第9讲 平面直角坐标系与函数初步 (含答案) 2025年中考数学知识点过关训练
文档属性
| 名称 | 第9讲 平面直角坐标系与函数初步 (含答案) 2025年中考数学知识点过关训练 |  | |
| 格式 | docx | ||
| 文件大小 | 157.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-10 07:32:02 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
第9讲 平面直角坐标系与函数初步
A熟知教材与迁移
1.台风是一种破坏性极大的自然灾害,气象台为了预报台风,首先应确定台风中心的位置.下列表述中能确定台风中心位置的是 ( )
A.在沿海地区
B.台湾省以东的洋面上
C.距离台州 200 km
D.北纬 28°,东经120°
2.函数 中自变量x的取值范围是 ( )
A. x≠3 B. x>3
C. x<3 D. x=3
3.如图,这是某市一天的气温随时间变化的情况,下列说法中正确的是 ( )
A.这一天的最低温度是-4℃
B.这一天12时温度最高
C.最高温比最低温高8℃
D.0时至8时气温呈下降趋势
4.若点 P(a+1,2-2a)关于x轴的对称点在第四象限,则a的取值范围可以在数轴上表示为 ( )
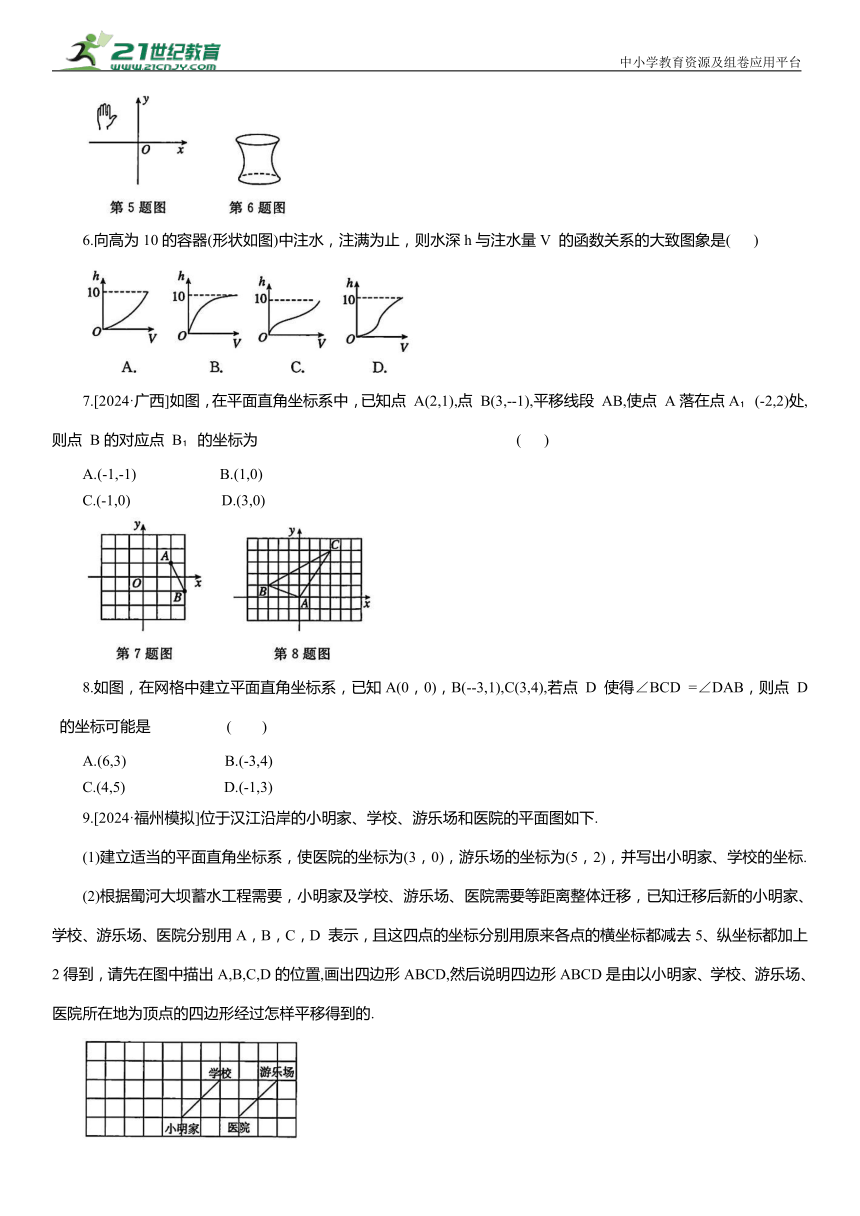
5.已知a+b>0,ab>0,则在下左图所示的平面直角坐标系中,小手盖住的点的坐标可能是( )
A.(a,b) B.(-a,b)
C.(-a,-b) D.(a,-b)
6.向高为10的容器(形状如图)中注水,注满为止,则水深h与注水量V 的函数关系的大致图象是( )
7.[2024·广西]如图,在平面直角坐标系中,已知点 A(2,1),点 B(3,--1),平移线段 AB,使点 A落在点A (-2,2)处,则点 B的对应点 B 的坐标为 ( )
A.(-1,-1) B.(1,0)
C.(-1,0) D.(3,0)
8.如图,在网格中建立平面直角坐标系,已知A(0,0),B(--3,1),C(3,4),若点 D 使得∠BCD =∠DAB,则点 D 的坐标可能是 ( )
A.(6,3) B.(-3,4)
C.(4,5) D.(-1,3)
9.[2024·福州模拟]位于汉江沿岸的小明家、学校、游乐场和医院的平面图如下.
(1)建立适当的平面直角坐标系,使医院的坐标为(3,0),游乐场的坐标为(5,2),并写出小明家、学校的坐标.
(2)根据蜀河大坝蓄水工程需要,小明家及学校、游乐场、医院需要等距离整体迁移,已知迁移后新的小明家、学校、游乐场、医院分别用A,B,C,D 表示,且这四点的坐标分别用原来各点的横坐标都减去5、纵坐标都加上2得到,请先在图中描出A,B,C,D的位置,画出四边形ABCD,然后说明四边形ABCD是由以小明家、学校、游乐场、医院所在地为顶点的四边形经过怎样平移得到的.
B掌握通性与通法
10.下面的三个问题中都有两个变量:
①汽车从 A 地匀速行驶到 B 地,汽车的剩余路程y与行驶时间x;②将水箱中的水匀速放出,直至放完,水箱中的剩余水量y与放水时间x;③用长度一定的绳子围成一个矩形,矩形的面积y与一边长x.
其中,变量 y与变量x之间的函数关系可以用下图所示的图象表示的是 ( )
A.①② B.①③
C.②③ D.①②③
11.已知函数 若 y=2,则x=
12.图1所示的摩天轮可抽象成一个圆,圆上一点离地面的高度 y(m)与旋转时间x(min)之间的关系如图2所示.
(1)根据图2填表:
x/ min 0 3 6 8 12
y/m
(2)变量y是x的函数吗 为什么
(3)根据图中的信息,写出摩天轮的直径.
13.在平面直角坐标系中.
(1)若点 M(m--6,2m+3)到两坐标轴的距离相等,求点 M 的坐标.
(2)若点 M(m--6,2m+3),点 N(5,2),且 MN∥y轴,求点 M 的坐标.
(3)若点 M(a,b),点 N(5,2),且 MN∥x轴,MN=3,求点 M的坐标.
C感悟思维与素养
14.[2024·温岭模拟] 如图,在矩形ABCD中,BC=1,∠ADB=60°,动点 P 沿折线AD→DB运动到点B,同时动点 Q 沿折线DB→BC 运动到点C,点P,Q在矩形边上的运动速度为1个单位/s,点P,Q在矩形对角线上的运动速度为 2 个单位/s.设运动时间为 t 秒,△PBQ的面积为S,则下列图象能大致反映S与t 之间函数关系的是 ( )
1. D 2. A 3. A4. C5. B 6. D 7. C 8. A
9.解:建立坐标系,如图.
(1)小明家、学校的坐标分别为(0,0),(2,2).
(2)如图,四边形ABCD 即为所求,将原来四边形先向左平移5个单位,再向上平移2个单位得到四边形ABCD.
10. A 11.2
12.解:(1)5705 545
(2)变量y是x的函数,因为由图2可知,每一个x值都对应唯一一个y值,所以根据函数的定义可判定变量y是x的函数.
(3)根据图中的信息,摩天轮上一点离地面的高度最小为5m,最大为70m,因此,摩天轮的直径为70-5=65(m).
13.(1)(-5,5)或(-15,-15) (2)(5,25) (3)(2,2)或(8,2)14. D
第9讲 平面直角坐标系与函数初步
A熟知教材与迁移
1.台风是一种破坏性极大的自然灾害,气象台为了预报台风,首先应确定台风中心的位置.下列表述中能确定台风中心位置的是 ( )
A.在沿海地区
B.台湾省以东的洋面上
C.距离台州 200 km
D.北纬 28°,东经120°
2.函数 中自变量x的取值范围是 ( )
A. x≠3 B. x>3
C. x<3 D. x=3
3.如图,这是某市一天的气温随时间变化的情况,下列说法中正确的是 ( )
A.这一天的最低温度是-4℃
B.这一天12时温度最高
C.最高温比最低温高8℃
D.0时至8时气温呈下降趋势
4.若点 P(a+1,2-2a)关于x轴的对称点在第四象限,则a的取值范围可以在数轴上表示为 ( )
5.已知a+b>0,ab>0,则在下左图所示的平面直角坐标系中,小手盖住的点的坐标可能是( )
A.(a,b) B.(-a,b)
C.(-a,-b) D.(a,-b)
6.向高为10的容器(形状如图)中注水,注满为止,则水深h与注水量V 的函数关系的大致图象是( )
7.[2024·广西]如图,在平面直角坐标系中,已知点 A(2,1),点 B(3,--1),平移线段 AB,使点 A落在点A (-2,2)处,则点 B的对应点 B 的坐标为 ( )
A.(-1,-1) B.(1,0)
C.(-1,0) D.(3,0)
8.如图,在网格中建立平面直角坐标系,已知A(0,0),B(--3,1),C(3,4),若点 D 使得∠BCD =∠DAB,则点 D 的坐标可能是 ( )
A.(6,3) B.(-3,4)
C.(4,5) D.(-1,3)
9.[2024·福州模拟]位于汉江沿岸的小明家、学校、游乐场和医院的平面图如下.
(1)建立适当的平面直角坐标系,使医院的坐标为(3,0),游乐场的坐标为(5,2),并写出小明家、学校的坐标.
(2)根据蜀河大坝蓄水工程需要,小明家及学校、游乐场、医院需要等距离整体迁移,已知迁移后新的小明家、学校、游乐场、医院分别用A,B,C,D 表示,且这四点的坐标分别用原来各点的横坐标都减去5、纵坐标都加上2得到,请先在图中描出A,B,C,D的位置,画出四边形ABCD,然后说明四边形ABCD是由以小明家、学校、游乐场、医院所在地为顶点的四边形经过怎样平移得到的.
B掌握通性与通法
10.下面的三个问题中都有两个变量:
①汽车从 A 地匀速行驶到 B 地,汽车的剩余路程y与行驶时间x;②将水箱中的水匀速放出,直至放完,水箱中的剩余水量y与放水时间x;③用长度一定的绳子围成一个矩形,矩形的面积y与一边长x.
其中,变量 y与变量x之间的函数关系可以用下图所示的图象表示的是 ( )
A.①② B.①③
C.②③ D.①②③
11.已知函数 若 y=2,则x=
12.图1所示的摩天轮可抽象成一个圆,圆上一点离地面的高度 y(m)与旋转时间x(min)之间的关系如图2所示.
(1)根据图2填表:
x/ min 0 3 6 8 12
y/m
(2)变量y是x的函数吗 为什么
(3)根据图中的信息,写出摩天轮的直径.
13.在平面直角坐标系中.
(1)若点 M(m--6,2m+3)到两坐标轴的距离相等,求点 M 的坐标.
(2)若点 M(m--6,2m+3),点 N(5,2),且 MN∥y轴,求点 M 的坐标.
(3)若点 M(a,b),点 N(5,2),且 MN∥x轴,MN=3,求点 M的坐标.
C感悟思维与素养
14.[2024·温岭模拟] 如图,在矩形ABCD中,BC=1,∠ADB=60°,动点 P 沿折线AD→DB运动到点B,同时动点 Q 沿折线DB→BC 运动到点C,点P,Q在矩形边上的运动速度为1个单位/s,点P,Q在矩形对角线上的运动速度为 2 个单位/s.设运动时间为 t 秒,△PBQ的面积为S,则下列图象能大致反映S与t 之间函数关系的是 ( )
1. D 2. A 3. A4. C5. B 6. D 7. C 8. A
9.解:建立坐标系,如图.
(1)小明家、学校的坐标分别为(0,0),(2,2).
(2)如图,四边形ABCD 即为所求,将原来四边形先向左平移5个单位,再向上平移2个单位得到四边形ABCD.
10. A 11.2
12.解:(1)5705 545
(2)变量y是x的函数,因为由图2可知,每一个x值都对应唯一一个y值,所以根据函数的定义可判定变量y是x的函数.
(3)根据图中的信息,摩天轮上一点离地面的高度最小为5m,最大为70m,因此,摩天轮的直径为70-5=65(m).
13.(1)(-5,5)或(-15,-15) (2)(5,25) (3)(2,2)或(8,2)14. D
同课章节目录
