第18讲直角三角形与勾股定理 (含答案) 2025年中考数学知识点过关训练
文档属性
| 名称 | 第18讲直角三角形与勾股定理 (含答案) 2025年中考数学知识点过关训练 | 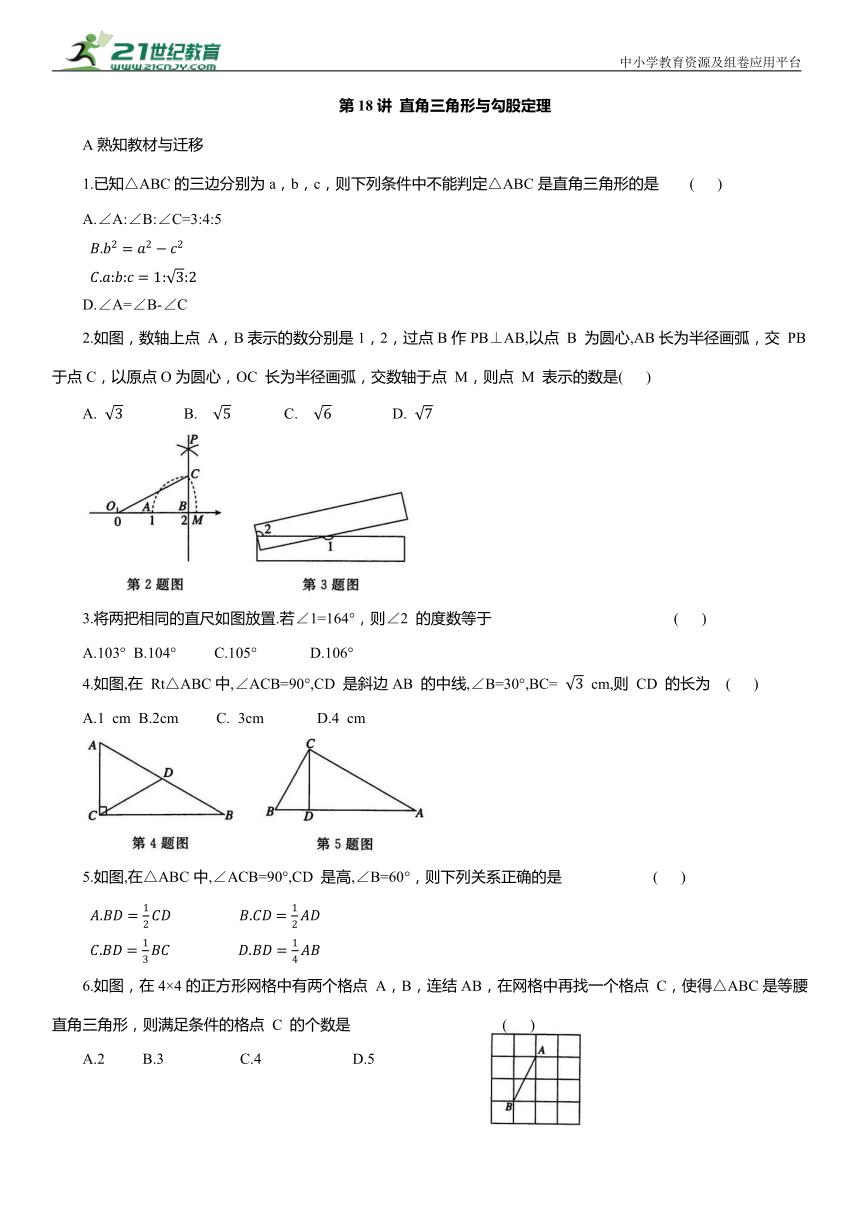 | |
| 格式 | docx | ||
| 文件大小 | 135.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-10 07:31:42 | ||
图片预览


文档简介
直角三角形与勾股定理
A熟知教材与迁移
1.已知△ABC的三边分别为a,b,c,则下列条件中不能判定△ABC是直角三角形的是 ( )
A.∠A:∠B:∠C=3:4:5
D.∠A=∠B-∠C
2.如图,数轴上点 A,B表示的数分别是1,2,过点B作PB⊥AB,以点 B 为圆心,AB长为半径画弧,交 PB于点C,以原点O为圆心,OC 长为半径画弧,交数轴于点 M,则点 M 表示的数是( )
A. B. C. D.
3.将两把相同的直尺如图放置.若∠1=164°,则∠2 的度数等于 ( )
A.103° B.104° C.105° D.106°
4.如图,在 Rt△ABC中,∠ACB=90°,CD 是斜边AB 的中线,∠B=30°,BC= cm,则 CD 的长为 ( )
A.1 cm B.2cm C. 3cm D.4 cm
5.如图,在△ABC中,∠ACB=90°,CD 是高,∠B=60°,则下列关系正确的是 ( )
6.如图,在4×4的正方形网格中有两个格点 A,B,连结AB,在网格中再找一个格点 C,使得△ABC是等腰直角三角形,则满足条件的格点 C 的个数是 ( )
A.2 B.3 C.4 D.5
7.在直角三角形 ABC中,∠B=90°,∠A=2∠C,则∠C的度数为 .
8.[2024·广州模拟] 如图,在等边三角形 ABC中,D为AB 的中点,DE⊥BC于点E,BE=5,则AB 的长是 .
9.如图,有一个水池,水面是一个边长为14 尺的正方形,在水池正中央有一根芦苇,它高出水面1尺,如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面.则水的深度是 尺.
10.[2024·南京模拟] 如图,在四边形ABCD中,∠C=90°,BD平分∠ABC,AD=3,E为AB 上一点,AE=4,ED=5,求证:AD=CD.
B掌握通性与通法
11.如图,一根竹竿 AB,斜靠在竖直的墙上,P是AB 的中点,A'B'表示竹竿AB 沿墙上下滑动过程中的某个位置,则OP 的长随竹竿AB 在滑动过程中的情况是 ( )
A.下滑时,OP 增大
B.上升时,OP 减小
C.无论怎样滑动,OP 不变
D.只要滑动,OP 就变化
12.如图,△ABC 与△CDE 均为直角三角形,AB交CD 于点 F,∠ACB=∠CDE=90°,∠B=30°,∠E=45°,∠ECB=α,则∠CFB= ( )
B.α+45°
C.105°-α
13.[2024·广州模拟]如图,在直角三角形 ABC中,∠ACB=90°,中线 AD⊥中线CE,且相交于F,已知AC=4,则AB的长为 ( )
A.2 B.4 D.
14.如图,在 Rt△ABC中,∠ACB=90°,分别以直角三角形的三条边为边,在直线 AB 同侧分别作正三角形,已知 则△ABC的面积是 ( )
A.5 B.11 C.17 D.22
15.如图,在△ABC中,AD 是BC 边上的高线,CE是AB 边上的中线,DG⊥CE于G,CD=AE.
(1)求证:CG=EG.
(2)已知 BC=13,CD=5,连结 ED,求△EDC的面积.
C感悟思维与素养
16.[2024·北京模拟] 如图,已知∠ABC=90°,D是直线AB 上的点,AD=BC.
(1)如图1,过点 A 作AF⊥AB,并截取 AF=BD,连结 DC,DF,CF,判断△CDF 的形状并证明.
(2)如图2,E 是直线BC 上一点,且CE=BD,直线 AE,CD 相交于点 P,∠APD 的度数是一个固定的值吗 若是,请求出它的度数;若不是,请说明理由.
中小学教育资源及组卷应用平台
1. A 2. B 3. D 4. A 5. D 6. B 7.30° 8.20 9.24
10.证明:∵AD=3,AE=4,ED=5,∴AD +AE =ED ,∴△ADE是直角三角形,∠A=90°.
又∵∠C=90°,BD平分∠ABC,∴AD=CD.
11. C 12. C 13. B 14. B 15.(1)证明略 (2)7.5
16.解:(1)△CDF 是等腰直角三角形,证明如下:
∵AF⊥AD,∠ABC=90°,∴∠FAD=∠DBC.
在△FAD与△DBC中,
∴△FAD≌△DBC(SAS),∴FD=DC,
∴△CDF是等腰三角形.
∵△FAD≌△DBC,∴∠FDA=∠DCB.
∵∠BDC+∠DCB=90°,∴∠BDC+∠FDA=90°,即∠CDF=90°,∴△CDF是等腰直角三角形.
(2)∠APD的度数是一个固定值45°,理由如下:
如图,作AF⊥AB于点A,使AF=BD,连结DF,CF.
∵AF⊥AD,∠ABC=90°,
∴∠FAD=∠DBC,
在△FAD与△DBC中,
∴△FAD≌△DBC(SAS),∴FD=DC,
∴△CDF是等腰三角形.
∵△FAD≌△DBC,∴∠FDA=∠DCB.
∵∠BDC+∠DCB=90°,∴∠BDC+∠FDA=90°,即∠FDC=90°,∴△CDF是等腰直角三角形,
,且AF=BD=CE,
∴四边形 AFCE 是平行四边形,
∴AE∥CF,∴∠APD=∠FCD=45°.
A熟知教材与迁移
1.已知△ABC的三边分别为a,b,c,则下列条件中不能判定△ABC是直角三角形的是 ( )
A.∠A:∠B:∠C=3:4:5
D.∠A=∠B-∠C
2.如图,数轴上点 A,B表示的数分别是1,2,过点B作PB⊥AB,以点 B 为圆心,AB长为半径画弧,交 PB于点C,以原点O为圆心,OC 长为半径画弧,交数轴于点 M,则点 M 表示的数是( )
A. B. C. D.
3.将两把相同的直尺如图放置.若∠1=164°,则∠2 的度数等于 ( )
A.103° B.104° C.105° D.106°
4.如图,在 Rt△ABC中,∠ACB=90°,CD 是斜边AB 的中线,∠B=30°,BC= cm,则 CD 的长为 ( )
A.1 cm B.2cm C. 3cm D.4 cm
5.如图,在△ABC中,∠ACB=90°,CD 是高,∠B=60°,则下列关系正确的是 ( )
6.如图,在4×4的正方形网格中有两个格点 A,B,连结AB,在网格中再找一个格点 C,使得△ABC是等腰直角三角形,则满足条件的格点 C 的个数是 ( )
A.2 B.3 C.4 D.5
7.在直角三角形 ABC中,∠B=90°,∠A=2∠C,则∠C的度数为 .
8.[2024·广州模拟] 如图,在等边三角形 ABC中,D为AB 的中点,DE⊥BC于点E,BE=5,则AB 的长是 .
9.如图,有一个水池,水面是一个边长为14 尺的正方形,在水池正中央有一根芦苇,它高出水面1尺,如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面.则水的深度是 尺.
10.[2024·南京模拟] 如图,在四边形ABCD中,∠C=90°,BD平分∠ABC,AD=3,E为AB 上一点,AE=4,ED=5,求证:AD=CD.
B掌握通性与通法
11.如图,一根竹竿 AB,斜靠在竖直的墙上,P是AB 的中点,A'B'表示竹竿AB 沿墙上下滑动过程中的某个位置,则OP 的长随竹竿AB 在滑动过程中的情况是 ( )
A.下滑时,OP 增大
B.上升时,OP 减小
C.无论怎样滑动,OP 不变
D.只要滑动,OP 就变化
12.如图,△ABC 与△CDE 均为直角三角形,AB交CD 于点 F,∠ACB=∠CDE=90°,∠B=30°,∠E=45°,∠ECB=α,则∠CFB= ( )
B.α+45°
C.105°-α
13.[2024·广州模拟]如图,在直角三角形 ABC中,∠ACB=90°,中线 AD⊥中线CE,且相交于F,已知AC=4,则AB的长为 ( )
A.2 B.4 D.
14.如图,在 Rt△ABC中,∠ACB=90°,分别以直角三角形的三条边为边,在直线 AB 同侧分别作正三角形,已知 则△ABC的面积是 ( )
A.5 B.11 C.17 D.22
15.如图,在△ABC中,AD 是BC 边上的高线,CE是AB 边上的中线,DG⊥CE于G,CD=AE.
(1)求证:CG=EG.
(2)已知 BC=13,CD=5,连结 ED,求△EDC的面积.
C感悟思维与素养
16.[2024·北京模拟] 如图,已知∠ABC=90°,D是直线AB 上的点,AD=BC.
(1)如图1,过点 A 作AF⊥AB,并截取 AF=BD,连结 DC,DF,CF,判断△CDF 的形状并证明.
(2)如图2,E 是直线BC 上一点,且CE=BD,直线 AE,CD 相交于点 P,∠APD 的度数是一个固定的值吗 若是,请求出它的度数;若不是,请说明理由.
中小学教育资源及组卷应用平台
1. A 2. B 3. D 4. A 5. D 6. B 7.30° 8.20 9.24
10.证明:∵AD=3,AE=4,ED=5,∴AD +AE =ED ,∴△ADE是直角三角形,∠A=90°.
又∵∠C=90°,BD平分∠ABC,∴AD=CD.
11. C 12. C 13. B 14. B 15.(1)证明略 (2)7.5
16.解:(1)△CDF 是等腰直角三角形,证明如下:
∵AF⊥AD,∠ABC=90°,∴∠FAD=∠DBC.
在△FAD与△DBC中,
∴△FAD≌△DBC(SAS),∴FD=DC,
∴△CDF是等腰三角形.
∵△FAD≌△DBC,∴∠FDA=∠DCB.
∵∠BDC+∠DCB=90°,∴∠BDC+∠FDA=90°,即∠CDF=90°,∴△CDF是等腰直角三角形.
(2)∠APD的度数是一个固定值45°,理由如下:
如图,作AF⊥AB于点A,使AF=BD,连结DF,CF.
∵AF⊥AD,∠ABC=90°,
∴∠FAD=∠DBC,
在△FAD与△DBC中,
∴△FAD≌△DBC(SAS),∴FD=DC,
∴△CDF是等腰三角形.
∵△FAD≌△DBC,∴∠FDA=∠DCB.
∵∠BDC+∠DCB=90°,∴∠BDC+∠FDA=90°,即∠FDC=90°,∴△CDF是等腰直角三角形,
,且AF=BD=CE,
∴四边形 AFCE 是平行四边形,
∴AE∥CF,∴∠APD=∠FCD=45°.
同课章节目录
