第19讲 相似三角形(1) (含答案) 2025年中考数学知识点过关训练
文档属性
| 名称 | 第19讲 相似三角形(1) (含答案) 2025年中考数学知识点过关训练 |  | |
| 格式 | docx | ||
| 文件大小 | 103.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-10 07:33:07 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
相似三角形(1)
A熟知教材与迁移
1.若 则 ab= ( )
A.6 B.
C.1 D.
2.下列各组线段中,不是成比例线段的为 ( )
A.1, , , B.3,6,2,4
C.4,6,5,10
3.已知 则 的值是 ( )
A. B.
C.3 D.
4.已知c是a 和b的比例中项,a=2,b=18,则c=( )
A.±6 B.6
C.4 D.±3
5.如图,已知 AB∥CD∥EF,若CE= ,EF=4,CD=6,则线段AB的长为 ( )
A.7 B.8 C.9 D.10
6.[2024·广州模拟]黄金分割由于其美学性质,受到摄影爱好者和艺术家的喜爱,摄影中有一种拍摄手法叫黄金构图法.其原理是:如图,将正方形 ABCD的底边BC 取中点E,以 E 为圆心,线段 DE为半径作圆,其与底边 BC 的延长线交于点 F,这样就把正方形 ABCD延伸为矩形 ABFG,称其为黄金矩形.若CF=8a,则AB= ( )
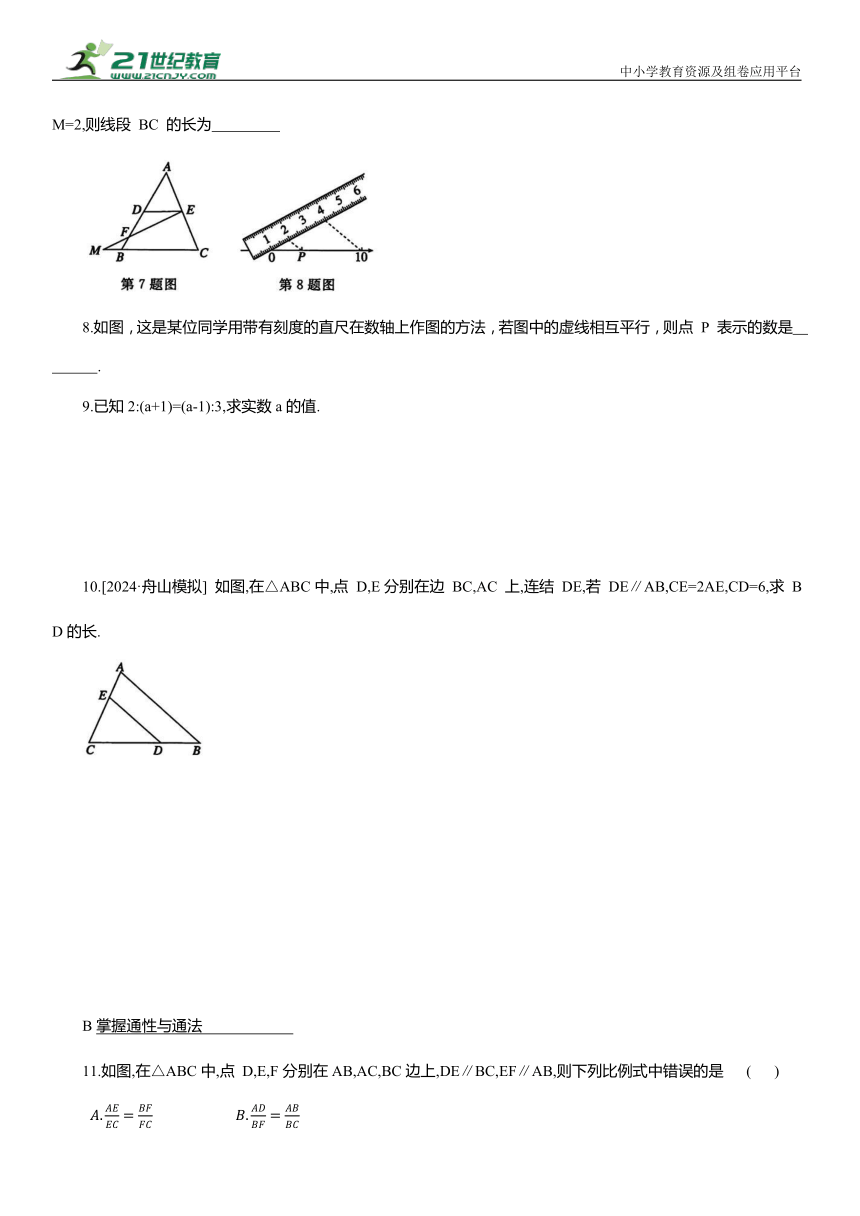
7.如图,D,E分别是边AB,AC的中点,点F在DB上,DF=2BF.连结EF 并延长,与CB 的延长线相交于点 M.若 BM=2,则线段 BC 的长为
8.如图,这是某位同学用带有刻度的直尺在数轴上作图的方法,若图中的虚线相互平行,则点 P 表示的数是 .
9.已知2:(a+1)=(a-1):3,求实数a的值.
10.[2024·舟山模拟] 如图,在△ABC中,点 D,E分别在边 BC,AC 上,连结 DE,若 DE∥AB,CE=2AE,CD=6,求 BD的长.
B掌握通性与通法
11.如图,在△ABC中,点 D,E,F分别在AB,AC,BC边上,DE∥BC,EF∥AB,则下列比例式中错误的是 ( )
12.某校开展“展青春风采,树强国信念”科普阅读活动.小明看到黄金分割比是一种数学上的比例关系,它具有严格的比例性、艺术性、和谐性,蕴藏着丰富的美学价值,应用时一般取0.618.特别奇妙的是在正五边形中,如图,连结 AB,AC,∠ACB 的平分线交边AB 于点 D,则点 D就是线段AB 的一个黄金分割点,即 0.618,已知AC=10 cm,那么该正五边形的周长为 ( )
A.19.1 cm B.25 cm
C.30.9 cm D.40 cm
13.已知 则k的值是 .
14.如图所示,在△ABC中,D为BC 的中点. E 为AB上一点, CE 和 AD 相交于点F,则
15.[2024·深圳模拟]如图,AD∥EG∥BC,EG分别交AB,DB,AC 于点E,F,G,已知AD=5,BC=10,AE=9,AB=12.求 EG,FG的长.
C感悟思维与素养
16.如图,O是△ABC的边BC 上一点,过点O的直线分别交射线 AB、线段 AC 于点 M,N,且
(用含m的代数式表示); (用含 n的代数式表示).
(2)若O是线段BC 的中点.求证:m+n=2.
(3)若 求m,n之间的关系(用含k的代数式表示).
1. A 2. C 3. D 4. A 5. C 6. C 7.8 8. 9.±
10.3 11. C 12. C 13.2或一1 14.3 15. EG= ,FG=
16.解:(1)∵AB=AM-BM,AC=AN+CN,AB∥=m,ACAN=n,
故答案为1-m,n-1.
(2)证明:设
∴AB= am,AC= bn,∴MB=MA-AB=a-am=(1-m)a,CN=AC-AN= bn-b=(n--1)b,
若点O是线段BC 的中点,如图1,过点 B作BH∥AC交MN于H,∴∠OBH=∠OCN.在△OBH与△OCN中,
∴△OBH≌△OCN(ASA),
∴BH=CN=(n-1)b.∵BH∥AN,∴△BMH∽△AMN,
即
(3)若 如图2,过点 B 作 BG∥AC 交 MN 于G,∴∠OBG=∠OCN.
∵∠BOG=∠CON,∴△OBG∽△OCN,
即
∵BG∥AN,∴△MBG∽△MAN,
即
相似三角形(1)
A熟知教材与迁移
1.若 则 ab= ( )
A.6 B.
C.1 D.
2.下列各组线段中,不是成比例线段的为 ( )
A.1, , , B.3,6,2,4
C.4,6,5,10
3.已知 则 的值是 ( )
A. B.
C.3 D.
4.已知c是a 和b的比例中项,a=2,b=18,则c=( )
A.±6 B.6
C.4 D.±3
5.如图,已知 AB∥CD∥EF,若CE= ,EF=4,CD=6,则线段AB的长为 ( )
A.7 B.8 C.9 D.10
6.[2024·广州模拟]黄金分割由于其美学性质,受到摄影爱好者和艺术家的喜爱,摄影中有一种拍摄手法叫黄金构图法.其原理是:如图,将正方形 ABCD的底边BC 取中点E,以 E 为圆心,线段 DE为半径作圆,其与底边 BC 的延长线交于点 F,这样就把正方形 ABCD延伸为矩形 ABFG,称其为黄金矩形.若CF=8a,则AB= ( )
7.如图,D,E分别是边AB,AC的中点,点F在DB上,DF=2BF.连结EF 并延长,与CB 的延长线相交于点 M.若 BM=2,则线段 BC 的长为
8.如图,这是某位同学用带有刻度的直尺在数轴上作图的方法,若图中的虚线相互平行,则点 P 表示的数是 .
9.已知2:(a+1)=(a-1):3,求实数a的值.
10.[2024·舟山模拟] 如图,在△ABC中,点 D,E分别在边 BC,AC 上,连结 DE,若 DE∥AB,CE=2AE,CD=6,求 BD的长.
B掌握通性与通法
11.如图,在△ABC中,点 D,E,F分别在AB,AC,BC边上,DE∥BC,EF∥AB,则下列比例式中错误的是 ( )
12.某校开展“展青春风采,树强国信念”科普阅读活动.小明看到黄金分割比是一种数学上的比例关系,它具有严格的比例性、艺术性、和谐性,蕴藏着丰富的美学价值,应用时一般取0.618.特别奇妙的是在正五边形中,如图,连结 AB,AC,∠ACB 的平分线交边AB 于点 D,则点 D就是线段AB 的一个黄金分割点,即 0.618,已知AC=10 cm,那么该正五边形的周长为 ( )
A.19.1 cm B.25 cm
C.30.9 cm D.40 cm
13.已知 则k的值是 .
14.如图所示,在△ABC中,D为BC 的中点. E 为AB上一点, CE 和 AD 相交于点F,则
15.[2024·深圳模拟]如图,AD∥EG∥BC,EG分别交AB,DB,AC 于点E,F,G,已知AD=5,BC=10,AE=9,AB=12.求 EG,FG的长.
C感悟思维与素养
16.如图,O是△ABC的边BC 上一点,过点O的直线分别交射线 AB、线段 AC 于点 M,N,且
(用含m的代数式表示); (用含 n的代数式表示).
(2)若O是线段BC 的中点.求证:m+n=2.
(3)若 求m,n之间的关系(用含k的代数式表示).
1. A 2. C 3. D 4. A 5. C 6. C 7.8 8. 9.±
10.3 11. C 12. C 13.2或一1 14.3 15. EG= ,FG=
16.解:(1)∵AB=AM-BM,AC=AN+CN,AB∥=m,ACAN=n,
故答案为1-m,n-1.
(2)证明:设
∴AB= am,AC= bn,∴MB=MA-AB=a-am=(1-m)a,CN=AC-AN= bn-b=(n--1)b,
若点O是线段BC 的中点,如图1,过点 B作BH∥AC交MN于H,∴∠OBH=∠OCN.在△OBH与△OCN中,
∴△OBH≌△OCN(ASA),
∴BH=CN=(n-1)b.∵BH∥AN,∴△BMH∽△AMN,
即
(3)若 如图2,过点 B 作 BG∥AC 交 MN 于G,∴∠OBG=∠OCN.
∵∠BOG=∠CON,∴△OBG∽△OCN,
即
∵BG∥AN,∴△MBG∽△MAN,
即
同课章节目录
