第15讲线段、角、相交线与平行线 (含答案) 2025年中考数学知识点过关训练
文档属性
| 名称 | 第15讲线段、角、相交线与平行线 (含答案) 2025年中考数学知识点过关训练 | 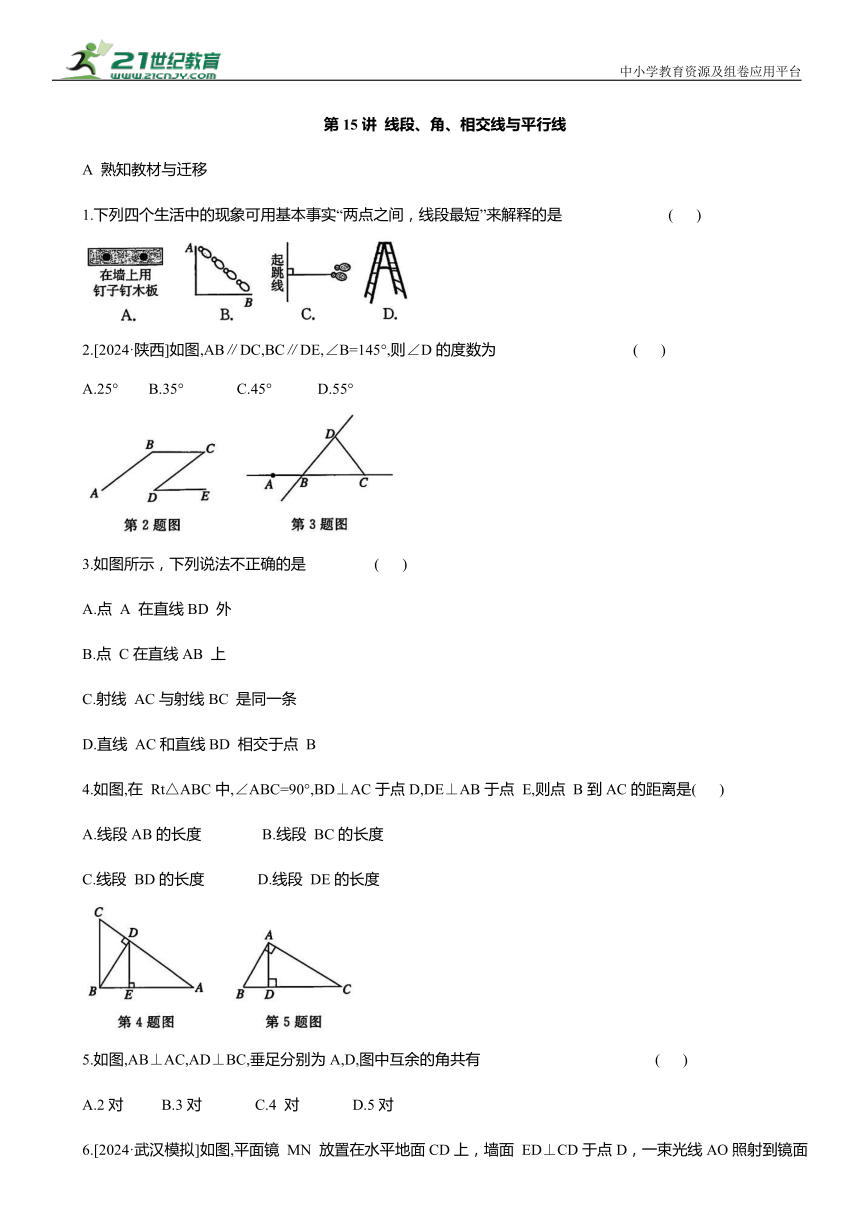 | |
| 格式 | docx | ||
| 文件大小 | 134.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-10 07:35:07 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
线段、角、相交线与平行线
A 熟知教材与迁移
1.下列四个生活中的现象可用基本事实“两点之间,线段最短”来解释的是 ( )
2.[2024·陕西]如图,AB∥DC,BC∥DE,∠B=145°,则∠D的度数为 ( )
A.25° B.35° C.45° D.55°
3.如图所示,下列说法不正确的是 ( )
A.点 A 在直线BD 外
B.点 C在直线AB 上
C.射线 AC与射线BC 是同一条
D.直线 AC和直线BD 相交于点 B
4.如图,在 Rt△ABC中,∠ABC=90°,BD⊥AC于点D,DE⊥AB于点 E,则点 B到AC的距离是( )
A.线段AB的长度 B.线段 BC的长度
C.线段 BD的长度 D.线段 DE的长度
5.如图,AB⊥AC,AD⊥BC,垂足分别为A,D,图中互余的角共有 ( )
A.2对 B.3对 C.4 对 D.5对
6.[2024·武汉模拟]如图,平面镜 MN 放置在水平地面CD上,墙面 ED⊥CD于点D,一束光线AO照射到镜面MN 上,反射光线为OB,点 B 在ED 上,若 则∠OBD 的度数为
7.如图,点 D,E分别在△ABC的边AB,AC上,且DE∥BC,点 F 在线段 BC 的延长线上.若∠ADE=28°,∠ACF=118°,则∠A= .
8.如图,点C位于点A 正北方向,点B位于点A 北偏东50°方向,点C位于点 B 北偏西 35°方向,则∠ABC 的度数为 °.
9.[2024·广州模拟] 如图,点A,O,C在一条直线上,OE 是∠BOC 的平分线,∠EOF=90°,∠1 比∠2 大75°.
(1)求∠2的度数.
(2)求∠COF 的度数.
B掌握通性与通法
10.下列说法中正确的个数为 ( )
①不相交的两条直线叫做平行线;
②在同一平面内,过一点有且只有一条直线与已知直线垂直;
③从直线外一点到这条直线的垂线段,叫做这点到直线的距离;
④两条直线被第三条直线所截,同位角相等.
A.0个 B.1个 C.2个 D.3个
11.右图所示的“箭头”图形中,AB∥CD,∠B=∠D=80°,∠E=∠F=47°,则图中∠G的度数是
( )
A.80° B.76° C.66° D.56°
12.[2024·丽水模拟]如图所示,把一根筷子一端放在水里,一端露出水面,筷子变弯了,它真的弯了吗 其实没有,这是光的折射现象,光从空气中射入水中,光的传播方向发生了改变.
(1)请指出与∠1是同旁内角的有哪些角 请指出与∠2是内错角的有哪些角
(2)若∠1=115°,测得∠BOM=145°,从水面上看斜插入水中的筷子,水下部分向上弯了多少度 请说明理由.
13.某风景区A,B,C,D四个景点在一条直线上,图中数据为各景点之间的距离(单位:千米).
(1)求景点 C,D之间的距离.(用含 m的代数式表示)
(2)若景点 C到景点A 的距离与景点 C 到景点D 的距离相等,求景点 B,D之间的距离.
14.如图,在四边形ABCD中,AB∥CD,BD平分∠ABC,∠1与∠2互补.
(1)求证:EF∥BD.
(2)若∠A= 65°,∠AEF = 80°,求∠CBD 的度数.
C感悟思维与素养
15.[2024·苏州模拟]【阅读理解】如图1,小明把一副三角板的直角顶点O重叠在一起.如图2,固定三角板 AOB,将三角板 COD 绕点O 以每秒15°的速度顺时针旋转,旋转时间为 t 秒,当OD 边与OB 边重合时停止转动.
【解决问题】
(1)在旋转过程中,请填出∠AOC,∠BOD 之间的数量关系 .
(2)当运动时间为9 秒时,图中有角平分线吗 找出并说明理由.
(3)当∠AOC,∠BOD 中一个角的度数是另一个角的两倍时,则称射线 OC 是∠AOB 的“优线”,请直接写出所有满足条件1. B 2. B 3. C 4. C 5. C 6.49°42′ 7.90° 8.95
9.(1)35° (2)55° 10. B 11. C
12.解:(1)与∠1是同旁内角的有∠AOE,∠MOE,∠ADE;与∠2是内错角的有∠MOE,∠AOE.
(2)∵AB∥CD,∴∠BOE=∠1=115°.∵∠BOM=145°,∴∠MOE=∠BOM-∠BOE=145°-115°=30°,∴往上弯了30°.
13.解:(1)9+2m-(6-m)=9+2m-6+m=3+3m,答:景点C,D之间的距离为(3+3m)千米.
(2)由题意得5+(6-m)=3+3m,解得m=2,∴BD=9+2m=13,答:景点 B,D之间的距离为13千米.
14.(1)证明略 (2)35°
15.解:(1)①如图1,∠AOC+∠BOD=180°.理由如下:由题意得,∠DOA=90°-∠AOC,∠COB=90°-∠AOC.
∴∠AOC+∠BOD=∠AOC+∠DOA+∠AOC+∠COB=
②如图 2,∠AOC+∠BOD=180°.理由如下:由题意得,∠DOA=90°-∠DOB,∠COB=90°-∠DOB.
∴∠AOC+∠BOD=∠DOA+∠DOB+∠COB+∠BOD=90°-∠DOB+∠DOB+90°-∠DOB+∠BOD=180°.故答案为∠AOC+∠BOD=180°.
(2)OD平分∠AOB,OB平分∠COD.理由:如图3所示,当运动时间为9秒时,
∴∠BOC=∠AOC-∠AOB=135°-90°=45°.∵∠COD=90°,∴∠BOD=∠COD-∠BOC=90°-45°=45°.
∴∠BOC=∠BOD=45°.∴OB平分∠COD.
又 ∴OD平分∠AOB.
(3)由题意得,∠AOB=90°,∠AOC=15°t.
当∠BOD=2∠AOC时,又∠AOC+∠BOD=180°,∴∠AOC=60°.∴15t=60,解得t=4.
当2∠BOD=∠AOC时,又∠AOC+∠BOD=180°,∴∠AOC=120°.∴15t=120,解得t=8.综上,t=4 或8.
线段、角、相交线与平行线
A 熟知教材与迁移
1.下列四个生活中的现象可用基本事实“两点之间,线段最短”来解释的是 ( )
2.[2024·陕西]如图,AB∥DC,BC∥DE,∠B=145°,则∠D的度数为 ( )
A.25° B.35° C.45° D.55°
3.如图所示,下列说法不正确的是 ( )
A.点 A 在直线BD 外
B.点 C在直线AB 上
C.射线 AC与射线BC 是同一条
D.直线 AC和直线BD 相交于点 B
4.如图,在 Rt△ABC中,∠ABC=90°,BD⊥AC于点D,DE⊥AB于点 E,则点 B到AC的距离是( )
A.线段AB的长度 B.线段 BC的长度
C.线段 BD的长度 D.线段 DE的长度
5.如图,AB⊥AC,AD⊥BC,垂足分别为A,D,图中互余的角共有 ( )
A.2对 B.3对 C.4 对 D.5对
6.[2024·武汉模拟]如图,平面镜 MN 放置在水平地面CD上,墙面 ED⊥CD于点D,一束光线AO照射到镜面MN 上,反射光线为OB,点 B 在ED 上,若 则∠OBD 的度数为
7.如图,点 D,E分别在△ABC的边AB,AC上,且DE∥BC,点 F 在线段 BC 的延长线上.若∠ADE=28°,∠ACF=118°,则∠A= .
8.如图,点C位于点A 正北方向,点B位于点A 北偏东50°方向,点C位于点 B 北偏西 35°方向,则∠ABC 的度数为 °.
9.[2024·广州模拟] 如图,点A,O,C在一条直线上,OE 是∠BOC 的平分线,∠EOF=90°,∠1 比∠2 大75°.
(1)求∠2的度数.
(2)求∠COF 的度数.
B掌握通性与通法
10.下列说法中正确的个数为 ( )
①不相交的两条直线叫做平行线;
②在同一平面内,过一点有且只有一条直线与已知直线垂直;
③从直线外一点到这条直线的垂线段,叫做这点到直线的距离;
④两条直线被第三条直线所截,同位角相等.
A.0个 B.1个 C.2个 D.3个
11.右图所示的“箭头”图形中,AB∥CD,∠B=∠D=80°,∠E=∠F=47°,则图中∠G的度数是
( )
A.80° B.76° C.66° D.56°
12.[2024·丽水模拟]如图所示,把一根筷子一端放在水里,一端露出水面,筷子变弯了,它真的弯了吗 其实没有,这是光的折射现象,光从空气中射入水中,光的传播方向发生了改变.
(1)请指出与∠1是同旁内角的有哪些角 请指出与∠2是内错角的有哪些角
(2)若∠1=115°,测得∠BOM=145°,从水面上看斜插入水中的筷子,水下部分向上弯了多少度 请说明理由.
13.某风景区A,B,C,D四个景点在一条直线上,图中数据为各景点之间的距离(单位:千米).
(1)求景点 C,D之间的距离.(用含 m的代数式表示)
(2)若景点 C到景点A 的距离与景点 C 到景点D 的距离相等,求景点 B,D之间的距离.
14.如图,在四边形ABCD中,AB∥CD,BD平分∠ABC,∠1与∠2互补.
(1)求证:EF∥BD.
(2)若∠A= 65°,∠AEF = 80°,求∠CBD 的度数.
C感悟思维与素养
15.[2024·苏州模拟]【阅读理解】如图1,小明把一副三角板的直角顶点O重叠在一起.如图2,固定三角板 AOB,将三角板 COD 绕点O 以每秒15°的速度顺时针旋转,旋转时间为 t 秒,当OD 边与OB 边重合时停止转动.
【解决问题】
(1)在旋转过程中,请填出∠AOC,∠BOD 之间的数量关系 .
(2)当运动时间为9 秒时,图中有角平分线吗 找出并说明理由.
(3)当∠AOC,∠BOD 中一个角的度数是另一个角的两倍时,则称射线 OC 是∠AOB 的“优线”,请直接写出所有满足条件1. B 2. B 3. C 4. C 5. C 6.49°42′ 7.90° 8.95
9.(1)35° (2)55° 10. B 11. C
12.解:(1)与∠1是同旁内角的有∠AOE,∠MOE,∠ADE;与∠2是内错角的有∠MOE,∠AOE.
(2)∵AB∥CD,∴∠BOE=∠1=115°.∵∠BOM=145°,∴∠MOE=∠BOM-∠BOE=145°-115°=30°,∴往上弯了30°.
13.解:(1)9+2m-(6-m)=9+2m-6+m=3+3m,答:景点C,D之间的距离为(3+3m)千米.
(2)由题意得5+(6-m)=3+3m,解得m=2,∴BD=9+2m=13,答:景点 B,D之间的距离为13千米.
14.(1)证明略 (2)35°
15.解:(1)①如图1,∠AOC+∠BOD=180°.理由如下:由题意得,∠DOA=90°-∠AOC,∠COB=90°-∠AOC.
∴∠AOC+∠BOD=∠AOC+∠DOA+∠AOC+∠COB=
②如图 2,∠AOC+∠BOD=180°.理由如下:由题意得,∠DOA=90°-∠DOB,∠COB=90°-∠DOB.
∴∠AOC+∠BOD=∠DOA+∠DOB+∠COB+∠BOD=90°-∠DOB+∠DOB+90°-∠DOB+∠BOD=180°.故答案为∠AOC+∠BOD=180°.
(2)OD平分∠AOB,OB平分∠COD.理由:如图3所示,当运动时间为9秒时,
∴∠BOC=∠AOC-∠AOB=135°-90°=45°.∵∠COD=90°,∴∠BOD=∠COD-∠BOC=90°-45°=45°.
∴∠BOC=∠BOD=45°.∴OB平分∠COD.
又 ∴OD平分∠AOB.
(3)由题意得,∠AOB=90°,∠AOC=15°t.
当∠BOD=2∠AOC时,又∠AOC+∠BOD=180°,∴∠AOC=60°.∴15t=60,解得t=4.
当2∠BOD=∠AOC时,又∠AOC+∠BOD=180°,∴∠AOC=120°.∴15t=120,解得t=8.综上,t=4 或8.
同课章节目录
