[专题集训 8]专题八 角平分线问题的模型(含答案)
文档属性
| 名称 | [专题集训 8]专题八 角平分线问题的模型(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 145.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-10 07:59:16 | ||
图片预览


文档简介
[专题集训 8]专题八 角平分线问题的模型
中小学教育资源及组卷应用平台
一、选择题
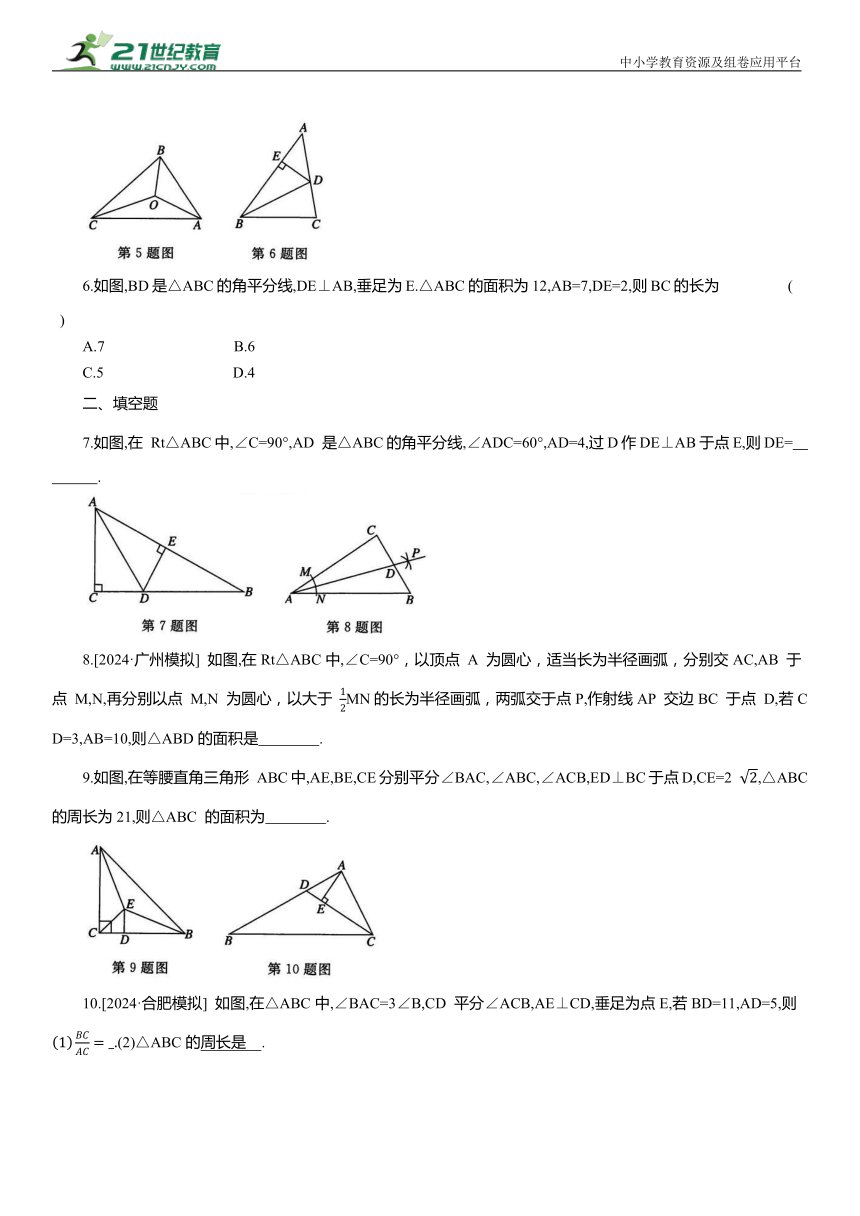
1.如图,OP 平分∠MON,PA⊥ON 于点 A,点 Q是射线OM 上的一个动点.若PA=3,则线段PQ的长不可能是 ( )
A.5 B.4
C.3 D.2
2.如图,在△ABC中,∠C=90°,AD平分∠BAC,BC=30,BD:CD=3:2,则点 D到AB的距离为( )
A.18 B.12
C.15 D.不能确定
3.如图,在△ABC中,AD 是∠BAC 的平分线,AB=8cm ,AC=6 cm,则 S△ABD : S△ACD为 ( )
A.9:16 B.3:4
C.16:9 D.4:3
4.在△ABC中,∠A=36°,AB=AC,用无刻度的直尺和圆规在 AC 边上找一点 D,使BD 平分∠ABC,下列画法不正确的是 ( )
5.[2024·上海模拟] 如图,△ABC 的三边 AB,BC,CA 的长分别是 20,30,40,其三条角平分线将△ABC 分为三个三角形,则 S△CAO等于 ( )
A.1:1:1
B.1:2:3
C.2:3:4
D.3:4:5
6.如图,BD是△ABC的角平分线,DE⊥AB,垂足为E.△ABC的面积为12,AB=7,DE=2,则BC的长为 ( )
A.7 B.6
C.5 D.4
二、填空题
7.如图,在 Rt△ABC中,∠C=90°,AD 是△ABC的角平分线,∠ADC=60°,AD=4,过D作DE⊥AB于点E,则DE= .
8.[2024·广州模拟] 如图,在Rt△ABC中,∠C=90°,以顶点 A 为圆心,适当长为半径画弧,分别交AC,AB 于点 M,N,再分别以点 M,N 为圆心,以大于 MN的长为半径画弧,两弧交于点P,作射线AP 交边BC 于点 D,若CD=3,AB=10,则△ABD的面积是 .
9.如图,在等腰直角三角形 ABC中,AE,BE,CE分别平分∠BAC,∠ABC,∠ACB,ED⊥BC于点D,CE=2 ,△ABC的周长为21,则△ABC 的面积为 .
10.[2024·合肥模拟] 如图,在△ABC中,∠BAC=3∠B,CD 平分∠ACB,AE⊥CD,垂足为点E,若BD=11,AD=5,则 (2)△ABC的周长是 .
三、解答题
11.如图,在△ABC中,点 D,E分别在AB,AC上,EF交DC 于点 F,∠3+∠2=180°,∠1=∠B.
(1)求证:DE∥BC.
(2)若 DE 平分∠ADC,∠3=3∠B,求∠2 的度数.
12.如图,在△ABC中,AB=AC,过 BC 的中点 D作DE⊥AB,DF⊥AC,垂足分别为点 E,F.
(1)求证:DE=DF.
(2)若∠BDE=55°,求∠BAC的度数.
13.[2024·西安模拟] 如图,BD是△ABC的角平分线,DE⊥AB,DF⊥BC,垂足分别为 E,F.
(1)∠EDB 与∠FDB 相等吗 请说明理由.
(2)若△ABC的面积为70,AB=16,DE=5,求BC的长.
14.如图1,在四边形 ABCD 中,AC 和 BD 相交于点O.
(1)如图 1,若 AD∥BC,DB 平分∠ADC,∠BCD=100°,则∠DBC= .
(2)如图2,若AD∥BC,DP平分∠ADB,CP平分∠ACB,求证:
(3)如图3,若 DP 平分∠ADB,CP 平分∠ACB,CQ和DQ 分别是△BCD 和△ADC的外角平分线,试探究∠P,∠DOC,∠Q之间的数量关系.
1. D 2. B 3. D 4. B 5. C 6. C 7.2 8.15 9.21
10.(1)
11.(1)证明:∵∠DFE+∠2=180°,∠3+∠2=180°,
∴∠DFE=∠3,∴BD∥EF,∴∠1=∠ADE.
∵∠1=∠B,∴∠ADE=∠B,∴DE∥BC.
(2)∠2=72°
12.解:(1)证明:如图,连结 AD,
∵D 是 BC 的中点,AB=AC,
∴AD平分∠BAC.
∵DE⊥AB,DF⊥AC,
∴DE=DF.
(2)∵DE⊥AB,∴∠BED=90°.∵∠BDE=55°,∴∠B=35°,∴∠C=35°,∴∠BAC=110°.
13.(1)∠EDB与∠FDB相等,理由略 (2)BC=12.
14.解:(1)∵AD∥BC,∴∠ADC+∠BCD=180°.
又∵∠BCD=100°,∴∠ADC=180°-∠BCD=80°.
∵DB平分∠ADC,∴∠ADB= ∠ADC=40°.
∵AD∥BC,∴∠DBC=∠ADB=40°.故答案为40°.
(2)证明:∵DP平分∠ADB,∴∠ADP=∠BDP,
∵CP平分∠ACB,∴∠ACP=∠BCP.
设∠ADP=∠BDP=α,∠ACP=∠BCP=β.
∵AD∥BC,∴∠DBC=∠ADB=2α,
∴∠DOC=∠DBC+∠ACB=2α+2β.如图,过点 P 作PE∥AD,则∠DPE=∠ADP=α.∵AD∥BC,
∴PE∥BC,∴∠CPE=∠BCP=β,
∴∠DPC=∠DPE+∠CPE=α+β,
(3)2∠P+2∠Q-∠DOC=180°,理由如下:
∵DP 平分∠ADB,CP 平分∠ACB,CQ 和 DQ 分别是△BCD和△ADC的外角平分线,
∴∠ADP=∠BDP,∠ACP=∠BCP,∠EDQ=∠CDQ,∠DCQ=∠FCQ.
设∠ADP=∠BDP=x,∠ACP=∠BCP=y,
∠EDQ=∠CDQ=z,∠DCQ=∠FCQ=ω,
贝
∠ODC=180°-∠ADB-∠CDE=180°-2x-2z,
∠OCD=180°-∠ACB-∠DCF=180°-2y-2ω,
∴∠DOC=180°-∠ODC-∠OCD=180°-(180°-2x-2z)
-(180°-2y-2w)=2x+2y+2z+2w-180°②,
∴∠P=180°-∠BDP-∠OCP-∠ODC-∠OCD=180°- -180°③,
由①×2-②+③×2得,2∠P+2∠Q-∠DOC=180°.
中小学教育资源及组卷应用平台
一、选择题
1.如图,OP 平分∠MON,PA⊥ON 于点 A,点 Q是射线OM 上的一个动点.若PA=3,则线段PQ的长不可能是 ( )
A.5 B.4
C.3 D.2
2.如图,在△ABC中,∠C=90°,AD平分∠BAC,BC=30,BD:CD=3:2,则点 D到AB的距离为( )
A.18 B.12
C.15 D.不能确定
3.如图,在△ABC中,AD 是∠BAC 的平分线,AB=8cm ,AC=6 cm,则 S△ABD : S△ACD为 ( )
A.9:16 B.3:4
C.16:9 D.4:3
4.在△ABC中,∠A=36°,AB=AC,用无刻度的直尺和圆规在 AC 边上找一点 D,使BD 平分∠ABC,下列画法不正确的是 ( )
5.[2024·上海模拟] 如图,△ABC 的三边 AB,BC,CA 的长分别是 20,30,40,其三条角平分线将△ABC 分为三个三角形,则 S△CAO等于 ( )
A.1:1:1
B.1:2:3
C.2:3:4
D.3:4:5
6.如图,BD是△ABC的角平分线,DE⊥AB,垂足为E.△ABC的面积为12,AB=7,DE=2,则BC的长为 ( )
A.7 B.6
C.5 D.4
二、填空题
7.如图,在 Rt△ABC中,∠C=90°,AD 是△ABC的角平分线,∠ADC=60°,AD=4,过D作DE⊥AB于点E,则DE= .
8.[2024·广州模拟] 如图,在Rt△ABC中,∠C=90°,以顶点 A 为圆心,适当长为半径画弧,分别交AC,AB 于点 M,N,再分别以点 M,N 为圆心,以大于 MN的长为半径画弧,两弧交于点P,作射线AP 交边BC 于点 D,若CD=3,AB=10,则△ABD的面积是 .
9.如图,在等腰直角三角形 ABC中,AE,BE,CE分别平分∠BAC,∠ABC,∠ACB,ED⊥BC于点D,CE=2 ,△ABC的周长为21,则△ABC 的面积为 .
10.[2024·合肥模拟] 如图,在△ABC中,∠BAC=3∠B,CD 平分∠ACB,AE⊥CD,垂足为点E,若BD=11,AD=5,则 (2)△ABC的周长是 .
三、解答题
11.如图,在△ABC中,点 D,E分别在AB,AC上,EF交DC 于点 F,∠3+∠2=180°,∠1=∠B.
(1)求证:DE∥BC.
(2)若 DE 平分∠ADC,∠3=3∠B,求∠2 的度数.
12.如图,在△ABC中,AB=AC,过 BC 的中点 D作DE⊥AB,DF⊥AC,垂足分别为点 E,F.
(1)求证:DE=DF.
(2)若∠BDE=55°,求∠BAC的度数.
13.[2024·西安模拟] 如图,BD是△ABC的角平分线,DE⊥AB,DF⊥BC,垂足分别为 E,F.
(1)∠EDB 与∠FDB 相等吗 请说明理由.
(2)若△ABC的面积为70,AB=16,DE=5,求BC的长.
14.如图1,在四边形 ABCD 中,AC 和 BD 相交于点O.
(1)如图 1,若 AD∥BC,DB 平分∠ADC,∠BCD=100°,则∠DBC= .
(2)如图2,若AD∥BC,DP平分∠ADB,CP平分∠ACB,求证:
(3)如图3,若 DP 平分∠ADB,CP 平分∠ACB,CQ和DQ 分别是△BCD 和△ADC的外角平分线,试探究∠P,∠DOC,∠Q之间的数量关系.
1. D 2. B 3. D 4. B 5. C 6. C 7.2 8.15 9.21
10.(1)
11.(1)证明:∵∠DFE+∠2=180°,∠3+∠2=180°,
∴∠DFE=∠3,∴BD∥EF,∴∠1=∠ADE.
∵∠1=∠B,∴∠ADE=∠B,∴DE∥BC.
(2)∠2=72°
12.解:(1)证明:如图,连结 AD,
∵D 是 BC 的中点,AB=AC,
∴AD平分∠BAC.
∵DE⊥AB,DF⊥AC,
∴DE=DF.
(2)∵DE⊥AB,∴∠BED=90°.∵∠BDE=55°,∴∠B=35°,∴∠C=35°,∴∠BAC=110°.
13.(1)∠EDB与∠FDB相等,理由略 (2)BC=12.
14.解:(1)∵AD∥BC,∴∠ADC+∠BCD=180°.
又∵∠BCD=100°,∴∠ADC=180°-∠BCD=80°.
∵DB平分∠ADC,∴∠ADB= ∠ADC=40°.
∵AD∥BC,∴∠DBC=∠ADB=40°.故答案为40°.
(2)证明:∵DP平分∠ADB,∴∠ADP=∠BDP,
∵CP平分∠ACB,∴∠ACP=∠BCP.
设∠ADP=∠BDP=α,∠ACP=∠BCP=β.
∵AD∥BC,∴∠DBC=∠ADB=2α,
∴∠DOC=∠DBC+∠ACB=2α+2β.如图,过点 P 作PE∥AD,则∠DPE=∠ADP=α.∵AD∥BC,
∴PE∥BC,∴∠CPE=∠BCP=β,
∴∠DPC=∠DPE+∠CPE=α+β,
(3)2∠P+2∠Q-∠DOC=180°,理由如下:
∵DP 平分∠ADB,CP 平分∠ACB,CQ 和 DQ 分别是△BCD和△ADC的外角平分线,
∴∠ADP=∠BDP,∠ACP=∠BCP,∠EDQ=∠CDQ,∠DCQ=∠FCQ.
设∠ADP=∠BDP=x,∠ACP=∠BCP=y,
∠EDQ=∠CDQ=z,∠DCQ=∠FCQ=ω,
贝
∠ODC=180°-∠ADB-∠CDE=180°-2x-2z,
∠OCD=180°-∠ACB-∠DCF=180°-2y-2ω,
∴∠DOC=180°-∠ODC-∠OCD=180°-(180°-2x-2z)
-(180°-2y-2w)=2x+2y+2z+2w-180°②,
∴∠P=180°-∠BDP-∠OCP-∠ODC-∠OCD=180°- -180°③,
由①×2-②+③×2得,2∠P+2∠Q-∠DOC=180°.
同课章节目录
