第16讲三角形与全等三角形 (含答案) 2025年中考数学知识点过关训练
文档属性
| 名称 | 第16讲三角形与全等三角形 (含答案) 2025年中考数学知识点过关训练 |  | |
| 格式 | docx | ||
| 文件大小 | 150.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-10 07:41:02 | ||
图片预览

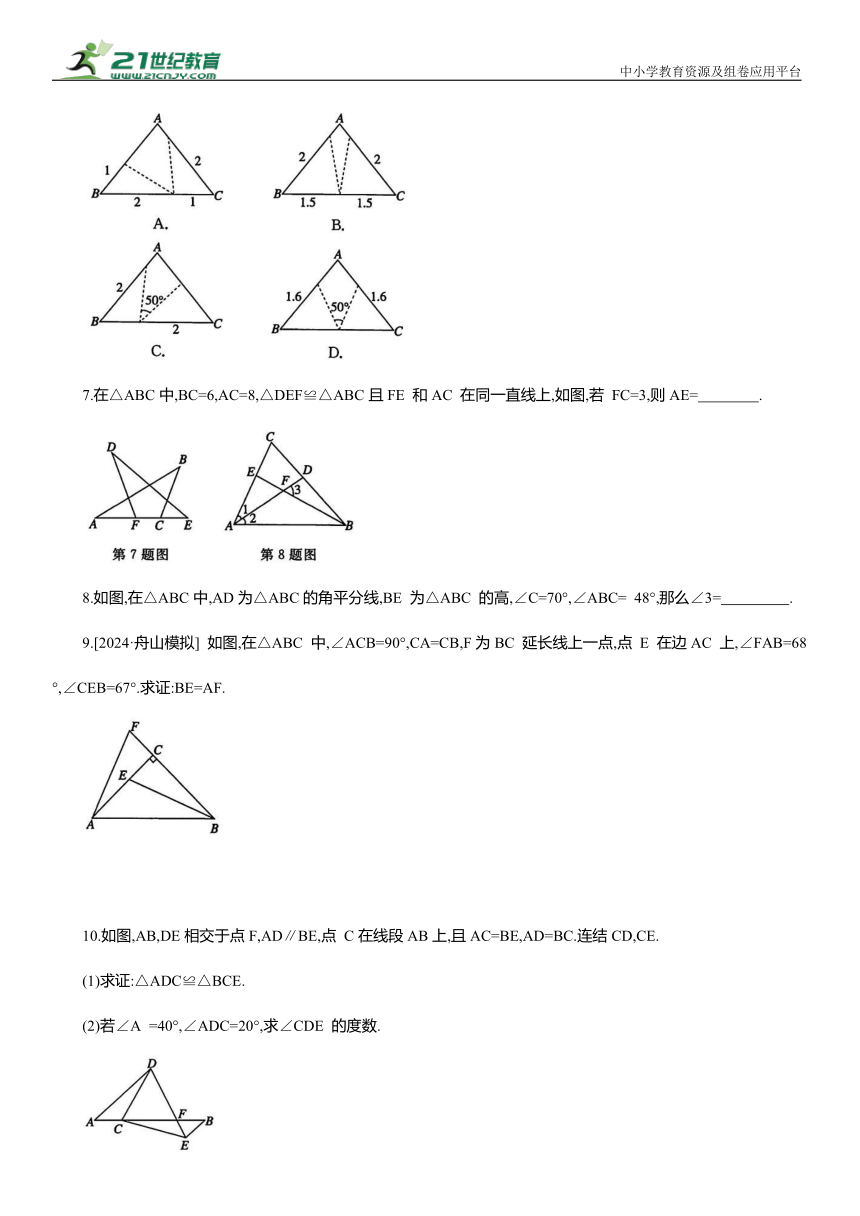
文档简介
中小学教育资源及组卷应用平台
三角形与全等三角形
A 熟知教材与迁移
1.下列图形中具有稳定性的图形是 ( )
2.在下列长度的四条线段中,能与长5cm ,12 cm的两条线段围成一个三角形的是 ( )
A.5cm B.7 cm C.15 cm D.17 cm
3.下列判断中错误的是 ( )
A.有两角和一边对应相等的两个三角形全等
B.有两边和一角对应相等的两个三角形全等
C.有两边和其中一边上的中线对应相等的两个三角形全等
D.有一边对应相等的两个等边三角形全等
4.如果将一副三角板按如图方式叠放,那么∠1等于 ( )
A.45° B.60° C.105° D.120°
5.如图,在△ABC中,AD 是高,AE 是角平分线,AF是中线,则下列说法中错误的是 ( )
A. BF=CF B.∠C+∠CAD=90°
C.∠BAF=∠CAF D. S△ABC=2S△ABF
6.在△ABC中,∠B=∠C=50°,将△ABC沿图中虚线剪开,剪下的两个三角形不一定全等的是( )
7.在△ABC中,BC=6,AC=8,△DEF≌△ABC且FE 和AC 在同一直线上,如图,若 FC=3,则AE= .
8.如图,在△ABC中,AD为△ABC的角平分线,BE 为△ABC 的高,∠C=70°,∠ABC= 48°,那么∠3= .
9.[2024·舟山模拟] 如图,在△ABC 中,∠ACB=90°,CA=CB,F为BC 延长线上一点,点 E 在边AC 上,∠FAB=68°,∠CEB=67°.求证:BE=AF.
10.如图,AB,DE相交于点F,AD∥BE,点 C在线段AB上,且AC=BE,AD=BC.连结CD,CE.
(1)求证:△ADC≌△BCE.
(2)若∠A =40°,∠ADC=20°,求∠CDE 的度数.
B掌握通性与通法
11.[2024·广州模拟]在探究证明“三角形的内角和是180°”时,综合实践小组的同学作了如图所示四种辅助线,其中不能证明“三角形内角和是180°”的是 ( )
过C作EF∥AB
B. 延长AC到F,过C作CE∥AB
C.过 AB 上一点 D 作 DE∥BC,DF∥AC
12.如图所示,在△ABC 中,D,E,F 分别为BC,AD,CE的中点,且 则阴影部分的面积为 ( )
A.3 cm B.4 cm C.5 cm D.6 cm
13.如图,在 Rt△ABC中,∠BAC=90°,AB=AC,D为BC 上一点,连结 AD.过点 B 作BE⊥AD于点E,过点 C作CF⊥AD交AD 的延长线于点 F.若 BE=4,CF=1,则 EF 的长度为
14.如图,在△ABC 中,D 是BC 的中点,AB=12,AC=8.用剪刀从点 D 入手进行裁剪,若沿 DA 剪成两个三角形,它们周长的差为 ;若点 E 在AB 上,沿 DE剪开得到两部分周长差为2,则AE= .
15.[2024·义乌模拟] 如图,在 Rt△ABC 中,∠ACB=90°,AC=BC,点 D 在边 BC 上(不与点 B,C重合),BE⊥AD,垂足为 E,过点 C 作CF⊥CE,交线段 AD 于点 F.
(1)试说明△CAF≌△CBE.
(2)如果 EF=2AF,取 EF 的中点 H ,连结CH,试说明DC=DB.
C感悟思维与素养
16.如图,△ABC的边BC 在直线 MN上,∠ABC 与 ∠ACN的平分线交于点D,∠BAC的平分线交 BD 于点 E.若∠MBA=α,∠AEB=β,∠D=γ,则下列关系正确的是 ( )
A.2α+2γ-β=180° B.2β+2γ-α=180°
C.α-2γ+β=180° D.β+2γ-α=180°
1. A 2. C 3. B 4. C 5. C 6. D 7.11 8.59° 9.略
10.(1)略 (2)50° 11. D 12. B 13.3 14.4 1或3
15.证明:(1)∵BE⊥AD于点E,CF⊥CE,
∴∠AEB=∠FCE=90°.∵∠ACB=90°,
∴∠ACF=∠BCE=90°-∠BCF.
∵∠CAF+∠ADC=90°,∠CBE+∠BDE=90°,且∠ADC=∠BDE,∴∠CAF=∠CBE,
在△CAF和△CBE中.
∴△CAF≌△CBE(ASA).
(2)如图,H为EF 的中点,连结CH,由(1)得△CAF≌△CBE,
∴CF=CE,AF=BE.
∵∠FCE=90°,H是EF的中点,
∴CH⊥EF,CH=FH=EH
∴∠CHD=∠BED=90°,EF=2CH.
∵EF=2AF,∴2CH=2AF,∴CH=AF,∴CH=BE,在△CDH 和△BDE中, ∴△CDH≌△BDE(AAS),∴DC=DB.
16. B
三角形与全等三角形
A 熟知教材与迁移
1.下列图形中具有稳定性的图形是 ( )
2.在下列长度的四条线段中,能与长5cm ,12 cm的两条线段围成一个三角形的是 ( )
A.5cm B.7 cm C.15 cm D.17 cm
3.下列判断中错误的是 ( )
A.有两角和一边对应相等的两个三角形全等
B.有两边和一角对应相等的两个三角形全等
C.有两边和其中一边上的中线对应相等的两个三角形全等
D.有一边对应相等的两个等边三角形全等
4.如果将一副三角板按如图方式叠放,那么∠1等于 ( )
A.45° B.60° C.105° D.120°
5.如图,在△ABC中,AD 是高,AE 是角平分线,AF是中线,则下列说法中错误的是 ( )
A. BF=CF B.∠C+∠CAD=90°
C.∠BAF=∠CAF D. S△ABC=2S△ABF
6.在△ABC中,∠B=∠C=50°,将△ABC沿图中虚线剪开,剪下的两个三角形不一定全等的是( )
7.在△ABC中,BC=6,AC=8,△DEF≌△ABC且FE 和AC 在同一直线上,如图,若 FC=3,则AE= .
8.如图,在△ABC中,AD为△ABC的角平分线,BE 为△ABC 的高,∠C=70°,∠ABC= 48°,那么∠3= .
9.[2024·舟山模拟] 如图,在△ABC 中,∠ACB=90°,CA=CB,F为BC 延长线上一点,点 E 在边AC 上,∠FAB=68°,∠CEB=67°.求证:BE=AF.
10.如图,AB,DE相交于点F,AD∥BE,点 C在线段AB上,且AC=BE,AD=BC.连结CD,CE.
(1)求证:△ADC≌△BCE.
(2)若∠A =40°,∠ADC=20°,求∠CDE 的度数.
B掌握通性与通法
11.[2024·广州模拟]在探究证明“三角形的内角和是180°”时,综合实践小组的同学作了如图所示四种辅助线,其中不能证明“三角形内角和是180°”的是 ( )
过C作EF∥AB
B. 延长AC到F,过C作CE∥AB
C.过 AB 上一点 D 作 DE∥BC,DF∥AC
12.如图所示,在△ABC 中,D,E,F 分别为BC,AD,CE的中点,且 则阴影部分的面积为 ( )
A.3 cm B.4 cm C.5 cm D.6 cm
13.如图,在 Rt△ABC中,∠BAC=90°,AB=AC,D为BC 上一点,连结 AD.过点 B 作BE⊥AD于点E,过点 C作CF⊥AD交AD 的延长线于点 F.若 BE=4,CF=1,则 EF 的长度为
14.如图,在△ABC 中,D 是BC 的中点,AB=12,AC=8.用剪刀从点 D 入手进行裁剪,若沿 DA 剪成两个三角形,它们周长的差为 ;若点 E 在AB 上,沿 DE剪开得到两部分周长差为2,则AE= .
15.[2024·义乌模拟] 如图,在 Rt△ABC 中,∠ACB=90°,AC=BC,点 D 在边 BC 上(不与点 B,C重合),BE⊥AD,垂足为 E,过点 C 作CF⊥CE,交线段 AD 于点 F.
(1)试说明△CAF≌△CBE.
(2)如果 EF=2AF,取 EF 的中点 H ,连结CH,试说明DC=DB.
C感悟思维与素养
16.如图,△ABC的边BC 在直线 MN上,∠ABC 与 ∠ACN的平分线交于点D,∠BAC的平分线交 BD 于点 E.若∠MBA=α,∠AEB=β,∠D=γ,则下列关系正确的是 ( )
A.2α+2γ-β=180° B.2β+2γ-α=180°
C.α-2γ+β=180° D.β+2γ-α=180°
1. A 2. C 3. B 4. C 5. C 6. D 7.11 8.59° 9.略
10.(1)略 (2)50° 11. D 12. B 13.3 14.4 1或3
15.证明:(1)∵BE⊥AD于点E,CF⊥CE,
∴∠AEB=∠FCE=90°.∵∠ACB=90°,
∴∠ACF=∠BCE=90°-∠BCF.
∵∠CAF+∠ADC=90°,∠CBE+∠BDE=90°,且∠ADC=∠BDE,∴∠CAF=∠CBE,
在△CAF和△CBE中.
∴△CAF≌△CBE(ASA).
(2)如图,H为EF 的中点,连结CH,由(1)得△CAF≌△CBE,
∴CF=CE,AF=BE.
∵∠FCE=90°,H是EF的中点,
∴CH⊥EF,CH=FH=EH
∴∠CHD=∠BED=90°,EF=2CH.
∵EF=2AF,∴2CH=2AF,∴CH=AF,∴CH=BE,在△CDH 和△BDE中, ∴△CDH≌△BDE(AAS),∴DC=DB.
16. B
同课章节目录
