期中模拟测试卷(含解析)-2024-2025学年数学九年级下册人教版
文档属性
| 名称 | 期中模拟测试卷(含解析)-2024-2025学年数学九年级下册人教版 |  | |
| 格式 | docx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-10 07:37:01 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
期中模拟测试卷-2024-2025学年数学九年级下册人教版
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列各点中,在反比例函数图象上的点是( )
A. B. C. D.
2.已知a是一个正数,点,,都在反比例函数的图象上,则0,,,的大小关系是( )
A. B.
C. D.
3.如图,直线,,,,则的长为( )
A.8 B.6 C.4 D.2.5
4.已知在温度不变的条件下,对汽缸顶部的活塞加压后,气体对汽缸壁所产生的压强与汽缸内气体的体积成反比例,p关于V的函数图象如图所示.现对其加压两次,若两次加压的压强差为,气体体积压缩了.设第一次加压后气体的体积为,可列方程为( )
A. B.
C. D.
5.在中,,若,则的值为( )
A. B. C.1 D.
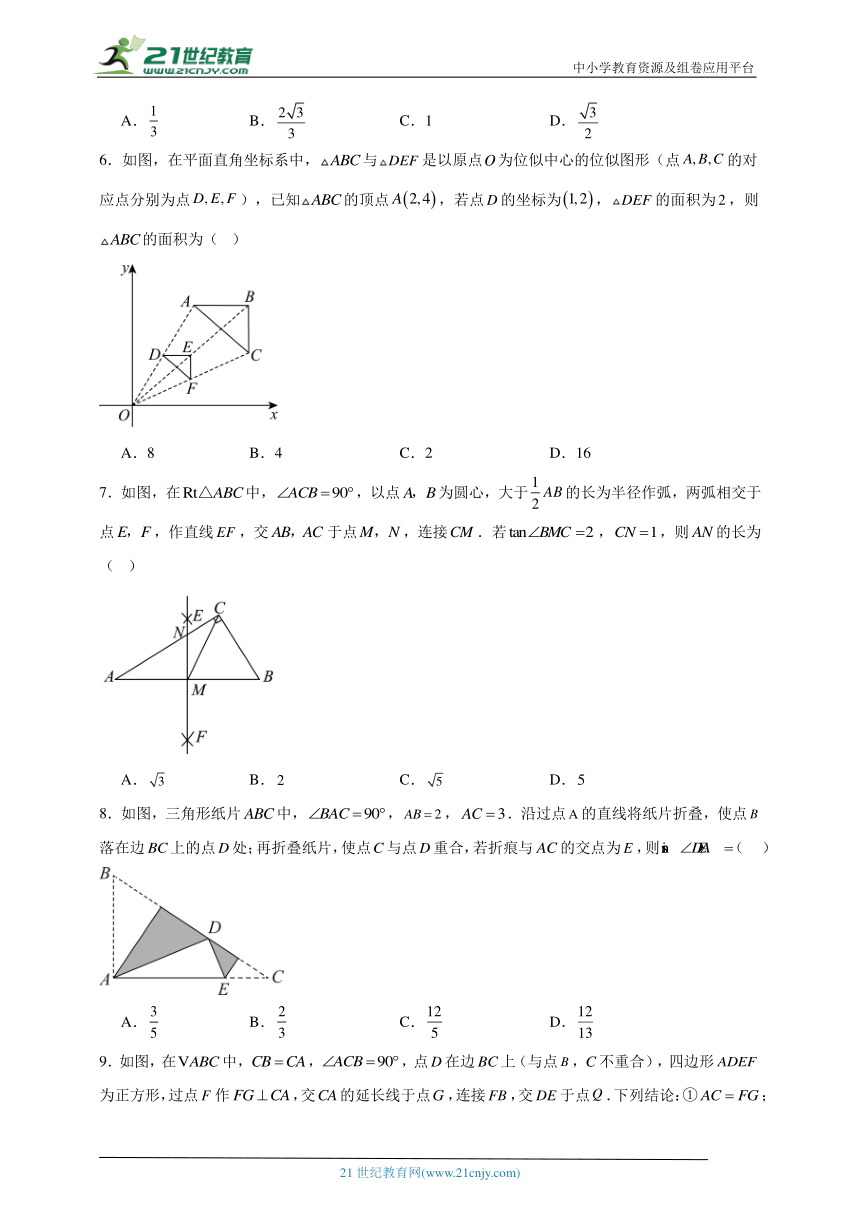
6.如图,在平面直角坐标系中,与是以原点为位似中心的位似图形(点的对应点分别为点),已知的顶点,若点的坐标为,的面积为,则的面积为( )
A.8 B.4 C.2 D.16
7.如图,在中,,以点为圆心,大于的长为半径作弧,两弧相交于点,作直线,交于点,连接.若,,则的长为( )
A. B. C. D.
8.如图,三角形纸片中,,,.沿过点的直线将纸片折叠,使点落在边上的点处;再折叠纸片,使点与点重合,若折痕与的交点为,则( )
A. B. C. D.
9.如图,在中,,,点在边上(与点,不重合),四边形为正方形,过点作,交的延长线于点,连接,交于点.下列结论:①;②;③;④,其中结论正确的个数是( )
A.4个 B.3个 C.2个 D.1个
二、填空题
10.若反比例函数的图象经过点,则的值为 .
11.已知一辆汽车匀速通过某段公路,所需时间(单位:)与行驶速度(单位:)成反比例关系,函数图象如图所示.若该路段限速,则该汽车通过该路段至少需要 .
12.如图,在四边形中,对角线平分,,点E在边上,.若,,,则的长为 .
13.如图,在平面直角坐标系中,正比例函数与反比例函数(k为常数,)的图象相交于A、C两点,过点A作轴于点B,连接,若的面积为4,则k的值为 .
14.如图,在矩形中,,,点M在直线上,连接,
(1)当,则 .
(2)当最大时, .
15.七巧板是我国一款传统的益智玩具,能够启迪智慧,陶冶情操.七巧板是由五块含45°角的直角三角形、一块正方形和一块平行四边形组成的.某同学利用图1中七巧板的部分图形拼成图2中的图形.若,则的值为 .
16.为出行方便,越来越多的市民使用起了共享单车,图1为单车实物图,图2为单车示意图,与地面平行,坐垫C可沿射线方向调节.已知,车轮半径为,当时,小明体验后觉得骑着比较舒适,此时坐垫C离地面高度约为 .(结果精确到1cm,参考数据:)
三、解答题
17.计算:
18.学习数学贵在解决实际问题某校数学兴趣小组准备利用所学数学知识来测量一个山脚下的信号塔的高度(图1).如图2,信号塔刚好在坡角为的斜坡底角处,斜坡的长为,在点D处测得信号塔最高点A的仰角为,平行于水平线,的长为,求信号塔的高(结果精确到.参考数据:).
19.如图,、交于点E,,且平分.
(1)求证:;
(2)若,求的长.
20.如图,中,,,点在上,交于点.
(1)如图1,求证:;
(2)如图2,点在上,,,分别交,于点,,找出图中与相等的线段,并证明;
(3)在(2)的条件下,若,求的值.
21.如图,一次函数的图象与反比例函数的图象交于点,,且一次函数与轴,轴分别交于点,.
(1)求反比例函数和一次函数的表达式;
(2)根据图象直接写出不等式的解集;
(3)在第三象限的反比例函数图象上有一点,使得,求点的坐标.
22.如图,在中,,,点在线段上(点不与点,重合),线段绕点顺时针旋转得到线段,连接,于点,与交于点.
(1)如图1,求证:;
(2)如图2,连接,求证:;
(3)如图3,设与交于点,与交于点,当时,求的面积.
23.如图,已知反比例函数与直线交于点,点C是x轴上的一点,连接.
(1)求反比例函数的表达式及直线的函数表达式;
(2)若,求点C的坐标;
(3)如图2,直线l绕若点旋转,直线l上有一动点P,过P作交反比例图象于M,作轴交反比例函数图象于N,连接,若在直线上刚好存在三个不同的P点且使得的面积为9时,请直接写出此时直线的斜率.
《期中模拟测试卷-2024-2025学年数学九年级下册人教版》参考答案
题号 1 2 3 4 5 6 7 8 9
答案 A A D C A A C D A
1.A
【分析】本题考查的是反比例函数图象上点的坐标特点,根据反比例函数图象上点的坐标特征对各选项进行逐一判断即可.
【详解】解:A、,此点在反比例函数的图象上,符合题意;
B、,此点不在反比例函数的图象上,不符合题意;
C、,此点不在反比例函数的图象上,不符合题意;
D、,此点不在反比例函数的图象上,不符合题意.
故选:A.
2.A
【分析】本题主要考查了反比例函数图象上点的坐标特征,依据题意,由点,,都在反比例函数的图象上,从而,,,结合a是一个正数和反比例函数的性质可得结论.
【详解】解:由题意,∵点,,都在反比例函数的图象上,
∴,,,
∵a是一个正数,
∴,,,
又∵反比例函数的图象分布在第二、第四象限,且在每个象限内y随x的增大而增大,
∴当时,,
∴.
故选:A.
3.D
【分析】本题考查了平行线分线段成比例定理,根据平行线分线段成比例定理得出,代入数据计算即可得解,熟练掌握平行线分线段成比例定理是解此题的关键.
【详解】解:∵直线,
∴,即,
∴,
故选:D.
4.C
【分析】本题主要考查了反比例函数的应用,分式方程的应用,解题的关键是熟练掌握待定系数法,求出反比例函数解析式,先求出反比例函数解析式为,根据第一次加压后气体的体积为,则第二次气体体积为,两次加压的压强差为,列出方程即可.
【详解】解:设p关于V的函数关系式为,
把代入得:,
∴p关于V的函数关系式为,
第一次加压后气体的体积为,则第二次气体体积为,
根据题意得:,
故选:C.
5.A
【分析】本题主要考查了余弦和正弦的定义,根据正弦的定义得到,再由余弦的定义即可得到答案.
【详解】解:∵在中,,,
∴,
故选:A.
6.A
【分析】本题主要考查位数图形的性质,掌握位数图形的性质,求出相似比是解题的关键.
先由得,,进而得,再利用位似的性质得,,然后根据三角形相似的性质解决问题.
【详解】解:∵,
∴,,
∴,
∵与是以原点为位似中心的位似图形,
∴,
∴,
∴,
故选:A.
7.C
【分析】本题考查了线段垂直平分线的性质,直角三角形斜边中线等于斜边一半,解直角三角形,勾股定理,平行线分线段成比例,,熟练掌握相关知识点是解题的关键.
作于点,由题意得垂直平分,得到,求出,得到,求出,即可得到答案.
【详解】解:如图,作于点,
由题意得垂直平分,
,
,
,
,
,
,
,
,
,
,
,
,
,
故选:C.
8.D
【分析】本题考查了折叠的性质,勾股定理,解直角三角形,熟练掌握相关知识点是解题的关键.
根据折叠的性质得到,,,,得到,根据勾股定理求出,得到,即可得到答案.
【详解】解:,
,
由折叠可得,,,,
,
,
,
,
,
,
,
故选:D.
9.A
【分析】由正方形的性质得出,证出,由证明,得出,①正确;证明四边形是矩形,得出,②正确;由等腰直角三角形的性质和矩形的性质得出,③正确;证出,得出对应边成比例,得出,④正确.
【详解】解:∵四边形为正方形,
,
,
,
,
,
在和中,,
,
∴,故①正确;
,
,
,
,
∴四边形是矩形,
,
∴,
∴,故②正确;
,
∴,故③正确;
,
,
,
,故④正确;
∴正确的有①②③④.
故选:A.
【点晴】本题考查正方形的性质,矩形的判定和性质,三角形全等的判定和性质,三角形相似的判定和性质等知识.利用数形结合的思想是解答本题的关键.
10.
【分析】本题考查的是反比例函数的性质,把点代入反比例函数解析式即可得到答案.
【详解】解:∵反比例函数的图象经过点,
∴,
解得:,
故答案为:
11./
【分析】本题考查了反比例函数的实际应用,现实生活中存在大量成反比例函数的两个变量,解答该类问题的关键是确定两个变量之间的函数关系,然后利用待定系数法求出它们的关系式.设反比例函数的解析式为,把代入得到反比例函数的解析式是,把代入解析式,得到汽车通过该段路段的时间最少是.
【详解】解:设反比例函数的解析式为,
把代入得,
解得,
则反比例函数的解析式是,
把代入解析式得,
则当汽车通过该段路段的时间最少是.
故答案为:.
12.
【分析】本题考查了全等三角形的判定与性质、相似三角形的判定与性质、等腰三角形的性质,根据角平分线的特点,在上截取,连结,构造全等三角形和相似三角形,由相似三角形的性质求出的长.
【详解】解:如图,在上取一点F,使,连接,
平分,
,
,
,
,,,
,
,
即,
,即,
,
,,
,,
,
,,
,
,
,
又,
,
.
故答案为:.
13.
【分析】本题主要考查了反比例函数中的几何意义,首先根据反比例函数中的几何意义可得:,再根据反比例函数的对称性可知:,据此即可求出的值.
【详解】解:∵正比例函数与反比例函数(k为常数,)的图象相交于A、C两点,
∴,
由反比例函数中的几何意义得:,
∴,
,
∵,
.
故答案为:.
14. / 3
【分析】①根据矩形的性质和勾股定理即可求解;
②作,过点A作于点E,则连接,取中点O,连接,,先证明,继而,因此,故的最大值转化为的最大值,由,知点E在以点O为圆心,为半径的圆上运动,由,故当三点共线时,取得最大值为18,故.
【详解】解:①∵,,
∴,
∵四边形是矩形,
∴,,
∴由勾股定理得:,,
∴,
故答案为:;
②作,过点A作于点E,则连接,取中点O,连接,,
∵四边形是矩形,
∴,,,
∵点O为中点,
∴,
∴由勾股定理得,
∵,
∴
∵四边形是矩形,
∴,
∴,
∴,
∴,
∴
∵
∴
∴,
∴,
∴,
∴的最大值转化为的最大值,
∵,
∴点E在以点O为圆心,为半径的圆上运动,
∵,
∴当三点共线时,取得最大值为18,
∴.
故答案为:3.
【点睛】本题考查了矩形的性质,勾股定理,相似三角形的判定与性质,三角形三边关系,构造相似三角形是解决本题的关键.
15.
【分析】本题主要考查了三角形内角和定理,用七巧板拼接图形以及特殊角的三角函数求值.
根据题意可得,再由平角的定义分别求出的度数,再由三角形内角和定理求出的度数,即可根据平角的定义求出答案.
【详解】解:如图所示,
由题意得,,
∵,
∴,,
∴,
∴,
,
故答案为:.
16./86厘米
【分析】本题考查了解直角三角形的应用,作出适当的辅助线,构造出直角三角形是解题的关键;作于H,作地面于P,利用三角函数求出即可.
【详解】解:如图,作于H,作地面于P,
由题知,,
∴,
∴坐垫C离地面高度约为,
故答案为:.
17.
【分析】本题主要考查了实数的运算,求特殊角三角函数值,先计算特殊角三角函数值,算术平方根,零指数幂和负整数指数幂,再去绝对值后计算加减法即可得到答案.
【详解】解;
.
18.
【分析】本题考查平行线的性质,解直角三角形的实际应用.延长交于点,在中,求出的长,在中,求出的长,利用求出的长即可.解题的关键是构造直角三角形.
【详解】解:延长交于点,则:,
∵,
∴
∵,
∴,
,
∴
在中,,
∴,
在中,,
∴.
答:信号塔的高为.
19.(1)见解析
(2)
【分析】本题考查了三角形相似的判定和性质,等腰三角形性质,角的平分线,熟练掌握相似的判定和性质是解题的关键.
(1)先证明,结合即可得证.
(2)根据,得到,结合,代入解答即可.
【详解】(1)证明:∵,
∴,
∵平分,
∴,
∴,
∵,
∴.
(2)解:∵,
∴.
∵,
∴.
∵,
∴.
解得.
20.(1)见详解
(2),见详解
(3)
【分析】本题主要考查了平行四边形的性质,垂直的性质,全等三角形的判定和性质,等腰直角三角形的性质,勾股定理等知识点,解题的关键是构造出辅助线,并熟练运用以上性质定理.
(1)利用平行四边形的性质,直角三角形的性质,垂直的性质即可求得结果;
(2)构造角平分线,利用平行四边形的性质和平行线的性质得出相关线段和角相等,证出,,进而可求得相等线段;
(3)构造辅助线,根据题目条件、平行四边形和等腰直角三角形的性质得出,设,表示出相关的线段长,利用勾股定理表示出和求出比值即可.
【详解】(1)证明:∵,,
∴,
∴,
中,,
∴,
∵,
∴,
∴.
(2)解:,理由如下:
如图,过点作平分,交于点,
中,,,
中,,,
∴,,
∵,
∴(ASA),
∴,,
∴,
∵,
∴,
∴,
∵,,
∴,
中,,
∴,
∵,
∴,
∴(ASA)
∴.
(3)解:
如图,过点作于点,
由(2)知,中,,,
∴,,
中,,
又∵,
∴,
∵,,
∴,,
设,则,,
∴中,,,
∵,
∴,
∴,
∴,
∴,
∴中,,
中,,
∴.
21.(1),
(2)或
(3)点坐标为
【分析】本题主要考查了反比例函数与一次函数的交点问题,熟知反比例函数及一次函数的图象与性质是解题的关键.
(1)将点坐标代入反比例函数解析式,求出,再将点坐标代入反比例函数解析式,求出点坐标,最后将,两点坐标代入一次函数解析式即可解决问题;
(2)利用反比例函数以及一次函数图象,即可解决问题;
(3)根据与的面积关系,可求出点的纵坐标,据此可解决问题.
【详解】(1)解:将代入得,
∴,
反比例函数的解析式为,
将代入得,,
点的坐标为.
将点和点的坐标代入得,,
解得,
一次函数的解析式为;
(2)解:根据所给函数图象可知,当或时,一次函数的图象在反比例函数图象的上方,即,
不等式的解集为:或.
(3)解:将代入得,,
点的坐标为,
,
.
将代入得,,
点的坐标为,
,
解得.
∵点在第三象限,
∴,
将代入得,,
点坐标为.
22.(1)见解析
(2)见解析
(3)
【分析】(1)由旋转的性质可得是等腰直角三角形,从而得出,,通过角度之间的转换得出,,即可得证;
(2)过点作交于点,即,证明和都是等腰直角三角形,得出,再证明,得出,即可得解;
(3)证明是等腰直角三角形,得出,,证明,求出,,,再证明,得出,即可得解.
【详解】(1)证明:线段是由旋转得到,
∴是等腰直角三角形,
,,
,
,
,
,
,
,,
,
,
;
(2)证明:过点作交于点,即,
,
,
,
,
和都是等腰直角三角形,
,
,
,
又,
,
,
;
(3)解:
,
是等腰直角三角形,
,
,,
由(2)问知:.
,,
,
,.
,
∵,
∴,
∴,
,
.
【点睛】本题考查了旋转的性质、等腰直角三角形的判定与性质、全等三角形的判定与性质、相似三角形的判定与性质等知识点,熟练掌握以上知识点并灵活运用,添加适当的辅助线是解此题的关键.
23.(1),
(2)或
(3)或或或
【分析】(1)待定系数法求出函数解析式即可;
(2)设直线与轴交于点,设,根据,列出方程进行求解即可;
(3)设直线的解析式为,把代入,得到,设,进而得到,,根据的面积为9,列出方程,根据直线上刚好存在三个不同的P点,得到有3个不相等的实数根,利用根与系数的关系进行求解即可.
【详解】(1)解:∵反比例函数与直线交于点,
∴,
∴,
∴,,
∴,解得:;
∴;
(2)设直线与轴交于点,设,
∵,
∴当时,,解得,
∴,
∴,
∵,
∴,即:,
∴,
∴或,
∴或;
(3)设直线的解析式为,把代入,得:,
∴,
∴,
设,
∵过P作交反比例图象于M,作轴交反比例函数图象于N,
∴到,,
∴,
∵的面积为9,
∴,
∴,
整理,得:,
设,则:,
∴;
①当时,,解得:或,
∴或,
即:或,
当时,,
∴有2个不相等的实数根,
∵直线上刚好存在三个不同的P点,
∴有2个相等的实数根,
∴,解得:或;
②当时,则:,解得:或,
∴或,
当时,;
当时,;
∵直线上刚好存在三个不同的P点,
∴或,
当时,解得:或;
当,无解;
综上:或或或.
【点睛】本题考查反比例函数与一次函数的交点问题,涉及待定系数法求函数解析式,分割法求面积,根与系数的关系等知识点,综合性强,计算量大,熟练掌握相关知识点,利用数形结合的思想进行求解,是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期中模拟测试卷-2024-2025学年数学九年级下册人教版
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列各点中,在反比例函数图象上的点是( )
A. B. C. D.
2.已知a是一个正数,点,,都在反比例函数的图象上,则0,,,的大小关系是( )
A. B.
C. D.
3.如图,直线,,,,则的长为( )
A.8 B.6 C.4 D.2.5
4.已知在温度不变的条件下,对汽缸顶部的活塞加压后,气体对汽缸壁所产生的压强与汽缸内气体的体积成反比例,p关于V的函数图象如图所示.现对其加压两次,若两次加压的压强差为,气体体积压缩了.设第一次加压后气体的体积为,可列方程为( )
A. B.
C. D.
5.在中,,若,则的值为( )
A. B. C.1 D.
6.如图,在平面直角坐标系中,与是以原点为位似中心的位似图形(点的对应点分别为点),已知的顶点,若点的坐标为,的面积为,则的面积为( )
A.8 B.4 C.2 D.16
7.如图,在中,,以点为圆心,大于的长为半径作弧,两弧相交于点,作直线,交于点,连接.若,,则的长为( )
A. B. C. D.
8.如图,三角形纸片中,,,.沿过点的直线将纸片折叠,使点落在边上的点处;再折叠纸片,使点与点重合,若折痕与的交点为,则( )
A. B. C. D.
9.如图,在中,,,点在边上(与点,不重合),四边形为正方形,过点作,交的延长线于点,连接,交于点.下列结论:①;②;③;④,其中结论正确的个数是( )
A.4个 B.3个 C.2个 D.1个
二、填空题
10.若反比例函数的图象经过点,则的值为 .
11.已知一辆汽车匀速通过某段公路,所需时间(单位:)与行驶速度(单位:)成反比例关系,函数图象如图所示.若该路段限速,则该汽车通过该路段至少需要 .
12.如图,在四边形中,对角线平分,,点E在边上,.若,,,则的长为 .
13.如图,在平面直角坐标系中,正比例函数与反比例函数(k为常数,)的图象相交于A、C两点,过点A作轴于点B,连接,若的面积为4,则k的值为 .
14.如图,在矩形中,,,点M在直线上,连接,
(1)当,则 .
(2)当最大时, .
15.七巧板是我国一款传统的益智玩具,能够启迪智慧,陶冶情操.七巧板是由五块含45°角的直角三角形、一块正方形和一块平行四边形组成的.某同学利用图1中七巧板的部分图形拼成图2中的图形.若,则的值为 .
16.为出行方便,越来越多的市民使用起了共享单车,图1为单车实物图,图2为单车示意图,与地面平行,坐垫C可沿射线方向调节.已知,车轮半径为,当时,小明体验后觉得骑着比较舒适,此时坐垫C离地面高度约为 .(结果精确到1cm,参考数据:)
三、解答题
17.计算:
18.学习数学贵在解决实际问题某校数学兴趣小组准备利用所学数学知识来测量一个山脚下的信号塔的高度(图1).如图2,信号塔刚好在坡角为的斜坡底角处,斜坡的长为,在点D处测得信号塔最高点A的仰角为,平行于水平线,的长为,求信号塔的高(结果精确到.参考数据:).
19.如图,、交于点E,,且平分.
(1)求证:;
(2)若,求的长.
20.如图,中,,,点在上,交于点.
(1)如图1,求证:;
(2)如图2,点在上,,,分别交,于点,,找出图中与相等的线段,并证明;
(3)在(2)的条件下,若,求的值.
21.如图,一次函数的图象与反比例函数的图象交于点,,且一次函数与轴,轴分别交于点,.
(1)求反比例函数和一次函数的表达式;
(2)根据图象直接写出不等式的解集;
(3)在第三象限的反比例函数图象上有一点,使得,求点的坐标.
22.如图,在中,,,点在线段上(点不与点,重合),线段绕点顺时针旋转得到线段,连接,于点,与交于点.
(1)如图1,求证:;
(2)如图2,连接,求证:;
(3)如图3,设与交于点,与交于点,当时,求的面积.
23.如图,已知反比例函数与直线交于点,点C是x轴上的一点,连接.
(1)求反比例函数的表达式及直线的函数表达式;
(2)若,求点C的坐标;
(3)如图2,直线l绕若点旋转,直线l上有一动点P,过P作交反比例图象于M,作轴交反比例函数图象于N,连接,若在直线上刚好存在三个不同的P点且使得的面积为9时,请直接写出此时直线的斜率.
《期中模拟测试卷-2024-2025学年数学九年级下册人教版》参考答案
题号 1 2 3 4 5 6 7 8 9
答案 A A D C A A C D A
1.A
【分析】本题考查的是反比例函数图象上点的坐标特点,根据反比例函数图象上点的坐标特征对各选项进行逐一判断即可.
【详解】解:A、,此点在反比例函数的图象上,符合题意;
B、,此点不在反比例函数的图象上,不符合题意;
C、,此点不在反比例函数的图象上,不符合题意;
D、,此点不在反比例函数的图象上,不符合题意.
故选:A.
2.A
【分析】本题主要考查了反比例函数图象上点的坐标特征,依据题意,由点,,都在反比例函数的图象上,从而,,,结合a是一个正数和反比例函数的性质可得结论.
【详解】解:由题意,∵点,,都在反比例函数的图象上,
∴,,,
∵a是一个正数,
∴,,,
又∵反比例函数的图象分布在第二、第四象限,且在每个象限内y随x的增大而增大,
∴当时,,
∴.
故选:A.
3.D
【分析】本题考查了平行线分线段成比例定理,根据平行线分线段成比例定理得出,代入数据计算即可得解,熟练掌握平行线分线段成比例定理是解此题的关键.
【详解】解:∵直线,
∴,即,
∴,
故选:D.
4.C
【分析】本题主要考查了反比例函数的应用,分式方程的应用,解题的关键是熟练掌握待定系数法,求出反比例函数解析式,先求出反比例函数解析式为,根据第一次加压后气体的体积为,则第二次气体体积为,两次加压的压强差为,列出方程即可.
【详解】解:设p关于V的函数关系式为,
把代入得:,
∴p关于V的函数关系式为,
第一次加压后气体的体积为,则第二次气体体积为,
根据题意得:,
故选:C.
5.A
【分析】本题主要考查了余弦和正弦的定义,根据正弦的定义得到,再由余弦的定义即可得到答案.
【详解】解:∵在中,,,
∴,
故选:A.
6.A
【分析】本题主要考查位数图形的性质,掌握位数图形的性质,求出相似比是解题的关键.
先由得,,进而得,再利用位似的性质得,,然后根据三角形相似的性质解决问题.
【详解】解:∵,
∴,,
∴,
∵与是以原点为位似中心的位似图形,
∴,
∴,
∴,
故选:A.
7.C
【分析】本题考查了线段垂直平分线的性质,直角三角形斜边中线等于斜边一半,解直角三角形,勾股定理,平行线分线段成比例,,熟练掌握相关知识点是解题的关键.
作于点,由题意得垂直平分,得到,求出,得到,求出,即可得到答案.
【详解】解:如图,作于点,
由题意得垂直平分,
,
,
,
,
,
,
,
,
,
,
,
,
,
故选:C.
8.D
【分析】本题考查了折叠的性质,勾股定理,解直角三角形,熟练掌握相关知识点是解题的关键.
根据折叠的性质得到,,,,得到,根据勾股定理求出,得到,即可得到答案.
【详解】解:,
,
由折叠可得,,,,
,
,
,
,
,
,
,
故选:D.
9.A
【分析】由正方形的性质得出,证出,由证明,得出,①正确;证明四边形是矩形,得出,②正确;由等腰直角三角形的性质和矩形的性质得出,③正确;证出,得出对应边成比例,得出,④正确.
【详解】解:∵四边形为正方形,
,
,
,
,
,
在和中,,
,
∴,故①正确;
,
,
,
,
∴四边形是矩形,
,
∴,
∴,故②正确;
,
∴,故③正确;
,
,
,
,故④正确;
∴正确的有①②③④.
故选:A.
【点晴】本题考查正方形的性质,矩形的判定和性质,三角形全等的判定和性质,三角形相似的判定和性质等知识.利用数形结合的思想是解答本题的关键.
10.
【分析】本题考查的是反比例函数的性质,把点代入反比例函数解析式即可得到答案.
【详解】解:∵反比例函数的图象经过点,
∴,
解得:,
故答案为:
11./
【分析】本题考查了反比例函数的实际应用,现实生活中存在大量成反比例函数的两个变量,解答该类问题的关键是确定两个变量之间的函数关系,然后利用待定系数法求出它们的关系式.设反比例函数的解析式为,把代入得到反比例函数的解析式是,把代入解析式,得到汽车通过该段路段的时间最少是.
【详解】解:设反比例函数的解析式为,
把代入得,
解得,
则反比例函数的解析式是,
把代入解析式得,
则当汽车通过该段路段的时间最少是.
故答案为:.
12.
【分析】本题考查了全等三角形的判定与性质、相似三角形的判定与性质、等腰三角形的性质,根据角平分线的特点,在上截取,连结,构造全等三角形和相似三角形,由相似三角形的性质求出的长.
【详解】解:如图,在上取一点F,使,连接,
平分,
,
,
,
,,,
,
,
即,
,即,
,
,,
,,
,
,,
,
,
,
又,
,
.
故答案为:.
13.
【分析】本题主要考查了反比例函数中的几何意义,首先根据反比例函数中的几何意义可得:,再根据反比例函数的对称性可知:,据此即可求出的值.
【详解】解:∵正比例函数与反比例函数(k为常数,)的图象相交于A、C两点,
∴,
由反比例函数中的几何意义得:,
∴,
,
∵,
.
故答案为:.
14. / 3
【分析】①根据矩形的性质和勾股定理即可求解;
②作,过点A作于点E,则连接,取中点O,连接,,先证明,继而,因此,故的最大值转化为的最大值,由,知点E在以点O为圆心,为半径的圆上运动,由,故当三点共线时,取得最大值为18,故.
【详解】解:①∵,,
∴,
∵四边形是矩形,
∴,,
∴由勾股定理得:,,
∴,
故答案为:;
②作,过点A作于点E,则连接,取中点O,连接,,
∵四边形是矩形,
∴,,,
∵点O为中点,
∴,
∴由勾股定理得,
∵,
∴
∵四边形是矩形,
∴,
∴,
∴,
∴,
∴
∵
∴
∴,
∴,
∴,
∴的最大值转化为的最大值,
∵,
∴点E在以点O为圆心,为半径的圆上运动,
∵,
∴当三点共线时,取得最大值为18,
∴.
故答案为:3.
【点睛】本题考查了矩形的性质,勾股定理,相似三角形的判定与性质,三角形三边关系,构造相似三角形是解决本题的关键.
15.
【分析】本题主要考查了三角形内角和定理,用七巧板拼接图形以及特殊角的三角函数求值.
根据题意可得,再由平角的定义分别求出的度数,再由三角形内角和定理求出的度数,即可根据平角的定义求出答案.
【详解】解:如图所示,
由题意得,,
∵,
∴,,
∴,
∴,
,
故答案为:.
16./86厘米
【分析】本题考查了解直角三角形的应用,作出适当的辅助线,构造出直角三角形是解题的关键;作于H,作地面于P,利用三角函数求出即可.
【详解】解:如图,作于H,作地面于P,
由题知,,
∴,
∴坐垫C离地面高度约为,
故答案为:.
17.
【分析】本题主要考查了实数的运算,求特殊角三角函数值,先计算特殊角三角函数值,算术平方根,零指数幂和负整数指数幂,再去绝对值后计算加减法即可得到答案.
【详解】解;
.
18.
【分析】本题考查平行线的性质,解直角三角形的实际应用.延长交于点,在中,求出的长,在中,求出的长,利用求出的长即可.解题的关键是构造直角三角形.
【详解】解:延长交于点,则:,
∵,
∴
∵,
∴,
,
∴
在中,,
∴,
在中,,
∴.
答:信号塔的高为.
19.(1)见解析
(2)
【分析】本题考查了三角形相似的判定和性质,等腰三角形性质,角的平分线,熟练掌握相似的判定和性质是解题的关键.
(1)先证明,结合即可得证.
(2)根据,得到,结合,代入解答即可.
【详解】(1)证明:∵,
∴,
∵平分,
∴,
∴,
∵,
∴.
(2)解:∵,
∴.
∵,
∴.
∵,
∴.
解得.
20.(1)见详解
(2),见详解
(3)
【分析】本题主要考查了平行四边形的性质,垂直的性质,全等三角形的判定和性质,等腰直角三角形的性质,勾股定理等知识点,解题的关键是构造出辅助线,并熟练运用以上性质定理.
(1)利用平行四边形的性质,直角三角形的性质,垂直的性质即可求得结果;
(2)构造角平分线,利用平行四边形的性质和平行线的性质得出相关线段和角相等,证出,,进而可求得相等线段;
(3)构造辅助线,根据题目条件、平行四边形和等腰直角三角形的性质得出,设,表示出相关的线段长,利用勾股定理表示出和求出比值即可.
【详解】(1)证明:∵,,
∴,
∴,
中,,
∴,
∵,
∴,
∴.
(2)解:,理由如下:
如图,过点作平分,交于点,
中,,,
中,,,
∴,,
∵,
∴(ASA),
∴,,
∴,
∵,
∴,
∴,
∵,,
∴,
中,,
∴,
∵,
∴,
∴(ASA)
∴.
(3)解:
如图,过点作于点,
由(2)知,中,,,
∴,,
中,,
又∵,
∴,
∵,,
∴,,
设,则,,
∴中,,,
∵,
∴,
∴,
∴,
∴,
∴中,,
中,,
∴.
21.(1),
(2)或
(3)点坐标为
【分析】本题主要考查了反比例函数与一次函数的交点问题,熟知反比例函数及一次函数的图象与性质是解题的关键.
(1)将点坐标代入反比例函数解析式,求出,再将点坐标代入反比例函数解析式,求出点坐标,最后将,两点坐标代入一次函数解析式即可解决问题;
(2)利用反比例函数以及一次函数图象,即可解决问题;
(3)根据与的面积关系,可求出点的纵坐标,据此可解决问题.
【详解】(1)解:将代入得,
∴,
反比例函数的解析式为,
将代入得,,
点的坐标为.
将点和点的坐标代入得,,
解得,
一次函数的解析式为;
(2)解:根据所给函数图象可知,当或时,一次函数的图象在反比例函数图象的上方,即,
不等式的解集为:或.
(3)解:将代入得,,
点的坐标为,
,
.
将代入得,,
点的坐标为,
,
解得.
∵点在第三象限,
∴,
将代入得,,
点坐标为.
22.(1)见解析
(2)见解析
(3)
【分析】(1)由旋转的性质可得是等腰直角三角形,从而得出,,通过角度之间的转换得出,,即可得证;
(2)过点作交于点,即,证明和都是等腰直角三角形,得出,再证明,得出,即可得解;
(3)证明是等腰直角三角形,得出,,证明,求出,,,再证明,得出,即可得解.
【详解】(1)证明:线段是由旋转得到,
∴是等腰直角三角形,
,,
,
,
,
,
,
,,
,
,
;
(2)证明:过点作交于点,即,
,
,
,
,
和都是等腰直角三角形,
,
,
,
又,
,
,
;
(3)解:
,
是等腰直角三角形,
,
,,
由(2)问知:.
,,
,
,.
,
∵,
∴,
∴,
,
.
【点睛】本题考查了旋转的性质、等腰直角三角形的判定与性质、全等三角形的判定与性质、相似三角形的判定与性质等知识点,熟练掌握以上知识点并灵活运用,添加适当的辅助线是解此题的关键.
23.(1),
(2)或
(3)或或或
【分析】(1)待定系数法求出函数解析式即可;
(2)设直线与轴交于点,设,根据,列出方程进行求解即可;
(3)设直线的解析式为,把代入,得到,设,进而得到,,根据的面积为9,列出方程,根据直线上刚好存在三个不同的P点,得到有3个不相等的实数根,利用根与系数的关系进行求解即可.
【详解】(1)解:∵反比例函数与直线交于点,
∴,
∴,
∴,,
∴,解得:;
∴;
(2)设直线与轴交于点,设,
∵,
∴当时,,解得,
∴,
∴,
∵,
∴,即:,
∴,
∴或,
∴或;
(3)设直线的解析式为,把代入,得:,
∴,
∴,
设,
∵过P作交反比例图象于M,作轴交反比例函数图象于N,
∴到,,
∴,
∵的面积为9,
∴,
∴,
整理,得:,
设,则:,
∴;
①当时,,解得:或,
∴或,
即:或,
当时,,
∴有2个不相等的实数根,
∵直线上刚好存在三个不同的P点,
∴有2个相等的实数根,
∴,解得:或;
②当时,则:,解得:或,
∴或,
当时,;
当时,;
∵直线上刚好存在三个不同的P点,
∴或,
当时,解得:或;
当,无解;
综上:或或或.
【点睛】本题考查反比例函数与一次函数的交点问题,涉及待定系数法求函数解析式,分割法求面积,根与系数的关系等知识点,综合性强,计算量大,熟练掌握相关知识点,利用数形结合的思想进行求解,是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
