初二下学期期中测试(二次根式到平行四边形——含答案)
文档属性
| 名称 | 初二下学期期中测试(二次根式到平行四边形——含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 193.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-10 00:00:00 | ||
图片预览


文档简介
初二下学期期中测试(二次根式到平行四边形)
姓名: 得分:
一、填空题(每题4分,共52分)
1.已知是整数,则满足条件的最小整数n为 .
2.把根号外的因式移到根号内,得 .
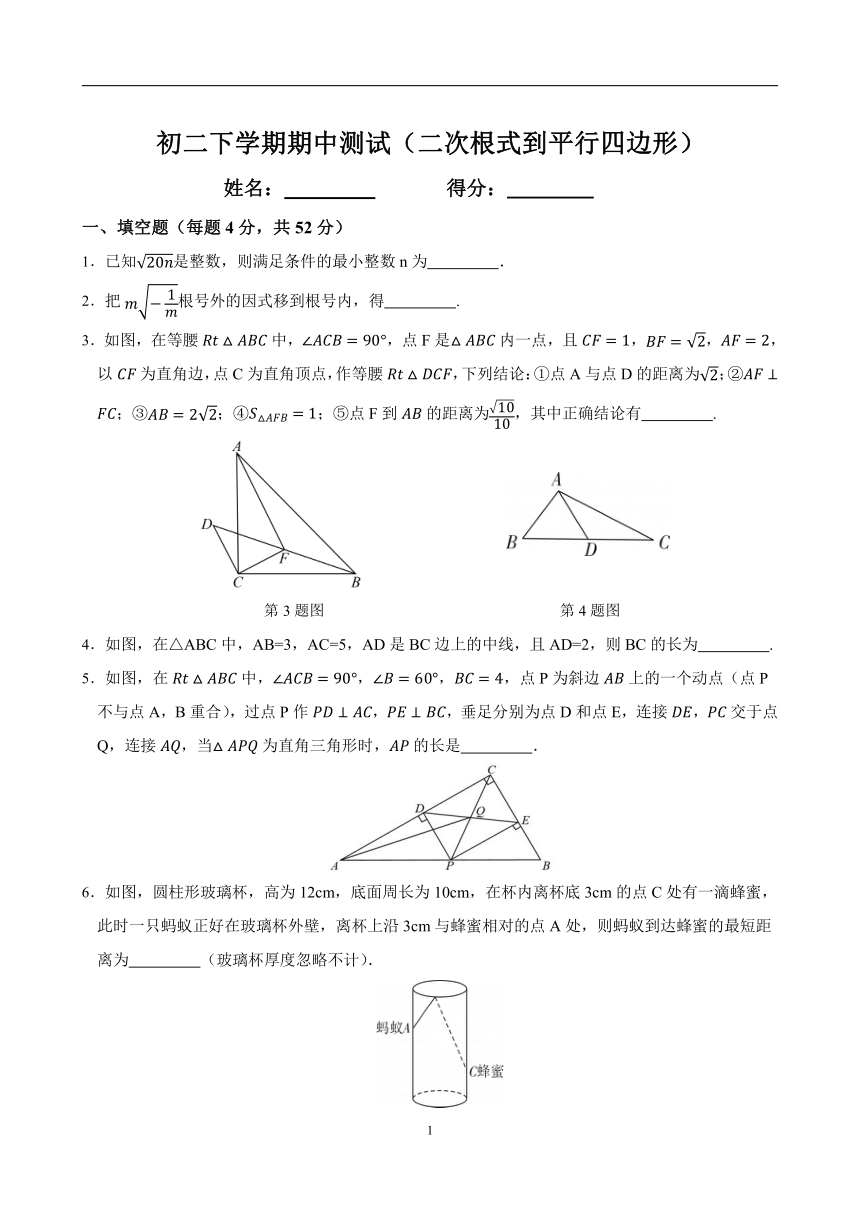
3.如图,在等腰中,,点F是内一点,且,,,以为直角边,点C为直角顶点,作等腰,下列结论:①点A与点D的距离为;②;③;④;⑤点F到的距离为,其中正确结论有 .
第3题图 第4题图
4.如图,在△ABC中,AB=3,AC=5,AD是BC边上的中线,且AD=2,则BC的长为 .
5.如图,在中,,,,点P为斜边上的一个动点(点P不与点A,B重合),过点P作,,垂足分别为点D和点E,连接,交于点Q,连接,当为直角三角形时,的长是 .
6.如图,圆柱形玻璃杯,高为12cm,底面周长为10cm,在杯内离杯底3cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在玻璃杯外壁,离杯上沿3cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为 (玻璃杯厚度忽略不计).
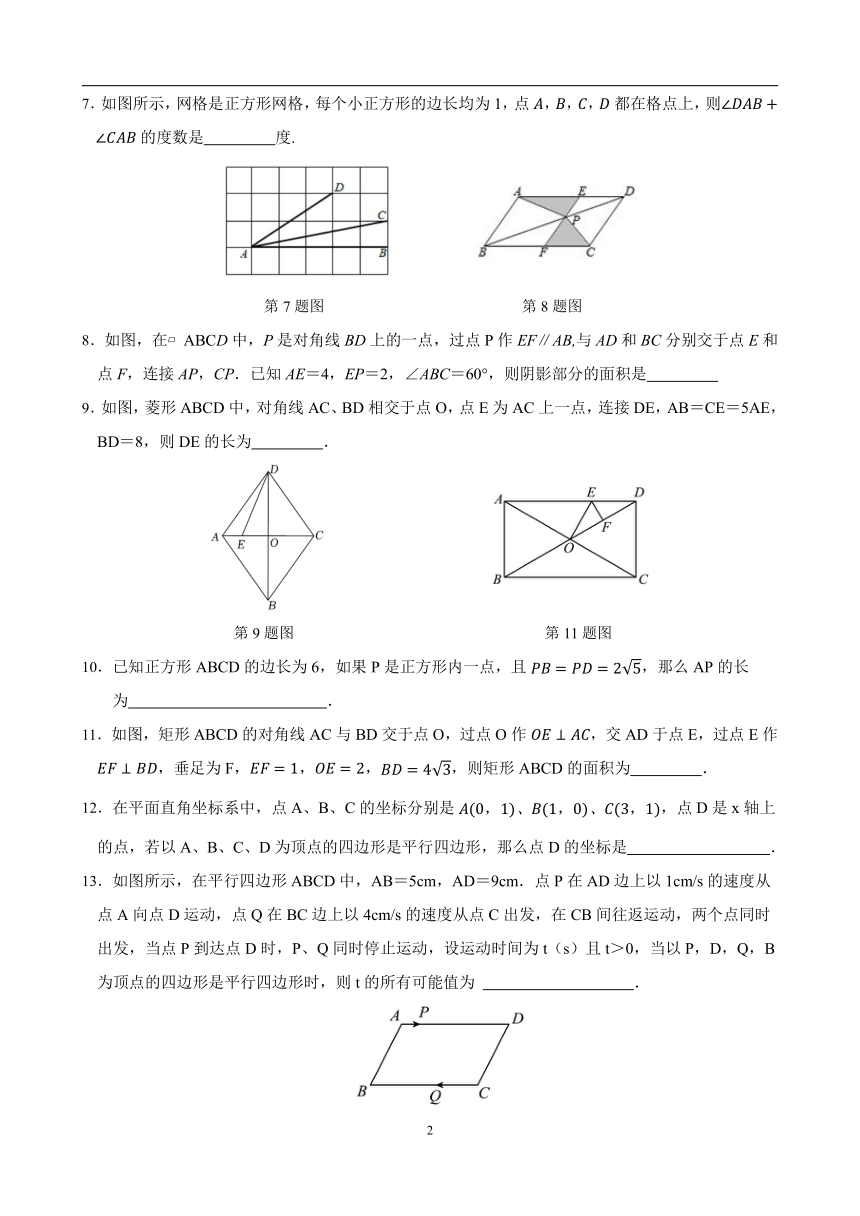
7.如图所示,网格是正方形网格,每个小正方形的边长均为1,点,,,都在格点上,则的度数是 度.
第7题图 第8题图
8.如图,在 ABCD中,P是对角线BD上的一点,过点P作EF∥AB,与AD和BC分别交于点E和点F,连接AP,CP.已知AE=4,EP=2,∠ABC=60°,则阴影部分的面积是
9.如图,菱形ABCD中,对角线AC、BD相交于点O,点E为AC上一点,连接DE,AB=CE=5AE,BD=8,则DE的长为 .
第9题图 第11题图
10.已知正方形ABCD的边长为6,如果P是正方形内一点,且,那么AP的长为 .
11.如图,矩形ABCD的对角线AC与BD交于点O,过点O作,交AD于点E,过点E作,垂足为F,,,,则矩形ABCD的面积为 .
12.在平面直角坐标系中,点A、B、C的坐标分别是,点D是x轴上的点,若以A、B、C、D为顶点的四边形是平行四边形,那么点D的坐标是 .
13.如图所示,在平行四边形ABCD中,AB=5cm,AD=9cm.点P在AD边上以1cm/s的速度从点A向点D运动,点Q在BC边上以4cm/s的速度从点C出发,在CB间往返运动,两个点同时出发,当点P到达点D时,P、Q同时停止运动,设运动时间为t(s)且t>0,当以P,D,Q,B为顶点的四边形是平行四边形时,则t的所有可能值为 .
二、计算题(17分)
14.计算:(每题4分,共12分)
(1) (2)(23)2 (3)
15.(5分)已知,,求代数式的值.
三、解答题
16.(9分)如图所示,在△ABC中,AB=5,BC=4,AC=3,点I为Rt△ABC三条角平分线的交点,则点I到边AB的距离是多少?
17.(11分)如图,已知正方形ABCD的边长为3,E、F分别是AB、BC边上的点,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM.若AE=1,求FM的长.
18.(11分)如图,菱形ABCD中,分别延长DC,BC至点E,F,使CE=CD,CF=CB,联结DB,BE,EF,FD.
(1)求证:四边形DBEF是矩形;
(2)如果∠A=60°,菱形ABCD的面积为,求DF的长.
答案解析部分
1.【答案】0
2.【答案】
3.【答案】①②④
4.【答案】
5.【答案】6或
6.【答案】13cm
7.【答案】45
8.【答案】
9.【答案】2
10.【答案】或或或
11.【答案】
12.【答案】(4,0)或( 2,0)
13.【答案】或 6或
14.【答案】(1)解:原式= ;
(2)解:原式= ;
(3)解:原式= .
15.【答案】解:∵,,
∴,,
∴,,
∴.
16.【答案】解:连接AI,BI,CI,过点I作IE⊥AC于E,IF⊥AB于F,ID⊥BC于D,
在△ABC中,
∵BC=4,CA=3,AB=5,
∴ AC2+ BC2=32+42=52=AB2 ,
∴ △ABC是直角三角形,∠C= 90°.
∵点I为△ABC的三条角平分线的交点,
∴ IE=IF= ID.
设IE=x,因为S△ABC=S△IAB十S△IAC+ S△ICB,
∴ ×4×3= IF×5+ IE×3+ ID×4,
∴ 5x+3x+4x= 12,解得x=1,
∴ 点I到AB的距离等于1.
17.【答案】解:∵ DAE逆时针旋转90°得到 DCE,
∴∠FCM=∠FCD+∠DCM=180°,
∴F、C、M三点共线,
∴DE=DM,∠EDM=90°,
∴∠EDF+∠FDM=90°,
∵∠EDF=45°,
∴∠FDM=∠EDF=45°,
在 DEF和 DMF中,
∴ DEF≌ DMF(SAS),
∴EF=MF,
设EF=MF=x,
∵AE=CM=1,且BC=3,
∴BM=BC+CM=4,
∴BF=BM-MF=BM-EF=4-x,
∵EB=AB-AE=3-1=2,
在Rt EBF中
即
解得x= ,
∴FM=
18.【答案】(1)证明:∵CE=CD,CF=CB,
∴四边形DBEF是平行四边形.
∵四边形ABCD是菱形,
∴CD=CB.
∴CE=CF,
∴BF=DE,
∴四边形DBEF是矩形.
(2)解:设DB为2a,
∵∠A=60°,菱形ABCD的面积为,
∴可得,
解得:a=2,∴DB=4,
∵∠DBC=60°,
∴DF=.
姓名: 得分:
一、填空题(每题4分,共52分)
1.已知是整数,则满足条件的最小整数n为 .
2.把根号外的因式移到根号内,得 .
3.如图,在等腰中,,点F是内一点,且,,,以为直角边,点C为直角顶点,作等腰,下列结论:①点A与点D的距离为;②;③;④;⑤点F到的距离为,其中正确结论有 .
第3题图 第4题图
4.如图,在△ABC中,AB=3,AC=5,AD是BC边上的中线,且AD=2,则BC的长为 .
5.如图,在中,,,,点P为斜边上的一个动点(点P不与点A,B重合),过点P作,,垂足分别为点D和点E,连接,交于点Q,连接,当为直角三角形时,的长是 .
6.如图,圆柱形玻璃杯,高为12cm,底面周长为10cm,在杯内离杯底3cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在玻璃杯外壁,离杯上沿3cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为 (玻璃杯厚度忽略不计).
7.如图所示,网格是正方形网格,每个小正方形的边长均为1,点,,,都在格点上,则的度数是 度.
第7题图 第8题图
8.如图,在 ABCD中,P是对角线BD上的一点,过点P作EF∥AB,与AD和BC分别交于点E和点F,连接AP,CP.已知AE=4,EP=2,∠ABC=60°,则阴影部分的面积是
9.如图,菱形ABCD中,对角线AC、BD相交于点O,点E为AC上一点,连接DE,AB=CE=5AE,BD=8,则DE的长为 .
第9题图 第11题图
10.已知正方形ABCD的边长为6,如果P是正方形内一点,且,那么AP的长为 .
11.如图,矩形ABCD的对角线AC与BD交于点O,过点O作,交AD于点E,过点E作,垂足为F,,,,则矩形ABCD的面积为 .
12.在平面直角坐标系中,点A、B、C的坐标分别是,点D是x轴上的点,若以A、B、C、D为顶点的四边形是平行四边形,那么点D的坐标是 .
13.如图所示,在平行四边形ABCD中,AB=5cm,AD=9cm.点P在AD边上以1cm/s的速度从点A向点D运动,点Q在BC边上以4cm/s的速度从点C出发,在CB间往返运动,两个点同时出发,当点P到达点D时,P、Q同时停止运动,设运动时间为t(s)且t>0,当以P,D,Q,B为顶点的四边形是平行四边形时,则t的所有可能值为 .
二、计算题(17分)
14.计算:(每题4分,共12分)
(1) (2)(23)2 (3)
15.(5分)已知,,求代数式的值.
三、解答题
16.(9分)如图所示,在△ABC中,AB=5,BC=4,AC=3,点I为Rt△ABC三条角平分线的交点,则点I到边AB的距离是多少?
17.(11分)如图,已知正方形ABCD的边长为3,E、F分别是AB、BC边上的点,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM.若AE=1,求FM的长.
18.(11分)如图,菱形ABCD中,分别延长DC,BC至点E,F,使CE=CD,CF=CB,联结DB,BE,EF,FD.
(1)求证:四边形DBEF是矩形;
(2)如果∠A=60°,菱形ABCD的面积为,求DF的长.
答案解析部分
1.【答案】0
2.【答案】
3.【答案】①②④
4.【答案】
5.【答案】6或
6.【答案】13cm
7.【答案】45
8.【答案】
9.【答案】2
10.【答案】或或或
11.【答案】
12.【答案】(4,0)或( 2,0)
13.【答案】或 6或
14.【答案】(1)解:原式= ;
(2)解:原式= ;
(3)解:原式= .
15.【答案】解:∵,,
∴,,
∴,,
∴.
16.【答案】解:连接AI,BI,CI,过点I作IE⊥AC于E,IF⊥AB于F,ID⊥BC于D,
在△ABC中,
∵BC=4,CA=3,AB=5,
∴ AC2+ BC2=32+42=52=AB2 ,
∴ △ABC是直角三角形,∠C= 90°.
∵点I为△ABC的三条角平分线的交点,
∴ IE=IF= ID.
设IE=x,因为S△ABC=S△IAB十S△IAC+ S△ICB,
∴ ×4×3= IF×5+ IE×3+ ID×4,
∴ 5x+3x+4x= 12,解得x=1,
∴ 点I到AB的距离等于1.
17.【答案】解:∵ DAE逆时针旋转90°得到 DCE,
∴∠FCM=∠FCD+∠DCM=180°,
∴F、C、M三点共线,
∴DE=DM,∠EDM=90°,
∴∠EDF+∠FDM=90°,
∵∠EDF=45°,
∴∠FDM=∠EDF=45°,
在 DEF和 DMF中,
∴ DEF≌ DMF(SAS),
∴EF=MF,
设EF=MF=x,
∵AE=CM=1,且BC=3,
∴BM=BC+CM=4,
∴BF=BM-MF=BM-EF=4-x,
∵EB=AB-AE=3-1=2,
在Rt EBF中
即
解得x= ,
∴FM=
18.【答案】(1)证明:∵CE=CD,CF=CB,
∴四边形DBEF是平行四边形.
∵四边形ABCD是菱形,
∴CD=CB.
∴CE=CF,
∴BF=DE,
∴四边形DBEF是矩形.
(2)解:设DB为2a,
∵∠A=60°,菱形ABCD的面积为,
∴可得,
解得:a=2,∴DB=4,
∵∠DBC=60°,
∴DF=.
同课章节目录
