期中模拟卷《二次根式到一次函数》(含答案)
文档属性
| 名称 | 期中模拟卷《二次根式到一次函数》(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 273.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-10 17:57:05 | ||
图片预览


文档简介
期中模拟卷
一、单选题
1.已知函数的图象如图所示,则函数的图象大致是( )
A. B. C. D.
2.一列火车从A站行驶3公里到B处以后,以每小时90公里的速度前进.则离开B处t小时后,火车离A站的路程s与时间t的关系是( )
A.s=3+90t B.s=90t C.s=3t D.s=90+3t
3.如图,在中,,D是中点,分别以,为边向外作正方形和正方形,连接,.若,则阴影部分的面积是( )
A.12 B.9 C. D.6
4.下列说法不正确的是( )
A.有一个角是直角的菱形是正方形 B.四条边都相等的四边形是正方形
C.对角线互相垂直的矩形是正方形 D.两条对角线相等的菱形是正方形
5.如果一个正方形的周长为(其中,),则该正方形的面积为( )
A. B. C. D.
6.已知一次函数y=kx﹣b,y随着x的增大而增大,且kb<0,则它的大致图象是( )
A. B. C. D.
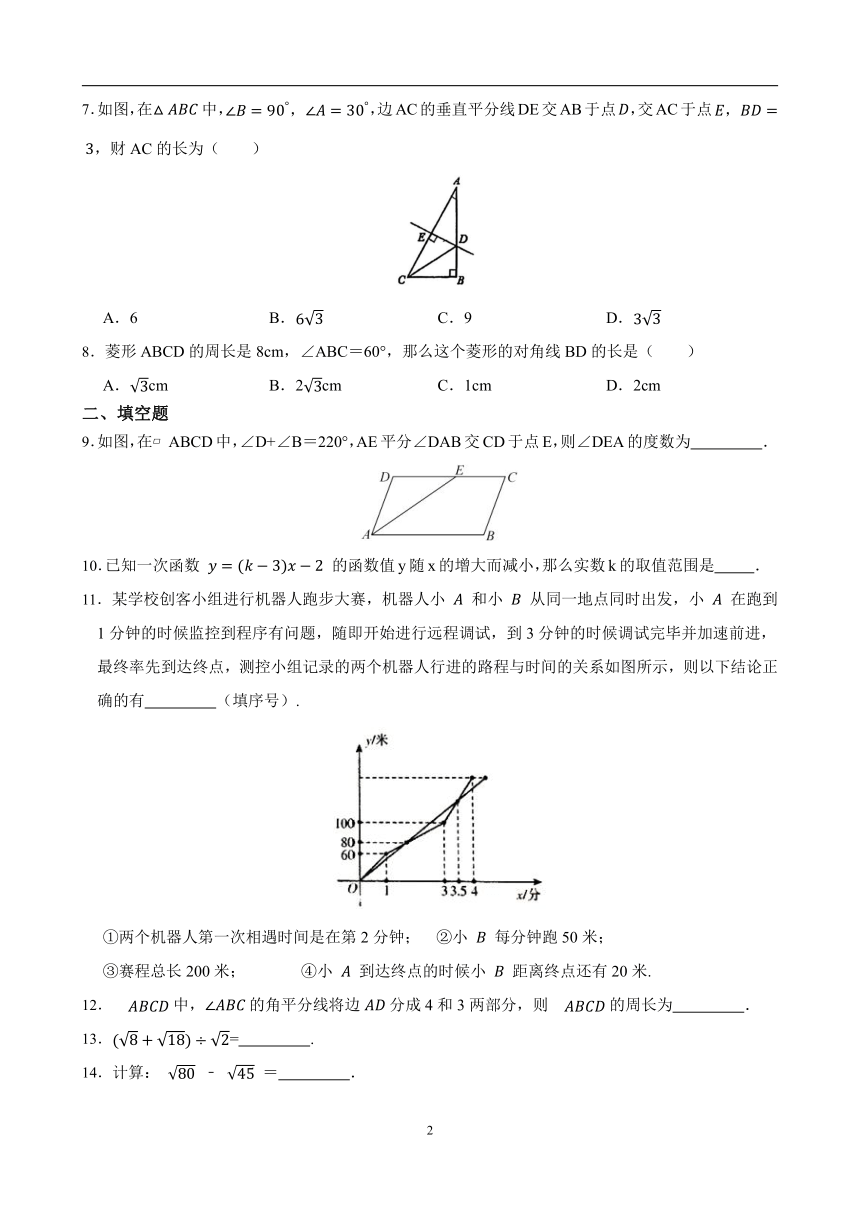
7.如图,在中,,边AC的垂直平分线DE交AB于点,交AC于点,财AC的长为( )
A.6 B. C.9 D.
8.菱形ABCD的周长是8cm,∠ABC=60°,那么这个菱形的对角线BD的长是( )
A.cm B.2cm C.1cm D.2cm
二、填空题
9.如图,在 ABCD中,∠D+∠B=220°,AE平分∠DAB交CD于点E,则∠DEA的度数为 .
10.已知一次函数 的函数值y随x的增大而减小,那么实数k的取值范围是 .
11.某学校创客小组进行机器人跑步大赛,机器人小 和小 从同一地点同时出发,小 在跑到1分钟的时候监控到程序有问题,随即开始进行远程调试,到3分钟的时候调试完毕并加速前进,最终率先到达终点,测控小组记录的两个机器人行进的路程与时间的关系如图所示,则以下结论正确的有 (填序号).
①两个机器人第一次相遇时间是在第2分钟; ②小 每分钟跑50米;
③赛程总长200米; ④小 到达终点的时候小 距离终点还有20米.
12.中,的角平分线将边分成4和3两部分,则的周长为 .
13.= .
14.计算: ﹣ = .
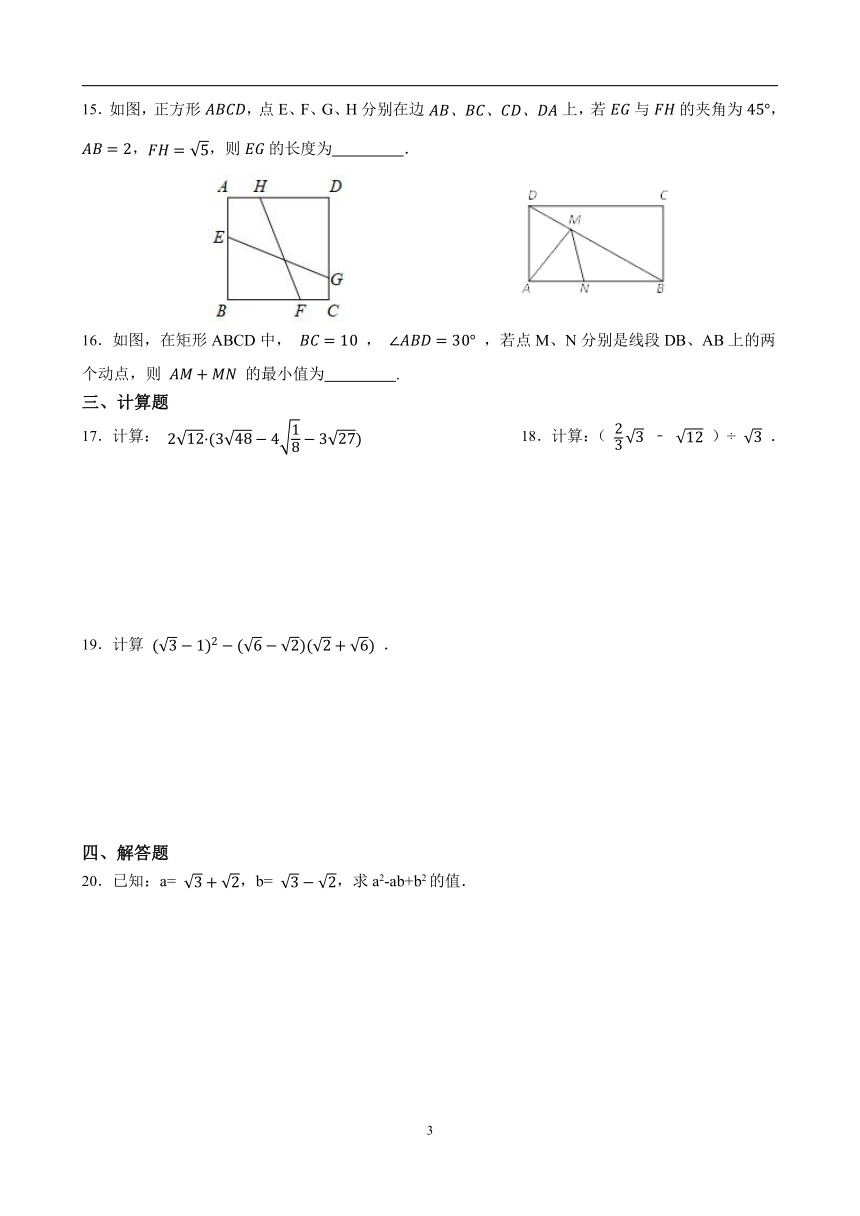
15.如图,正方形,点E、F、G、H分别在边上,若与的夹角为,,,则的长度为 .
16.如图,在矩形ABCD中, , ,若点M、N分别是线段DB、AB上的两个动点,则 的最小值为 .
三、计算题
17.计算: 18.计算:( ﹣ )÷ .
19.计算 .
四、解答题
20.已知:a= ,b= ,求a2-ab+b2的值.
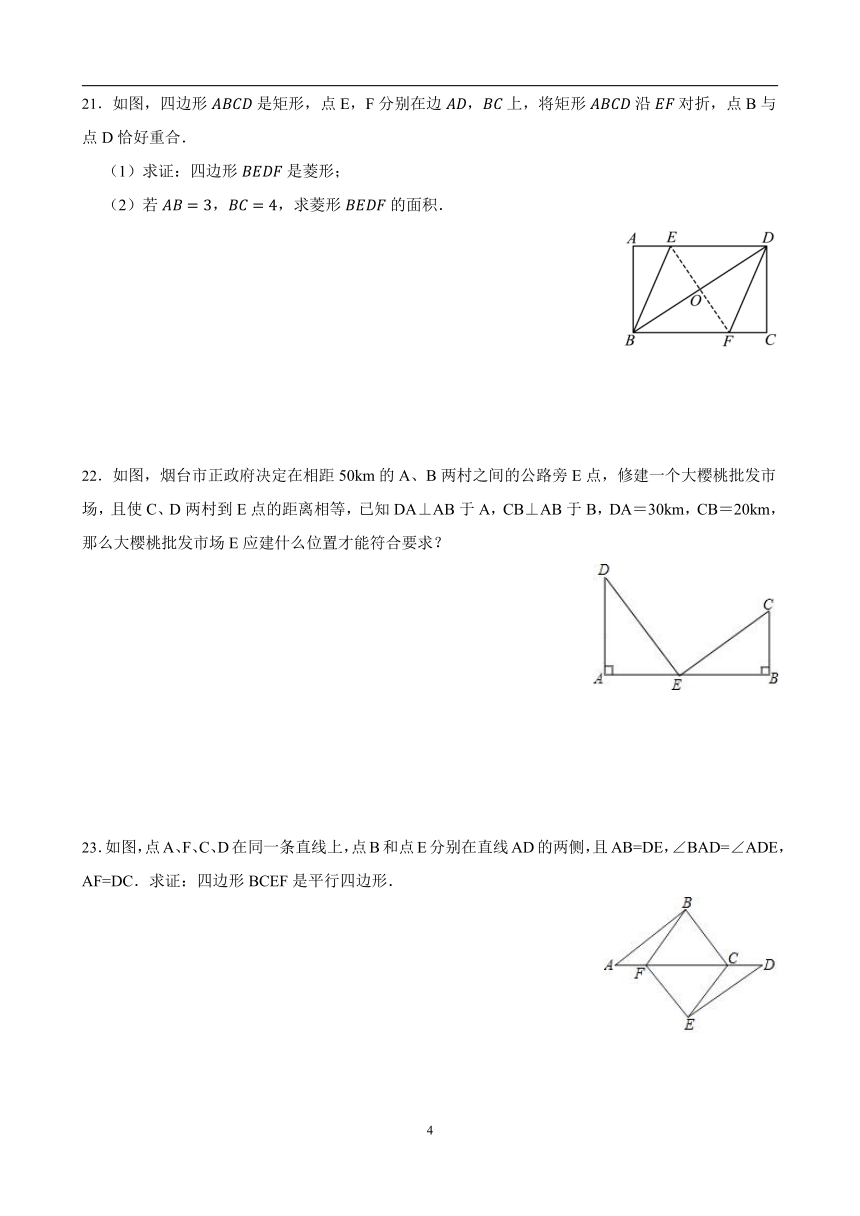
21.如图,四边形是矩形,点E,F分别在边,上,将矩形沿对折,点B与点D恰好重合.
(1)求证:四边形是菱形;
(2)若,,求菱形的面积.
22.如图,烟台市正政府决定在相距50km的A、B两村之间的公路旁E点,修建一个大樱桃批发市场,且使C、D两村到E点的距离相等,已知DA⊥AB于A,CB⊥AB于B,DA=30km,CB=20km,那么大樱桃批发市场E应建什么位置才能符合要求?
23.如图,点A、F、C、D在同一条直线上,点B和点E分别在直线AD的两侧,且AB=DE,∠BAD=∠ADE,AF=DC.求证:四边形BCEF是平行四边形.
24. 如图,直线与轴交于点,与轴交于点,直线与轴交于点,与轴交于点,与直线交于点,.
(1)求直线的解析式;
(2)直线上是否存在点,使得?若存在,求出点的坐标,若不存在,请说明理由.
25.某社区采购春节慰问礼品,购买了甲、乙两种类型的粮油套装.甲种粮油套装单价比乙种粮油套装单价多元,用元购买甲种粮油套装和用元购买乙种粮油套装的数量相同.
(1)求甲、乙两种粮油套装的单价分别是多少元?
(2)社区准备再次购买甲种和乙种粮油套装共件,购买乙种粮油套装不超过甲种粮油套装的倍,且商家给出了两种粮油套装均打八折的优惠.问购买甲种和乙种粮油套装各多少件时花费最少?最少花费是多少元?
26.如图,在矩形ABCD中,AB=4cm,AD=12cm.点P在边 AD 上以每秒1cm的速度从点 A 向点D运动,点Q在边BC 上以每秒4cm的速度从点C出发,在CB间往返运动,两点同时出发,当点P到达点 D 时停止,求经过多长时间,四边形ABQP为矩形
答案解析部分
1.【答案】D
2.【答案】A
3.【答案】B
4.【答案】B
5.【答案】A
6.【答案】D
7.【答案】B
8.【答案】B
9.【答案】35°
10.【答案】
11.【答案】①④
12.【答案】20或22
13.【答案】5
14.【答案】
15.【答案】
16.【答案】15
17.【答案】解:原式= ,
= ,
= .
18.【答案】解:原式=( ﹣2 )÷
=﹣ ÷
=﹣ .
19.【答案】解:
=
=
=
20.【答案】解:a2-ab+b2=(a+b)2-3ab
∵a+b=,ab=1,
∴原式=(a+b)2-3ab=()2-3×1=9
21.【答案】(1)证明:四边形是矩形,
,
,
将矩形沿对折,点B与点D恰好重合,
,,,
,
,
,
四边形是菱形
(2)解:四边形是矩形,
,,
设菱形边长是x,则,
在中,,
,
解得,
,
菱形的面积是,
答:菱形的面积为.
22.【答案】解:设大樱桃批发市场E应建在离A站x千米的地方,则千米.
在直角中,根据勾股定理得:,
∴,
在直角中,根据勾股定理得:,
∴.
又∵C、D两村到E点的距离相等,
∴,
∴,
所以,
解得.
∴大樱桃批发市场E应建在离A站20千米的地方.
23.【答案】证明:在△AFB和△DCE中,
,
∴△AFB≌△DCE(SAS),
∴FB=CE,∠AFB=∠DCE,
∴∠BFC=∠ECF,
∴FB∥CE,
即FB CE,
∴四边形BCEF是平行四边形
24.【答案】(1)解:直线与轴交于点,与轴交于点,
,,
,
,
,
设直线的解析式为,
把、的坐标代入得,
解得,
直线的解析式为;
(2)解:存在,
令,则,
解得,
,
,
,
,
,
,. ,
,
,
设,
当在的下方时,,
,
此时;
当在的上方时,,
,
此时;
综上,点的坐标为或.
25.【答案】(1)解:设乙种粮油套装的单价为元,则甲种粮油套装的单价为元,
由题意可得,,
解得,
经检验,是原方程的解,符合题意,
∴,
答:甲种粮油套装的单价为元,乙种粮油套装的单价为元
(2)解:设购买了甲种粮油套装件,则乙种粮油套装件,费用为元,
则,
∵购买乙种粮油套装不超过甲种粮油套装的倍,
∴,
解得,
∴当时,即购买甲种粮油套装件,乙种粮油套装件,花费最少,
此时,元.
26.【答案】解:四边形ABCD为矩形, AD=12cm,
∴AD=BC= 12cm,AD//BC,∠A=90°,
∴当 AP= BQ时,四边形ABQP是矩形.
点P从点A到达点D所需时间:12÷1=12(秒),点Q从点C到达点B所需时间:12÷4=3(秒),
t秒时AP=t.
①当0∴t=12-4t,
解得:;
②当3≤t<6时,BQ=4t-12,
t=4t-12,
解得:t=4;
③当6≤t<9时,BQ=36-4t,
∴t=36-4t,
解得:;
④当9≤t≤12时,BQ=4t-36,
t=4t-36,
解得:t=12.
综上所述,当t为s或4s或s或12s时,四边形A BQP为矩形.
一、单选题
1.已知函数的图象如图所示,则函数的图象大致是( )
A. B. C. D.
2.一列火车从A站行驶3公里到B处以后,以每小时90公里的速度前进.则离开B处t小时后,火车离A站的路程s与时间t的关系是( )
A.s=3+90t B.s=90t C.s=3t D.s=90+3t
3.如图,在中,,D是中点,分别以,为边向外作正方形和正方形,连接,.若,则阴影部分的面积是( )
A.12 B.9 C. D.6
4.下列说法不正确的是( )
A.有一个角是直角的菱形是正方形 B.四条边都相等的四边形是正方形
C.对角线互相垂直的矩形是正方形 D.两条对角线相等的菱形是正方形
5.如果一个正方形的周长为(其中,),则该正方形的面积为( )
A. B. C. D.
6.已知一次函数y=kx﹣b,y随着x的增大而增大,且kb<0,则它的大致图象是( )
A. B. C. D.
7.如图,在中,,边AC的垂直平分线DE交AB于点,交AC于点,财AC的长为( )
A.6 B. C.9 D.
8.菱形ABCD的周长是8cm,∠ABC=60°,那么这个菱形的对角线BD的长是( )
A.cm B.2cm C.1cm D.2cm
二、填空题
9.如图,在 ABCD中,∠D+∠B=220°,AE平分∠DAB交CD于点E,则∠DEA的度数为 .
10.已知一次函数 的函数值y随x的增大而减小,那么实数k的取值范围是 .
11.某学校创客小组进行机器人跑步大赛,机器人小 和小 从同一地点同时出发,小 在跑到1分钟的时候监控到程序有问题,随即开始进行远程调试,到3分钟的时候调试完毕并加速前进,最终率先到达终点,测控小组记录的两个机器人行进的路程与时间的关系如图所示,则以下结论正确的有 (填序号).
①两个机器人第一次相遇时间是在第2分钟; ②小 每分钟跑50米;
③赛程总长200米; ④小 到达终点的时候小 距离终点还有20米.
12.中,的角平分线将边分成4和3两部分,则的周长为 .
13.= .
14.计算: ﹣ = .
15.如图,正方形,点E、F、G、H分别在边上,若与的夹角为,,,则的长度为 .
16.如图,在矩形ABCD中, , ,若点M、N分别是线段DB、AB上的两个动点,则 的最小值为 .
三、计算题
17.计算: 18.计算:( ﹣ )÷ .
19.计算 .
四、解答题
20.已知:a= ,b= ,求a2-ab+b2的值.
21.如图,四边形是矩形,点E,F分别在边,上,将矩形沿对折,点B与点D恰好重合.
(1)求证:四边形是菱形;
(2)若,,求菱形的面积.
22.如图,烟台市正政府决定在相距50km的A、B两村之间的公路旁E点,修建一个大樱桃批发市场,且使C、D两村到E点的距离相等,已知DA⊥AB于A,CB⊥AB于B,DA=30km,CB=20km,那么大樱桃批发市场E应建什么位置才能符合要求?
23.如图,点A、F、C、D在同一条直线上,点B和点E分别在直线AD的两侧,且AB=DE,∠BAD=∠ADE,AF=DC.求证:四边形BCEF是平行四边形.
24. 如图,直线与轴交于点,与轴交于点,直线与轴交于点,与轴交于点,与直线交于点,.
(1)求直线的解析式;
(2)直线上是否存在点,使得?若存在,求出点的坐标,若不存在,请说明理由.
25.某社区采购春节慰问礼品,购买了甲、乙两种类型的粮油套装.甲种粮油套装单价比乙种粮油套装单价多元,用元购买甲种粮油套装和用元购买乙种粮油套装的数量相同.
(1)求甲、乙两种粮油套装的单价分别是多少元?
(2)社区准备再次购买甲种和乙种粮油套装共件,购买乙种粮油套装不超过甲种粮油套装的倍,且商家给出了两种粮油套装均打八折的优惠.问购买甲种和乙种粮油套装各多少件时花费最少?最少花费是多少元?
26.如图,在矩形ABCD中,AB=4cm,AD=12cm.点P在边 AD 上以每秒1cm的速度从点 A 向点D运动,点Q在边BC 上以每秒4cm的速度从点C出发,在CB间往返运动,两点同时出发,当点P到达点 D 时停止,求经过多长时间,四边形ABQP为矩形
答案解析部分
1.【答案】D
2.【答案】A
3.【答案】B
4.【答案】B
5.【答案】A
6.【答案】D
7.【答案】B
8.【答案】B
9.【答案】35°
10.【答案】
11.【答案】①④
12.【答案】20或22
13.【答案】5
14.【答案】
15.【答案】
16.【答案】15
17.【答案】解:原式= ,
= ,
= .
18.【答案】解:原式=( ﹣2 )÷
=﹣ ÷
=﹣ .
19.【答案】解:
=
=
=
20.【答案】解:a2-ab+b2=(a+b)2-3ab
∵a+b=,ab=1,
∴原式=(a+b)2-3ab=()2-3×1=9
21.【答案】(1)证明:四边形是矩形,
,
,
将矩形沿对折,点B与点D恰好重合,
,,,
,
,
,
四边形是菱形
(2)解:四边形是矩形,
,,
设菱形边长是x,则,
在中,,
,
解得,
,
菱形的面积是,
答:菱形的面积为.
22.【答案】解:设大樱桃批发市场E应建在离A站x千米的地方,则千米.
在直角中,根据勾股定理得:,
∴,
在直角中,根据勾股定理得:,
∴.
又∵C、D两村到E点的距离相等,
∴,
∴,
所以,
解得.
∴大樱桃批发市场E应建在离A站20千米的地方.
23.【答案】证明:在△AFB和△DCE中,
,
∴△AFB≌△DCE(SAS),
∴FB=CE,∠AFB=∠DCE,
∴∠BFC=∠ECF,
∴FB∥CE,
即FB CE,
∴四边形BCEF是平行四边形
24.【答案】(1)解:直线与轴交于点,与轴交于点,
,,
,
,
,
设直线的解析式为,
把、的坐标代入得,
解得,
直线的解析式为;
(2)解:存在,
令,则,
解得,
,
,
,
,
,
,. ,
,
,
设,
当在的下方时,,
,
此时;
当在的上方时,,
,
此时;
综上,点的坐标为或.
25.【答案】(1)解:设乙种粮油套装的单价为元,则甲种粮油套装的单价为元,
由题意可得,,
解得,
经检验,是原方程的解,符合题意,
∴,
答:甲种粮油套装的单价为元,乙种粮油套装的单价为元
(2)解:设购买了甲种粮油套装件,则乙种粮油套装件,费用为元,
则,
∵购买乙种粮油套装不超过甲种粮油套装的倍,
∴,
解得,
∴当时,即购买甲种粮油套装件,乙种粮油套装件,花费最少,
此时,元.
26.【答案】解:四边形ABCD为矩形, AD=12cm,
∴AD=BC= 12cm,AD//BC,∠A=90°,
∴当 AP= BQ时,四边形ABQP是矩形.
点P从点A到达点D所需时间:12÷1=12(秒),点Q从点C到达点B所需时间:12÷4=3(秒),
t秒时AP=t.
①当0
解得:;
②当3≤t<6时,BQ=4t-12,
t=4t-12,
解得:t=4;
③当6≤t<9时,BQ=36-4t,
∴t=36-4t,
解得:;
④当9≤t≤12时,BQ=4t-36,
t=4t-36,
解得:t=12.
综上所述,当t为s或4s或s或12s时,四边形A BQP为矩形.
同课章节目录
