人教版物理选修1-1第三章第二节法拉第电磁感应定律同步训练
文档属性
| 名称 | 人教版物理选修1-1第三章第二节法拉第电磁感应定律同步训练 |
|
|
| 格式 | doc | ||
| 文件大小 | 360.5KB | ||
| 资源类型 | 素材 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2016-05-25 00:00:00 | ||
图片预览


文档简介
登陆21世纪教育 助您教考全无忧
人教版物理选修1-1第三章
第二节法拉第电磁感应定律同步训练
一.选择题(共15小题)
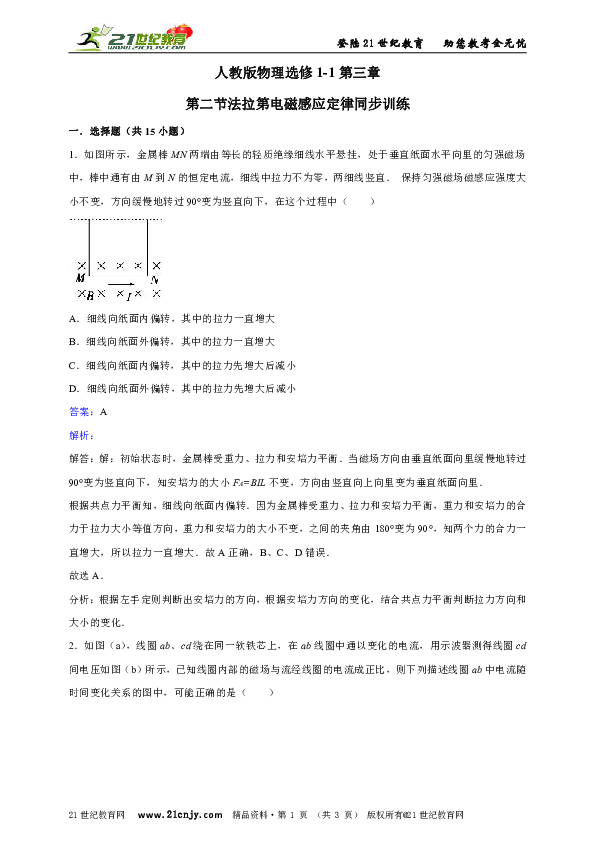
1.如图所示,金属棒MN两端由等长的轻质绝缘细线水平悬挂,处于垂直纸面水平向里的匀强磁场中,棒中通有由M到N的恒定电流,细线中拉力不为零,两细线竖直. 保持匀强磁场磁感应强度大小不变,方向缓慢地转过90°变为竖直向下,在这个过程中( )
A.细线向纸面内偏转,其中的拉力一直增大
B.细线向纸面外偏转,其中的拉力一直增大
C.细线向纸面内偏转,其中的拉力先增大后减小
D.细线向纸面外偏转,其中的拉力先增大后减小
答案:A
解析:
解答:解:初始状态时,金属棒受重力、拉力和安培力平衡.当磁场方向由垂直纸面向里缓慢地转过90°变为竖直向下,知安培力的大小FA=BIL不变,方向由竖直向上向里变为垂直纸面向里.
根据共点力平衡知,细线向纸面内偏转.因为金属棒受重力、拉力和安培力平衡,重力和安培力的合力于拉力大小等值方向,重力和安培力的大小不变,之间的夹角由180°变为90°,知两个力的合力一直增大,所以拉力一直增大.故A正确,B、C、D错误.
故选A.
分析:根据左手定则判断出安培力的方向,根据安培力方向的变化,结合共点力平衡判断拉力方向和大小的变化.
2.如图(a),线圈ab、cd绕在同一软铁芯上,在ab线圈中通以变化的电流,用示波器测得线圈cd间电压如图(b)所示,已知线圈内部的磁场与流经线圈的电流成正比,则下列描述线圈ab中电流随时间变化关系的图中,可能正确的是( )
A. B.
C. D.
答案:
解析:
解答:解:因为线圈cd中每个时间段内电流大小不变化,则每个时间段内产生的感应电动势不变;
根据法拉第电磁感应定律得:E=NS,
电流为:I= ,
则线圈ab中每个时间段内电流的磁场均匀变化.正确反应这一关系的图象只有C.故C正确,A、B、D错误.
故选:C.
分析:线圈cd与示波器连接,在每个时间段内电流不随时间变化,则根据法拉第电磁感应定律,产生感应电流的磁场均匀变化,由此判断线圈ab电流的变化.
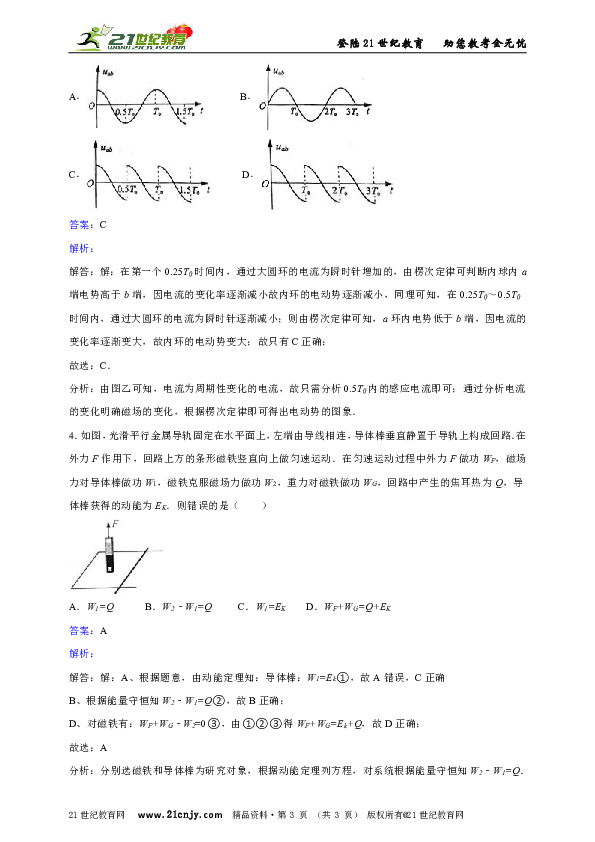
3.如图甲,R0为定值电阻,两金属圆环固定在同一绝缘平面内.左端连接在一周期为T0的正弦交流电源上,经二极管整流后,通过R0的电流i始终向左,其大小按图乙所示规律变化.规定内圆环a端电势高于b端时,a、b间的电压uab为正,下列uab﹣t图象可能正确的是( )
A. B.
C. D.
答案:C
解析:
解答:解:在第一个0.25T0时间内,通过大圆环的电流为瞬时针增加的,由楞次定律可判断内球内a端电势高于b端,因电流的变化率逐渐减小故内环的电动势逐渐减小,同理可知,在0.25T0~0.5T0时间内,通过大圆环的电流为瞬时针逐渐减小;则由楞次定律可知,a环内电势低于b端,因电流的变化率逐渐变大,故内环的电动势变大;故只有C正确;
故选:C.
分析:由图乙可知,电流为周期性变化的电流,故只需分析0.5T0内的感应电流即可;通过分析电流的变化明确磁场的变化,根据楞次定律即可得出电动势的图象.
4.如图,光滑平行金属导轨固定在水平面上,左端由导线相连,导体棒垂直静置于导轨上构成回路.在外力F作用下,回路上方的条形磁铁竖直向上做匀速运动.在匀速运动过程中外力F做功WF,磁场力对导体棒做功W1,磁铁克服磁场力做功W2,重力对磁铁做功WG,回路中产生的焦耳热为Q,导体棒获得的动能为EK.则错误的是( )
A.W1=Q B.W2﹣W1=Q C.W1=EK D.WF+WG=Q+EK
答案:A
解析:
解答:解:A、根据题意,由动能定理知:导体棒:W1=Ek①,故A错误,C正确
B、根据能量守恒知W2﹣W1=Q②,故B正确;
D、对磁铁有:WF+WG﹣W2=0③,由①②③得WF+WG=Ek+Q,故D正确;
故选:A
分析:分别选磁铁和导体棒为研究对象,根据动能定理列方程,对系统根据能量守恒知W2﹣W1=Q.
5.把一条形磁铁插入同一个闭合线圈中,第一次是迅速的,第二次是缓慢的,两次初、末位置均相同,则在两次插入的过程中( )
A.磁通量变化率相同 B.磁通量变化量相同
C.产生的感应电流相同 D.产生的感应电动势相同
答案:B
解析:
解答:解:A、当条形磁铁插入线圈的瞬间,穿过线圈的磁通量增加,产生感应电流.条形磁铁第一次迅速插入线圈时,磁通量增加快;条形磁铁第二次缓慢插入线圈时,磁通量增加慢,磁通量变化率不同,但磁通量变化量相同.故A错误,B正确;
C、根据法拉第电磁感应定律第一次线圈中产生的感应电动势大,再欧姆定律可知第一次感应电流大,故C错误;D错误;
故选:B
分析:根据产生感应电流的条件分析有无感应电流产生.再根据法拉第电磁感应定律分析感应电动势的大小,由欧姆定律分析感应电流的大小.再由q=It可确定导体某横截面的电荷量等于磁通量的变化与电阻的比值.
6.一个闭合线圈放在变化的磁场中,线圈产生的感应电动势为E,若仅将磁通量的变化率增加为原来的4倍,则线圈产生的感应电动势变为( )
A.4E B.2E C.E D.E/2
答案:
解析:
解答:解:根据法拉第电磁感应定律:E=n,可知仅将磁通量的变化率增加为原来的4倍时,线圈中的感应电动势变为4E,故BCD错误,A正确.
故选A.
分析:法拉第电磁感应定律:当穿过回路的磁通量发生变化时,回路中的感生电动势E感的大小和穿过回路的磁通量变化率等成正比,公式为:E=n.
7.如图所示,匀强磁场垂直于矩形线框abcd,磁场的磁感应强度为B,矩形面积为S.现使矩形框以ab边为轴转动90°角,则在这个过程中,穿过线框的磁通量变化量的数值是( )
A.0 B.0.5BS C.BS D.2BS
答案:C
解析:
解答:解:当线圈平面与磁场方向垂直时,Φ=BS.
当线圈绕ab轴转动至与磁场方向平行时,线圈平面与磁场方向的夹角为0度,则Φ=0.
根据Φ=BSsinθ知,在此转动过程中,穿过线圈平面的磁通量变化量为BS,故C正确,ABD错误.
故选:C.
分析:通过线圈的磁通量可以根据Φ=BSsinθ进行求解,θ为线圈平面与磁场方向的夹角.
8.矩形导线框abcd放在匀强磁场中处于静止状态,如图(甲)所示.磁感线方向与导线框所在平面垂直,磁感应强度B随时间变化的图象如图(乙)所示.t=0时刻,磁感应强度的方向垂直导线框平面向里,在0﹣4s时间内,导线框ad边所受安培力随时间变化的图象(规定以向左为安培力正方向)可能是图中的( )
A. B.
C. D.
答案:D
解析:
解答:解:t=0时刻,磁感应强度的方向垂直线框平面向里,在0到1S内,穿过线框的磁通量变小,由楞次定律可得,感应电流方向是顺时针,再由左手定则可得线框的ad边的安培力水平向左.
当在1S到2S内,磁感应强度的方向垂直线框平面向外,穿过线框的磁通量变大,由楞次定律可得,感应电流方向是顺时针,再由左手定则可得线框的ad边的安培力水平向右.在下一个周期内,重复出现安培力先向左后向右.根据F=BIL知,在0到1s内电流的大小不变,磁感应强度均匀减小,则安培力均匀减小,在1到2s内,电流的大小不变,磁感应强度均匀增大,则安培力均匀增大.故D正确,A、B、C错误.
故选D.
分析:穿过线圈的磁通量发生变化,导致线圈中产生感应电动势,从而形成感应电流.由题意可知,磁感应强度是随着时间均匀变化的,所以感应电流是恒定的,则线框ad边所受的安培力与磁感应强度有一定的关系.
9.闭合回路由电阻R与导线组成,其内部磁场大小按B﹣t图变化,方向如图,则回路中( )
A.电流方向为逆时针方向 B.电流强度越来越大
C.磁通量的变化率恒定不变 D.产生的感应电动势越来越大
答案:C
解析:
解答:解:由图象可知,磁感应随时间均匀增大,则由 =BS可知,磁通量随时间均匀增加,故其变化率恒定不变,故C正确;
由楞次定律可知,电流方向为顺时针,故A不正确;
由法拉第电磁感应定律可知,E==S,故感应电动势保持不变,电流强度不变,故BD均错;
故选C.
分析:由B﹣t图象可知磁感应强度的变化情况,则由磁通量的定义可知磁通量的变化率;再由楞次定律可判断电流方向;由法拉第电磁感应定律可求得感应电动势.
10.如图所示,甲图中的电容器C原来不带电,除电阻R外,其余部分电阻均不计,光滑且足够长的导轨水平放置,现给导体棒ab水平向右的初速度v,则甲、乙、丙三种情形下ab棒最终的运动状态是( )
A.三种情形下导体棒ab最终均作匀速运动
B.甲、丙中导体棒ab最终将以不同的速度作匀速运动,乙中导体棒ab最终静止
C.甲、丙中导体棒ab最终将以相同的速度作匀速运动,乙中导体棒ab最终静止
D.三种情形下导体棒ab最终均静止
答案:B
解析:
解答:解:甲图中ab棒产生感应电动势对C充电,C两板间电势差与感应电电动势相同时,没有电流做向右的匀速直线运动;
乙图中导体棒在初速度作用下,切割磁感线,产生电动势,出现安培力,阻碍其向前运动,其动能正转化为热能,最终会静止;
图丙中,导体棒先受到向左的安培力作用向右做减速运动,速度减为零后再在安培力作用下向左做加速运动,当导体棒产生的感应电动势与电源的电动势相等时,电路中没有电流,ab棒向左做匀速运动.由此得选项B正确,ACD错误
故选:B
分析:明确三种图中的电容器,电阻,电源在电路中的作用,电容器被充电后两板间的电压达到感应电动势便不再充电;电阻发热耗能,电池提供电流.
11.如图甲所示,线圈A、B紧靠在一起,当给线圈A通以如图乙所示的电流(规定由b进入a流出为电流正方向)时,则电压表的示数变化情况(规定电流由c进入电压表为正方向)应为下列图中的( )
A.B.C.D.
答案:C
解析:
解答:解:规定由b进入a流出为电流正方向,
0﹣1s,电流为正值,随时间均匀增大,根据右手螺旋定则判断出线圈A产生的磁场左端是S极,右端是N极,
由于产生原磁场的电流在增大所以原磁场穿过线圈B的磁通量均匀增大,
根据楞次定律判断出线圈B中感应电流方向是从d经过电压表再经过c,也就是在图中电压为正值.
根据法拉第地磁感应定律得出产生的感应电动势为不变,为定值.
依次求出1﹣4s过程中电压变化情况.
故选:C.
分析:根据右手螺旋定则判断出线圈A产生的磁场极性.
由于产生原磁场的电流在增大,根据楞次定律判断线圈B中感应电流方向,
根据法拉第地磁感应定律得出感应电动势的大小不变.
12.某同学在实验里熟悉各种仪器的使用.他将一条形磁铁放在水平转盘上,如图(甲)所示,磁铁可随转盘转动,另将一磁感应强度传感器固定在转盘旁边.当转盘(及磁铁)转动时,引起磁感应强度测量值周期性地变化,该变化的周期与转盘转动周期一致.经过操作,该同学在计算机上得到了如图(乙)所示的图象.该同学猜测磁感应强度传感器内有一线圈,当测得磁感应强度最大时就是穿过线圈的磁通量最大时,按照这种猜测( )
A.在t=0.1s时刻,线圈内产生的感应电流的方向发生了变化
B.在t=0.15s时刻,线圈内产生的感应电流的方向发生了变化
C.在t=0.1s时刻,线圈内产生的感应电流的大小达到了最大值
D.在t=0.15s时刻,线圈内产生的感应电流的大小达到了最大值
答案:A
解析:
解答:解:A、在t=0.1s时刻,线圈内磁场最强,磁通量最大,接着磁通量会变小,但磁场方向没变,所以根据楞次定律得知,线圈内产生感应电流的方向发生变化,故A正确;
B、在t=0.15s时刻,线圈内B为零,磁通量为零,接着磁通量会变大,由于磁场方向发生变化,所以根据楞次定律得知产生感应电流的方向不会发生变化,故B错误;
C、在t=0.1s时刻,线圈内磁场最强,图线的斜率为零,故磁感应强度的变化率为零,此时磁通量变化率为零,产生的感应电动势为零,感应电流则为零,故C错误;
D、在t=0.15s时刻,线圈内磁场最弱,图线的斜率不是最大,故此时磁感应强度的变化率不是最大,则磁通量变化率不是最大,产生的感应电动势就不是最大,感应电流的大小没有达到最大.故D错误;
故选:A
分析:利用楞次定律的“增反减同”来确定感应电流的方向,由图象可知磁感应强度的变化,从而得出感应磁场方向,再由安培定则来确定感应电流方向.法拉第电磁感应定律可得出在磁通量变化率最大时,电流最强.
13.一圆环形铝质金属圈(阻值不随温度变化)放在匀强磁场中,设第1s内磁感线垂直于金属圈平面(即垂直于纸面)向里,如图甲所示.若磁感应强度B随时间t变化的关系如图乙所示,那么第3s内金属圈中( )
A.感应电流逐渐增大,沿逆时针方向
B.感应电流恒定,沿顺时针方向
C.圆环各微小段受力大小不变,方向沿半径指向圆心
D.圆环各微小段受力逐渐增大,方向沿半径指向圆心
答案:D
解析:
解答:解:A、B、第3s内,向里的磁场逐渐增大,根据楞次定律可得,感应电流的磁场方向向外,感应电流沿逆时针方向;由于磁场是均匀增大的,根据法拉第电磁感应定律可知,感应电动势的大小不变,所以感应电流不变.故AB错误;
C、D、圆环各微小段受力:F=BIL,由于磁场逐渐增大,所以圆环各微小段受力逐渐增大;由左手定则可得,安培力的方向沿半径指向圆心.故C错误;D正确.
故选:D
分析:穿过线圈的磁通量发生变化,导致线圈中产生感应电动势,从而形成感应电流.由题意可知,磁感应强度是随着时间均匀变化的,所以感应电流是恒定的,则线框ad边所受的安培力与磁感应强度有一定的关系.
14.如图所示,bacd为导体做成的框架,其平面与水平面成θ角,质量为m的导体棒PQ与ab、cd接触良好,回路的电阻为R,整个装置放于垂直框架平面的变化磁场中,磁感应强度B的变化情况如图乙所示,PQ能够始终保持静止,则0~t2时间内,PQ受到的安培力F和摩擦力Ff随时间变化的图象可能不正确的是(取平行斜面向上为正方向)( )
A.B.C.D.
答案:B
解析:
解答:解:根据法拉第电磁感应定律可知在线圈中产生恒定的感应电流,开始导体棒PQ受到沿导轨向上的安培力,
若开始安培力小于导体棒重力沿导轨向下的分力mgsinθ,则摩擦力为:f=mgsinθ﹣F安,随着安培力的减小,摩擦力f逐渐逐渐增大,
当安培力反向时,f=mgsinθ+F安,安培力逐渐增大,故摩擦力也是逐渐增大;
若安培力大于mgsinθ,则安培力为:f=F安﹣mgsinθ,由于安培力逐渐减小,故摩擦力逐渐减小,
当F安=mgsinθ时,摩擦力为零并开始反向变为:f=mgsinθ﹣F安,随着安培力的变化将逐渐增大,
故选:B.
分析:由图乙可知磁场均匀变化,根据法拉第电磁感应定律可知在线圈中产生恒定的感应电流,根据左手定则可知导体棒开始受到沿斜面向上逐渐减小的安培力,当B=0时,安培力为零,当磁场反向时,导体棒受到沿导轨向下的逐渐增大的安培力,分析清楚安培力的情况,然后对导体棒进行正确受力分析,即可正确判断摩擦力的变化情况.
15.一闭合线圈固定在垂直于纸面的均匀磁场中,设向里为磁感应强度B的正方向,线圈中的箭头为电流i的正方向,如图(a)所示.已知线圈中感应电流i随时间而变化的图象如图(b)所示,则磁感应强度B随时间而变化的图象可能是下图中的( )
A. B.
C. D.
答案:A
解析:
解答:解:A、在0~t内,磁场方向垂直纸面向外,且均匀增大,根据法拉第电磁感应定律,则产生的感应电动势为定值,电流为定值,根据楞次定律,感应电流的方向为顺时针方向,则电流为负值.
在t~t内,磁场方向垂直纸面向外,且均匀减小,感应电流为定值,根据楞次定律,感应电流的方向为逆时针方向,则电流为正值.
在t~t 内,磁场方向垂直纸面向里,且均匀增大,电流为定值,根据楞次定律,感应电流的方向为逆时针方向,则电流为正值.
在t~2t内,磁场方向垂直纸面向里,且均匀减小,感应电流为定值,根据楞次定律,感应电流的方向为顺时针方向,则电流为负值,故A正确.
B、在0~t内,磁场方向垂直纸面向外,且均匀减小,根据法拉第电磁感应定律,则产生的感应电动势为定值,电流为定值,根据楞次定律,感应电流的方向为逆时针方向,则电流为正值,故B错误;
C、在0~t内,磁场方向垂直纸面向外,且非均匀增大,根据法拉第电磁感应定律,则产生的感应电动势不是定值,电流不是定值,故C错误.
D、磁场的方向不变,则与图中电流方向不符.故D错误.
故选:A.
分析:线圈中因磁通量发生变化,才导致线圈产生感应电动势,从而形成感应电流.由楞次定律可推断出磁场的变化及磁通量的变化.
二.填空题(共5小题)
16. 1831年 (选填“奥斯特”或“法拉第”)发现了电磁感应现象.大量实验表明,回路中所产生的感应电动势大小与穿过该回路的磁通量的 (选填“变化量”或“变化率”)成正比.
答案:法拉第,变化率
解析:
解答:解:在奥斯特发现电流周围存在磁场后,法拉第发现了电磁感应现象;
根据E=n,知感应电动势的大小与穿过回路的磁通量的变化率成正比.
故答案为:法拉第,变化率.
分析:根据法拉第发现了电磁感应现象,而奥斯特发现电流周围存在磁场,并根据法拉第电磁感应定律,E=n,从而即可求解.
17.如图所示,使闭合矩形线圈在匀强磁场中绕垂直于磁场方向的转轴匀速转动,在线圈中就会产生交流电.已知磁场的磁感应强度为B,线圈abcd面积为S,线圈转动的角速度为ω.当线圈转到如图位置时,线圈中的感应电动势为 ;当线圈从图示位置转过90°时,线圈中的感应电动势为 .
答案:0,BSω
解析:
解答:解:当线框平面与磁场垂直时,穿过线框的磁通量变化率为零,感应电动势为零;
当线框从中性面位置转过90°,线框平面与中性面垂直,产生的感应电动势为BSω;
故答案为:0,BSω
分析:线框位于中性面时,穿过线框的磁通量最大,磁通量的变化率为零,感应电动势为零;
由法拉第电磁感应定律可以求出感应电动势.
18.如图所示,线圈内有理想边界的磁场,当磁感应强度均匀增加时,有一带电粒子静止于水平放置的平行板电容器中间,则此粒子电性是 ,若增大磁感应强度的变化率,则带电粒子将 (填“向上运动”“向下运动”或静止”)
答案:负,向上运动
解析:
解答:解:当磁场均匀增加时,由楞次定律可判断上极板带正电.所以平行板电容器的板间的电场方向向下,带电粒子受重力和电场力平衡,所以粒子带负电.
若增大磁感应强度的变化率,感应电动势增大,粒子受的电场力增大,则带电粒子将向上运动.
故答案为:负,向上运动
分析:带电粒子受重力和电场力平衡,由楞次定律可判断极板带电性质,由法拉第电磁感应定律可得出感应电动势变化,从而知道电场力的变化.
19.如图所示,A、B两个闭合线圈用同样的导线制成,匝数都为10匝,半径rA=2rB图示区域内有磁感应强度均匀减小的匀强磁场,则A、B线圈中产生的感应电动势之比为EA:EB= ,线圈中的感应电流之比IA:IB= .
答案:1:1,1:2
解析:
解答:解:根据法拉第电磁感应定律E=n=n,题中n相同,相同,面积S也相同,
则得到A、B环中感应电动势EA:EB=1:1.
根据电阻定律R=ρ,L=n 2πr,ρ、S相同,则电阻之比为:RA:RB=rA:rB=2:1,
根据欧姆定律I=E/R得产生的感应电流之比为:IA:IB=1:2.
故答案为:1:1,1:2.
分析:根据法拉第电磁感应定律E=n=n,研究A、B环中感应电动势EA:EB.根据电阻定律求出两环电阻之比,再欧姆定律求解电流之比IA:IB.
20.金属线圈ABC构成一个等腰直角三角形,腰长为a,绕垂直于纸面通过A的轴在纸面内匀速转动,角速度ω,如图所示.如加上一个垂直纸面向里的磁感应强度为B的匀强磁场,则B、A间的电势差UBA= ,B、C间的电势差UBC= .
答案:Bωa2,Bωa2
解析:
解答:解:AC、BC、AB均绕垂直于A的轴以角速度ω匀速转动,△ABC中磁通量不变,所以线圈中没有电流.
但当单独考虑每条边时,三边均切割磁感线,均有感应电动势产生,且B点电势大于C点电势和A点电势.
则有UBA=EBA=BL=BωLAB2=Bωa2,
UCA=ECA=BωLAC2=Bωa2,
UBC=UBA﹣UCA=Bωa2﹣Bωa2=Bωa2.
故答案为:Bωa2,Bωa2.
分析:根据法拉第电磁感应定律,求得感应电动势的大小,再结合闭合电路欧姆定律,及楞次定律从而确定两点的电势差,从而即可求解.
三.解答题(共5小题)
21.如图所示,一个单匝矩形线圈水平放在桌面上,再线圈中心上方有一竖直的条形磁体,此时线圈内的磁通量为0.05Wb.在0.5s的时间内,将该条形磁体从图示位置竖放到线圈内的桌面上,此时线圈内的磁通量为0.10Wb.试求此过程:
(1)线圈内磁通量的变化量;
(2)线圈中产生的感应电动势大小.
答案:(1)线圈的磁通量的变化量0.05Wb;
(2)线圈产生的感应电动势的大小为0.1V
解析:
解答:解:(1)磁通量的变化为:
△Φ=Φ′﹣Φ=0.10﹣0.05=0.05Wb;
(2)由法拉第电磁感应定律可得感应电动势为:
E=n=1×=0.1V;
答:(1)线圈的磁通量的变化量0.05Wb;
(2)线圈产生的感应电动势的大小为0.1V.
分析:(1)由磁通量的定义式可以求出磁通量的变化;
(2)由法拉第电磁感应定律可以求出感应电动势.
22.在应用法拉第电磁感应定律求感应电动势时有两种方法,请你分别写出这两种表达式并指出表达式的应用范围.
答案:由法拉第电磁感应定律可知;E=n,即E与磁通量的变化率成正比,即电动势取决于磁通量的变化快慢,此公式应用于平均感应电动势的计算;
对于导体切割磁感线产生感应电动势的情况,常采用E=BLv来计算,使用条件为B、L、v两两垂直的情况,不垂直式进行正交分解,取垂直的分量.此公式既可以计算匀强磁场中导体运动产生的平均感应电动势,也可以计算非匀强磁场瞬时感应电动势.
解析:
解答:解:由法拉第电磁感应定律可知;E=n,即E与磁通量的变化率成正比,即电动势取决于磁通量的变化快慢,此公式应用于平均感应电动势的计算;
对于导体切割磁感线产生感应电动势的情况,常采用E=BLv来计算,使用条件为B、L、v两两垂直的情况,不垂直式进行正交分解,取垂直的分量.此公式既可以计算匀强磁场中导体运动产生的平均感应电动势,也可以计算非匀强磁场瞬时感应电动势.
分析:由法拉第电磁感应定律可知,闭合电路中产生的感应电动势的大小与磁通量的变化率成正比,一般公式为:E=n,其中n为线圈的匝数;对于导体切割磁感线产生感应电动势的情况,常采用E=BLv来计算
23.如图甲,100匝的线圈(图中只画了2匝)两端A、B与一个阻值R=48Ω的电阻相连,其线圈的电阻r=2Ω,线圈内有指向纸内方向的磁场,线圈中的磁通量在按图乙所示规律变化.
(1)如果A、B两端与一理想电压表相连,哪端该接电压表标+号的接线柱?
(2)该线圈产生的感应电动势等于多少?
(3)如果A、B两端与一理想电压表相连,则电压表的示数为多少?
答案:(1)如果A、B两端与一理想电压表相连,A端该接电压表标+号的接线柱;
(2)该线圈产生的感应电动势等于50V;
(3)如果A、B两端与一理想电压表相连,则电压表的示数为48V
解析:
解答:解:(1)线圈相当于电源,由楞次定律可知A相当于电源的正极,B相当于电源的负极.故A应该与理想电压表的+号接线柱相连.
(2)由法拉第电磁感应定律得:E=n=100x=50V
(3)由闭合电路的欧姆定律得:==1A
又由部分电路的欧姆定律得:U=IR=1×48=48V
答:(1)如果A、B两端与一理想电压表相连,A端该接电压表标+号的接线柱;
(2)该线圈产生的感应电动势等于50V;
(3)如果A、B两端与一理想电压表相连,则电压表的示数为48V.
分析:(1)根据楞次定律判断感应电流的方向.线圈相当于电源,即可判断电压表的接法.
(2、3)由图求出磁通量的变化率.根据法拉第电磁感应定律求出回路中感应电动势,得到电压表的读数;
24.一个面积为0.2m2的100匝线圈处在匀强磁场中,磁场方问垂直于线圈平面,已知磁感应强度随时间变化的规律为B=(2+0.2t)T,定值电阻R=6Ω,线圈电阻r=4Ω,求:
(1)线圈中磁通量的变化率和回路的感应电动势;
(2)a、b两点间电压Uab.
答案:(1)磁通量变化率为0.04Wb/s;回路的感应电动势为4V;
(2)ab两点间电压Uab为2.4V
解析:
解答:解:(1)磁通量的变化率=S=0.2×0.2=0.04Wb/s.
根据法拉第电磁感应定律得,感应电动势E=n=100×0.04V=4V.
(2)根据欧姆定律得,ab间的电压U=R=×6V=2.4V.
答:(1)磁通量变化率为0.04Wb/s;回路的感应电动势为4V;
(2)ab两点间电压Uab为2.4V.
分析:根据磁感应强度的变化率求出磁通量的变化率,结合法拉第电磁感应定律求出回路中的感应电动势,通过欧姆定律求出ab两点间的电压.
25.一个300匝的线圈,穿过它的磁通量在0.01s内由6×10﹣2Wb均匀地减小到3×10﹣2Wb.求线圈中的感应电动势的大小.
答案:线圈中的感应电动势为900V
解析:
解答:解:根据法拉第电磁感应定律得:
E=N=300×=900V;
答:线圈中的感应电动势为900V.
分析:线圈的磁通量变化时,产生感应电动势,由法拉第电磁感应定律可得感应电动势大小.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 17 页 (共 17 页) 版权所有@21世纪教育网
人教版物理选修1-1第三章
第二节法拉第电磁感应定律同步训练
一.选择题(共15小题)
1.如图所示,金属棒MN两端由等长的轻质绝缘细线水平悬挂,处于垂直纸面水平向里的匀强磁场中,棒中通有由M到N的恒定电流,细线中拉力不为零,两细线竖直. 保持匀强磁场磁感应强度大小不变,方向缓慢地转过90°变为竖直向下,在这个过程中( )
A.细线向纸面内偏转,其中的拉力一直增大
B.细线向纸面外偏转,其中的拉力一直增大
C.细线向纸面内偏转,其中的拉力先增大后减小
D.细线向纸面外偏转,其中的拉力先增大后减小
答案:A
解析:
解答:解:初始状态时,金属棒受重力、拉力和安培力平衡.当磁场方向由垂直纸面向里缓慢地转过90°变为竖直向下,知安培力的大小FA=BIL不变,方向由竖直向上向里变为垂直纸面向里.
根据共点力平衡知,细线向纸面内偏转.因为金属棒受重力、拉力和安培力平衡,重力和安培力的合力于拉力大小等值方向,重力和安培力的大小不变,之间的夹角由180°变为90°,知两个力的合力一直增大,所以拉力一直增大.故A正确,B、C、D错误.
故选A.
分析:根据左手定则判断出安培力的方向,根据安培力方向的变化,结合共点力平衡判断拉力方向和大小的变化.
2.如图(a),线圈ab、cd绕在同一软铁芯上,在ab线圈中通以变化的电流,用示波器测得线圈cd间电压如图(b)所示,已知线圈内部的磁场与流经线圈的电流成正比,则下列描述线圈ab中电流随时间变化关系的图中,可能正确的是( )
A. B.
C. D.
答案:
解析:
解答:解:因为线圈cd中每个时间段内电流大小不变化,则每个时间段内产生的感应电动势不变;
根据法拉第电磁感应定律得:E=NS,
电流为:I= ,
则线圈ab中每个时间段内电流的磁场均匀变化.正确反应这一关系的图象只有C.故C正确,A、B、D错误.
故选:C.
分析:线圈cd与示波器连接,在每个时间段内电流不随时间变化,则根据法拉第电磁感应定律,产生感应电流的磁场均匀变化,由此判断线圈ab电流的变化.
3.如图甲,R0为定值电阻,两金属圆环固定在同一绝缘平面内.左端连接在一周期为T0的正弦交流电源上,经二极管整流后,通过R0的电流i始终向左,其大小按图乙所示规律变化.规定内圆环a端电势高于b端时,a、b间的电压uab为正,下列uab﹣t图象可能正确的是( )
A. B.
C. D.
答案:C
解析:
解答:解:在第一个0.25T0时间内,通过大圆环的电流为瞬时针增加的,由楞次定律可判断内球内a端电势高于b端,因电流的变化率逐渐减小故内环的电动势逐渐减小,同理可知,在0.25T0~0.5T0时间内,通过大圆环的电流为瞬时针逐渐减小;则由楞次定律可知,a环内电势低于b端,因电流的变化率逐渐变大,故内环的电动势变大;故只有C正确;
故选:C.
分析:由图乙可知,电流为周期性变化的电流,故只需分析0.5T0内的感应电流即可;通过分析电流的变化明确磁场的变化,根据楞次定律即可得出电动势的图象.
4.如图,光滑平行金属导轨固定在水平面上,左端由导线相连,导体棒垂直静置于导轨上构成回路.在外力F作用下,回路上方的条形磁铁竖直向上做匀速运动.在匀速运动过程中外力F做功WF,磁场力对导体棒做功W1,磁铁克服磁场力做功W2,重力对磁铁做功WG,回路中产生的焦耳热为Q,导体棒获得的动能为EK.则错误的是( )
A.W1=Q B.W2﹣W1=Q C.W1=EK D.WF+WG=Q+EK
答案:A
解析:
解答:解:A、根据题意,由动能定理知:导体棒:W1=Ek①,故A错误,C正确
B、根据能量守恒知W2﹣W1=Q②,故B正确;
D、对磁铁有:WF+WG﹣W2=0③,由①②③得WF+WG=Ek+Q,故D正确;
故选:A
分析:分别选磁铁和导体棒为研究对象,根据动能定理列方程,对系统根据能量守恒知W2﹣W1=Q.
5.把一条形磁铁插入同一个闭合线圈中,第一次是迅速的,第二次是缓慢的,两次初、末位置均相同,则在两次插入的过程中( )
A.磁通量变化率相同 B.磁通量变化量相同
C.产生的感应电流相同 D.产生的感应电动势相同
答案:B
解析:
解答:解:A、当条形磁铁插入线圈的瞬间,穿过线圈的磁通量增加,产生感应电流.条形磁铁第一次迅速插入线圈时,磁通量增加快;条形磁铁第二次缓慢插入线圈时,磁通量增加慢,磁通量变化率不同,但磁通量变化量相同.故A错误,B正确;
C、根据法拉第电磁感应定律第一次线圈中产生的感应电动势大,再欧姆定律可知第一次感应电流大,故C错误;D错误;
故选:B
分析:根据产生感应电流的条件分析有无感应电流产生.再根据法拉第电磁感应定律分析感应电动势的大小,由欧姆定律分析感应电流的大小.再由q=It可确定导体某横截面的电荷量等于磁通量的变化与电阻的比值.
6.一个闭合线圈放在变化的磁场中,线圈产生的感应电动势为E,若仅将磁通量的变化率增加为原来的4倍,则线圈产生的感应电动势变为( )
A.4E B.2E C.E D.E/2
答案:
解析:
解答:解:根据法拉第电磁感应定律:E=n,可知仅将磁通量的变化率增加为原来的4倍时,线圈中的感应电动势变为4E,故BCD错误,A正确.
故选A.
分析:法拉第电磁感应定律:当穿过回路的磁通量发生变化时,回路中的感生电动势E感的大小和穿过回路的磁通量变化率等成正比,公式为:E=n.
7.如图所示,匀强磁场垂直于矩形线框abcd,磁场的磁感应强度为B,矩形面积为S.现使矩形框以ab边为轴转动90°角,则在这个过程中,穿过线框的磁通量变化量的数值是( )
A.0 B.0.5BS C.BS D.2BS
答案:C
解析:
解答:解:当线圈平面与磁场方向垂直时,Φ=BS.
当线圈绕ab轴转动至与磁场方向平行时,线圈平面与磁场方向的夹角为0度,则Φ=0.
根据Φ=BSsinθ知,在此转动过程中,穿过线圈平面的磁通量变化量为BS,故C正确,ABD错误.
故选:C.
分析:通过线圈的磁通量可以根据Φ=BSsinθ进行求解,θ为线圈平面与磁场方向的夹角.
8.矩形导线框abcd放在匀强磁场中处于静止状态,如图(甲)所示.磁感线方向与导线框所在平面垂直,磁感应强度B随时间变化的图象如图(乙)所示.t=0时刻,磁感应强度的方向垂直导线框平面向里,在0﹣4s时间内,导线框ad边所受安培力随时间变化的图象(规定以向左为安培力正方向)可能是图中的( )
A. B.
C. D.
答案:D
解析:
解答:解:t=0时刻,磁感应强度的方向垂直线框平面向里,在0到1S内,穿过线框的磁通量变小,由楞次定律可得,感应电流方向是顺时针,再由左手定则可得线框的ad边的安培力水平向左.
当在1S到2S内,磁感应强度的方向垂直线框平面向外,穿过线框的磁通量变大,由楞次定律可得,感应电流方向是顺时针,再由左手定则可得线框的ad边的安培力水平向右.在下一个周期内,重复出现安培力先向左后向右.根据F=BIL知,在0到1s内电流的大小不变,磁感应强度均匀减小,则安培力均匀减小,在1到2s内,电流的大小不变,磁感应强度均匀增大,则安培力均匀增大.故D正确,A、B、C错误.
故选D.
分析:穿过线圈的磁通量发生变化,导致线圈中产生感应电动势,从而形成感应电流.由题意可知,磁感应强度是随着时间均匀变化的,所以感应电流是恒定的,则线框ad边所受的安培力与磁感应强度有一定的关系.
9.闭合回路由电阻R与导线组成,其内部磁场大小按B﹣t图变化,方向如图,则回路中( )
A.电流方向为逆时针方向 B.电流强度越来越大
C.磁通量的变化率恒定不变 D.产生的感应电动势越来越大
答案:C
解析:
解答:解:由图象可知,磁感应随时间均匀增大,则由 =BS可知,磁通量随时间均匀增加,故其变化率恒定不变,故C正确;
由楞次定律可知,电流方向为顺时针,故A不正确;
由法拉第电磁感应定律可知,E==S,故感应电动势保持不变,电流强度不变,故BD均错;
故选C.
分析:由B﹣t图象可知磁感应强度的变化情况,则由磁通量的定义可知磁通量的变化率;再由楞次定律可判断电流方向;由法拉第电磁感应定律可求得感应电动势.
10.如图所示,甲图中的电容器C原来不带电,除电阻R外,其余部分电阻均不计,光滑且足够长的导轨水平放置,现给导体棒ab水平向右的初速度v,则甲、乙、丙三种情形下ab棒最终的运动状态是( )
A.三种情形下导体棒ab最终均作匀速运动
B.甲、丙中导体棒ab最终将以不同的速度作匀速运动,乙中导体棒ab最终静止
C.甲、丙中导体棒ab最终将以相同的速度作匀速运动,乙中导体棒ab最终静止
D.三种情形下导体棒ab最终均静止
答案:B
解析:
解答:解:甲图中ab棒产生感应电动势对C充电,C两板间电势差与感应电电动势相同时,没有电流做向右的匀速直线运动;
乙图中导体棒在初速度作用下,切割磁感线,产生电动势,出现安培力,阻碍其向前运动,其动能正转化为热能,最终会静止;
图丙中,导体棒先受到向左的安培力作用向右做减速运动,速度减为零后再在安培力作用下向左做加速运动,当导体棒产生的感应电动势与电源的电动势相等时,电路中没有电流,ab棒向左做匀速运动.由此得选项B正确,ACD错误
故选:B
分析:明确三种图中的电容器,电阻,电源在电路中的作用,电容器被充电后两板间的电压达到感应电动势便不再充电;电阻发热耗能,电池提供电流.
11.如图甲所示,线圈A、B紧靠在一起,当给线圈A通以如图乙所示的电流(规定由b进入a流出为电流正方向)时,则电压表的示数变化情况(规定电流由c进入电压表为正方向)应为下列图中的( )
A.B.C.D.
答案:C
解析:
解答:解:规定由b进入a流出为电流正方向,
0﹣1s,电流为正值,随时间均匀增大,根据右手螺旋定则判断出线圈A产生的磁场左端是S极,右端是N极,
由于产生原磁场的电流在增大所以原磁场穿过线圈B的磁通量均匀增大,
根据楞次定律判断出线圈B中感应电流方向是从d经过电压表再经过c,也就是在图中电压为正值.
根据法拉第地磁感应定律得出产生的感应电动势为不变,为定值.
依次求出1﹣4s过程中电压变化情况.
故选:C.
分析:根据右手螺旋定则判断出线圈A产生的磁场极性.
由于产生原磁场的电流在增大,根据楞次定律判断线圈B中感应电流方向,
根据法拉第地磁感应定律得出感应电动势的大小不变.
12.某同学在实验里熟悉各种仪器的使用.他将一条形磁铁放在水平转盘上,如图(甲)所示,磁铁可随转盘转动,另将一磁感应强度传感器固定在转盘旁边.当转盘(及磁铁)转动时,引起磁感应强度测量值周期性地变化,该变化的周期与转盘转动周期一致.经过操作,该同学在计算机上得到了如图(乙)所示的图象.该同学猜测磁感应强度传感器内有一线圈,当测得磁感应强度最大时就是穿过线圈的磁通量最大时,按照这种猜测( )
A.在t=0.1s时刻,线圈内产生的感应电流的方向发生了变化
B.在t=0.15s时刻,线圈内产生的感应电流的方向发生了变化
C.在t=0.1s时刻,线圈内产生的感应电流的大小达到了最大值
D.在t=0.15s时刻,线圈内产生的感应电流的大小达到了最大值
答案:A
解析:
解答:解:A、在t=0.1s时刻,线圈内磁场最强,磁通量最大,接着磁通量会变小,但磁场方向没变,所以根据楞次定律得知,线圈内产生感应电流的方向发生变化,故A正确;
B、在t=0.15s时刻,线圈内B为零,磁通量为零,接着磁通量会变大,由于磁场方向发生变化,所以根据楞次定律得知产生感应电流的方向不会发生变化,故B错误;
C、在t=0.1s时刻,线圈内磁场最强,图线的斜率为零,故磁感应强度的变化率为零,此时磁通量变化率为零,产生的感应电动势为零,感应电流则为零,故C错误;
D、在t=0.15s时刻,线圈内磁场最弱,图线的斜率不是最大,故此时磁感应强度的变化率不是最大,则磁通量变化率不是最大,产生的感应电动势就不是最大,感应电流的大小没有达到最大.故D错误;
故选:A
分析:利用楞次定律的“增反减同”来确定感应电流的方向,由图象可知磁感应强度的变化,从而得出感应磁场方向,再由安培定则来确定感应电流方向.法拉第电磁感应定律可得出在磁通量变化率最大时,电流最强.
13.一圆环形铝质金属圈(阻值不随温度变化)放在匀强磁场中,设第1s内磁感线垂直于金属圈平面(即垂直于纸面)向里,如图甲所示.若磁感应强度B随时间t变化的关系如图乙所示,那么第3s内金属圈中( )
A.感应电流逐渐增大,沿逆时针方向
B.感应电流恒定,沿顺时针方向
C.圆环各微小段受力大小不变,方向沿半径指向圆心
D.圆环各微小段受力逐渐增大,方向沿半径指向圆心
答案:D
解析:
解答:解:A、B、第3s内,向里的磁场逐渐增大,根据楞次定律可得,感应电流的磁场方向向外,感应电流沿逆时针方向;由于磁场是均匀增大的,根据法拉第电磁感应定律可知,感应电动势的大小不变,所以感应电流不变.故AB错误;
C、D、圆环各微小段受力:F=BIL,由于磁场逐渐增大,所以圆环各微小段受力逐渐增大;由左手定则可得,安培力的方向沿半径指向圆心.故C错误;D正确.
故选:D
分析:穿过线圈的磁通量发生变化,导致线圈中产生感应电动势,从而形成感应电流.由题意可知,磁感应强度是随着时间均匀变化的,所以感应电流是恒定的,则线框ad边所受的安培力与磁感应强度有一定的关系.
14.如图所示,bacd为导体做成的框架,其平面与水平面成θ角,质量为m的导体棒PQ与ab、cd接触良好,回路的电阻为R,整个装置放于垂直框架平面的变化磁场中,磁感应强度B的变化情况如图乙所示,PQ能够始终保持静止,则0~t2时间内,PQ受到的安培力F和摩擦力Ff随时间变化的图象可能不正确的是(取平行斜面向上为正方向)( )
A.B.C.D.
答案:B
解析:
解答:解:根据法拉第电磁感应定律可知在线圈中产生恒定的感应电流,开始导体棒PQ受到沿导轨向上的安培力,
若开始安培力小于导体棒重力沿导轨向下的分力mgsinθ,则摩擦力为:f=mgsinθ﹣F安,随着安培力的减小,摩擦力f逐渐逐渐增大,
当安培力反向时,f=mgsinθ+F安,安培力逐渐增大,故摩擦力也是逐渐增大;
若安培力大于mgsinθ,则安培力为:f=F安﹣mgsinθ,由于安培力逐渐减小,故摩擦力逐渐减小,
当F安=mgsinθ时,摩擦力为零并开始反向变为:f=mgsinθ﹣F安,随着安培力的变化将逐渐增大,
故选:B.
分析:由图乙可知磁场均匀变化,根据法拉第电磁感应定律可知在线圈中产生恒定的感应电流,根据左手定则可知导体棒开始受到沿斜面向上逐渐减小的安培力,当B=0时,安培力为零,当磁场反向时,导体棒受到沿导轨向下的逐渐增大的安培力,分析清楚安培力的情况,然后对导体棒进行正确受力分析,即可正确判断摩擦力的变化情况.
15.一闭合线圈固定在垂直于纸面的均匀磁场中,设向里为磁感应强度B的正方向,线圈中的箭头为电流i的正方向,如图(a)所示.已知线圈中感应电流i随时间而变化的图象如图(b)所示,则磁感应强度B随时间而变化的图象可能是下图中的( )
A. B.
C. D.
答案:A
解析:
解答:解:A、在0~t内,磁场方向垂直纸面向外,且均匀增大,根据法拉第电磁感应定律,则产生的感应电动势为定值,电流为定值,根据楞次定律,感应电流的方向为顺时针方向,则电流为负值.
在t~t内,磁场方向垂直纸面向外,且均匀减小,感应电流为定值,根据楞次定律,感应电流的方向为逆时针方向,则电流为正值.
在t~t 内,磁场方向垂直纸面向里,且均匀增大,电流为定值,根据楞次定律,感应电流的方向为逆时针方向,则电流为正值.
在t~2t内,磁场方向垂直纸面向里,且均匀减小,感应电流为定值,根据楞次定律,感应电流的方向为顺时针方向,则电流为负值,故A正确.
B、在0~t内,磁场方向垂直纸面向外,且均匀减小,根据法拉第电磁感应定律,则产生的感应电动势为定值,电流为定值,根据楞次定律,感应电流的方向为逆时针方向,则电流为正值,故B错误;
C、在0~t内,磁场方向垂直纸面向外,且非均匀增大,根据法拉第电磁感应定律,则产生的感应电动势不是定值,电流不是定值,故C错误.
D、磁场的方向不变,则与图中电流方向不符.故D错误.
故选:A.
分析:线圈中因磁通量发生变化,才导致线圈产生感应电动势,从而形成感应电流.由楞次定律可推断出磁场的变化及磁通量的变化.
二.填空题(共5小题)
16. 1831年 (选填“奥斯特”或“法拉第”)发现了电磁感应现象.大量实验表明,回路中所产生的感应电动势大小与穿过该回路的磁通量的 (选填“变化量”或“变化率”)成正比.
答案:法拉第,变化率
解析:
解答:解:在奥斯特发现电流周围存在磁场后,法拉第发现了电磁感应现象;
根据E=n,知感应电动势的大小与穿过回路的磁通量的变化率成正比.
故答案为:法拉第,变化率.
分析:根据法拉第发现了电磁感应现象,而奥斯特发现电流周围存在磁场,并根据法拉第电磁感应定律,E=n,从而即可求解.
17.如图所示,使闭合矩形线圈在匀强磁场中绕垂直于磁场方向的转轴匀速转动,在线圈中就会产生交流电.已知磁场的磁感应强度为B,线圈abcd面积为S,线圈转动的角速度为ω.当线圈转到如图位置时,线圈中的感应电动势为 ;当线圈从图示位置转过90°时,线圈中的感应电动势为 .
答案:0,BSω
解析:
解答:解:当线框平面与磁场垂直时,穿过线框的磁通量变化率为零,感应电动势为零;
当线框从中性面位置转过90°,线框平面与中性面垂直,产生的感应电动势为BSω;
故答案为:0,BSω
分析:线框位于中性面时,穿过线框的磁通量最大,磁通量的变化率为零,感应电动势为零;
由法拉第电磁感应定律可以求出感应电动势.
18.如图所示,线圈内有理想边界的磁场,当磁感应强度均匀增加时,有一带电粒子静止于水平放置的平行板电容器中间,则此粒子电性是 ,若增大磁感应强度的变化率,则带电粒子将 (填“向上运动”“向下运动”或静止”)
答案:负,向上运动
解析:
解答:解:当磁场均匀增加时,由楞次定律可判断上极板带正电.所以平行板电容器的板间的电场方向向下,带电粒子受重力和电场力平衡,所以粒子带负电.
若增大磁感应强度的变化率,感应电动势增大,粒子受的电场力增大,则带电粒子将向上运动.
故答案为:负,向上运动
分析:带电粒子受重力和电场力平衡,由楞次定律可判断极板带电性质,由法拉第电磁感应定律可得出感应电动势变化,从而知道电场力的变化.
19.如图所示,A、B两个闭合线圈用同样的导线制成,匝数都为10匝,半径rA=2rB图示区域内有磁感应强度均匀减小的匀强磁场,则A、B线圈中产生的感应电动势之比为EA:EB= ,线圈中的感应电流之比IA:IB= .
答案:1:1,1:2
解析:
解答:解:根据法拉第电磁感应定律E=n=n,题中n相同,相同,面积S也相同,
则得到A、B环中感应电动势EA:EB=1:1.
根据电阻定律R=ρ,L=n 2πr,ρ、S相同,则电阻之比为:RA:RB=rA:rB=2:1,
根据欧姆定律I=E/R得产生的感应电流之比为:IA:IB=1:2.
故答案为:1:1,1:2.
分析:根据法拉第电磁感应定律E=n=n,研究A、B环中感应电动势EA:EB.根据电阻定律求出两环电阻之比,再欧姆定律求解电流之比IA:IB.
20.金属线圈ABC构成一个等腰直角三角形,腰长为a,绕垂直于纸面通过A的轴在纸面内匀速转动,角速度ω,如图所示.如加上一个垂直纸面向里的磁感应强度为B的匀强磁场,则B、A间的电势差UBA= ,B、C间的电势差UBC= .
答案:Bωa2,Bωa2
解析:
解答:解:AC、BC、AB均绕垂直于A的轴以角速度ω匀速转动,△ABC中磁通量不变,所以线圈中没有电流.
但当单独考虑每条边时,三边均切割磁感线,均有感应电动势产生,且B点电势大于C点电势和A点电势.
则有UBA=EBA=BL=BωLAB2=Bωa2,
UCA=ECA=BωLAC2=Bωa2,
UBC=UBA﹣UCA=Bωa2﹣Bωa2=Bωa2.
故答案为:Bωa2,Bωa2.
分析:根据法拉第电磁感应定律,求得感应电动势的大小,再结合闭合电路欧姆定律,及楞次定律从而确定两点的电势差,从而即可求解.
三.解答题(共5小题)
21.如图所示,一个单匝矩形线圈水平放在桌面上,再线圈中心上方有一竖直的条形磁体,此时线圈内的磁通量为0.05Wb.在0.5s的时间内,将该条形磁体从图示位置竖放到线圈内的桌面上,此时线圈内的磁通量为0.10Wb.试求此过程:
(1)线圈内磁通量的变化量;
(2)线圈中产生的感应电动势大小.
答案:(1)线圈的磁通量的变化量0.05Wb;
(2)线圈产生的感应电动势的大小为0.1V
解析:
解答:解:(1)磁通量的变化为:
△Φ=Φ′﹣Φ=0.10﹣0.05=0.05Wb;
(2)由法拉第电磁感应定律可得感应电动势为:
E=n=1×=0.1V;
答:(1)线圈的磁通量的变化量0.05Wb;
(2)线圈产生的感应电动势的大小为0.1V.
分析:(1)由磁通量的定义式可以求出磁通量的变化;
(2)由法拉第电磁感应定律可以求出感应电动势.
22.在应用法拉第电磁感应定律求感应电动势时有两种方法,请你分别写出这两种表达式并指出表达式的应用范围.
答案:由法拉第电磁感应定律可知;E=n,即E与磁通量的变化率成正比,即电动势取决于磁通量的变化快慢,此公式应用于平均感应电动势的计算;
对于导体切割磁感线产生感应电动势的情况,常采用E=BLv来计算,使用条件为B、L、v两两垂直的情况,不垂直式进行正交分解,取垂直的分量.此公式既可以计算匀强磁场中导体运动产生的平均感应电动势,也可以计算非匀强磁场瞬时感应电动势.
解析:
解答:解:由法拉第电磁感应定律可知;E=n,即E与磁通量的变化率成正比,即电动势取决于磁通量的变化快慢,此公式应用于平均感应电动势的计算;
对于导体切割磁感线产生感应电动势的情况,常采用E=BLv来计算,使用条件为B、L、v两两垂直的情况,不垂直式进行正交分解,取垂直的分量.此公式既可以计算匀强磁场中导体运动产生的平均感应电动势,也可以计算非匀强磁场瞬时感应电动势.
分析:由法拉第电磁感应定律可知,闭合电路中产生的感应电动势的大小与磁通量的变化率成正比,一般公式为:E=n,其中n为线圈的匝数;对于导体切割磁感线产生感应电动势的情况,常采用E=BLv来计算
23.如图甲,100匝的线圈(图中只画了2匝)两端A、B与一个阻值R=48Ω的电阻相连,其线圈的电阻r=2Ω,线圈内有指向纸内方向的磁场,线圈中的磁通量在按图乙所示规律变化.
(1)如果A、B两端与一理想电压表相连,哪端该接电压表标+号的接线柱?
(2)该线圈产生的感应电动势等于多少?
(3)如果A、B两端与一理想电压表相连,则电压表的示数为多少?
答案:(1)如果A、B两端与一理想电压表相连,A端该接电压表标+号的接线柱;
(2)该线圈产生的感应电动势等于50V;
(3)如果A、B两端与一理想电压表相连,则电压表的示数为48V
解析:
解答:解:(1)线圈相当于电源,由楞次定律可知A相当于电源的正极,B相当于电源的负极.故A应该与理想电压表的+号接线柱相连.
(2)由法拉第电磁感应定律得:E=n=100x=50V
(3)由闭合电路的欧姆定律得:==1A
又由部分电路的欧姆定律得:U=IR=1×48=48V
答:(1)如果A、B两端与一理想电压表相连,A端该接电压表标+号的接线柱;
(2)该线圈产生的感应电动势等于50V;
(3)如果A、B两端与一理想电压表相连,则电压表的示数为48V.
分析:(1)根据楞次定律判断感应电流的方向.线圈相当于电源,即可判断电压表的接法.
(2、3)由图求出磁通量的变化率.根据法拉第电磁感应定律求出回路中感应电动势,得到电压表的读数;
24.一个面积为0.2m2的100匝线圈处在匀强磁场中,磁场方问垂直于线圈平面,已知磁感应强度随时间变化的规律为B=(2+0.2t)T,定值电阻R=6Ω,线圈电阻r=4Ω,求:
(1)线圈中磁通量的变化率和回路的感应电动势;
(2)a、b两点间电压Uab.
答案:(1)磁通量变化率为0.04Wb/s;回路的感应电动势为4V;
(2)ab两点间电压Uab为2.4V
解析:
解答:解:(1)磁通量的变化率=S=0.2×0.2=0.04Wb/s.
根据法拉第电磁感应定律得,感应电动势E=n=100×0.04V=4V.
(2)根据欧姆定律得,ab间的电压U=R=×6V=2.4V.
答:(1)磁通量变化率为0.04Wb/s;回路的感应电动势为4V;
(2)ab两点间电压Uab为2.4V.
分析:根据磁感应强度的变化率求出磁通量的变化率,结合法拉第电磁感应定律求出回路中的感应电动势,通过欧姆定律求出ab两点间的电压.
25.一个300匝的线圈,穿过它的磁通量在0.01s内由6×10﹣2Wb均匀地减小到3×10﹣2Wb.求线圈中的感应电动势的大小.
答案:线圈中的感应电动势为900V
解析:
解答:解:根据法拉第电磁感应定律得:
E=N=300×=900V;
答:线圈中的感应电动势为900V.
分析:线圈的磁通量变化时,产生感应电动势,由法拉第电磁感应定律可得感应电动势大小.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 17 页 (共 17 页) 版权所有@21世纪教育网
