第四单元比例(知识梳理+拔高训练)二2024-2025学年六年级数学下学期培优检测卷(人教版)
文档属性
| 名称 | 第四单元比例(知识梳理+拔高训练)二2024-2025学年六年级数学下学期培优检测卷(人教版) |

|
|
| 格式 | docx | ||
| 文件大小 | 710.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-09 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
第四单元比例(知识梳理+拔高训练)二
知识梳理
知识点01:正比例
两个相关联的量,一个量变化,另一个量也随着变化,如果这两个量中相对应的两个数的比值(也就是商)一定,那么这两个量就叫作成正比例的量,它们的关系叫作正比例关系。
若用字母x和y表示两个相关联的量,用字母k表示它们的比值,则正比例关系可以表示为=k(一定)。
判断两个量是否成正比例的方法:首先判断两个量是不是相关联的量,再判断两个量中相对应的两个数的比值是否一定,最后判断两个量是否成正比例。
知识点02:反比例
两个相关联的量,一个量变化,另一个量也随着变化,如果这两个量中相对应的两个数的积一定,那么这两个量就叫作成反比例的量,它们的关系叫作反比例关系。
若用字母x和y表示两个相关联的量,用字母k表示它们的积,则反比例关系可以表示为xy=k(一定)。
判断两个量是否成反比例的方法:首先判断两个量是不是相关联的量,再判断两个量中相对应的两个数的积是否一定,最后判断两个量是否成反比例。
拔高训练
一、填空题(共20分)
1.(2分)比例的两个外项的积是810,其中一个内项是15,另一个内项是( )。
2.(2分)在20以内的合数中选4个数组成一个比例,可以是( )。
3.(2分)小明卡牌数量的40%等于小亮卡牌数量的75%,那么小明卡牌数量与小亮卡牌数量的最简整数比是( )。
4.(2分)A×B=C,A一定时,B和C成( )比例,C一定时,A和B成( )比例。
5.(2分)东东沿着直尺的方向将橡皮筋拉紧(如图,AC是橡皮筋示意图,B是橡皮筋上的一点)。如果点A的位置固定不变,沿着原来的方向将橡皮筋拉长,使点C的位置在15cm处,此时点B的位置在( )cm处。
6.(2分)为了庆祝六一节每张卡片减价20%,用同样多的钱可以多买6张,原来可以买( )张卡片。
7.(2分)在比例尺是1∶20000的图纸上,量得休闲广场的长是4厘米,宽是3厘米。休闲广场实际的面积是( )公顷。
8.(2分)将长为6厘米,宽3厘米的长方形按5∶1放大,得到的图形面积是( )平方厘米。
9.(2分)填表。
比例尺 图上距离 实际距离
1∶50000 ( )cm 3.2km
( ) 2.6cm 104km
10.(2分)一个长方形的周长是24分米,长和宽都是质数,这个长方形的面积是( )平方分米。将这个长方形按1∶2缩小后,缩小后的面积是原来长方形面积的( )。
二、判断题(共10分)
11.(2分)比例尺1∶1表示图上距离和实际距离相等。( )
12.(2分)比的前项和后项都扩大到原来的5倍,得到一个新的比,这两个比能组成比例。( )
13.(2分)工作时间一定,生产每个零件所用的时间和零件总数成反比例。( )
14.(2分)根据4×3=2×6,可以写出其中一个比例4∶6=3∶2。( )
15.(2分)淘气和爷爷的今年年龄的岁数比是,淘气今年的年龄是4岁,爷爷今年的年龄是58岁。( )
三、选择题(共10分)
16.(2分)盒子里有黑、白两种棋子,先放入一些白棋子,这样使得盒子中黑、白棋子的比是2∶5,然后又放入一些黑棋子,这样使得盒子中的黑、白棋子的比是3∶5。如果放入的黑棋子和白棋子的数量比是3∶7,那么原来盒子中黑、白棋子的数量之比是( )。
A.6∶5 B.5∶6 C.4∶3 D.3∶4
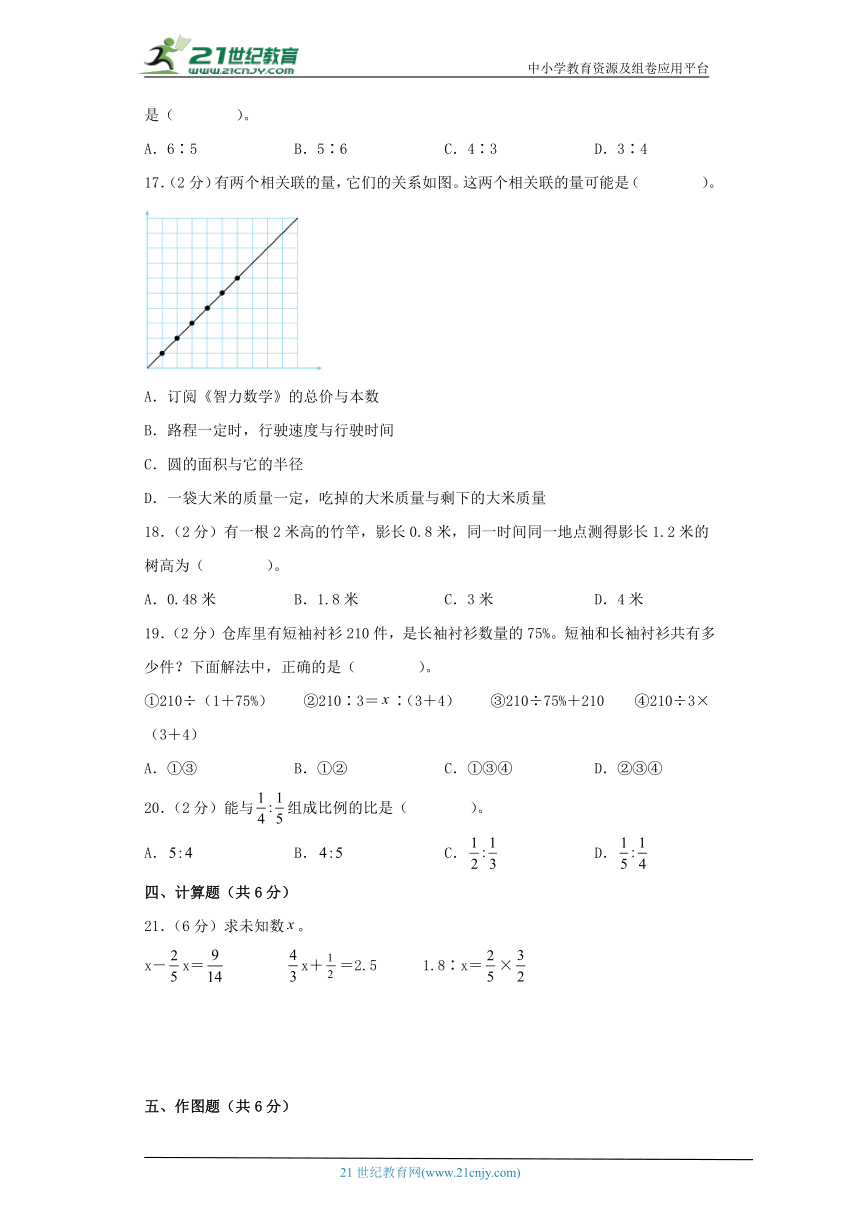
17.(2分)有两个相关联的量,它们的关系如图。这两个相关联的量可能是( )。
A.订阅《智力数学》的总价与本数
B.路程一定时,行驶速度与行驶时间
C.圆的面积与它的半径
D.一袋大米的质量一定,吃掉的大米质量与剩下的大米质量
18.(2分)有一根2米高的竹竿,影长0.8米,同一时间同一地点测得影长1.2米的树高为( )。
A.0.48米 B.1.8米 C.3米 D.4米
19.(2分)仓库里有短袖衬衫210件,是长袖衬衫数量的75%。短袖和长袖衬衫共有多少件?下面解法中,正确的是( )。
①210÷(1+75%) ②210∶3=∶(3+4) ③210÷75%+210 ④210÷3×(3+4)
A.①③ B.①② C.①③④ D.②③④
20.(2分)能与组成比例的比是( )。
A. B. C. D.
四、计算题(共6分)
21.(6分)求未知数。
x-x= x+=2.5 1.8∶x=×
五、作图题(共6分)
22.(6分)篮球场长28米,宽15米。下图是比例尺为1∶250的篮球场平面图,小明、小丽、小红在篮球场上的大致位置如图所示。小明在距边线2.5米的3分线上,小丽在3分线的中点上,小红在距底线4米的3分线上。请标出他们的准确位置。
六、解答题(共48分)
23.(6分)李叔叔承包了两块水稻田,面积分别为0.5公顷和0.8公顷。秋收时,两块水稻田的产量分别为3.75吨和6吨。两块水稻田的产量与面积之比,是否可以组成比例?如果可以组成比例,指出比例的内项和外项。
24.(6分)餐馆给餐具消毒,要用100毫升消毒液配成消毒水,如果消毒液与水的比是,应加入多少升水?
25.(6分)在比例尺为1∶5000000的地图上量的甲、乙两地的距离是12.6厘米,客车和货车分别从两地同时出发相向而行,5小时后两车相遇。已知客车的速度是每小时70千米,货车的速度是每小时多少千米?
26.(6分)某工程队铺一条管道,前6天铺了240米,照这样计算,还要8天才能把管道铺完,这条管道一共长多少米?(用比例知识解答)
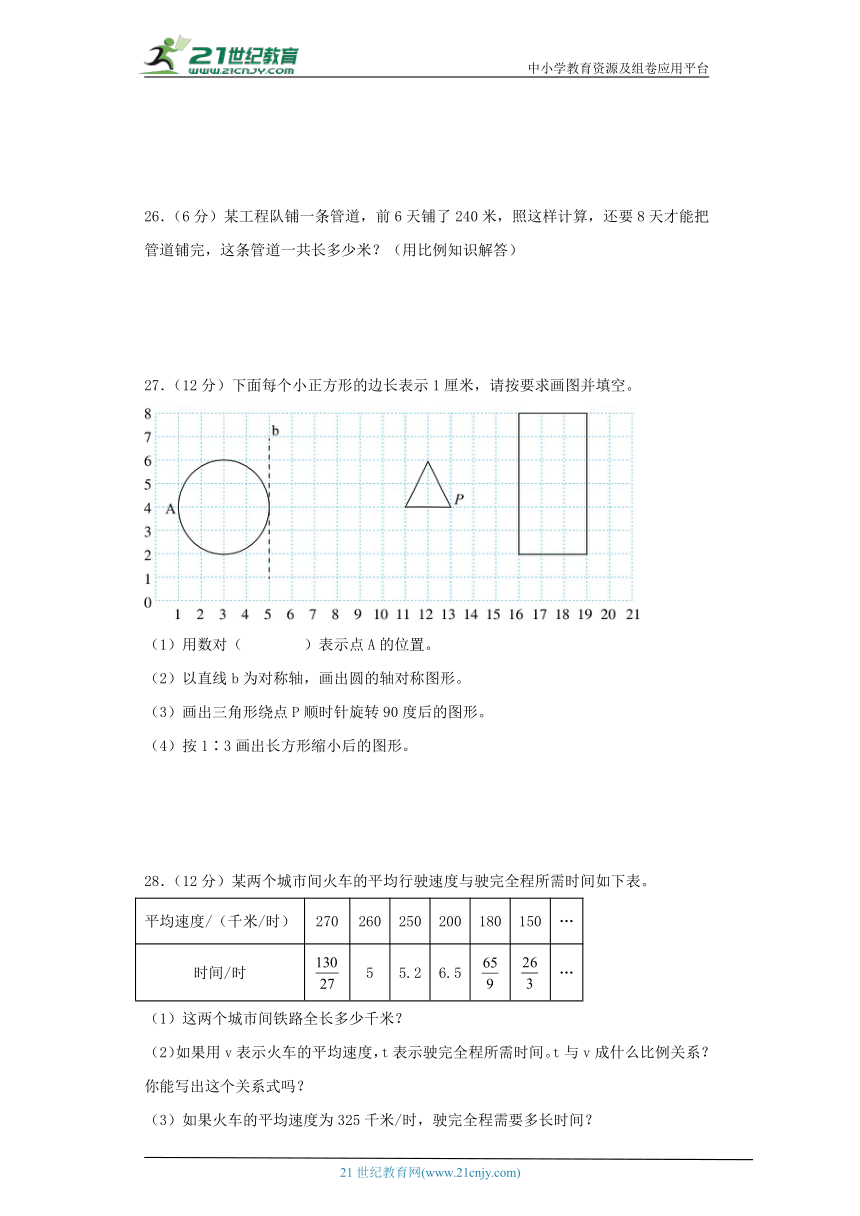
27.(12分)下面每个小正方形的边长表示1厘米,请按要求画图并填空。
(1)用数对( )表示点A的位置。
(2)以直线b为对称轴,画出圆的轴对称图形。
(3)画出三角形绕点P顺时针旋转90度后的图形。
(4)按1∶3画出长方形缩小后的图形。
28.(12分)某两个城市间火车的平均行驶速度与驶完全程所需时间如下表。
平均速度/(千米/时) 270 260 250 200 180 150 …
时间/时 5 5.2 6.5 …
(1)这两个城市间铁路全长多少千米?
(2)如果用v表示火车的平均速度,t表示驶完全程所需时间。t与v成什么比例关系?你能写出这个关系式吗?
(3)如果火车的平均速度为325千米/时,驶完全程需要多长时间?
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案
1.54
【分析】比例的基本性质:在比例里,两个外项的积等于两个内项的积。
已知一个比例的两个外项的积是810,根据比例的基本性质,那么这个比例的两个内项的积也是810;用两个内项的积除以已知的内项,即可求出另一个内项。
【详解】810÷15=54
另一个内项是54。
2.4∶6=10∶15
【分析】先列举出20以内的所有合数,再从中找出4个合数,两两相乘,积相等的即可根据比例的基本性质组成一个比例。
一个数,如果除了1和它本身还有别的因数,那么这样的数叫做合数。
比例的基本性质:在比例里,两个外项的积等于两个内项的积。
【详解】20以内的合数有:4,6,8,9,10,12,14,15,16,18,20;
4×15=60
6×10=60
4×15=6×10
可以组成比例:4∶6=10∶15。(答案不唯一)
3.15∶8
【分析】根据小明卡牌数量的40%等于小亮卡牌数量的75%,写成等式的形式为小明卡牌数量×40%=小亮卡牌数量×75%,再根据比例的基本性质:在比例中,两个外项的积等于两个内项的积,把等式改写成比例的形式,据此解答。
【详解】因为小明卡牌数量×40%=小亮卡牌数量×75%
所以小明卡牌数量∶小亮卡牌数量=75%∶40%
75%∶40%
=0.75∶0.4
=(0.75×100)∶(0.4×100)
=75∶40
=(75÷5)∶(40÷5)
=15∶8
因此小明卡牌数量与小亮卡牌数量的最简整数比是15∶8。
4. 正 反
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例。
【详解】A×B=C,A一定时,B和C成正比例,C一定时,A和B成反比例。
【点睛】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再作判断。
5.10
【分析】因为橡皮的弹性一定,所以原来B、C点的位置和拉长后B、C点的位置存在正比例关系,所以设此时点B的位置在xcm处,即可算出答案。
【详解】解:设此时点B的位置在xcm处。
6∶9=x∶15
9x=6×15
9x=90
9x÷9=90÷9
x=10
【点睛】此题考查了正比例关系以及解比例的应用。
6.24
【分析】先设原来卡片的单价是1,把原来卡片的单价看作单位“1”,现在每张卡片减价20%,则现在每张卡片的价格是原来的(1-20%),用原价乘(1-20%),求出现在每张卡片的价格;
根据“用同样多的钱”可知,总钱数不变,即单价×数量=总价(一定),乘积一定,则单价和数量成反比例关系,据此列出反比例方程,并求解。
【详解】设原来卡片的单价是1,现在卡片的单价是:
1×(1-20%)
=1×0.8
=0.8
解:设原来可以买张卡片。
1×=0.8×(+6)
=0.8+4.8
-0.8=4.8
0.2=4.8
=4.8÷0.2
=24
原来可以买24张卡片。
【点睛】先确定总钱数不变,再根据单价、数量、总价之间的关系,得出单价和数量成反比例关系,据此列出相应的比例方程。
7.48
【分析】实际距离=图上距离÷比例尺,据此求出休闲广场实际的长和宽。根据“长方形面积=长×宽”求出广场的实际面积。1公顷=10000平方米,据此将面积单位换算到公顷。
【详解】4÷=4×20000=80000(厘米)=800(米)
3÷=3×20000=60000(厘米)=600(米)
800×600=480000(平方米)=48(公顷)
所以,休闲广场的实际面积是48公顷。
8.450
【分析】根据图上距离=实际距离×比例尺,因为按5∶1放大,所以长方形的长是6×5=30(厘米),宽是3×5=15(厘米),再根据长方形的面积=长×宽,求出扩大后的长方形的面积即可。
【详解】6×5=30(厘米)
3×5=15(厘米)
30×15=450(平方厘米)
得到的图形的面积是450平方厘米。
9.6.4;1∶4000000
【分析】根据比例尺=图上距离∶实际距离,实际距离=图上距离÷比例尺,图上距离=实际距离×比例尺,代入数据解答即可。
【详解】3.2km=320000cm
320000×=6.4(cm)
2.6cm∶104km
=2.6cm∶10400000cm
=(2.6×10÷26)∶(10400000×10÷26)
=1∶4000000
比例尺 图上距离 实际距离
1∶50000 6.4cm 3.2km
1∶4000000 2.6cm 104km
10. 35
【分析】根据长方形的周长=(长+宽)×2,用24÷2即可求出长方形长与宽的和,也就是12分米,然后将12分别拆成2个数相加,符合长、宽都是质数的只有12=5+7,所以长是7分米,宽是5分米;长方形按1∶2缩小,则长和宽分别缩小到原来的,用7÷2即可求出现在的长,用5÷2即可求出现在的宽,最后根据长方形的面积=长×宽,分别求出缩小前后长方形的面积,再用缩小后的面积除以缩小前的面积,即可求出缩小后的面积是原来长方形面积的几分之几。
【详解】24÷2=12(分米)
长和宽都是质数,
所以12=5+7
长是7分米,宽是5分米;
5÷2=2.5(分米)
7÷2=3.5(分米)
5×7=35(平方分米)
2.5×3.5=8.75(平方分米)
8.75÷35=
一个长方形的周长是24分米,长和宽都是质数,这个长方形的面积是35平方分米。将这个长方形按1∶2缩小后,缩小后的面积是原来长方形面积的。
【点睛】本题主要考查了长方形周长和面积公式的灵活应用、质数的认识、图形的缩小等,要熟练掌握每个知识点。
11.√
【分析】根据比例尺的意义可知,图上距离和实际距离的比,叫做这幅图的比例尺;即:图上距离∶实际距离=图上距离÷比例尺;据此解答。
【详解】由分析可得:图上距离和实际距离的比叫做比例尺;所以比例尺1∶1,说明图上距离和实际距离相等,原题说法正确。
故答案为:√
12.√
【分析】比的基本性质:比的前项和后项同时乘或除以相同的数(0除外),比值不变。
表示两个比相等的式子叫做比例。根据比例的意义可知,比值相等的两个比可以组成比例。
【详解】如:8∶5=8÷5=
(8×5)∶(5×5)=40∶25
40∶25=40÷25=
比值相等,则8∶5=40∶25;
所以,比的前项和后项都扩大到原来的5倍,得到一个新的比,这两个比能组成比例。
原题说法正确。
故答案为:√
13.√
【分析】判断两种相关联的量成不成比例,成什么比例,就看这两种量是对应的比值一定, 还是对应的乘积一定,如果是比值一定,就成正比例;如果是乘积一定,就成反比例;如果是其它的量一定或乘积、比值不一定,就不成比例。
【详解】因生产每个零件所用的时间×零件总数=总工作时间(一定)
原题说法正确。
故答案为:√
【点睛】此题属于根据正、反比例的意义,辨识两种相关联的量成不成比例,成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定,还是对应的其它量一定,再做出判断。
14.×
【分析】根据比例的基本性质可知,在比例里,两个外项的积等于两个内项的积。题目中写出的比例是4∶6=3∶2,利用比例的基本性质判断即可。
【详解】若比例4∶6=3∶2成立,
则6×3=4×2应该成立才对,但6×3=18,4×2=8,18≠8,显然6×3=4×2不成立。
所以题目中写出的比例是错误的。
故答案为:×
【点睛】此题的解题关键是灵活运用比例的基本性质求解。
15.√
【分析】可设爷爷今年的年龄是x岁,根据题意,可列出比例式:2∶29=4∶x,解此比例即可知爷爷今年的年龄。再进行判断即可。
【详解】解:设爷爷今年的年龄是x岁。
2∶29=4∶x
2x=29×4
2x÷2=29×4÷2
x=58
原题说法正确。
故答案为:√
【点睛】本题考查了比例的应用,列出比例式2∶29=4∶x是解答的关键。
16.D
【分析】设原来有黑棋子x个,白棋子y个。先放入一些白棋子,这样使得盒子中黑、白棋子的比是2∶5,黑棋子没有发生改变,则现在的白棋子是黑棋子的,则白棋子有个,则放进白棋子的的数量=现在白棋子的数量-原来白棋子的数量=个。然后又放入一些黑棋子,这样使得盒子中的黑、白棋子的比是3∶5,白棋子的数量没有发生改变,现在黑棋子的数量是白棋子的,则现在黑棋子的数量为个,那么放进去的黑棋子的数量=现在黑棋子的数量-原来黑棋子的数量=个。根据放入的黑棋子和白棋子的数量比是3∶7列出比例,再根据比例的基本性质化简比例得出,根据比例的基本性子,x∶y=3∶4。
【详解】设:原来有黑棋子x个,白棋子y个。
x∶y=3∶4
原来盒子中黑、白棋子的数量之比是3∶4
故答案为:D
17.A
【分析】正比例关系的图像是一条直线,由图可以看出这两个量成正比例关系,判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例。
【详解】A.《智力数学》订阅的总价÷本数=单价(一定),商一定,所以《智力数学》订阅的总价和本数成正比例;
B.行驶速度×时间=总路程(一定),是对应的乘积一定,所以速度和所用的时间成反比例;
C.因为圆的面积÷它的半径=π×半径(不一定),是圆的面积与它的半径的比值不一定,既不符合正比例的意义,也不符合反比例的意义;
D.因为吃掉的大米质量+剩下的质量=大米的总量(一定),既不符合正比例才意义,也不符合反比例的意义;
故答案为:A
18.C
【分析】根据同一时间同一地点杆高与影长成正比例可知,竹竿的高与竹竿的影长的比值与树的高与树的影长的比值相等,即2∶0.8的比值和树的高∶1.2的比值相等,根据这个数量关系可列比例解答。
【详解】解:设树高x米。
x∶1.2=2∶0.8
0.8x=1.2×2
0.8x=2.4
0.8x÷0.8=2.4÷0.8
x=3
树高3米。
故答案为:C
19.D
【分析】①210÷(1+75%),意思是210件短袖衬衫比长袖衬衫的数量多75%,把长袖衬衫的数量看作单位“1”,则短袖衬衫是长袖衬衫数量的(1+75%),单位“1”未知,用短袖衬衫的数量除以(1+75%),求出长袖衬衫的数量。
②将75%化成,=3∶4,把210件短袖衬衫的数量看作3份,长袖衬衫的数量看作4份,一共是(3+4)份;根据衬衫数量∶份数=一份数(一定),列出正比例方程;
③把长袖衬衫的数量看作单位“1”,210件短袖衬衫是长袖衬衫数量的75%,单位“1”未知,用短袖衬衫的数量除以75%,求出长袖衬衫的数量,再加上短袖衬衫的数量,即是短袖和长袖衬衫的总数量。
④将75%化成,=3∶4,把210件短袖衬衫的数量看作3份,长袖衬衫的数量看作4份,一共是(3+4)份;用短袖衬衫的数量除以3,求出一份数,再用一份数乘总份数,即可求出短袖和长袖衬衫的总数量。
【详解】①210÷(1+75%),表示210件短袖衬衫比长袖衬衫的数量多75%,不符合题意,解法错误;
②75%==3∶4
解:设短袖和长袖衬衫共有件。
210∶3=∶(3+4)
3=210×(3+4)
3=1470
=1470÷3
=490
短袖和长袖衬衫共有490件,解法正确;
③210÷75%+210
=210÷0.75+210
=280+210
=490(件)
短袖和长袖衬衫共有490件,解法正确;
④75%==3∶4
210÷3×(3+4)
=70×7
=490(件)
短袖和长袖衬衫共有490件,解法正确;
综上所述,解法正确的是②③④。
故答案为:D
20.A
【分析】根据比例的性质,比例的两内项积等于两个外项的积,据此解答即可。
【详解】A.=1,=1,即=,=5∶4,故符合题意。
B.=,=,不等于,故不符合题意。
C.,,不等于,即不等于,故不符合题意。
D.,,不等于,即不等于,故不符合题意。
能与∶组成比例的比是5∶4。
故答案为:A
21.x=;x=;x=3
【分析】(1)先化简方程左边,得到x=,再两边同时除以即可;
(2)先左右两边同时减去,再两边同时除以即可;
(3)先计算方程右边,得到1.8∶x=,再根据比例的基本性质,化成3x=1.8×5,最后两边同时除以3即可。
【详解】x-x=
解:x=
x÷=÷
x=×
x=
x+=2.5
解:x+-=-
x=2
x÷=2÷
x=2×
x=
1.8∶x=×
解:1.8∶x=
3x=1.8×5
3x=9
3x÷3=9÷3
x=3
22.见详解
【分析】先确定底线和边线的位置,再根据公式:图上距离=实际距离×比例尺,算出小明距边线的图上距离,小红距底线的图上距离,最后标出他们的位置即可。
【详解】小明:2.5米=250厘米
250×=1(厘米)
小丽:
3分线的中点上
小红:4米=400厘米
400×=1.6(厘米)
他们的准确位置如图所示:
23.可以组成比例,3.75∶0.5=6∶0.8,其中3.75和0.8是外项,0.5和6是内项。
【分析】表示两个比相等的式子叫做比例。组成比例的四个数,两端的两项叫作比例的外项,中间的两项叫作比例的内项。
【详解】第一块水稻田的产量与面积之比是3.75∶0.5,比值是7.5;第二块水稻田的产量与面积之比是6∶0.8,比值是7.5;所以可以组成比例为3.75∶0.5=6∶0.8。其中3.75和0.8是外项,0.5和6是内项。(答案不唯一)
24.15升
【分析】由题意可知,设应加入x升水,根据消毒液的体积∶水的体积=1∶150,据此列比例解答即可。
【详解】解:设应加入x升水。
100毫升=0.1升
0.1∶x=1∶150
x=0.1×150
x=15
答:应加入15升水。
25.56千米
【分析】根据实际距离=图上距离÷比例尺,据此求出甲、乙两地的实际距离;然后设货车的速度是每小时x千米,再根据相遇问题中的等量关系:速度和×相遇时间=路程和,据此列方程解答即可。
【详解】解:设货车的速度是每小时x千米。
12.6÷=12.6×5000000=63000000(厘米)
63000000厘米=630千米
(70+x)×5=630
(70+x)×5÷5=630÷5
70+x=126
70+x-70=126-70
x=56
答:货车的速度是每小时56千米。
26.560米
【分析】根据题意可知,铺路的长度∶天数=每天铺路的长度(一定),比值一定,则铺路的长度与天数成正比例关系,据此列出正比例方程,并求解。
【详解】解:设这条管道一共长米。
240∶6=∶(6+8)
6=240×(6+8)
6=240×14
6=3360
=3360÷6
=560
答:这条管道一共长560米。
27.(1)(1,4)
(2)图见详解
(3)图见详解
(4)图见详解
【分析】(1)根据用数对表示点的位置的方法,数对的第一个数字表示列数,第二个数字表示行数,即可用数对表示出点A的位置;
(2)根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴b的右侧合适位置找到圆心,再画一个半径是2格的圆即可;
(3)根据旋转的特征,图形绕P点顺时针旋转90度,点P的位置不变,其余各部分均绕此点按相同的方向旋转相同的度数即可画出旋转后的图形;
(4)根据图形放大与缩小的意义,长方形按1:3缩小后的图形,是长和宽分别为2和1的长方形,据此画图即可。
【详解】(1)由分析可知:点A的位置用数对可表示为(1,4)。
(2)、(3)、(4)作图如下:
28.(1)1300千米
(2)因为速度×时间=路程(一定),所以v与t成反比例关系。关系式:vt=1300
(3)4小时
【分析】(1)根据路程=速度×时间,应用一组对应的平均速度和时间,计算出铁路全长;
(2)各组数据中平均速度与时间的乘积是定值1300千米,速度×时间=路程,根据反比例的概念解答;
(3)vt=1300,当v=325时,计算出t,据此解答。
【详解】(1)(千米)
答:这两个城市间铁路全长1300千米。
(2)(千米)
(千米)
(千米)
……
因为速度×时间=路程(一定),所以v与t成反比例关系。关系式:vt=1300。
(3)(小时)
答:如果火车的平均速度为325千米/时,驶完全程需要4小时。
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
中小学教育资源及组卷应用平台
第四单元比例(知识梳理+拔高训练)二
知识梳理
知识点01:正比例
两个相关联的量,一个量变化,另一个量也随着变化,如果这两个量中相对应的两个数的比值(也就是商)一定,那么这两个量就叫作成正比例的量,它们的关系叫作正比例关系。
若用字母x和y表示两个相关联的量,用字母k表示它们的比值,则正比例关系可以表示为=k(一定)。
判断两个量是否成正比例的方法:首先判断两个量是不是相关联的量,再判断两个量中相对应的两个数的比值是否一定,最后判断两个量是否成正比例。
知识点02:反比例
两个相关联的量,一个量变化,另一个量也随着变化,如果这两个量中相对应的两个数的积一定,那么这两个量就叫作成反比例的量,它们的关系叫作反比例关系。
若用字母x和y表示两个相关联的量,用字母k表示它们的积,则反比例关系可以表示为xy=k(一定)。
判断两个量是否成反比例的方法:首先判断两个量是不是相关联的量,再判断两个量中相对应的两个数的积是否一定,最后判断两个量是否成反比例。
拔高训练
一、填空题(共20分)
1.(2分)比例的两个外项的积是810,其中一个内项是15,另一个内项是( )。
2.(2分)在20以内的合数中选4个数组成一个比例,可以是( )。
3.(2分)小明卡牌数量的40%等于小亮卡牌数量的75%,那么小明卡牌数量与小亮卡牌数量的最简整数比是( )。
4.(2分)A×B=C,A一定时,B和C成( )比例,C一定时,A和B成( )比例。
5.(2分)东东沿着直尺的方向将橡皮筋拉紧(如图,AC是橡皮筋示意图,B是橡皮筋上的一点)。如果点A的位置固定不变,沿着原来的方向将橡皮筋拉长,使点C的位置在15cm处,此时点B的位置在( )cm处。
6.(2分)为了庆祝六一节每张卡片减价20%,用同样多的钱可以多买6张,原来可以买( )张卡片。
7.(2分)在比例尺是1∶20000的图纸上,量得休闲广场的长是4厘米,宽是3厘米。休闲广场实际的面积是( )公顷。
8.(2分)将长为6厘米,宽3厘米的长方形按5∶1放大,得到的图形面积是( )平方厘米。
9.(2分)填表。
比例尺 图上距离 实际距离
1∶50000 ( )cm 3.2km
( ) 2.6cm 104km
10.(2分)一个长方形的周长是24分米,长和宽都是质数,这个长方形的面积是( )平方分米。将这个长方形按1∶2缩小后,缩小后的面积是原来长方形面积的( )。
二、判断题(共10分)
11.(2分)比例尺1∶1表示图上距离和实际距离相等。( )
12.(2分)比的前项和后项都扩大到原来的5倍,得到一个新的比,这两个比能组成比例。( )
13.(2分)工作时间一定,生产每个零件所用的时间和零件总数成反比例。( )
14.(2分)根据4×3=2×6,可以写出其中一个比例4∶6=3∶2。( )
15.(2分)淘气和爷爷的今年年龄的岁数比是,淘气今年的年龄是4岁,爷爷今年的年龄是58岁。( )
三、选择题(共10分)
16.(2分)盒子里有黑、白两种棋子,先放入一些白棋子,这样使得盒子中黑、白棋子的比是2∶5,然后又放入一些黑棋子,这样使得盒子中的黑、白棋子的比是3∶5。如果放入的黑棋子和白棋子的数量比是3∶7,那么原来盒子中黑、白棋子的数量之比是( )。
A.6∶5 B.5∶6 C.4∶3 D.3∶4
17.(2分)有两个相关联的量,它们的关系如图。这两个相关联的量可能是( )。
A.订阅《智力数学》的总价与本数
B.路程一定时,行驶速度与行驶时间
C.圆的面积与它的半径
D.一袋大米的质量一定,吃掉的大米质量与剩下的大米质量
18.(2分)有一根2米高的竹竿,影长0.8米,同一时间同一地点测得影长1.2米的树高为( )。
A.0.48米 B.1.8米 C.3米 D.4米
19.(2分)仓库里有短袖衬衫210件,是长袖衬衫数量的75%。短袖和长袖衬衫共有多少件?下面解法中,正确的是( )。
①210÷(1+75%) ②210∶3=∶(3+4) ③210÷75%+210 ④210÷3×(3+4)
A.①③ B.①② C.①③④ D.②③④
20.(2分)能与组成比例的比是( )。
A. B. C. D.
四、计算题(共6分)
21.(6分)求未知数。
x-x= x+=2.5 1.8∶x=×
五、作图题(共6分)
22.(6分)篮球场长28米,宽15米。下图是比例尺为1∶250的篮球场平面图,小明、小丽、小红在篮球场上的大致位置如图所示。小明在距边线2.5米的3分线上,小丽在3分线的中点上,小红在距底线4米的3分线上。请标出他们的准确位置。
六、解答题(共48分)
23.(6分)李叔叔承包了两块水稻田,面积分别为0.5公顷和0.8公顷。秋收时,两块水稻田的产量分别为3.75吨和6吨。两块水稻田的产量与面积之比,是否可以组成比例?如果可以组成比例,指出比例的内项和外项。
24.(6分)餐馆给餐具消毒,要用100毫升消毒液配成消毒水,如果消毒液与水的比是,应加入多少升水?
25.(6分)在比例尺为1∶5000000的地图上量的甲、乙两地的距离是12.6厘米,客车和货车分别从两地同时出发相向而行,5小时后两车相遇。已知客车的速度是每小时70千米,货车的速度是每小时多少千米?
26.(6分)某工程队铺一条管道,前6天铺了240米,照这样计算,还要8天才能把管道铺完,这条管道一共长多少米?(用比例知识解答)
27.(12分)下面每个小正方形的边长表示1厘米,请按要求画图并填空。
(1)用数对( )表示点A的位置。
(2)以直线b为对称轴,画出圆的轴对称图形。
(3)画出三角形绕点P顺时针旋转90度后的图形。
(4)按1∶3画出长方形缩小后的图形。
28.(12分)某两个城市间火车的平均行驶速度与驶完全程所需时间如下表。
平均速度/(千米/时) 270 260 250 200 180 150 …
时间/时 5 5.2 6.5 …
(1)这两个城市间铁路全长多少千米?
(2)如果用v表示火车的平均速度,t表示驶完全程所需时间。t与v成什么比例关系?你能写出这个关系式吗?
(3)如果火车的平均速度为325千米/时,驶完全程需要多长时间?
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案
1.54
【分析】比例的基本性质:在比例里,两个外项的积等于两个内项的积。
已知一个比例的两个外项的积是810,根据比例的基本性质,那么这个比例的两个内项的积也是810;用两个内项的积除以已知的内项,即可求出另一个内项。
【详解】810÷15=54
另一个内项是54。
2.4∶6=10∶15
【分析】先列举出20以内的所有合数,再从中找出4个合数,两两相乘,积相等的即可根据比例的基本性质组成一个比例。
一个数,如果除了1和它本身还有别的因数,那么这样的数叫做合数。
比例的基本性质:在比例里,两个外项的积等于两个内项的积。
【详解】20以内的合数有:4,6,8,9,10,12,14,15,16,18,20;
4×15=60
6×10=60
4×15=6×10
可以组成比例:4∶6=10∶15。(答案不唯一)
3.15∶8
【分析】根据小明卡牌数量的40%等于小亮卡牌数量的75%,写成等式的形式为小明卡牌数量×40%=小亮卡牌数量×75%,再根据比例的基本性质:在比例中,两个外项的积等于两个内项的积,把等式改写成比例的形式,据此解答。
【详解】因为小明卡牌数量×40%=小亮卡牌数量×75%
所以小明卡牌数量∶小亮卡牌数量=75%∶40%
75%∶40%
=0.75∶0.4
=(0.75×100)∶(0.4×100)
=75∶40
=(75÷5)∶(40÷5)
=15∶8
因此小明卡牌数量与小亮卡牌数量的最简整数比是15∶8。
4. 正 反
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例。
【详解】A×B=C,A一定时,B和C成正比例,C一定时,A和B成反比例。
【点睛】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再作判断。
5.10
【分析】因为橡皮的弹性一定,所以原来B、C点的位置和拉长后B、C点的位置存在正比例关系,所以设此时点B的位置在xcm处,即可算出答案。
【详解】解:设此时点B的位置在xcm处。
6∶9=x∶15
9x=6×15
9x=90
9x÷9=90÷9
x=10
【点睛】此题考查了正比例关系以及解比例的应用。
6.24
【分析】先设原来卡片的单价是1,把原来卡片的单价看作单位“1”,现在每张卡片减价20%,则现在每张卡片的价格是原来的(1-20%),用原价乘(1-20%),求出现在每张卡片的价格;
根据“用同样多的钱”可知,总钱数不变,即单价×数量=总价(一定),乘积一定,则单价和数量成反比例关系,据此列出反比例方程,并求解。
【详解】设原来卡片的单价是1,现在卡片的单价是:
1×(1-20%)
=1×0.8
=0.8
解:设原来可以买张卡片。
1×=0.8×(+6)
=0.8+4.8
-0.8=4.8
0.2=4.8
=4.8÷0.2
=24
原来可以买24张卡片。
【点睛】先确定总钱数不变,再根据单价、数量、总价之间的关系,得出单价和数量成反比例关系,据此列出相应的比例方程。
7.48
【分析】实际距离=图上距离÷比例尺,据此求出休闲广场实际的长和宽。根据“长方形面积=长×宽”求出广场的实际面积。1公顷=10000平方米,据此将面积单位换算到公顷。
【详解】4÷=4×20000=80000(厘米)=800(米)
3÷=3×20000=60000(厘米)=600(米)
800×600=480000(平方米)=48(公顷)
所以,休闲广场的实际面积是48公顷。
8.450
【分析】根据图上距离=实际距离×比例尺,因为按5∶1放大,所以长方形的长是6×5=30(厘米),宽是3×5=15(厘米),再根据长方形的面积=长×宽,求出扩大后的长方形的面积即可。
【详解】6×5=30(厘米)
3×5=15(厘米)
30×15=450(平方厘米)
得到的图形的面积是450平方厘米。
9.6.4;1∶4000000
【分析】根据比例尺=图上距离∶实际距离,实际距离=图上距离÷比例尺,图上距离=实际距离×比例尺,代入数据解答即可。
【详解】3.2km=320000cm
320000×=6.4(cm)
2.6cm∶104km
=2.6cm∶10400000cm
=(2.6×10÷26)∶(10400000×10÷26)
=1∶4000000
比例尺 图上距离 实际距离
1∶50000 6.4cm 3.2km
1∶4000000 2.6cm 104km
10. 35
【分析】根据长方形的周长=(长+宽)×2,用24÷2即可求出长方形长与宽的和,也就是12分米,然后将12分别拆成2个数相加,符合长、宽都是质数的只有12=5+7,所以长是7分米,宽是5分米;长方形按1∶2缩小,则长和宽分别缩小到原来的,用7÷2即可求出现在的长,用5÷2即可求出现在的宽,最后根据长方形的面积=长×宽,分别求出缩小前后长方形的面积,再用缩小后的面积除以缩小前的面积,即可求出缩小后的面积是原来长方形面积的几分之几。
【详解】24÷2=12(分米)
长和宽都是质数,
所以12=5+7
长是7分米,宽是5分米;
5÷2=2.5(分米)
7÷2=3.5(分米)
5×7=35(平方分米)
2.5×3.5=8.75(平方分米)
8.75÷35=
一个长方形的周长是24分米,长和宽都是质数,这个长方形的面积是35平方分米。将这个长方形按1∶2缩小后,缩小后的面积是原来长方形面积的。
【点睛】本题主要考查了长方形周长和面积公式的灵活应用、质数的认识、图形的缩小等,要熟练掌握每个知识点。
11.√
【分析】根据比例尺的意义可知,图上距离和实际距离的比,叫做这幅图的比例尺;即:图上距离∶实际距离=图上距离÷比例尺;据此解答。
【详解】由分析可得:图上距离和实际距离的比叫做比例尺;所以比例尺1∶1,说明图上距离和实际距离相等,原题说法正确。
故答案为:√
12.√
【分析】比的基本性质:比的前项和后项同时乘或除以相同的数(0除外),比值不变。
表示两个比相等的式子叫做比例。根据比例的意义可知,比值相等的两个比可以组成比例。
【详解】如:8∶5=8÷5=
(8×5)∶(5×5)=40∶25
40∶25=40÷25=
比值相等,则8∶5=40∶25;
所以,比的前项和后项都扩大到原来的5倍,得到一个新的比,这两个比能组成比例。
原题说法正确。
故答案为:√
13.√
【分析】判断两种相关联的量成不成比例,成什么比例,就看这两种量是对应的比值一定, 还是对应的乘积一定,如果是比值一定,就成正比例;如果是乘积一定,就成反比例;如果是其它的量一定或乘积、比值不一定,就不成比例。
【详解】因生产每个零件所用的时间×零件总数=总工作时间(一定)
原题说法正确。
故答案为:√
【点睛】此题属于根据正、反比例的意义,辨识两种相关联的量成不成比例,成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定,还是对应的其它量一定,再做出判断。
14.×
【分析】根据比例的基本性质可知,在比例里,两个外项的积等于两个内项的积。题目中写出的比例是4∶6=3∶2,利用比例的基本性质判断即可。
【详解】若比例4∶6=3∶2成立,
则6×3=4×2应该成立才对,但6×3=18,4×2=8,18≠8,显然6×3=4×2不成立。
所以题目中写出的比例是错误的。
故答案为:×
【点睛】此题的解题关键是灵活运用比例的基本性质求解。
15.√
【分析】可设爷爷今年的年龄是x岁,根据题意,可列出比例式:2∶29=4∶x,解此比例即可知爷爷今年的年龄。再进行判断即可。
【详解】解:设爷爷今年的年龄是x岁。
2∶29=4∶x
2x=29×4
2x÷2=29×4÷2
x=58
原题说法正确。
故答案为:√
【点睛】本题考查了比例的应用,列出比例式2∶29=4∶x是解答的关键。
16.D
【分析】设原来有黑棋子x个,白棋子y个。先放入一些白棋子,这样使得盒子中黑、白棋子的比是2∶5,黑棋子没有发生改变,则现在的白棋子是黑棋子的,则白棋子有个,则放进白棋子的的数量=现在白棋子的数量-原来白棋子的数量=个。然后又放入一些黑棋子,这样使得盒子中的黑、白棋子的比是3∶5,白棋子的数量没有发生改变,现在黑棋子的数量是白棋子的,则现在黑棋子的数量为个,那么放进去的黑棋子的数量=现在黑棋子的数量-原来黑棋子的数量=个。根据放入的黑棋子和白棋子的数量比是3∶7列出比例,再根据比例的基本性质化简比例得出,根据比例的基本性子,x∶y=3∶4。
【详解】设:原来有黑棋子x个,白棋子y个。
x∶y=3∶4
原来盒子中黑、白棋子的数量之比是3∶4
故答案为:D
17.A
【分析】正比例关系的图像是一条直线,由图可以看出这两个量成正比例关系,判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例。
【详解】A.《智力数学》订阅的总价÷本数=单价(一定),商一定,所以《智力数学》订阅的总价和本数成正比例;
B.行驶速度×时间=总路程(一定),是对应的乘积一定,所以速度和所用的时间成反比例;
C.因为圆的面积÷它的半径=π×半径(不一定),是圆的面积与它的半径的比值不一定,既不符合正比例的意义,也不符合反比例的意义;
D.因为吃掉的大米质量+剩下的质量=大米的总量(一定),既不符合正比例才意义,也不符合反比例的意义;
故答案为:A
18.C
【分析】根据同一时间同一地点杆高与影长成正比例可知,竹竿的高与竹竿的影长的比值与树的高与树的影长的比值相等,即2∶0.8的比值和树的高∶1.2的比值相等,根据这个数量关系可列比例解答。
【详解】解:设树高x米。
x∶1.2=2∶0.8
0.8x=1.2×2
0.8x=2.4
0.8x÷0.8=2.4÷0.8
x=3
树高3米。
故答案为:C
19.D
【分析】①210÷(1+75%),意思是210件短袖衬衫比长袖衬衫的数量多75%,把长袖衬衫的数量看作单位“1”,则短袖衬衫是长袖衬衫数量的(1+75%),单位“1”未知,用短袖衬衫的数量除以(1+75%),求出长袖衬衫的数量。
②将75%化成,=3∶4,把210件短袖衬衫的数量看作3份,长袖衬衫的数量看作4份,一共是(3+4)份;根据衬衫数量∶份数=一份数(一定),列出正比例方程;
③把长袖衬衫的数量看作单位“1”,210件短袖衬衫是长袖衬衫数量的75%,单位“1”未知,用短袖衬衫的数量除以75%,求出长袖衬衫的数量,再加上短袖衬衫的数量,即是短袖和长袖衬衫的总数量。
④将75%化成,=3∶4,把210件短袖衬衫的数量看作3份,长袖衬衫的数量看作4份,一共是(3+4)份;用短袖衬衫的数量除以3,求出一份数,再用一份数乘总份数,即可求出短袖和长袖衬衫的总数量。
【详解】①210÷(1+75%),表示210件短袖衬衫比长袖衬衫的数量多75%,不符合题意,解法错误;
②75%==3∶4
解:设短袖和长袖衬衫共有件。
210∶3=∶(3+4)
3=210×(3+4)
3=1470
=1470÷3
=490
短袖和长袖衬衫共有490件,解法正确;
③210÷75%+210
=210÷0.75+210
=280+210
=490(件)
短袖和长袖衬衫共有490件,解法正确;
④75%==3∶4
210÷3×(3+4)
=70×7
=490(件)
短袖和长袖衬衫共有490件,解法正确;
综上所述,解法正确的是②③④。
故答案为:D
20.A
【分析】根据比例的性质,比例的两内项积等于两个外项的积,据此解答即可。
【详解】A.=1,=1,即=,=5∶4,故符合题意。
B.=,=,不等于,故不符合题意。
C.,,不等于,即不等于,故不符合题意。
D.,,不等于,即不等于,故不符合题意。
能与∶组成比例的比是5∶4。
故答案为:A
21.x=;x=;x=3
【分析】(1)先化简方程左边,得到x=,再两边同时除以即可;
(2)先左右两边同时减去,再两边同时除以即可;
(3)先计算方程右边,得到1.8∶x=,再根据比例的基本性质,化成3x=1.8×5,最后两边同时除以3即可。
【详解】x-x=
解:x=
x÷=÷
x=×
x=
x+=2.5
解:x+-=-
x=2
x÷=2÷
x=2×
x=
1.8∶x=×
解:1.8∶x=
3x=1.8×5
3x=9
3x÷3=9÷3
x=3
22.见详解
【分析】先确定底线和边线的位置,再根据公式:图上距离=实际距离×比例尺,算出小明距边线的图上距离,小红距底线的图上距离,最后标出他们的位置即可。
【详解】小明:2.5米=250厘米
250×=1(厘米)
小丽:
3分线的中点上
小红:4米=400厘米
400×=1.6(厘米)
他们的准确位置如图所示:
23.可以组成比例,3.75∶0.5=6∶0.8,其中3.75和0.8是外项,0.5和6是内项。
【分析】表示两个比相等的式子叫做比例。组成比例的四个数,两端的两项叫作比例的外项,中间的两项叫作比例的内项。
【详解】第一块水稻田的产量与面积之比是3.75∶0.5,比值是7.5;第二块水稻田的产量与面积之比是6∶0.8,比值是7.5;所以可以组成比例为3.75∶0.5=6∶0.8。其中3.75和0.8是外项,0.5和6是内项。(答案不唯一)
24.15升
【分析】由题意可知,设应加入x升水,根据消毒液的体积∶水的体积=1∶150,据此列比例解答即可。
【详解】解:设应加入x升水。
100毫升=0.1升
0.1∶x=1∶150
x=0.1×150
x=15
答:应加入15升水。
25.56千米
【分析】根据实际距离=图上距离÷比例尺,据此求出甲、乙两地的实际距离;然后设货车的速度是每小时x千米,再根据相遇问题中的等量关系:速度和×相遇时间=路程和,据此列方程解答即可。
【详解】解:设货车的速度是每小时x千米。
12.6÷=12.6×5000000=63000000(厘米)
63000000厘米=630千米
(70+x)×5=630
(70+x)×5÷5=630÷5
70+x=126
70+x-70=126-70
x=56
答:货车的速度是每小时56千米。
26.560米
【分析】根据题意可知,铺路的长度∶天数=每天铺路的长度(一定),比值一定,则铺路的长度与天数成正比例关系,据此列出正比例方程,并求解。
【详解】解:设这条管道一共长米。
240∶6=∶(6+8)
6=240×(6+8)
6=240×14
6=3360
=3360÷6
=560
答:这条管道一共长560米。
27.(1)(1,4)
(2)图见详解
(3)图见详解
(4)图见详解
【分析】(1)根据用数对表示点的位置的方法,数对的第一个数字表示列数,第二个数字表示行数,即可用数对表示出点A的位置;
(2)根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴b的右侧合适位置找到圆心,再画一个半径是2格的圆即可;
(3)根据旋转的特征,图形绕P点顺时针旋转90度,点P的位置不变,其余各部分均绕此点按相同的方向旋转相同的度数即可画出旋转后的图形;
(4)根据图形放大与缩小的意义,长方形按1:3缩小后的图形,是长和宽分别为2和1的长方形,据此画图即可。
【详解】(1)由分析可知:点A的位置用数对可表示为(1,4)。
(2)、(3)、(4)作图如下:
28.(1)1300千米
(2)因为速度×时间=路程(一定),所以v与t成反比例关系。关系式:vt=1300
(3)4小时
【分析】(1)根据路程=速度×时间,应用一组对应的平均速度和时间,计算出铁路全长;
(2)各组数据中平均速度与时间的乘积是定值1300千米,速度×时间=路程,根据反比例的概念解答;
(3)vt=1300,当v=325时,计算出t,据此解答。
【详解】(1)(千米)
答:这两个城市间铁路全长1300千米。
(2)(千米)
(千米)
(千米)
……
因为速度×时间=路程(一定),所以v与t成反比例关系。关系式:vt=1300。
(3)(小时)
答:如果火车的平均速度为325千米/时,驶完全程需要4小时。
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
