北师大版六年级下册数学第四单元正比例与反比例选择题训练(含解析)
文档属性
| 名称 | 北师大版六年级下册数学第四单元正比例与反比例选择题训练(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 439.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-10 06:37:17 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
北师大版六年级下册数学第四单元正比例与反比例选择题训练
1.下列选项中的两个量成反比例关系的是( )。
A.人的体重和身高 B.梯形面积一定,它的上底和下底
C.路程一定,行驶速度和时间 D.订《意林(少年版)》的份数和总钱数
2.六(2)班举行50米×8往返跑测试。折返点在起点的北偏东45°方向。下面说法错误的是( )。
A.跑步速度与所用时间成正比例
B.跑步速度与所用时间成反比例
C.向折返点跑是北偏东45°方向
D.向起点跑是南偏西45°方向
3.下面每组中的两个量,成正比例关系的是( )。
A.一袋大米50千克,大米的袋数和总质量 B.小明的年龄和身高
C.小丽从家到学校,走了的路程和未走的路程 D.行驶一段路程,行驶的速度和所用的时间
4.下面几组相关联的量中,成反比例关系的是( )。
A.小明的年龄和妈妈的年龄。 B.平行四边形的面积一定,它的底和高。
C.班级的出勤率一定,出勤人数和总人数。 D.读一本书,已经读了的页数与未读的页数。
5.若圆柱的侧面积是314cm2,则不与圆柱的高成反比例的是( )。
A.底面积 B.底面直径 C.底面周长 D.底面半径
6.一个圆柱若高增加2分米,则表面积增加25.12平方分米,体积增加。原来圆柱的表面积为( )平方分米。
A.188.4 B.157 C.150.72 D.125.6
7.若,则x和y( )。
A.成正比例 B.成反比例 C.不成比例 D.无法确定
8.下面说法错误的有( )个。
①乘积为1的两个数一定互为倒数。
②一本书的已读页数和未读页数成反比例。
③一副三角尺能拼出145°的角。
④两个等底等高的三角形就可以拼出平行四边形。
A.1 B.2 C.3 D.4
9.x、y均不为0,下列和成反比例关系的是( )。
A. B. C. D.
10.小李加工一批零件,工作时间与加工零件的个数的关系如下图,下列说法错误的是( )。
A.加工零件的个数与工作时间成正比例关系。
B.N表示400个零件。
C.M表示3.2小时。
D.如果有一点P表示5小时做了600个零件,那么点P一定会和点E、F、G一样在射线l上。
11.下面各题中的两种量,成正比例关系的有( )组。
①圆柱的体积一定,圆柱的底面积和高。
②张老师的身高和体重。
③圆的面积和半径。
④看电影所付票费与看电影的人数。
⑤等边三角形的周长与边长。
A.1 B.2 C.3 D.4
12.下面各种量中,成反比例关系的是( )。
A.一本书的页数一定,已读的页数和剩下的页数
B.跳高运动员跳的高度和他的身高
C.长方形的面积一定,它的长和宽
D.每千克大米的价格一定,大米的总价和数量
13.下面各选项中,两个量成反比例的是( )。
A.长方形的周长一定,长和宽 B.速度一定,路程和时间
C.总价一定,单价和数量 D.时间一定,每分打字个数和打字总个数
14.如果x和y(x、y均不为0)是两种相关联的量,那么下面表示x和y成正比例关系的是( )。
A.x-y B.y+x C. D.
15.在出勤率、出勤人数、全班人数这三个量中,当( )一定时,另外两个量成反比例。
A.全班人数 B.出勤人数 C.出勤率 D.以上都可以
16.下列选项中,两个量不成反比例的是( )。
A.乐乐放学回家,已走的路程和剩下的路程 B.等分一块蛋糕,每个人分到的蛋糕大小与人数
C.长方形的面积一定,它的长和宽 D.百米赛跑,跑步的速度和时间
17.下面的两个量中,成反比例关系的是( )。
A.比例尺一定,图上距离和实际距离。
B.正方形的周长和边长。
C.全班的总人数一定,参加朱子文化诵读活动的人数和剩下的人数。
D.将500毫升的水倒入不同的圆柱形容器中,容器中水面的高度与容器的底面积。
18.下面是四位同学关于“两个量是否成正比例”的说法,正确的是( )。
笑笑:“路程与时间的比值一定,路程与时间成正比例。”
奇思:“长方形的面积一定,长方形的长与宽成正比例。”
淘气:“小明的年龄会随爸爸年龄的变化而变化,爸爸的年龄与小明的年龄成正比例。”
妙想:“书的单价一定,买书应付金额与所买书的数量成正比例。”
A.只有笑笑 B.有笑笑和淘气 C.有笑笑和妙想 D.有笑笑、妙想和奇思
19.若6y=x(x、y不为0),则x与y( )。
A.成正比例 B.成反比例 C.不成比例 D.无关
20.下列选项中,两种量成反比例关系的是( )。
A.同学的年龄一定,他们的身高和体重 B.单价一定,购买的数量和所用的钱数
C.圆的面积一定,它的半径和圆周率 D.三角形面积一定,它的底和高
21.下列各种关系中,成反比例关系的是( )。
A.在一定时间里,每分钟生产零件个数和生产零件的总个数 B.长方形的长不变,面积和宽
C.圆锥的体积一定,圆锥的高和圆锥的底面积 D.一捆10米长的彩带,用去的长度与剩下的长度
22.下面关于正比例和反比例的四个说法,正确的是( )。
①正比例的图象是一条直线 ②一个人的年龄和体重既不成正比例也不成反比例
③圆锥的底面积一定,它的体积和高成反比例
④从学校去劳动实践基地的路程一定,已走的路程和剩下的路程不成比例。
A.①②③ B.①②④ C.②③④ D.①③④
23.下面说法正确的有( )。
①一个质数和一个合数的和一定是奇数;
②分数的分子和分母同时乘或除以同一个数,分数的大小不变;
③圆的周长一定,圆的半径和圆周率成反比例。
A.0个 B.1个 C.2个 D.3个
24.一列火车从甲地开往乙地,10小时行驶了800千米,离乙地还有160千米,照这样行完全程还需要几小时?
解答此题时,同学们有以下几种方法,其中解答错误的是( )。
A.设还需要x小时。= B.设还需要x小时。10∶800=160∶x
C.160÷(800÷10) D.10÷(800÷160)
25.下面各式中,表示x和y成反比例的是( )。
A.x+y=6 B.x=6+y C. D.y=6x
26.下列关系中,( )成反比例。
A.正方体的体积和它的棱长 B.三角形的面积一定,它的底和高
C.圆的面积一定,它的半径和圆周率 D.汽车行驶的速度和时间
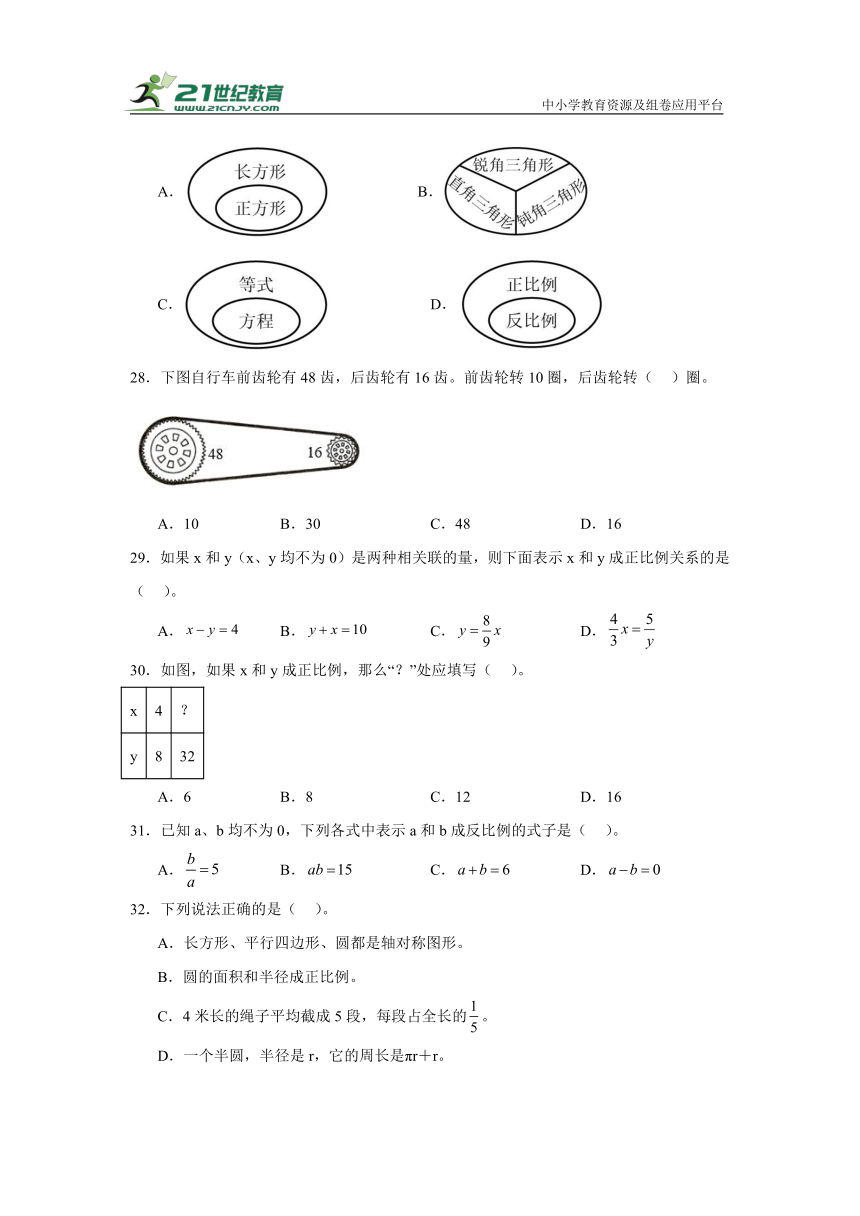
27.小学阶段学了很多数学知识,它们之间有密切的联系。下面不能正确表示它们之间关系的是( )。
A. B.
C. D.
28.下图自行车前齿轮有48齿,后齿轮有16齿。前齿轮转10圈,后齿轮转( )圈。
A.10 B.30 C.48 D.16
29.如果x和y(x、y均不为0)是两种相关联的量,则下面表示x和y成正比例关系的是( )。
A. B. C. D.
30.如图,如果x和y成正比例,那么“?”处应填写( )。
x 4 ?
y 8 32
A.6 B.8 C.12 D.16
31.已知a、b均不为0,下列各式中表示a和b成反比例的式子是( )。
A. B. C. D.
32.下列说法正确的是( )。
A.长方形、平行四边形、圆都是轴对称图形。
B.圆的面积和半径成正比例。
C.4米长的绳子平均截成5段,每段占全长的。
D.一个半圆,半径是r,它的周长是πr+r。
33.已知=c(a,b均不为0),当哪个量一定时,另外两个量成反比例?( )
A.a B.b C.c D.都不是
34.龙龙制作了一个摩天轮模型,模型高度与摩天轮的实际高度之比是3∶400,现测得模型的高度为27cm,则摩天轮的实际高度是( )米。
A.27 B.33 C.36 D.42
35.下图表示两辆汽车所行驶的路程与相应时间关系的图象,下列关于图象描述错误的是( )。
A.两辆汽车行驶的路程和时间都成正比例
B.从昆明到大理大约有350千米,甲车从昆明到大理大约要4个小时
C.从图象上看甲车的速度比乙车快
D.从图象上看乙车的速度比甲车快
36.甲与乙是成反比例的量,如果甲增加25%,乙就会( )。
A.增加25% B.减少25% C.增加20% D.减少20%
37.下列各式中(a、b均不为0)a和b成反比例的是( )。
A.a×8= B.9a=6b C.a×-1÷b=0 D.
38.下面说法中,成正比例关系的有( )个。
①图上距离和实际距离;②圆的直径一定时,圆的周长与π;③长方形的周长是20cm,它的长与宽;④六(1)班同学参加广播操比赛,每行人数和行数;⑤铺地面积一定时,方砖的面积和需要的块数;⑥在梯形中,当上下底之和一定时,面积与高。
A.4 B.3 C.2 D.1
39.若、不为,则与( )。
A.成正比例 B.成反比例 C.不成比例 D.既成正比例又成反比例
40.下面数量关系中( )能构成正比例,( )能构成反比例。
①路程÷速度=时间(一定) ②总价=单价×数量 ③K=2 ④A×B=C(一定) ⑤A+B=C(一定)
A.①④ B.②③ C.③④ D.④⑤
41.下列各图中,能表示出两个量成正比例关系的是( )。
A. B.
C. D.
42.下面每组中两个相关联的量,成正比例关系的是( )。
A.六(1)班有36个学生,班级的男生人数和女生人数。
B.六(1)班有36个学生,平均分成若干组,每组人数和分的组数。
C.圆锥的体积一定,圆锥的底面积和高。
D.圆锥的高一定,圆锥的底面积和体积。
43.在①x+y=12,②y=2x,③=y,④25%∶y=x∶40中,表示x和y成反比例的式子有( )个。
A.1 B.2 C.3 D.4
44.下面四种说法中,( )是错误的。
A.等边三角形的周长与边长成正比例
B.看一本书,已看的页数与剩下的页数成反比例
C.比例尺一定,图上距离与实际距离成正比例
D.平行四边形的面积一定,底与对应的高成反比例
45.下列各式中(a、b均不为0),a和b成反比例的是( )。
A.a×9= B.7a=4b
C.a×3=4÷b D. =b
46.,且和都不为0。当一定时,和( )。
A.成正比例 B.成反比例 C.不成比例 D.以上都不对
47.下列各式中(a、b均不为0),a和b成反比例的是( )。
A.a×8= B.9a=6b C.2a﹣5=b D.a×﹣1÷b=0
48.下面各题中,两种量成正比例关系的是( );两种量成反比例关系的是( );两种量不成比例关系的是( )。
①时间一定,每分打字个数和打字总个数 ②梯形的面积一定,它的上底和下底的和与高 ③正方形的边长和面积
A.①②③ B.①③② C.③②① D.②③①
49.下列各项中,两种量成反比例关系的是( )
A.车轮周长一定,车轮行驶的路程和转数
B.一(5)班今天的出勤人数和未出勤人数
C.工作时间一定,加工零件总数和加工每个零件的时间
D.圆柱体的高一定,它的底面积和体积
50.下面说法正确的有( )
①圆锥的侧面展开后是一个等腰三角形.
②在比例式中,两个外项的积与两个内项的积的比是1:1.
③平行四边形的对称轴有两条.
④甲数能被乙数整除,乙数一定是甲乙两数的最大公约数.
⑤工作时间一定,制造每个零件的时间和零件个数成正比例.
⑥24个铁圆锥,可以熔铸成等底等高的圆柱体的8个.
A.①②④⑤ B.②④⑤ C.②④⑤⑥ D.②④⑥
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
《北师大版六年级下册数学第四单元正比例与反比例选择题训练》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C A A B A C A C B D
题号 11 12 13 14 15 16 17 18 19 20
答案 B C C C B A D C A D
题号 21 22 23 24 25 26 27 28 29 30
答案 C B A B C B D B C D
题号 31 32 33 34 35 36 37 38 39 40
答案 B C B C D D C C A A
题号 41 42 43 44 45 46 47 48 49 50
答案 C D B B C B D A C D
1.C
【分析】判断两种相关联的量之间成什么比例,就看这两个量是对应的比值(商)一定,还是对应的乘积一定;如果是比值(商)一定,这两种相关联的量成正比例;如果是乘积一定,这两种相关联的量成反比例。
如果既不是比值一定,也不是乘积一定,则这两种相关联的量不成比例。
【详解】A.人的体重和身高的比值或乘积都不一定,所以人的体重和身高不成比例关系;
B.(上底+下底)×高÷2=梯形面积(一定),它的上底与下底之和与高成反比例,但它的上底和下底不成比例;
C.行驶速度×时间=路程(一定),乘积一定,所以行驶速度和时间成反比例关系;
D.订《意林(少年版)》的总钱数÷份数=《意林(少年版)》的单价(一定),商一定,所以订《意林(少年版)》的份数和总钱数成正比例关系。
故答案为:C
2.A
【分析】根据正比例和反比例的判定方法:判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例。以及根据方向的相对性:方向相反,角度相同。即北相反是南,东相反是西。结合选项逐一分析解答即可。
【详解】A.因为速度×时间=路程,是乘积一定,所以跑步速度与所用时间成反比例,所以本选项说法错误;
B.因为速度×时间=路程,是乘积一定,所以跑步速度与所用时间成反比例。所以本选项说法正确。
C.根据方向知识可知,折返点在起点的北偏东45°方向,所以向折返点跑是北偏东45°方向跑,所以本选项说法正确。
D.根据方向的相对性知识可知,折返点在起点的北偏东45°方向,向起点跑是南偏西45°方向,所以本选项说法正确。
故答案为:A
3.A
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值(或商)一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例。如果既不是比值(或商)一定,也不是乘积一定,则这两种相关联的量不成比例。
【详解】A.大米的总质量÷大米的袋数=一袋大米50千克(一定),商一定,所以大米的袋数和总质量成正比例关系;
B.人的身高与年龄的比值、以及乘积都是不一定的,所以小明的年龄与身高有关系,但不成比例;
C.走了的路程+未走的路程=小丽从家到学校的路程(一定),和一定,所以走了的路程和未走的路程不成比例。
D.行驶的速度×所用的时间=行驶一段的路程(一定),乘积一定,所以行驶的速度和所用的时间成反比例关系。
故答案为:A
4.B
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例。逐项分析。
【详解】A.妈妈的年龄与小明的年龄差一定,所以小明的年龄和妈妈的年龄不成比例,不符合题意;
B.平行四边形的底×高=平行四边形的面积(一定),乘积一定,所以平行四边形的底和高成反比例,符合题意;
C.出勤人数÷总人数=出勤率(一定),商一定,所以出勤人数和总人数成正比例,不符合题意;
D.已经读了的页数+未读的页数=这本书的总页数(一定),和一定,所以已经读了的页数与未读的页数不成比例,不符合题意。
故答案为:B
5.A
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的积一定,如果是比值一定,就成正比例;如果是积一定,则成反比例。因为圆柱的侧面积=圆柱的底面周长×高,从“若圆柱的侧面积是314cm2”可知,侧面积是一定的。据此逐项判断即可。
【详解】圆柱的侧面积是314cm2,设圆柱的底面半径分别是1cm和2cm,根据圆柱的高:h=S÷(2πr),圆的面积:S=πr2,填表如下:
侧面积 314cm2 314cm2
高 50cm 25cm
半径 1cm 2cm
直径 2cm 4cm
底面周长 6.28cm 12.56cm
底面积 3.14cm2 12.56cm2
观察表格中数据的变化情况,可得:
A.底面积和高:因为3.14×50≠12.56×25,即侧面积一定时,圆柱的底面积和高的积不一定,所以底面积和高不成反比例;
B.底面直径和高:因为2×50=4×25,即侧面积一定时,圆柱的底面直径和高的积一定,所以底面直径和高成反比例;
C.底面周长和高:因为6.28×50=12.56×25,即侧面积一定时,圆柱的底面周长和高的积一定,所以底面周长和高成反比例;
D.底面半径和高:因为1×50=2×25,即侧面积一定时,圆柱的底面半径和高的积一定,所以底面半径和高成反比例。
故答案为:A
6.C
【分析】根据题意可知,这个圆柱的高增加2分米,表面积增加25.12平方分米,表面积增加的是高为2分米的圆柱的侧面积,根据圆柱的侧面积公式:侧面积=底面周长×高;底面周长=侧面积÷高;再根据圆的周长公式:周长=π×直径;直径=周长÷π;据此可以求出圆柱的底面直径,又知高增加2分米,体积增加,因为圆柱的底面积不变,所以圆柱的体积与高成正比例,也就是圆柱高的是2分米,据此可以求出圆柱的高,然后根据圆柱的表面积侧面积底面积×2,把数据代入公式解答。
【详解】圆柱的底面直径:
(分米)
圆柱的高:
(分米)
圆柱的表面积:3.14×4×10+3.14×(4÷2)2×2
=12.56×10+3.14×22×2
=125.6+3.14×4×2
=125.6+12.56×2
=125.6+25.12
=150.72(平方分米)
一个圆柱若高增加2分米,则表面积增加25.12平方分米,体积增加。原来圆柱的表面积为150.72平方分米。
故答案为:C
7.A
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【详解】
2x×5=3y
10x=3y
x∶y=(一定)
x和y的比值一定,所以x和y成正比例。
故答案为:A。
8.C
【分析】①根据倒数的定义:乘积是1的两个数互为倒数;解答。
②根据两个相关联的量,乘积一定,我们说这个相关联的量成反比例关系,据此判断。
③一副三角尺的角的度数有:30°、45°、90°、60°,可拼到的角有60°-45°=l5°,60°+45°=105°,60°+90°=150°,90°+45°=135°,90°+30°=120°,30°+45°=75°,据此分析解答。
④两个三角形的底和高相等时,只能确定三角形的面积,不能确定三角形的形状,形状不一定完全相同,据此解答。
【详解】①乘积为1的两个数一定互为倒数。故原说法正确;
②已读页数+未读页数=一本书的页数,所以一本书的已读页数和未读页数不成比例。故原说法错误;
③一副三角尺的角的度数有:30°、45°、90°、60°,所以这些角的和,没有拼成145度。故原说法错误;
④两个完全一样的三角形可以拼成一个平行四边形,而两个等底等高的三角形面积相等,只是面积相同,但形状不一定相同,所以两个等底等高的三角形不一定能拼成一个平行四边形,选项说法错误。
所以说法错误的有3个。
故答案为:C
9.B
【分析】两种相关联的量,一种量变化另一种量随着变化,无论怎么变,如果x÷y=k(一定),x和y成正比例关系;如果xy=k(一定),x和y成反比例关系;除此之外不成比例关系。据此将需要转化的选项转化后进行分析。
【详解】A.,两边同时÷,可得,x和y成正比例关系;
B.,两边同时×,可得,x和y成反比例关系;
C.,和一定,x和y不成比例关系;
D.,两边同时÷,可得,x和y成正比例关系。
和成反比例关系的是。
故答案为:B
10.D
【分析】根据判断两种相关联的量成正反比例的方法,两种相关联的量比值一定(且不为0),则这两种量为正比例关系;两种相关联的量积一定,则这两种量为反比例关系。还可以根据两种成正比例的量相交的点在同一条直线上判断两种量是否成正比例。再根据加工零件个数工作时间=工作效率,代入图中相关数据,分别判断各选项是否符合图意。
【详解】A.由图可知,这两种相关联的量相交的点在同一条直线上,符合正比例关系的特征。即该说法正确。
加工1.5小时的零件个数是150个,则工作效率为(个/时)
B.由图可知,加工1.5小时的零件个数是150个,则工作效率为150÷1.5=100(个/时),根据加工零件个数=工作效率工作时间,则(个),所以该说法正确。
C.根据工作时间=加工零件个数工作效率,则(小时),所以该说法正确。
D.(个/时)这两个量的比值是120,与图中的两种相关联的比值是100,比值不同,则点P不会和点E、F、G一样在射线l上。所以该说法错误。
故答案为:D
11.B
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。据此判断即可。
【详解】①圆柱的体积=底面积×高,圆柱的体积一定,圆柱的底面积和高成反比例关系;
②张老师的身高和体重,不成比例;
③圆的面积÷半径的平方=π,所以圆的面积和半径不成比例;
④看电影所付票费÷看电影的人数=每张票的价格,每张票的价格一定,所以看电影所付票费与看电影的人数成正比例关系;
⑤等边三角形的周长÷边长=3,商一定,所以等边三角形的周长与边长成正比例关系。
则上面各题中的两种量,成正比例关系的有2组。
故答案为:B
12.C
【分析】两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫作成正比例的量,它们的关系叫作正比例关系。如果这两种量中相对应的两个数的乘积一定,这两种量就叫作成反比例的量,它们的关系叫作反比例关系;不满足正、反比例的意义的不成比例;据此解答。
【详解】A.已读的页数+剩下的页数=一本书的页数,和一定,所以一本书的页数一定,已读的页数和剩下的页数不成比例;
B.跳高运动员跳的高度和他的身高的比值或乘积均不一定,所以跳高运动员跳的高度和他的身高不成比例;
C.长×宽=长方形的面积,长方形的面积一定也就是长和宽的乘积一定,所以长方形的面积一定,它的长和宽成反比例关系;
D.大米的总价÷数量=每千克大米的价格,每千克大米的价格一定也就是大米的总价与数量的比值一定,所以每千克大米的价格一定,大米的总价和数量成正比例关系。
故答案为:C
13.C
【分析】两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫作成正比例的量,它们的关系叫作正比例关系。如果这两种量中相对应的两个数的乘积一定,这两种量就叫作成反比例的量,它们的关系叫作反比例关系;不满足正、反比例的意义的不成比例;据此解答。
【详解】A.根据长方形的周长=(长+宽)×2得(长+宽)=长方形的周长÷2,长方形的周长一定,则长方形的周长÷2一定,也就是长与宽的和一定,长方形的周长一定,长和宽不成比例;
B.根据速度=路程÷时间,速度一定,也就是路程和时间的比值一定,所以速度一定,路程和时间成正比例关系;
C.根据总价=单价×数量,总价一定,则单价与数量的乘积一定,所以总价一定,单价和数量成反比例关系;
D.打字总个数÷每分打字个数=打字时间,打字时间一定,也就是打字总个数与每分打字个数的比值一定,所以时间一定,每分打字个数和打字总个数成正比例关系。
故答案为:C
14.C
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【详解】A.x-y表示x和y的差,所以x和y不成比例;
B.y+x表示x和y的和,所以x和y不成比例;
C.,则(一定),所以x和y成正比例关系;
D.,则(一定),所以x和y成反比例关系;
故答案为:C
15.B
【分析】判断两种相关联的量之间成什么比例,就看这两个量是对应的比值(商)一定,还是对应的乘积一定;如果是比值(商)一定,这两种相关联的量成正比例;如果是乘积一定,这两种相关联的量成反比例。
【详解】A.出勤人数÷出勤率=全班人数(一定),商一定,则出勤人数和出勤率成正比例,不符合题意;
B.全班人数×出勤率=出勤人数(一定),积一定,则全班人数和出勤率成反比例,符合题意;
C.出勤人数÷全班人数=出勤率(一定),商一定,则出勤人数和全班人数成正比例,不符合题意。
故答案为:B
16.A
【分析】两个相关联的量,一个量变化,另一个量也随之变化,且它们乘积一定,则这两个量成反比例关系,据此逐一分析各项即可。
【详解】A.因为已走的路程+剩下的路程=总路程(一定),已走的路程和剩下的路程的和一定,所以它们不成比例关系;
B.因为每个人分到的蛋糕大小×人数=蛋糕的总份数(一定),它们的乘积一定,所以每个人分到的蛋糕大小与人数成反比例关系;
C.因为长×宽=长方形的面积(一定),它们的乘积一定,所以长方形的长和宽成反比例关系;
D.因为速度×时间=路程(一定),它们的乘积一定,所以速度和时间成反比例关系。
故答案为:A
17.D
【分析】两种相关联的量,如果它们的比值或商一定,则这两种量成正比例关系;如果它们的乘积一定,则这两种量成反比例关系。据此逐项分析。
【详解】A.图上距离∶实际距离=比例尺(一定),比例尺一定,即图上距离和实际距离的比值一定,则图上距离和实际距离成正比例关系;
B.正方形的周长÷边长=4,商一定,则正方形的周长和边长成正比例关系;
C.参加朱子文化诵读活动的人数+剩下的人数=全班总人数(一定),和一定,则参加朱子文化诵读活动的人数和剩下的人数不成比例;
D.根据题意,圆柱的底面积×水面的高度=500毫升,积一定,则容器中水面的高度与容器的底面积成反比例关系。
故答案为:D
18.C
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。据此判断即可。
【详解】路程÷时间=速度,速度一定,则路程与时间成正比例;笑笑的说法正确;
长方形的面积=长×宽,面积一定,长和宽成反比例;奇思的说法错误;
小明和爸爸的年龄差不变,爸爸的年龄与小明的年龄不成比例;淘气的说法错误;
总价÷数量=单价,单价一定,所以买书应付金额与所买书的数量成正比例;妙想的说法正确;
只有笑笑和妙想的说法正确。
故答案为:C
19.A
【分析】两种相关联的量,一种量变化,另一种量随之变化,如果这两种量的比值一定,则这两种量成正比例关系;如果这两种量的乘积一定,则这两种量成反比例关系。
【详解】若6y=x,则x÷y=6(一定),比值一定,x和y成正比例。
故答案为:A
20.D
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例。
【详解】A.人的身高和体重虽是两种相关联的量,但是它们的乘积或比值都不一定,所以不成比例;
B.所用的钱数÷购买的数量=单价(一定),是比值一定,所以单价一定,购买的数量和所用的钱数成正比例;
C.因为圆的面积=πr2,当圆的面积一定时,圆周率也是一个定值,所以这里圆的半径与圆周率不成比例;
D.三角形的底×高=面积×2(一定),是对应的乘积一定,所以底和高成反比例。
故答案为:D
21.C
【分析】两种相关联的量,若两种量的比值一定,两种量成正比例;若两种量的乘积一定,则两种量成反比例,据此逐一分析判断即可。
【详解】由分析可得:
A.生产零件的总个数÷每分钟生产零件个数=生产零件的总时间(一定),由此可知对应的商一定,所以在一定时间里,每分钟生产零件个数和生产零件的总个数成正比例关系;
B.长方形的面积÷宽=长(一定),由此可知对应的商一定,所以长方形的长不变,面积和宽成正比例关系;
C.×圆锥底面积×高=圆锥的体积(一定),由此可知对应的积一定,所以圆锥的体积一定,圆锥的高和圆锥的底面积成反比例;
D.用去的长度+剩下的长度=10(一定),既不是积一定,也不是商一定,所以一捆10米长的彩带,用去的长度与剩下的长度不成比例;
故答案为:C
22.B
【分析】x÷y=k(一定),x和y成正比例关系,正比例图像是一条经过原点的直线;xy=k(一定),x和y成反比例关系,据此分析。
【详解】①正比例的图象是一条直线,说法正确;
②一个人的年龄和体重既不成正比例也不成反比例,说法正确;
③圆柱的体积÷高=底面积÷3,圆锥的底面积一定,它的体积和高成正比例,原说法错误;
④已走的路程+剩下的路程=总路程,从学校去劳动实践基地的路程一定,已走的路程和剩下的路程不成比例,说法正确。
正确的是①②④。
故答案为:B
23.A
【分析】只有1和它本身两个因数的数叫做质数;一个数如果除了1和它本身还有别的因数,这样的数叫做合数;整数中,不是2的倍数的数叫做奇数。
分数的基本性质:分子和分母同时乘(或除以)同一个数(0除外),分数大小不变。
圆的周长.两个相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的乘积一定,这两种量就成反比例关系。
【详解】①×,,6是偶数不是奇数。
②×,分数的分子和分母同时乘或除以同一个数(0除外),分数大小不变。
③×,,周长一定,半径和圆周率都不变,不成比例。
所以说法正确的个数为0个。
故答案为:A
【点睛】考查了质数、合数、奇数的含义;分数的基本性质以及圆的周长公式、反比例的辨别,熟练掌握基础知识是关键。
24.B
【分析】根据速度=路程÷时间,用800÷10即可求出火车的速度,然后根据时间=路程÷速度,用160÷(800÷10)即可求出行完全程还需要多少小时;
如果列方程解决问题,则设完全程还需要x小时,速度不变,路程和时间成正比例,列比例为:800∶10=160∶x;
也可以用800÷160求出800千米里面有几个160千米,也就是5个,5个160千米需要花10小时,则用10÷5即可求出160千米需要花多少小时;据此解答。
【详解】根据分析可知,用列算式解答可以是160÷(800÷10)和10÷(800÷160);
如果用列方程解决问题,设还需要x小时。列方程为:10∶800=160∶x,也就是=。
其中解答错误的是:设还需要x小时。10∶800=160∶x。
故答案为:B
【点睛】本题主要考查了灵活解应用题的方法,掌握正比例的应用是解答本题的关键。
25.C
【分析】判断两种相关联的量成不成比例,成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,就成反比例,如果是其它的量一定或乘积、比值不一定,就不成比例。
【详解】A.因为x+y=6即x与y的和一定,所以x、y不成比例;
B.由x=6+y可得:x-y=6,即x与y的差一定,所以x、y不成比例;
C.由可得:xy=2×3=6,即x、y的乘积一定,所以x、y成反比例关系;
D.由y=6x可得:,即x、y的比值一定,所以x、y成正比例关系;
故答案为:C
【点睛】此题属于根据正、反比例的意义,辨识两种相关联的量成不成比例,成什么比例,就看这两种量是否都是变量,且对应的比值一定,或是对应的乘积一定,再做出判断。
26.B
【分析】两种相关联的量,如果它们的乘积一定,则这两种量成反比例关系。据此解答。
【详解】A.正方体的体积÷棱长=棱长×棱长,正方体的体积和棱长的积不一定,则正方体的体积和它的棱长不成反比例;
B.三角形的底×高=面积×2,三角形的面积一定,则它的底和高的积一定,所以它的底和高成反比例;
C.圆的面积S=πr2,圆的面积一定,圆周率一定,则圆的半径也一定,所以它的半径和圆周率不成比例;
D.速度×时间=路程,路程不一定,也就是汽车行驶的速度和时间的积不一定,则汽车行驶的速度和时间不成反比例。
故答案为:B
【点睛】本题考查反比例的辨认。根据反比例的意义,灵活运用正方体的体积、三角形的面积、圆的面积和行程问题的公式是解题的关键。
27.D
【分析】正方形是特殊的长方形;
三角形按角分类分为:锐角三角形、直角三角形、钝角三角形;
含有未知数的等式叫方程;
如果一个量变化另一个量也随之变化,并且这两个量的比值一定,那么这两个量成正比例关系;如果一个量变化另一个量也随之变化,并且这两个量的乘积一定,那么这两个量成反比例关系;据此解答。
【详解】A.,因为正方形是特殊的长方形,所以关系图正确;
B.,因为三角形按角分类分为:锐角三角形、直角三角形、钝角三角形,所以关系图正确;
C.,因为含有未知数的等式叫方程,方程一定是等式,而等式不一定是方程,所以关系图正确;
D.,因为如果一个量变化另一个量也随之变化,并且这两个量的比值一定,那么这两个量成正比例关系;如果一个量变化另一个量也随之变化,并且这两个量的乘积一定,那么这两个量成反比例关系;正比例和反比例不一样,所以关系图不正确。
故答案为:D
【点睛】本题考查长方形与正方形的关系、三角形的分类、方程与等式的关系、正比例与反比例的意义。
28.B
【分析】前轮和后轮走过的路程是一定的,齿轮的齿数与转过的圈数成反比例,设后齿轮转x圈;列比例:48×10=16x,解比例,即可解答。
【详解】解:四个后齿轮转x圈。
48×10=16x
16x=480
x=480÷16
x=30
下图自行车前齿轮有48齿,后齿轮有16齿。前齿轮转10圈,后齿轮转30圈。
故答案为:B
【点睛】解答这类问题,关键是先判断出题目中的两个相关的量是成正比例还是成反比例,再进行解答。
29.C
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。再逐项分析,即可解答。
【详解】A.x-y=4(一定),差一定,x和y不成比例;不符合题意;
B.y+x=10(一定),和一定,x和y不成比例;不符合题意;
C.y=x
x÷y=
x∶y=(一定),x和y成正比例;符合题意;
D.x=
4xy=3×5
xy=
xy=(一定),x和y成反比例;不符合题意。
如果x和y(x、y均不为0)是两种相关联的量,则表示x和y成正比例关系的是y=x。
故答案为:C
【点睛】熟练掌握正比例意义和辨别、反比例意义和辨别是解答本题的关键。
30.D
【分析】两种相关联的量,如果它们的比值或商一定,则这两种量成正比例关系。x和y成正比例,则x和y的比值一定。设“?”处的数是x,可以列出比例,解出这个比例即可。
【详解】解:设“?”处的数是x。
8x=4×32
8x=128
x=128÷8
x=16
则“?”处应填写16。
故答案为:D
【点睛】根据正比例的意义列出比例是解题的关键。
31.B
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例。据此逐项分析,进行解答。
【详解】A.=5(一定),比值一定,a和b成正比例关系,不符合题意;
B.ab=15(一定),乘积一定,a和b成反比例,符合题意;
C.a+b=6(一定),和一定,a和b不成比例,不符合题意;
D.a-b=0(一定),差一定,a和b不成比例,不符合题意。
已知a、b均不为0,表示a和b成反比例的式子是ab=15。
故答案为:B
【点睛】本题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再作判断。
32.C
【分析】A.轴对称:在平面内,如果一个图形沿一条直线对折,对折后的两部分都能完全重合,这样的图形叫做轴对称图形,这条直线就是其对称轴;
B.判断圆的面积和半径是否成正比例,就看这两种量是否是对应的比值一定,如果是比值一定,就成正比例,如果不是比值一定或比值不一定,就不成正比例;
C.把4米长的绳子平均剪成5段,每段为全长的五分之一;
D.已知一个半圆的半径是r,根据一个半圆的周长等于一个圆周长的一半加上直径,则用2πr÷2+2r即可求出半圆的周长。
【详解】A.长方形、圆是轴对称图形,平行四边形不是轴对称图形,原题说法错误;
B.因为圆的面积S=πr2,所以S:r2=π(一定),即圆的面积与半径的平方的比值一定,但圆的面积与半径的比值不是一定的。不符合正比例的意义,圆的面积和半径不成正比例,原题说法错误;
C.1÷5=,每段占全长的,原题说法正确;
D.2πr÷2+2r=πr+2r,它的周长是πr+2r,原题说法错误。
故答案为:C
【点睛】此题考查了轴对称的意义、辨识成正、反比例的量、分数的意义以及圆周长公式的灵活应用。
33.B
【分析】两个相关联的量乘积一定,这两个量成反比例;两个相关联的量对应的比值一定,这两个量成正比例;据此解答。
【详解】=c(a,b均不为0),c也不为0,则b=ac,。
当c一定时,b和a成正比例;当a一定时,b和c成正比例;当b一定时,a和c成反比例。
故答案为:B
【点睛】熟练掌握正比例、反比例的意义是解答本题的关键。
34.C
【分析】设摩天轮的实际高度是x米,根据摩天轮的实际高度与模型高度的比值是一定,即两种量成正比例,由此设出未知数,列比例解答问题。
【详解】解:设摩天轮的实际高度是x米,由题意得:
27厘米=0.27米
0.27: x =3:400
3x=0.27×400
3x÷3=0.27×400÷3
x=108÷3
x=36
摩天轮的实际高度是36米
故答案为:C
【点睛】本题考查了正反比例应用题,关键是得出摩天轮实际高度与模型高度的比值是一定的。
35.D
【分析】A.当两个相关联的量成正比例关系的时候,它的图象是经过原点的直线,由此即可判断;
B.根据图像可知,当甲车走4小时的时候,走了360千米,所以,当甲车走350千米的时候,大约要走4小时;
C和D.由于甲、乙两车的路程和时间成正比例关系,根据公式:路程÷时间=速度,分别求出甲、乙两车的速度,之后进行比较即可。
【详解】由分析可知:
A.甲、乙两辆汽车图像都是经过原点的直线,符合正比例图象特征,所以两辆汽车行驶的路程和时间都成正比例关系;不符合题意;
B.甲车从昆明到大理大约有350千米,大约要4小时,不符合题意;
C.甲车:360÷4=90(千米/小时);乙车:360÷8=45(千米/小时)
90>45,甲车的速度快,不符合题意;
D.甲车的速度>乙车的速度,符合题意。
故答案为:D
【点睛】本题主要考查正比例图象的分析,学会分析正比例图象是解题的关键。
36.D
【分析】甲与乙成反比例,则乘积一定,假设甲是4,乙是5,即甲×乙=4×5=20,如果甲增加25%,则此时甲是4×(1+25%),求出增加后的甲,由于甲×乙=20,乙=20÷甲,求出乙现在的量,再用乙现在的量与原来乙的量的差,除以原来乙的量,再乘100%,即可解答。
【详解】假设甲是4,乙数是5
4×5=20
甲增加25%;
甲现在的量:4×(1+25%)
=4×1.25
=5
乙现在的量:20÷5=4
(5-4)÷5×100%
=1÷5×100%
=0.2×100%
=20%
故答案为:D
【点睛】利用反比例的意义以及求一个数比另一个数多或少百分之几的知识进行解答。
37.C
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。据此逐项分析即可。
【详解】A.a×8=,那么b∶a=40,比值一定,所以a和b成正比例;
B.9a=6b,那么a∶b=,比值一定,所以a和b成正比例;
C.a×-1÷b=0,那么=,即ab=3×1=3,积一定,所以a和b成反比例;
D.,a和b的比值或积不一定,所以a和b不成比例。
故答案为:C
【点睛】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
38.C
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【详解】①比例尺=图上距离∶实际距离;比例尺一定,图上距离和实际距离成正比例;
②圆的周长=π×直径;π是定值,圆的周长与π不成比例;
③长方形周长=(长+宽)÷2;长方形周长是20cm,长和宽不成比例;
④总人数=每行人数×行数;六(1)班同学参加广播操比赛总人数一定,每行人数和行数成反比例;
⑤铺地面积=方砖面积×块数;铺地面积一定,方砖面积与块数成反比例;
⑥梯形面积=(上底+下底)×高÷2;梯形面积×2÷高=上底+下底;上底+下底一定,梯形面积与高成正比例;
只有①和⑥成正比例关系。
故答案为:C
【点睛】利用正比例意义和辨别,反比例意义和辨别进行解答。
39.A
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定, 还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【详解】因为、不为,所以(一定)。
所以与成正比例。
故答案为:A
【点睛】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
40.A
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【详解】①路程÷速度=时间(一定),比值一定,路程和速度成正比例;
②总价=单价×数量;总价没有注明一定不一定,单价和数量不成比例;
③k=2,是一个值;
④A×B=C(一定),积一定,A 和B成反比例;
⑤A+B=C(一定),是和一定,A和B不成比例。
故答案为:A
【点睛】利用正比例意义以及辨别和反比例意义以及辨别进行解答。
41.C
【分析】首先要知道成正比例关系的图象特点是一条经过原点的直线,相关联的两个量应是比值或商一定;据此即可作出正确选择。
【详解】A.不是一条直线,不符合题意;
B.是一条曲线,不是直线,不符合题意;
C.是一条经过原点的直线,符合题意;
D.不是一条直线,不符合题意。
故答案为:C。
【点睛】本题主要考查正比例的图像,熟练掌握正比例的图像并灵活运用。
42.D
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【详解】A.男生人数+女生人数=36(一定),和一定,不是比值或乘积一定,所以班级的男生人数和女生人数这两个量不成比例;
B.每组人数×分的组数=36(一定),积一定,所以六(1)班有36个学生,平均分成若干组,每组人数和分的组数成反比例;
C.圆锥的底面积×高=圆锥的体积×3(一定),积一定,所以圆锥的底面积和高成反比例;
D.圆锥的体积÷底面积=×高(一定),比值一定,所以圆锥的底面积和体积成正比例。
故答案为:D
【点睛】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
43.B
【分析】根据反比例的意义,如果两种相关系的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的乘积一定,这两种量就叫做反比例的量,它们的关系叫做反比例,以此判断。
【详解】①x+y=12,是和一定,所以x和y不成反比例;
②y=2x,则=2,是比值一定,所以x和y成正比例;
③=y,则xy=7,是积一定,所以x和y成反比例;
④25%∶y=x∶40中,根据比例的基本性质得:xy=25%×40,积一定,所以x和y成反比例。
表示x和y成反比例的式子有2个。
故答案为:B
【点睛】本题考查反比例的意义,灵活运用反比例意义解答问题。
44.B
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例;据此解答即可。
【详解】A.因为等边三角形的周长=边长×3,所以等边三角形周长÷边长=3 (一定),比值一定,则等边三角形的周长和边长成正比例;故原题说法正确。
B.已看的页数+剩下的页数=总页数(一定),和一定,则已看的页数和剩下的页数不成比例关系;故原题说法错误。
C.图上距离÷实际距离=比例尺(一定),比值一定,所以图上距离和实际距离成正比例关系;故原题说法正确。
D.根据平行四边形的底×高=平行四边形面积(一定),乘积一定,则平行四边形的底和对应的高成反比例关系;故原题说法正确。
故答案为: B
【点睛】本题主要考查辨识成正比例的量和成反比例的量。掌握方法认真解答即可。
45.C
【分析】如果用字母x和y表示两种相关联的量,用k表示它们的比值,正比例关系可以用以下关系式表示:y∶x=k(一定);如果用字母x和y表示两种相关联的量,用k表示它们的积,反比例关系可以用下面关系式表示:xy=k(一定),据此判断。
【详解】A.由a×9=可得,b÷a=45,b与a成正比例;
B.由7a=4b可得,a÷b=,a与b成正比例;
C.由a×3=4÷b可得,a×b=,a与b成反比例;
D.由=b可得,a÷b=10,a与b成正比例。
故答案为:C
【点睛】此题主要考查学生对反比例的理解与判定方法。
46.B
【分析】判断和成不成比例,成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,就成反比例,如果是其它的量一定或乘积、比值不一定,就不成比例,据此进行判断并选择。
【详解】因为则有,一定,则就一定,和对应的乘积一定,所以和成反比例。
故答案为:B
【点睛】掌握两种量成正比例、反比例的方法是解答此题的关键。
47.D
【分析】根据正反比例的意义,分析数量关系,找出一定的量,然后看那两个变量是比值一定还是乘积一定,从而判定成什么比例关系。
【详解】A.因为a×8=,所以a÷b=,a和b成正比例;
B.因为9a=6b,所以a÷b=,a和b成正比例;
C.2a﹣5=b,即2a﹣b=5,是差一定,不成比例;
D.a×﹣1÷b=0,即a×b=3,是比值一定,所以a和b成反比例。
故答案为:D
【点睛】此题属于辨识成正、反比例的量,解题的关键是确定两个相关联的量是对应的比值一定,还是对应的乘积一定。
48.A
【解析】如果两个相关量的比值(也就是商)一定时,那么这两个量成正比例。如果两个相关量的乘积一定,那么它们成反比例。
【详解】① =时间 比值一定,成正比例。
② (上底+下底)×高=梯形面积 积一定,成反比例。
③ 正方形的面积=边长×边长,所以不成比例。
故答案为:A
【点睛】本题主要考查正比例和反比例的定义以及运用。易错点要区别正反比例的不同。相关两个量,积一定时成反比例;比值一定时成正比例。不符合这两者要求的即是不成比例。
49.C
【分析】判断两种量是否成反比例,就看这两种量是否是:①相关联;②一种量变化,另一种量也随着变化,变化方向相反;③对应的乘积一定;如果这两种相关联的量都是变量,且对应的乘积一定,就成反比例;如果乘积不一定,就不成反比例.据此逐项分析再进行选择.
【详解】A、车轮行驶的路程:转数=车轮的周长(一定),是比值一定,车轮行驶的路程和转数成正比例;
B、因为乙(5)班今天的出勤人数+未出勤人数=全班的人数(一定),是和一定,所以一(5)班今天的出勤人数和未出勤不成比例;
C、因为生产每个零件的时间×零件个数=总工作时间(一定),是乘积一定,所以生产每个零件的时间和零件个数成反比例;
D、因为圆柱的体积=底面积×高,所以圆柱的体积÷底面积=高(一定),符合正比例的意义,不符合反比例的意义,所以圆柱的高一定,底面积与体积不成反比例;
50.D
【详解】试题分析:(1)因为用一个扇形和一个圆可以制作一个圆锥,扇形是圆锥的侧面,圆是底面,由此得出结论.
(2)依据比例的基本性质,即两内项之积等于两外项之积,即可判断题目的正误.
(3)依据轴对称图形的定义即可作答.
(4)甲数能被乙数整除,说明甲数是乙数的整数倍,求两个数为倍数关系时的最大公约数:两个数为倍数关系,最大公约数为较小的数;由此解答问题即可.
(5)判断两种相关联的量成不成比例,成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,就成反比例,如果是其它的量一定或乘积、比值不一定,就不成比例.
(6)本题是把圆锥熔铸成等底等高的圆柱体,由于一个圆柱的体积是与它等底等高的圆锥体积的3倍,也就是说,要3个这样的圆锥才能熔铸成1个等底等高的圆柱体,所以原题就是求24里面有几个3,于是即可判断题干的正误.
解:(1)圆锥的侧面展开后是一个扇形,不是等腰三角形,故此说法错误;
(2)在比例中,两内项之积等于两外项之积,所以两内项之积与两外项之积的比为1:1,故此说法正确;
(3)平行四边形不是轴对称图形,也就没有对称轴,故此说法错误;
(4)由题意得,甲÷乙=整数(0除外),可知甲数是乙数的倍数,所以甲和乙的最大公约数是乙;故此说法正确;
(5)因为生产每个零件的时间×零件个数=总工作时间(一定),是乘积一定,所以生产每个零件的时间和零件个数成反比例;故此说法错误;
(6)据分析可得:24÷3=8(个),故此说法正确;
点评:(1)此题主要回顾圆锥的特征和制作过程,以此做出判断.
(2)此题主要考查比例的基本性质的灵活应用.
(3)此题主要考查轴对称图形的意义的掌握,即在平面内,如果一个图形沿一条直线对折,对折后的两部分都能完全重合,这样的图形叫做轴对称图形,这条直线就是其对称轴.
(4)此题主要考查求两个数为倍数关系时的最大公约数:两个数为倍数关系,最大公约数为较小的数.
(5)本题考查反比例的意义.
(6)此题是考查圆柱、圆锥的关系,要注意圆柱和圆锥在等底等高的条件下体积有3倍或的关系.
中小学教育资源及组卷应用平台
北师大版六年级下册数学第四单元正比例与反比例选择题训练
1.下列选项中的两个量成反比例关系的是( )。
A.人的体重和身高 B.梯形面积一定,它的上底和下底
C.路程一定,行驶速度和时间 D.订《意林(少年版)》的份数和总钱数
2.六(2)班举行50米×8往返跑测试。折返点在起点的北偏东45°方向。下面说法错误的是( )。
A.跑步速度与所用时间成正比例
B.跑步速度与所用时间成反比例
C.向折返点跑是北偏东45°方向
D.向起点跑是南偏西45°方向
3.下面每组中的两个量,成正比例关系的是( )。
A.一袋大米50千克,大米的袋数和总质量 B.小明的年龄和身高
C.小丽从家到学校,走了的路程和未走的路程 D.行驶一段路程,行驶的速度和所用的时间
4.下面几组相关联的量中,成反比例关系的是( )。
A.小明的年龄和妈妈的年龄。 B.平行四边形的面积一定,它的底和高。
C.班级的出勤率一定,出勤人数和总人数。 D.读一本书,已经读了的页数与未读的页数。
5.若圆柱的侧面积是314cm2,则不与圆柱的高成反比例的是( )。
A.底面积 B.底面直径 C.底面周长 D.底面半径
6.一个圆柱若高增加2分米,则表面积增加25.12平方分米,体积增加。原来圆柱的表面积为( )平方分米。
A.188.4 B.157 C.150.72 D.125.6
7.若,则x和y( )。
A.成正比例 B.成反比例 C.不成比例 D.无法确定
8.下面说法错误的有( )个。
①乘积为1的两个数一定互为倒数。
②一本书的已读页数和未读页数成反比例。
③一副三角尺能拼出145°的角。
④两个等底等高的三角形就可以拼出平行四边形。
A.1 B.2 C.3 D.4
9.x、y均不为0,下列和成反比例关系的是( )。
A. B. C. D.
10.小李加工一批零件,工作时间与加工零件的个数的关系如下图,下列说法错误的是( )。
A.加工零件的个数与工作时间成正比例关系。
B.N表示400个零件。
C.M表示3.2小时。
D.如果有一点P表示5小时做了600个零件,那么点P一定会和点E、F、G一样在射线l上。
11.下面各题中的两种量,成正比例关系的有( )组。
①圆柱的体积一定,圆柱的底面积和高。
②张老师的身高和体重。
③圆的面积和半径。
④看电影所付票费与看电影的人数。
⑤等边三角形的周长与边长。
A.1 B.2 C.3 D.4
12.下面各种量中,成反比例关系的是( )。
A.一本书的页数一定,已读的页数和剩下的页数
B.跳高运动员跳的高度和他的身高
C.长方形的面积一定,它的长和宽
D.每千克大米的价格一定,大米的总价和数量
13.下面各选项中,两个量成反比例的是( )。
A.长方形的周长一定,长和宽 B.速度一定,路程和时间
C.总价一定,单价和数量 D.时间一定,每分打字个数和打字总个数
14.如果x和y(x、y均不为0)是两种相关联的量,那么下面表示x和y成正比例关系的是( )。
A.x-y B.y+x C. D.
15.在出勤率、出勤人数、全班人数这三个量中,当( )一定时,另外两个量成反比例。
A.全班人数 B.出勤人数 C.出勤率 D.以上都可以
16.下列选项中,两个量不成反比例的是( )。
A.乐乐放学回家,已走的路程和剩下的路程 B.等分一块蛋糕,每个人分到的蛋糕大小与人数
C.长方形的面积一定,它的长和宽 D.百米赛跑,跑步的速度和时间
17.下面的两个量中,成反比例关系的是( )。
A.比例尺一定,图上距离和实际距离。
B.正方形的周长和边长。
C.全班的总人数一定,参加朱子文化诵读活动的人数和剩下的人数。
D.将500毫升的水倒入不同的圆柱形容器中,容器中水面的高度与容器的底面积。
18.下面是四位同学关于“两个量是否成正比例”的说法,正确的是( )。
笑笑:“路程与时间的比值一定,路程与时间成正比例。”
奇思:“长方形的面积一定,长方形的长与宽成正比例。”
淘气:“小明的年龄会随爸爸年龄的变化而变化,爸爸的年龄与小明的年龄成正比例。”
妙想:“书的单价一定,买书应付金额与所买书的数量成正比例。”
A.只有笑笑 B.有笑笑和淘气 C.有笑笑和妙想 D.有笑笑、妙想和奇思
19.若6y=x(x、y不为0),则x与y( )。
A.成正比例 B.成反比例 C.不成比例 D.无关
20.下列选项中,两种量成反比例关系的是( )。
A.同学的年龄一定,他们的身高和体重 B.单价一定,购买的数量和所用的钱数
C.圆的面积一定,它的半径和圆周率 D.三角形面积一定,它的底和高
21.下列各种关系中,成反比例关系的是( )。
A.在一定时间里,每分钟生产零件个数和生产零件的总个数 B.长方形的长不变,面积和宽
C.圆锥的体积一定,圆锥的高和圆锥的底面积 D.一捆10米长的彩带,用去的长度与剩下的长度
22.下面关于正比例和反比例的四个说法,正确的是( )。
①正比例的图象是一条直线 ②一个人的年龄和体重既不成正比例也不成反比例
③圆锥的底面积一定,它的体积和高成反比例
④从学校去劳动实践基地的路程一定,已走的路程和剩下的路程不成比例。
A.①②③ B.①②④ C.②③④ D.①③④
23.下面说法正确的有( )。
①一个质数和一个合数的和一定是奇数;
②分数的分子和分母同时乘或除以同一个数,分数的大小不变;
③圆的周长一定,圆的半径和圆周率成反比例。
A.0个 B.1个 C.2个 D.3个
24.一列火车从甲地开往乙地,10小时行驶了800千米,离乙地还有160千米,照这样行完全程还需要几小时?
解答此题时,同学们有以下几种方法,其中解答错误的是( )。
A.设还需要x小时。= B.设还需要x小时。10∶800=160∶x
C.160÷(800÷10) D.10÷(800÷160)
25.下面各式中,表示x和y成反比例的是( )。
A.x+y=6 B.x=6+y C. D.y=6x
26.下列关系中,( )成反比例。
A.正方体的体积和它的棱长 B.三角形的面积一定,它的底和高
C.圆的面积一定,它的半径和圆周率 D.汽车行驶的速度和时间
27.小学阶段学了很多数学知识,它们之间有密切的联系。下面不能正确表示它们之间关系的是( )。
A. B.
C. D.
28.下图自行车前齿轮有48齿,后齿轮有16齿。前齿轮转10圈,后齿轮转( )圈。
A.10 B.30 C.48 D.16
29.如果x和y(x、y均不为0)是两种相关联的量,则下面表示x和y成正比例关系的是( )。
A. B. C. D.
30.如图,如果x和y成正比例,那么“?”处应填写( )。
x 4 ?
y 8 32
A.6 B.8 C.12 D.16
31.已知a、b均不为0,下列各式中表示a和b成反比例的式子是( )。
A. B. C. D.
32.下列说法正确的是( )。
A.长方形、平行四边形、圆都是轴对称图形。
B.圆的面积和半径成正比例。
C.4米长的绳子平均截成5段,每段占全长的。
D.一个半圆,半径是r,它的周长是πr+r。
33.已知=c(a,b均不为0),当哪个量一定时,另外两个量成反比例?( )
A.a B.b C.c D.都不是
34.龙龙制作了一个摩天轮模型,模型高度与摩天轮的实际高度之比是3∶400,现测得模型的高度为27cm,则摩天轮的实际高度是( )米。
A.27 B.33 C.36 D.42
35.下图表示两辆汽车所行驶的路程与相应时间关系的图象,下列关于图象描述错误的是( )。
A.两辆汽车行驶的路程和时间都成正比例
B.从昆明到大理大约有350千米,甲车从昆明到大理大约要4个小时
C.从图象上看甲车的速度比乙车快
D.从图象上看乙车的速度比甲车快
36.甲与乙是成反比例的量,如果甲增加25%,乙就会( )。
A.增加25% B.减少25% C.增加20% D.减少20%
37.下列各式中(a、b均不为0)a和b成反比例的是( )。
A.a×8= B.9a=6b C.a×-1÷b=0 D.
38.下面说法中,成正比例关系的有( )个。
①图上距离和实际距离;②圆的直径一定时,圆的周长与π;③长方形的周长是20cm,它的长与宽;④六(1)班同学参加广播操比赛,每行人数和行数;⑤铺地面积一定时,方砖的面积和需要的块数;⑥在梯形中,当上下底之和一定时,面积与高。
A.4 B.3 C.2 D.1
39.若、不为,则与( )。
A.成正比例 B.成反比例 C.不成比例 D.既成正比例又成反比例
40.下面数量关系中( )能构成正比例,( )能构成反比例。
①路程÷速度=时间(一定) ②总价=单价×数量 ③K=2 ④A×B=C(一定) ⑤A+B=C(一定)
A.①④ B.②③ C.③④ D.④⑤
41.下列各图中,能表示出两个量成正比例关系的是( )。
A. B.
C. D.
42.下面每组中两个相关联的量,成正比例关系的是( )。
A.六(1)班有36个学生,班级的男生人数和女生人数。
B.六(1)班有36个学生,平均分成若干组,每组人数和分的组数。
C.圆锥的体积一定,圆锥的底面积和高。
D.圆锥的高一定,圆锥的底面积和体积。
43.在①x+y=12,②y=2x,③=y,④25%∶y=x∶40中,表示x和y成反比例的式子有( )个。
A.1 B.2 C.3 D.4
44.下面四种说法中,( )是错误的。
A.等边三角形的周长与边长成正比例
B.看一本书,已看的页数与剩下的页数成反比例
C.比例尺一定,图上距离与实际距离成正比例
D.平行四边形的面积一定,底与对应的高成反比例
45.下列各式中(a、b均不为0),a和b成反比例的是( )。
A.a×9= B.7a=4b
C.a×3=4÷b D. =b
46.,且和都不为0。当一定时,和( )。
A.成正比例 B.成反比例 C.不成比例 D.以上都不对
47.下列各式中(a、b均不为0),a和b成反比例的是( )。
A.a×8= B.9a=6b C.2a﹣5=b D.a×﹣1÷b=0
48.下面各题中,两种量成正比例关系的是( );两种量成反比例关系的是( );两种量不成比例关系的是( )。
①时间一定,每分打字个数和打字总个数 ②梯形的面积一定,它的上底和下底的和与高 ③正方形的边长和面积
A.①②③ B.①③② C.③②① D.②③①
49.下列各项中,两种量成反比例关系的是( )
A.车轮周长一定,车轮行驶的路程和转数
B.一(5)班今天的出勤人数和未出勤人数
C.工作时间一定,加工零件总数和加工每个零件的时间
D.圆柱体的高一定,它的底面积和体积
50.下面说法正确的有( )
①圆锥的侧面展开后是一个等腰三角形.
②在比例式中,两个外项的积与两个内项的积的比是1:1.
③平行四边形的对称轴有两条.
④甲数能被乙数整除,乙数一定是甲乙两数的最大公约数.
⑤工作时间一定,制造每个零件的时间和零件个数成正比例.
⑥24个铁圆锥,可以熔铸成等底等高的圆柱体的8个.
A.①②④⑤ B.②④⑤ C.②④⑤⑥ D.②④⑥
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
《北师大版六年级下册数学第四单元正比例与反比例选择题训练》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C A A B A C A C B D
题号 11 12 13 14 15 16 17 18 19 20
答案 B C C C B A D C A D
题号 21 22 23 24 25 26 27 28 29 30
答案 C B A B C B D B C D
题号 31 32 33 34 35 36 37 38 39 40
答案 B C B C D D C C A A
题号 41 42 43 44 45 46 47 48 49 50
答案 C D B B C B D A C D
1.C
【分析】判断两种相关联的量之间成什么比例,就看这两个量是对应的比值(商)一定,还是对应的乘积一定;如果是比值(商)一定,这两种相关联的量成正比例;如果是乘积一定,这两种相关联的量成反比例。
如果既不是比值一定,也不是乘积一定,则这两种相关联的量不成比例。
【详解】A.人的体重和身高的比值或乘积都不一定,所以人的体重和身高不成比例关系;
B.(上底+下底)×高÷2=梯形面积(一定),它的上底与下底之和与高成反比例,但它的上底和下底不成比例;
C.行驶速度×时间=路程(一定),乘积一定,所以行驶速度和时间成反比例关系;
D.订《意林(少年版)》的总钱数÷份数=《意林(少年版)》的单价(一定),商一定,所以订《意林(少年版)》的份数和总钱数成正比例关系。
故答案为:C
2.A
【分析】根据正比例和反比例的判定方法:判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例。以及根据方向的相对性:方向相反,角度相同。即北相反是南,东相反是西。结合选项逐一分析解答即可。
【详解】A.因为速度×时间=路程,是乘积一定,所以跑步速度与所用时间成反比例,所以本选项说法错误;
B.因为速度×时间=路程,是乘积一定,所以跑步速度与所用时间成反比例。所以本选项说法正确。
C.根据方向知识可知,折返点在起点的北偏东45°方向,所以向折返点跑是北偏东45°方向跑,所以本选项说法正确。
D.根据方向的相对性知识可知,折返点在起点的北偏东45°方向,向起点跑是南偏西45°方向,所以本选项说法正确。
故答案为:A
3.A
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值(或商)一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例。如果既不是比值(或商)一定,也不是乘积一定,则这两种相关联的量不成比例。
【详解】A.大米的总质量÷大米的袋数=一袋大米50千克(一定),商一定,所以大米的袋数和总质量成正比例关系;
B.人的身高与年龄的比值、以及乘积都是不一定的,所以小明的年龄与身高有关系,但不成比例;
C.走了的路程+未走的路程=小丽从家到学校的路程(一定),和一定,所以走了的路程和未走的路程不成比例。
D.行驶的速度×所用的时间=行驶一段的路程(一定),乘积一定,所以行驶的速度和所用的时间成反比例关系。
故答案为:A
4.B
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例。逐项分析。
【详解】A.妈妈的年龄与小明的年龄差一定,所以小明的年龄和妈妈的年龄不成比例,不符合题意;
B.平行四边形的底×高=平行四边形的面积(一定),乘积一定,所以平行四边形的底和高成反比例,符合题意;
C.出勤人数÷总人数=出勤率(一定),商一定,所以出勤人数和总人数成正比例,不符合题意;
D.已经读了的页数+未读的页数=这本书的总页数(一定),和一定,所以已经读了的页数与未读的页数不成比例,不符合题意。
故答案为:B
5.A
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的积一定,如果是比值一定,就成正比例;如果是积一定,则成反比例。因为圆柱的侧面积=圆柱的底面周长×高,从“若圆柱的侧面积是314cm2”可知,侧面积是一定的。据此逐项判断即可。
【详解】圆柱的侧面积是314cm2,设圆柱的底面半径分别是1cm和2cm,根据圆柱的高:h=S÷(2πr),圆的面积:S=πr2,填表如下:
侧面积 314cm2 314cm2
高 50cm 25cm
半径 1cm 2cm
直径 2cm 4cm
底面周长 6.28cm 12.56cm
底面积 3.14cm2 12.56cm2
观察表格中数据的变化情况,可得:
A.底面积和高:因为3.14×50≠12.56×25,即侧面积一定时,圆柱的底面积和高的积不一定,所以底面积和高不成反比例;
B.底面直径和高:因为2×50=4×25,即侧面积一定时,圆柱的底面直径和高的积一定,所以底面直径和高成反比例;
C.底面周长和高:因为6.28×50=12.56×25,即侧面积一定时,圆柱的底面周长和高的积一定,所以底面周长和高成反比例;
D.底面半径和高:因为1×50=2×25,即侧面积一定时,圆柱的底面半径和高的积一定,所以底面半径和高成反比例。
故答案为:A
6.C
【分析】根据题意可知,这个圆柱的高增加2分米,表面积增加25.12平方分米,表面积增加的是高为2分米的圆柱的侧面积,根据圆柱的侧面积公式:侧面积=底面周长×高;底面周长=侧面积÷高;再根据圆的周长公式:周长=π×直径;直径=周长÷π;据此可以求出圆柱的底面直径,又知高增加2分米,体积增加,因为圆柱的底面积不变,所以圆柱的体积与高成正比例,也就是圆柱高的是2分米,据此可以求出圆柱的高,然后根据圆柱的表面积侧面积底面积×2,把数据代入公式解答。
【详解】圆柱的底面直径:
(分米)
圆柱的高:
(分米)
圆柱的表面积:3.14×4×10+3.14×(4÷2)2×2
=12.56×10+3.14×22×2
=125.6+3.14×4×2
=125.6+12.56×2
=125.6+25.12
=150.72(平方分米)
一个圆柱若高增加2分米,则表面积增加25.12平方分米,体积增加。原来圆柱的表面积为150.72平方分米。
故答案为:C
7.A
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【详解】
2x×5=3y
10x=3y
x∶y=(一定)
x和y的比值一定,所以x和y成正比例。
故答案为:A。
8.C
【分析】①根据倒数的定义:乘积是1的两个数互为倒数;解答。
②根据两个相关联的量,乘积一定,我们说这个相关联的量成反比例关系,据此判断。
③一副三角尺的角的度数有:30°、45°、90°、60°,可拼到的角有60°-45°=l5°,60°+45°=105°,60°+90°=150°,90°+45°=135°,90°+30°=120°,30°+45°=75°,据此分析解答。
④两个三角形的底和高相等时,只能确定三角形的面积,不能确定三角形的形状,形状不一定完全相同,据此解答。
【详解】①乘积为1的两个数一定互为倒数。故原说法正确;
②已读页数+未读页数=一本书的页数,所以一本书的已读页数和未读页数不成比例。故原说法错误;
③一副三角尺的角的度数有:30°、45°、90°、60°,所以这些角的和,没有拼成145度。故原说法错误;
④两个完全一样的三角形可以拼成一个平行四边形,而两个等底等高的三角形面积相等,只是面积相同,但形状不一定相同,所以两个等底等高的三角形不一定能拼成一个平行四边形,选项说法错误。
所以说法错误的有3个。
故答案为:C
9.B
【分析】两种相关联的量,一种量变化另一种量随着变化,无论怎么变,如果x÷y=k(一定),x和y成正比例关系;如果xy=k(一定),x和y成反比例关系;除此之外不成比例关系。据此将需要转化的选项转化后进行分析。
【详解】A.,两边同时÷,可得,x和y成正比例关系;
B.,两边同时×,可得,x和y成反比例关系;
C.,和一定,x和y不成比例关系;
D.,两边同时÷,可得,x和y成正比例关系。
和成反比例关系的是。
故答案为:B
10.D
【分析】根据判断两种相关联的量成正反比例的方法,两种相关联的量比值一定(且不为0),则这两种量为正比例关系;两种相关联的量积一定,则这两种量为反比例关系。还可以根据两种成正比例的量相交的点在同一条直线上判断两种量是否成正比例。再根据加工零件个数工作时间=工作效率,代入图中相关数据,分别判断各选项是否符合图意。
【详解】A.由图可知,这两种相关联的量相交的点在同一条直线上,符合正比例关系的特征。即该说法正确。
加工1.5小时的零件个数是150个,则工作效率为(个/时)
B.由图可知,加工1.5小时的零件个数是150个,则工作效率为150÷1.5=100(个/时),根据加工零件个数=工作效率工作时间,则(个),所以该说法正确。
C.根据工作时间=加工零件个数工作效率,则(小时),所以该说法正确。
D.(个/时)这两个量的比值是120,与图中的两种相关联的比值是100,比值不同,则点P不会和点E、F、G一样在射线l上。所以该说法错误。
故答案为:D
11.B
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。据此判断即可。
【详解】①圆柱的体积=底面积×高,圆柱的体积一定,圆柱的底面积和高成反比例关系;
②张老师的身高和体重,不成比例;
③圆的面积÷半径的平方=π,所以圆的面积和半径不成比例;
④看电影所付票费÷看电影的人数=每张票的价格,每张票的价格一定,所以看电影所付票费与看电影的人数成正比例关系;
⑤等边三角形的周长÷边长=3,商一定,所以等边三角形的周长与边长成正比例关系。
则上面各题中的两种量,成正比例关系的有2组。
故答案为:B
12.C
【分析】两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫作成正比例的量,它们的关系叫作正比例关系。如果这两种量中相对应的两个数的乘积一定,这两种量就叫作成反比例的量,它们的关系叫作反比例关系;不满足正、反比例的意义的不成比例;据此解答。
【详解】A.已读的页数+剩下的页数=一本书的页数,和一定,所以一本书的页数一定,已读的页数和剩下的页数不成比例;
B.跳高运动员跳的高度和他的身高的比值或乘积均不一定,所以跳高运动员跳的高度和他的身高不成比例;
C.长×宽=长方形的面积,长方形的面积一定也就是长和宽的乘积一定,所以长方形的面积一定,它的长和宽成反比例关系;
D.大米的总价÷数量=每千克大米的价格,每千克大米的价格一定也就是大米的总价与数量的比值一定,所以每千克大米的价格一定,大米的总价和数量成正比例关系。
故答案为:C
13.C
【分析】两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫作成正比例的量,它们的关系叫作正比例关系。如果这两种量中相对应的两个数的乘积一定,这两种量就叫作成反比例的量,它们的关系叫作反比例关系;不满足正、反比例的意义的不成比例;据此解答。
【详解】A.根据长方形的周长=(长+宽)×2得(长+宽)=长方形的周长÷2,长方形的周长一定,则长方形的周长÷2一定,也就是长与宽的和一定,长方形的周长一定,长和宽不成比例;
B.根据速度=路程÷时间,速度一定,也就是路程和时间的比值一定,所以速度一定,路程和时间成正比例关系;
C.根据总价=单价×数量,总价一定,则单价与数量的乘积一定,所以总价一定,单价和数量成反比例关系;
D.打字总个数÷每分打字个数=打字时间,打字时间一定,也就是打字总个数与每分打字个数的比值一定,所以时间一定,每分打字个数和打字总个数成正比例关系。
故答案为:C
14.C
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【详解】A.x-y表示x和y的差,所以x和y不成比例;
B.y+x表示x和y的和,所以x和y不成比例;
C.,则(一定),所以x和y成正比例关系;
D.,则(一定),所以x和y成反比例关系;
故答案为:C
15.B
【分析】判断两种相关联的量之间成什么比例,就看这两个量是对应的比值(商)一定,还是对应的乘积一定;如果是比值(商)一定,这两种相关联的量成正比例;如果是乘积一定,这两种相关联的量成反比例。
【详解】A.出勤人数÷出勤率=全班人数(一定),商一定,则出勤人数和出勤率成正比例,不符合题意;
B.全班人数×出勤率=出勤人数(一定),积一定,则全班人数和出勤率成反比例,符合题意;
C.出勤人数÷全班人数=出勤率(一定),商一定,则出勤人数和全班人数成正比例,不符合题意。
故答案为:B
16.A
【分析】两个相关联的量,一个量变化,另一个量也随之变化,且它们乘积一定,则这两个量成反比例关系,据此逐一分析各项即可。
【详解】A.因为已走的路程+剩下的路程=总路程(一定),已走的路程和剩下的路程的和一定,所以它们不成比例关系;
B.因为每个人分到的蛋糕大小×人数=蛋糕的总份数(一定),它们的乘积一定,所以每个人分到的蛋糕大小与人数成反比例关系;
C.因为长×宽=长方形的面积(一定),它们的乘积一定,所以长方形的长和宽成反比例关系;
D.因为速度×时间=路程(一定),它们的乘积一定,所以速度和时间成反比例关系。
故答案为:A
17.D
【分析】两种相关联的量,如果它们的比值或商一定,则这两种量成正比例关系;如果它们的乘积一定,则这两种量成反比例关系。据此逐项分析。
【详解】A.图上距离∶实际距离=比例尺(一定),比例尺一定,即图上距离和实际距离的比值一定,则图上距离和实际距离成正比例关系;
B.正方形的周长÷边长=4,商一定,则正方形的周长和边长成正比例关系;
C.参加朱子文化诵读活动的人数+剩下的人数=全班总人数(一定),和一定,则参加朱子文化诵读活动的人数和剩下的人数不成比例;
D.根据题意,圆柱的底面积×水面的高度=500毫升,积一定,则容器中水面的高度与容器的底面积成反比例关系。
故答案为:D
18.C
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。据此判断即可。
【详解】路程÷时间=速度,速度一定,则路程与时间成正比例;笑笑的说法正确;
长方形的面积=长×宽,面积一定,长和宽成反比例;奇思的说法错误;
小明和爸爸的年龄差不变,爸爸的年龄与小明的年龄不成比例;淘气的说法错误;
总价÷数量=单价,单价一定,所以买书应付金额与所买书的数量成正比例;妙想的说法正确;
只有笑笑和妙想的说法正确。
故答案为:C
19.A
【分析】两种相关联的量,一种量变化,另一种量随之变化,如果这两种量的比值一定,则这两种量成正比例关系;如果这两种量的乘积一定,则这两种量成反比例关系。
【详解】若6y=x,则x÷y=6(一定),比值一定,x和y成正比例。
故答案为:A
20.D
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例。
【详解】A.人的身高和体重虽是两种相关联的量,但是它们的乘积或比值都不一定,所以不成比例;
B.所用的钱数÷购买的数量=单价(一定),是比值一定,所以单价一定,购买的数量和所用的钱数成正比例;
C.因为圆的面积=πr2,当圆的面积一定时,圆周率也是一个定值,所以这里圆的半径与圆周率不成比例;
D.三角形的底×高=面积×2(一定),是对应的乘积一定,所以底和高成反比例。
故答案为:D
21.C
【分析】两种相关联的量,若两种量的比值一定,两种量成正比例;若两种量的乘积一定,则两种量成反比例,据此逐一分析判断即可。
【详解】由分析可得:
A.生产零件的总个数÷每分钟生产零件个数=生产零件的总时间(一定),由此可知对应的商一定,所以在一定时间里,每分钟生产零件个数和生产零件的总个数成正比例关系;
B.长方形的面积÷宽=长(一定),由此可知对应的商一定,所以长方形的长不变,面积和宽成正比例关系;
C.×圆锥底面积×高=圆锥的体积(一定),由此可知对应的积一定,所以圆锥的体积一定,圆锥的高和圆锥的底面积成反比例;
D.用去的长度+剩下的长度=10(一定),既不是积一定,也不是商一定,所以一捆10米长的彩带,用去的长度与剩下的长度不成比例;
故答案为:C
22.B
【分析】x÷y=k(一定),x和y成正比例关系,正比例图像是一条经过原点的直线;xy=k(一定),x和y成反比例关系,据此分析。
【详解】①正比例的图象是一条直线,说法正确;
②一个人的年龄和体重既不成正比例也不成反比例,说法正确;
③圆柱的体积÷高=底面积÷3,圆锥的底面积一定,它的体积和高成正比例,原说法错误;
④已走的路程+剩下的路程=总路程,从学校去劳动实践基地的路程一定,已走的路程和剩下的路程不成比例,说法正确。
正确的是①②④。
故答案为:B
23.A
【分析】只有1和它本身两个因数的数叫做质数;一个数如果除了1和它本身还有别的因数,这样的数叫做合数;整数中,不是2的倍数的数叫做奇数。
分数的基本性质:分子和分母同时乘(或除以)同一个数(0除外),分数大小不变。
圆的周长.两个相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的乘积一定,这两种量就成反比例关系。
【详解】①×,,6是偶数不是奇数。
②×,分数的分子和分母同时乘或除以同一个数(0除外),分数大小不变。
③×,,周长一定,半径和圆周率都不变,不成比例。
所以说法正确的个数为0个。
故答案为:A
【点睛】考查了质数、合数、奇数的含义;分数的基本性质以及圆的周长公式、反比例的辨别,熟练掌握基础知识是关键。
24.B
【分析】根据速度=路程÷时间,用800÷10即可求出火车的速度,然后根据时间=路程÷速度,用160÷(800÷10)即可求出行完全程还需要多少小时;
如果列方程解决问题,则设完全程还需要x小时,速度不变,路程和时间成正比例,列比例为:800∶10=160∶x;
也可以用800÷160求出800千米里面有几个160千米,也就是5个,5个160千米需要花10小时,则用10÷5即可求出160千米需要花多少小时;据此解答。
【详解】根据分析可知,用列算式解答可以是160÷(800÷10)和10÷(800÷160);
如果用列方程解决问题,设还需要x小时。列方程为:10∶800=160∶x,也就是=。
其中解答错误的是:设还需要x小时。10∶800=160∶x。
故答案为:B
【点睛】本题主要考查了灵活解应用题的方法,掌握正比例的应用是解答本题的关键。
25.C
【分析】判断两种相关联的量成不成比例,成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,就成反比例,如果是其它的量一定或乘积、比值不一定,就不成比例。
【详解】A.因为x+y=6即x与y的和一定,所以x、y不成比例;
B.由x=6+y可得:x-y=6,即x与y的差一定,所以x、y不成比例;
C.由可得:xy=2×3=6,即x、y的乘积一定,所以x、y成反比例关系;
D.由y=6x可得:,即x、y的比值一定,所以x、y成正比例关系;
故答案为:C
【点睛】此题属于根据正、反比例的意义,辨识两种相关联的量成不成比例,成什么比例,就看这两种量是否都是变量,且对应的比值一定,或是对应的乘积一定,再做出判断。
26.B
【分析】两种相关联的量,如果它们的乘积一定,则这两种量成反比例关系。据此解答。
【详解】A.正方体的体积÷棱长=棱长×棱长,正方体的体积和棱长的积不一定,则正方体的体积和它的棱长不成反比例;
B.三角形的底×高=面积×2,三角形的面积一定,则它的底和高的积一定,所以它的底和高成反比例;
C.圆的面积S=πr2,圆的面积一定,圆周率一定,则圆的半径也一定,所以它的半径和圆周率不成比例;
D.速度×时间=路程,路程不一定,也就是汽车行驶的速度和时间的积不一定,则汽车行驶的速度和时间不成反比例。
故答案为:B
【点睛】本题考查反比例的辨认。根据反比例的意义,灵活运用正方体的体积、三角形的面积、圆的面积和行程问题的公式是解题的关键。
27.D
【分析】正方形是特殊的长方形;
三角形按角分类分为:锐角三角形、直角三角形、钝角三角形;
含有未知数的等式叫方程;
如果一个量变化另一个量也随之变化,并且这两个量的比值一定,那么这两个量成正比例关系;如果一个量变化另一个量也随之变化,并且这两个量的乘积一定,那么这两个量成反比例关系;据此解答。
【详解】A.,因为正方形是特殊的长方形,所以关系图正确;
B.,因为三角形按角分类分为:锐角三角形、直角三角形、钝角三角形,所以关系图正确;
C.,因为含有未知数的等式叫方程,方程一定是等式,而等式不一定是方程,所以关系图正确;
D.,因为如果一个量变化另一个量也随之变化,并且这两个量的比值一定,那么这两个量成正比例关系;如果一个量变化另一个量也随之变化,并且这两个量的乘积一定,那么这两个量成反比例关系;正比例和反比例不一样,所以关系图不正确。
故答案为:D
【点睛】本题考查长方形与正方形的关系、三角形的分类、方程与等式的关系、正比例与反比例的意义。
28.B
【分析】前轮和后轮走过的路程是一定的,齿轮的齿数与转过的圈数成反比例,设后齿轮转x圈;列比例:48×10=16x,解比例,即可解答。
【详解】解:四个后齿轮转x圈。
48×10=16x
16x=480
x=480÷16
x=30
下图自行车前齿轮有48齿,后齿轮有16齿。前齿轮转10圈,后齿轮转30圈。
故答案为:B
【点睛】解答这类问题,关键是先判断出题目中的两个相关的量是成正比例还是成反比例,再进行解答。
29.C
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。再逐项分析,即可解答。
【详解】A.x-y=4(一定),差一定,x和y不成比例;不符合题意;
B.y+x=10(一定),和一定,x和y不成比例;不符合题意;
C.y=x
x÷y=
x∶y=(一定),x和y成正比例;符合题意;
D.x=
4xy=3×5
xy=
xy=(一定),x和y成反比例;不符合题意。
如果x和y(x、y均不为0)是两种相关联的量,则表示x和y成正比例关系的是y=x。
故答案为:C
【点睛】熟练掌握正比例意义和辨别、反比例意义和辨别是解答本题的关键。
30.D
【分析】两种相关联的量,如果它们的比值或商一定,则这两种量成正比例关系。x和y成正比例,则x和y的比值一定。设“?”处的数是x,可以列出比例,解出这个比例即可。
【详解】解:设“?”处的数是x。
8x=4×32
8x=128
x=128÷8
x=16
则“?”处应填写16。
故答案为:D
【点睛】根据正比例的意义列出比例是解题的关键。
31.B
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例。据此逐项分析,进行解答。
【详解】A.=5(一定),比值一定,a和b成正比例关系,不符合题意;
B.ab=15(一定),乘积一定,a和b成反比例,符合题意;
C.a+b=6(一定),和一定,a和b不成比例,不符合题意;
D.a-b=0(一定),差一定,a和b不成比例,不符合题意。
已知a、b均不为0,表示a和b成反比例的式子是ab=15。
故答案为:B
【点睛】本题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再作判断。
32.C
【分析】A.轴对称:在平面内,如果一个图形沿一条直线对折,对折后的两部分都能完全重合,这样的图形叫做轴对称图形,这条直线就是其对称轴;
B.判断圆的面积和半径是否成正比例,就看这两种量是否是对应的比值一定,如果是比值一定,就成正比例,如果不是比值一定或比值不一定,就不成正比例;
C.把4米长的绳子平均剪成5段,每段为全长的五分之一;
D.已知一个半圆的半径是r,根据一个半圆的周长等于一个圆周长的一半加上直径,则用2πr÷2+2r即可求出半圆的周长。
【详解】A.长方形、圆是轴对称图形,平行四边形不是轴对称图形,原题说法错误;
B.因为圆的面积S=πr2,所以S:r2=π(一定),即圆的面积与半径的平方的比值一定,但圆的面积与半径的比值不是一定的。不符合正比例的意义,圆的面积和半径不成正比例,原题说法错误;
C.1÷5=,每段占全长的,原题说法正确;
D.2πr÷2+2r=πr+2r,它的周长是πr+2r,原题说法错误。
故答案为:C
【点睛】此题考查了轴对称的意义、辨识成正、反比例的量、分数的意义以及圆周长公式的灵活应用。
33.B
【分析】两个相关联的量乘积一定,这两个量成反比例;两个相关联的量对应的比值一定,这两个量成正比例;据此解答。
【详解】=c(a,b均不为0),c也不为0,则b=ac,。
当c一定时,b和a成正比例;当a一定时,b和c成正比例;当b一定时,a和c成反比例。
故答案为:B
【点睛】熟练掌握正比例、反比例的意义是解答本题的关键。
34.C
【分析】设摩天轮的实际高度是x米,根据摩天轮的实际高度与模型高度的比值是一定,即两种量成正比例,由此设出未知数,列比例解答问题。
【详解】解:设摩天轮的实际高度是x米,由题意得:
27厘米=0.27米
0.27: x =3:400
3x=0.27×400
3x÷3=0.27×400÷3
x=108÷3
x=36
摩天轮的实际高度是36米
故答案为:C
【点睛】本题考查了正反比例应用题,关键是得出摩天轮实际高度与模型高度的比值是一定的。
35.D
【分析】A.当两个相关联的量成正比例关系的时候,它的图象是经过原点的直线,由此即可判断;
B.根据图像可知,当甲车走4小时的时候,走了360千米,所以,当甲车走350千米的时候,大约要走4小时;
C和D.由于甲、乙两车的路程和时间成正比例关系,根据公式:路程÷时间=速度,分别求出甲、乙两车的速度,之后进行比较即可。
【详解】由分析可知:
A.甲、乙两辆汽车图像都是经过原点的直线,符合正比例图象特征,所以两辆汽车行驶的路程和时间都成正比例关系;不符合题意;
B.甲车从昆明到大理大约有350千米,大约要4小时,不符合题意;
C.甲车:360÷4=90(千米/小时);乙车:360÷8=45(千米/小时)
90>45,甲车的速度快,不符合题意;
D.甲车的速度>乙车的速度,符合题意。
故答案为:D
【点睛】本题主要考查正比例图象的分析,学会分析正比例图象是解题的关键。
36.D
【分析】甲与乙成反比例,则乘积一定,假设甲是4,乙是5,即甲×乙=4×5=20,如果甲增加25%,则此时甲是4×(1+25%),求出增加后的甲,由于甲×乙=20,乙=20÷甲,求出乙现在的量,再用乙现在的量与原来乙的量的差,除以原来乙的量,再乘100%,即可解答。
【详解】假设甲是4,乙数是5
4×5=20
甲增加25%;
甲现在的量:4×(1+25%)
=4×1.25
=5
乙现在的量:20÷5=4
(5-4)÷5×100%
=1÷5×100%
=0.2×100%
=20%
故答案为:D
【点睛】利用反比例的意义以及求一个数比另一个数多或少百分之几的知识进行解答。
37.C
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。据此逐项分析即可。
【详解】A.a×8=,那么b∶a=40,比值一定,所以a和b成正比例;
B.9a=6b,那么a∶b=,比值一定,所以a和b成正比例;
C.a×-1÷b=0,那么=,即ab=3×1=3,积一定,所以a和b成反比例;
D.,a和b的比值或积不一定,所以a和b不成比例。
故答案为:C
【点睛】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
38.C
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【详解】①比例尺=图上距离∶实际距离;比例尺一定,图上距离和实际距离成正比例;
②圆的周长=π×直径;π是定值,圆的周长与π不成比例;
③长方形周长=(长+宽)÷2;长方形周长是20cm,长和宽不成比例;
④总人数=每行人数×行数;六(1)班同学参加广播操比赛总人数一定,每行人数和行数成反比例;
⑤铺地面积=方砖面积×块数;铺地面积一定,方砖面积与块数成反比例;
⑥梯形面积=(上底+下底)×高÷2;梯形面积×2÷高=上底+下底;上底+下底一定,梯形面积与高成正比例;
只有①和⑥成正比例关系。
故答案为:C
【点睛】利用正比例意义和辨别,反比例意义和辨别进行解答。
39.A
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定, 还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【详解】因为、不为,所以(一定)。
所以与成正比例。
故答案为:A
【点睛】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
40.A
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【详解】①路程÷速度=时间(一定),比值一定,路程和速度成正比例;
②总价=单价×数量;总价没有注明一定不一定,单价和数量不成比例;
③k=2,是一个值;
④A×B=C(一定),积一定,A 和B成反比例;
⑤A+B=C(一定),是和一定,A和B不成比例。
故答案为:A
【点睛】利用正比例意义以及辨别和反比例意义以及辨别进行解答。
41.C
【分析】首先要知道成正比例关系的图象特点是一条经过原点的直线,相关联的两个量应是比值或商一定;据此即可作出正确选择。
【详解】A.不是一条直线,不符合题意;
B.是一条曲线,不是直线,不符合题意;
C.是一条经过原点的直线,符合题意;
D.不是一条直线,不符合题意。
故答案为:C。
【点睛】本题主要考查正比例的图像,熟练掌握正比例的图像并灵活运用。
42.D
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【详解】A.男生人数+女生人数=36(一定),和一定,不是比值或乘积一定,所以班级的男生人数和女生人数这两个量不成比例;
B.每组人数×分的组数=36(一定),积一定,所以六(1)班有36个学生,平均分成若干组,每组人数和分的组数成反比例;
C.圆锥的底面积×高=圆锥的体积×3(一定),积一定,所以圆锥的底面积和高成反比例;
D.圆锥的体积÷底面积=×高(一定),比值一定,所以圆锥的底面积和体积成正比例。
故答案为:D
【点睛】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
43.B
【分析】根据反比例的意义,如果两种相关系的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的乘积一定,这两种量就叫做反比例的量,它们的关系叫做反比例,以此判断。
【详解】①x+y=12,是和一定,所以x和y不成反比例;
②y=2x,则=2,是比值一定,所以x和y成正比例;
③=y,则xy=7,是积一定,所以x和y成反比例;
④25%∶y=x∶40中,根据比例的基本性质得:xy=25%×40,积一定,所以x和y成反比例。
表示x和y成反比例的式子有2个。
故答案为:B
【点睛】本题考查反比例的意义,灵活运用反比例意义解答问题。
44.B
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例;据此解答即可。
【详解】A.因为等边三角形的周长=边长×3,所以等边三角形周长÷边长=3 (一定),比值一定,则等边三角形的周长和边长成正比例;故原题说法正确。
B.已看的页数+剩下的页数=总页数(一定),和一定,则已看的页数和剩下的页数不成比例关系;故原题说法错误。
C.图上距离÷实际距离=比例尺(一定),比值一定,所以图上距离和实际距离成正比例关系;故原题说法正确。
D.根据平行四边形的底×高=平行四边形面积(一定),乘积一定,则平行四边形的底和对应的高成反比例关系;故原题说法正确。
故答案为: B
【点睛】本题主要考查辨识成正比例的量和成反比例的量。掌握方法认真解答即可。
45.C
【分析】如果用字母x和y表示两种相关联的量,用k表示它们的比值,正比例关系可以用以下关系式表示:y∶x=k(一定);如果用字母x和y表示两种相关联的量,用k表示它们的积,反比例关系可以用下面关系式表示:xy=k(一定),据此判断。
【详解】A.由a×9=可得,b÷a=45,b与a成正比例;
B.由7a=4b可得,a÷b=,a与b成正比例;
C.由a×3=4÷b可得,a×b=,a与b成反比例;
D.由=b可得,a÷b=10,a与b成正比例。
故答案为:C
【点睛】此题主要考查学生对反比例的理解与判定方法。
46.B
【分析】判断和成不成比例,成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,就成反比例,如果是其它的量一定或乘积、比值不一定,就不成比例,据此进行判断并选择。
【详解】因为则有,一定,则就一定,和对应的乘积一定,所以和成反比例。
故答案为:B
【点睛】掌握两种量成正比例、反比例的方法是解答此题的关键。
47.D
【分析】根据正反比例的意义,分析数量关系,找出一定的量,然后看那两个变量是比值一定还是乘积一定,从而判定成什么比例关系。
【详解】A.因为a×8=,所以a÷b=,a和b成正比例;
B.因为9a=6b,所以a÷b=,a和b成正比例;
C.2a﹣5=b,即2a﹣b=5,是差一定,不成比例;
D.a×﹣1÷b=0,即a×b=3,是比值一定,所以a和b成反比例。
故答案为:D
【点睛】此题属于辨识成正、反比例的量,解题的关键是确定两个相关联的量是对应的比值一定,还是对应的乘积一定。
48.A
【解析】如果两个相关量的比值(也就是商)一定时,那么这两个量成正比例。如果两个相关量的乘积一定,那么它们成反比例。
【详解】① =时间 比值一定,成正比例。
② (上底+下底)×高=梯形面积 积一定,成反比例。
③ 正方形的面积=边长×边长,所以不成比例。
故答案为:A
【点睛】本题主要考查正比例和反比例的定义以及运用。易错点要区别正反比例的不同。相关两个量,积一定时成反比例;比值一定时成正比例。不符合这两者要求的即是不成比例。
49.C
【分析】判断两种量是否成反比例,就看这两种量是否是:①相关联;②一种量变化,另一种量也随着变化,变化方向相反;③对应的乘积一定;如果这两种相关联的量都是变量,且对应的乘积一定,就成反比例;如果乘积不一定,就不成反比例.据此逐项分析再进行选择.
【详解】A、车轮行驶的路程:转数=车轮的周长(一定),是比值一定,车轮行驶的路程和转数成正比例;
B、因为乙(5)班今天的出勤人数+未出勤人数=全班的人数(一定),是和一定,所以一(5)班今天的出勤人数和未出勤不成比例;
C、因为生产每个零件的时间×零件个数=总工作时间(一定),是乘积一定,所以生产每个零件的时间和零件个数成反比例;
D、因为圆柱的体积=底面积×高,所以圆柱的体积÷底面积=高(一定),符合正比例的意义,不符合反比例的意义,所以圆柱的高一定,底面积与体积不成反比例;
50.D
【详解】试题分析:(1)因为用一个扇形和一个圆可以制作一个圆锥,扇形是圆锥的侧面,圆是底面,由此得出结论.
(2)依据比例的基本性质,即两内项之积等于两外项之积,即可判断题目的正误.
(3)依据轴对称图形的定义即可作答.
(4)甲数能被乙数整除,说明甲数是乙数的整数倍,求两个数为倍数关系时的最大公约数:两个数为倍数关系,最大公约数为较小的数;由此解答问题即可.
(5)判断两种相关联的量成不成比例,成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,就成反比例,如果是其它的量一定或乘积、比值不一定,就不成比例.
(6)本题是把圆锥熔铸成等底等高的圆柱体,由于一个圆柱的体积是与它等底等高的圆锥体积的3倍,也就是说,要3个这样的圆锥才能熔铸成1个等底等高的圆柱体,所以原题就是求24里面有几个3,于是即可判断题干的正误.
解:(1)圆锥的侧面展开后是一个扇形,不是等腰三角形,故此说法错误;
(2)在比例中,两内项之积等于两外项之积,所以两内项之积与两外项之积的比为1:1,故此说法正确;
(3)平行四边形不是轴对称图形,也就没有对称轴,故此说法错误;
(4)由题意得,甲÷乙=整数(0除外),可知甲数是乙数的倍数,所以甲和乙的最大公约数是乙;故此说法正确;
(5)因为生产每个零件的时间×零件个数=总工作时间(一定),是乘积一定,所以生产每个零件的时间和零件个数成反比例;故此说法错误;
(6)据分析可得:24÷3=8(个),故此说法正确;
点评:(1)此题主要回顾圆锥的特征和制作过程,以此做出判断.
(2)此题主要考查比例的基本性质的灵活应用.
(3)此题主要考查轴对称图形的意义的掌握,即在平面内,如果一个图形沿一条直线对折,对折后的两部分都能完全重合,这样的图形叫做轴对称图形,这条直线就是其对称轴.
(4)此题主要考查求两个数为倍数关系时的最大公约数:两个数为倍数关系,最大公约数为较小的数.
(5)本题考查反比例的意义.
(6)此题是考查圆柱、圆锥的关系,要注意圆柱和圆锥在等底等高的条件下体积有3倍或的关系.
