3.2 简单图形坐标表示 课件(共27张PPT)
文档属性
| 名称 | 3.2 简单图形坐标表示 课件(共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-10 00:00:00 | ||
图片预览







文档简介
(共27张PPT)
第一章 直角三角形
3.2 简单图形坐标表示
01
教学目标
02
新知导入
03
新知讲解
04
课堂练习
05
课堂小结
06
作业布置
01
教学目标
01
02
03
1.能根据坐标描出点的位置;
2、能建立适当的平面直角坐标系描述物体的位置.
02
新知导入
文字密码游戏:
密码是:“嘿,我真聪明!”
如图“家”字的位置记作(1,9),请你破解密码:(3,3),(5,5),(2,7),(2,2),(1,8),(8,7),(8,8)
03
新知探究
动脑筋
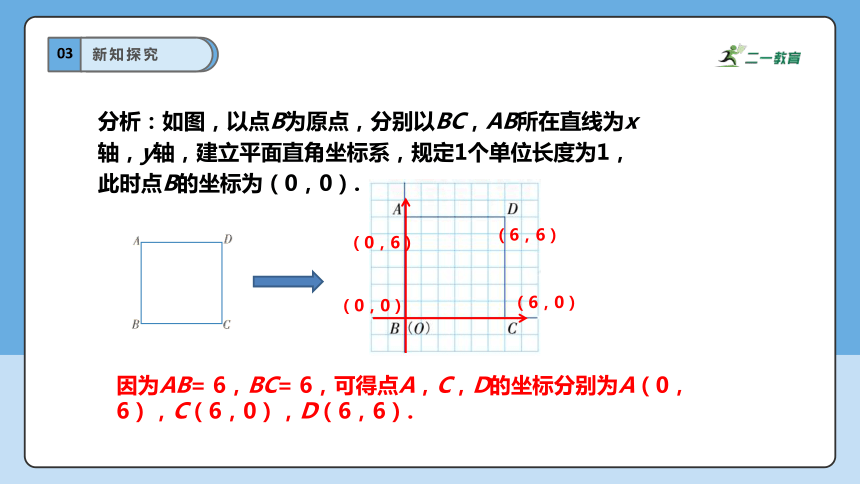
如图, 已知正方形ABCD的边长为6.
(1)如果以点B为原点,以BC所在直线为x轴,建立平面直角坐标系,那么y轴是哪条直线?写出正方形的顶点A,B,C,D的坐标.
03
新知探究
因为AB= 6,BC= 6,可得点A,C,D的坐标分别为A(0,6),C(6,0),D(6,6).
分析:如图,以点B为原点,分别以BC,AB所在直线为x轴,y轴,建立平面直角坐标系,规定1个单位长度为1,此时点B的坐标为(0,0).
(0,6)
(0,0)
(6,6)
(6,0)
03
新知讲解
(2)如果以正方形的中心为原点,建立平面直角坐标系, 那么x轴和y轴分别是哪条直线?此时正方形的顶点A, B,C,D的坐标分别是多少?
03
新知讲解
分析:如图,以正方形的中心O为坐标原点,分别以过正方形的中心且垂直两组对边的两条对称轴为x轴,y轴,建立平面直角坐标系.
此时,点A,B,C,D的坐标分别为A(-3,3),
B(-3,-3),C(3,-3),D(3,3).
(0,0)
(-3,3)
(-3,-3)
(3,-3)
(3,3)
●
A
C
●
D
●
B
03
新知讲解
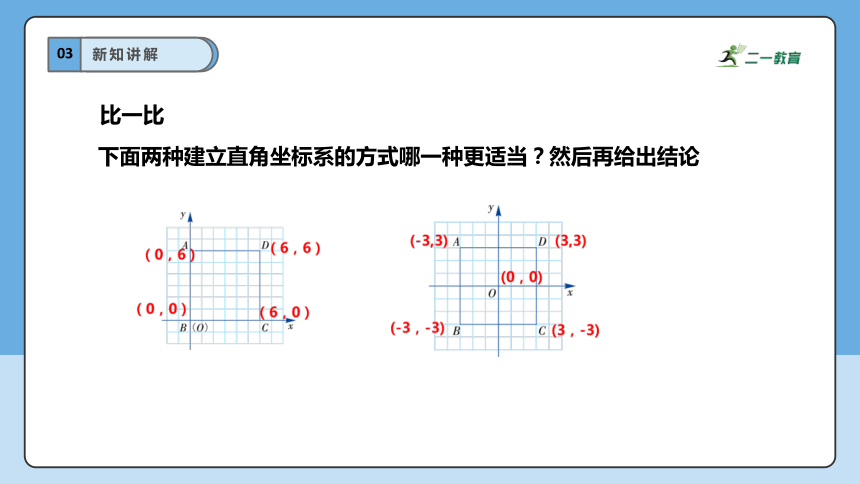
下面两种建立直角坐标系的方式哪一种更适当?然后再给出结论
比一比
03
新知讲解
由上得知,建立的平面直角坐标系不同,则正方形的顶点A,B,C,D的坐标也不同.你认为怎样建立直角坐标系才比较适当?
①以某已知点为原点.
②以图形中某线所在的直线为x轴(或y轴)
③以已知线段中点为原点.
④以两直线交点为原点.
⑤利用图形的轴对称性,以对称轴为x轴或y轴.
温馨提示:
没有一成不变的模式,但选择适当的坐标系,可使计算降低难度!
新课探究
例
例1、如图,矩形ABCD的长和宽分别为8和6,试建立适当的平面直角坐标系表示矩形ABCD各顶点的坐标,并作出矩形ABCD.
03
新知讲解
解:如图所示,以点B为坐标原点,分别以BC,AB 所在直线为x 轴,y轴,建立平面直角坐标系. 规定1个单位长度为1. 点B的坐标为(0,0).
因为BC=8,AB=6,可得点A,C,D的坐标分别为:
A(0,6),C(8,0),D(8,6).
●
A
C
●
D
●
依次连接A,B,C,D , 则图中的四边形就是所求作的矩形.
03
新知讲解
建立适当的直角坐标系求点的坐标
(1)分析条件,选择适当的点作为坐标原点
(2)过原点作两条互相垂直的数轴作为x轴与y轴;
(3)确定正方向、单位长度。
归纳总结
03
新知讲解
例2、如图是一个机器零件的尺寸规格示意图, 试建立适当的平面直角坐标系表示其各顶点的坐标,并作出这个示意图.
03
新知讲解
解:过点D 作AB 的垂线,垂足为点O,以点O 为原点,分别以AB,DO所在直线为x轴,y轴,建立平面直角坐标系,如图.
规定1 个单位长度为100 mm,则四边形ABCD 的顶点坐标分别为:A(-1,0),B(4,0),C(3,2), D(0,2). 依次连接A,B,C,D , 则图中的四边形ABCD即为所求作的图形.
y
x
(-1,0)
(4,0)
(3,2)
(0,2)
03
新知讲解
归纳总结:
(1)建立平面直角坐标系,用坐标描述简单图形的一个根本原则是在建立平面直角坐标系时,应使点的坐标最简明.
(2)解题的关键是把求坐标的问题转化为求线段的长的问题.
04
课堂练习
【知识技能类作业】必做题:
1.如图是小刚画的一张脸,他对妹妹说“如果我用(0,2)表示左眼,用(2,2)表示右眼,那么嘴的位置可以表示成( )
A.(1,0) B.(-1,0)
C.(-1,1) D.(1,-1)
A
04
课堂练习
【知识技能类作业】选做题:
2.如图,正方形ABCD的边长等于4,那么A,B,C,D四个顶点坐标分别为________、________、________、________.
(0,0)
(0,4)
(-4,0)
(-4,4)
04
课堂练习
【综合拓展类作业】
3.将例1再建立另外一个平面直角坐标系,作出矩形ABCD.
04
课堂练习
【综合拓展类作业】
解:如图所示,分别以AB,AD的中点所在直线为x 轴,y轴,建立平面直角坐标系,两直线交点为原点.规定1个单位长度为1.
因为AD=8,AB=6,可得点A,C,D的坐标分别为:
A(-4,3),B(-4,-3),C(4,-3),D(4,3).
依次连接A,B,C,D , 则图中的四边形就是所求作的矩形.
●
A
C
●
D
●
B
05
课堂小结
简单的坐标表示
1.根据点的坐标确定点的位置,并运用它描点作图.
2.建立适当的直角坐标系,并用坐标表示简单图形各顶点的位置
简单图形的坐标表示
坐标原点的选取
平面直角坐标系的建立
用坐标表示简单几何图形各顶点的位置
06
作业布置
【知识技能类作业】必做题:
1.在平面直角坐标系内,已知点A(2,2),B(2,-3),点P在y轴上,且△APB为直角三角形,则点P的个数为( )
A.1个 B.2个 C.3个 D.4个
D
06
作业布置
【知识技能类作业】选做题:
2、如图所示,坐在象棋棋盘上建立直角坐标系,使“帅”位于点(﹣2,﹣2),“马”位于点(1,﹣2),则“兵”位于点 .
(-4,1)
06
作业布置
【综合拓展类作业】
3.如图, Rt△ABC的两直角边AB, BC 的长分别为6,5, 试建立适当的平面直角坐标系来表示Rt△ABC各顶点的坐标.
06
作业布置
【综合拓展类作业】
解:以点B为原点, 分别以BC,AB所在直线为x轴, y轴,建立平面直角坐标系,如下图所示.
从上图可知Rt△ABC各顶点的坐标分别为:
A(0,6),B(0 ,0),
C(5,0).
Thanks!
https://www.21cnjy.com/recruitment/home/fine
第一章 直角三角形
3.2 简单图形坐标表示
01
教学目标
02
新知导入
03
新知讲解
04
课堂练习
05
课堂小结
06
作业布置
01
教学目标
01
02
03
1.能根据坐标描出点的位置;
2、能建立适当的平面直角坐标系描述物体的位置.
02
新知导入
文字密码游戏:
密码是:“嘿,我真聪明!”
如图“家”字的位置记作(1,9),请你破解密码:(3,3),(5,5),(2,7),(2,2),(1,8),(8,7),(8,8)
03
新知探究
动脑筋
如图, 已知正方形ABCD的边长为6.
(1)如果以点B为原点,以BC所在直线为x轴,建立平面直角坐标系,那么y轴是哪条直线?写出正方形的顶点A,B,C,D的坐标.
03
新知探究
因为AB= 6,BC= 6,可得点A,C,D的坐标分别为A(0,6),C(6,0),D(6,6).
分析:如图,以点B为原点,分别以BC,AB所在直线为x轴,y轴,建立平面直角坐标系,规定1个单位长度为1,此时点B的坐标为(0,0).
(0,6)
(0,0)
(6,6)
(6,0)
03
新知讲解
(2)如果以正方形的中心为原点,建立平面直角坐标系, 那么x轴和y轴分别是哪条直线?此时正方形的顶点A, B,C,D的坐标分别是多少?
03
新知讲解
分析:如图,以正方形的中心O为坐标原点,分别以过正方形的中心且垂直两组对边的两条对称轴为x轴,y轴,建立平面直角坐标系.
此时,点A,B,C,D的坐标分别为A(-3,3),
B(-3,-3),C(3,-3),D(3,3).
(0,0)
(-3,3)
(-3,-3)
(3,-3)
(3,3)
●
A
C
●
D
●
B
03
新知讲解
下面两种建立直角坐标系的方式哪一种更适当?然后再给出结论
比一比
03
新知讲解
由上得知,建立的平面直角坐标系不同,则正方形的顶点A,B,C,D的坐标也不同.你认为怎样建立直角坐标系才比较适当?
①以某已知点为原点.
②以图形中某线所在的直线为x轴(或y轴)
③以已知线段中点为原点.
④以两直线交点为原点.
⑤利用图形的轴对称性,以对称轴为x轴或y轴.
温馨提示:
没有一成不变的模式,但选择适当的坐标系,可使计算降低难度!
新课探究
例
例1、如图,矩形ABCD的长和宽分别为8和6,试建立适当的平面直角坐标系表示矩形ABCD各顶点的坐标,并作出矩形ABCD.
03
新知讲解
解:如图所示,以点B为坐标原点,分别以BC,AB 所在直线为x 轴,y轴,建立平面直角坐标系. 规定1个单位长度为1. 点B的坐标为(0,0).
因为BC=8,AB=6,可得点A,C,D的坐标分别为:
A(0,6),C(8,0),D(8,6).
●
A
C
●
D
●
依次连接A,B,C,D , 则图中的四边形就是所求作的矩形.
03
新知讲解
建立适当的直角坐标系求点的坐标
(1)分析条件,选择适当的点作为坐标原点
(2)过原点作两条互相垂直的数轴作为x轴与y轴;
(3)确定正方向、单位长度。
归纳总结
03
新知讲解
例2、如图是一个机器零件的尺寸规格示意图, 试建立适当的平面直角坐标系表示其各顶点的坐标,并作出这个示意图.
03
新知讲解
解:过点D 作AB 的垂线,垂足为点O,以点O 为原点,分别以AB,DO所在直线为x轴,y轴,建立平面直角坐标系,如图.
规定1 个单位长度为100 mm,则四边形ABCD 的顶点坐标分别为:A(-1,0),B(4,0),C(3,2), D(0,2). 依次连接A,B,C,D , 则图中的四边形ABCD即为所求作的图形.
y
x
(-1,0)
(4,0)
(3,2)
(0,2)
03
新知讲解
归纳总结:
(1)建立平面直角坐标系,用坐标描述简单图形的一个根本原则是在建立平面直角坐标系时,应使点的坐标最简明.
(2)解题的关键是把求坐标的问题转化为求线段的长的问题.
04
课堂练习
【知识技能类作业】必做题:
1.如图是小刚画的一张脸,他对妹妹说“如果我用(0,2)表示左眼,用(2,2)表示右眼,那么嘴的位置可以表示成( )
A.(1,0) B.(-1,0)
C.(-1,1) D.(1,-1)
A
04
课堂练习
【知识技能类作业】选做题:
2.如图,正方形ABCD的边长等于4,那么A,B,C,D四个顶点坐标分别为________、________、________、________.
(0,0)
(0,4)
(-4,0)
(-4,4)
04
课堂练习
【综合拓展类作业】
3.将例1再建立另外一个平面直角坐标系,作出矩形ABCD.
04
课堂练习
【综合拓展类作业】
解:如图所示,分别以AB,AD的中点所在直线为x 轴,y轴,建立平面直角坐标系,两直线交点为原点.规定1个单位长度为1.
因为AD=8,AB=6,可得点A,C,D的坐标分别为:
A(-4,3),B(-4,-3),C(4,-3),D(4,3).
依次连接A,B,C,D , 则图中的四边形就是所求作的矩形.
●
A
C
●
D
●
B
05
课堂小结
简单的坐标表示
1.根据点的坐标确定点的位置,并运用它描点作图.
2.建立适当的直角坐标系,并用坐标表示简单图形各顶点的位置
简单图形的坐标表示
坐标原点的选取
平面直角坐标系的建立
用坐标表示简单几何图形各顶点的位置
06
作业布置
【知识技能类作业】必做题:
1.在平面直角坐标系内,已知点A(2,2),B(2,-3),点P在y轴上,且△APB为直角三角形,则点P的个数为( )
A.1个 B.2个 C.3个 D.4个
D
06
作业布置
【知识技能类作业】选做题:
2、如图所示,坐在象棋棋盘上建立直角坐标系,使“帅”位于点(﹣2,﹣2),“马”位于点(1,﹣2),则“兵”位于点 .
(-4,1)
06
作业布置
【综合拓展类作业】
3.如图, Rt△ABC的两直角边AB, BC 的长分别为6,5, 试建立适当的平面直角坐标系来表示Rt△ABC各顶点的坐标.
06
作业布置
【综合拓展类作业】
解:以点B为原点, 分别以BC,AB所在直线为x轴, y轴,建立平面直角坐标系,如下图所示.
从上图可知Rt△ABC各顶点的坐标分别为:
A(0,6),B(0 ,0),
C(5,0).
Thanks!
https://www.21cnjy.com/recruitment/home/fine
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
