湖南省永州市祁阳市浯溪一中2024-2025学年下学期4月考九年级数学试卷(含答案)
文档属性
| 名称 | 湖南省永州市祁阳市浯溪一中2024-2025学年下学期4月考九年级数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-10 08:36:30 | ||
图片预览



文档简介
湖南省祁阳市浯溪一中2024-2025学年下学期4月考九年级数学试卷
时间:120分钟 满分:120分
一.选择题(共10小题,满分30分,每小题3分)
1.﹣2025的相反数是( )
A.2025 B.﹣2025 C. D.
2.一个由长方体截去一部分后得到的几何体如图水平放置,其左视图是( )
A. B. C. D.
3.下列计算正确的是( )
A.a6÷a3=a2 B.a2+2a2=3a2 C.(2a)3=6a3 D.(a+1)2=a2+1
4.2025年初,祁阳市常住人口为119.1万人,其中数据“119.1万”用科学记数法表示为( )
A.11.91×105 B.1.191×105
C.1.191×106 D.0.1191×107
5.规定以下两种变换:①f(m,n)=(m,﹣n),如f(2,1)=(2,﹣1);②g(m,n)=(﹣m,﹣n),如g(2,1)=(﹣2,﹣1).按照以上变换,那么g[f(﹣2,3)]等于( )
A.(2,3) B.(2,﹣3) C.(﹣2,3) D.(﹣2,﹣3)
6.如图,AC∥BD,AD与BC相交于点O,若∠AOB=70°,∠B=32°,则∠A的度数为( )
A.32° B.70° C.38° D.45°
第6题图 第7题图 第8题图 第10题图
7.如图,某同学用一个等边三角形ABC和一个正五边形BCDEF设计了一个宝石徽章,其中BC为两个图形的公共边,连接AE,CF交于点G,下列说法错误的是( )
A.AC⊥CF B.DE∥CF C.△EFG是等腰三角形 D.AE垂直平分BC
8.如图,已知圆O的直径为6,CD为圆O的直径,且CD⊥AB,∠D=15°.则OE的长为( )
A.3 B.3 C. D.
9.在申请加入中国共青团的过程中,团课笔试是一个重要的环节.某校组织65名申请入团的同学进行团课笔试,其中有32人笔试合格.小轩已经查出自己的成绩,他想判断自己笔试是否合格,只需要知道65人笔试成绩的( )
A.中位数 B.平均数 C.众数 D.方差
10.如图,把正方形ABCD放在平面直角坐标系中,点D是坐标原点,点C,A分别在x,y轴的正半轴上且,点O是对角线AC,BD的交点,过点O作射线OM,ON分别交边BC,CD于点E,F,且OF⊥OE于点O,OC,EF交于点G.给出下列结论:①△COE≌△DOF;②△EOF∽△BOC;③四边形CEOF的面积总是正方形ABCD面积的;④DF2+BE2=2OE2;⑤当时,点G的坐标为(6,2).其中正确结论的个数是( )
A.2 B.3 C.4 D.5
二.填空题(共8小题,满分24分,每小题3分)
11.若二次根式有意义,则x的取值范围是 .
12.方程的解是 .
13.已知一元二次方程x2﹣2x+1=9有一个实数根是﹣2,则方程的另一个根是 .
14.圆周率π是无限不循环小数.历史上,祖冲之、刘徽、韦达、欧拉等数学家都对π有过深入的研究.目前,超级计算机已计算出π的小数部分超过31.4万亿位.有学者发现,随着π小数部分位数的增加,0﹣9这10个数字出现的频率趋于稳定接近相同,从π的小数部分随机取出一个数字,估计数字是3的概率为 .
第14题图 第15题图 第16题图 第17题图
15.如图,在平行四边形ABCD中,以点A为圆心,AB长为半径画弧,交AD于点E;分别以点B,E为圆心,大于BE长为半径画弧,两弧相交于点F,射线AF交BC于点G.若AB=10,BE=12,则AG的长为 .
16.现有不等臂跷跷板AB,当AB的一端点A碰到地面时(如图(1)),另一端点B到地面距离为3米;当AB的另一端点B碰到地面时(如图(2)),端点A到地面距离为2米,那么跷跷板AB的支撑点O到地面的距离OH= 米.
17.已知:如图,DE∥BC,AD:BD=1:2,则S△ADE:S四边形BCED= .
18.一次数学考试共有8道判断题,每道题10分,满分80分.规定正确的画√,错误的画×.甲、乙、丙、丁四名同学的解答及得分情况如表所示,则m的值为 .
题号学生 1 2 3 4 5 6 7 8 得分
甲 × √ × √ × × √ × 60
乙 × × √ √ √ × × √ 50
丙 √ × × × √ √ √ × 50
丁 × √ × √ √ × √ √ m
三.解答题(共8小题,满分66分)
19.(6分)计算:.
20.(6分)解不等式组:.
21.(8分)为了解学生的睡眠情况,某校随机抽取部分学生对他们最近两周的睡眠情况进行调查,得到他们每日平均睡眠时长x(单位:h)的一组数据,将所得数据分为四组(A:x<8;B:8≤x<9;C:9≤x<10;D:x≥10),并绘制成如下两幅不完整的统计图.
根据以上信息,解答下列问题:
(1)本次一共抽样调查了 名学生.
(2)求出扇形统计图中D组所对应的扇形圆心角的度数.
(3)将条形统计图补充完整.
(4)若该校共有1200名学生,请估计最近两周有多少名学生的每日平均睡眠时长大于或等于9h.
22.(8分)如图, ABCD的对角线AC,BD交于点O,点E在边CB的延长线上,且∠EAC=90°,AE2=EB EC.求证:
(1)△AEB △CEA;
(2)四边形ABCD是矩形.
23.(9分)为抗击疫情,人们众志成城,响应号召,某药店销售普通口罩和W95口罩.
(1)计划W95口罩每包售价比普通口罩贵16元,14包普通口罩和6包W95口罩总售价相同,求普通口罩和W95口罩每包售价;
(2)已知普通口罩每包进价6元,按(1)中售价销售一段时间后,发现普通口罩的日均销售量为120包,当每包降价1元时,日均销售量增加20包.该药店秉承让利于民的原则,对普通口罩进行降价销售,但要保证当天普通口罩的利润为640元,求此时普通口罩每包售价.
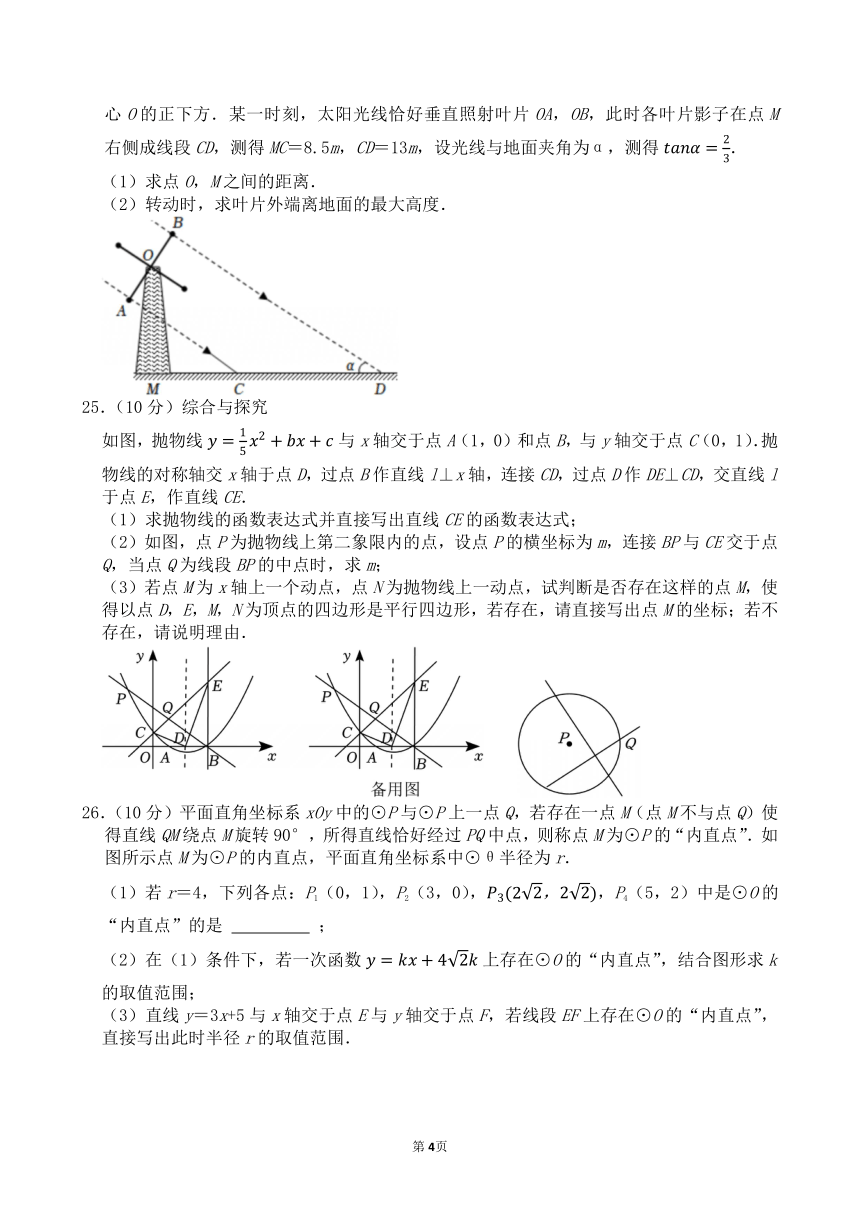
24.(9分)如图是某风车示意图,其相同的四个叶片均匀分布,水平地面上的点M在旋转中心O的正下方.某一时刻,太阳光线恰好垂直照射叶片OA,OB,此时各叶片影子在点M右侧成线段CD,测得MC=8.5m,CD=13m,设光线与地面夹角为α,测得.
(1)求点O,M之间的距离.
(2)转动时,求叶片外端离地面的最大高度.
25.(10分)综合与探究
如图,抛物线与x轴交于点A(1,0)和点B,与y轴交于点C(0,1).抛物线的对称轴交x轴于点D,过点B作直线l⊥x轴,连接CD,过点D作DE⊥CD,交直线l于点E,作直线CE.
(1)求抛物线的函数表达式并直接写出直线CE的函数表达式;
(2)如图,点P为抛物线上第二象限内的点,设点P的横坐标为m,连接BP与CE交于点Q,当点Q为线段BP的中点时,求m;
(3)若点M为x轴上一个动点,点N为抛物线上一动点,试判断是否存在这样的点M,使得以点D,E,M,N为顶点的四边形是平行四边形,若存在,请直接写出点M的坐标;若不存在,请说明理由.
26.(10分)平面直角坐标系xOy中的⊙P与⊙P上一点Q,若存在一点M(点M不与点Q)使得直线QM绕点M旋转90°,所得直线恰好经过PQ中点,则称点M为⊙P的“内直点”.如图所示点M为⊙P的内直点,平面直角坐标系中⊙θ半径为r.
(1)若r=4,下列各点:P1(0,1),P2(3,0),,P4(5,2)中是⊙O的“内直点”的是 ;
(2)在(1)条件下,若一次函数上存在⊙O的“内直点”,结合图形求k的取值范围;
(3)直线y=3x+5与x轴交于点E与y轴交于点F,若线段EF上存在⊙O的“内直点”,直接写出此时半径r的取值范围.
参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 A. D B C. A C A D A D
7.【解析】A、∵五边形BCDEF是一个正五边形,且△ABC是一个等边三角形,∴内角和为(5﹣2)×180°=540°,BC=BF,∠ACB=60°,∴∠CBF=540°÷5=108°,∴,∴∠ACF=∠ACB+∠BCF=60°+36°=96°≠90°,∴AC不垂直于CF,此选项错误,但符合题意;B、由A选项得∠BFC=36°,∴∠CFE=∠BFE﹣∠BFC=108°﹣36°=72°,∴∠CFE+∠FED=72°+108°=180°,∴DE∥CF,此选项正确,但不符合题意;C、如图,连接BE、CE,∵五边形BCDEF是一个正五边形,且△ABC是一个等边三角形,∴EF=BF=CD=DE=AB=AC,∠BFE=∠CDE=108°,在△BFE和△CDE中,,∴△BFE≌△CDE(SAS),∴∠FEB=∠DEC;同理可证△ABE≌△ACE(SSS),∴∠BEA=∠CEA,∴∠FEB+∠BEA=∠DEC+∠CEA,∴,∵由B选项得∠CFE=72°,∴∠FGE=180°﹣∠CFE﹣∠FEA=180°﹣72°﹣54°=54°,∴FG=FE,∴△EFG是等腰三角形.此选项正确,但不符合题意;D、∵△BFE≌△CDE,∴BE=CE,∵AB=AC,∴AE是BC的垂直平分线.此选项正确,但不符合题意.故选:A.
10.【解析】∵正方形ABCD,∴OD=OC=OB=OA,AD=CD=BC,∠ODF=∠OCE=45°,∠DOC=90°,∵∠DOF+∠FOC=90°=∠FOC+∠COE,∴∠DOF=∠COE,∵∠DOF=∠COE,OD=OC,∠ODF=∠OCE=45°,∴△DOF≌△COE(ASA),①正确,故符合要求;∴S△DOF=S△COE,OF=OE,DF=CE,∴CF=BE,∴,③正确,故符合要求;∵,∠FOE=90°=∠COB,∴△EOF∽△BOC,②正确,故符合要求;由勾股定理得,EF2=CF2+CE2,EF2=OE2+OF2,∴CF2+CE2=OE2+OF2,即DF2+BE2=2OE2,④正确,故符合要求;由勾股定理得,,解得,AD=CD=8,
如图,作GH⊥CD于H,∵,∴,∵∠GHC=90°=∠ADC,∠GCH=∠ACD,∴△GCH∽△ACD,∴,即,解得,GH=2,CH=2,∴G(6,2),⑤正确,故符合要求;故选:D.
11.x,12.x=3.13. 4.14..15. 16.16. 1.2.17. 1:8.18. 60.【解析】∵乙、丙第2,5题答案相同,且总得分相同,∴第2,5两题答案正确;又∵甲得分60分,即甲错两题且第2题、第5题答案均与乙、丙不同,∴其余6题答案均正确,∴这8道判断的答案分别是:×√√×√,对比丁的答案,可知其2,8两题错误,∴m=6×10=60.
19.解:=9+1.
20.解:,解不等式①得:x>﹣4,解不等式②得:x<3,则不等式组的解集为﹣4<x<3.
21.解:(1)本次调查的学生人数为16÷32%=50(名),故答案为:50;(2)表示D组的扇形圆心角的度数为360°14.4°;(3)A组人数为50﹣(16+28+2)=4(名),补全图形如下:
(4)1200720(名).答:估计该校最近两周有720名学生的每日平均睡眠时长大于或等于9h.
22.证明:(1)∵AE2=EB EC,∴,∵∠E=∠E,∴△AEB∽△CEA;
(2)由(1)可知,△AEB∽△CEA,∴∠EAB=∠ECA,∵∠EAC=90°,∴∠EAB+∠BAC=90°,∴∠ECA+∠BAC=90°,∴∠ABC=90°,∴平行四边形ABCD为矩形.
23.解:(1)设普通口罩每包的售价为x元,W95口罩每包的售价为y元,依题意得:,
解得:.答:普通口罩每包的售价为12元,W95口罩每包的售价为28元.
(2)设普通口罩每包售价为m元,则普通口罩每包的销售利润为(m﹣6)元,日均销售量为120+20(12﹣m)=(360﹣20m)包,依题意得:(m﹣6)(360﹣20m)=640,整理得:m2﹣24m+140=0,解得:m1=10,m2=14.又∵对普通口罩进行降价销售,∴m=10.
答:此时普通口罩每包售价为10元.
24.解:(1)如图,过点O作AC、BD的平行线,交CD于H,由题意可知,点O是AB的中点,∵OH∥AC∥BD,∴,∴点H是CD的中点,∵CD=13m,∴,∴MH=MC+CH=8.5+6.5=15(m),由题意可知:∠OHM=∠BDC=α∴,∴,解得OM=10m,∴点O、M之间的距离等于10m;(2)过点O作水平线OJ交BD于点J,过点B作BI⊥OJ,垂足为I,延长MO,使得OK=OB,∵BI⊥OJ,∴∠BIO=∠BIJ=90°,由题意可知:∠OBJ=∠OBI+∠JBI=90°,又∵∠BOI+∠OBI=90°,∴∠BOI=∠JBI,∴△BIO∽△JIB,∴,∴,,∵OJ∥CD,OH∥DJ,∴四边形OHDJ是平行四边形,∴OJ=HD=6.5m,∵,∴IJ=4.5m,BI=3m,OI=2m,在Rt△OBI中,由勾股定理得:OB2=OI2+BI2,∴,∴,∴,∴叶片外端离地面的最大高度等于.
25.解:(1)由题意得:,解得:,则抛物线的表达式为:yx2x+1,
则抛物线的对称轴为直线x=3,即点D(3,0),令yx2x+1=0,则x=1或5,
即点B(5,0),则BD=2,OD=2,OC=1,∵∠CDO+∠EDB=90°,∠EDB+∠DEB=90°,
∴∠CDO=∠DEB,∴tan∠CDO=tan∠DEB,即,即,
解得:BE=6,则点E(5,6),由点C、E的坐标得,直线CE的表达式为:y=x+1;
(2)设点P(m,m2m+1),
而点B(5,0),
∵点Q为线段BP的中点,由中点坐标公式得:点Q(,m2m),
将点Q的坐标代入直线CE的表达式得:m2m1,
解得:m(不合题意的值已舍去);
(3)存在,理由:设点N(m,m2m+1),点M(x,0),
当DE为对角线时,中点坐标公式得:,
解得:,即点M的坐标为:(5,0)或(5,0);
当EN或EM为对角线时,同理可得:或,
解得:x=1±,即点M的坐标为:(1,0)或(1,0);
综上,点M的坐标为:(1,0)或(1,0)或:(5,0)或(5,0).
26.解:(1)如图,
设半径OQ的中点为A,则点A的轨迹是以O为圆心,2为半径的圆,
∵∠AMQ=90°,∴点M的轨迹是以OA为直径的圆(不包括与半径为2和4相切的点),
∴点M在圆环内,∵OP1<2,OP3=4,OP4>5
∴点P1,P3,P4不是⊙O的“内置点”,∵2<OP2<4,∴P2是⊙O的“内置点”,故答案为:P2;
(2)如图2,∵y=kx+4k(x+4),∴直线y=kx+4过C(﹣4,0),
设直线y=kx+4与半径为4的圆且与点A和点B,连接OA,OB,∴∠OAC=∠OBC=90°,
∵OA=OB=4,∴sin∠OCB=sin∠OCA,∴∠OCA=∠OCB=45°,
∴kBC=1,kAC=﹣1,∴0<k<1或﹣1<k<0;
(3)如图3,直线y=3x+5记作直线l,直线l与x轴交于点B,交y轴于点C,当直线l与⊙O相切于点A,连接OA,可得OB,OC=5,BC,∠CAO=90°,∵sin∠ACO,
∴,∴OA,如图4,当r=10时,EF和圆环交于点C,
∴.
第1页
时间:120分钟 满分:120分
一.选择题(共10小题,满分30分,每小题3分)
1.﹣2025的相反数是( )
A.2025 B.﹣2025 C. D.
2.一个由长方体截去一部分后得到的几何体如图水平放置,其左视图是( )
A. B. C. D.
3.下列计算正确的是( )
A.a6÷a3=a2 B.a2+2a2=3a2 C.(2a)3=6a3 D.(a+1)2=a2+1
4.2025年初,祁阳市常住人口为119.1万人,其中数据“119.1万”用科学记数法表示为( )
A.11.91×105 B.1.191×105
C.1.191×106 D.0.1191×107
5.规定以下两种变换:①f(m,n)=(m,﹣n),如f(2,1)=(2,﹣1);②g(m,n)=(﹣m,﹣n),如g(2,1)=(﹣2,﹣1).按照以上变换,那么g[f(﹣2,3)]等于( )
A.(2,3) B.(2,﹣3) C.(﹣2,3) D.(﹣2,﹣3)
6.如图,AC∥BD,AD与BC相交于点O,若∠AOB=70°,∠B=32°,则∠A的度数为( )
A.32° B.70° C.38° D.45°
第6题图 第7题图 第8题图 第10题图
7.如图,某同学用一个等边三角形ABC和一个正五边形BCDEF设计了一个宝石徽章,其中BC为两个图形的公共边,连接AE,CF交于点G,下列说法错误的是( )
A.AC⊥CF B.DE∥CF C.△EFG是等腰三角形 D.AE垂直平分BC
8.如图,已知圆O的直径为6,CD为圆O的直径,且CD⊥AB,∠D=15°.则OE的长为( )
A.3 B.3 C. D.
9.在申请加入中国共青团的过程中,团课笔试是一个重要的环节.某校组织65名申请入团的同学进行团课笔试,其中有32人笔试合格.小轩已经查出自己的成绩,他想判断自己笔试是否合格,只需要知道65人笔试成绩的( )
A.中位数 B.平均数 C.众数 D.方差
10.如图,把正方形ABCD放在平面直角坐标系中,点D是坐标原点,点C,A分别在x,y轴的正半轴上且,点O是对角线AC,BD的交点,过点O作射线OM,ON分别交边BC,CD于点E,F,且OF⊥OE于点O,OC,EF交于点G.给出下列结论:①△COE≌△DOF;②△EOF∽△BOC;③四边形CEOF的面积总是正方形ABCD面积的;④DF2+BE2=2OE2;⑤当时,点G的坐标为(6,2).其中正确结论的个数是( )
A.2 B.3 C.4 D.5
二.填空题(共8小题,满分24分,每小题3分)
11.若二次根式有意义,则x的取值范围是 .
12.方程的解是 .
13.已知一元二次方程x2﹣2x+1=9有一个实数根是﹣2,则方程的另一个根是 .
14.圆周率π是无限不循环小数.历史上,祖冲之、刘徽、韦达、欧拉等数学家都对π有过深入的研究.目前,超级计算机已计算出π的小数部分超过31.4万亿位.有学者发现,随着π小数部分位数的增加,0﹣9这10个数字出现的频率趋于稳定接近相同,从π的小数部分随机取出一个数字,估计数字是3的概率为 .
第14题图 第15题图 第16题图 第17题图
15.如图,在平行四边形ABCD中,以点A为圆心,AB长为半径画弧,交AD于点E;分别以点B,E为圆心,大于BE长为半径画弧,两弧相交于点F,射线AF交BC于点G.若AB=10,BE=12,则AG的长为 .
16.现有不等臂跷跷板AB,当AB的一端点A碰到地面时(如图(1)),另一端点B到地面距离为3米;当AB的另一端点B碰到地面时(如图(2)),端点A到地面距离为2米,那么跷跷板AB的支撑点O到地面的距离OH= 米.
17.已知:如图,DE∥BC,AD:BD=1:2,则S△ADE:S四边形BCED= .
18.一次数学考试共有8道判断题,每道题10分,满分80分.规定正确的画√,错误的画×.甲、乙、丙、丁四名同学的解答及得分情况如表所示,则m的值为 .
题号学生 1 2 3 4 5 6 7 8 得分
甲 × √ × √ × × √ × 60
乙 × × √ √ √ × × √ 50
丙 √ × × × √ √ √ × 50
丁 × √ × √ √ × √ √ m
三.解答题(共8小题,满分66分)
19.(6分)计算:.
20.(6分)解不等式组:.
21.(8分)为了解学生的睡眠情况,某校随机抽取部分学生对他们最近两周的睡眠情况进行调查,得到他们每日平均睡眠时长x(单位:h)的一组数据,将所得数据分为四组(A:x<8;B:8≤x<9;C:9≤x<10;D:x≥10),并绘制成如下两幅不完整的统计图.
根据以上信息,解答下列问题:
(1)本次一共抽样调查了 名学生.
(2)求出扇形统计图中D组所对应的扇形圆心角的度数.
(3)将条形统计图补充完整.
(4)若该校共有1200名学生,请估计最近两周有多少名学生的每日平均睡眠时长大于或等于9h.
22.(8分)如图, ABCD的对角线AC,BD交于点O,点E在边CB的延长线上,且∠EAC=90°,AE2=EB EC.求证:
(1)△AEB △CEA;
(2)四边形ABCD是矩形.
23.(9分)为抗击疫情,人们众志成城,响应号召,某药店销售普通口罩和W95口罩.
(1)计划W95口罩每包售价比普通口罩贵16元,14包普通口罩和6包W95口罩总售价相同,求普通口罩和W95口罩每包售价;
(2)已知普通口罩每包进价6元,按(1)中售价销售一段时间后,发现普通口罩的日均销售量为120包,当每包降价1元时,日均销售量增加20包.该药店秉承让利于民的原则,对普通口罩进行降价销售,但要保证当天普通口罩的利润为640元,求此时普通口罩每包售价.
24.(9分)如图是某风车示意图,其相同的四个叶片均匀分布,水平地面上的点M在旋转中心O的正下方.某一时刻,太阳光线恰好垂直照射叶片OA,OB,此时各叶片影子在点M右侧成线段CD,测得MC=8.5m,CD=13m,设光线与地面夹角为α,测得.
(1)求点O,M之间的距离.
(2)转动时,求叶片外端离地面的最大高度.
25.(10分)综合与探究
如图,抛物线与x轴交于点A(1,0)和点B,与y轴交于点C(0,1).抛物线的对称轴交x轴于点D,过点B作直线l⊥x轴,连接CD,过点D作DE⊥CD,交直线l于点E,作直线CE.
(1)求抛物线的函数表达式并直接写出直线CE的函数表达式;
(2)如图,点P为抛物线上第二象限内的点,设点P的横坐标为m,连接BP与CE交于点Q,当点Q为线段BP的中点时,求m;
(3)若点M为x轴上一个动点,点N为抛物线上一动点,试判断是否存在这样的点M,使得以点D,E,M,N为顶点的四边形是平行四边形,若存在,请直接写出点M的坐标;若不存在,请说明理由.
26.(10分)平面直角坐标系xOy中的⊙P与⊙P上一点Q,若存在一点M(点M不与点Q)使得直线QM绕点M旋转90°,所得直线恰好经过PQ中点,则称点M为⊙P的“内直点”.如图所示点M为⊙P的内直点,平面直角坐标系中⊙θ半径为r.
(1)若r=4,下列各点:P1(0,1),P2(3,0),,P4(5,2)中是⊙O的“内直点”的是 ;
(2)在(1)条件下,若一次函数上存在⊙O的“内直点”,结合图形求k的取值范围;
(3)直线y=3x+5与x轴交于点E与y轴交于点F,若线段EF上存在⊙O的“内直点”,直接写出此时半径r的取值范围.
参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 A. D B C. A C A D A D
7.【解析】A、∵五边形BCDEF是一个正五边形,且△ABC是一个等边三角形,∴内角和为(5﹣2)×180°=540°,BC=BF,∠ACB=60°,∴∠CBF=540°÷5=108°,∴,∴∠ACF=∠ACB+∠BCF=60°+36°=96°≠90°,∴AC不垂直于CF,此选项错误,但符合题意;B、由A选项得∠BFC=36°,∴∠CFE=∠BFE﹣∠BFC=108°﹣36°=72°,∴∠CFE+∠FED=72°+108°=180°,∴DE∥CF,此选项正确,但不符合题意;C、如图,连接BE、CE,∵五边形BCDEF是一个正五边形,且△ABC是一个等边三角形,∴EF=BF=CD=DE=AB=AC,∠BFE=∠CDE=108°,在△BFE和△CDE中,,∴△BFE≌△CDE(SAS),∴∠FEB=∠DEC;同理可证△ABE≌△ACE(SSS),∴∠BEA=∠CEA,∴∠FEB+∠BEA=∠DEC+∠CEA,∴,∵由B选项得∠CFE=72°,∴∠FGE=180°﹣∠CFE﹣∠FEA=180°﹣72°﹣54°=54°,∴FG=FE,∴△EFG是等腰三角形.此选项正确,但不符合题意;D、∵△BFE≌△CDE,∴BE=CE,∵AB=AC,∴AE是BC的垂直平分线.此选项正确,但不符合题意.故选:A.
10.【解析】∵正方形ABCD,∴OD=OC=OB=OA,AD=CD=BC,∠ODF=∠OCE=45°,∠DOC=90°,∵∠DOF+∠FOC=90°=∠FOC+∠COE,∴∠DOF=∠COE,∵∠DOF=∠COE,OD=OC,∠ODF=∠OCE=45°,∴△DOF≌△COE(ASA),①正确,故符合要求;∴S△DOF=S△COE,OF=OE,DF=CE,∴CF=BE,∴,③正确,故符合要求;∵,∠FOE=90°=∠COB,∴△EOF∽△BOC,②正确,故符合要求;由勾股定理得,EF2=CF2+CE2,EF2=OE2+OF2,∴CF2+CE2=OE2+OF2,即DF2+BE2=2OE2,④正确,故符合要求;由勾股定理得,,解得,AD=CD=8,
如图,作GH⊥CD于H,∵,∴,∵∠GHC=90°=∠ADC,∠GCH=∠ACD,∴△GCH∽△ACD,∴,即,解得,GH=2,CH=2,∴G(6,2),⑤正确,故符合要求;故选:D.
11.x,12.x=3.13. 4.14..15. 16.16. 1.2.17. 1:8.18. 60.【解析】∵乙、丙第2,5题答案相同,且总得分相同,∴第2,5两题答案正确;又∵甲得分60分,即甲错两题且第2题、第5题答案均与乙、丙不同,∴其余6题答案均正确,∴这8道判断的答案分别是:×√√×√,对比丁的答案,可知其2,8两题错误,∴m=6×10=60.
19.解:=9+1.
20.解:,解不等式①得:x>﹣4,解不等式②得:x<3,则不等式组的解集为﹣4<x<3.
21.解:(1)本次调查的学生人数为16÷32%=50(名),故答案为:50;(2)表示D组的扇形圆心角的度数为360°14.4°;(3)A组人数为50﹣(16+28+2)=4(名),补全图形如下:
(4)1200720(名).答:估计该校最近两周有720名学生的每日平均睡眠时长大于或等于9h.
22.证明:(1)∵AE2=EB EC,∴,∵∠E=∠E,∴△AEB∽△CEA;
(2)由(1)可知,△AEB∽△CEA,∴∠EAB=∠ECA,∵∠EAC=90°,∴∠EAB+∠BAC=90°,∴∠ECA+∠BAC=90°,∴∠ABC=90°,∴平行四边形ABCD为矩形.
23.解:(1)设普通口罩每包的售价为x元,W95口罩每包的售价为y元,依题意得:,
解得:.答:普通口罩每包的售价为12元,W95口罩每包的售价为28元.
(2)设普通口罩每包售价为m元,则普通口罩每包的销售利润为(m﹣6)元,日均销售量为120+20(12﹣m)=(360﹣20m)包,依题意得:(m﹣6)(360﹣20m)=640,整理得:m2﹣24m+140=0,解得:m1=10,m2=14.又∵对普通口罩进行降价销售,∴m=10.
答:此时普通口罩每包售价为10元.
24.解:(1)如图,过点O作AC、BD的平行线,交CD于H,由题意可知,点O是AB的中点,∵OH∥AC∥BD,∴,∴点H是CD的中点,∵CD=13m,∴,∴MH=MC+CH=8.5+6.5=15(m),由题意可知:∠OHM=∠BDC=α∴,∴,解得OM=10m,∴点O、M之间的距离等于10m;(2)过点O作水平线OJ交BD于点J,过点B作BI⊥OJ,垂足为I,延长MO,使得OK=OB,∵BI⊥OJ,∴∠BIO=∠BIJ=90°,由题意可知:∠OBJ=∠OBI+∠JBI=90°,又∵∠BOI+∠OBI=90°,∴∠BOI=∠JBI,∴△BIO∽△JIB,∴,∴,,∵OJ∥CD,OH∥DJ,∴四边形OHDJ是平行四边形,∴OJ=HD=6.5m,∵,∴IJ=4.5m,BI=3m,OI=2m,在Rt△OBI中,由勾股定理得:OB2=OI2+BI2,∴,∴,∴,∴叶片外端离地面的最大高度等于.
25.解:(1)由题意得:,解得:,则抛物线的表达式为:yx2x+1,
则抛物线的对称轴为直线x=3,即点D(3,0),令yx2x+1=0,则x=1或5,
即点B(5,0),则BD=2,OD=2,OC=1,∵∠CDO+∠EDB=90°,∠EDB+∠DEB=90°,
∴∠CDO=∠DEB,∴tan∠CDO=tan∠DEB,即,即,
解得:BE=6,则点E(5,6),由点C、E的坐标得,直线CE的表达式为:y=x+1;
(2)设点P(m,m2m+1),
而点B(5,0),
∵点Q为线段BP的中点,由中点坐标公式得:点Q(,m2m),
将点Q的坐标代入直线CE的表达式得:m2m1,
解得:m(不合题意的值已舍去);
(3)存在,理由:设点N(m,m2m+1),点M(x,0),
当DE为对角线时,中点坐标公式得:,
解得:,即点M的坐标为:(5,0)或(5,0);
当EN或EM为对角线时,同理可得:或,
解得:x=1±,即点M的坐标为:(1,0)或(1,0);
综上,点M的坐标为:(1,0)或(1,0)或:(5,0)或(5,0).
26.解:(1)如图,
设半径OQ的中点为A,则点A的轨迹是以O为圆心,2为半径的圆,
∵∠AMQ=90°,∴点M的轨迹是以OA为直径的圆(不包括与半径为2和4相切的点),
∴点M在圆环内,∵OP1<2,OP3=4,OP4>5
∴点P1,P3,P4不是⊙O的“内置点”,∵2<OP2<4,∴P2是⊙O的“内置点”,故答案为:P2;
(2)如图2,∵y=kx+4k(x+4),∴直线y=kx+4过C(﹣4,0),
设直线y=kx+4与半径为4的圆且与点A和点B,连接OA,OB,∴∠OAC=∠OBC=90°,
∵OA=OB=4,∴sin∠OCB=sin∠OCA,∴∠OCA=∠OCB=45°,
∴kBC=1,kAC=﹣1,∴0<k<1或﹣1<k<0;
(3)如图3,直线y=3x+5记作直线l,直线l与x轴交于点B,交y轴于点C,当直线l与⊙O相切于点A,连接OA,可得OB,OC=5,BC,∠CAO=90°,∵sin∠ACO,
∴,∴OA,如图4,当r=10时,EF和圆环交于点C,
∴.
第1页
同课章节目录
