北京市顺义牛栏山第一中学2024-2025学年高二下学期3月月考数学试卷(含答案)
文档属性
| 名称 | 北京市顺义牛栏山第一中学2024-2025学年高二下学期3月月考数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 69.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-10 10:38:39 | ||
图片预览




文档简介
2024-2025学年北京市顺义区牛栏山一中高二(下)3月月考
数学试卷
一、单选题:本题共10小题,每小题4分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知,则的值为( )
A. B. C. D.
2.甲、乙、丙、丁四名学生代表高二班参加校运动会米接力比赛,则他们的出场顺序的方案数可以表示为( )
A. B. C. D.
3.若,且,则等于( )
A. B. C. D.
4.展开式中第四项的系数为,则等于( )
A. B. C. D.
5.对于的展开式,下列说法正确的是( )
A. 的展开式中共有项.
B. 展开式中的第四项与的展开式中的第四项不同.
C. 的展开式中奇数项与偶数项的系数相等.
D. 的展开式中系数为有理数的项共有四项.
6.一场元旦联欢晚会上共有个舞蹈节目,个歌曲节目,个语言类节目,则个舞蹈类节目两两不相邻的节目安排种类数为( )
A. B. C. D.
7.春节期间小明与爸爸、妈妈、爷爷、奶奶一家五人来到电影院观看哪吒,已知五人的电影票座位是依次相邻的,且爷爷、奶奶、小明三人相邻,则符合要求的坐法的种类数为( )
A. B. C. D.
8.盒子中共有个红球和个黄球,从中随机取出个球,则取出的红球多于黄球的概率为( )
A. B. C. D.
9.北京市某高中高一年级名学生参加“传承诗词文化,赓续青春华章”古诗词知识竞赛,比赛包含“唐诗”、“宋词”、“元曲”三个项目,规定每个项目至少有一名学生参加,则符合要求的参赛方法种类数
为( )
A. B. C. D.
10.在平面直角坐标系中,已知,,动点满足,且,则下列说法正确的是( )
A. 点的轨迹为圆. B. 点到原点的最短距离为.
C. 点的轨迹所围成的图形的面积为. D. 点的轨迹是一个正方形.
二、填空题:本题共5小题,每小题5分,共25分。
11.已知离散型随机变量的分布列如下表,则 ______.
12.若事件,相互独立,其中,,则 ______.
13.二十四节气是中国古代用来指导农事的补充历法,是中华民族劳动人民长期经验积累的智慧结晶春、夏、秋、冬每个季节各包含六个节气李华同学计划从中随机选取个节气开展知识讲座,则两个节气恰好在同一季节的概率为______;若已知选取的个节气均属于春季,则其中包含“立春”的概率为______“立春”是春季的六个节气之一
14.的展开式中含项的系数为______;展开式中各项的系数和为______.
15.若曲线上存在两个不同点处的切线重合,则称这条切线为曲线的“自公切线”,下列方程的曲线有“自公切线”的是______.
;
;
;
.
三、解答题:本题共6小题,共85分。解答应写出文字说明,证明过程或演算步骤。
16.本小题分
已知二项式的展开式中,各项二项式系数之和为.
求的值及展开式中的常数项;
求展开式中所有项的系数和;
求展开式中二项式系数最大的项.
17.本小题分
“猜灯谜”是我国传统节日元宵节的特色活动某公司组织猜灯谜比赛,根据谜底不同分为“字谜”、“事谜”、“物谜”三种类型,每个人每类灯谜只能猜一个小张猜对“字谜”、“事谜”、“物谜”的概率分别为、、,假设每类灯谜猜对与否互不影响.
求小张恰好猜对一类灯谜的概率;只列式不化简
求小张至少猜对一个灯谜的概率只列式不化简
18.本小题分
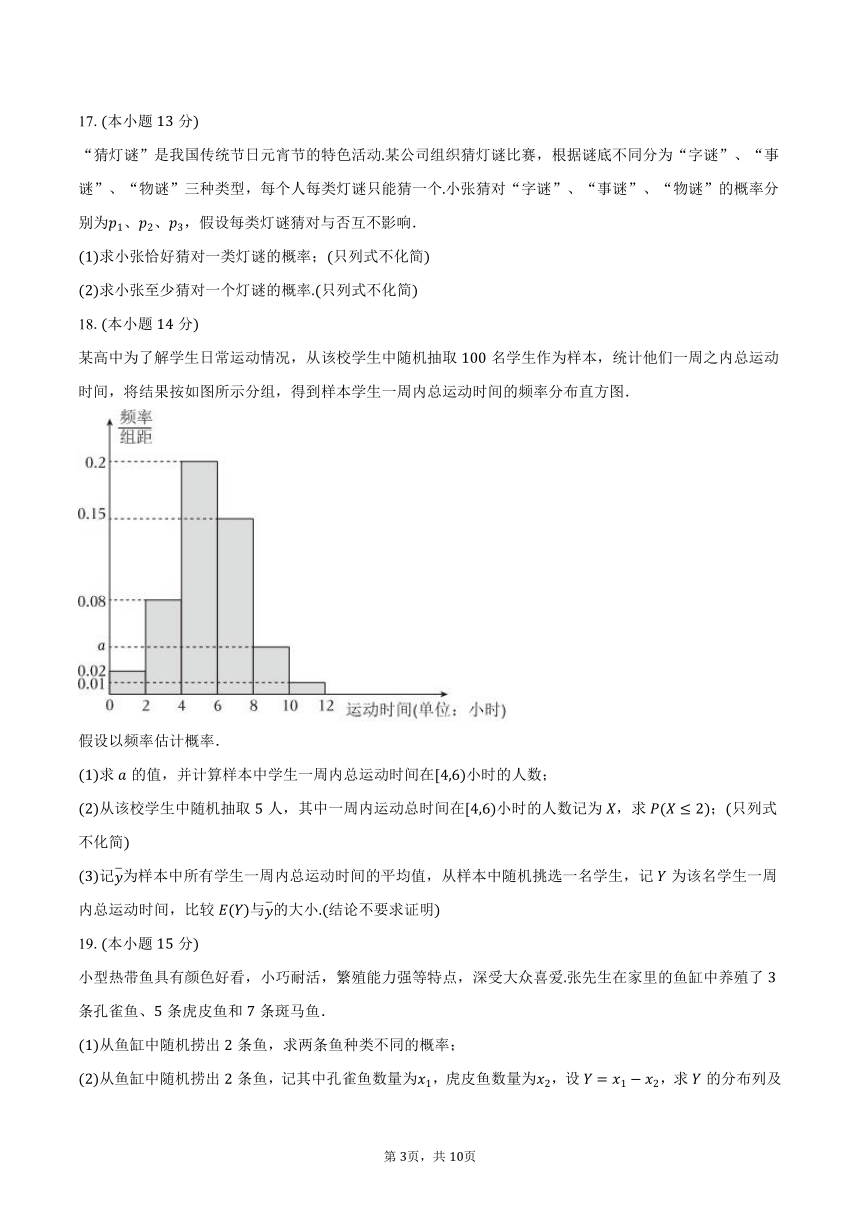
某高中为了解学生日常运动情况,从该校学生中随机抽取名学生作为样本,统计他们一周之内总运动时间,将结果按如图所示分组,得到样本学生一周内总运动时间的频率分布直方图.
假设以频率估计概率.
求的值,并计算样本中学生一周内总运动时间在小时的人数;
从该校学生中随机抽取人,其中一周内运动总时间在小时的人数记为,求;只列式不化简
记为样本中所有学生一周内总运动时间的平均值,从样本中随机挑选一名学生,记为该名学生一周内总运动时间,比较与的大小结论不要求证明
19.本小题分
小型热带鱼具有颜色好看,小巧耐活,繁殖能力强等特点,深受大众喜爱张先生在家里的鱼缸中养殖了条孔雀鱼、条虎皮鱼和条斑马鱼.
从鱼缸中随机捞出条鱼,求两条鱼种类不同的概率;
从鱼缸中随机捞出条鱼,记其中孔雀鱼数量为,虎皮鱼数量为,设,求的分布列及其期望;
若张先生又从市场购买了孔雀鱼、虎皮鱼和斑马鱼各条并投入鱼缸,此时从鱼缸中随机捞出条鱼,记其中孔雀鱼数量减去虎皮鱼数量之差为,比较中与的大小结论不要求证明.
20.本小题分
已知椭圆,点.
求椭圆的离心率和短轴长;
设直线:与椭圆有两个不同的交点,,且,求实数的取值范围.
21.本小题分
如图,设是由个实数组成的行列数表,其中表示数表中第行第列的实数,满足:,且;,,,
记为所有这样的数表组成的集合对于任意,记,;记为的一个子集,定义“变换”为:对于任意,若,则令,不变;若,则令,不变数表经过“变换”所得新数表记为.
对如数表,直接写出一个集合,使其满足;
证明:对于任意,存在集合满足;
证明:对于任意,存在集合满足且,
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.解:二项式的展开式中,各项二项式系数之和为.
则,解得,
所以该二项式为,
则通项公式为:.
令,解得,
所以该二项式的展开式中的常数项为.
取,故展开式中所有项的系数和,
由于,故展开式中二项式系数最大为,故二项式系数最大的项为
.
17.解:根据题意,设小张猜对“字谜”、“事谜”、“物谜“分别为事件,,,
则,,,且事件,,相互独立.
设小张恰好猜对一类灯谜为事件,
则
.
根据题意,设小张至少猜对一个灯谜为事件,
则事件的对立事件为小张没有猜对一个灯谜,即,
故.
18.解:根据题意可得,解得;
因为在小时的频率为,
所以所求人数为;
因为学生一周内总运动时间落在区间的概率,
今从该校学生中随机抽取人,记其中一周总运动时间在的人数为
则,
所以
.
因为为样本中所有学生一周内总运动时间的平均值,
若从这人当中再随机抽取人,记其一周运动时间为,
则由于是从同一个样本中取值,所以.
19.解:鱼缸中一共有条鱼,从中任选两条,总情况有,
设事件表示“两条鱼种类不同”,则表示“两条鱼种类相同”,
所以,
所以;
其中孔雀鱼数量为,虎皮鱼数量为,
当时,则,或,,此时概率,
当时,则,,此时概率,
当时,则,,此时概率,
当时,则,,此时概率,
当时,则,,此时概率,
故的分布列为:
;
记其中孔雀鱼数量为,虎皮鱼数量为,设,
则当时,则,或,,此时概率,
当时,则,,此时概率,
当时,则,,此时概率,
当时,则,,此时概率,
当时,则,,此时概率,
故的分布列为:
,
故,
故E.
20.解:因为椭圆,
所以,,
故,所以
故离心率为,短轴长为;
由,
得.
因为直线与椭圆有两个交点,
所以,
即,
设,,
则,
所以,
所以线段的中点,易知,
直线的斜率,
由,得,
所以,
解得
将代入到中,
得,即,且
解得,
综上所述,实数的取值范围是.
21.解:根据题目:设是由个实数组成的行列数表,
其中表示数表中第行第列的实数,满足:,且;,,,,
当时满足条件,变换后的数表为
, , ,符合题意;
当时,变换后的数表为
,,,符合题意;
当时,变换后的数表为
,,,不符合题意;
当时,变换后的数表为
,不符合题意;
当时,变换后的数表为
,不符合题意;
当时,变换后的数表为
,符合题意;
当时,变换后的数表为
,不符合题意;
当时,变换后的数表为
,不符合题意;
以上任意符合题意的集合都可以作为集合,即,,,.
证明:根据题目:记为所有这样的数表组成的集合.对于任意,
记,;记为的一个子集,
定义“变换”为:对于任意,若,
则令,不变;若,则令,不变.
数表经过“变换”所得新数表记为.
因为,且;,,.
,,
定义,
即将列中第一行的数大于等于第二行的数的列的列数构成集合,
则变换后每一列中只剩一个不超过的数,,符合题意.
这就证明了对于任意,存在集合满足;
证明:每一列的数对可能为,,,,,,,
对于,,的列的列数不属于,对于,,的列的列数属于,这样的变换后相应的这些列中的数字都变成或者.
如果的列如果有偶数列,则随意将其中的列的列数加入,
这些列中有第一行的数字变为,第二行的数字还是,另外的列的列数不在中的列第一行的数字为,第二行的数字为,
则,,
如果的列如果有奇数列,则随意将其中的列的列数加入,
这些列中有第一行的数字变为,第二行的数字还是,另外的列的列数不在中的列第一行的数字为,第二行的数字为,
则,,符合题意,
这样就证明了对于任意,存在集合满足且.
第1页,共1页
数学试卷
一、单选题:本题共10小题,每小题4分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知,则的值为( )
A. B. C. D.
2.甲、乙、丙、丁四名学生代表高二班参加校运动会米接力比赛,则他们的出场顺序的方案数可以表示为( )
A. B. C. D.
3.若,且,则等于( )
A. B. C. D.
4.展开式中第四项的系数为,则等于( )
A. B. C. D.
5.对于的展开式,下列说法正确的是( )
A. 的展开式中共有项.
B. 展开式中的第四项与的展开式中的第四项不同.
C. 的展开式中奇数项与偶数项的系数相等.
D. 的展开式中系数为有理数的项共有四项.
6.一场元旦联欢晚会上共有个舞蹈节目,个歌曲节目,个语言类节目,则个舞蹈类节目两两不相邻的节目安排种类数为( )
A. B. C. D.
7.春节期间小明与爸爸、妈妈、爷爷、奶奶一家五人来到电影院观看哪吒,已知五人的电影票座位是依次相邻的,且爷爷、奶奶、小明三人相邻,则符合要求的坐法的种类数为( )
A. B. C. D.
8.盒子中共有个红球和个黄球,从中随机取出个球,则取出的红球多于黄球的概率为( )
A. B. C. D.
9.北京市某高中高一年级名学生参加“传承诗词文化,赓续青春华章”古诗词知识竞赛,比赛包含“唐诗”、“宋词”、“元曲”三个项目,规定每个项目至少有一名学生参加,则符合要求的参赛方法种类数
为( )
A. B. C. D.
10.在平面直角坐标系中,已知,,动点满足,且,则下列说法正确的是( )
A. 点的轨迹为圆. B. 点到原点的最短距离为.
C. 点的轨迹所围成的图形的面积为. D. 点的轨迹是一个正方形.
二、填空题:本题共5小题,每小题5分,共25分。
11.已知离散型随机变量的分布列如下表,则 ______.
12.若事件,相互独立,其中,,则 ______.
13.二十四节气是中国古代用来指导农事的补充历法,是中华民族劳动人民长期经验积累的智慧结晶春、夏、秋、冬每个季节各包含六个节气李华同学计划从中随机选取个节气开展知识讲座,则两个节气恰好在同一季节的概率为______;若已知选取的个节气均属于春季,则其中包含“立春”的概率为______“立春”是春季的六个节气之一
14.的展开式中含项的系数为______;展开式中各项的系数和为______.
15.若曲线上存在两个不同点处的切线重合,则称这条切线为曲线的“自公切线”,下列方程的曲线有“自公切线”的是______.
;
;
;
.
三、解答题:本题共6小题,共85分。解答应写出文字说明,证明过程或演算步骤。
16.本小题分
已知二项式的展开式中,各项二项式系数之和为.
求的值及展开式中的常数项;
求展开式中所有项的系数和;
求展开式中二项式系数最大的项.
17.本小题分
“猜灯谜”是我国传统节日元宵节的特色活动某公司组织猜灯谜比赛,根据谜底不同分为“字谜”、“事谜”、“物谜”三种类型,每个人每类灯谜只能猜一个小张猜对“字谜”、“事谜”、“物谜”的概率分别为、、,假设每类灯谜猜对与否互不影响.
求小张恰好猜对一类灯谜的概率;只列式不化简
求小张至少猜对一个灯谜的概率只列式不化简
18.本小题分
某高中为了解学生日常运动情况,从该校学生中随机抽取名学生作为样本,统计他们一周之内总运动时间,将结果按如图所示分组,得到样本学生一周内总运动时间的频率分布直方图.
假设以频率估计概率.
求的值,并计算样本中学生一周内总运动时间在小时的人数;
从该校学生中随机抽取人,其中一周内运动总时间在小时的人数记为,求;只列式不化简
记为样本中所有学生一周内总运动时间的平均值,从样本中随机挑选一名学生,记为该名学生一周内总运动时间,比较与的大小结论不要求证明
19.本小题分
小型热带鱼具有颜色好看,小巧耐活,繁殖能力强等特点,深受大众喜爱张先生在家里的鱼缸中养殖了条孔雀鱼、条虎皮鱼和条斑马鱼.
从鱼缸中随机捞出条鱼,求两条鱼种类不同的概率;
从鱼缸中随机捞出条鱼,记其中孔雀鱼数量为,虎皮鱼数量为,设,求的分布列及其期望;
若张先生又从市场购买了孔雀鱼、虎皮鱼和斑马鱼各条并投入鱼缸,此时从鱼缸中随机捞出条鱼,记其中孔雀鱼数量减去虎皮鱼数量之差为,比较中与的大小结论不要求证明.
20.本小题分
已知椭圆,点.
求椭圆的离心率和短轴长;
设直线:与椭圆有两个不同的交点,,且,求实数的取值范围.
21.本小题分
如图,设是由个实数组成的行列数表,其中表示数表中第行第列的实数,满足:,且;,,,
记为所有这样的数表组成的集合对于任意,记,;记为的一个子集,定义“变换”为:对于任意,若,则令,不变;若,则令,不变数表经过“变换”所得新数表记为.
对如数表,直接写出一个集合,使其满足;
证明:对于任意,存在集合满足;
证明:对于任意,存在集合满足且,
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.解:二项式的展开式中,各项二项式系数之和为.
则,解得,
所以该二项式为,
则通项公式为:.
令,解得,
所以该二项式的展开式中的常数项为.
取,故展开式中所有项的系数和,
由于,故展开式中二项式系数最大为,故二项式系数最大的项为
.
17.解:根据题意,设小张猜对“字谜”、“事谜”、“物谜“分别为事件,,,
则,,,且事件,,相互独立.
设小张恰好猜对一类灯谜为事件,
则
.
根据题意,设小张至少猜对一个灯谜为事件,
则事件的对立事件为小张没有猜对一个灯谜,即,
故.
18.解:根据题意可得,解得;
因为在小时的频率为,
所以所求人数为;
因为学生一周内总运动时间落在区间的概率,
今从该校学生中随机抽取人,记其中一周总运动时间在的人数为
则,
所以
.
因为为样本中所有学生一周内总运动时间的平均值,
若从这人当中再随机抽取人,记其一周运动时间为,
则由于是从同一个样本中取值,所以.
19.解:鱼缸中一共有条鱼,从中任选两条,总情况有,
设事件表示“两条鱼种类不同”,则表示“两条鱼种类相同”,
所以,
所以;
其中孔雀鱼数量为,虎皮鱼数量为,
当时,则,或,,此时概率,
当时,则,,此时概率,
当时,则,,此时概率,
当时,则,,此时概率,
当时,则,,此时概率,
故的分布列为:
;
记其中孔雀鱼数量为,虎皮鱼数量为,设,
则当时,则,或,,此时概率,
当时,则,,此时概率,
当时,则,,此时概率,
当时,则,,此时概率,
当时,则,,此时概率,
故的分布列为:
,
故,
故E.
20.解:因为椭圆,
所以,,
故,所以
故离心率为,短轴长为;
由,
得.
因为直线与椭圆有两个交点,
所以,
即,
设,,
则,
所以,
所以线段的中点,易知,
直线的斜率,
由,得,
所以,
解得
将代入到中,
得,即,且
解得,
综上所述,实数的取值范围是.
21.解:根据题目:设是由个实数组成的行列数表,
其中表示数表中第行第列的实数,满足:,且;,,,,
当时满足条件,变换后的数表为
, , ,符合题意;
当时,变换后的数表为
,,,符合题意;
当时,变换后的数表为
,,,不符合题意;
当时,变换后的数表为
,不符合题意;
当时,变换后的数表为
,不符合题意;
当时,变换后的数表为
,符合题意;
当时,变换后的数表为
,不符合题意;
当时,变换后的数表为
,不符合题意;
以上任意符合题意的集合都可以作为集合,即,,,.
证明:根据题目:记为所有这样的数表组成的集合.对于任意,
记,;记为的一个子集,
定义“变换”为:对于任意,若,
则令,不变;若,则令,不变.
数表经过“变换”所得新数表记为.
因为,且;,,.
,,
定义,
即将列中第一行的数大于等于第二行的数的列的列数构成集合,
则变换后每一列中只剩一个不超过的数,,符合题意.
这就证明了对于任意,存在集合满足;
证明:每一列的数对可能为,,,,,,,
对于,,的列的列数不属于,对于,,的列的列数属于,这样的变换后相应的这些列中的数字都变成或者.
如果的列如果有偶数列,则随意将其中的列的列数加入,
这些列中有第一行的数字变为,第二行的数字还是,另外的列的列数不在中的列第一行的数字为,第二行的数字为,
则,,
如果的列如果有奇数列,则随意将其中的列的列数加入,
这些列中有第一行的数字变为,第二行的数字还是,另外的列的列数不在中的列第一行的数字为,第二行的数字为,
则,,符合题意,
这样就证明了对于任意,存在集合满足且.
第1页,共1页
同课章节目录
