期中练习卷(含解析)-2024-2025学年数学七年级下册北师大版(2024)
文档属性
| 名称 | 期中练习卷(含解析)-2024-2025学年数学七年级下册北师大版(2024) |  | |
| 格式 | docx | ||
| 文件大小 | 920.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-10 18:27:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
期中练习卷-2024-2025学年数学七年级下册北师大版(2024)
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列说法正确的是( )
A.“明天下雨的概率为”,意味着明天有的时间下雨
B.经过有信号灯的十字路口时,遇到红灯是随机事件
C.汽车累积行驶没有出现故障,是必然事件
D.若抛掷图钉钉尖向上的概率为,则抛掷100次图钉,钉尖向上的次数为40次
2.一个选择题有四个选项,其中只有一个是正确的,随机选一个,选择正确的概率是( )
A.0 B. C. D.1
3.下列运算正确的是( )
A. B. C. D.
4.如图,在下列给出的条件中,不能判定的是( )
A. B. C. D.
5.现定义运算“”,对于任意有理数,都有.例如:,由此可知等于( )
A. B. C. D.
6.如图,边长为a的大正方形剪去一个边长为b的小正方形后,将剩余部分通过割补拼成新的图形.根据图形能验证的等式为( )
A. B.
C. D.
7.下列说法中,正确的个数有( )
①在同一平面内,不相交的两条直线一定平行;
②过一点有且只有一条直线与已知直线平行;
③过一点有且只有一条直线与已知直线垂直;
④两条平行线被第三条直线所截,一对内错角的角平分线互相平行.
A.1个 B.2个 C.3个 D.4个
8.如图,已知,点B在上,点C在上,点A在上方,,点E在的反向延长线上,且,设,则的度数用含x的式子一定可以表示为( )
A. B. C. D.
二、填空题
9.未来三天必有降雨,则“明天下雨”是 事件.(填“必然”“不可能”或“随机”)
10.若有意义,则a的取值范围是 .
11.计算 .
12.某种绿豆在相同条件下发芽的试验结果如下表,根据表中数据估计这种绿豆发芽的概率约是 .(结果精确到)
每批粒数 2 10 50 100 500 1000 2000 3000
发芽的粒数 2 9 44 92 463 928 1866 2794
发芽的频率 1
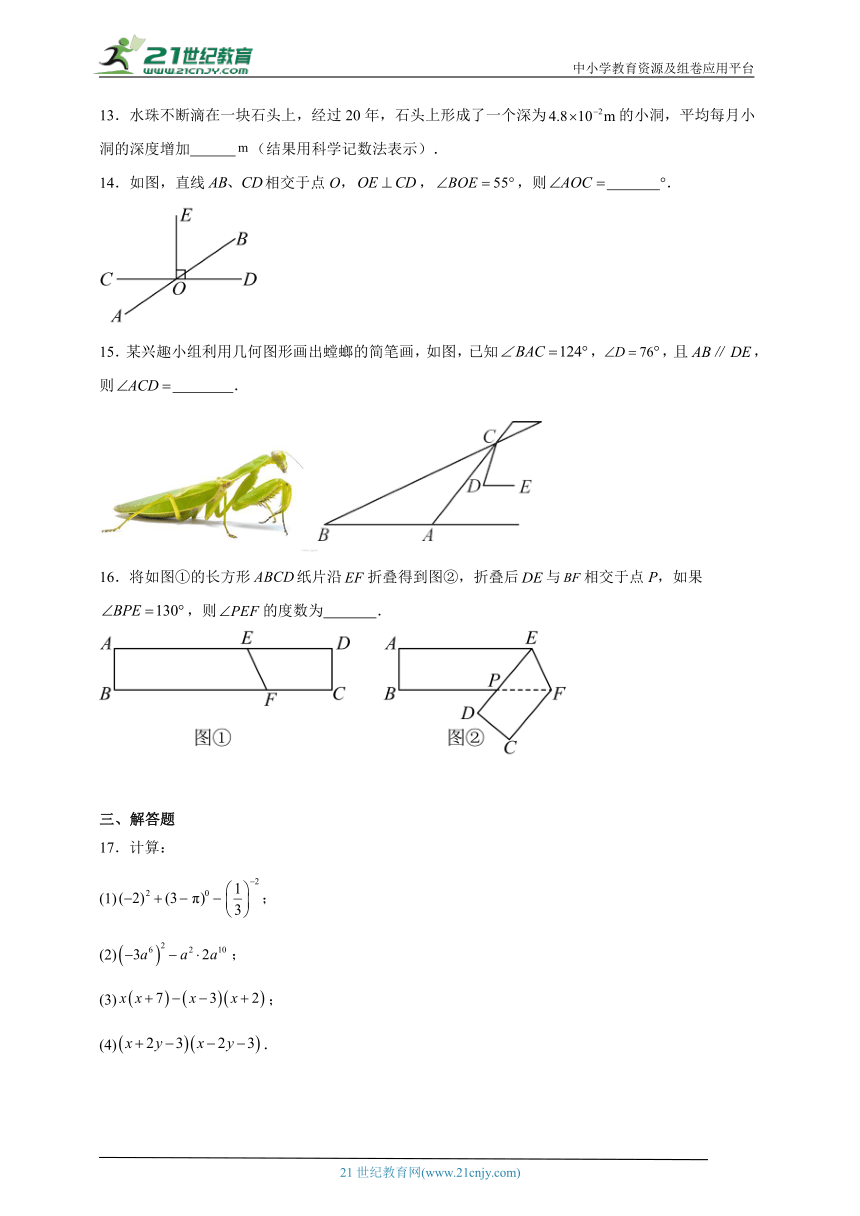
13.水珠不断滴在一块石头上,经过20年,石头上形成了一个深为的小洞,平均每月小洞的深度增加 (结果用科学记数法表示).
14.如图,直线相交于点O,,,则 °.
15.某兴趣小组利用几何图形画出螳螂的简笔画,如图,已知,,且,则 .
16.将如图①的长方形纸片沿折叠得到图②,折叠后与相交于点P,如果,则的度数为 .
三、解答题
17.计算:
(1);
(2);
(3);
(4).
18.1个袋子中装有1个白球和1个黑球,它们除颜色外其他完全相同.甲、乙两人去摸球,每人摸1次,1次摸出1个球.
(1)如果摸出球后放回摇匀,并规定摸出黑球的人获胜,那么这个游戏对双方公平吗?
(2)若摸出球后不放回,同样规定摸出黑球的人获胜,则这个游戏的公平性是否和摸出球后放回摇匀时的一样?
(3)若袋子中装有除颜色外其他完全相同的5个白球和5个黑球,甲、乙两人先后去摸球,一人摸1次,1次摸出1个球,摸出后放回摇匀,并规定摸出黑球的人获胜.这个游戏对双方公平吗?为什么?
19.观察下列各式:
;
;
;
……
不难发现规律:比任意一个偶数大3的数与此偶数的平方差能被3整除.
(1)的结果是3的______倍.
(2)设偶数为,试说明比大7的数与的平方差能被7整除.
20.如图,直线与相交于点,平分,且,射线在内部.
(1)求的度数;
(2)若,求的度数.
21.数学实验课上同学们分两组进行相同的摸球实验:在一个不透明的袋子里装有大小质地完全相同的黑、白、红、黄四种颜色的球若干个,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.第一小组进行了若干次试验后,将他们的实验结果整理绘制成如下两幅不完整的统计图.
根据以上信息,解答下列问题:
(1)补全条形统计图,并求第一小组摸出黄球的频率;
(2)求第一小组摸出黑球所对应的扇形的圆心角的度数;
(3)若第二小组与第一小组的试验次数相同,他们两组的实验结果一定会一样吗?为什么?
22.如图,在四边形中,,E为延长线上一点,交于点F,,,试说明.
证明:(____________________)
且(____________________)
在中,
在中,
,
__________(等式的性质)
(____________________)
______________________________(等量代换)
(____________________)
23.问题呈现
(1)分别计算图1、2中阴影部分的面积.
知识应用
(2)某公园是长为米,宽为米的长方形,规划部门计划在其内部修建一座边长为米的正方形雕像,左右两边修两条宽为a米的长方形道路,剩余的阴影部分种植草坪进行绿化,尺寸如图3所示.
①求绿化的面积;
②若,种植草坪的价格为30元/平方米,问绿化应投入的资金是多少元?
24.如图①,过直线外一点C作,连接,.
(1)求的度数;
(2)如图②,若的平分线交于点D,点E是线段上一动点(不与A,D重合),连接.若,试探究和之间的数量关系,并说明理由;
(3)过点B引一条射线交于点H,满足,现将绕点B每秒的速度顺时针转动,绕点H每秒的速度顺时针转动,它们同时开始运动,设运动时间为.若转动后的两条射线交于点P,过P作交射线于点Q.若在转动过程中,与的比值是定值,求此时的度数.
《期中练习卷-2024-2025学年数学七年级下册北师大版(2024)》参考答案
题号 1 2 3 4 5 6 7 8
答案 B C A B C B B A
1.B
【分析】本题考查概率的意义,事件的分类.根据概率的意义,事件分类逐个判断即可得到答案.
【详解】解:A、“明天下雨的概率为”是说明天大约有可能下雨,原说法错误,不符合题意;
B、经过有信号灯的十字路口时,遇到红灯是随机事件,原说法正确,符合题意;
C、汽车累积行驶没有出现故障,是随机事件,原说法错误,不符合题意;
D、抛掷图钉钉尖向上的概率为,则抛掷100次图钉,钉尖向上的次数可能为40次,原说法错误,不符合题意.
故选:B.
2.C
【分析】本题主要考查了简单的概率计算,解题的关键在于能够熟练掌握概率计算公式.
根据一共有4个答案,那么就有4种等可能性的结果,其中只有1个正确答案,那么只有一种是正确的结果,由此利用概率公式计算即可.
【详解】解:∵一共有4个答案,其中只有1个正确答案,
∴选择正确的概率是.
故选C.
3.A
【分析】本题主要考查同底数幂的乘法,同底数幂的除法,单项式乘单项式,幂的乘方.利用同底数幂的除法的法则,同底数幂的乘法的法则,单项式乘单项式的法则,幂的乘方的法则对各项进行运算即可.
【详解】解:A、,故本选项符合题意;
B、,故本选项不符合题意;
C、,故本选项不符合题意;
D、,故本选项不符合题意;
故选:A.
4.B
【分析】本题考查了平行线的判定,熟练掌握判定定理是解题的关键.根据平行线的判定解答即可.
【详解】解:∵,
∴(内错角相等,两直线平行)
故A正确,不符合题意;
,
∴(同位角相等,两直线平行)
故B不正确,符合题意;
∴(内错角相等,两直线平行)
故C正确,不符合题意;
,
(同旁内角互补,两直线平行)
故D正确,不符合题意;
故选:B.
5.C
【分析】本题主要考查了整式的四则混合运算,根据新定义代入,然后根据完全平方公式以及平方差公式展开,最后合并同类项即可.
【详解】解:根据题意可知:
,
故选:C
6.B
【分析】本题考查了利用几何方法验证平方差公式,解决问题的关键是根据拼接前后不同的几何图形的面积不变得到等量关系.边长为a的大正方形剪去一个边长为b的小正方形后的面积为,新的图形面积等于,由于两图中阴影部分面积相等,即可得到结论.
【详解】解∶左边阴影部分的面积为,右边阴影部分的面积为,
∵前后两个图形中阴影部分的面积相等,
∴验证的等式为,
故选∶B.
7.B
【分析】结合平行线的定义与性质,垂线的性质和平行公理进行判定即可.本题主要考查了平行线的定义与性质,垂线的性质和平行公理,熟练掌握相关知识点是解题的关键.
【详解】解:①在同一平面内,不相交的两条直线一定平行,故该说法是正确的,
②经过一点有且只有一条直线与已知直线平行,应强调在经过直线外一点,故该说法是错误的.
③经过一点有且只有一条直线与已知直线垂直,应强调在同一个平面内,故该说法是是错误的.
④④两条平行线被第三条直线所截,一对内错角的角平分线互相平行,故该说法是正确的.
故选B.
8.A
【分析】本题考查平行线的性质与判定,过点作,利用平行线性质得到,过点作,利用平行线性质得到进行求解,即可解题.
【详解】解:过点作,
,
,
,
,
,
,
,即
过点作,
,,
,
,
,
,
,
.
故选:A.
9.随机
【分析】本题考查了事件的分类,正确理解必然事件、不可能事件、随机事件的概念是解决本题的关键.
必然事件指在一定条件下一定发生的事件;不可能事件是指在一定条件下,一定不发生的事件;不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件,据此判断即可.
【详解】解:未来三天必有降雨,但是明天可能下雨也可能不下雨,这一事件属于随机事件;
故答案为:随机.
10.且
【分析】考查了零指数幂,根据零指数幂有意义的条件,可得,依此即可求解.
【详解】解:∵有意义,
∴,
解得且.
故答案为:且.
11.
【分析】本题主要考查了同底数幂相乘和积的乘方的逆用,掌握相关运算法则是解题关键.根据同底数幂相乘和积的乘方的逆用即可计算答案.
【详解】解:
.
故答案为:.
12.
【分析】本题考查了用频率估计概率.分析表格频率特点是关键.
根据大量重复实验时,事件发生的频率在某个固定位置左右摆动,并且摆动的幅度越来越小,根据这个频率稳定性定理,可以用频率的集中趋势来估计概率,这个固定的近似值就是这个事件的概率,对表格进行分析即可解答.
【详解】观察发现,随着试验次数的增多,绿豆发芽的频率逐渐稳定到左右,
绿豆发芽的概率约是(结果精确到).
故答案为:.
13.
【分析】此题考查了科学记数法,幂的运算,关键是理解运用科学记数法.科学记数法的表示形式为的形式,其中,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.
用除以即可求得平均每月的深度,改为科学记数法表示即可.
【详解】解:.
∴平均每月小洞的深度增加.
故答案为:.
14.35
【分析】本题主要考查了角度的和差计算.根据题意,先由,,即可得到的度数,再由对顶角的关系即可求出.
【详解】解:∵,
∴,
又∵,
∴,
则.
故答案为:35.
15./20度
【分析】本题考查平行公理的推理,平行线的性质.
过点C作,则,由平行公理的推论得到,从而,再根据即可求解.
【详解】解:过点C作,
∴
∵,,
∴,
∴,
∵.
故答案为:
16./65度
【分析】本题考查平行线的性质,与角平分线有关的计算,根据折痕为角平分线,以及平行线的性质,进行求解即可.
【详解】解:的长方形纸片沿折叠得到图②,
∴,
∴,
∴;
故答案为:.
17.(1)
(2)
(3)
(4)
【分析】本题主要考查零指数幂,负整数指数幂,整式的运算,熟练掌握运算法则是解题的关键.
(1)根据零指数幂,负整数指数幂进行计算即可;
(2)根据积的乘方以及同底数幂的乘法进行计算即可;
(3)根据整式的运算法则进行计算即可;
(4)根据完全平方公式的运算法则进行计算即可.
【详解】(1)解:原式
;
(2)解:原式
;
(3)解:原式
;
(4)解:原式
.
18.(1)这个游戏对双方公平
(2)这个游戏的公平性和摸出球后放回时的一样
(3)这个游戏对双方是公平的,理由见解析
【分析】此题目是关于游戏公平性的问题,解题的关键是熟练掌握每种情况下的概率.
(1)因为口袋里有1个白球和1个黑球,它们除颜色外其他完全相同,每次摸出一个球后放回,每个人摸出黑球的概率都是,所以对双方公平;
(2)由于是摸出后不放回,则总的结果为甲黑乙白,或甲白乙黑,每人摸出黑球的可能性都是,所以这个游戏对双方是公平的;
(3)因为口袋里有5个白球和5个黑球,它们除颜色外其他完全相同,每人摸出黑球的可能性都是,所以这个游戏对双方是公平的.
【详解】(1)解:由于是摸出后放回,每个人摸出黑球的概率都是,所以对双方公平;
(2)解:由于是摸出后不放回,则总的结果为甲黑乙白,或甲白乙黑,则他们获胜的概率和放回时一样都是,对双方公平;
(3)解:游戏对双方公平,因为袋子中白球和黑球各有5个,每人摸出黑球的可能性都是,所以这个游戏对双方是公平的.
19.(1)27
(2)见解析
【分析】本题主要考查了运用平方差公式分解因式,分解因式的应用;
(1)计算出的结果,即可;
(2)根据“比大7的数与的平方差”列式,再利用平方差公式计算即可.
【详解】(1)解:,
即的结果是3的27倍,
故答案为:27;
(2)解:偶数为,比大7的数为,
∴,
∵为整数,
∴能被7整除,
∴比大7的数与的平方差能被7整除.
20.(1);
(2).
【分析】本题考查了余角的定义,邻补角的定义,角的倍数的运算,掌握邻补角的定义是解题的关键.
(1)根据角平分线的定义可知的度数,再利用邻补角的定义即可得到的度数;
(2)根据角的倍数即可得到的度数,再利用余角的定义即可求得的度数.
【详解】(1)解:∵,平分,
∴,
∵,
∴
即的度数为;
(2)解:∵ ,
∴,
∵,
∴,
∴.
21.(1)条形统计图见解析;
(2)
(3)不一定;理由见解析
【分析】本题主要考查了条形统计图和扇形统计图的信息关联,熟练掌握统计图的特点,是解题的关键.
(1)先根据条形统计图和扇形统计图求出摸球的总数,然后求出摸出白球的频数,补全条形统计图即可;根据摸出黄球的频数和摸球总数求出摸出黄球的频率即可;
(2)根据第一小组摸出黑球所占的百分比求出所对应的扇形的圆心角的度数即可;
(3)根据实验的随机性进行回答即可.
【详解】(1)解:实验总次数为:(次),
摸出白球的频数为:,
摸出黄球的频率为:,
补全条形统计图,如图所示:
(2)解:第一小组摸出黑球所对应的扇形的圆心角的度数为:
;
(3)解:因为进行实验时具有随机性,所以当第二小组与第一小组的试验次数相同时,他们摸出的各种球的频率很接近,但不会完全相同,因此他们两组的实验结果不一定会完全一样.
22.见解析
【分析】本题主要考查了平行线的性质与判定,对顶角相等,先根据已知条件和对顶角相等证明,再由三角形内角和定理和等式的性质推出,进而由平行线的性质推出,据此根据内错角相等,两直线平行可证明结论.
【详解】证明:(已知),
且(对顶角相等),
,
在中,,
在中,,
,,
(等式的性质)
(两直线平行,同位角相等)
(等量代换)
(内错角相等,两直线平行)
23.(1)图1:;图2:;(2)①绿化的面积为平方米;②180000元
【分析】本题考查的是多项式的乘法与图形面积,完全平方公式的应用,熟练的利用图形面积差列出正确的运算式是解本题的关键.
(1)根据长方形面积公式列式计算即可;
(2)①根据图形的面积之差列式:,再计算即可;
②代入数据计算即可求解.
【详解】(1)解:如图1,
阴影部分的面积为
;
如图2,
阴影部分的面积为
;
(2)①由题意可得:
平方米;
答:绿化的面积为平方米;
②若,种植草坪的价格为30元/平方米,
∴绿化应投入的资金是:
元.
24.(1)
(2),理由见解析
(3)
【分析】本题主要考查了平行线的性质与判定,角平分线的定义,熟知平行线的性质是解题的关键.
(1)根据平行线的性质得到,则,再由平角的定义可得答案;
(2)由角平分线的定义得到,再由三角形内角和定理和角的和差关系结合已知条件证明,即可得到;
(3)根据平行线的性质和已知条件求出;则可表示出,,过点P作,则,可得,设(k为常数),则,进而得到,再由的度数与时间t无关,推出,则.
【详解】(1)解:∵,
∴,
∵,
∴,
∵,
∴;
(2)解:,理由如下:
∵平分,
∴,
∵,
∴,
∵,
∴,
∴;
(3)解:∵,
∴,
∵,
∴;
由题意得,,
∴,,
如图所示,过点P作,则,
∴,
∴,
设(k为常数),则,
∴,
∵的度数与时间t无关,
∴,
∴,
∴.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期中练习卷-2024-2025学年数学七年级下册北师大版(2024)
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列说法正确的是( )
A.“明天下雨的概率为”,意味着明天有的时间下雨
B.经过有信号灯的十字路口时,遇到红灯是随机事件
C.汽车累积行驶没有出现故障,是必然事件
D.若抛掷图钉钉尖向上的概率为,则抛掷100次图钉,钉尖向上的次数为40次
2.一个选择题有四个选项,其中只有一个是正确的,随机选一个,选择正确的概率是( )
A.0 B. C. D.1
3.下列运算正确的是( )
A. B. C. D.
4.如图,在下列给出的条件中,不能判定的是( )
A. B. C. D.
5.现定义运算“”,对于任意有理数,都有.例如:,由此可知等于( )
A. B. C. D.
6.如图,边长为a的大正方形剪去一个边长为b的小正方形后,将剩余部分通过割补拼成新的图形.根据图形能验证的等式为( )
A. B.
C. D.
7.下列说法中,正确的个数有( )
①在同一平面内,不相交的两条直线一定平行;
②过一点有且只有一条直线与已知直线平行;
③过一点有且只有一条直线与已知直线垂直;
④两条平行线被第三条直线所截,一对内错角的角平分线互相平行.
A.1个 B.2个 C.3个 D.4个
8.如图,已知,点B在上,点C在上,点A在上方,,点E在的反向延长线上,且,设,则的度数用含x的式子一定可以表示为( )
A. B. C. D.
二、填空题
9.未来三天必有降雨,则“明天下雨”是 事件.(填“必然”“不可能”或“随机”)
10.若有意义,则a的取值范围是 .
11.计算 .
12.某种绿豆在相同条件下发芽的试验结果如下表,根据表中数据估计这种绿豆发芽的概率约是 .(结果精确到)
每批粒数 2 10 50 100 500 1000 2000 3000
发芽的粒数 2 9 44 92 463 928 1866 2794
发芽的频率 1
13.水珠不断滴在一块石头上,经过20年,石头上形成了一个深为的小洞,平均每月小洞的深度增加 (结果用科学记数法表示).
14.如图,直线相交于点O,,,则 °.
15.某兴趣小组利用几何图形画出螳螂的简笔画,如图,已知,,且,则 .
16.将如图①的长方形纸片沿折叠得到图②,折叠后与相交于点P,如果,则的度数为 .
三、解答题
17.计算:
(1);
(2);
(3);
(4).
18.1个袋子中装有1个白球和1个黑球,它们除颜色外其他完全相同.甲、乙两人去摸球,每人摸1次,1次摸出1个球.
(1)如果摸出球后放回摇匀,并规定摸出黑球的人获胜,那么这个游戏对双方公平吗?
(2)若摸出球后不放回,同样规定摸出黑球的人获胜,则这个游戏的公平性是否和摸出球后放回摇匀时的一样?
(3)若袋子中装有除颜色外其他完全相同的5个白球和5个黑球,甲、乙两人先后去摸球,一人摸1次,1次摸出1个球,摸出后放回摇匀,并规定摸出黑球的人获胜.这个游戏对双方公平吗?为什么?
19.观察下列各式:
;
;
;
……
不难发现规律:比任意一个偶数大3的数与此偶数的平方差能被3整除.
(1)的结果是3的______倍.
(2)设偶数为,试说明比大7的数与的平方差能被7整除.
20.如图,直线与相交于点,平分,且,射线在内部.
(1)求的度数;
(2)若,求的度数.
21.数学实验课上同学们分两组进行相同的摸球实验:在一个不透明的袋子里装有大小质地完全相同的黑、白、红、黄四种颜色的球若干个,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.第一小组进行了若干次试验后,将他们的实验结果整理绘制成如下两幅不完整的统计图.
根据以上信息,解答下列问题:
(1)补全条形统计图,并求第一小组摸出黄球的频率;
(2)求第一小组摸出黑球所对应的扇形的圆心角的度数;
(3)若第二小组与第一小组的试验次数相同,他们两组的实验结果一定会一样吗?为什么?
22.如图,在四边形中,,E为延长线上一点,交于点F,,,试说明.
证明:(____________________)
且(____________________)
在中,
在中,
,
__________(等式的性质)
(____________________)
______________________________(等量代换)
(____________________)
23.问题呈现
(1)分别计算图1、2中阴影部分的面积.
知识应用
(2)某公园是长为米,宽为米的长方形,规划部门计划在其内部修建一座边长为米的正方形雕像,左右两边修两条宽为a米的长方形道路,剩余的阴影部分种植草坪进行绿化,尺寸如图3所示.
①求绿化的面积;
②若,种植草坪的价格为30元/平方米,问绿化应投入的资金是多少元?
24.如图①,过直线外一点C作,连接,.
(1)求的度数;
(2)如图②,若的平分线交于点D,点E是线段上一动点(不与A,D重合),连接.若,试探究和之间的数量关系,并说明理由;
(3)过点B引一条射线交于点H,满足,现将绕点B每秒的速度顺时针转动,绕点H每秒的速度顺时针转动,它们同时开始运动,设运动时间为.若转动后的两条射线交于点P,过P作交射线于点Q.若在转动过程中,与的比值是定值,求此时的度数.
《期中练习卷-2024-2025学年数学七年级下册北师大版(2024)》参考答案
题号 1 2 3 4 5 6 7 8
答案 B C A B C B B A
1.B
【分析】本题考查概率的意义,事件的分类.根据概率的意义,事件分类逐个判断即可得到答案.
【详解】解:A、“明天下雨的概率为”是说明天大约有可能下雨,原说法错误,不符合题意;
B、经过有信号灯的十字路口时,遇到红灯是随机事件,原说法正确,符合题意;
C、汽车累积行驶没有出现故障,是随机事件,原说法错误,不符合题意;
D、抛掷图钉钉尖向上的概率为,则抛掷100次图钉,钉尖向上的次数可能为40次,原说法错误,不符合题意.
故选:B.
2.C
【分析】本题主要考查了简单的概率计算,解题的关键在于能够熟练掌握概率计算公式.
根据一共有4个答案,那么就有4种等可能性的结果,其中只有1个正确答案,那么只有一种是正确的结果,由此利用概率公式计算即可.
【详解】解:∵一共有4个答案,其中只有1个正确答案,
∴选择正确的概率是.
故选C.
3.A
【分析】本题主要考查同底数幂的乘法,同底数幂的除法,单项式乘单项式,幂的乘方.利用同底数幂的除法的法则,同底数幂的乘法的法则,单项式乘单项式的法则,幂的乘方的法则对各项进行运算即可.
【详解】解:A、,故本选项符合题意;
B、,故本选项不符合题意;
C、,故本选项不符合题意;
D、,故本选项不符合题意;
故选:A.
4.B
【分析】本题考查了平行线的判定,熟练掌握判定定理是解题的关键.根据平行线的判定解答即可.
【详解】解:∵,
∴(内错角相等,两直线平行)
故A正确,不符合题意;
,
∴(同位角相等,两直线平行)
故B不正确,符合题意;
∴(内错角相等,两直线平行)
故C正确,不符合题意;
,
(同旁内角互补,两直线平行)
故D正确,不符合题意;
故选:B.
5.C
【分析】本题主要考查了整式的四则混合运算,根据新定义代入,然后根据完全平方公式以及平方差公式展开,最后合并同类项即可.
【详解】解:根据题意可知:
,
故选:C
6.B
【分析】本题考查了利用几何方法验证平方差公式,解决问题的关键是根据拼接前后不同的几何图形的面积不变得到等量关系.边长为a的大正方形剪去一个边长为b的小正方形后的面积为,新的图形面积等于,由于两图中阴影部分面积相等,即可得到结论.
【详解】解∶左边阴影部分的面积为,右边阴影部分的面积为,
∵前后两个图形中阴影部分的面积相等,
∴验证的等式为,
故选∶B.
7.B
【分析】结合平行线的定义与性质,垂线的性质和平行公理进行判定即可.本题主要考查了平行线的定义与性质,垂线的性质和平行公理,熟练掌握相关知识点是解题的关键.
【详解】解:①在同一平面内,不相交的两条直线一定平行,故该说法是正确的,
②经过一点有且只有一条直线与已知直线平行,应强调在经过直线外一点,故该说法是错误的.
③经过一点有且只有一条直线与已知直线垂直,应强调在同一个平面内,故该说法是是错误的.
④④两条平行线被第三条直线所截,一对内错角的角平分线互相平行,故该说法是正确的.
故选B.
8.A
【分析】本题考查平行线的性质与判定,过点作,利用平行线性质得到,过点作,利用平行线性质得到进行求解,即可解题.
【详解】解:过点作,
,
,
,
,
,
,
,即
过点作,
,,
,
,
,
,
,
.
故选:A.
9.随机
【分析】本题考查了事件的分类,正确理解必然事件、不可能事件、随机事件的概念是解决本题的关键.
必然事件指在一定条件下一定发生的事件;不可能事件是指在一定条件下,一定不发生的事件;不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件,据此判断即可.
【详解】解:未来三天必有降雨,但是明天可能下雨也可能不下雨,这一事件属于随机事件;
故答案为:随机.
10.且
【分析】考查了零指数幂,根据零指数幂有意义的条件,可得,依此即可求解.
【详解】解:∵有意义,
∴,
解得且.
故答案为:且.
11.
【分析】本题主要考查了同底数幂相乘和积的乘方的逆用,掌握相关运算法则是解题关键.根据同底数幂相乘和积的乘方的逆用即可计算答案.
【详解】解:
.
故答案为:.
12.
【分析】本题考查了用频率估计概率.分析表格频率特点是关键.
根据大量重复实验时,事件发生的频率在某个固定位置左右摆动,并且摆动的幅度越来越小,根据这个频率稳定性定理,可以用频率的集中趋势来估计概率,这个固定的近似值就是这个事件的概率,对表格进行分析即可解答.
【详解】观察发现,随着试验次数的增多,绿豆发芽的频率逐渐稳定到左右,
绿豆发芽的概率约是(结果精确到).
故答案为:.
13.
【分析】此题考查了科学记数法,幂的运算,关键是理解运用科学记数法.科学记数法的表示形式为的形式,其中,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.
用除以即可求得平均每月的深度,改为科学记数法表示即可.
【详解】解:.
∴平均每月小洞的深度增加.
故答案为:.
14.35
【分析】本题主要考查了角度的和差计算.根据题意,先由,,即可得到的度数,再由对顶角的关系即可求出.
【详解】解:∵,
∴,
又∵,
∴,
则.
故答案为:35.
15./20度
【分析】本题考查平行公理的推理,平行线的性质.
过点C作,则,由平行公理的推论得到,从而,再根据即可求解.
【详解】解:过点C作,
∴
∵,,
∴,
∴,
∵.
故答案为:
16./65度
【分析】本题考查平行线的性质,与角平分线有关的计算,根据折痕为角平分线,以及平行线的性质,进行求解即可.
【详解】解:的长方形纸片沿折叠得到图②,
∴,
∴,
∴;
故答案为:.
17.(1)
(2)
(3)
(4)
【分析】本题主要考查零指数幂,负整数指数幂,整式的运算,熟练掌握运算法则是解题的关键.
(1)根据零指数幂,负整数指数幂进行计算即可;
(2)根据积的乘方以及同底数幂的乘法进行计算即可;
(3)根据整式的运算法则进行计算即可;
(4)根据完全平方公式的运算法则进行计算即可.
【详解】(1)解:原式
;
(2)解:原式
;
(3)解:原式
;
(4)解:原式
.
18.(1)这个游戏对双方公平
(2)这个游戏的公平性和摸出球后放回时的一样
(3)这个游戏对双方是公平的,理由见解析
【分析】此题目是关于游戏公平性的问题,解题的关键是熟练掌握每种情况下的概率.
(1)因为口袋里有1个白球和1个黑球,它们除颜色外其他完全相同,每次摸出一个球后放回,每个人摸出黑球的概率都是,所以对双方公平;
(2)由于是摸出后不放回,则总的结果为甲黑乙白,或甲白乙黑,每人摸出黑球的可能性都是,所以这个游戏对双方是公平的;
(3)因为口袋里有5个白球和5个黑球,它们除颜色外其他完全相同,每人摸出黑球的可能性都是,所以这个游戏对双方是公平的.
【详解】(1)解:由于是摸出后放回,每个人摸出黑球的概率都是,所以对双方公平;
(2)解:由于是摸出后不放回,则总的结果为甲黑乙白,或甲白乙黑,则他们获胜的概率和放回时一样都是,对双方公平;
(3)解:游戏对双方公平,因为袋子中白球和黑球各有5个,每人摸出黑球的可能性都是,所以这个游戏对双方是公平的.
19.(1)27
(2)见解析
【分析】本题主要考查了运用平方差公式分解因式,分解因式的应用;
(1)计算出的结果,即可;
(2)根据“比大7的数与的平方差”列式,再利用平方差公式计算即可.
【详解】(1)解:,
即的结果是3的27倍,
故答案为:27;
(2)解:偶数为,比大7的数为,
∴,
∵为整数,
∴能被7整除,
∴比大7的数与的平方差能被7整除.
20.(1);
(2).
【分析】本题考查了余角的定义,邻补角的定义,角的倍数的运算,掌握邻补角的定义是解题的关键.
(1)根据角平分线的定义可知的度数,再利用邻补角的定义即可得到的度数;
(2)根据角的倍数即可得到的度数,再利用余角的定义即可求得的度数.
【详解】(1)解:∵,平分,
∴,
∵,
∴
即的度数为;
(2)解:∵ ,
∴,
∵,
∴,
∴.
21.(1)条形统计图见解析;
(2)
(3)不一定;理由见解析
【分析】本题主要考查了条形统计图和扇形统计图的信息关联,熟练掌握统计图的特点,是解题的关键.
(1)先根据条形统计图和扇形统计图求出摸球的总数,然后求出摸出白球的频数,补全条形统计图即可;根据摸出黄球的频数和摸球总数求出摸出黄球的频率即可;
(2)根据第一小组摸出黑球所占的百分比求出所对应的扇形的圆心角的度数即可;
(3)根据实验的随机性进行回答即可.
【详解】(1)解:实验总次数为:(次),
摸出白球的频数为:,
摸出黄球的频率为:,
补全条形统计图,如图所示:
(2)解:第一小组摸出黑球所对应的扇形的圆心角的度数为:
;
(3)解:因为进行实验时具有随机性,所以当第二小组与第一小组的试验次数相同时,他们摸出的各种球的频率很接近,但不会完全相同,因此他们两组的实验结果不一定会完全一样.
22.见解析
【分析】本题主要考查了平行线的性质与判定,对顶角相等,先根据已知条件和对顶角相等证明,再由三角形内角和定理和等式的性质推出,进而由平行线的性质推出,据此根据内错角相等,两直线平行可证明结论.
【详解】证明:(已知),
且(对顶角相等),
,
在中,,
在中,,
,,
(等式的性质)
(两直线平行,同位角相等)
(等量代换)
(内错角相等,两直线平行)
23.(1)图1:;图2:;(2)①绿化的面积为平方米;②180000元
【分析】本题考查的是多项式的乘法与图形面积,完全平方公式的应用,熟练的利用图形面积差列出正确的运算式是解本题的关键.
(1)根据长方形面积公式列式计算即可;
(2)①根据图形的面积之差列式:,再计算即可;
②代入数据计算即可求解.
【详解】(1)解:如图1,
阴影部分的面积为
;
如图2,
阴影部分的面积为
;
(2)①由题意可得:
平方米;
答:绿化的面积为平方米;
②若,种植草坪的价格为30元/平方米,
∴绿化应投入的资金是:
元.
24.(1)
(2),理由见解析
(3)
【分析】本题主要考查了平行线的性质与判定,角平分线的定义,熟知平行线的性质是解题的关键.
(1)根据平行线的性质得到,则,再由平角的定义可得答案;
(2)由角平分线的定义得到,再由三角形内角和定理和角的和差关系结合已知条件证明,即可得到;
(3)根据平行线的性质和已知条件求出;则可表示出,,过点P作,则,可得,设(k为常数),则,进而得到,再由的度数与时间t无关,推出,则.
【详解】(1)解:∵,
∴,
∵,
∴,
∵,
∴;
(2)解:,理由如下:
∵平分,
∴,
∵,
∴,
∵,
∴,
∴;
(3)解:∵,
∴,
∵,
∴;
由题意得,,
∴,,
如图所示,过点P作,则,
∴,
∴,
设(k为常数),则,
∴,
∵的度数与时间t无关,
∴,
∴,
∴.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
