[专题集训11]专题十一 三角形相似的几种模型(含答案)
文档属性
| 名称 | [专题集训11]专题十一 三角形相似的几种模型(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 131.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-10 20:00:37 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
[专题集训11]专题十一 三角形相似的几种模型
一、选择题
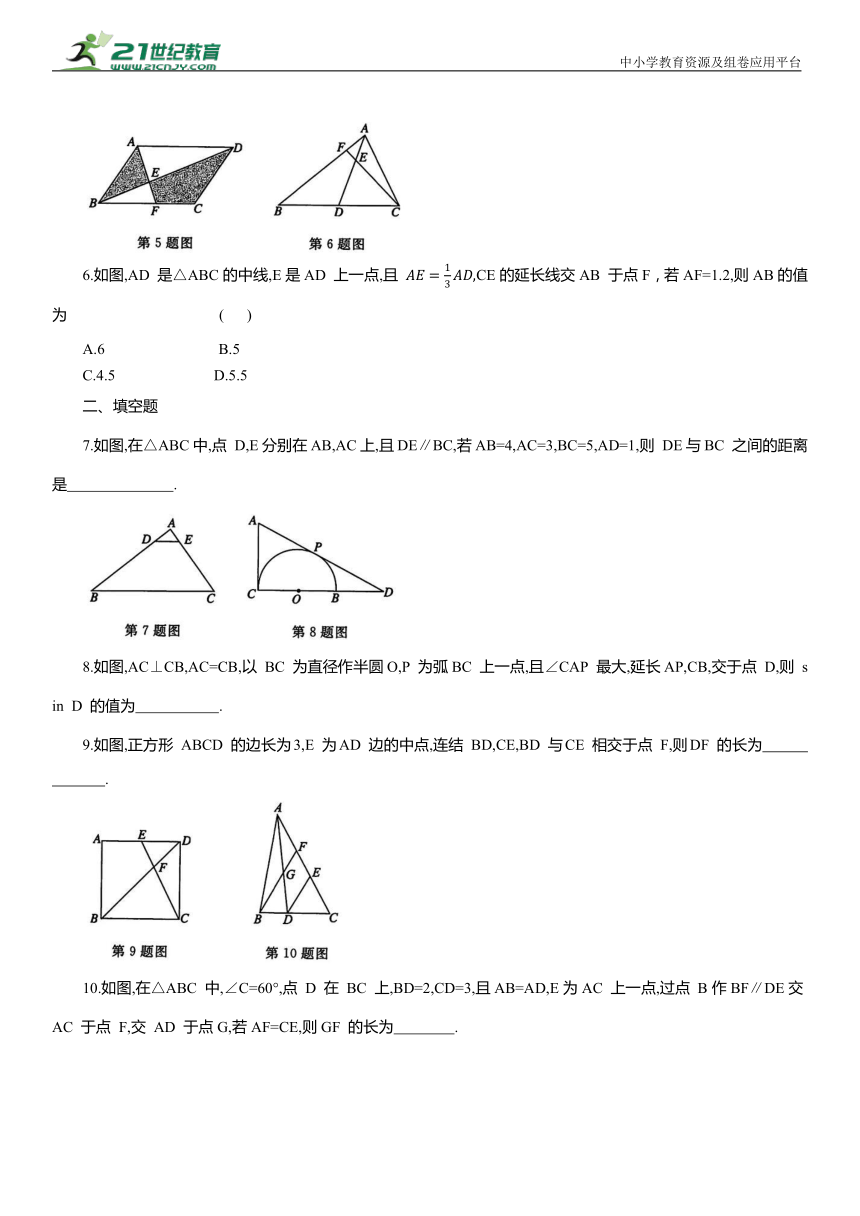
1.[2024·金华模拟] 如图,在△ABC中,点 D,E分别在AB,AC边上,DE∥BC,若AD:DB=3:1,则AE:AC= ( )
A.3:1 B.3:4
C.3:5 D.2:3
2.如图,D,E 分别是△ABC 边 AB,AC 上的点,∠ADE=∠ACB,若AD=2,AB=6,AC=4,则AE的长是 ( )
A.3 B.
C.2 D.
3.[2024·宁波模拟] 如图,∠1=∠2,添加一个条件能判定△ABC∽△ADE的是 ( )
①∠C=∠E;②∠B=∠ADE;
A.①②③ B.①②④
C.②③④ D.①②③④
4.如图,在 Rt△ABC中,∠ABC=90°,BD⊥AC于D,如果△BCD 和△ABD的面积比为9:16,CD=12,那么 BD的长是 ( )
A.8 B.12
C.16 D.4
5.[2024·徐州模拟] 如图,在平行四边形 ABCD中,F 是 BC 的中点,AF 与 BD 交于点 E,则△ABE与四边形EFCD 的面积之比为 ( )
A. B.
C. D.
6.如图,AD 是△ABC的中线,E是AD 上一点,且 CE的延长线交AB 于点F,若AF=1.2,则AB的值为 ( )
A.6 B.5
C.4.5 D.5.5
二、填空题
7.如图,在△ABC中,点 D,E分别在AB,AC上,且DE∥BC,若AB=4,AC=3,BC=5,AD=1,则 DE与BC 之间的距离是 .
8.如图,AC⊥CB,AC=CB,以 BC 为直径作半圆O,P 为弧BC 上一点,且∠CAP 最大,延长AP,CB,交于点 D,则 sin D 的值为 .
9.如图,正方形 ABCD 的边长为3,E 为AD 边的中点,连结 BD,CE,BD 与CE 相交于点 F,则DF 的长为 .
10.如图,在△ABC 中,∠C=60°,点 D 在 BC 上,BD=2,CD=3,且AB=AD,E为AC 上一点,过点 B作BF∥DE交AC 于点 F,交 AD 于点G,若AF=CE,则GF 的长为 .
三、解答题
11.如图,在△ABC 和△DEC 中,∠A =∠D,∠BCE=∠ACD.
(1)求证:△ABC∽△DEC.
(2)若S△ABC : S△DEC =4 : 9,BC=6,求 EC的长.
12.如图,在△ABC 中,BC 边上的中线 AE 与∠ABC的平分线BD 交于F 点,AD=AF.
(1)求证:△ABF∽△CBD.
(2)求证:CD=2EF.
(3)若 DF=2,求 BF.
13.在 Rt△ABC中,∠ABC=90°,AB=nBC,P 为AB 上的一点(不与端点重合),过点 P 作PM⊥AB交AC 于点M,得到△APM.
(1)【问题发现】如图1,当n=1时,P 为AB 的中点时,CM与BP 的数量关系为 .
(2)【类比探究】如图2,当n=2时,△APM绕点A 顺时针旋转,连结 CM,BP,则在旋转过程中CM与BP 之间的数量关系是否发生变化 请说明理由.
(3)【拓展延伸】在(2)的条件下,已知 AB=4,AP=2,当△APM绕点A 顺时针旋转至 B,P,M 三点共线时,请直接写出线段 BM的长.
1. B 2. A 3. B 4. C 5. C 6. A
7. 8. 9. 10.
11.解:(1)证明:∵∠BCE=∠ACD.
∴∠BCE+∠ACE=∠ACD+∠ACE,∴∠ACB=∠DCE.
又∵∠A=∠D,∴△ABC∽△DEC.
又∵BC=6,∴CE=9.
12.(1)证明略 (2)证明略
13.解:(1)当n=1时,
∵P为AB的中点,∴
∵PM⊥AB,∴∠APM=90°,∴∠APM=∠ABC,
∴PM∥BC,∴△APM∽△ABC,∴APM=AB=
故答案为
的数量关系不变,理由如下:
当n=2时,AB=2BC,
则
由勾股定理可得
旋转之前
由旋转得∠CAB=∠MAP,
即∠BAP+∠CAP=∠CAM+∠CAP,
∴∠BAP=∠CAM,∴△ABP∽△ACM,
(3)∵AB=4,AP=2,∴BC=2,PM=1,由勾股定理可得
∵△APM绕点A 顺时针旋转至B,P,M三点共线,
∴∠APM=90°,PM=1,∠APB=180°-90°=90°,
当△APM旋转至直线AB 上方时,如图1,则
当△APM旋转至直线AB 下方时,如图2,则
综上所述,线段 BM的长为 或
[专题集训11]专题十一 三角形相似的几种模型
一、选择题
1.[2024·金华模拟] 如图,在△ABC中,点 D,E分别在AB,AC边上,DE∥BC,若AD:DB=3:1,则AE:AC= ( )
A.3:1 B.3:4
C.3:5 D.2:3
2.如图,D,E 分别是△ABC 边 AB,AC 上的点,∠ADE=∠ACB,若AD=2,AB=6,AC=4,则AE的长是 ( )
A.3 B.
C.2 D.
3.[2024·宁波模拟] 如图,∠1=∠2,添加一个条件能判定△ABC∽△ADE的是 ( )
①∠C=∠E;②∠B=∠ADE;
A.①②③ B.①②④
C.②③④ D.①②③④
4.如图,在 Rt△ABC中,∠ABC=90°,BD⊥AC于D,如果△BCD 和△ABD的面积比为9:16,CD=12,那么 BD的长是 ( )
A.8 B.12
C.16 D.4
5.[2024·徐州模拟] 如图,在平行四边形 ABCD中,F 是 BC 的中点,AF 与 BD 交于点 E,则△ABE与四边形EFCD 的面积之比为 ( )
A. B.
C. D.
6.如图,AD 是△ABC的中线,E是AD 上一点,且 CE的延长线交AB 于点F,若AF=1.2,则AB的值为 ( )
A.6 B.5
C.4.5 D.5.5
二、填空题
7.如图,在△ABC中,点 D,E分别在AB,AC上,且DE∥BC,若AB=4,AC=3,BC=5,AD=1,则 DE与BC 之间的距离是 .
8.如图,AC⊥CB,AC=CB,以 BC 为直径作半圆O,P 为弧BC 上一点,且∠CAP 最大,延长AP,CB,交于点 D,则 sin D 的值为 .
9.如图,正方形 ABCD 的边长为3,E 为AD 边的中点,连结 BD,CE,BD 与CE 相交于点 F,则DF 的长为 .
10.如图,在△ABC 中,∠C=60°,点 D 在 BC 上,BD=2,CD=3,且AB=AD,E为AC 上一点,过点 B作BF∥DE交AC 于点 F,交 AD 于点G,若AF=CE,则GF 的长为 .
三、解答题
11.如图,在△ABC 和△DEC 中,∠A =∠D,∠BCE=∠ACD.
(1)求证:△ABC∽△DEC.
(2)若S△ABC : S△DEC =4 : 9,BC=6,求 EC的长.
12.如图,在△ABC 中,BC 边上的中线 AE 与∠ABC的平分线BD 交于F 点,AD=AF.
(1)求证:△ABF∽△CBD.
(2)求证:CD=2EF.
(3)若 DF=2,求 BF.
13.在 Rt△ABC中,∠ABC=90°,AB=nBC,P 为AB 上的一点(不与端点重合),过点 P 作PM⊥AB交AC 于点M,得到△APM.
(1)【问题发现】如图1,当n=1时,P 为AB 的中点时,CM与BP 的数量关系为 .
(2)【类比探究】如图2,当n=2时,△APM绕点A 顺时针旋转,连结 CM,BP,则在旋转过程中CM与BP 之间的数量关系是否发生变化 请说明理由.
(3)【拓展延伸】在(2)的条件下,已知 AB=4,AP=2,当△APM绕点A 顺时针旋转至 B,P,M 三点共线时,请直接写出线段 BM的长.
1. B 2. A 3. B 4. C 5. C 6. A
7. 8. 9. 10.
11.解:(1)证明:∵∠BCE=∠ACD.
∴∠BCE+∠ACE=∠ACD+∠ACE,∴∠ACB=∠DCE.
又∵∠A=∠D,∴△ABC∽△DEC.
又∵BC=6,∴CE=9.
12.(1)证明略 (2)证明略
13.解:(1)当n=1时,
∵P为AB的中点,∴
∵PM⊥AB,∴∠APM=90°,∴∠APM=∠ABC,
∴PM∥BC,∴△APM∽△ABC,∴APM=AB=
故答案为
的数量关系不变,理由如下:
当n=2时,AB=2BC,
则
由勾股定理可得
旋转之前
由旋转得∠CAB=∠MAP,
即∠BAP+∠CAP=∠CAM+∠CAP,
∴∠BAP=∠CAM,∴△ABP∽△ACM,
(3)∵AB=4,AP=2,∴BC=2,PM=1,由勾股定理可得
∵△APM绕点A 顺时针旋转至B,P,M三点共线,
∴∠APM=90°,PM=1,∠APB=180°-90°=90°,
当△APM旋转至直线AB 上方时,如图1,则
当△APM旋转至直线AB 下方时,如图2,则
综上所述,线段 BM的长为 或
同课章节目录
