[专题集训17]专题十七 几何图形中函数思想的运用 (含答案) 2025年中考数学知识点过关训练
文档属性
| 名称 | [专题集训17]专题十七 几何图形中函数思想的运用 (含答案) 2025年中考数学知识点过关训练 |  | |
| 格式 | docx | ||
| 文件大小 | 232.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-10 19:58:04 | ||
图片预览

文档简介
[专题集训17]专题十七 几何图形中函数思想的运用
一、选择题
1.在 Rt△ABC中,∠C=90°,若各边都扩大为原来的3 倍,则 tan A 的值 ( )
A.缩小为原来的 B.扩大为原来的3倍
C.不变 D.不能确定
2.用一根长为40厘米的绳子围成一个面积为a平方厘米的矩形,那么a的值不可能为 ( )
A.120 B.100 C.40 D.20
3.如图,在△ABC中,点 D 在AB 边上,DE∥BC,与边AC交于点 E,连结 BE.记△ADE,△BCE的面积分别为S ,S ,下列说法正确的是 ( )
A.若2AD>AB,则
B.若2AD>AB,则
C.若2ADD.若2AD4.如图,在△ABC中,∠ACB=90°,AC=BC=3,D是边AB上的动点(点D 与点 A,B不重合),过点 D作DE⊥AB交射线 BC 于点 E,连结 AE,F是AE 的中点,过点 D,F作直线,交 AC于点G,连结CF,CD.当点 E 在边 BC 上时,设 DB=x,CE=y,那么y关于x的函数关系式是 ( )
5.题目“如图,在矩形 ABCD中,AB=9,BC=15,P,Q分别是BC,CD上的点.”张老师要求添加条件后,编制一道题目并解决,甲、乙两人的做法如下.下列判断正确的是 ( )
甲:若 CQ=4,则在 BC 上存在 2 个点 P,使△ABP 与△PCQ相似;
乙:若AP⊥PQ,则CQ的最大值为
A.甲对,乙错 B.甲错,乙对
C.甲、乙都对 D.甲、乙都错
二、填空题
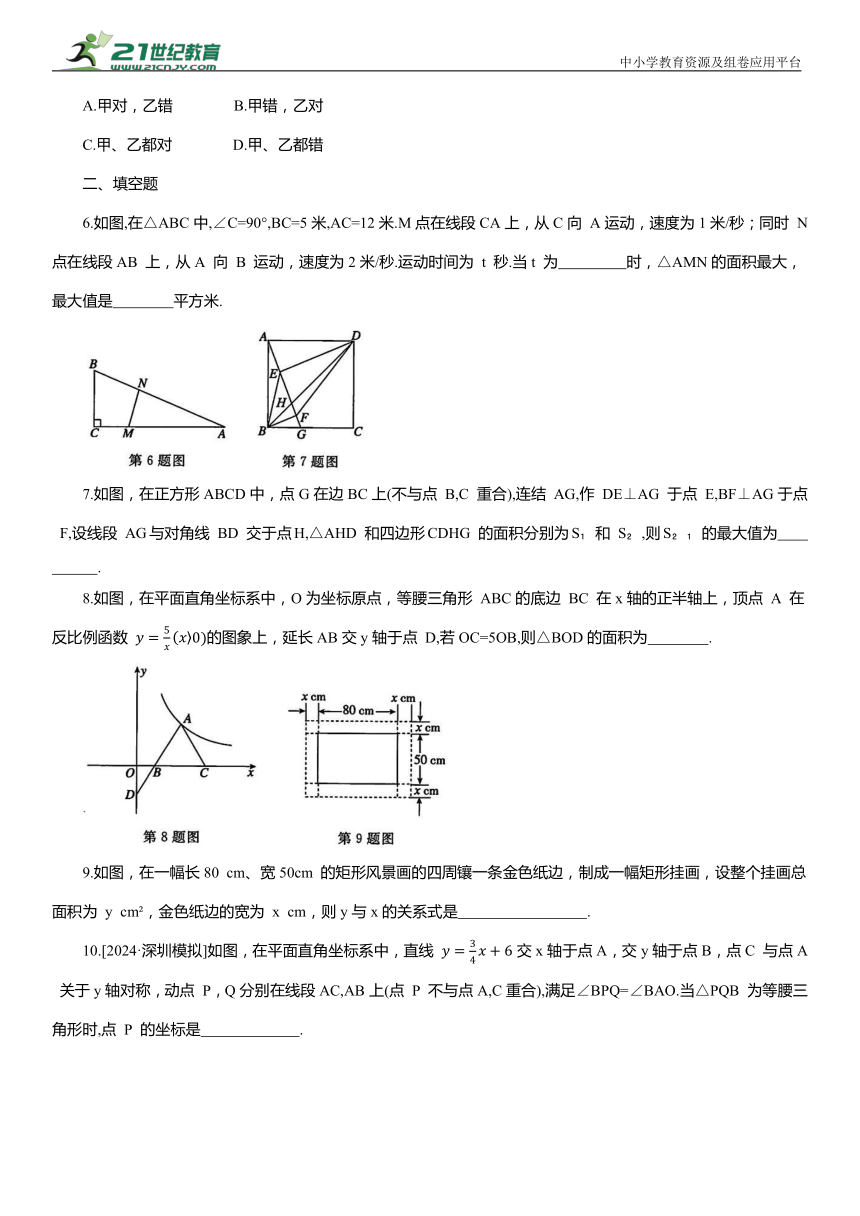
6.如图,在△ABC中,∠C=90°,BC=5米,AC=12米.M点在线段CA上,从C向 A运动,速度为1米/秒;同时 N点在线段AB 上,从A 向 B 运动,速度为2米/秒.运动时间为 t 秒.当t 为 时,△AMN的面积最大,最大值是 平方米.
7.如图,在正方形ABCD中,点G在边BC上(不与点 B,C 重合),连结 AG,作 DE⊥AG 于点 E,BF⊥AG于点 F,设线段 AG与对角线 BD 交于点H,△AHD 和四边形CDHG 的面积分别为S 和 S ,则S 的最大值为 .
8.如图,在平面直角坐标系中,O为坐标原点,等腰三角形 ABC的底边 BC 在x轴的正半轴上,顶点 A 在反比例函数 的图象上,延长AB交y轴于点 D,若OC=5OB,则△BOD的面积为 .
9.如图,在一幅长80 cm、宽50cm 的矩形风景画的四周镶一条金色纸边,制成一幅矩形挂画,设整个挂画总面积为 y cm ,金色纸边的宽为 x cm,则y与x的关系式是 .
10.[2024·深圳模拟]如图,在平面直角坐标系中,直线 交x轴于点A,交y轴于点B,点C 与点A 关于y轴对称,动点 P,Q分别在线段AC,AB上(点 P 不与点A,C重合),满足∠BPQ=∠BAO.当△PQB 为等腰三角形时,点 P 的坐标是 .
11.如图,在△ABC中,AB=1,CD⊥AB于点D,E是线段CD 上的动点,点F 在直线AB 的下方,∠ACB=∠FEB=90°,∠A=∠EFB=30°,设CE=x,△BDF的面积为y,则y关于x的函数关系式为 .
三、解答题
12.[2024·杭州模拟]如图,一架无人机沿水平直线飞行进行测绘工作,在点 P 处测得正前方水平地面上某建筑物AB 的顶端A 的俯角为30°,面向 AB方向继续飞行5米到达点 Q,测得该建筑物底端B 的俯角为45°,已知建筑物 AB 的高为3米,求无人机飞行的高度.(结果精确到1米,参考数据:
13.[2024·丽水模拟]我国著名数学家华罗庚曾说过:“数缺形时少直观,形少数时难入微;数形结合百般好,隔离分家万事休.”数学中,数和形是两个最主要的研究对象,它们之间有着十分密切的联系,在一定条件下,数和形之间可以相互转化,相互渗透.在我校的数学课上,同学们针对四边形面积求解的问题进行了探究:
【问题提出】
(1)如图1,在 ABCD中,∠A=45°,AB=8,AD=6,E是AD 的中点,点 F 在DC 上,且 DF=5,求四边形ABFE 的面积.(结果保留根号)
【问题解决】
(2)如图2所示,现规划在一处滩地上建一个五边形河畔公园ABCDE,按设计要求,要在五边形河畔公园 ABCDE 内挖一个四边形人工湖OPMN,使点 O,P,M,N 分别在边 BC,CD,AE,AB 上,且满足 BO=2AN=2CP,AM=OC.已知在五边形 ABCDE 中,∠A=∠B=∠C=90°,AB=800m,BC=1200 m,CD=600m,AE=900 m,为满足人工湖周边各功能场所及绿化用地需要,想让人工湖的面积尽可能小.请问:是否存在符合设计要求的面积最小的四边形人工湖 OPMN 若存在,求四边形 OPMN面积的最小值及这时点 N 到点A 的距离;若不存在,请说明理由.
中小学教育资源及组卷应用平台
1-5CADAB,6.6 , 7.- 8.-
0 10.(2,0)或(- ,0)
12.无人机飞行的高度约为14米.
13.解:(1)如图1,过点A作AH⊥CD交CD 的延长线于点 H,过点E作EG⊥CH 于点G,∴∠H=90°.
∵四边形 ABCD 是平行四边形,
∴CD=AB=8,AB∥CD,∴∠ADH=∠BAD=45°.
在 Rt△ADH中,AD=6,
∴AH=AD·sin∠ADH=6×sin45°=3
∵E是AD的中点, 同理
∵DF=5,∴FC=CD-DF=3,∴S四边形ABFE=S□ABCD-S△DEF
(2)存在,如图2,分别延长AE与CD,交于点 K,则四边形ABCK是矩形,∴AK=BC=1200m,AB=CK=800m,
设AN= xm,则PC= xm,BO=2xm,BN=(800-x) m,AM=OC=(1200-2x)m,
∴MK=AK-AM=1200--(1200-2x)=2xm,PK=CK-CP=(800-x)m,
.M
-
∴当x=350时,S四边形OPMN最小为470 000 m ,AM=1200-2x=1200-2×350=500<900,CP=x=350<600,
∴符合设计要求的四边形OPMN面积的最小值为470 000 m ,此时点 N 到点 A 的距离为350 m.
一、选择题
1.在 Rt△ABC中,∠C=90°,若各边都扩大为原来的3 倍,则 tan A 的值 ( )
A.缩小为原来的 B.扩大为原来的3倍
C.不变 D.不能确定
2.用一根长为40厘米的绳子围成一个面积为a平方厘米的矩形,那么a的值不可能为 ( )
A.120 B.100 C.40 D.20
3.如图,在△ABC中,点 D 在AB 边上,DE∥BC,与边AC交于点 E,连结 BE.记△ADE,△BCE的面积分别为S ,S ,下列说法正确的是 ( )
A.若2AD>AB,则
B.若2AD>AB,则
C.若2AD
5.题目“如图,在矩形 ABCD中,AB=9,BC=15,P,Q分别是BC,CD上的点.”张老师要求添加条件后,编制一道题目并解决,甲、乙两人的做法如下.下列判断正确的是 ( )
甲:若 CQ=4,则在 BC 上存在 2 个点 P,使△ABP 与△PCQ相似;
乙:若AP⊥PQ,则CQ的最大值为
A.甲对,乙错 B.甲错,乙对
C.甲、乙都对 D.甲、乙都错
二、填空题
6.如图,在△ABC中,∠C=90°,BC=5米,AC=12米.M点在线段CA上,从C向 A运动,速度为1米/秒;同时 N点在线段AB 上,从A 向 B 运动,速度为2米/秒.运动时间为 t 秒.当t 为 时,△AMN的面积最大,最大值是 平方米.
7.如图,在正方形ABCD中,点G在边BC上(不与点 B,C 重合),连结 AG,作 DE⊥AG 于点 E,BF⊥AG于点 F,设线段 AG与对角线 BD 交于点H,△AHD 和四边形CDHG 的面积分别为S 和 S ,则S 的最大值为 .
8.如图,在平面直角坐标系中,O为坐标原点,等腰三角形 ABC的底边 BC 在x轴的正半轴上,顶点 A 在反比例函数 的图象上,延长AB交y轴于点 D,若OC=5OB,则△BOD的面积为 .
9.如图,在一幅长80 cm、宽50cm 的矩形风景画的四周镶一条金色纸边,制成一幅矩形挂画,设整个挂画总面积为 y cm ,金色纸边的宽为 x cm,则y与x的关系式是 .
10.[2024·深圳模拟]如图,在平面直角坐标系中,直线 交x轴于点A,交y轴于点B,点C 与点A 关于y轴对称,动点 P,Q分别在线段AC,AB上(点 P 不与点A,C重合),满足∠BPQ=∠BAO.当△PQB 为等腰三角形时,点 P 的坐标是 .
11.如图,在△ABC中,AB=1,CD⊥AB于点D,E是线段CD 上的动点,点F 在直线AB 的下方,∠ACB=∠FEB=90°,∠A=∠EFB=30°,设CE=x,△BDF的面积为y,则y关于x的函数关系式为 .
三、解答题
12.[2024·杭州模拟]如图,一架无人机沿水平直线飞行进行测绘工作,在点 P 处测得正前方水平地面上某建筑物AB 的顶端A 的俯角为30°,面向 AB方向继续飞行5米到达点 Q,测得该建筑物底端B 的俯角为45°,已知建筑物 AB 的高为3米,求无人机飞行的高度.(结果精确到1米,参考数据:
13.[2024·丽水模拟]我国著名数学家华罗庚曾说过:“数缺形时少直观,形少数时难入微;数形结合百般好,隔离分家万事休.”数学中,数和形是两个最主要的研究对象,它们之间有着十分密切的联系,在一定条件下,数和形之间可以相互转化,相互渗透.在我校的数学课上,同学们针对四边形面积求解的问题进行了探究:
【问题提出】
(1)如图1,在 ABCD中,∠A=45°,AB=8,AD=6,E是AD 的中点,点 F 在DC 上,且 DF=5,求四边形ABFE 的面积.(结果保留根号)
【问题解决】
(2)如图2所示,现规划在一处滩地上建一个五边形河畔公园ABCDE,按设计要求,要在五边形河畔公园 ABCDE 内挖一个四边形人工湖OPMN,使点 O,P,M,N 分别在边 BC,CD,AE,AB 上,且满足 BO=2AN=2CP,AM=OC.已知在五边形 ABCDE 中,∠A=∠B=∠C=90°,AB=800m,BC=1200 m,CD=600m,AE=900 m,为满足人工湖周边各功能场所及绿化用地需要,想让人工湖的面积尽可能小.请问:是否存在符合设计要求的面积最小的四边形人工湖 OPMN 若存在,求四边形 OPMN面积的最小值及这时点 N 到点A 的距离;若不存在,请说明理由.
中小学教育资源及组卷应用平台
1-5CADAB,6.6 , 7.- 8.-
0 10.(2,0)或(- ,0)
12.无人机飞行的高度约为14米.
13.解:(1)如图1,过点A作AH⊥CD交CD 的延长线于点 H,过点E作EG⊥CH 于点G,∴∠H=90°.
∵四边形 ABCD 是平行四边形,
∴CD=AB=8,AB∥CD,∴∠ADH=∠BAD=45°.
在 Rt△ADH中,AD=6,
∴AH=AD·sin∠ADH=6×sin45°=3
∵E是AD的中点, 同理
∵DF=5,∴FC=CD-DF=3,∴S四边形ABFE=S□ABCD-S△DEF
(2)存在,如图2,分别延长AE与CD,交于点 K,则四边形ABCK是矩形,∴AK=BC=1200m,AB=CK=800m,
设AN= xm,则PC= xm,BO=2xm,BN=(800-x) m,AM=OC=(1200-2x)m,
∴MK=AK-AM=1200--(1200-2x)=2xm,PK=CK-CP=(800-x)m,
.M
-
∴当x=350时,S四边形OPMN最小为470 000 m ,AM=1200-2x=1200-2×350=500<900,CP=x=350<600,
∴符合设计要求的四边形OPMN面积的最小值为470 000 m ,此时点 N 到点 A 的距离为350 m.
同课章节目录
