[专题集训12]]专题十二 正方形中的构图 (含答案) 2025年中考数学知识点过关训练
文档属性
| 名称 | [专题集训12]]专题十二 正方形中的构图 (含答案) 2025年中考数学知识点过关训练 |  | |
| 格式 | docx | ||
| 文件大小 | 132.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-10 20:51:20 | ||
图片预览

文档简介
[专题集训12]]专题十二 正方形中的构图
一、选择题
1.如图,四边形ABCD是正方形,延长AB到点E,使AE=AC,连结CE,则∠E的度数是 ( )
A.25° B.45° C.67.5° D.75°
2.如图,AC 是正方形ABCD 的对角线,AE 平分∠CAB交DC 的延长线于点E,交 BC 于点F,则 的值为 ( )
A. C.2 D.
3.[2024·宁波模拟]四张正方形纸片如图放置,知道下列哪两个点之间的距离,可求最大正方形与最小正方形的面积之和 ( )
A.点 K,F B.点 K,E
C.点 C,F D.点C,E
4.如图,四边形 ABCD是正方形,点 E 在 AD上,连结 BE,过点 A 作 BE的垂线交CD于点 F,点G为垂足,下列选项中的结论,不正确的是 ( )
A. AE=DF B.∠DFA=∠AEB
C. AG=GF D. S△ABG=S四边形EGFD
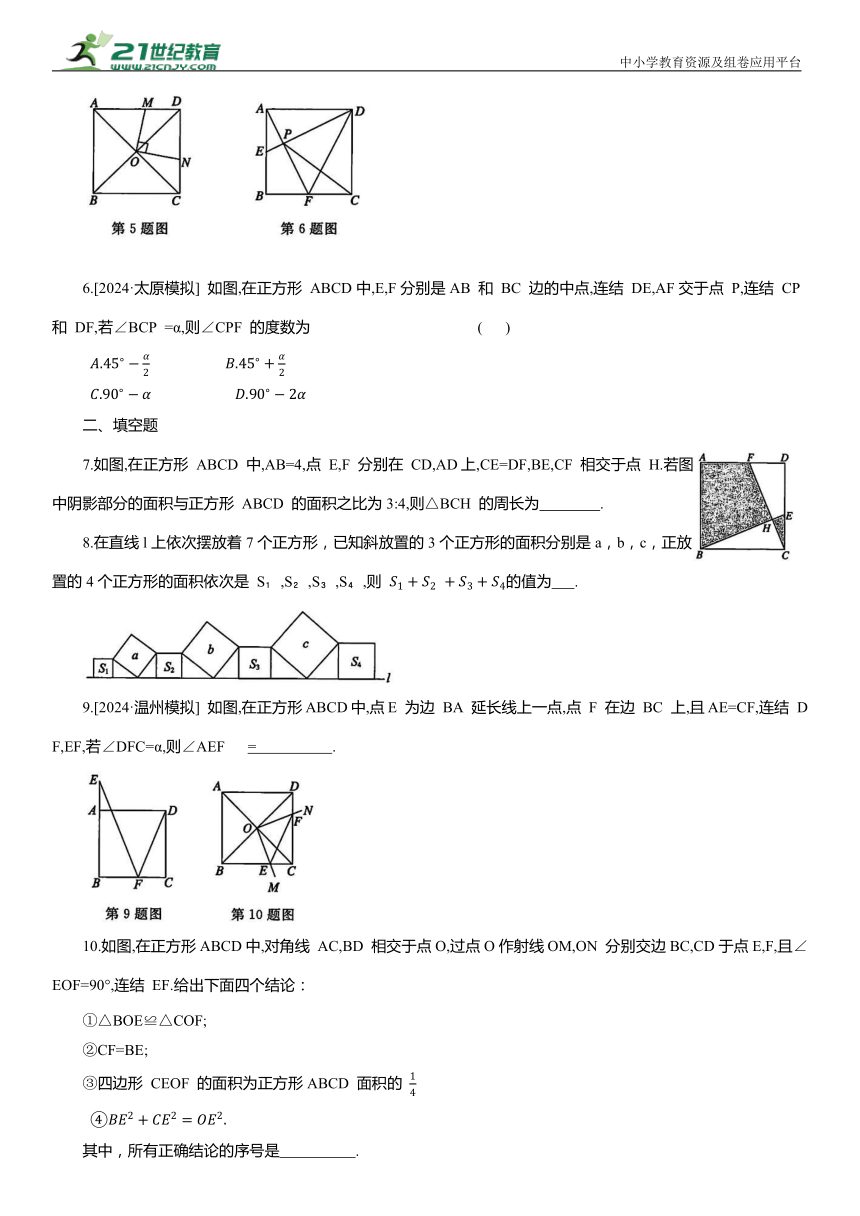
5.如图,在正方形 ABCD中,对角线 AC 与 BD 相交于点O,点 M在AD 边上,连结OM,过点O作ON⊥OM,交 CD于点 N.若四边形 MOND 的面积是4,则 AB的长为 ( )
A. B.2 C.4 D.8
6.[2024·太原模拟] 如图,在正方形 ABCD中,E,F分别是AB 和 BC 边的中点,连结 DE,AF交于点 P,连结 CP 和 DF,若∠BCP =α,则∠CPF 的度数为 ( )
二、填空题
7.如图,在正方形 ABCD 中,AB=4,点 E,F 分别在 CD,AD上,CE=DF,BE,CF 相交于点 H.若图中阴影部分的面积与正方形 ABCD 的面积之比为3:4,则△BCH 的周长为 .
8.在直线l上依次摆放着7个正方形,已知斜放置的3个正方形的面积分别是a,b,c,正放置的4个正方形的面积依次是 S ,S ,S ,S ,则 的值为 .
9.[2024·温州模拟] 如图,在正方形ABCD中,点E 为边 BA 延长线上一点,点 F 在边 BC 上,且AE=CF,连结 DF,EF,若∠DFC=α,则∠AEF = .
10.如图,在正方形ABCD中,对角线 AC,BD 相交于点O,过点O作射线OM,ON 分别交边BC,CD于点E,F,且∠EOF=90°,连结 EF.给出下面四个结论:
①△BOE≌△COF;
②CF=BE;
③四边形 CEOF 的面积为正方形ABCD 面积的
其中,所有正确结论的序号是 .
三、解答题
11.如图,在正方形ABCD中,点 E,F在对角线AC上,且AE=CF,连结ED,DF,BE,BF.求证:四边形 BEDF 为菱形.
12.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示,“赵爽弦图”是由四个全等的直角三角形与一个小正方形拼成的一个大正方形,如果小正方形的面积为6,大正方形的面积为23,直角三角形中短直角边长为 a,较长直角边长为 b,求 的值.
13.[2024·长沙模拟] 如图,在正方形 ABCD中,E为AD 上一点,连结 BE,BE的垂直平分线交AB 于点 M,交 CD 于点 N,垂足为 O,点 F 在DC 上,且 MF∥AD.
(1)求证:BE=MN.
(2)若AB=8,AE=6,求 BM的长.
中小学教育资源及组卷应用平台
专题集训12[专题十二 正方形中的构图]
1. C 2. A 3. C 4. C 5. C 6. A
7.2 +4 8. a+c 9.α-45° 10.①②③
11.证明:如图,连结 BD交AC 于点O,
∵四边形ABCD 是正方形,
∴OB=OD,OA=OC.
∵AE=CF,∴OE=OF,
∴四边形 BEDF 是平行四边形,
∵四边形ABCD是正方形,
∴AC⊥BD,∴平行四边形 BEDF 是菱形.
12.解:由题意得
∴ ,
13.解:(1)证明:∵四边形 ABCD为正方形,
∴AB=AD,AB∥CD,∠A=∠D=90°.
又∵MF∥AD,∴四边形AMFD为矩形,
∴∠MFD=∠MFN=90°,∴AD=MF,∴AB=MF.
∵BE的垂直平分线交AB 于点M,交CD于点N,垂足为O,
∴∠FMN+∠BMO=∠BMO+∠MBO=90°,
∴∠FMN=∠MBO.在△ABE和△FMN中,
∴△ABE≌△FMN(ASA),∴BE=MN.
(2)∵∠MOB=∠A=90°,∠ABE 是公共角,
∴根据勾股定理得,
∵MN 是BE 的垂直平分线,
一、选择题
1.如图,四边形ABCD是正方形,延长AB到点E,使AE=AC,连结CE,则∠E的度数是 ( )
A.25° B.45° C.67.5° D.75°
2.如图,AC 是正方形ABCD 的对角线,AE 平分∠CAB交DC 的延长线于点E,交 BC 于点F,则 的值为 ( )
A. C.2 D.
3.[2024·宁波模拟]四张正方形纸片如图放置,知道下列哪两个点之间的距离,可求最大正方形与最小正方形的面积之和 ( )
A.点 K,F B.点 K,E
C.点 C,F D.点C,E
4.如图,四边形 ABCD是正方形,点 E 在 AD上,连结 BE,过点 A 作 BE的垂线交CD于点 F,点G为垂足,下列选项中的结论,不正确的是 ( )
A. AE=DF B.∠DFA=∠AEB
C. AG=GF D. S△ABG=S四边形EGFD
5.如图,在正方形 ABCD中,对角线 AC 与 BD 相交于点O,点 M在AD 边上,连结OM,过点O作ON⊥OM,交 CD于点 N.若四边形 MOND 的面积是4,则 AB的长为 ( )
A. B.2 C.4 D.8
6.[2024·太原模拟] 如图,在正方形 ABCD中,E,F分别是AB 和 BC 边的中点,连结 DE,AF交于点 P,连结 CP 和 DF,若∠BCP =α,则∠CPF 的度数为 ( )
二、填空题
7.如图,在正方形 ABCD 中,AB=4,点 E,F 分别在 CD,AD上,CE=DF,BE,CF 相交于点 H.若图中阴影部分的面积与正方形 ABCD 的面积之比为3:4,则△BCH 的周长为 .
8.在直线l上依次摆放着7个正方形,已知斜放置的3个正方形的面积分别是a,b,c,正放置的4个正方形的面积依次是 S ,S ,S ,S ,则 的值为 .
9.[2024·温州模拟] 如图,在正方形ABCD中,点E 为边 BA 延长线上一点,点 F 在边 BC 上,且AE=CF,连结 DF,EF,若∠DFC=α,则∠AEF = .
10.如图,在正方形ABCD中,对角线 AC,BD 相交于点O,过点O作射线OM,ON 分别交边BC,CD于点E,F,且∠EOF=90°,连结 EF.给出下面四个结论:
①△BOE≌△COF;
②CF=BE;
③四边形 CEOF 的面积为正方形ABCD 面积的
其中,所有正确结论的序号是 .
三、解答题
11.如图,在正方形ABCD中,点 E,F在对角线AC上,且AE=CF,连结ED,DF,BE,BF.求证:四边形 BEDF 为菱形.
12.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示,“赵爽弦图”是由四个全等的直角三角形与一个小正方形拼成的一个大正方形,如果小正方形的面积为6,大正方形的面积为23,直角三角形中短直角边长为 a,较长直角边长为 b,求 的值.
13.[2024·长沙模拟] 如图,在正方形 ABCD中,E为AD 上一点,连结 BE,BE的垂直平分线交AB 于点 M,交 CD 于点 N,垂足为 O,点 F 在DC 上,且 MF∥AD.
(1)求证:BE=MN.
(2)若AB=8,AE=6,求 BM的长.
中小学教育资源及组卷应用平台
专题集训12[专题十二 正方形中的构图]
1. C 2. A 3. C 4. C 5. C 6. A
7.2 +4 8. a+c 9.α-45° 10.①②③
11.证明:如图,连结 BD交AC 于点O,
∵四边形ABCD 是正方形,
∴OB=OD,OA=OC.
∵AE=CF,∴OE=OF,
∴四边形 BEDF 是平行四边形,
∵四边形ABCD是正方形,
∴AC⊥BD,∴平行四边形 BEDF 是菱形.
12.解:由题意得
∴ ,
13.解:(1)证明:∵四边形 ABCD为正方形,
∴AB=AD,AB∥CD,∠A=∠D=90°.
又∵MF∥AD,∴四边形AMFD为矩形,
∴∠MFD=∠MFN=90°,∴AD=MF,∴AB=MF.
∵BE的垂直平分线交AB 于点M,交CD于点N,垂足为O,
∴∠FMN+∠BMO=∠BMO+∠MBO=90°,
∴∠FMN=∠MBO.在△ABE和△FMN中,
∴△ABE≌△FMN(ASA),∴BE=MN.
(2)∵∠MOB=∠A=90°,∠ABE 是公共角,
∴根据勾股定理得,
∵MN 是BE 的垂直平分线,
同课章节目录
