专题提升卷(七) 相似三角形综合 (含答案) 2025年中考数学知识点过关训练
文档属性
| 名称 | 专题提升卷(七) 相似三角形综合 (含答案) 2025年中考数学知识点过关训练 | 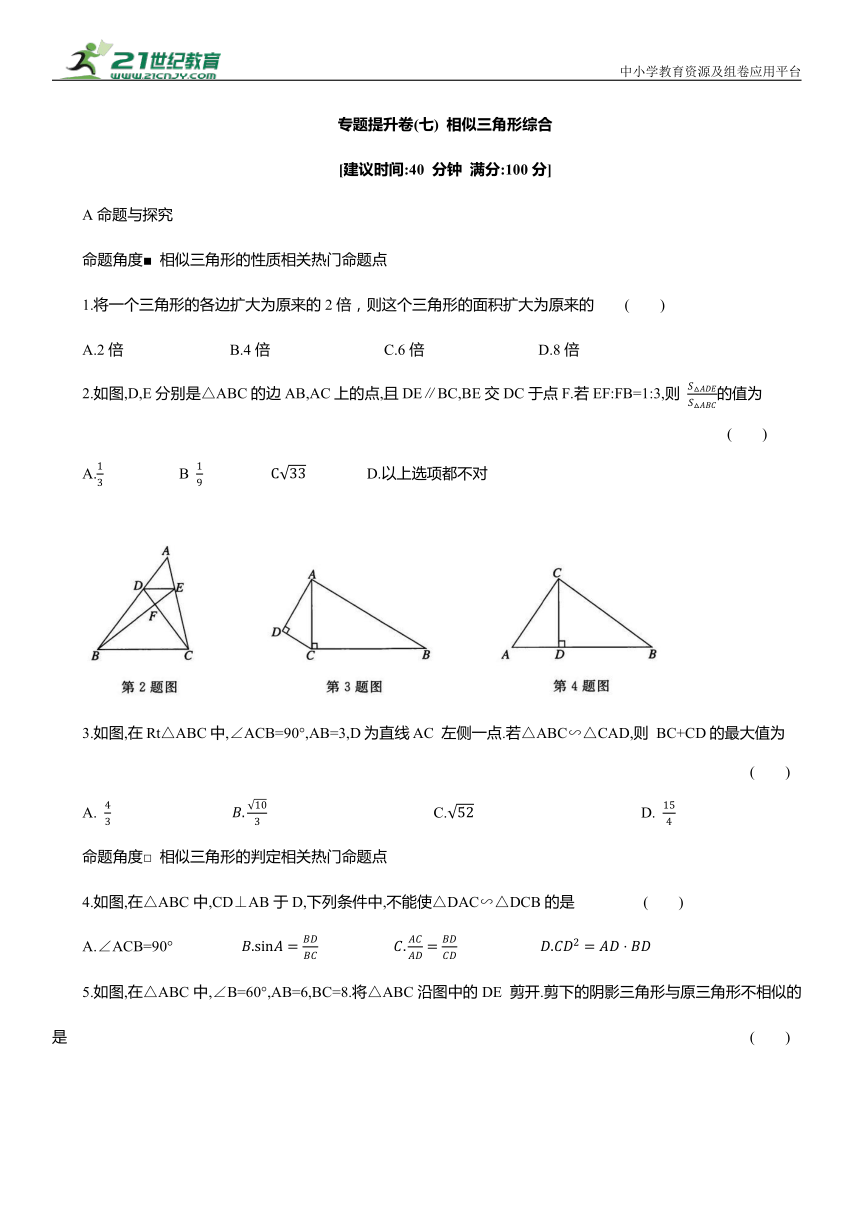 | |
| 格式 | docx | ||
| 文件大小 | 213.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-10 21:09:04 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
专题提升卷(七) 相似三角形综合
[建议时间:40 分钟 满分:100分]
A命题与探究
命题角度■ 相似三角形的性质相关热门命题点
1.将一个三角形的各边扩大为原来的2倍,则这个三角形的面积扩大为原来的 ( )
A.2倍 B.4倍 C.6倍 D.8倍
2.如图,D,E分别是△ABC的边AB,AC上的点,且DE∥BC,BE交DC于点F.若EF:FB=1:3,则 的值为 ( )
A. B D.以上选项都不对
3.如图,在Rt△ABC中,∠ACB=90°,AB=3,D为直线AC 左侧一点.若△ABC∽△CAD,则 BC+CD的最大值为 ( )
A. C. D.
命题角度□ 相似三角形的判定相关热门命题点
4.如图,在△ABC中,CD⊥AB于D,下列条件中,不能使△DAC∽△DCB的是 ( )
A.∠ACB=90°
5.如图,在△ABC中,∠B=60°,AB=6,BC=8.将△ABC沿图中的DE 剪开.剪下的阴影三角形与原三角形不相似的是 ( )
6.如图,在钝角三角形 ABC中,AB=3cm,AC=6cm,动点 D从点A 出发沿AB 以1cm/s的速度向点 B运动,同时动点E从点C 出发沿CA 以2cm/s的速度向点A 运动,当以A,D,E为顶点的三角形与△ABC相似时,运动时间是 ( )
A.3s 或4.8s B. 3s C.4. 5s D.1. 5s 或2.4s
如图,AB,CD相交于点O,且OC=45,OD=30,OB=36,当OA= 时,△AOC 与△BOD相似.
命题角度目 相似三角形的性质与判定综合热门命题点
8.[2024·辽宁] 如图,在△ABC中,. 若 9:4,则AE:CE 的值是 ( )
A.4:5 B.5:4 C.7:9 D.9:7
9.(12分)如图,在 中, ,点 D在AB边上,点 E在AC边上(点E不与A,C重合),且
(1)求证:AD·AB=AE·AC.
(2)若 求 的值.
(3)若AB=6,AC=4,求 AD长的取值范围.
10.(10分)[2024·上海] 如图,在矩形ABCD中,E为边CD 上一点,且AE⊥BD.
(1)求证:
(2)F为线段AE 延长线上一点,且满足 求证:CE=AD.
命题角度相似三角形的应用相关热门命题点
11.《孙子算经》中记载一题:“今有竿,不知长短,度其影,得一丈五尺.别立一表,长一尺五寸,影得五寸.问:竿长几何 ”其大意是:今有一根木杆,不知道其长度,量它的影子,等于15 尺,另外再立一根标杆,杆长1.5尺,量得标杆的影子为0.5尺,则木杆的长为 ( )
A.5尺 B.15尺 C.30尺 D.45尺
12.凸透镜成像的原理如右图所示, 若物体 H 到焦点F 的距离与焦点 到凸透镜中心线 DB的距离之比为3:2,则物体被缩小到原来的 ( )
IB仿真与预测
13.在研究相似问题时,嘉嘉和淇淇两同学的观点如下:
嘉嘉:将边长为1的正方形按图1的方式向外扩张,得到新正方形,它们的对应边间距为1,则新正方形与原正方形相似,同时也位似;
淇淇:将边长为1的正方形按图2的方式向外扩张,得到新正方形,每条对角线向其延长线两个方向各延伸1,则新正方形与原正方形相似,同时也位似.
对于两人的观点,下列说法正确的是 ( )
A.两人都对 B.两人都不对 C.嘉嘉对,淇淇不对 D.嘉嘉不对,淇淇对
14.如图,在平行四边形ABCD中,E,F分别为AB,BC的中点,AF与DE 相交于点G,则 的值是 ( )
A. B. C. D.
15.我国非物质文化遗产“皮影戏”又称“影子戏”,射灯发出的光线沿直线传播照在不透明的皮影人上,在皮影人后面的屏幕上形成中心投影,通过操纵皮影人来完成各种造型和场景的表演.如图,已知皮影人在C处,屏幕在E处,皮影人与屏幕相距1m,射灯A 与皮影人相距2m.若保持皮影人在C处位置不变,要使屏幕上的影子的像高DE增大一倍至FE,则射灯A应向皮影人靠近至G 的距离AG为 .
16.如图,在Rt△ABC中,∠ACB=90°,AC=4cm,BC=3cm,点 P 由点B 出发沿BA方向向点A 匀速运动,速度为1cm/s,同时点Q由A 出发沿AC 方向向点C匀速运动,速度为1cm/s,连结 PQ.设运动的时间为t(s),其中017.(12分)(1)在△ABC中,D,E分别是边BC,AB的中点,AD,CE相交于点G.
求证
提示:连结ED.
请根据提示,结合图1,写出完整的证明过程.
结论应用:
(2)如图2,在Rt△ABC中,∠ACB=90°,AC=6,D,E分别是边AB,BC的中点,CD,AE相交于点G.若 则 BC= .
(3)如图3,在△ABC中,D,E分别是边AB,BC的中点,CD,AE相交于点G.过点G作GF∥BC交AB 于点 F,如果△ABC的面积是9,那么△AFG 的面积是 .
18.(12分)如图,在△ABC中,点 D,E分别在边 BC,AC上,AD与BE相交于点O,且.
(1)求证:①∠EAD=∠ABE.②BE=EC.
(2)若 BD:CD=4:3,CE=8,求线段AE的长.
19.(12分)如图,在△ABC中,AD是角平分线,点 E在边AC 上,且. ,连结 DE.
(1)求证:△ABD∽△ADE.
(2)若∠BAC=α,求∠EDC.(结果用α表示)
(3)若AB=5,AD=4,DE=2,求 EC的长.
1. B 2. B 3. D 4. C 5. D 6. D 7.54或 8. C
9.(1)证明:∵∠AED=∠B,∠A=∠A,
∴△AED∽△ABC,∴AD:AC=AE:AB,
即AD·AB=AE·AC.
10.证明:(1)∵四边形 ABCD为矩形,
∴∠BAD=90°,∠ADE=90°,AB=DC,
∴∠ABD+∠ADB=90°.∵AE⊥BD,
∴∠DAE+∠ADB=90°,∴∠ABD=∠DAE.
∵∠BAD=∠ADE=90°,∴△ADE∽△BAD,
(2)连结AC,交 BD 于点O,如图.
∵四边形ABCD是矩形,
∴∠ADE=90°,
∴∠DAE+∠AED=90°.
∵AE⊥BD,
∴∠DAE+∠ADB=90°,
∴∠ADB=∠AED,
∵∠FEC=∠AED,
∴∠ADO=∠FEC.∵四边形ABCD为矩形,
∴OA=OD=EF=CF,∴∠ADO=∠OAD,∠FEC=∠FCE.
∵∠ADO=∠FEC,∴∠ADO=∠OAD=∠FEC=∠FCE.
在△ODA 和△FEC中,∵
∴△ODA≌△FEC(AAS),∴CE=AD.
11. D 12. D 13. A 14. A 15. m 16. 或
17.解:(1)证明:如图1,
∵在△ABC中,D,E分别是边 BC,AB的中点,
∴△DEG∽△ACG,
(2)如图2,连结ED,
∵在△ABC中,D,E 分别是边 AB,BC的中点,
∴△GED∽△GAC,
∴CD=GC+GD=5.
在Rt△ABC中,∠ACB=90°,AC=6,D是AB的中点,则AB=2CD=10,
.故答案为8.
(3)如图3,连结ED,
∵在△ABC中,D,E分别是边AB,BC的中点,
∵GF∥BC,∴△AFG∽△ABE,∴ ∧∞=( )°=
∵E是BC 的中点,△ABC的面积是9,
故答案为2.
18.解:(1)证明:(
∵∠AEO=∠BEA,∴△AEO∽△BEA,
∴∠EAD=∠ABE.
②∵AB=AD,∴∠ABD=∠ADB.
∵∠ABD=∠ABE+∠CBE,∠ADB=∠EAD+∠C,
由①知∠EAD=∠ABE,
∴∠CBE=∠C,∴BE=EC.
(2)过点A作AF⊥BD于点F,交 BE于点G,连结GD,如图,
∵AB=AD,AF⊥BD,∴BF=FD,
即AF为BD 的垂直平分线,∴GB=GD,
∴∠GBC=∠GDB,由(1)②知∠CBE=∠C,
∴∠GDB=∠C,∴GD∥EC,∴△BGD∽△BEC,
19.解:(1)证明:∵
∵AD是△ABC的角平分线,
∴∠BAD=∠DAE,∴△ABD∽△ADE.
(2)∵△ABD∽△ADE,∴∠ADB=∠AED,
∴∠EDC=∠AED-∠C=∠ADB-∠C=∠DAC= ∠BAC.∵∠BAC=α,∴∠EDC= a.
(3)∵AD =AE·AB,AB=5,AD=4,DE=2,
设EC=x,则
∵∠EDC=∠DAC,∠C=∠C,∴△EDC∽△DAC,
解得 (不符合题意,舍去),
∴EC的长是
专题提升卷(七) 相似三角形综合
[建议时间:40 分钟 满分:100分]
A命题与探究
命题角度■ 相似三角形的性质相关热门命题点
1.将一个三角形的各边扩大为原来的2倍,则这个三角形的面积扩大为原来的 ( )
A.2倍 B.4倍 C.6倍 D.8倍
2.如图,D,E分别是△ABC的边AB,AC上的点,且DE∥BC,BE交DC于点F.若EF:FB=1:3,则 的值为 ( )
A. B D.以上选项都不对
3.如图,在Rt△ABC中,∠ACB=90°,AB=3,D为直线AC 左侧一点.若△ABC∽△CAD,则 BC+CD的最大值为 ( )
A. C. D.
命题角度□ 相似三角形的判定相关热门命题点
4.如图,在△ABC中,CD⊥AB于D,下列条件中,不能使△DAC∽△DCB的是 ( )
A.∠ACB=90°
5.如图,在△ABC中,∠B=60°,AB=6,BC=8.将△ABC沿图中的DE 剪开.剪下的阴影三角形与原三角形不相似的是 ( )
6.如图,在钝角三角形 ABC中,AB=3cm,AC=6cm,动点 D从点A 出发沿AB 以1cm/s的速度向点 B运动,同时动点E从点C 出发沿CA 以2cm/s的速度向点A 运动,当以A,D,E为顶点的三角形与△ABC相似时,运动时间是 ( )
A.3s 或4.8s B. 3s C.4. 5s D.1. 5s 或2.4s
如图,AB,CD相交于点O,且OC=45,OD=30,OB=36,当OA= 时,△AOC 与△BOD相似.
命题角度目 相似三角形的性质与判定综合热门命题点
8.[2024·辽宁] 如图,在△ABC中,. 若 9:4,则AE:CE 的值是 ( )
A.4:5 B.5:4 C.7:9 D.9:7
9.(12分)如图,在 中, ,点 D在AB边上,点 E在AC边上(点E不与A,C重合),且
(1)求证:AD·AB=AE·AC.
(2)若 求 的值.
(3)若AB=6,AC=4,求 AD长的取值范围.
10.(10分)[2024·上海] 如图,在矩形ABCD中,E为边CD 上一点,且AE⊥BD.
(1)求证:
(2)F为线段AE 延长线上一点,且满足 求证:CE=AD.
命题角度相似三角形的应用相关热门命题点
11.《孙子算经》中记载一题:“今有竿,不知长短,度其影,得一丈五尺.别立一表,长一尺五寸,影得五寸.问:竿长几何 ”其大意是:今有一根木杆,不知道其长度,量它的影子,等于15 尺,另外再立一根标杆,杆长1.5尺,量得标杆的影子为0.5尺,则木杆的长为 ( )
A.5尺 B.15尺 C.30尺 D.45尺
12.凸透镜成像的原理如右图所示, 若物体 H 到焦点F 的距离与焦点 到凸透镜中心线 DB的距离之比为3:2,则物体被缩小到原来的 ( )
IB仿真与预测
13.在研究相似问题时,嘉嘉和淇淇两同学的观点如下:
嘉嘉:将边长为1的正方形按图1的方式向外扩张,得到新正方形,它们的对应边间距为1,则新正方形与原正方形相似,同时也位似;
淇淇:将边长为1的正方形按图2的方式向外扩张,得到新正方形,每条对角线向其延长线两个方向各延伸1,则新正方形与原正方形相似,同时也位似.
对于两人的观点,下列说法正确的是 ( )
A.两人都对 B.两人都不对 C.嘉嘉对,淇淇不对 D.嘉嘉不对,淇淇对
14.如图,在平行四边形ABCD中,E,F分别为AB,BC的中点,AF与DE 相交于点G,则 的值是 ( )
A. B. C. D.
15.我国非物质文化遗产“皮影戏”又称“影子戏”,射灯发出的光线沿直线传播照在不透明的皮影人上,在皮影人后面的屏幕上形成中心投影,通过操纵皮影人来完成各种造型和场景的表演.如图,已知皮影人在C处,屏幕在E处,皮影人与屏幕相距1m,射灯A 与皮影人相距2m.若保持皮影人在C处位置不变,要使屏幕上的影子的像高DE增大一倍至FE,则射灯A应向皮影人靠近至G 的距离AG为 .
16.如图,在Rt△ABC中,∠ACB=90°,AC=4cm,BC=3cm,点 P 由点B 出发沿BA方向向点A 匀速运动,速度为1cm/s,同时点Q由A 出发沿AC 方向向点C匀速运动,速度为1cm/s,连结 PQ.设运动的时间为t(s),其中0
求证
提示:连结ED.
请根据提示,结合图1,写出完整的证明过程.
结论应用:
(2)如图2,在Rt△ABC中,∠ACB=90°,AC=6,D,E分别是边AB,BC的中点,CD,AE相交于点G.若 则 BC= .
(3)如图3,在△ABC中,D,E分别是边AB,BC的中点,CD,AE相交于点G.过点G作GF∥BC交AB 于点 F,如果△ABC的面积是9,那么△AFG 的面积是 .
18.(12分)如图,在△ABC中,点 D,E分别在边 BC,AC上,AD与BE相交于点O,且.
(1)求证:①∠EAD=∠ABE.②BE=EC.
(2)若 BD:CD=4:3,CE=8,求线段AE的长.
19.(12分)如图,在△ABC中,AD是角平分线,点 E在边AC 上,且. ,连结 DE.
(1)求证:△ABD∽△ADE.
(2)若∠BAC=α,求∠EDC.(结果用α表示)
(3)若AB=5,AD=4,DE=2,求 EC的长.
1. B 2. B 3. D 4. C 5. D 6. D 7.54或 8. C
9.(1)证明:∵∠AED=∠B,∠A=∠A,
∴△AED∽△ABC,∴AD:AC=AE:AB,
即AD·AB=AE·AC.
10.证明:(1)∵四边形 ABCD为矩形,
∴∠BAD=90°,∠ADE=90°,AB=DC,
∴∠ABD+∠ADB=90°.∵AE⊥BD,
∴∠DAE+∠ADB=90°,∴∠ABD=∠DAE.
∵∠BAD=∠ADE=90°,∴△ADE∽△BAD,
(2)连结AC,交 BD 于点O,如图.
∵四边形ABCD是矩形,
∴∠ADE=90°,
∴∠DAE+∠AED=90°.
∵AE⊥BD,
∴∠DAE+∠ADB=90°,
∴∠ADB=∠AED,
∵∠FEC=∠AED,
∴∠ADO=∠FEC.∵四边形ABCD为矩形,
∴OA=OD=EF=CF,∴∠ADO=∠OAD,∠FEC=∠FCE.
∵∠ADO=∠FEC,∴∠ADO=∠OAD=∠FEC=∠FCE.
在△ODA 和△FEC中,∵
∴△ODA≌△FEC(AAS),∴CE=AD.
11. D 12. D 13. A 14. A 15. m 16. 或
17.解:(1)证明:如图1,
∵在△ABC中,D,E分别是边 BC,AB的中点,
∴△DEG∽△ACG,
(2)如图2,连结ED,
∵在△ABC中,D,E 分别是边 AB,BC的中点,
∴△GED∽△GAC,
∴CD=GC+GD=5.
在Rt△ABC中,∠ACB=90°,AC=6,D是AB的中点,则AB=2CD=10,
.故答案为8.
(3)如图3,连结ED,
∵在△ABC中,D,E分别是边AB,BC的中点,
∵GF∥BC,∴△AFG∽△ABE,∴ ∧∞=( )°=
∵E是BC 的中点,△ABC的面积是9,
故答案为2.
18.解:(1)证明:(
∵∠AEO=∠BEA,∴△AEO∽△BEA,
∴∠EAD=∠ABE.
②∵AB=AD,∴∠ABD=∠ADB.
∵∠ABD=∠ABE+∠CBE,∠ADB=∠EAD+∠C,
由①知∠EAD=∠ABE,
∴∠CBE=∠C,∴BE=EC.
(2)过点A作AF⊥BD于点F,交 BE于点G,连结GD,如图,
∵AB=AD,AF⊥BD,∴BF=FD,
即AF为BD 的垂直平分线,∴GB=GD,
∴∠GBC=∠GDB,由(1)②知∠CBE=∠C,
∴∠GDB=∠C,∴GD∥EC,∴△BGD∽△BEC,
19.解:(1)证明:∵
∵AD是△ABC的角平分线,
∴∠BAD=∠DAE,∴△ABD∽△ADE.
(2)∵△ABD∽△ADE,∴∠ADB=∠AED,
∴∠EDC=∠AED-∠C=∠ADB-∠C=∠DAC= ∠BAC.∵∠BAC=α,∴∠EDC= a.
(3)∵AD =AE·AB,AB=5,AD=4,DE=2,
设EC=x,则
∵∠EDC=∠DAC,∠C=∠C,∴△EDC∽△DAC,
解得 (不符合题意,舍去),
∴EC的长是
同课章节目录
