专题提升卷(九) 平行四边形与特殊平行四边形综合(一)——平行四边形和矩形、菱形(含答案)
文档属性
| 名称 | 专题提升卷(九) 平行四边形与特殊平行四边形综合(一)——平行四边形和矩形、菱形(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 192.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-10 21:08:50 | ||
图片预览

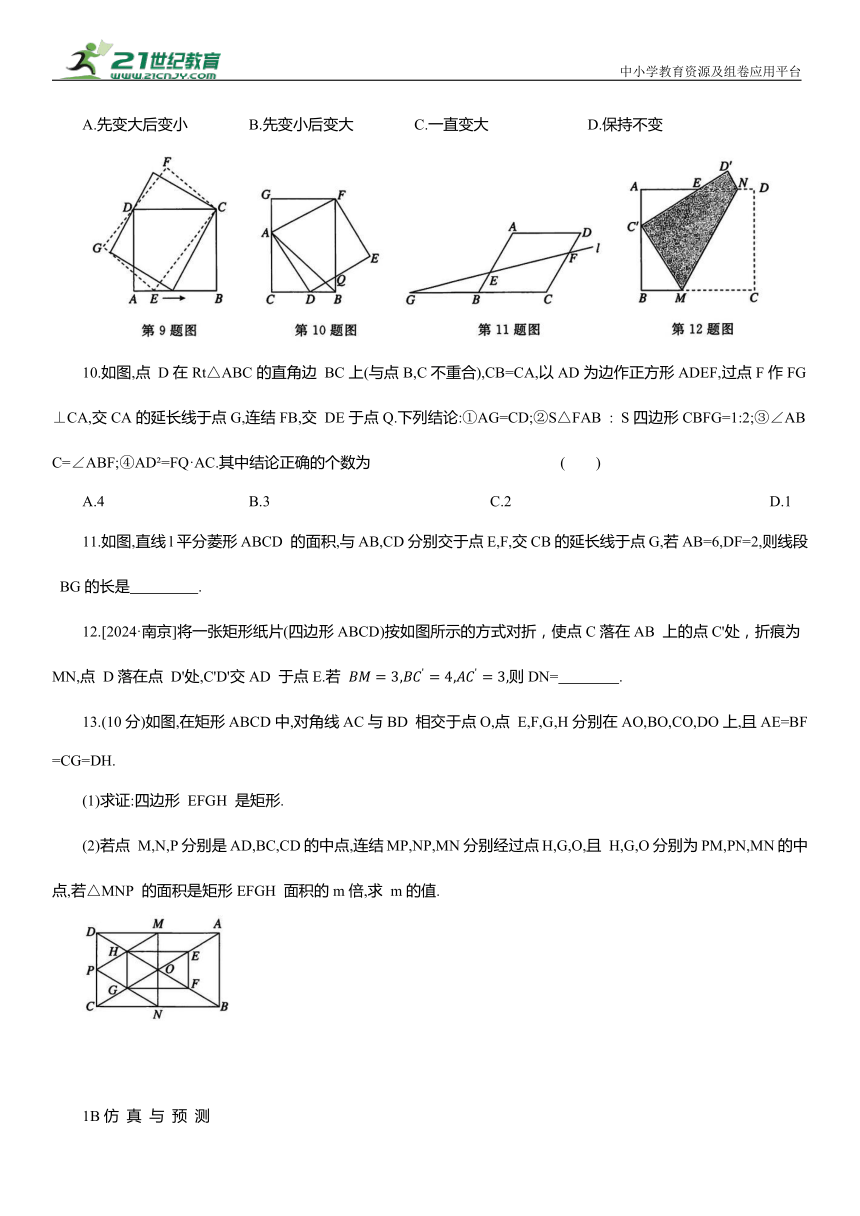
文档简介
中小学教育资源及组卷应用平台
专题提升卷(九) 平行四边形与特殊平行四边形综合(一)——平行四边形和矩形、菱形
[建议时间:40 分钟 满分:100分]
IA命 题 与 探究
命题角度■ 平行四边形与特殊平行四边形中心对称性热门命题点
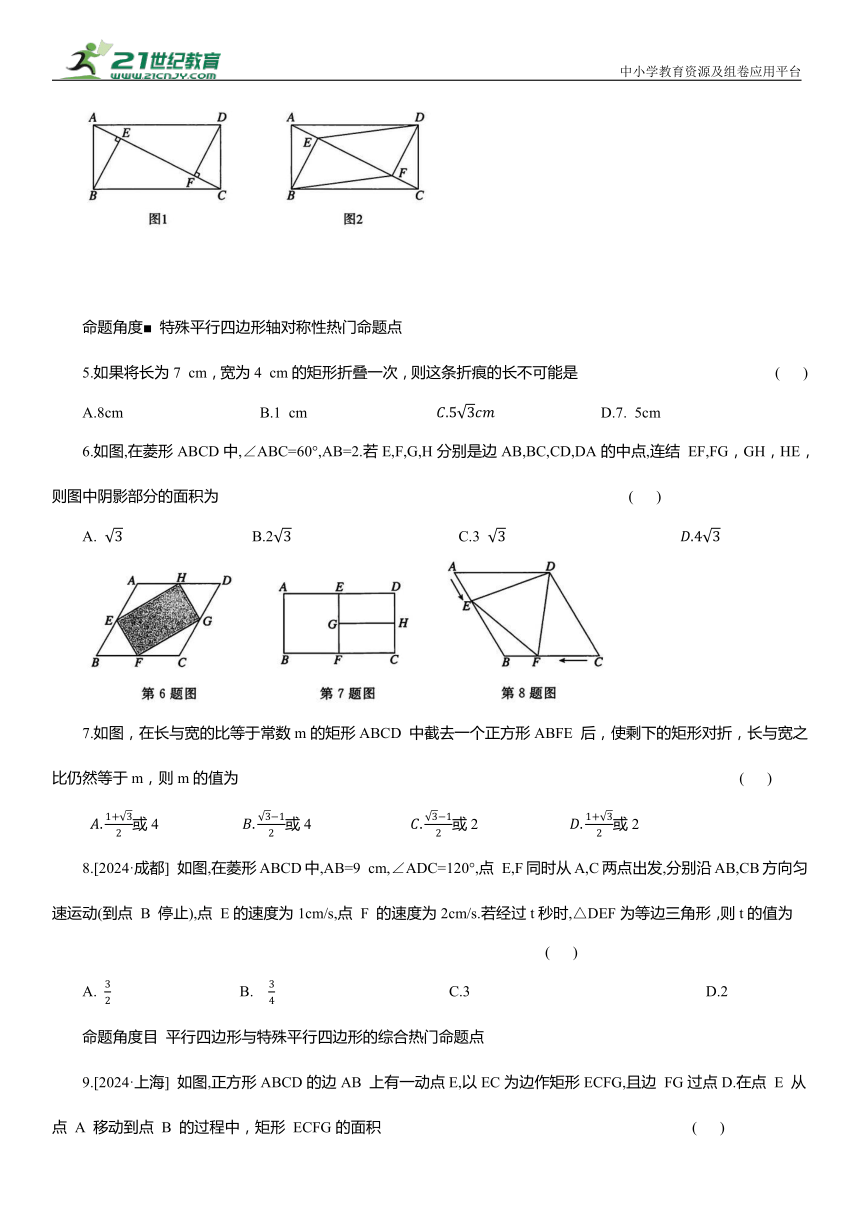
1.如图, ABCD的对角线AC,BD交于点O,AC⊥BC,已知 ABCD的面积为48,OA=3,则CD的长为( )
A.6 B.8 C.10 D.12
2.如图,点O是菱形ABCD 的对称中心,连结OA,OB,OA=4,OB=6,EF为过点O的一条直线,点 E,F分别在AD,BC上,则图中阴影部分的面积为 ( )
A.24 B.16 C.18 D.12
3.如图,在矩形ABCD中,AB=6,BC=8,E,F是对角线AC上的两点,AE=CF=2,点 P 在边AD 上运动(不与点A,D重合),连结点 P 与AC 的中点O并延长交BC 于点Q,连结PE,PF,QE,QF.在点 P从点 D运动到点A 的整个过程中,四边形 PEQF 的形状变化依次是 ( )
A.平行四边形→菱形→矩形→平行四边形
B.平行四边形→矩形→菱形→平行四边形
C.平行四边形→菱形→平行四边形→矩形→平行四边形
D.平行四边形→矩形→平行四边形→菱形→平行四边形
4.(10分)已知,在矩形ABCD中,AC是对角线,BE⊥AC于点E,DF⊥AC于点F.
(1)如图1,求证:AE=CF.
(2)如图2,连结 DE,BF, 在不添加任何辅助线的情况下,请直接写出图2中所有面积为△BCF 面积4倍的三角形.
命题角度■ 特殊平行四边形轴对称性热门命题点
5.如果将长为7 cm,宽为4 cm的矩形折叠一次,则这条折痕的长不可能是 ( )
A.8cm B.1 cm D.7. 5cm
6.如图,在菱形ABCD中,∠ABC=60°,AB=2.若E,F,G,H分别是边AB,BC,CD,DA的中点,连结 EF,FG,GH,HE,则图中阴影部分的面积为 ( )
A. B.2 C.3
7.如图,在长与宽的比等于常数m的矩形ABCD 中截去一个正方形ABFE 后,使剩下的矩形对折,长与宽之比仍然等于m,则m的值为 ( )
或4 或4 或2 或2
8.[2024·成都] 如图,在菱形ABCD中,AB=9 cm,∠ADC=120°,点 E,F同时从A,C两点出发,分别沿AB,CB方向匀速运动(到点 B 停止),点 E的速度为1cm/s,点 F 的速度为2cm/s.若经过t秒时,△DEF为等边三角形,则t的值为 ( )
A. B. C.3 D.2
命题角度目 平行四边形与特殊平行四边形的综合热门命题点
9.[2024·上海] 如图,正方形ABCD的边AB 上有一动点E,以EC为边作矩形ECFG,且边 FG过点D.在点 E 从点 A 移动到点 B 的过程中,矩形 ECFG的面积 ( )
A.先变大后变小 B.先变小后变大 C.一直变大 D.保持不变
10.如图,点 D在Rt△ABC的直角边 BC上(与点B,C不重合),CB=CA,以AD为边作正方形ADEF,过点F作FG⊥CA,交CA的延长线于点G,连结FB,交 DE于点Q.下列结论:①AG=CD;②S△FAB : S四边形CBFG=1:2;③∠ABC=∠ABF;④AD =FQ·AC.其中结论正确的个数为 ( )
A.4 B.3 C.2 D.1
11.如图,直线l平分菱形ABCD 的面积,与AB,CD分别交于点E,F,交CB的延长线于点G,若AB=6,DF=2,则线段 BG的长是 .
12.[2024·南京]将一张矩形纸片(四边形ABCD)按如图所示的方式对折,使点C落在AB 上的点C'处,折痕为MN,点 D落在点 D'处,C'D'交AD 于点E.若 则DN= .
13.(10分)如图,在矩形ABCD中,对角线AC与BD 相交于点O,点 E,F,G,H分别在AO,BO,CO,DO上,且AE=BF=CG=DH.
(1)求证:四边形 EFGH 是矩形.
(2)若点 M,N,P分别是AD,BC,CD的中点,连结MP,NP,MN分别经过点H,G,O,且 H,G,O分别为PM,PN,MN的中点,若△MNP 的面积是矩形EFGH 面积的m倍,求 m的值.
1B仿 真 与 预 测
14.如图,在矩形 ABCD中,点 E 在DC 上,将矩形沿AE 折叠,使点 D 落在 BC 边上的点 F 处,若AB=6,BC=10,则 tan∠EAF的值为 ( )
A. B. C. D
15.如图,在矩形ABCD中,AB=4,AD=6,P,Q分别是边AD,BC上的动点,点 P从A 出发到D 停止运动,点Q从C 出发到B 停止运动,若P,Q两点以相同的速度同时出发,匀速运动,下列结论中不正确的是( )
A.存在四边形 APQB 是矩形 B.存在四边形APQB是正方形
C.存在四边形APCQ是菱形 D.存在四边形APCQ是矩形
16.如图,在菱形ABCD中,∠ABC=120°,AB=2 ,E,F分别是AD,BC边上的两个动点,连结AF,EF,若FA平分∠BFE,则DE的最大值为 .(结果保留根号)
17.在菱形ABCD中,∠B=120°,AB=2,M为对角线AC 的中点,N为边AB 上一动点,若△AMN为等腰三角形,则BN 的长为 .
18.(11 分)如图,四边形 ABCD 是矩形,点 E,F 分别在边AD,BC上,将矩形 ABCD沿EF 对折,点B 与点 D 恰好重合.
(1)求证:四边形 BEDF 是菱形.
(2)若AB=3,BC=4,求菱形 BEDF 的面积.
19.(12 分)如图,在 中,点E,F在AC上,且 ,GH过点O分别与AB,CD交于点G,H,证明:
(2)GH,EF互相平分.
20.(12分)如图,在菱形ABCD中,对角线AC与BD 相交于点O, ,动点 P 从点 D 出发沿 DC 方向匀速运动,运动速度为 ,动点 Q 同时从点O 出发沿OB 方向匀速运动,运动速度为 ,当 P到达C时,P,Q两点停止运动,连结AP,AQ,PQ.设时间为 ,解答下列问题:
(1)当 时,求t的值.
(2)设 的面积为 请写出y与t 的函数关系式.
1. C 2. D 3. C
4.解:(1)证明:∵四边形 ABCD是矩形,∴AB=CD,AB∥CD,∴∠BAE=∠DCF.又∵BE⊥AC,DF⊥AC,
∴∠AEB=∠CFD=90°.
在△ABE和△CDF中,
∴△ABE≌△CDF(AAS),∴AE=CF.
(2)△ABF,△BCE,△ADF,△CDE
5. C 6. A 7. D 8. C 9. D 10. A 11.6 12.
13.(1)证明:∵四边形 ABCD 是矩形,
∴AB=CD,AO=BO=DO=CO.
∵AE=BF=CG=DH,∴HO=FO=EO=GO,
∴四边形 EFGH 是平行四边形,HF=EG,
∴四边形 EFGH 是矩形.
(2)m=1
14. D 15. B 16.2 -3 17.2- 或1
18.(1)证明:∵四边形 ABCD 是矩形,
∴AD∥BC,∴∠DEF=∠BFE.
∵将矩形 ABCD沿EF 对折,点 B 与点D 恰好重合,
∴DE=BE,DF=BF,∠DEF=∠BEF,
∴∠BFE=∠BEF,∴BE=BF,
∴DE=BE=BF=DF,∴四边形 BEDF 是菱形.
(2)
19.证明:(1)在□ABCD中,
∵AB∥CD,∴∠BAC=∠ACD,AO=CO.
在△AOG与△COH中,∵
∴△AOG≌△COH(ASA),∴AG=CH.
(2)连结EH,GF(图略),在 ABCD中,
∵AB∥CD,∴∠GAE=∠HCF.
∵AF=CE,∴AF-EF=CE--EF,即AE=CF,在△AGE与△CHF中,.
∴△AGE≌△CHF(SAS),∴GE=HF,∠AEG=∠CFH,
∴∠GEO=∠HFO,∴EG∥FH,
∴四边形GFHE是平行四边形,∴GH,EF互相平分.
20.解:(1)由题意得OQ= tcm,DP=2t cm,
∵四边形ABCD是菱形,AC=12cm,BD=16cm,
∴AC⊥BD,AO=OC=6cm,BO=OD=8cm,∴CD=10cm.
在 Rt△APD中,
t 的值为
(2)过点 P作PE⊥BD于点 E,如图.
∵∠BDP=∠BDP,∠COD=∠PED=90°,
∴△ODC∽△EDP,
即
∴y与t的函数关系式为
专题提升卷(九) 平行四边形与特殊平行四边形综合(一)——平行四边形和矩形、菱形
[建议时间:40 分钟 满分:100分]
IA命 题 与 探究
命题角度■ 平行四边形与特殊平行四边形中心对称性热门命题点
1.如图, ABCD的对角线AC,BD交于点O,AC⊥BC,已知 ABCD的面积为48,OA=3,则CD的长为( )
A.6 B.8 C.10 D.12
2.如图,点O是菱形ABCD 的对称中心,连结OA,OB,OA=4,OB=6,EF为过点O的一条直线,点 E,F分别在AD,BC上,则图中阴影部分的面积为 ( )
A.24 B.16 C.18 D.12
3.如图,在矩形ABCD中,AB=6,BC=8,E,F是对角线AC上的两点,AE=CF=2,点 P 在边AD 上运动(不与点A,D重合),连结点 P 与AC 的中点O并延长交BC 于点Q,连结PE,PF,QE,QF.在点 P从点 D运动到点A 的整个过程中,四边形 PEQF 的形状变化依次是 ( )
A.平行四边形→菱形→矩形→平行四边形
B.平行四边形→矩形→菱形→平行四边形
C.平行四边形→菱形→平行四边形→矩形→平行四边形
D.平行四边形→矩形→平行四边形→菱形→平行四边形
4.(10分)已知,在矩形ABCD中,AC是对角线,BE⊥AC于点E,DF⊥AC于点F.
(1)如图1,求证:AE=CF.
(2)如图2,连结 DE,BF, 在不添加任何辅助线的情况下,请直接写出图2中所有面积为△BCF 面积4倍的三角形.
命题角度■ 特殊平行四边形轴对称性热门命题点
5.如果将长为7 cm,宽为4 cm的矩形折叠一次,则这条折痕的长不可能是 ( )
A.8cm B.1 cm D.7. 5cm
6.如图,在菱形ABCD中,∠ABC=60°,AB=2.若E,F,G,H分别是边AB,BC,CD,DA的中点,连结 EF,FG,GH,HE,则图中阴影部分的面积为 ( )
A. B.2 C.3
7.如图,在长与宽的比等于常数m的矩形ABCD 中截去一个正方形ABFE 后,使剩下的矩形对折,长与宽之比仍然等于m,则m的值为 ( )
或4 或4 或2 或2
8.[2024·成都] 如图,在菱形ABCD中,AB=9 cm,∠ADC=120°,点 E,F同时从A,C两点出发,分别沿AB,CB方向匀速运动(到点 B 停止),点 E的速度为1cm/s,点 F 的速度为2cm/s.若经过t秒时,△DEF为等边三角形,则t的值为 ( )
A. B. C.3 D.2
命题角度目 平行四边形与特殊平行四边形的综合热门命题点
9.[2024·上海] 如图,正方形ABCD的边AB 上有一动点E,以EC为边作矩形ECFG,且边 FG过点D.在点 E 从点 A 移动到点 B 的过程中,矩形 ECFG的面积 ( )
A.先变大后变小 B.先变小后变大 C.一直变大 D.保持不变
10.如图,点 D在Rt△ABC的直角边 BC上(与点B,C不重合),CB=CA,以AD为边作正方形ADEF,过点F作FG⊥CA,交CA的延长线于点G,连结FB,交 DE于点Q.下列结论:①AG=CD;②S△FAB : S四边形CBFG=1:2;③∠ABC=∠ABF;④AD =FQ·AC.其中结论正确的个数为 ( )
A.4 B.3 C.2 D.1
11.如图,直线l平分菱形ABCD 的面积,与AB,CD分别交于点E,F,交CB的延长线于点G,若AB=6,DF=2,则线段 BG的长是 .
12.[2024·南京]将一张矩形纸片(四边形ABCD)按如图所示的方式对折,使点C落在AB 上的点C'处,折痕为MN,点 D落在点 D'处,C'D'交AD 于点E.若 则DN= .
13.(10分)如图,在矩形ABCD中,对角线AC与BD 相交于点O,点 E,F,G,H分别在AO,BO,CO,DO上,且AE=BF=CG=DH.
(1)求证:四边形 EFGH 是矩形.
(2)若点 M,N,P分别是AD,BC,CD的中点,连结MP,NP,MN分别经过点H,G,O,且 H,G,O分别为PM,PN,MN的中点,若△MNP 的面积是矩形EFGH 面积的m倍,求 m的值.
1B仿 真 与 预 测
14.如图,在矩形 ABCD中,点 E 在DC 上,将矩形沿AE 折叠,使点 D 落在 BC 边上的点 F 处,若AB=6,BC=10,则 tan∠EAF的值为 ( )
A. B. C. D
15.如图,在矩形ABCD中,AB=4,AD=6,P,Q分别是边AD,BC上的动点,点 P从A 出发到D 停止运动,点Q从C 出发到B 停止运动,若P,Q两点以相同的速度同时出发,匀速运动,下列结论中不正确的是( )
A.存在四边形 APQB 是矩形 B.存在四边形APQB是正方形
C.存在四边形APCQ是菱形 D.存在四边形APCQ是矩形
16.如图,在菱形ABCD中,∠ABC=120°,AB=2 ,E,F分别是AD,BC边上的两个动点,连结AF,EF,若FA平分∠BFE,则DE的最大值为 .(结果保留根号)
17.在菱形ABCD中,∠B=120°,AB=2,M为对角线AC 的中点,N为边AB 上一动点,若△AMN为等腰三角形,则BN 的长为 .
18.(11 分)如图,四边形 ABCD 是矩形,点 E,F 分别在边AD,BC上,将矩形 ABCD沿EF 对折,点B 与点 D 恰好重合.
(1)求证:四边形 BEDF 是菱形.
(2)若AB=3,BC=4,求菱形 BEDF 的面积.
19.(12 分)如图,在 中,点E,F在AC上,且 ,GH过点O分别与AB,CD交于点G,H,证明:
(2)GH,EF互相平分.
20.(12分)如图,在菱形ABCD中,对角线AC与BD 相交于点O, ,动点 P 从点 D 出发沿 DC 方向匀速运动,运动速度为 ,动点 Q 同时从点O 出发沿OB 方向匀速运动,运动速度为 ,当 P到达C时,P,Q两点停止运动,连结AP,AQ,PQ.设时间为 ,解答下列问题:
(1)当 时,求t的值.
(2)设 的面积为 请写出y与t 的函数关系式.
1. C 2. D 3. C
4.解:(1)证明:∵四边形 ABCD是矩形,∴AB=CD,AB∥CD,∴∠BAE=∠DCF.又∵BE⊥AC,DF⊥AC,
∴∠AEB=∠CFD=90°.
在△ABE和△CDF中,
∴△ABE≌△CDF(AAS),∴AE=CF.
(2)△ABF,△BCE,△ADF,△CDE
5. C 6. A 7. D 8. C 9. D 10. A 11.6 12.
13.(1)证明:∵四边形 ABCD 是矩形,
∴AB=CD,AO=BO=DO=CO.
∵AE=BF=CG=DH,∴HO=FO=EO=GO,
∴四边形 EFGH 是平行四边形,HF=EG,
∴四边形 EFGH 是矩形.
(2)m=1
14. D 15. B 16.2 -3 17.2- 或1
18.(1)证明:∵四边形 ABCD 是矩形,
∴AD∥BC,∴∠DEF=∠BFE.
∵将矩形 ABCD沿EF 对折,点 B 与点D 恰好重合,
∴DE=BE,DF=BF,∠DEF=∠BEF,
∴∠BFE=∠BEF,∴BE=BF,
∴DE=BE=BF=DF,∴四边形 BEDF 是菱形.
(2)
19.证明:(1)在□ABCD中,
∵AB∥CD,∴∠BAC=∠ACD,AO=CO.
在△AOG与△COH中,∵
∴△AOG≌△COH(ASA),∴AG=CH.
(2)连结EH,GF(图略),在 ABCD中,
∵AB∥CD,∴∠GAE=∠HCF.
∵AF=CE,∴AF-EF=CE--EF,即AE=CF,在△AGE与△CHF中,.
∴△AGE≌△CHF(SAS),∴GE=HF,∠AEG=∠CFH,
∴∠GEO=∠HFO,∴EG∥FH,
∴四边形GFHE是平行四边形,∴GH,EF互相平分.
20.解:(1)由题意得OQ= tcm,DP=2t cm,
∵四边形ABCD是菱形,AC=12cm,BD=16cm,
∴AC⊥BD,AO=OC=6cm,BO=OD=8cm,∴CD=10cm.
在 Rt△APD中,
t 的值为
(2)过点 P作PE⊥BD于点 E,如图.
∵∠BDP=∠BDP,∠COD=∠PED=90°,
∴△ODC∽△EDP,
即
∴y与t的函数关系式为
同课章节目录
