专题提升卷(十) 平行四边形与特殊平行四边形综合(二)——正方形(含答案)
文档属性
| 名称 | 专题提升卷(十) 平行四边形与特殊平行四边形综合(二)——正方形(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 196.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
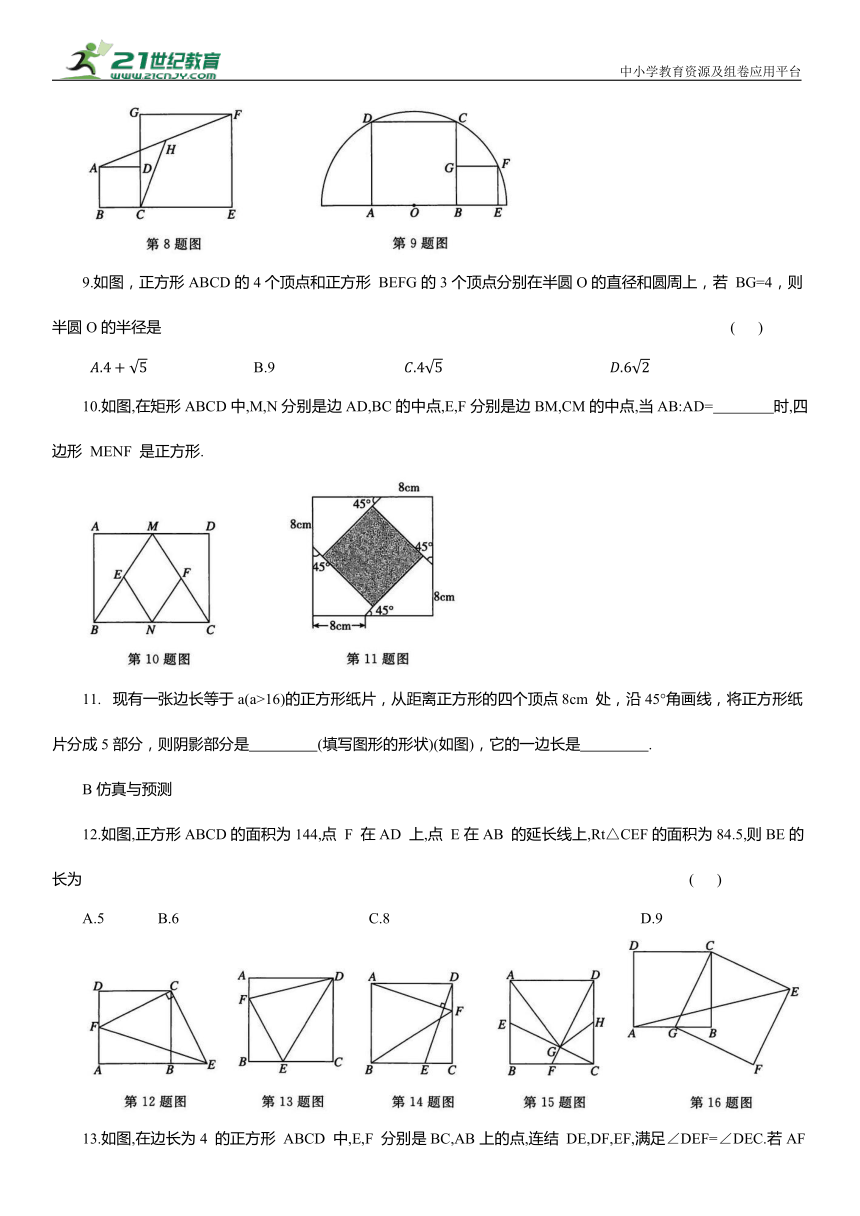
| 更新时间 | 2025-04-10 21:08:34 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
专题提升卷(十) 平行四边形与特殊平行四边形综合(二)——正方形
[建议时间:40分钟 满分:100分]
A命题与探究|
命题角度■ 正方形的轴对称性热门命题点
1.如图,正方形ABCD的边长为2,E为AB边的中点,点F在BC边上,点 B关于直线EF 的对称点记为B',连结 B'D,B'E,B'F.当点 F在BC 边上移动使得四边形BEB'F 成为正方形时,B'D 的长为 ( )
A. B. D.3
2.如图,N为正方形ABCD 对角线BD上的任意一点(不包括 B,D两点),过点 N作NG⊥BC,NM⊥DC,垂足分别为G,M,若四边形 NGCM的周长为( ,则正方形ABCD的面积是 ( )
3.(8分)如图,正方形ABCD的对角线AC,BD 相交于点O,CE∥BD,DE∥AC.
(1)求证:四边形OCED 是正方形.
(2)若 则点 E到边AB 的距离为 .
命题角度■ 正方形中的垂直问题热门命题点
4.将五个边长都为2cm的正方形按如图所示摆放,点A,B,C,D分别是四个正方形的中心(对角线的交点),则图中四块阴影面积的和为 ( )
5.如图,正方形ABCD的边长为8,在各边上顺次截取AE=BF=CG=DH=5,则四边形 EFGH的面积是( )
A.30 B.34 C.36 D.40
6.如图,正方形ABCD的四个顶点分别在四条平行线 上,这四条直线中相邻两条直线之间的距离依次为 若 则正方形ABCD的面积为 ( )
A.24 B.36 C.52 D.48
7.(8分)如图,四边形ABCD是正方形,G是BC 上的任意一点, 于点E,BF∥DE,且交 AG于点 F.
(1)求证:
(2)求证:
命题角度目 正方形的综合热门命题点
8.如图,在正方形ABCD和正方形CEFG 中,点 D在CG上,BC=1,H 是AF 的中点,CH=3,那么CE的长是 ( )
A.3 B.4
9.如图,正方形ABCD的4个顶点和正方形 BEFG的3个顶点分别在半圆O的直径和圆周上,若 BG=4,则半圆O的半径是 ( )
B.9
10.如图,在矩形ABCD中,M,N分别是边AD,BC的中点,E,F分别是边BM,CM的中点,当AB:AD= 时,四边形 MENF 是正方形.
现有一张边长等于a(a>16)的正方形纸片,从距离正方形的四个顶点8cm 处,沿45°角画线,将正方形纸片分成5部分,则阴影部分是 (填写图形的形状)(如图),它的一边长是 .
B仿真与预测
12.如图,正方形ABCD的面积为144,点 F 在AD 上,点 E在AB 的延长线上,Rt△CEF的面积为84.5,则BE的长为 ( )
A.5 B.6 C.8 D.9
13.如图,在边长为4 的正方形 ABCD 中,E,F 分别是BC,AB上的点,连结 DE,DF,EF,满足∠DEF=∠DEC.若AF=1,则 EF的长为 ( )
B C
14.如图,正方形ABCD的边长为6,E为BC上一点,连结DE,过点A作DE 的垂线交CD 于点F,连结 BF.若CE=2,则 BF 的长为 ( )
C.8
15.如图,在正方形ABCD中,E,F,H分别是AB,BC,CD的中点,CE,DF交于G,连结AG,HG.有下列结论:①CE⊥DF;②AG=AD;③∠CHG=∠DAG;④HG= AD.其中正确的结论个数为 ( )
A.1 B.2 C.3 D.4
16.如图,已知四边形ABCD和四边形CEFG均为正方形,且G是AB的中点,连结AE,若AB=2,则AE的长为 .
17.(8分)如图,M是正方形ABCD 边AB 上一点,DN⊥CM于N,DN=2CN=2,求 BN的长度.
18.(10分)如图,在正方形ABCD中,E为CD的中点,连结AC,过点C作( 交AE 的延长线于点F,求 的值及 的值.
19.(12分)如图,四边形AECF 是菱形,对角线 AC,EF 交于点O,D,B 是对角线EF 所在直线上两点,且 连结AD,AB,CD,CB,
(1)求证:四边形 ABCD 是正方形.
(2)若正方形ABCD的面积为72, 求点 F 到线段AE 的距离.
20.(12分)点 E 是正方形ABCD 的对角线BD 上一点,过点 E作 交CD 于点F,AE的延长线交BC于点G,AF交BD 于点 H.
(1)如图1,证明:
(2)如图2,若. 求CF的长.
1. A 2. D
3.解:(1)证明:∵CE∥BD,DE∥AC,
∴四边形OCED 是平行四边形.
在正方形 ABCD中,AC⊥BD,OD=OC,
∴∠COD=90°,∴四边形OCED是正方形.
(2)1.5
4. B 5. B 6. C
7.证明:(1)∵四边形ABCD是正方形,
∴∠DAE+∠BAF=90°.
∵DE⊥AG,∴∠DAE+∠ADE=90°.
∴∠BAF=∠ADE.
(2)∵BF∥DE,∠AED=∠FED=90°,∴∠BFA=90°.
在△AED和△BFA中,
∴△AED≌△BFA(AAS).∴AE=BF,DE=AF.
∵AF-AE=EF,∴DE-BF=EF.
8. D 9. C 10.1:2 11.正方形 8 cm 12. A 13. B14. D 15. C 16. 17. BN=
19.(1)证明:∵菱形AECF 的对角线AC 和EF 交于点O,
∴AC⊥EF,OA=OC,OE=OF.∵BF=DE,∴BO=DO.
又∵AC⊥BD,∴四边形ABCD 是菱形,
∵∠ADO=45°,∴∠DAO=∠ADO=45°,
∴AO=DO,∴AC=BD,∴四边形ABCD是正方形.
(2)点 F 到线段AE 的距离为
20.解:(1)证明:如图,连结CE.
∵四边形ABCD 是正方形,
∴点A,C关于BD对称,
∴CE=AE,∠DCE=∠DAE.
∵∠AEF+∠FDA=180°,
∴∠EFD+∠EAD=180°,
又∠EFC+∠DFE=180°,
∴∠EAD=∠EFC,∴∠DCE=∠CFE,
∴EC=FE,∴AE=FE.
(2)由四边形 ABCD是正方形,
得AD=AB=2,∠EBA=∠EDF=45°,BD= AB=2
由AD=ED,得AB=DE,∠EAD=∠DEA,
∴∠BAD-∠DAE=∠FEA-∠DEA,即∠BAE=∠DEF,
∴△EBA≌△FDE,∴DF=BE=BD-DE=2 -2,
专题提升卷(十) 平行四边形与特殊平行四边形综合(二)——正方形
[建议时间:40分钟 满分:100分]
A命题与探究|
命题角度■ 正方形的轴对称性热门命题点
1.如图,正方形ABCD的边长为2,E为AB边的中点,点F在BC边上,点 B关于直线EF 的对称点记为B',连结 B'D,B'E,B'F.当点 F在BC 边上移动使得四边形BEB'F 成为正方形时,B'D 的长为 ( )
A. B. D.3
2.如图,N为正方形ABCD 对角线BD上的任意一点(不包括 B,D两点),过点 N作NG⊥BC,NM⊥DC,垂足分别为G,M,若四边形 NGCM的周长为( ,则正方形ABCD的面积是 ( )
3.(8分)如图,正方形ABCD的对角线AC,BD 相交于点O,CE∥BD,DE∥AC.
(1)求证:四边形OCED 是正方形.
(2)若 则点 E到边AB 的距离为 .
命题角度■ 正方形中的垂直问题热门命题点
4.将五个边长都为2cm的正方形按如图所示摆放,点A,B,C,D分别是四个正方形的中心(对角线的交点),则图中四块阴影面积的和为 ( )
5.如图,正方形ABCD的边长为8,在各边上顺次截取AE=BF=CG=DH=5,则四边形 EFGH的面积是( )
A.30 B.34 C.36 D.40
6.如图,正方形ABCD的四个顶点分别在四条平行线 上,这四条直线中相邻两条直线之间的距离依次为 若 则正方形ABCD的面积为 ( )
A.24 B.36 C.52 D.48
7.(8分)如图,四边形ABCD是正方形,G是BC 上的任意一点, 于点E,BF∥DE,且交 AG于点 F.
(1)求证:
(2)求证:
命题角度目 正方形的综合热门命题点
8.如图,在正方形ABCD和正方形CEFG 中,点 D在CG上,BC=1,H 是AF 的中点,CH=3,那么CE的长是 ( )
A.3 B.4
9.如图,正方形ABCD的4个顶点和正方形 BEFG的3个顶点分别在半圆O的直径和圆周上,若 BG=4,则半圆O的半径是 ( )
B.9
10.如图,在矩形ABCD中,M,N分别是边AD,BC的中点,E,F分别是边BM,CM的中点,当AB:AD= 时,四边形 MENF 是正方形.
现有一张边长等于a(a>16)的正方形纸片,从距离正方形的四个顶点8cm 处,沿45°角画线,将正方形纸片分成5部分,则阴影部分是 (填写图形的形状)(如图),它的一边长是 .
B仿真与预测
12.如图,正方形ABCD的面积为144,点 F 在AD 上,点 E在AB 的延长线上,Rt△CEF的面积为84.5,则BE的长为 ( )
A.5 B.6 C.8 D.9
13.如图,在边长为4 的正方形 ABCD 中,E,F 分别是BC,AB上的点,连结 DE,DF,EF,满足∠DEF=∠DEC.若AF=1,则 EF的长为 ( )
B C
14.如图,正方形ABCD的边长为6,E为BC上一点,连结DE,过点A作DE 的垂线交CD 于点F,连结 BF.若CE=2,则 BF 的长为 ( )
C.8
15.如图,在正方形ABCD中,E,F,H分别是AB,BC,CD的中点,CE,DF交于G,连结AG,HG.有下列结论:①CE⊥DF;②AG=AD;③∠CHG=∠DAG;④HG= AD.其中正确的结论个数为 ( )
A.1 B.2 C.3 D.4
16.如图,已知四边形ABCD和四边形CEFG均为正方形,且G是AB的中点,连结AE,若AB=2,则AE的长为 .
17.(8分)如图,M是正方形ABCD 边AB 上一点,DN⊥CM于N,DN=2CN=2,求 BN的长度.
18.(10分)如图,在正方形ABCD中,E为CD的中点,连结AC,过点C作( 交AE 的延长线于点F,求 的值及 的值.
19.(12分)如图,四边形AECF 是菱形,对角线 AC,EF 交于点O,D,B 是对角线EF 所在直线上两点,且 连结AD,AB,CD,CB,
(1)求证:四边形 ABCD 是正方形.
(2)若正方形ABCD的面积为72, 求点 F 到线段AE 的距离.
20.(12分)点 E 是正方形ABCD 的对角线BD 上一点,过点 E作 交CD 于点F,AE的延长线交BC于点G,AF交BD 于点 H.
(1)如图1,证明:
(2)如图2,若. 求CF的长.
1. A 2. D
3.解:(1)证明:∵CE∥BD,DE∥AC,
∴四边形OCED 是平行四边形.
在正方形 ABCD中,AC⊥BD,OD=OC,
∴∠COD=90°,∴四边形OCED是正方形.
(2)1.5
4. B 5. B 6. C
7.证明:(1)∵四边形ABCD是正方形,
∴∠DAE+∠BAF=90°.
∵DE⊥AG,∴∠DAE+∠ADE=90°.
∴∠BAF=∠ADE.
(2)∵BF∥DE,∠AED=∠FED=90°,∴∠BFA=90°.
在△AED和△BFA中,
∴△AED≌△BFA(AAS).∴AE=BF,DE=AF.
∵AF-AE=EF,∴DE-BF=EF.
8. D 9. C 10.1:2 11.正方形 8 cm 12. A 13. B14. D 15. C 16. 17. BN=
19.(1)证明:∵菱形AECF 的对角线AC 和EF 交于点O,
∴AC⊥EF,OA=OC,OE=OF.∵BF=DE,∴BO=DO.
又∵AC⊥BD,∴四边形ABCD 是菱形,
∵∠ADO=45°,∴∠DAO=∠ADO=45°,
∴AO=DO,∴AC=BD,∴四边形ABCD是正方形.
(2)点 F 到线段AE 的距离为
20.解:(1)证明:如图,连结CE.
∵四边形ABCD 是正方形,
∴点A,C关于BD对称,
∴CE=AE,∠DCE=∠DAE.
∵∠AEF+∠FDA=180°,
∴∠EFD+∠EAD=180°,
又∠EFC+∠DFE=180°,
∴∠EAD=∠EFC,∴∠DCE=∠CFE,
∴EC=FE,∴AE=FE.
(2)由四边形 ABCD是正方形,
得AD=AB=2,∠EBA=∠EDF=45°,BD= AB=2
由AD=ED,得AB=DE,∠EAD=∠DEA,
∴∠BAD-∠DAE=∠FEA-∠DEA,即∠BAE=∠DEF,
∴△EBA≌△FDE,∴DF=BE=BD-DE=2 -2,
同课章节目录
