专题提升卷(十一) 圆的综合(一) (含答案) 2025年中考数学知识点过关训练
文档属性
| 名称 | 专题提升卷(十一) 圆的综合(一) (含答案) 2025年中考数学知识点过关训练 |  | |
| 格式 | docx | ||
| 文件大小 | 177.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-10 21:08:19 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
专题提升卷(十一) 圆的综合(一)
[建议时间:40分钟 满分:100分]
A命题与探究
命题角度■ 圆与三角形的综合热门命题点
1.[2024·重庆] 如图,AB是⊙O的弦,OC⊥AB交⊙O于点C,D是⊙O上一点,连结 BD,CD.若∠D=28°,则∠OAB 的度数为 ( )
A.28° B.34° C.56° D.62°
2.[2024·盐城] 如图,△ABC是⊙O的内接三角形,∠C=40°,连结OA,OB,则∠OAB= .
3.正三角形的边长为6,则它的内切圆的半径大小是 .
4.如图,已知△ABC是等边三角形,O是边 BC 的中点,⊙O分别与边AB,AC切于点D 和点E,连结 DE.若AB=4,则 DE的长为 .
5.如图,在△ABC中,∠ACB=90°,CD⊥AB,△ABC,△ADC,△DBC的内切圆半径分别记为r,r ,r ,若 则r= .
命题角度□ 圆与四边形的综合热门命题点
6.如图,四边形ABCD外切于⊙O,且AB=10,CD=15,则四边形 ABCD的周长为 ( )
A.60 B.55 C.45 D.50
7.如图,点A,B,C在⊙O上,P为 上任意一点,∠A=m,则∠D+∠E等于 ( )
A.2m
8.如图,菱形ABCD的顶点B,C,D在⊙O上,且AB与⊙O相切,若⊙O的半径为1,则菱形ABCD的周长为( )
B.4 C.6 D.8
9.(10分)如图,四边形ABCD是⊙O的内接四边形, D是 的中点.
(1)求 的度数.
(2)求证:四边形 AOCD 是菱形.
10.(11分)[2024·甘肃]如图,AB是⊙O的直径, 点 E在AD 的延长线上,且
(1)求证:BE 是⊙O的切线.
(2)当⊙O的半径为2, 时,求 的值.
命题角度目 圆、三角形、四边形的综合热门命题点
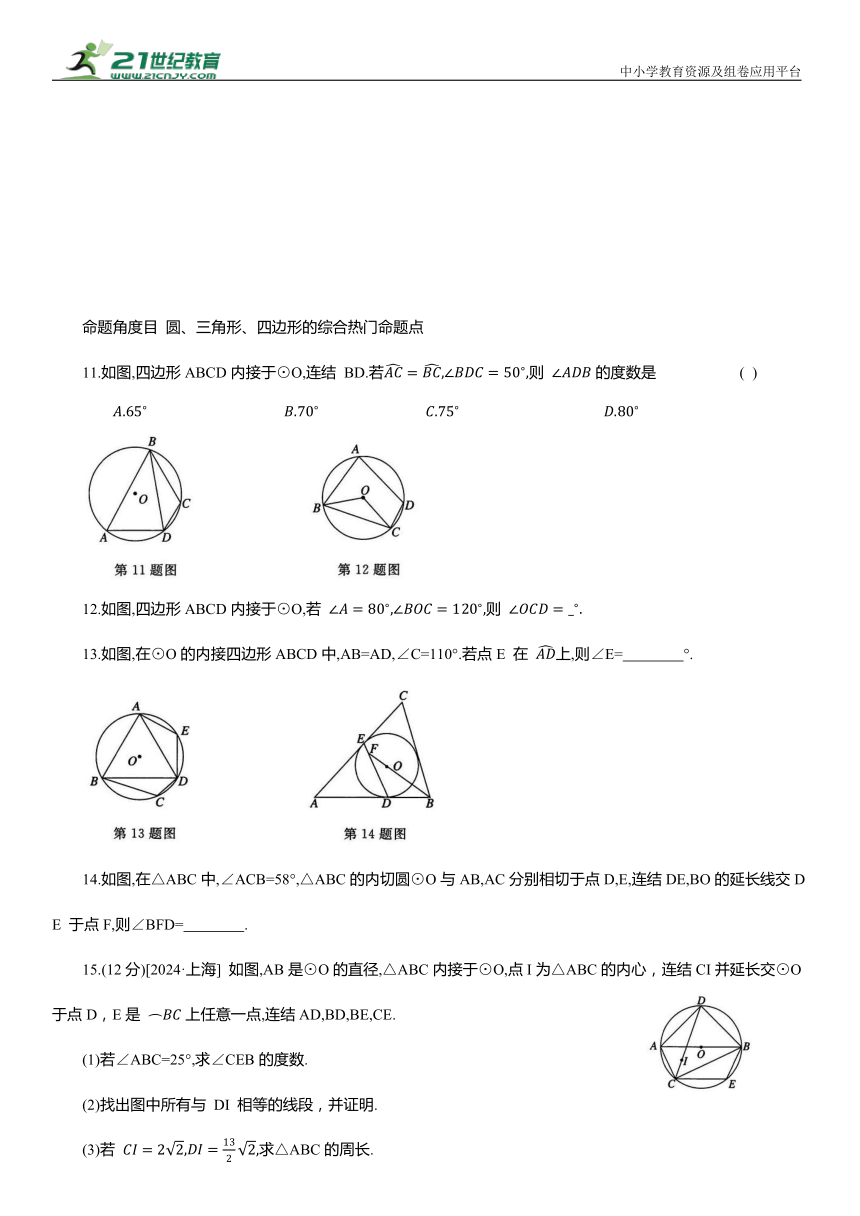
11.如图,四边形ABCD内接于⊙O,连结 BD.若则 的度数是 ( )
12.如图,四边形ABCD内接于⊙O,若 则
13.如图,在⊙O的内接四边形ABCD中,AB=AD,∠C=110°.若点E 在 上,则∠E= °.
14.如图,在△ABC中,∠ACB=58°,△ABC的内切圆⊙O与AB,AC分别相切于点D,E,连结DE,BO的延长线交DE 于点F,则∠BFD= .
15.(12分)[2024·上海] 如图,AB是⊙O的直径,△ABC内接于⊙O,点I为△ABC的内心,连结CI并延长交⊙O于点D,E是 上任意一点,连结AD,BD,BE,CE.
(1)若∠ABC=25°,求∠CEB的度数.
(2)找出图中所有与 DI 相等的线段,并证明.
(3)若 求△ABC的周长.
B仿真与预测
16.如图,AD是⊙O的切线,D是切点,C是⊙O上的一点,连结CD,AC,AC交⊙O于点B,若∠C=25°,则∠A 的度数是 ( )
A.20° B.25° C.30° D.40°
17.如图,△ABC 内接于⊙O,AD是直径,若∠B=25°,则∠CAD= °.
18.如图,△ABC 内接于⊙O,CD 是⊙O的直径,连结 BD,AO.已知∠DCA=40°,则∠ABC 的度数是
19.(10分)“托勒密定理”由依巴谷提出,其指出圆的内接四边形中,两条对角线的乘积等于两组对边乘积之和.如图,⊙O中有圆内接四边形ABCD,已知. 求AD的长度.
20.(12分)如图,圆外接于 过点C作( 于点D,延长CD交圆于点E,连结BE,过点 B的切线交AC 的延长线于点 F.
(1)证明:
(2)若 求 BF的长.
1. B 2.50° 3. 4.3 5. 6. D 7. C 8. B
9.(1)∠B=60° (2)证明略
10.(1)证明:设 AB与CD 相交于点F,连结 BD,OC,OD,如图所示,
∵OC=OD,
∴点O,B在CD的垂直平分线上,
∴OB垂直平分CD,
∵∠ADC=∠AEB,∴CD∥BE,
∴∠ABE=∠AFD=90°,∴AB⊥BE.
∵AB是⊙O的直径,∴BE是⊙O的切线.
11. D 12.70 13.125 14.29°
15.(1)∠CEB=115° (2)DI=AD=BD,证明略 (3)30
16. D 17.65 18.50°
19.解:过点 B作BE⊥CD,垂足为 E,
过点 B作BG⊥AC,垂足为G,如图.
∵∠BDC=60°,
∴∠BDC=∠BAC=60°.
在Rt△BDE中,BD=8,
∵CD=5,∴CE=CD-DE=5-4=1,
在 Rt△BCE中,
在 Rt△ABG中,.
在 Rt△BCG中,
∵四边形 ABCD是⊙O的内接四边形,
∴AD·BC+AB·CD=AC·BD,
解得
20.(1)证明:∵∠ACB=90°,∴AB是直径,∠A+∠ABC=90°.
∵BF是圆的切线,∴∠ABF=90°,
∴∠ABC+∠CBF=90°,∴∠A=∠CBF.
∵∠A=∠BEC,∴∠CBF=∠BEC.
专题提升卷(十一) 圆的综合(一)
[建议时间:40分钟 满分:100分]
A命题与探究
命题角度■ 圆与三角形的综合热门命题点
1.[2024·重庆] 如图,AB是⊙O的弦,OC⊥AB交⊙O于点C,D是⊙O上一点,连结 BD,CD.若∠D=28°,则∠OAB 的度数为 ( )
A.28° B.34° C.56° D.62°
2.[2024·盐城] 如图,△ABC是⊙O的内接三角形,∠C=40°,连结OA,OB,则∠OAB= .
3.正三角形的边长为6,则它的内切圆的半径大小是 .
4.如图,已知△ABC是等边三角形,O是边 BC 的中点,⊙O分别与边AB,AC切于点D 和点E,连结 DE.若AB=4,则 DE的长为 .
5.如图,在△ABC中,∠ACB=90°,CD⊥AB,△ABC,△ADC,△DBC的内切圆半径分别记为r,r ,r ,若 则r= .
命题角度□ 圆与四边形的综合热门命题点
6.如图,四边形ABCD外切于⊙O,且AB=10,CD=15,则四边形 ABCD的周长为 ( )
A.60 B.55 C.45 D.50
7.如图,点A,B,C在⊙O上,P为 上任意一点,∠A=m,则∠D+∠E等于 ( )
A.2m
8.如图,菱形ABCD的顶点B,C,D在⊙O上,且AB与⊙O相切,若⊙O的半径为1,则菱形ABCD的周长为( )
B.4 C.6 D.8
9.(10分)如图,四边形ABCD是⊙O的内接四边形, D是 的中点.
(1)求 的度数.
(2)求证:四边形 AOCD 是菱形.
10.(11分)[2024·甘肃]如图,AB是⊙O的直径, 点 E在AD 的延长线上,且
(1)求证:BE 是⊙O的切线.
(2)当⊙O的半径为2, 时,求 的值.
命题角度目 圆、三角形、四边形的综合热门命题点
11.如图,四边形ABCD内接于⊙O,连结 BD.若则 的度数是 ( )
12.如图,四边形ABCD内接于⊙O,若 则
13.如图,在⊙O的内接四边形ABCD中,AB=AD,∠C=110°.若点E 在 上,则∠E= °.
14.如图,在△ABC中,∠ACB=58°,△ABC的内切圆⊙O与AB,AC分别相切于点D,E,连结DE,BO的延长线交DE 于点F,则∠BFD= .
15.(12分)[2024·上海] 如图,AB是⊙O的直径,△ABC内接于⊙O,点I为△ABC的内心,连结CI并延长交⊙O于点D,E是 上任意一点,连结AD,BD,BE,CE.
(1)若∠ABC=25°,求∠CEB的度数.
(2)找出图中所有与 DI 相等的线段,并证明.
(3)若 求△ABC的周长.
B仿真与预测
16.如图,AD是⊙O的切线,D是切点,C是⊙O上的一点,连结CD,AC,AC交⊙O于点B,若∠C=25°,则∠A 的度数是 ( )
A.20° B.25° C.30° D.40°
17.如图,△ABC 内接于⊙O,AD是直径,若∠B=25°,则∠CAD= °.
18.如图,△ABC 内接于⊙O,CD 是⊙O的直径,连结 BD,AO.已知∠DCA=40°,则∠ABC 的度数是
19.(10分)“托勒密定理”由依巴谷提出,其指出圆的内接四边形中,两条对角线的乘积等于两组对边乘积之和.如图,⊙O中有圆内接四边形ABCD,已知. 求AD的长度.
20.(12分)如图,圆外接于 过点C作( 于点D,延长CD交圆于点E,连结BE,过点 B的切线交AC 的延长线于点 F.
(1)证明:
(2)若 求 BF的长.
1. B 2.50° 3. 4.3 5. 6. D 7. C 8. B
9.(1)∠B=60° (2)证明略
10.(1)证明:设 AB与CD 相交于点F,连结 BD,OC,OD,如图所示,
∵OC=OD,
∴点O,B在CD的垂直平分线上,
∴OB垂直平分CD,
∵∠ADC=∠AEB,∴CD∥BE,
∴∠ABE=∠AFD=90°,∴AB⊥BE.
∵AB是⊙O的直径,∴BE是⊙O的切线.
11. D 12.70 13.125 14.29°
15.(1)∠CEB=115° (2)DI=AD=BD,证明略 (3)30
16. D 17.65 18.50°
19.解:过点 B作BE⊥CD,垂足为 E,
过点 B作BG⊥AC,垂足为G,如图.
∵∠BDC=60°,
∴∠BDC=∠BAC=60°.
在Rt△BDE中,BD=8,
∵CD=5,∴CE=CD-DE=5-4=1,
在 Rt△BCE中,
在 Rt△ABG中,.
在 Rt△BCG中,
∵四边形 ABCD是⊙O的内接四边形,
∴AD·BC+AB·CD=AC·BD,
解得
20.(1)证明:∵∠ACB=90°,∴AB是直径,∠A+∠ABC=90°.
∵BF是圆的切线,∴∠ABF=90°,
∴∠ABC+∠CBF=90°,∴∠A=∠CBF.
∵∠A=∠BEC,∴∠CBF=∠BEC.
同课章节目录
