2025年中考数学复习专题提升卷(十三) 图形的变换与几何作图的综合(含答案)
文档属性
| 名称 | 2025年中考数学复习专题提升卷(十三) 图形的变换与几何作图的综合(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 349.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-10 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
专题提升卷(十三) 图形的变换与几何作图的综合
[建议时间:40分钟 满分:100分]
IA 命题与 探究
命题角度■ 对称变换
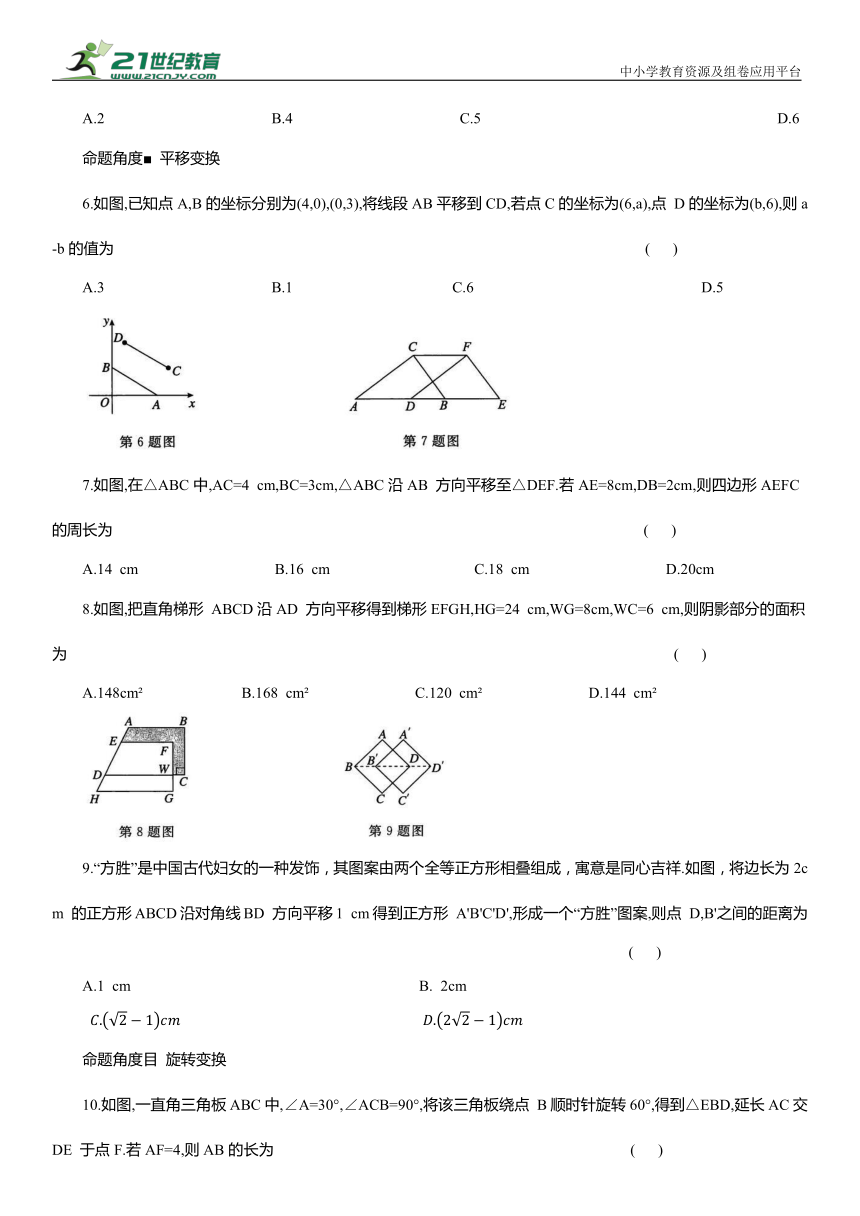
1.下列图形中,是中心对称图形但不是轴对称图形的是 ( )
2.如图,在 ABCD中,E为边AD上一点,将△DEC沿CE 翻折得到△FEC,点 F 在AC上,且满足AF=EF.若∠D=48°,则∠ACE 为 ( )
A.59° B.54° C.52° D.48°
3.如图,这是战机在空中展示的轴对称队形.以飞机 B,C所在直线为x轴、队形的对称轴为y轴,建立平面直角坐标系.若飞机 E 的坐标为(40,a),则飞机 D 的坐标为 ( )
A.(40,-a) B.(-40,a) C.(-40,-a) D.(a,-40)
4.如图,在正方形ABCD中,AB=12,将△ADE沿AE 对折至△AFE,延长EF 交BC 于点G,点G恰好是BC 边的中点,则 ED的长是 ( )
A.3 B.4 C.4.5 D.5
5.如图,将矩形纸片ABCD对折,使边AB与DC,BC与AD 分别重合,展开后得到四边形EFGH.若AB=2,BC=4,则四边形EFGH 的面积为 ( )
A.2 B.4 C.5 D.6
命题角度■ 平移变换
6.如图,已知点A,B的坐标分别为(4,0),(0,3),将线段AB平移到CD,若点C的坐标为(6,a),点 D的坐标为(b,6),则a-b的值为 ( )
A.3 B.1 C.6 D.5
7.如图,在△ABC中,AC=4 cm,BC=3cm,△ABC沿AB 方向平移至△DEF.若AE=8cm,DB=2cm,则四边形AEFC的周长为 ( )
A.14 cm B.16 cm C.18 cm D.20cm
8.如图,把直角梯形 ABCD沿AD 方向平移得到梯形EFGH,HG=24 cm,WG=8cm,WC=6 cm,则阴影部分的面积为 ( )
A.148cm B.168 cm C.120 cm D.144 cm
9.“方胜”是中国古代妇女的一种发饰,其图案由两个全等正方形相叠组成,寓意是同心吉祥.如图,将边长为2cm 的正方形ABCD沿对角线BD 方向平移1 cm得到正方形 A'B'C'D',形成一个“方胜”图案,则点 D,B'之间的距离为 ( )
A.1 cm B. 2cm
命题角度目 旋转变换
10.如图,一直角三角板ABC中,∠A=30°,∠ACB=90°,将该三角板绕点 B顺时针旋转60°,得到△EBD,延长AC交DE 于点F.若AF=4,则AB的长为 ( )
A.2 B. C.3 D.2
11.在平面直角坐标系中,已知点E(-6,2),F(-2,-2),以原点O为位似中心,位似比为 ,把△EFO缩小,则点 F 的对应点 F'的坐标是 ( )
A.(-1,-1) B.(1,1)
C.(-4,-4)或(4,4) D.(-1,-1)或(1,1)
12.如图,将矩形ABCD绕点B 旋转得到矩形GBEF,在旋转过程中,FG恰好过点C,过点G作MN 平行于AD交AB,CD于M,N两点.若AB=3,BC=5,则图中阴影部分的面积的是 ( )
A.3 B.4 C.5 D.
命题角度四 几何作图
13.(10分)如图,△DEF和等腰直角三角形ABC 的顶点都在方格纸的格点上.
(1)将△DEF向左平移6格得到△GBC,请画出△GBC.
将(1)中的△GBC绕点B 逆时针旋转90°得到△HBA,请画出△HBA;若∠ACG=α,则∠HAC的大小可用含α的代数式表示为 .
14.如图,在 中,. ,将 ABCD绕顶点B 顺时针旋转得到 ,当C'D'经过点 C 时,点 A′到AB 的距离为 .
B仿真与预测
15.[2024·成都] 如图,在 Rt△ABC中, .以点A为圆心,适当长为半径画弧,分别交 AC,AB于点M,N,再分别以 M,N为圆心,大于 的长为半径画弧,两弧在∠CAB的内部相交于点 P,画射线 AP与BC 交于点D,DE⊥AB,垂足为E.则下列结论错误的是
A.∠CAD=∠BAD B. CD=DE D. CD: BD=3:5
16.已知在△ABC中,AB17.(8分)尺规作图(保留作图痕迹,不要求写出作法).
如图,已知线段m,n.求作△ABC,使∠A=90°,AB=m,BC=n.
18.(12分)如图,在矩形 ABCD中,AC是对角线.
(1)实践与操作:利用尺规作线段AC的垂直平分线,垂足为点O,交边AD于点E,交边 BC于点 F(要求:尺规作图并保留作图痕迹,不写作法,标明字母).
(2)猜想与证明:试猜想线段AE与CF 的数量关系,并加以证明.
19.(12分)下图是由小正方形组成的网格,每个小正方形的顶点叫做格点,请用无刻度的直尺在给定网格中完成画图.
(1)在图1中,A,B,C三点均在格点上,请确定圆心O的位置,使A,B,C三点都在⊙O上.
(2)在图2中,点C在⊙O上,请在直径AB下方的圆上画出点E,使 ,并说明理由.
20.(13分)如图,O是等边三角形ABC 内的一点,将CO绕点C 顺时针旋转 得到CD,连结OD,AO,BO,AD.
(1)求证:
(2)若 求 的度数.
1. A 2. B 3. B 4. B 5. B 6. B 7. C 8. B 9. D 10. D11. D 12. A
13.解:(1)如图,△GBC即为所求的三角形.
14.2 15. C 16. D 17.略 18.(1)略(2)AE=CF,证明略
19.解:(1)如图1,点 O 即为所求.
(2)如图2,点 E 即为所求.连结BC,
∵AB为⊙O 的直径,∴∠ACB=90°.∵E为AB的中点,
∴点 E 即为所求.
20.(1)证明:∵CO绕点C顺时针旋转60°得到 CD,
∴CO=CD,∠OCD=60°.
∵△ABC是等边三角形,∴CA=CB,∠BCA=∠OCD=60°,∴∠BCO=∠ACD.
在△BCO和△ACD中,CB=CA,∠BCO=∠ACD,CO=CD,∴△BCO≌△ACD(SAS),∴BO=AD.
(2)∠BOC=150°
专题提升卷(十三) 图形的变换与几何作图的综合
[建议时间:40分钟 满分:100分]
IA 命题与 探究
命题角度■ 对称变换
1.下列图形中,是中心对称图形但不是轴对称图形的是 ( )
2.如图,在 ABCD中,E为边AD上一点,将△DEC沿CE 翻折得到△FEC,点 F 在AC上,且满足AF=EF.若∠D=48°,则∠ACE 为 ( )
A.59° B.54° C.52° D.48°
3.如图,这是战机在空中展示的轴对称队形.以飞机 B,C所在直线为x轴、队形的对称轴为y轴,建立平面直角坐标系.若飞机 E 的坐标为(40,a),则飞机 D 的坐标为 ( )
A.(40,-a) B.(-40,a) C.(-40,-a) D.(a,-40)
4.如图,在正方形ABCD中,AB=12,将△ADE沿AE 对折至△AFE,延长EF 交BC 于点G,点G恰好是BC 边的中点,则 ED的长是 ( )
A.3 B.4 C.4.5 D.5
5.如图,将矩形纸片ABCD对折,使边AB与DC,BC与AD 分别重合,展开后得到四边形EFGH.若AB=2,BC=4,则四边形EFGH 的面积为 ( )
A.2 B.4 C.5 D.6
命题角度■ 平移变换
6.如图,已知点A,B的坐标分别为(4,0),(0,3),将线段AB平移到CD,若点C的坐标为(6,a),点 D的坐标为(b,6),则a-b的值为 ( )
A.3 B.1 C.6 D.5
7.如图,在△ABC中,AC=4 cm,BC=3cm,△ABC沿AB 方向平移至△DEF.若AE=8cm,DB=2cm,则四边形AEFC的周长为 ( )
A.14 cm B.16 cm C.18 cm D.20cm
8.如图,把直角梯形 ABCD沿AD 方向平移得到梯形EFGH,HG=24 cm,WG=8cm,WC=6 cm,则阴影部分的面积为 ( )
A.148cm B.168 cm C.120 cm D.144 cm
9.“方胜”是中国古代妇女的一种发饰,其图案由两个全等正方形相叠组成,寓意是同心吉祥.如图,将边长为2cm 的正方形ABCD沿对角线BD 方向平移1 cm得到正方形 A'B'C'D',形成一个“方胜”图案,则点 D,B'之间的距离为 ( )
A.1 cm B. 2cm
命题角度目 旋转变换
10.如图,一直角三角板ABC中,∠A=30°,∠ACB=90°,将该三角板绕点 B顺时针旋转60°,得到△EBD,延长AC交DE 于点F.若AF=4,则AB的长为 ( )
A.2 B. C.3 D.2
11.在平面直角坐标系中,已知点E(-6,2),F(-2,-2),以原点O为位似中心,位似比为 ,把△EFO缩小,则点 F 的对应点 F'的坐标是 ( )
A.(-1,-1) B.(1,1)
C.(-4,-4)或(4,4) D.(-1,-1)或(1,1)
12.如图,将矩形ABCD绕点B 旋转得到矩形GBEF,在旋转过程中,FG恰好过点C,过点G作MN 平行于AD交AB,CD于M,N两点.若AB=3,BC=5,则图中阴影部分的面积的是 ( )
A.3 B.4 C.5 D.
命题角度四 几何作图
13.(10分)如图,△DEF和等腰直角三角形ABC 的顶点都在方格纸的格点上.
(1)将△DEF向左平移6格得到△GBC,请画出△GBC.
将(1)中的△GBC绕点B 逆时针旋转90°得到△HBA,请画出△HBA;若∠ACG=α,则∠HAC的大小可用含α的代数式表示为 .
14.如图,在 中,. ,将 ABCD绕顶点B 顺时针旋转得到 ,当C'D'经过点 C 时,点 A′到AB 的距离为 .
B仿真与预测
15.[2024·成都] 如图,在 Rt△ABC中, .以点A为圆心,适当长为半径画弧,分别交 AC,AB于点M,N,再分别以 M,N为圆心,大于 的长为半径画弧,两弧在∠CAB的内部相交于点 P,画射线 AP与BC 交于点D,DE⊥AB,垂足为E.则下列结论错误的是
A.∠CAD=∠BAD B. CD=DE D. CD: BD=3:5
16.已知在△ABC中,AB
如图,已知线段m,n.求作△ABC,使∠A=90°,AB=m,BC=n.
18.(12分)如图,在矩形 ABCD中,AC是对角线.
(1)实践与操作:利用尺规作线段AC的垂直平分线,垂足为点O,交边AD于点E,交边 BC于点 F(要求:尺规作图并保留作图痕迹,不写作法,标明字母).
(2)猜想与证明:试猜想线段AE与CF 的数量关系,并加以证明.
19.(12分)下图是由小正方形组成的网格,每个小正方形的顶点叫做格点,请用无刻度的直尺在给定网格中完成画图.
(1)在图1中,A,B,C三点均在格点上,请确定圆心O的位置,使A,B,C三点都在⊙O上.
(2)在图2中,点C在⊙O上,请在直径AB下方的圆上画出点E,使 ,并说明理由.
20.(13分)如图,O是等边三角形ABC 内的一点,将CO绕点C 顺时针旋转 得到CD,连结OD,AO,BO,AD.
(1)求证:
(2)若 求 的度数.
1. A 2. B 3. B 4. B 5. B 6. B 7. C 8. B 9. D 10. D11. D 12. A
13.解:(1)如图,△GBC即为所求的三角形.
14.2 15. C 16. D 17.略 18.(1)略(2)AE=CF,证明略
19.解:(1)如图1,点 O 即为所求.
(2)如图2,点 E 即为所求.连结BC,
∵AB为⊙O 的直径,∴∠ACB=90°.∵E为AB的中点,
∴点 E 即为所求.
20.(1)证明:∵CO绕点C顺时针旋转60°得到 CD,
∴CO=CD,∠OCD=60°.
∵△ABC是等边三角形,∴CA=CB,∠BCA=∠OCD=60°,∴∠BCO=∠ACD.
在△BCO和△ACD中,CB=CA,∠BCO=∠ACD,CO=CD,∴△BCO≌△ACD(SAS),∴BO=AD.
(2)∠BOC=150°
同课章节目录
