2025年中考数学核心素养命题100题 专题八 从模型观念的素养角度去思考命题(含答案)
文档属性
| 名称 | 2025年中考数学核心素养命题100题 专题八 从模型观念的素养角度去思考命题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 156.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-10 21:17:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
专题八 从模型观念的素养角度去思考命题
第81题在形成方程的过程中感悟数学的模型思想的模型观念素养(中华优秀传统文化)————元一次方程的应用
《孙子算经》中有这样一道题,大意为:今有100头鹿,每户分一头鹿后,还有剩余,将剩下的鹿按每3户共分一头,恰好分完,问:有多少户人家 若设有x户人家,则下列方程正确的是 ( )
A. x+3=100
C. x+3x=100
变式43 《诗经》是我国第一部诗歌总集,其中《颂》的部分有40篇,比《风》的篇数少 ,求《风》的篇数.若设《风》有x篇,则根据题意列方程 ( )
第82题 在形成不等式的过程中感悟数学的模型思想的模型观念素养————元一次不等式的应用一部电梯的额定限载量为1000千克.两人要用电梯把一批重物从底层搬到顶层,这两人的身体质量分别为60千克和80千克,每箱货物的质量为50千克,设每次搬x箱重物,则下面所列关系正确的是 ( )
A. 50x+60+80=1000 B. 50x+60+80≤1000
C. 50x+60+80<1000 D. 50x+60+80≥1000
第83题 在形成方程的过程中感悟数学的模型思想的模型观念素养(中华优秀传统文化)——二元一次方程的应用我国古代数学名著《算法统宗》中记载:“今有里长值月,议云每里科出银五钱依帐买物以辨酒席,多银三两五钱.每里科出四钱亦多五钱,问合用银并里数若干”.意为:里长们(“里”是指古代的一种基层行政单位)在月度会上商议出银子购买物资办酒席之事.若每里出5钱,则多出35 钱;若每里出4钱,则多出5钱.问办酒席需多少银子,里的数量有多少个 若设里的数量有x个,办酒席需要用y钱银子,则可列方程组( )
变式44 我国古代数学著作《增删算法统宗》记载:绳索量竿问题,“一条竿子一条索,索比竿子长一托,折回索子去量竿,却比竿子短一托”.其大意为:现有一根竿和一条绳索,用绳索去量竿,绳索比竿长5尺,如果将绳索对半折后再去量竿,就比竿短5尺.设竿长x尺,绳索长 y尺,则符合题意的方程组是 ( )
第84 题 在形成方程的过程中感悟数学的模型思想的模型观念素养(中华优秀传统文化)——分式方程的应用
为了大力弘扬中华优秀传统文化,某校决定开展名著阅读活动,用3 600元购买“四大名著”若干套后,发现这批图书满足不了学生的阅读需求,图书管理员在购买第二批时正赶上图书城八折销售该套书,于是用2400元购买的套数只比第一批少4套,设第一批购买的“四大名著”每套的价格为x元,则符合题意的方程是 ( )
变式45 赛龙舟是端午节的主要习俗之一,也是中国民俗传统与运动精神的完美结合.2019年起,深圳大沙河生态长廊龙舟邀请赛连续4年举办,已然成为深圳市标志性的体育赛事.2022年龙舟邀请赛设置了标准龙舟(22人龙舟)500米直道竞速赛项目,其中甲、乙两队参加比赛(比赛起点相同),甲队每秒的速度比乙队快0.5米,结果甲队比乙队提前14秒到达终点.设甲队的速度为x米/秒,下列方程正确的是 ( )
第85题 在形成函数的过程中感悟数学的模型思想的模型观念素养——分段函数的应用
A,B两地相距240km,甲货车从A 地以40 km/h的速度匀速前往 B地,到达 B地后停止.在甲货车出发的同时,乙货车从 B地沿同一公路匀速前往A 地,到达A地后停止.两车之间的路程y(km)与甲货车出发时间x(h)之间的函数关系如右图中的折线所示,则下列说法错误的是 ( )
A. 两货车2.4 h相遇
B. 两货车相遇时,甲货车比乙货车少行驶48km
C. 乙货车的速度为60 km/h
D. 乙货车到达 A 地时,甲货车距离 B 地96 km
变式46 甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米,先到终点的人原地休息.已知甲先出发4分钟,在整个步行过程中,甲、乙两人的距离y(米)与甲出发的时间t(分)之间的关系如右图所示,下列结论:①甲步行的速度为60米/分;②乙走完全程用了30分钟;③乙用12分钟追上甲;④乙到达终点时,甲离终点还有360米.其中正确的结论有 .(填序号)
第86题在形成函数的过程中感悟数学的模型思想的模型观念素养——反比例函数的应用
生活中做拉面的过程渗透着数学知识,一定体积的面团做成拉面,面条总长度与面条粗细(横截面面积)存在一定的函数关系.项目化学习小组的同学用一块面团进行了试验,并将数据整理如下:
面条粗细 s/cm … 0.4 0.3 0.2 0.1 …
面条总长度 y/cm … 33 44 66 132 …
根据以上数据可知,当面条总长度为220 cm时,面条粗细为 cn c m^{2}.
变式47 如图所示,小华设计了一个探究杠杆平衡条件的实验:在一根匀质的木杆中点O左侧固定位置B 处悬挂重物A,在中点O右侧用一个弹簧秤向下拉,改变弹簧秤与点O的距离x(cm),观察弹簧秤的示数y(N)的变化情况.实验数据记录如下:
x/ cm … 10 15 20 25 30 …
y/N … 30 20 15 12 10 …
猜测 y与x 之间的函数关系,并求出函数关系式为 .
第87题 能够根据实际问题的条件建构具体的模型并解决问题的模型观念素养——祖暅原理
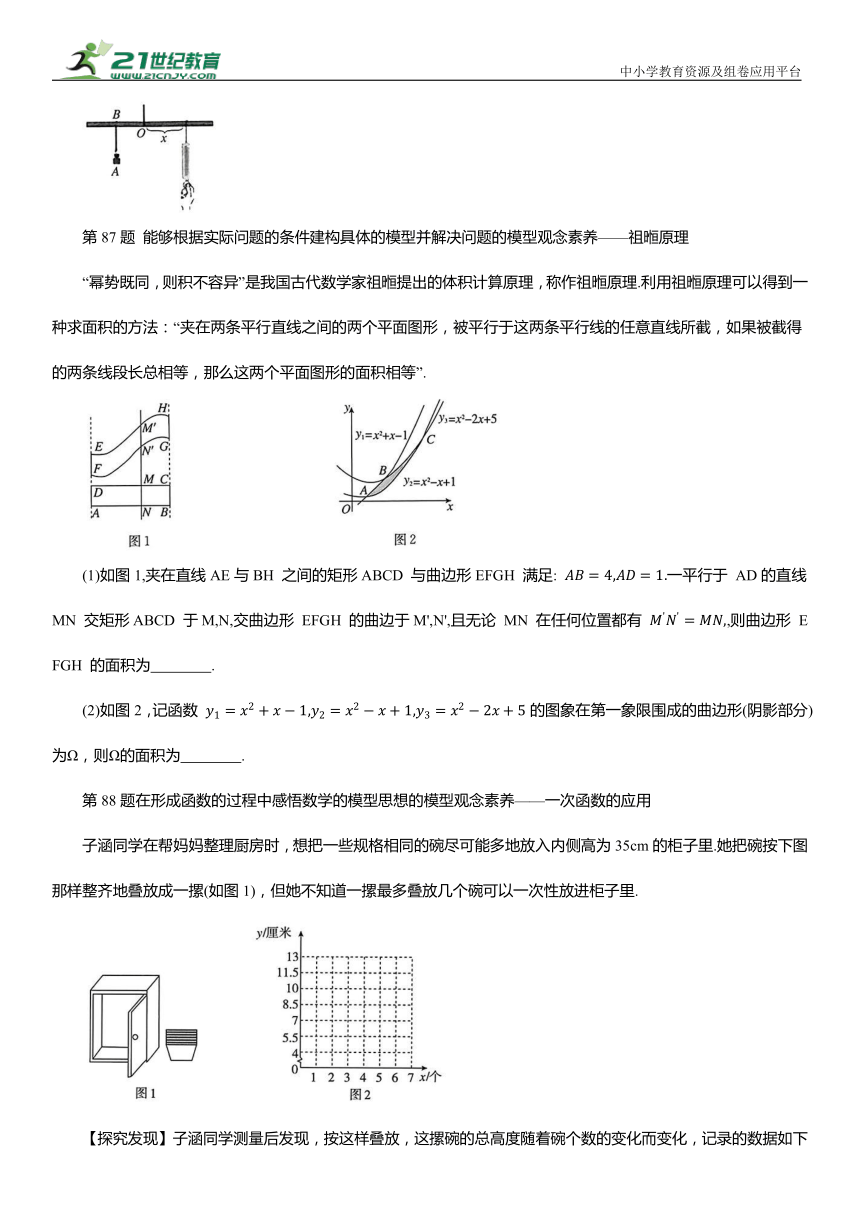
“幂势既同,则积不容异”是我国古代数学家祖暅提出的体积计算原理,称作祖暅原理.利用祖暅原理可以得到一种求面积的方法:“夹在两条平行直线之间的两个平面图形,被平行于这两条平行线的任意直线所截,如果被截得的两条线段长总相等,那么这两个平面图形的面积相等”.
(1)如图1,夹在直线AE与BH 之间的矩形ABCD 与曲边形EFGH 满足: 一平行于 AD的直线MN 交矩形ABCD 于M,N,交曲边形 EFGH 的曲边于M',N',且无论 MN 在任何位置都有 ,则曲边形 EFGH 的面积为 .
(2)如图2,记函数 的图象在第一象限围成的曲边形(阴影部分)为Ω,则Ω的面积为 .
第88题在形成函数的过程中感悟数学的模型思想的模型观念素养——一次函数的应用
子涵同学在帮妈妈整理厨房时,想把一些规格相同的碗尽可能多地放入内侧高为35cm的柜子里.她把碗按下图那样整齐地叠放成一摞(如图1),但她不知道一摞最多叠放几个碗可以一次性放进柜子里.
【探究发现】子涵同学测量后发现,按这样叠放,这摞碗的总高度随着碗个数的变化而变化,记录的数据如下表.
碗的个数x/个 1 2 3 4 5
这摞碗的总高度y/厘米 5.5 7 8.5 10 11.5
【建立模型】
(1)请根据表中信息,在平面直角坐标系(如图2)中描出对应点,并指出这些点的分布规律.
(2)求y与x的函数关系式,并求当碗的个数为12时这摞碗的总高度.
【结论应用】(3)请帮子涵同学算一算,一摞最多叠几个碗可以一次性放进柜子里
变式48 综合与实践
【问题情境】
新学期,两摞规格相同的数学课本整齐地叠放在讲台上,左边一摞有3本,右边一摞有6本,请根据图中所给出的数据信息,解答下列问题:
【知识运用】
(1)求每本书的厚度和课桌的高度分别是多少厘米
(2)当课本数为x(本)时,请写出叠放在桌面上的一摞同样的数学课本高出地面的距离.(用含x的代数式表示)
【综合应用】
(3)若桌面上有54本与题(1)中相同的数学课本,整齐叠放成摞,若有16名同学各从中取走1本,求余下的数学课本高出地面的距离.
第89题在形成方程、函数的过程中感悟数学的模型思想的模型观念素养——二元一次方程与二次函数的应用
如图1,一小球从斜面顶端由静止开始沿斜面下滚,呈匀加速运动状态,速度每秒增加2cm;然后在水平地面上继续滚动,呈匀减速运动状态,滚动速度每秒减小0.8cm.速度v(cm/s)与时间t(s)的关系如图2中的实线所示.(提示:根据物理学知识可知,物体匀加速运动时的路程=平均速度 时间 其中v 是开始时的速度,v 是t秒时的速度.匀减速运动时的路程和平均速度类似可得.)
(1)当 时,求解下面的问题.
①求 m的值.
②写出滚动的路程s(单位:cm)关于滚动时间t(单位:s)的函数解析式.
(2)若小球滚动最大的路程是350cm,则小球在水平地面上滚动了多长时间
变式49 如图,钢球(不计大小)在一个光滑的“V”型轨道上滚动,其中右侧轨道长为25 m,左侧轨道长为30m.钢球先由静止开始沿右侧斜面滚下,速度每秒增加8m,到达底端后又沿着左侧轨道向上滚动,速度每秒减少 a m.(提示:钢球滚动的距离=平均速度 时间t. 其中 表示开始的速度, 表示t秒时的速度.)
(1)若钢球在右侧轨道滚动2s,则
(2)写出钢球在右侧轨道滚动的距离s(单位:m)与时间t(单位:s)之间的函数解析式,并求出t的取值范围.
(3)若钢球滚出左侧轨道,求a的取值范围.
第90题在形成函数的过程中感悟数学的模型思想的模型观念素养——二次函数的应用
综合与实践
【问题提出】
某班开展课外锻炼,有7位同学组队参加跳长绳运动,如何才能顺利开展活动呢
【实践活动】
在体育老师的指导下,队员们进行了以下实践:
步骤一:收集身高数据如下:
队员 甲 乙 丙 丁 戊 己 庚
身高/m 1.70 1.70 1.73 1.60 1.68 1.80 1.60
步骤二:为增加甩绳的稳定度,确定两位身高较高且相近的甲、乙队员甩绳,其余队员跳绳;
步骤三:所有队员站成一排,跳绳队员按照中间高、两端低的方式排列,同时7名队员每两人间的距离至少为0.5m 才能保证安全;
步骤四:如图1,两位甩绳队员通过多次实践发现,当两人的水平距离AC=4m,手离地面的高度 CD=1.2m,绳子最高点距离地面2m时,效果最佳.
【问题解决】
如图2,当绳子甩动到最高点时的形状近似看成一条抛物线,若以AC所在直线为x轴,AB 所在的直线为y轴,建立平面直角坐标系.
(1)求抛物线的解析式.
(2)最高的队员位于AC中点,其余跳绳队员对称安排在其两侧.
①当跳绳队员之间正好保持0.5m的距离时,长绳能否高过所有跳绳队员的头顶
②在保证安全的情况下,求最左边的跳绳队员与离他最近的甩绳队员之间距离的取值范围.
变式50 综合与实践.
某数学兴趣小组对数学学习中有关汽车的刹车距离有疑惑,于是他们走进汽车研发中心考查刹车距离.
【知识背景】“道路千万条,安全第一条.”刹车系统是车辆行驶安全的重要保障,由于惯性的作用,行驶中的汽车在刹车后还要继续向前行驶一段距离才能停止,这段距离称为刹车距离.
【探究发现】汽车研发中心设计了一款新型汽车,现在模拟汽车在高速公路上以某一速度行驶时,对它的刹车性能进行测试.兴趣小组成员记录其中一组数据如下:
刹车后行驶的时间t 0 1 2 3
刹车后行驶的距离y 0 27 48 63
发现:①开始刹车后行驶的距离y(单位:m)与刹车后行驶的时间t(单位:s)之间成二次函数关系.
②汽车刹车后行驶的距离y随刹车后行驶的时间t的增大而增大,当刹车后行驶的距离最远时,汽车完全停止.
【问题解决】请根据以上信息,解决下列问题:
(1)求y关于t的函数解析式.(不要求写出自变量的取值范围)
(2)求汽车刹车4s 后行驶的距离.
(3)若汽车司机发现正前方80m处有一辆抛锚的车停在路面上时,立刻刹车,问该车在不变道的情况下是否会撞到抛锚的车 试说明理由.
81. D 变式43 D 82. B 83. D 变式44 B 84. B变式45 C 85. D 变式46 ①②③④86.0.06变式
87.(1)4 (2)3 【解析】(1)由祖暅原理,得曲边形 EFGH 的面积=矩形ABCD的面积,
∴曲边形 EFGH 的面积=AB×AD=4.
(2)联立函数,求得点 A(1,1),B(2,5),C(4,13),
yEF-yEM=2x-2,yFG - yMσ=-x+4,
当x=1时,yAB-yAH=0,当x=2时,yAB-yAH=2,
当x=4时,yBC-yHC=0,
88.(1)略 (2)y=1.5x+4 当碗的个数为12时,这摞碗的总高度为22厘米
(3)一摞最多叠20个碗可以一次性放进柜子里.
变式48 解:(1)每本书的厚度为(88-86.5)÷(6-3)=0.5(cm);课桌的高度为86.5-3×0.5=85(cm).
(2)高出地面的距离为(85+0.5x) cm.
(3)余下的数学课本高出地面的距离是104 cm.
89.(1)①m的值是
(2)小球在水平地面上滚动了25秒.
变式49 (1)16,8
90.(1)抛物线的解析式为
(2)①长绳能高过所有跳绳队员的头顶.
②最左边的跳绳队员与离他最近的甩绳队员之间距离的取值范围为
变式50 (1)y关于t的函数解析式为
(2)汽车刹车4s 后,行驶了 72 m.
(3)不会.理由如下:
∴当t=5时,汽车停下,行驶了75 m.
∵75<80,∴该车在不变道的情况下不会撞到抛锚的车.
专题八 从模型观念的素养角度去思考命题
第81题在形成方程的过程中感悟数学的模型思想的模型观念素养(中华优秀传统文化)————元一次方程的应用
《孙子算经》中有这样一道题,大意为:今有100头鹿,每户分一头鹿后,还有剩余,将剩下的鹿按每3户共分一头,恰好分完,问:有多少户人家 若设有x户人家,则下列方程正确的是 ( )
A. x+3=100
C. x+3x=100
变式43 《诗经》是我国第一部诗歌总集,其中《颂》的部分有40篇,比《风》的篇数少 ,求《风》的篇数.若设《风》有x篇,则根据题意列方程 ( )
第82题 在形成不等式的过程中感悟数学的模型思想的模型观念素养————元一次不等式的应用一部电梯的额定限载量为1000千克.两人要用电梯把一批重物从底层搬到顶层,这两人的身体质量分别为60千克和80千克,每箱货物的质量为50千克,设每次搬x箱重物,则下面所列关系正确的是 ( )
A. 50x+60+80=1000 B. 50x+60+80≤1000
C. 50x+60+80<1000 D. 50x+60+80≥1000
第83题 在形成方程的过程中感悟数学的模型思想的模型观念素养(中华优秀传统文化)——二元一次方程的应用我国古代数学名著《算法统宗》中记载:“今有里长值月,议云每里科出银五钱依帐买物以辨酒席,多银三两五钱.每里科出四钱亦多五钱,问合用银并里数若干”.意为:里长们(“里”是指古代的一种基层行政单位)在月度会上商议出银子购买物资办酒席之事.若每里出5钱,则多出35 钱;若每里出4钱,则多出5钱.问办酒席需多少银子,里的数量有多少个 若设里的数量有x个,办酒席需要用y钱银子,则可列方程组( )
变式44 我国古代数学著作《增删算法统宗》记载:绳索量竿问题,“一条竿子一条索,索比竿子长一托,折回索子去量竿,却比竿子短一托”.其大意为:现有一根竿和一条绳索,用绳索去量竿,绳索比竿长5尺,如果将绳索对半折后再去量竿,就比竿短5尺.设竿长x尺,绳索长 y尺,则符合题意的方程组是 ( )
第84 题 在形成方程的过程中感悟数学的模型思想的模型观念素养(中华优秀传统文化)——分式方程的应用
为了大力弘扬中华优秀传统文化,某校决定开展名著阅读活动,用3 600元购买“四大名著”若干套后,发现这批图书满足不了学生的阅读需求,图书管理员在购买第二批时正赶上图书城八折销售该套书,于是用2400元购买的套数只比第一批少4套,设第一批购买的“四大名著”每套的价格为x元,则符合题意的方程是 ( )
变式45 赛龙舟是端午节的主要习俗之一,也是中国民俗传统与运动精神的完美结合.2019年起,深圳大沙河生态长廊龙舟邀请赛连续4年举办,已然成为深圳市标志性的体育赛事.2022年龙舟邀请赛设置了标准龙舟(22人龙舟)500米直道竞速赛项目,其中甲、乙两队参加比赛(比赛起点相同),甲队每秒的速度比乙队快0.5米,结果甲队比乙队提前14秒到达终点.设甲队的速度为x米/秒,下列方程正确的是 ( )
第85题 在形成函数的过程中感悟数学的模型思想的模型观念素养——分段函数的应用
A,B两地相距240km,甲货车从A 地以40 km/h的速度匀速前往 B地,到达 B地后停止.在甲货车出发的同时,乙货车从 B地沿同一公路匀速前往A 地,到达A地后停止.两车之间的路程y(km)与甲货车出发时间x(h)之间的函数关系如右图中的折线所示,则下列说法错误的是 ( )
A. 两货车2.4 h相遇
B. 两货车相遇时,甲货车比乙货车少行驶48km
C. 乙货车的速度为60 km/h
D. 乙货车到达 A 地时,甲货车距离 B 地96 km
变式46 甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米,先到终点的人原地休息.已知甲先出发4分钟,在整个步行过程中,甲、乙两人的距离y(米)与甲出发的时间t(分)之间的关系如右图所示,下列结论:①甲步行的速度为60米/分;②乙走完全程用了30分钟;③乙用12分钟追上甲;④乙到达终点时,甲离终点还有360米.其中正确的结论有 .(填序号)
第86题在形成函数的过程中感悟数学的模型思想的模型观念素养——反比例函数的应用
生活中做拉面的过程渗透着数学知识,一定体积的面团做成拉面,面条总长度与面条粗细(横截面面积)存在一定的函数关系.项目化学习小组的同学用一块面团进行了试验,并将数据整理如下:
面条粗细 s/cm … 0.4 0.3 0.2 0.1 …
面条总长度 y/cm … 33 44 66 132 …
根据以上数据可知,当面条总长度为220 cm时,面条粗细为 cn c m^{2}.
变式47 如图所示,小华设计了一个探究杠杆平衡条件的实验:在一根匀质的木杆中点O左侧固定位置B 处悬挂重物A,在中点O右侧用一个弹簧秤向下拉,改变弹簧秤与点O的距离x(cm),观察弹簧秤的示数y(N)的变化情况.实验数据记录如下:
x/ cm … 10 15 20 25 30 …
y/N … 30 20 15 12 10 …
猜测 y与x 之间的函数关系,并求出函数关系式为 .
第87题 能够根据实际问题的条件建构具体的模型并解决问题的模型观念素养——祖暅原理
“幂势既同,则积不容异”是我国古代数学家祖暅提出的体积计算原理,称作祖暅原理.利用祖暅原理可以得到一种求面积的方法:“夹在两条平行直线之间的两个平面图形,被平行于这两条平行线的任意直线所截,如果被截得的两条线段长总相等,那么这两个平面图形的面积相等”.
(1)如图1,夹在直线AE与BH 之间的矩形ABCD 与曲边形EFGH 满足: 一平行于 AD的直线MN 交矩形ABCD 于M,N,交曲边形 EFGH 的曲边于M',N',且无论 MN 在任何位置都有 ,则曲边形 EFGH 的面积为 .
(2)如图2,记函数 的图象在第一象限围成的曲边形(阴影部分)为Ω,则Ω的面积为 .
第88题在形成函数的过程中感悟数学的模型思想的模型观念素养——一次函数的应用
子涵同学在帮妈妈整理厨房时,想把一些规格相同的碗尽可能多地放入内侧高为35cm的柜子里.她把碗按下图那样整齐地叠放成一摞(如图1),但她不知道一摞最多叠放几个碗可以一次性放进柜子里.
【探究发现】子涵同学测量后发现,按这样叠放,这摞碗的总高度随着碗个数的变化而变化,记录的数据如下表.
碗的个数x/个 1 2 3 4 5
这摞碗的总高度y/厘米 5.5 7 8.5 10 11.5
【建立模型】
(1)请根据表中信息,在平面直角坐标系(如图2)中描出对应点,并指出这些点的分布规律.
(2)求y与x的函数关系式,并求当碗的个数为12时这摞碗的总高度.
【结论应用】(3)请帮子涵同学算一算,一摞最多叠几个碗可以一次性放进柜子里
变式48 综合与实践
【问题情境】
新学期,两摞规格相同的数学课本整齐地叠放在讲台上,左边一摞有3本,右边一摞有6本,请根据图中所给出的数据信息,解答下列问题:
【知识运用】
(1)求每本书的厚度和课桌的高度分别是多少厘米
(2)当课本数为x(本)时,请写出叠放在桌面上的一摞同样的数学课本高出地面的距离.(用含x的代数式表示)
【综合应用】
(3)若桌面上有54本与题(1)中相同的数学课本,整齐叠放成摞,若有16名同学各从中取走1本,求余下的数学课本高出地面的距离.
第89题在形成方程、函数的过程中感悟数学的模型思想的模型观念素养——二元一次方程与二次函数的应用
如图1,一小球从斜面顶端由静止开始沿斜面下滚,呈匀加速运动状态,速度每秒增加2cm;然后在水平地面上继续滚动,呈匀减速运动状态,滚动速度每秒减小0.8cm.速度v(cm/s)与时间t(s)的关系如图2中的实线所示.(提示:根据物理学知识可知,物体匀加速运动时的路程=平均速度 时间 其中v 是开始时的速度,v 是t秒时的速度.匀减速运动时的路程和平均速度类似可得.)
(1)当 时,求解下面的问题.
①求 m的值.
②写出滚动的路程s(单位:cm)关于滚动时间t(单位:s)的函数解析式.
(2)若小球滚动最大的路程是350cm,则小球在水平地面上滚动了多长时间
变式49 如图,钢球(不计大小)在一个光滑的“V”型轨道上滚动,其中右侧轨道长为25 m,左侧轨道长为30m.钢球先由静止开始沿右侧斜面滚下,速度每秒增加8m,到达底端后又沿着左侧轨道向上滚动,速度每秒减少 a m.(提示:钢球滚动的距离=平均速度 时间t. 其中 表示开始的速度, 表示t秒时的速度.)
(1)若钢球在右侧轨道滚动2s,则
(2)写出钢球在右侧轨道滚动的距离s(单位:m)与时间t(单位:s)之间的函数解析式,并求出t的取值范围.
(3)若钢球滚出左侧轨道,求a的取值范围.
第90题在形成函数的过程中感悟数学的模型思想的模型观念素养——二次函数的应用
综合与实践
【问题提出】
某班开展课外锻炼,有7位同学组队参加跳长绳运动,如何才能顺利开展活动呢
【实践活动】
在体育老师的指导下,队员们进行了以下实践:
步骤一:收集身高数据如下:
队员 甲 乙 丙 丁 戊 己 庚
身高/m 1.70 1.70 1.73 1.60 1.68 1.80 1.60
步骤二:为增加甩绳的稳定度,确定两位身高较高且相近的甲、乙队员甩绳,其余队员跳绳;
步骤三:所有队员站成一排,跳绳队员按照中间高、两端低的方式排列,同时7名队员每两人间的距离至少为0.5m 才能保证安全;
步骤四:如图1,两位甩绳队员通过多次实践发现,当两人的水平距离AC=4m,手离地面的高度 CD=1.2m,绳子最高点距离地面2m时,效果最佳.
【问题解决】
如图2,当绳子甩动到最高点时的形状近似看成一条抛物线,若以AC所在直线为x轴,AB 所在的直线为y轴,建立平面直角坐标系.
(1)求抛物线的解析式.
(2)最高的队员位于AC中点,其余跳绳队员对称安排在其两侧.
①当跳绳队员之间正好保持0.5m的距离时,长绳能否高过所有跳绳队员的头顶
②在保证安全的情况下,求最左边的跳绳队员与离他最近的甩绳队员之间距离的取值范围.
变式50 综合与实践.
某数学兴趣小组对数学学习中有关汽车的刹车距离有疑惑,于是他们走进汽车研发中心考查刹车距离.
【知识背景】“道路千万条,安全第一条.”刹车系统是车辆行驶安全的重要保障,由于惯性的作用,行驶中的汽车在刹车后还要继续向前行驶一段距离才能停止,这段距离称为刹车距离.
【探究发现】汽车研发中心设计了一款新型汽车,现在模拟汽车在高速公路上以某一速度行驶时,对它的刹车性能进行测试.兴趣小组成员记录其中一组数据如下:
刹车后行驶的时间t 0 1 2 3
刹车后行驶的距离y 0 27 48 63
发现:①开始刹车后行驶的距离y(单位:m)与刹车后行驶的时间t(单位:s)之间成二次函数关系.
②汽车刹车后行驶的距离y随刹车后行驶的时间t的增大而增大,当刹车后行驶的距离最远时,汽车完全停止.
【问题解决】请根据以上信息,解决下列问题:
(1)求y关于t的函数解析式.(不要求写出自变量的取值范围)
(2)求汽车刹车4s 后行驶的距离.
(3)若汽车司机发现正前方80m处有一辆抛锚的车停在路面上时,立刻刹车,问该车在不变道的情况下是否会撞到抛锚的车 试说明理由.
81. D 变式43 D 82. B 83. D 变式44 B 84. B变式45 C 85. D 变式46 ①②③④86.0.06变式
87.(1)4 (2)3 【解析】(1)由祖暅原理,得曲边形 EFGH 的面积=矩形ABCD的面积,
∴曲边形 EFGH 的面积=AB×AD=4.
(2)联立函数,求得点 A(1,1),B(2,5),C(4,13),
yEF-yEM=2x-2,yFG - yMσ=-x+4,
当x=1时,yAB-yAH=0,当x=2时,yAB-yAH=2,
当x=4时,yBC-yHC=0,
88.(1)略 (2)y=1.5x+4 当碗的个数为12时,这摞碗的总高度为22厘米
(3)一摞最多叠20个碗可以一次性放进柜子里.
变式48 解:(1)每本书的厚度为(88-86.5)÷(6-3)=0.5(cm);课桌的高度为86.5-3×0.5=85(cm).
(2)高出地面的距离为(85+0.5x) cm.
(3)余下的数学课本高出地面的距离是104 cm.
89.(1)①m的值是
(2)小球在水平地面上滚动了25秒.
变式49 (1)16,8
90.(1)抛物线的解析式为
(2)①长绳能高过所有跳绳队员的头顶.
②最左边的跳绳队员与离他最近的甩绳队员之间距离的取值范围为
变式50 (1)y关于t的函数解析式为
(2)汽车刹车4s 后,行驶了 72 m.
(3)不会.理由如下:
∴当t=5时,汽车停下,行驶了75 m.
∵75<80,∴该车在不变道的情况下不会撞到抛锚的车.
同课章节目录
