2025年中考数学核心素养命题100题 专题二 从几何直观的素养角度去思考命题(含答案)
文档属性
| 名称 | 2025年中考数学核心素养命题100题 专题二 从几何直观的素养角度去思考命题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 233.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-10 21:15:50 | ||
图片预览

文档简介
专题二 从几何直观的素养角度去思考命题
第13题 理解数轴的作用与意义的几何直观素养——数轴是数的直观模型
不等式 的解集在数轴上表示正确的是 ( )
第14题 能够解释代数表示的几何意义的几何直观素养——反比例函数k的几何意义
如图,点A 在反比例函数 图象的一支上,点B 在反比例函数 图象的一支上,点C,D在x轴上.若四边形ABCD是面积为9的正方形,则实数k的值为 ( )
A. 6 B. 3
变式9 如图,直线l∥x轴,并分别与双曲线 相交于点 A 和点B,C为x轴上的一个动点,若 则 的值是 ( )
A. 4 B. 8 C. - 4 D. - 8
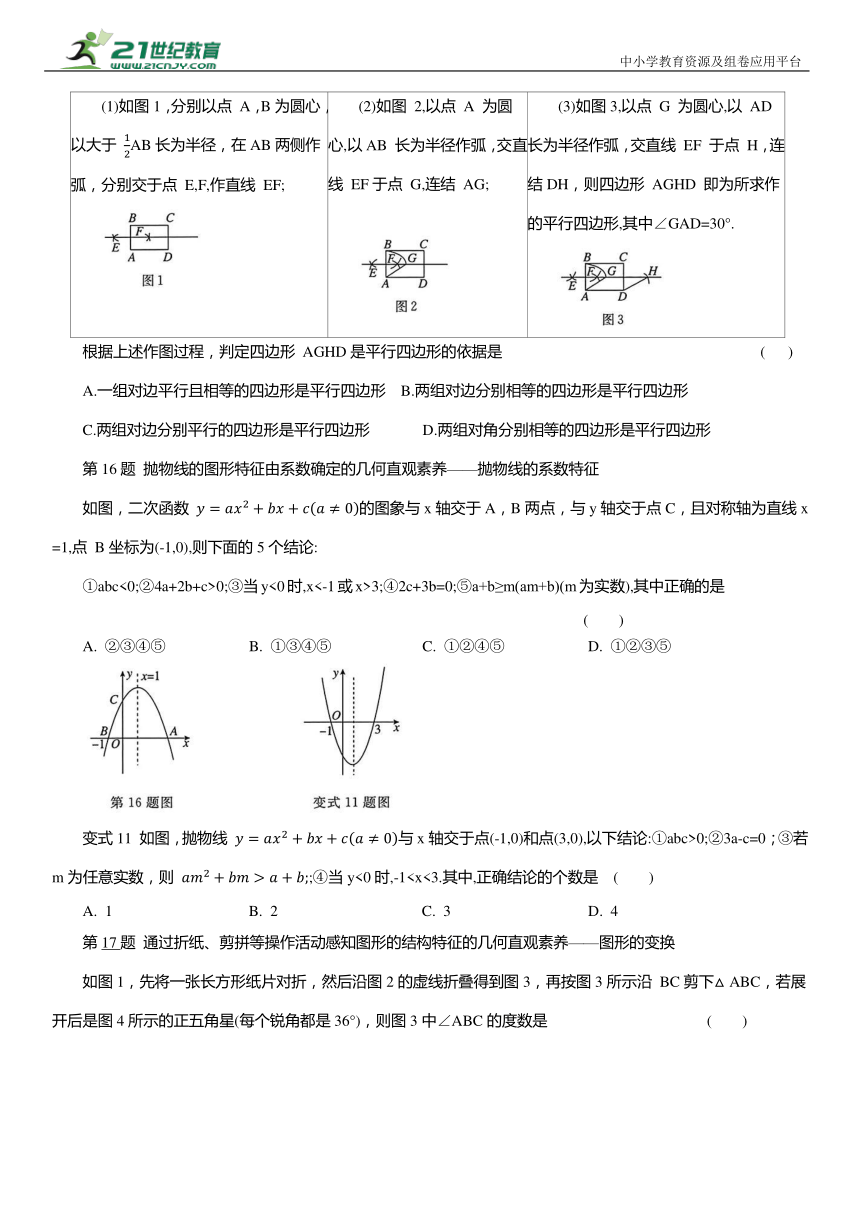
第15题 通过画图表示和解释图形的几何直观素养——平行四边形的判定
如图,以△ABC的顶点A 为圆心,以BC长为半径作弧;再以顶点C为圆心,以AB长为半径作弧,两弧交于点 D,则四边形ABCD是平行四边形的理由是 ( )
A.两组对边分别平行的四边形是平行四边形
B.两组对边分别相等的四边形是平行四边形
C.对角线互相平分的四边形是平行四边形
D.一组对边平行且相等的四边形是平行四边形
变式10 综合实践课上,嘉嘉设计了“利用已知矩形ABCD,用尺规作有一个内角为 角的平行四边形”.他的作法如下:
(1)如图1,分别以点 A,B为圆心,以大于 AB长为半径,在AB两侧作弧,分别交于点 E,F,作直线 EF; (2)如图 2,以点 A 为圆心,以AB 长为半径作弧,交直线 EF于点 G,连结 AG; (3)如图3,以点 G 为圆心,以 AD 长为半径作弧,交直线 EF 于点 H,连结DH,则四边形 AGHD 即为所求作的平行四边形,其中∠GAD=30°.
根据上述作图过程,判定四边形 AGHD是平行四边形的依据是 ( )
A.一组对边平行且相等的四边形是平行四边形 B.两组对边分别相等的四边形是平行四边形
C.两组对边分别平行的四边形是平行四边形 D.两组对角分别相等的四边形是平行四边形
第16题 抛物线的图形特征由系数确定的几何直观素养——抛物线的系数特征
如图,二次函数 的图象与x轴交于A,B两点,与y轴交于点C,且对称轴为直线x=1,点 B坐标为(-1,0),则下面的5个结论:
①abc<0;②4a+2b+c>0;③当y<0时,x<-1或x>3;④2c+3b=0;⑤a+b≥m(am+b)(m为实数),其中正确的是 ( )
A. ②③④⑤ B. ①③④⑤ C. ①②④⑤ D. ①②③⑤
变式11 如图,抛物线 与x轴交于点(-1,0)和点(3,0),以下结论:①abc>0;②3a-c=0;③若m为任意实数,则 ;④当y<0时,-1A. 1 B. 2 C. 3 D. 4
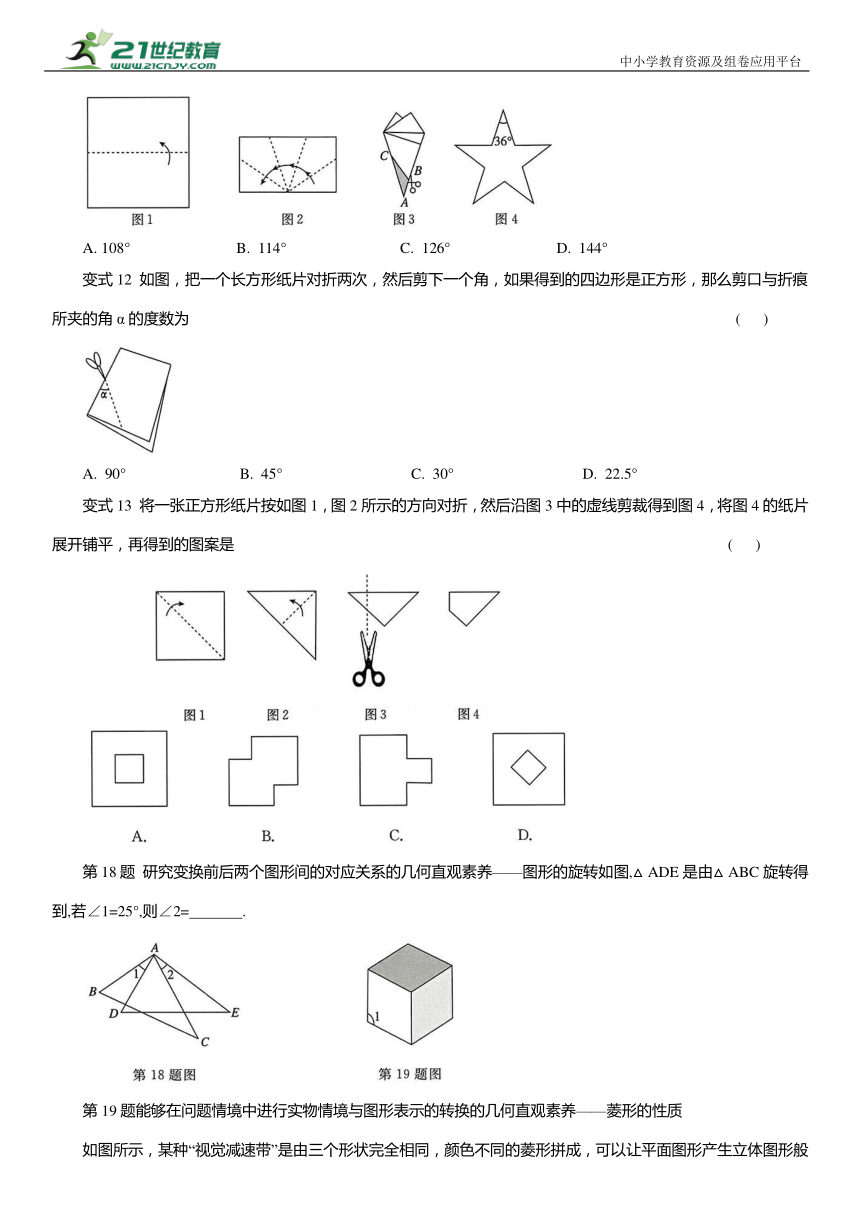
第17题 通过折纸、剪拼等操作活动感知图形的结构特征的几何直观素养——图形的变换
如图1,先将一张长方形纸片对折,然后沿图2的虚线折叠得到图3,再按图3所示沿 BC剪下△ABC,若展开后是图4所示的正五角星(每个锐角都是36°),则图3中∠ABC的度数是 ( )
108° B. 114° C. 126° D. 144°
变式12 如图,把一个长方形纸片对折两次,然后剪下一个角,如果得到的四边形是正方形,那么剪口与折痕所夹的角α的度数为 ( )
A. 90° B. 45° C. 30° D. 22.5°
变式13 将一张正方形纸片按如图1,图2所示的方向对折,然后沿图3中的虚线剪裁得到图4,将图4的纸片展开铺平,再得到的图案是 ( )
第18题 研究变换前后两个图形间的对应关系的几何直观素养——图形的旋转如图,△ADE是由△ABC旋转得到,若∠1=25°,则∠2= .
第19题能够在问题情境中进行实物情境与图形表示的转换的几何直观素养——菱形的性质
如图所示,某种“视觉减速带”是由三个形状完全相同,颜色不同的菱形拼成,可以让平面图形产生立体图形般的视觉效果.则∠1的度数为 .
第20题 通过折纸感知图形的结构特征的几何直观素养——轴对称
如图,将直角三角形纸片 折叠,使点C的对应点 与斜边AB 的中点O 重合,折痕为 EF.若 ,则折痕 EF 的长度为 .
变式14 如图,在 Rt△ABC中, ,D为斜边AB的中点,连结CD,CD=5,BC=6,将 沿CD翻折,使B落在点E 处,点 F 为直角边AC上一点,连结DF,将△ADF沿DF 翻折,使点A 与点E 重合,则AF= .
第21题 能够利用画图解释几何命题进行几何推理的几何直观素养——网格中的几何直观
下图是由边长为1的小正方形构成的7×7网格,每个小正方形的顶点叫做格点,△ABC的顶点在格点上,仅用无刻度直尺在网格中完成下列作图.(不写作法,保留痕迹)
(1)图1中,在 BC上画一点D,使∠BAD=45°.
(2)图2中,点P,M为格点,在AC上画一点E,使得PE+ME最小,并直接写出 的值.
变式15 如图,在 的正方形网格中,每个小正方形的顶点称为格点.点A,B,C,D都在格点上.请按要求画图.
(1)如图1,在线段AB上找一点 P,使 最小.
(2)如图2,在线段AB上找一点Q,使DQ⊥AB,画出线段DQ.
(3)在(2)的条件下,若CE⊥AB,则 DQ与CE的位置关系为 .(填“平行”“相交”或“垂直”)
第22题 能够利用图表工具分析问题情境中的数量关系的几何直观素养——分段函数
已知学校、书店、陈列馆依次在同一条直线上,书店离学校7.2km,陈列馆离学校12km.小明从学校出发,匀速骑行0.6h到达书店,在书店停留0.4h后,匀速骑行0.5h到达陈列馆,在陈列馆参观学习一段时间,然后回学校,回学校途中,匀速骑行0.5h后减速,继续匀速骑行回到学校.右图中x表示时间,y表示离学校的距离.图象反映了这个过程中小明离学校的距离与时间之间的对应关系.
请根据相关信息,回答下列问题:
(1)①填表:
小明离开学校的时间/h 0.3 0.6 0.8 5
小明离学校的距离/km 7.2
②填空:小明从陈列馆回学校途中,减速前的骑行速度为 km/h.
③填空:当小明离学校的距离为3 km时,他离开学校的时间为 h.
④当0≤x≤1.5时,请直接写出小明离学校的距离y关于时间x的函数解析式.
(2)当小明到达书店前0.1h时,同学小红从书店出发匀速直接前往陈列馆,如果小红步行的速度为
3.2km/h,那么她在前往陈列馆的途中遇到小明时离学校的距离是多少 (直接写出结果即可)
变式16 甲、乙两车分别从相距200km的A,B两地相向而行,乙车比甲车先出发 ,两车分别以各自的速度匀速行驶.甲从A地出发,行驶80km到达C地(A,B,C三地在同一直线上)时,因有事停留了 后,按原速度继续前往B地,乙车从B地经过4h直达A地的同时,甲车也到达了B地.甲、乙两车距A地的路程分别记为 它们与乙车行驶的时间x(h)的函数关系如图所示.
(1)分别求出甲、乙两车的速度及 y 关于x的函数表达式.
中小学教育资源及组卷应用平台
(2)试求乙车在出发多长时间后与甲车相遇.
13. A 14. C 变式9 D 15. B 变式10 A 16. D变式11 B 17. C 变式12 B 变式13 B 18.25°19.120° 20. 变式14
21.解:(1)如图,点 D 即为所作:理由如下:
AB=AE,∴∠BAE=90°.
∴AF⊥EF,∴F为BE 中点,AF平分∠BAE,
∴∠BAD=45°.
(2)如图,取格点F,连结PF交AC于E,此时点 E即为所作.理由:由图可知,四边形AMCF是正方形,
∴直线 AC是线段 MF 的垂直平分线,
∴EM=EF,
∴PE+EM=PE+EF,
∵P,E,F共线,PE+EF=PF,
∴此时 PE+EM最小.
以 M为原点,MC所在直线为x轴建立直角坐标系,则A(0,4),C(4,0),P(-1,2),F(4,4),设直线 AC的解析式为y= kx+b(k≠0),
则 解得
∴直线AC的解析式为y=-x+4,
同理可求,直线 PF 的解析式为
联立解得∴E( . ).
变式15 (1)图略 (2)图略 (3)平行
22.解:(1)①3.6,7.2,4. ②16 ③ 或
(2)9.6 km
变式16 解:(1)甲车速度为 乙车速度为200÷4=50(km/h).根据题意,y =200-50x.
(2)当甲车行驶80 km到达C地时, 此时乙车行驶的路程为
∵甲车有事停留了 h,
∴甲车停留时,乙车又行驶了
∵62.5+62.5+80>200,∴乙车在甲车停留时和甲车相遇.
,∴乙车在出发2.4h后与甲车相遇.
第13题 理解数轴的作用与意义的几何直观素养——数轴是数的直观模型
不等式 的解集在数轴上表示正确的是 ( )
第14题 能够解释代数表示的几何意义的几何直观素养——反比例函数k的几何意义
如图,点A 在反比例函数 图象的一支上,点B 在反比例函数 图象的一支上,点C,D在x轴上.若四边形ABCD是面积为9的正方形,则实数k的值为 ( )
A. 6 B. 3
变式9 如图,直线l∥x轴,并分别与双曲线 相交于点 A 和点B,C为x轴上的一个动点,若 则 的值是 ( )
A. 4 B. 8 C. - 4 D. - 8
第15题 通过画图表示和解释图形的几何直观素养——平行四边形的判定
如图,以△ABC的顶点A 为圆心,以BC长为半径作弧;再以顶点C为圆心,以AB长为半径作弧,两弧交于点 D,则四边形ABCD是平行四边形的理由是 ( )
A.两组对边分别平行的四边形是平行四边形
B.两组对边分别相等的四边形是平行四边形
C.对角线互相平分的四边形是平行四边形
D.一组对边平行且相等的四边形是平行四边形
变式10 综合实践课上,嘉嘉设计了“利用已知矩形ABCD,用尺规作有一个内角为 角的平行四边形”.他的作法如下:
(1)如图1,分别以点 A,B为圆心,以大于 AB长为半径,在AB两侧作弧,分别交于点 E,F,作直线 EF; (2)如图 2,以点 A 为圆心,以AB 长为半径作弧,交直线 EF于点 G,连结 AG; (3)如图3,以点 G 为圆心,以 AD 长为半径作弧,交直线 EF 于点 H,连结DH,则四边形 AGHD 即为所求作的平行四边形,其中∠GAD=30°.
根据上述作图过程,判定四边形 AGHD是平行四边形的依据是 ( )
A.一组对边平行且相等的四边形是平行四边形 B.两组对边分别相等的四边形是平行四边形
C.两组对边分别平行的四边形是平行四边形 D.两组对角分别相等的四边形是平行四边形
第16题 抛物线的图形特征由系数确定的几何直观素养——抛物线的系数特征
如图,二次函数 的图象与x轴交于A,B两点,与y轴交于点C,且对称轴为直线x=1,点 B坐标为(-1,0),则下面的5个结论:
①abc<0;②4a+2b+c>0;③当y<0时,x<-1或x>3;④2c+3b=0;⑤a+b≥m(am+b)(m为实数),其中正确的是 ( )
A. ②③④⑤ B. ①③④⑤ C. ①②④⑤ D. ①②③⑤
变式11 如图,抛物线 与x轴交于点(-1,0)和点(3,0),以下结论:①abc>0;②3a-c=0;③若m为任意实数,则 ;④当y<0时,-1
第17题 通过折纸、剪拼等操作活动感知图形的结构特征的几何直观素养——图形的变换
如图1,先将一张长方形纸片对折,然后沿图2的虚线折叠得到图3,再按图3所示沿 BC剪下△ABC,若展开后是图4所示的正五角星(每个锐角都是36°),则图3中∠ABC的度数是 ( )
108° B. 114° C. 126° D. 144°
变式12 如图,把一个长方形纸片对折两次,然后剪下一个角,如果得到的四边形是正方形,那么剪口与折痕所夹的角α的度数为 ( )
A. 90° B. 45° C. 30° D. 22.5°
变式13 将一张正方形纸片按如图1,图2所示的方向对折,然后沿图3中的虚线剪裁得到图4,将图4的纸片展开铺平,再得到的图案是 ( )
第18题 研究变换前后两个图形间的对应关系的几何直观素养——图形的旋转如图,△ADE是由△ABC旋转得到,若∠1=25°,则∠2= .
第19题能够在问题情境中进行实物情境与图形表示的转换的几何直观素养——菱形的性质
如图所示,某种“视觉减速带”是由三个形状完全相同,颜色不同的菱形拼成,可以让平面图形产生立体图形般的视觉效果.则∠1的度数为 .
第20题 通过折纸感知图形的结构特征的几何直观素养——轴对称
如图,将直角三角形纸片 折叠,使点C的对应点 与斜边AB 的中点O 重合,折痕为 EF.若 ,则折痕 EF 的长度为 .
变式14 如图,在 Rt△ABC中, ,D为斜边AB的中点,连结CD,CD=5,BC=6,将 沿CD翻折,使B落在点E 处,点 F 为直角边AC上一点,连结DF,将△ADF沿DF 翻折,使点A 与点E 重合,则AF= .
第21题 能够利用画图解释几何命题进行几何推理的几何直观素养——网格中的几何直观
下图是由边长为1的小正方形构成的7×7网格,每个小正方形的顶点叫做格点,△ABC的顶点在格点上,仅用无刻度直尺在网格中完成下列作图.(不写作法,保留痕迹)
(1)图1中,在 BC上画一点D,使∠BAD=45°.
(2)图2中,点P,M为格点,在AC上画一点E,使得PE+ME最小,并直接写出 的值.
变式15 如图,在 的正方形网格中,每个小正方形的顶点称为格点.点A,B,C,D都在格点上.请按要求画图.
(1)如图1,在线段AB上找一点 P,使 最小.
(2)如图2,在线段AB上找一点Q,使DQ⊥AB,画出线段DQ.
(3)在(2)的条件下,若CE⊥AB,则 DQ与CE的位置关系为 .(填“平行”“相交”或“垂直”)
第22题 能够利用图表工具分析问题情境中的数量关系的几何直观素养——分段函数
已知学校、书店、陈列馆依次在同一条直线上,书店离学校7.2km,陈列馆离学校12km.小明从学校出发,匀速骑行0.6h到达书店,在书店停留0.4h后,匀速骑行0.5h到达陈列馆,在陈列馆参观学习一段时间,然后回学校,回学校途中,匀速骑行0.5h后减速,继续匀速骑行回到学校.右图中x表示时间,y表示离学校的距离.图象反映了这个过程中小明离学校的距离与时间之间的对应关系.
请根据相关信息,回答下列问题:
(1)①填表:
小明离开学校的时间/h 0.3 0.6 0.8 5
小明离学校的距离/km 7.2
②填空:小明从陈列馆回学校途中,减速前的骑行速度为 km/h.
③填空:当小明离学校的距离为3 km时,他离开学校的时间为 h.
④当0≤x≤1.5时,请直接写出小明离学校的距离y关于时间x的函数解析式.
(2)当小明到达书店前0.1h时,同学小红从书店出发匀速直接前往陈列馆,如果小红步行的速度为
3.2km/h,那么她在前往陈列馆的途中遇到小明时离学校的距离是多少 (直接写出结果即可)
变式16 甲、乙两车分别从相距200km的A,B两地相向而行,乙车比甲车先出发 ,两车分别以各自的速度匀速行驶.甲从A地出发,行驶80km到达C地(A,B,C三地在同一直线上)时,因有事停留了 后,按原速度继续前往B地,乙车从B地经过4h直达A地的同时,甲车也到达了B地.甲、乙两车距A地的路程分别记为 它们与乙车行驶的时间x(h)的函数关系如图所示.
(1)分别求出甲、乙两车的速度及 y 关于x的函数表达式.
中小学教育资源及组卷应用平台
(2)试求乙车在出发多长时间后与甲车相遇.
13. A 14. C 变式9 D 15. B 变式10 A 16. D变式11 B 17. C 变式12 B 变式13 B 18.25°19.120° 20. 变式14
21.解:(1)如图,点 D 即为所作:理由如下:
AB=AE,∴∠BAE=90°.
∴AF⊥EF,∴F为BE 中点,AF平分∠BAE,
∴∠BAD=45°.
(2)如图,取格点F,连结PF交AC于E,此时点 E即为所作.理由:由图可知,四边形AMCF是正方形,
∴直线 AC是线段 MF 的垂直平分线,
∴EM=EF,
∴PE+EM=PE+EF,
∵P,E,F共线,PE+EF=PF,
∴此时 PE+EM最小.
以 M为原点,MC所在直线为x轴建立直角坐标系,则A(0,4),C(4,0),P(-1,2),F(4,4),设直线 AC的解析式为y= kx+b(k≠0),
则 解得
∴直线AC的解析式为y=-x+4,
同理可求,直线 PF 的解析式为
联立解得∴E( . ).
变式15 (1)图略 (2)图略 (3)平行
22.解:(1)①3.6,7.2,4. ②16 ③ 或
(2)9.6 km
变式16 解:(1)甲车速度为 乙车速度为200÷4=50(km/h).根据题意,y =200-50x.
(2)当甲车行驶80 km到达C地时, 此时乙车行驶的路程为
∵甲车有事停留了 h,
∴甲车停留时,乙车又行驶了
∵62.5+62.5+80>200,∴乙车在甲车停留时和甲车相遇.
,∴乙车在出发2.4h后与甲车相遇.
同课章节目录
