2025年中考数学核心素养命题100题 专题三 从空间观念的素养角度去思考命题(含答案)
文档属性
| 名称 | 2025年中考数学核心素养命题100题 专题三 从空间观念的素养角度去思考命题(含答案) | 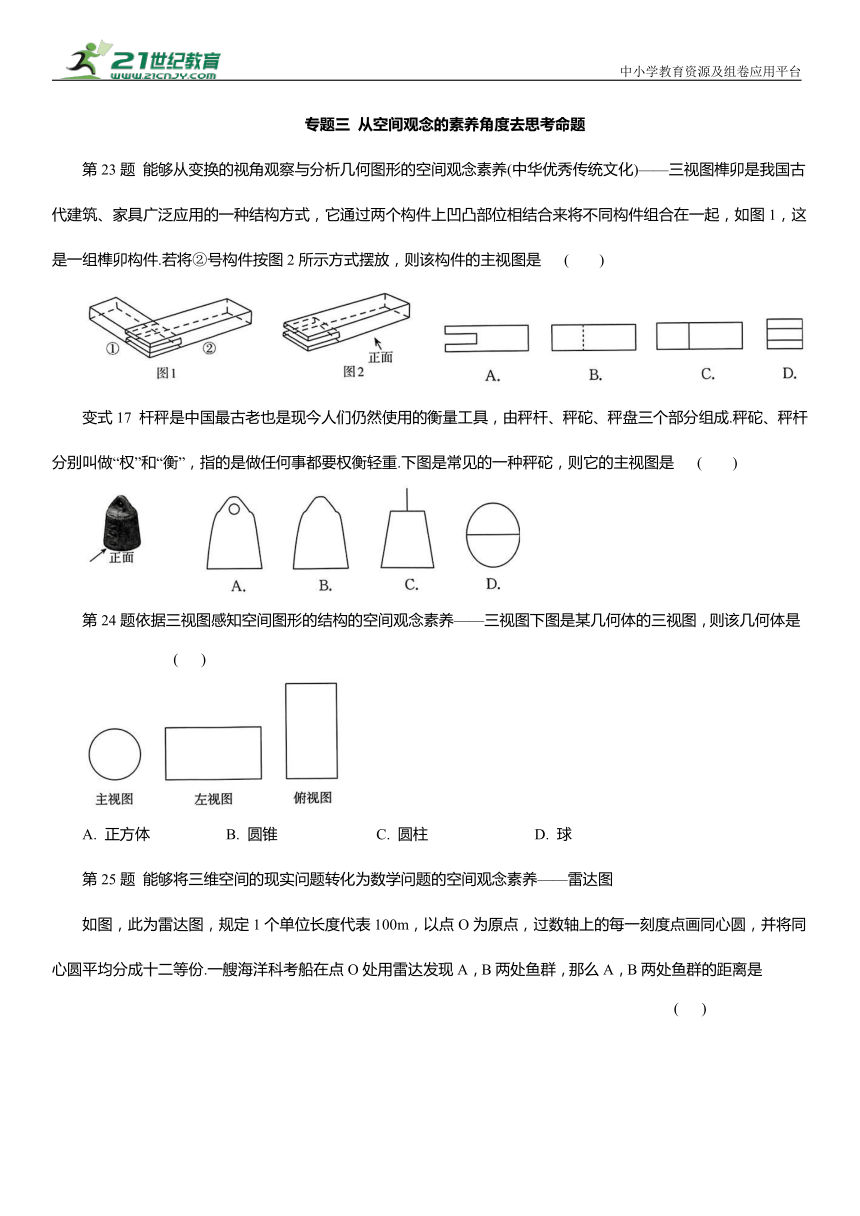 | |
| 格式 | docx | ||
| 文件大小 | 243.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-10 21:15:25 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
专题三 从空间观念的素养角度去思考命题
第23题 能够从变换的视角观察与分析几何图形的空间观念素养(中华优秀传统文化)——三视图榫卯是我国古代建筑、家具广泛应用的一种结构方式,它通过两个构件上凹凸部位相结合来将不同构件组合在一起,如图1,这是一组榫卯构件.若将②号构件按图2所示方式摆放,则该构件的主视图是 ( )
变式17 杆秤是中国最古老也是现今人们仍然使用的衡量工具,由秤杆、秤砣、秤盘三个部分组成.秤砣、秤杆分别叫做“权”和“衡”,指的是做任何事都要权衡轻重.下图是常见的一种秤砣,则它的主视图是 ( )
第24题依据三视图感知空间图形的结构的空间观念素养——三视图下图是某几何体的三视图,则该几何体是 ( )
A. 正方体 B. 圆锥 C. 圆柱 D. 球
第25题 能够将三维空间的现实问题转化为数学问题的空间观念素养——雷达图
如图,此为雷达图,规定1个单位长度代表100m,以点O为原点,过数轴上的每一刻度点画同心圆,并将同心圆平均分成十二等份.一艘海洋科考船在点O处用雷达发现A,B两处鱼群,那么A,B两处鱼群的距离是 ( )
A. 5m B. 400m C. 500 m D. 300 m
变式18 以水平数轴的原点为圆心,过正半轴 Ox上的每一刻度点画同心圆,将 Ox轴绕点O逆时针依次旋转 后得到如图所示的“圆”坐标系,其中点 B,C,D的坐标分别为( 5, 则点 A 的坐标为 ( )
第26题 利用长度和角度研究物体的位置关系的空间观念素养——方位角
如图,一航班沿北偏东60°方向从A地飞往C地,到达C地上空时,由于天气情况不适合着陆,准备备降B地,已知C地在B 地的北偏西45°方向,则其改变航向时∠α的度数为 ( )
A. 60° B. 75° C. 80°
变式19 如图,嘉淇一家驾车从A 地出发,沿着北偏东60°的方向行驶,到达 B地后沿着南偏东 的方向行驶来到C地,且C地恰好位于A 地正东方向上,则下列说法正确的是 ( )
B. A 地在B 地的南偏西 30°方向上
C. B 地在C 地的北偏西40°方向上
第27题 能够对几何图形进行多元表征并生成新的图形的空间观念素养——函数图象
图1是变量y与变量x的函数关系的图象,图2是变量z与变量y的函数关系的图象,则z与x的函数关系的图象可能是 ( )
变式20 变量y与x、变量z与y之间的函数关系分别如图1,图2所示,则表示变量z与x之间的函数关系的图象可能是 ( )
第28题 能够利用角度研究两条直线的位置关系的空间观念素养——平行线的性质
如图,平行于主光轴MN的光线AB和CD经过凹透镜的折射后,折射光线 BE,DF的反向延长线交于主光轴MN 上一点 P.若 ,则∠EPF 的度数是 .
第29题 通过空间物体结构得到几何图形的空间观念素养——抛物线形结构
窗格是中国传统建筑装饰的重要构成因素,是中国传统建筑文化的重要组成部分.下图是由大小相等的圆弧型“青瓦”组成的一个窗格图案的部分截面示意图,将其放置在平面直角坐标系中,点A,B,C均为弧的端点,若点 A 的坐标为 ,点B的坐标为(-3,0),则点 C的坐标为 .
第30题 能够从变换的视角观察与分析几何图形的空间观念素养——等腰三角形的性质
有一副直角三角板ABC,DEF,其中. 如图,将三角板 DEF 的顶点E 放在AB上,移动三角板DEF,当点 E从点A 沿AB 向点B 移动的过程中,点 E,C,D始终保持在一条直线上.若直线 DF 与直线AB 交于点M,当△MEF 为等腰三角形时,∠ACE的度数为 .
第31题 根据描述画出相应的平面图形的空间观念素养——网格作图
图1、图2、图3均是5×5的正方形网格,每个小正方形的顶点叫做格点, 的顶点均在格点上.在给定的网格中,只用无刻度的直尺,在图1、图2、图3中,按下列要求画图,只保留作图痕迹,不要求写出画法.
(1)在图1中画 的中线CD.
(2)在图2中 BC边上找一点E,连结AE,使AE平分. 的面积.
(3)在图3中 的内部找一点F,使
变式21 已知在: 的正方形网格中,每一个小正方形的边长为1个单位长度.
(1)如图1,点A,B都在格点上,在图中画出以AB为斜边的等腰直角三角形ABC,并且点C在格点上.
(2)如图2,点D,E,G都在格点上,点F 在小正方形的边上, 求线段GF的长.
第32题 能够利用角度和长度研究现实问题的空间观念素养———测高如图,某数学兴趣小组为了测量古树DE的高度,采用了如下的方法:先从与古树底端 D在同一水平线上的点A 出发,沿斜面坡度为 的斜坡AB前进 米到达点 B,再沿水平方向继续前进一段距离后到达点 C.在点 C处测得古树DE 的顶端E 的俯角为 底部 D的俯角为 求古树 DE 的高度.(计算结果精确到1米,参考数据: )
变式22 如图,某学习小组在学习了解直角三角形及其应用的知识后,尝试利用所学知识测量河对岸大树AB的高度,他在点C处测得大树顶端A的仰角为 ,再从点C出发沿斜坡走 米到达斜坡上的点 D,在点 D处测得树顶端 A 的仰角为 ,若斜坡CF 的坡比为 (点E,C,B在同一水平线上)
(1)求从点 C到点 D 的过程中上升的高度.
(2)求大树 AB的高度.(结果保留根号)
23. A 变式17 A 24. C 25. C 变式18 B 26. B
变式19 A 27. C 变式20 A 28.70° 29.(1,-2
30.15°或82.5° 【解析】根据题意可知∠F=45°,∠DEF=90°,
①当EM=FM时,如图,
②当EF=FM时,如图,
∴∠MEF+∠M=45°,
∴∠MEF=22.5°,
112.5°.
∵∠A+∠ACE=∠DEM,
综上所述,∠ACE的度数为 15°或82.5°.
31.(1)略(2)略 (3)略
变式21 解:(1)如图1,∴△ABC即为所求作.
(2)如图2,连结EG,由(1)得,△DEG是等腰直角三角形,
在 Rt△FEG中,
32.11米 变式 22 (1)3米 米
专题三 从空间观念的素养角度去思考命题
第23题 能够从变换的视角观察与分析几何图形的空间观念素养(中华优秀传统文化)——三视图榫卯是我国古代建筑、家具广泛应用的一种结构方式,它通过两个构件上凹凸部位相结合来将不同构件组合在一起,如图1,这是一组榫卯构件.若将②号构件按图2所示方式摆放,则该构件的主视图是 ( )
变式17 杆秤是中国最古老也是现今人们仍然使用的衡量工具,由秤杆、秤砣、秤盘三个部分组成.秤砣、秤杆分别叫做“权”和“衡”,指的是做任何事都要权衡轻重.下图是常见的一种秤砣,则它的主视图是 ( )
第24题依据三视图感知空间图形的结构的空间观念素养——三视图下图是某几何体的三视图,则该几何体是 ( )
A. 正方体 B. 圆锥 C. 圆柱 D. 球
第25题 能够将三维空间的现实问题转化为数学问题的空间观念素养——雷达图
如图,此为雷达图,规定1个单位长度代表100m,以点O为原点,过数轴上的每一刻度点画同心圆,并将同心圆平均分成十二等份.一艘海洋科考船在点O处用雷达发现A,B两处鱼群,那么A,B两处鱼群的距离是 ( )
A. 5m B. 400m C. 500 m D. 300 m
变式18 以水平数轴的原点为圆心,过正半轴 Ox上的每一刻度点画同心圆,将 Ox轴绕点O逆时针依次旋转 后得到如图所示的“圆”坐标系,其中点 B,C,D的坐标分别为( 5, 则点 A 的坐标为 ( )
第26题 利用长度和角度研究物体的位置关系的空间观念素养——方位角
如图,一航班沿北偏东60°方向从A地飞往C地,到达C地上空时,由于天气情况不适合着陆,准备备降B地,已知C地在B 地的北偏西45°方向,则其改变航向时∠α的度数为 ( )
A. 60° B. 75° C. 80°
变式19 如图,嘉淇一家驾车从A 地出发,沿着北偏东60°的方向行驶,到达 B地后沿着南偏东 的方向行驶来到C地,且C地恰好位于A 地正东方向上,则下列说法正确的是 ( )
B. A 地在B 地的南偏西 30°方向上
C. B 地在C 地的北偏西40°方向上
第27题 能够对几何图形进行多元表征并生成新的图形的空间观念素养——函数图象
图1是变量y与变量x的函数关系的图象,图2是变量z与变量y的函数关系的图象,则z与x的函数关系的图象可能是 ( )
变式20 变量y与x、变量z与y之间的函数关系分别如图1,图2所示,则表示变量z与x之间的函数关系的图象可能是 ( )
第28题 能够利用角度研究两条直线的位置关系的空间观念素养——平行线的性质
如图,平行于主光轴MN的光线AB和CD经过凹透镜的折射后,折射光线 BE,DF的反向延长线交于主光轴MN 上一点 P.若 ,则∠EPF 的度数是 .
第29题 通过空间物体结构得到几何图形的空间观念素养——抛物线形结构
窗格是中国传统建筑装饰的重要构成因素,是中国传统建筑文化的重要组成部分.下图是由大小相等的圆弧型“青瓦”组成的一个窗格图案的部分截面示意图,将其放置在平面直角坐标系中,点A,B,C均为弧的端点,若点 A 的坐标为 ,点B的坐标为(-3,0),则点 C的坐标为 .
第30题 能够从变换的视角观察与分析几何图形的空间观念素养——等腰三角形的性质
有一副直角三角板ABC,DEF,其中. 如图,将三角板 DEF 的顶点E 放在AB上,移动三角板DEF,当点 E从点A 沿AB 向点B 移动的过程中,点 E,C,D始终保持在一条直线上.若直线 DF 与直线AB 交于点M,当△MEF 为等腰三角形时,∠ACE的度数为 .
第31题 根据描述画出相应的平面图形的空间观念素养——网格作图
图1、图2、图3均是5×5的正方形网格,每个小正方形的顶点叫做格点, 的顶点均在格点上.在给定的网格中,只用无刻度的直尺,在图1、图2、图3中,按下列要求画图,只保留作图痕迹,不要求写出画法.
(1)在图1中画 的中线CD.
(2)在图2中 BC边上找一点E,连结AE,使AE平分. 的面积.
(3)在图3中 的内部找一点F,使
变式21 已知在: 的正方形网格中,每一个小正方形的边长为1个单位长度.
(1)如图1,点A,B都在格点上,在图中画出以AB为斜边的等腰直角三角形ABC,并且点C在格点上.
(2)如图2,点D,E,G都在格点上,点F 在小正方形的边上, 求线段GF的长.
第32题 能够利用角度和长度研究现实问题的空间观念素养———测高如图,某数学兴趣小组为了测量古树DE的高度,采用了如下的方法:先从与古树底端 D在同一水平线上的点A 出发,沿斜面坡度为 的斜坡AB前进 米到达点 B,再沿水平方向继续前进一段距离后到达点 C.在点 C处测得古树DE 的顶端E 的俯角为 底部 D的俯角为 求古树 DE 的高度.(计算结果精确到1米,参考数据: )
变式22 如图,某学习小组在学习了解直角三角形及其应用的知识后,尝试利用所学知识测量河对岸大树AB的高度,他在点C处测得大树顶端A的仰角为 ,再从点C出发沿斜坡走 米到达斜坡上的点 D,在点 D处测得树顶端 A 的仰角为 ,若斜坡CF 的坡比为 (点E,C,B在同一水平线上)
(1)求从点 C到点 D 的过程中上升的高度.
(2)求大树 AB的高度.(结果保留根号)
23. A 变式17 A 24. C 25. C 变式18 B 26. B
变式19 A 27. C 变式20 A 28.70° 29.(1,-2
30.15°或82.5° 【解析】根据题意可知∠F=45°,∠DEF=90°,
①当EM=FM时,如图,
②当EF=FM时,如图,
∴∠MEF+∠M=45°,
∴∠MEF=22.5°,
112.5°.
∵∠A+∠ACE=∠DEM,
综上所述,∠ACE的度数为 15°或82.5°.
31.(1)略(2)略 (3)略
变式21 解:(1)如图1,∴△ABC即为所求作.
(2)如图2,连结EG,由(1)得,△DEG是等腰直角三角形,
在 Rt△FEG中,
32.11米 变式 22 (1)3米 米
同课章节目录
