2025年中考数学“17—22题”解答小卷(九)(含答案)
文档属性
| 名称 | 2025年中考数学“17—22题”解答小卷(九)(含答案) | 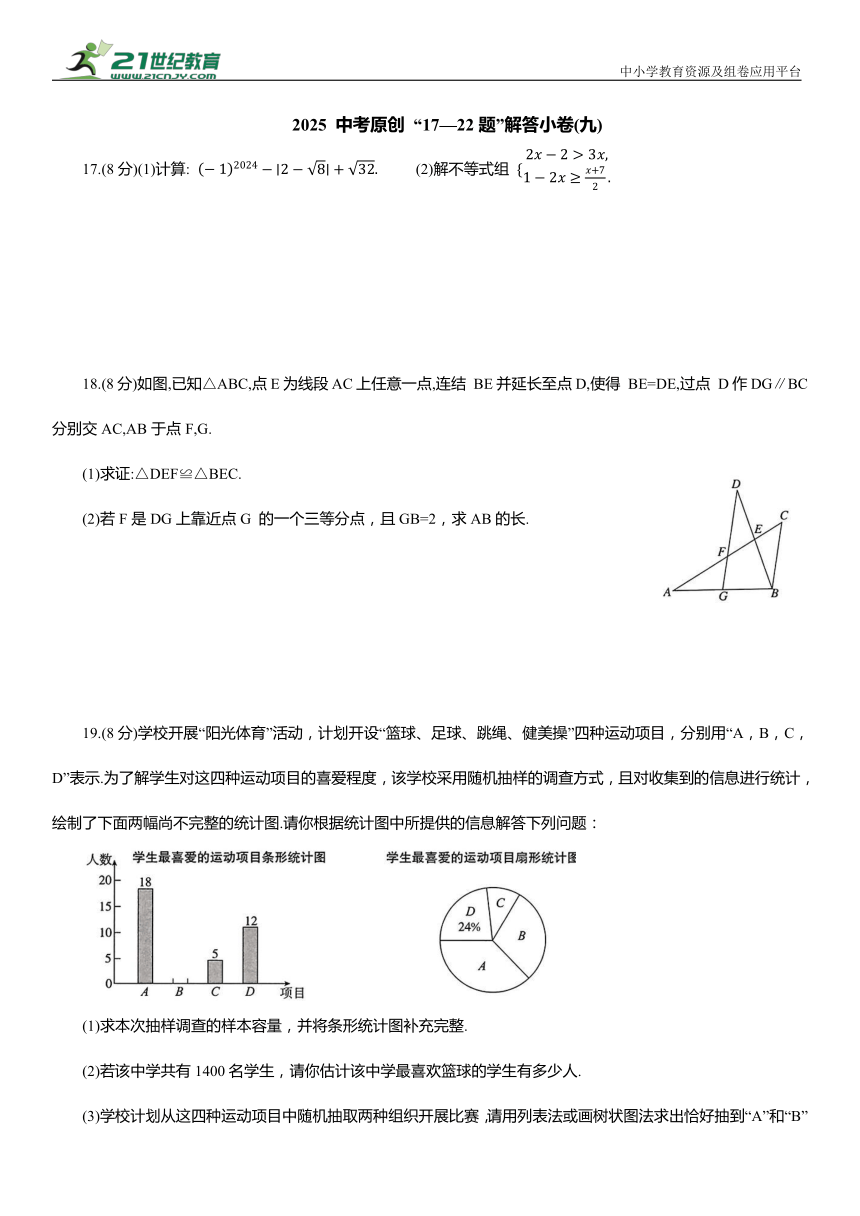 | |
| 格式 | docx | ||
| 文件大小 | 188.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-10 21:22:20 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
2025 中考原创 “17—22题”解答小卷(九)
17.(8分)(1)计算: (2)解不等式组
18.(8分)如图,已知△ABC,点E为线段AC上任意一点,连结 BE并延长至点D,使得 BE=DE,过点 D作DG∥BC分别交AC,AB于点F,G.
(1)求证:△DEF≌△BEC.
(2)若F是DG上靠近点G 的一个三等分点,且GB=2,求AB的长.
19.(8分)学校开展“阳光体育”活动,计划开设“篮球、足球、跳绳、健美操”四种运动项目,分别用“A,B,C,D”表示.为了解学生对这四种运动项目的喜爱程度,该学校采用随机抽样的调查方式,且对收集到的信息进行统计,绘制了下面两幅尚不完整的统计图.请你根据统计图中所提供的信息解答下列问题:
(1)求本次抽样调查的样本容量,并将条形统计图补充完整.
(2)若该中学共有1400名学生,请你估计该中学最喜欢篮球的学生有多少人.
(3)学校计划从这四种运动项目中随机抽取两种组织开展比赛,请用列表法或画树状图法求出恰好抽到“A”和“B”这两种运动项目的概率.
20.(8分)图1是一台笔记本电脑实物图,如图2,当笔记本电脑的张角∠AEB=135°时,顶部边缘A 处离桌面的高度AC的长为15 cm,当合起笔记本时,若笔记本电脑的张角∠FEB=30°(A的对应点是点F,AE=EF).
(1)求顶部边缘 F 处离桌面的高度FD 的长为多少厘米.(结果保留根号)
(2)求两次边缘顶部A 与F 之间的距离约为多少厘米.
(参考数据: 结果精确到1 cm),
21.(8分)某商场购进两种不同类型的护眼灯,若用6 240元和8400元购进A 型和B 型护眼灯的数量相同,其中每台A 型护眼灯比B 型护眼灯便宜27元.
(1)求该商场购进每台A 型和B 型护眼灯的价格.
(2)该商场经过调查发现,A型护眼灯售价为98元时,可以卖出100台.每涨价1元,则每天少售出2台.求每台 A 型护眼灯涨价多少元时销售利润最大.
22.(10分)如图,已知△ABC为等腰三角形,AB=AC,BC=16,作腰AC的垂直平分线DE 交AC 于点E,截取AD=10.
(1)如图1,若∠DAC=∠B,求AC的长.
(2)如图2,若∠ADC=2∠B,求 sin B的值.
17.(1)原式: (2)x<-2
18.(1)证明略 (2)AB 的长是4
19.解:(1)本次抽样调查的样本容量为12÷24%=50.
B项目的人数为50-18-5-12=15,补全的条形统计图略
(2)该中学最喜欢篮球的学生约有504人 (3)
21.(1)A型护眼灯每台的价格是78元,B型护眼灯每台的价格是105元 (2)每台 A型护眼灯涨价15元时销售利润最大
22.(1)AC=4 或
2025 中考原创 “17—22题”解答小卷(九)
17.(8分)(1)计算: (2)解不等式组
18.(8分)如图,已知△ABC,点E为线段AC上任意一点,连结 BE并延长至点D,使得 BE=DE,过点 D作DG∥BC分别交AC,AB于点F,G.
(1)求证:△DEF≌△BEC.
(2)若F是DG上靠近点G 的一个三等分点,且GB=2,求AB的长.
19.(8分)学校开展“阳光体育”活动,计划开设“篮球、足球、跳绳、健美操”四种运动项目,分别用“A,B,C,D”表示.为了解学生对这四种运动项目的喜爱程度,该学校采用随机抽样的调查方式,且对收集到的信息进行统计,绘制了下面两幅尚不完整的统计图.请你根据统计图中所提供的信息解答下列问题:
(1)求本次抽样调查的样本容量,并将条形统计图补充完整.
(2)若该中学共有1400名学生,请你估计该中学最喜欢篮球的学生有多少人.
(3)学校计划从这四种运动项目中随机抽取两种组织开展比赛,请用列表法或画树状图法求出恰好抽到“A”和“B”这两种运动项目的概率.
20.(8分)图1是一台笔记本电脑实物图,如图2,当笔记本电脑的张角∠AEB=135°时,顶部边缘A 处离桌面的高度AC的长为15 cm,当合起笔记本时,若笔记本电脑的张角∠FEB=30°(A的对应点是点F,AE=EF).
(1)求顶部边缘 F 处离桌面的高度FD 的长为多少厘米.(结果保留根号)
(2)求两次边缘顶部A 与F 之间的距离约为多少厘米.
(参考数据: 结果精确到1 cm),
21.(8分)某商场购进两种不同类型的护眼灯,若用6 240元和8400元购进A 型和B 型护眼灯的数量相同,其中每台A 型护眼灯比B 型护眼灯便宜27元.
(1)求该商场购进每台A 型和B 型护眼灯的价格.
(2)该商场经过调查发现,A型护眼灯售价为98元时,可以卖出100台.每涨价1元,则每天少售出2台.求每台 A 型护眼灯涨价多少元时销售利润最大.
22.(10分)如图,已知△ABC为等腰三角形,AB=AC,BC=16,作腰AC的垂直平分线DE 交AC 于点E,截取AD=10.
(1)如图1,若∠DAC=∠B,求AC的长.
(2)如图2,若∠ADC=2∠B,求 sin B的值.
17.(1)原式: (2)x<-2
18.(1)证明略 (2)AB 的长是4
19.解:(1)本次抽样调查的样本容量为12÷24%=50.
B项目的人数为50-18-5-12=15,补全的条形统计图略
(2)该中学最喜欢篮球的学生约有504人 (3)
21.(1)A型护眼灯每台的价格是78元,B型护眼灯每台的价格是105元 (2)每台 A型护眼灯涨价15元时销售利润最大
22.(1)AC=4 或
同课章节目录
