第23 讲 多边形与平行四边形 (含答案) 2025年中考数学知识点过关训练
文档属性
| 名称 | 第23 讲 多边形与平行四边形 (含答案) 2025年中考数学知识点过关训练 | 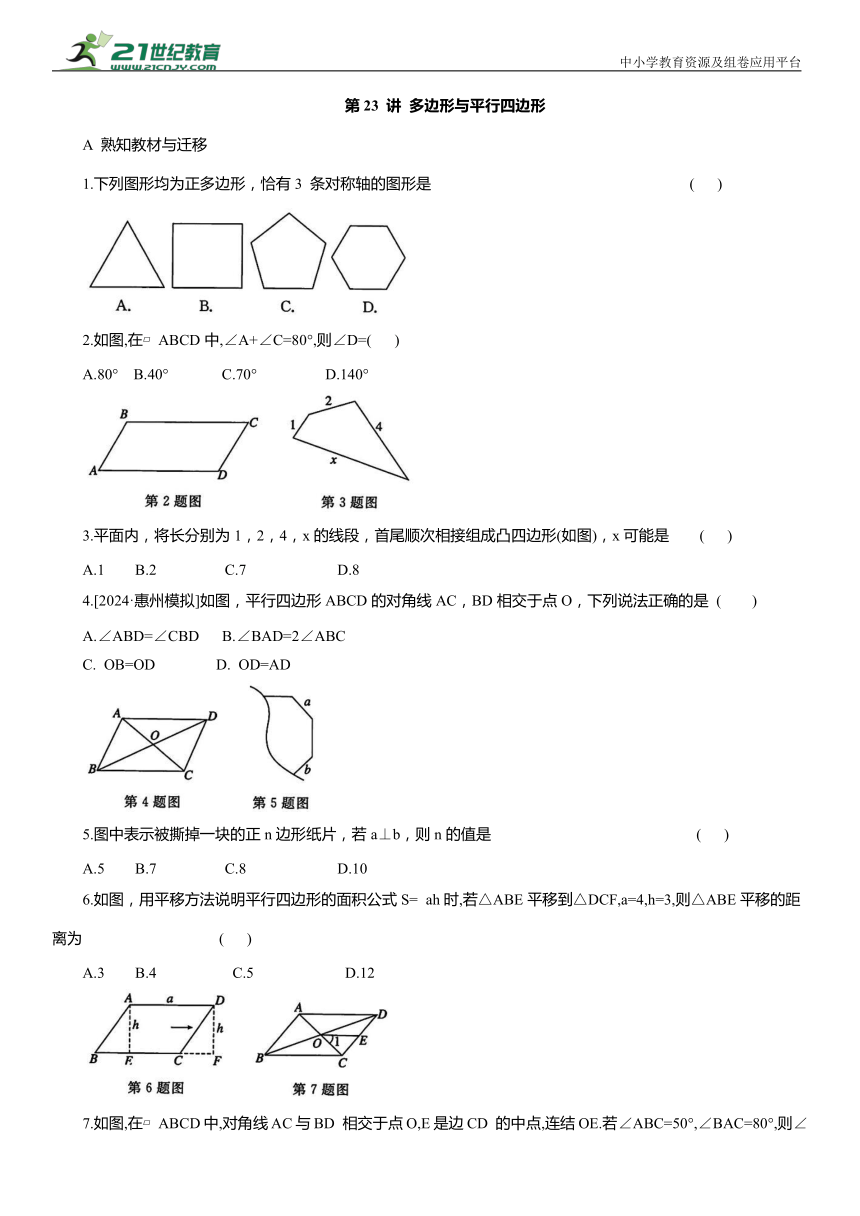 | |
| 格式 | docx | ||
| 文件大小 | 257.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-10 21:19:45 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第23 讲 多边形与平行四边形
A 熟知教材与迁移
1.下列图形均为正多边形,恰有3 条对称轴的图形是 ( )
2.如图,在 ABCD中,∠A+∠C=80°,则∠D=( )
A.80° B.40° C.70° D.140°
3.平面内,将长分别为1,2,4,x的线段,首尾顺次相接组成凸四边形(如图),x可能是 ( )
A.1 B.2 C.7 D.8
4.[2024·惠州模拟]如图,平行四边形ABCD的对角线AC,BD相交于点O,下列说法正确的是 ( )
A.∠ABD=∠CBD B.∠BAD=2∠ABC
C. OB=OD D. OD=AD
5.图中表示被撕掉一块的正n边形纸片,若a⊥b,则n的值是 ( )
A.5 B.7 C.8 D.10
6.如图,用平移方法说明平行四边形的面积公式S= ah时,若△ABE平移到△DCF,a=4,h=3,则△ABE平移的距离为 ( )
A.3 B.4 C.5 D.12
7.如图,在 ABCD中,对角线AC与BD 相交于点O,E是边CD 的中点,连结OE.若∠ABC=50°,∠BAC=80°,则∠1 的度数为 .
8.如图 1,在平行四边形 ABCD 中,AD>AB,∠ABC为锐角.要在对角线 BD上找点N,M,使四边形 ANCM为平行四边形,现有图2中的甲、乙两种方案,则正确的方案是 .
9.[2024·广东]如果一个多边形的每一个外角都是 40°,那么这个多边形的边数为 .
10.[2024·武汉] 如图,在 ABCD中,点 E,F 分别在边BC,AD上,AF=CE.
(1)求证:△ABE≌△CDF.
(2)连结 EF.请添加一个与线段相关的条件,使四边形 ABEF 是平行四边形.(不需要说明理由)
B掌握通性与通法
11.[2024·邯郸模拟]阅读下面的材料:
定理:三角形的中位线平行于第三边,并且等于第三边的一半.
已知:如图1,在△ABC中,D,E分别是边AB,AC的中点.
求证:DE∥BC,且
证明:延长DE到点F,使 EF=DE,连结CF,甲、乙两人后续证明的部分思路如下:
甲:如图2,先证明△ADE≌△CFE,再推理得出四边形 DBCF 是平行四边形.
乙:如图3,连结 DC,AF.先后证明四边形 AD-CF,DBCF 分别是平行四边形.
下列判断正确的是 ( )
A.甲思路正确,乙思路错误
B.甲思路错误,乙思路正确
C.甲、乙两人思路都正确
D.甲、乙两人思路都错误
12.如图,□ABCD的对角线AC,BD相交于点O,∠ADC的平分线与边AB 相交于点P,E是PD的中点,若AD=4,CD=6,则 EO的长为( )
A.1 B.2 C.3 D.4
13.如图,在正六边形ABCDEF中,M,N是对角线BE 上的两点.添加下列条件中的一个:①BM=EN; ② ∠FAN = ∠CDM; ③ AM = DN;④∠AMB=∠DNE.能使四边形 AMDN 是平行四边形的是 .(填上所有符合条件的序号)
14.[2024·北京] 如图,在四边形ABCD中,E 是AB 的中点,DB,CE 交于点 F,DF=FB,AF∥DC.
(1)求证:四边形AFCD为平行四边形.
(2)若∠EFB=90°,tan∠FEB=3,EF=1,求BC的长.
15.如图,在 ABCD中,E是AD 的中点,连结CE并延长交BA 的延长线于点 F.
(1)求证:AF=AB.
(2) G 是 线段 AF 上一点, 满足∠FCG =∠FCD,CG交AD 于点H,若AG=2,FG=6,求GH 的长.
C感悟思维与素养
16.[2024·成都]如图,在平行四边形ABCD中,AB=2,AD=4,E,F分别是边CD,AD上的动点,且CE=DF.当AE+CF的值最小时,CE=
1. A 2. D 3. B 4. C 5. C 6. B 7.50° 8.甲、乙 9.9
10.解:(1)证明:∵四边形 ABCD是平行四边形,
∴AB=CD,AD=BC,∠B=∠D.∵AF=CE,
∴AD-AF=BC-CE,∴DF=BE.在△ABE与△CDF中,
∵∠B=∠2D,∴△ABE≌△CDF(SAS).
(2)添加 BE=CE,理由如下:∵AF=CE,BE=CE,
∴AF=BE.∵四边形ABCD是平行四边形,∴AD∥BC,
∴四边形 ABEF 是平行四边形.
11. C 12. A 13.①②④ 14.(1)证明略
15.解:(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,CD∥AB,∴∠D=∠FAD,∠DCE=∠F.
∵E是AD的中点,∴DE=AE,
∴△CDE≌△FAE(AAS),∴CE=EF.
∵ B.
(2)∵AG=2,FG=6,
∴AF=FG+AG=6+2=8,∴AB=AF=8.
∵四边形ABCD是平行四边形,∴CD=AB=8.
∵∠DCE=∠F,∠FCG=∠FCD,∴∠F=∠FCG,
∴CG=FG=6.∵CD∥AF,∴△DCH∽△AGH,
即 ,∴GH=1.2.
16.
第23 讲 多边形与平行四边形
A 熟知教材与迁移
1.下列图形均为正多边形,恰有3 条对称轴的图形是 ( )
2.如图,在 ABCD中,∠A+∠C=80°,则∠D=( )
A.80° B.40° C.70° D.140°
3.平面内,将长分别为1,2,4,x的线段,首尾顺次相接组成凸四边形(如图),x可能是 ( )
A.1 B.2 C.7 D.8
4.[2024·惠州模拟]如图,平行四边形ABCD的对角线AC,BD相交于点O,下列说法正确的是 ( )
A.∠ABD=∠CBD B.∠BAD=2∠ABC
C. OB=OD D. OD=AD
5.图中表示被撕掉一块的正n边形纸片,若a⊥b,则n的值是 ( )
A.5 B.7 C.8 D.10
6.如图,用平移方法说明平行四边形的面积公式S= ah时,若△ABE平移到△DCF,a=4,h=3,则△ABE平移的距离为 ( )
A.3 B.4 C.5 D.12
7.如图,在 ABCD中,对角线AC与BD 相交于点O,E是边CD 的中点,连结OE.若∠ABC=50°,∠BAC=80°,则∠1 的度数为 .
8.如图 1,在平行四边形 ABCD 中,AD>AB,∠ABC为锐角.要在对角线 BD上找点N,M,使四边形 ANCM为平行四边形,现有图2中的甲、乙两种方案,则正确的方案是 .
9.[2024·广东]如果一个多边形的每一个外角都是 40°,那么这个多边形的边数为 .
10.[2024·武汉] 如图,在 ABCD中,点 E,F 分别在边BC,AD上,AF=CE.
(1)求证:△ABE≌△CDF.
(2)连结 EF.请添加一个与线段相关的条件,使四边形 ABEF 是平行四边形.(不需要说明理由)
B掌握通性与通法
11.[2024·邯郸模拟]阅读下面的材料:
定理:三角形的中位线平行于第三边,并且等于第三边的一半.
已知:如图1,在△ABC中,D,E分别是边AB,AC的中点.
求证:DE∥BC,且
证明:延长DE到点F,使 EF=DE,连结CF,甲、乙两人后续证明的部分思路如下:
甲:如图2,先证明△ADE≌△CFE,再推理得出四边形 DBCF 是平行四边形.
乙:如图3,连结 DC,AF.先后证明四边形 AD-CF,DBCF 分别是平行四边形.
下列判断正确的是 ( )
A.甲思路正确,乙思路错误
B.甲思路错误,乙思路正确
C.甲、乙两人思路都正确
D.甲、乙两人思路都错误
12.如图,□ABCD的对角线AC,BD相交于点O,∠ADC的平分线与边AB 相交于点P,E是PD的中点,若AD=4,CD=6,则 EO的长为( )
A.1 B.2 C.3 D.4
13.如图,在正六边形ABCDEF中,M,N是对角线BE 上的两点.添加下列条件中的一个:①BM=EN; ② ∠FAN = ∠CDM; ③ AM = DN;④∠AMB=∠DNE.能使四边形 AMDN 是平行四边形的是 .(填上所有符合条件的序号)
14.[2024·北京] 如图,在四边形ABCD中,E 是AB 的中点,DB,CE 交于点 F,DF=FB,AF∥DC.
(1)求证:四边形AFCD为平行四边形.
(2)若∠EFB=90°,tan∠FEB=3,EF=1,求BC的长.
15.如图,在 ABCD中,E是AD 的中点,连结CE并延长交BA 的延长线于点 F.
(1)求证:AF=AB.
(2) G 是 线段 AF 上一点, 满足∠FCG =∠FCD,CG交AD 于点H,若AG=2,FG=6,求GH 的长.
C感悟思维与素养
16.[2024·成都]如图,在平行四边形ABCD中,AB=2,AD=4,E,F分别是边CD,AD上的动点,且CE=DF.当AE+CF的值最小时,CE=
1. A 2. D 3. B 4. C 5. C 6. B 7.50° 8.甲、乙 9.9
10.解:(1)证明:∵四边形 ABCD是平行四边形,
∴AB=CD,AD=BC,∠B=∠D.∵AF=CE,
∴AD-AF=BC-CE,∴DF=BE.在△ABE与△CDF中,
∵∠B=∠2D,∴△ABE≌△CDF(SAS).
(2)添加 BE=CE,理由如下:∵AF=CE,BE=CE,
∴AF=BE.∵四边形ABCD是平行四边形,∴AD∥BC,
∴四边形 ABEF 是平行四边形.
11. C 12. A 13.①②④ 14.(1)证明略
15.解:(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,CD∥AB,∴∠D=∠FAD,∠DCE=∠F.
∵E是AD的中点,∴DE=AE,
∴△CDE≌△FAE(AAS),∴CE=EF.
∵ B.
(2)∵AG=2,FG=6,
∴AF=FG+AG=6+2=8,∴AB=AF=8.
∵四边形ABCD是平行四边形,∴CD=AB=8.
∵∠DCE=∠F,∠FCG=∠FCD,∴∠F=∠FCG,
∴CG=FG=6.∵CD∥AF,∴△DCH∽△AGH,
即 ,∴GH=1.2.
16.
同课章节目录
