第22 讲 锐角三角函数的应用 (含答案) 2025年中考数学知识点过关训练
文档属性
| 名称 | 第22 讲 锐角三角函数的应用 (含答案) 2025年中考数学知识点过关训练 | 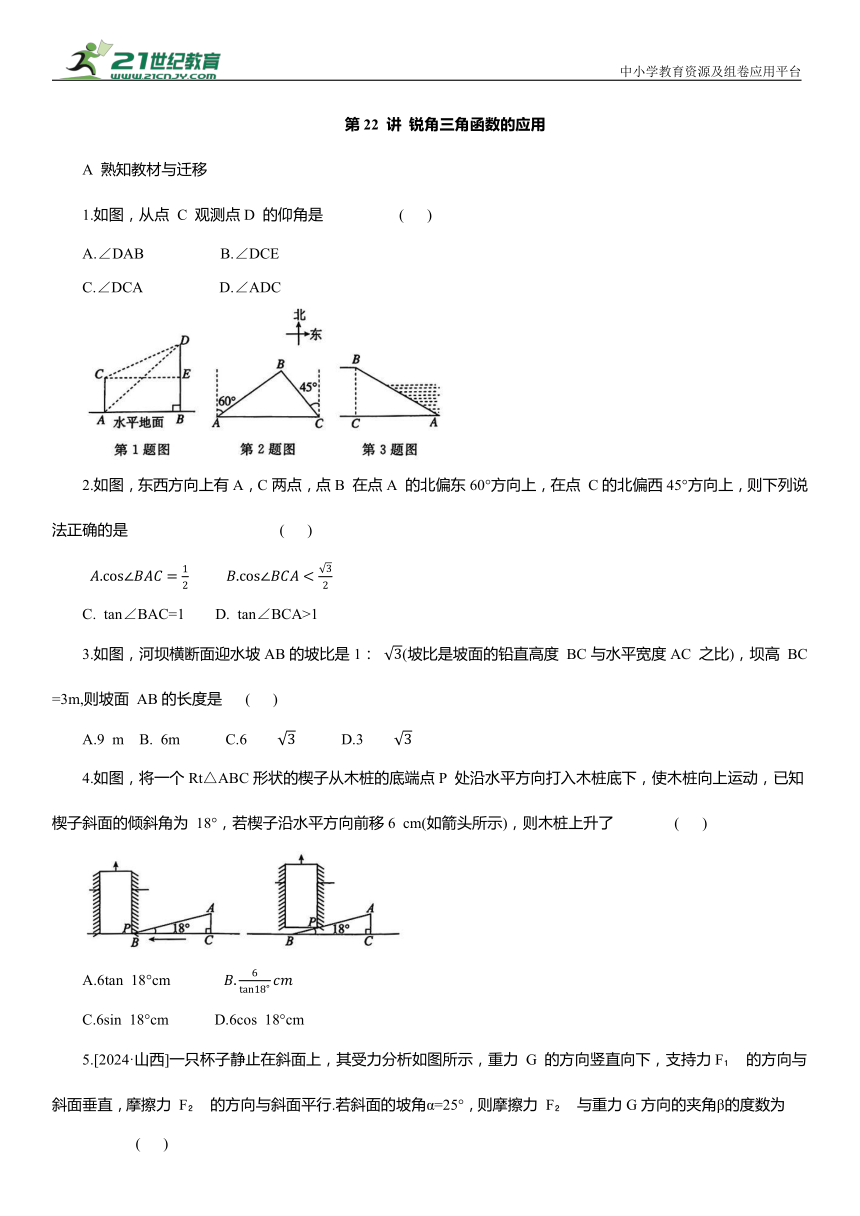 | |
| 格式 | docx | ||
| 文件大小 | 260.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-10 21:19:22 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第22 讲 锐角三角函数的应用
A 熟知教材与迁移
1.如图,从点 C 观测点D 的仰角是 ( )
A.∠DAB B.∠DCE
C.∠DCA D.∠ADC
2.如图,东西方向上有A,C两点,点B 在点A 的北偏东60°方向上,在点 C的北偏西45°方向上,则下列说法正确的是 ( )
C. tan∠BAC=1 D. tan∠BCA>1
3.如图,河坝横断面迎水坡AB的坡比是1: (坡比是坡面的铅直高度 BC与水平宽度AC 之比),坝高 BC=3m,则坡面 AB的长度是 ( )
A.9 m B. 6m C.6 D.3
4.如图,将一个Rt△ABC形状的楔子从木桩的底端点P 处沿水平方向打入木桩底下,使木桩向上运动,已知楔子斜面的倾斜角为 18°,若楔子沿水平方向前移6 cm(如箭头所示),则木桩上升了 ( )
A.6tan 18°cm
C.6sin 18°cm D.6cos 18°cm
5.[2024·山西]一只杯子静止在斜面上,其受力分析如图所示,重力 G 的方向竖直向下,支持力F 的方向与斜面垂直,摩擦力 F 的方向与斜面平行.若斜面的坡角α=25°,则摩擦力 F 与重力G方向的夹角β的度数为 ( )
A.155° B.125° C.115° D.65°
6.如图,它是源于我国汉代数学家赵爽的弦图,它是由四个全等直角三角形与一个小正方形拼成的一个大正方形.若小正方形的面积为1,大正方形的面积为25,直角三角形中较小的锐角为α,则 cosα的值为 ( )
A. B.
C. D.
7.[2024·成都模拟]课外活动小组测量学校旗杆的高度,如图,当太阳光线与地面成30°角时,测得旗杆 AB在地面上的投影BC 长为24米,则旗杆AB的高度约是 米.(结果保留一位小数,
8.如图所示的衣架可以近似看成一个等腰三角形ABC,其中AB=AC,∠ABC=27°,BC=40 cm,则高 AD 为 cm.(参考数据:sin 27°≈0.45, cos 27°≈0.89,t an27°≈0.51)
9.如图,已知公路l上A,B两点之间的距离为20米,点 B在C的南偏西30°的方向上,A在C的南偏西60°方向上,则点 C到公路l的距离为 米.
10.[2024·贵州]综合与实践:小星学习解直角三角形知识后,结合光的折射规律进行了如下综合性学习.
【实验操作】
第一步:将长方体空水槽放置在水平桌面上,一束光线从水槽边沿 A 处投射到底部B 处,入射光线与水槽内壁AC的夹角为∠A;
第二步:向水槽注水,水面上升到 AC的中点E处时,停止注水.(直线 NN'为法线,AO为入射光线,OD为折射光线.)
【测量数据】
如图,点 A,B,C,D,E,F,O,N,N'在同一平面内,测得AC=20cm,∠A=45°,折射角∠DON=32°.
【问题解决】
根据以上实验操作和测量的数据,解答下列问题:
(1)求 BC的长.
(2)求 B,D 之间的距离.(结果精确到0.1 cm)
(参考数据:
B 掌握通性与通法
11.爬坡时坡面与水平面夹角为α,则每爬1m 耗能(1.025-cosα) J,若某人爬了 1 000 m,该坡角为30°,则他耗能(参考数据: 1.414) ( )
A.58 J B.159J C.1 025 J D.1 732 J
12.如图,已知点 B,D,C在同一直线的水平地面上,在点 C处测得建筑物AB 的顶端A 的仰角为α,在点 D 处测得建筑物AB 的顶端A 的仰角为β,若CD=a,则建筑物AB的高度为
( )
13.[2024·广州]如图1,在水平地面上,一辆小车用一根绕过定滑轮的绳子将物体竖直向上提起.起始位置示意图如图 2,此时测得点 A 到BC 所在直线的距离AC=3m,∠CAB=60°,停止位置示意图如图3,此时测得∠CDB=37°(点C,A,D在同一直线上,且直线 CD 与地面平行),图3中所有点在同一平面内.定滑轮半径忽略不计,运动过程中绳子总长不变.
(1)求 AB的长.
(2)求物体上升的高度CE.(结果精确到0.1m)(参考数据:
C感悟思维与素养
14.[2024·北京]中国的探月工程激发了同学们对太空的兴趣.某晚,淇淇在家透过窗户的最高点 P 恰好看到一颗星星,此时淇淇距窗户的水平距离BQ=4m ,仰角为α;淇淇向前走了3m后到达点 D,透过点 P 恰好看到月亮,仰角为β,如图,这是示意图.已知淇淇的眼睛与水平地面BQ的距离AB=CD=1.6m ,点 P 到 BQ 的距离PQ=2.6 m,AC 的延长线交 PQ 于点 E.(注:图中所有点均在同一平面内)
(1)求β的大小及 tanα的值.
(2)求CP 的长及sin∠APC的值.
1. B 2. B 3. B 4. A 5. C 6. D 7.13.9 8.10.2 9.10 10.(1)20cm (2)3. 8cm 11. B 12. D
13.(1)6m (2)2.7m
14.解:(1)由题意可得 PQ⊥AE,PQ=2.6m,AB=CD=EQ=1. 6m,AE=BQ=4m,AC=BD=3m,
∴CE=4-3=1(m),PE=2.6-1.6=1(m),∠CEP=90°.
∴CE=PE,∴β=∠PCE=45°;tanα=tan∠PAE=PE=
(2)∵CE=PE=1m,∠CEP=90°,∴CP= +1 = (m).如图,过点 C作CH⊥AP于H,
∵tan α= tan ∠PAE= 设CH= xm,则AH=4xm,
第22 讲 锐角三角函数的应用
A 熟知教材与迁移
1.如图,从点 C 观测点D 的仰角是 ( )
A.∠DAB B.∠DCE
C.∠DCA D.∠ADC
2.如图,东西方向上有A,C两点,点B 在点A 的北偏东60°方向上,在点 C的北偏西45°方向上,则下列说法正确的是 ( )
C. tan∠BAC=1 D. tan∠BCA>1
3.如图,河坝横断面迎水坡AB的坡比是1: (坡比是坡面的铅直高度 BC与水平宽度AC 之比),坝高 BC=3m,则坡面 AB的长度是 ( )
A.9 m B. 6m C.6 D.3
4.如图,将一个Rt△ABC形状的楔子从木桩的底端点P 处沿水平方向打入木桩底下,使木桩向上运动,已知楔子斜面的倾斜角为 18°,若楔子沿水平方向前移6 cm(如箭头所示),则木桩上升了 ( )
A.6tan 18°cm
C.6sin 18°cm D.6cos 18°cm
5.[2024·山西]一只杯子静止在斜面上,其受力分析如图所示,重力 G 的方向竖直向下,支持力F 的方向与斜面垂直,摩擦力 F 的方向与斜面平行.若斜面的坡角α=25°,则摩擦力 F 与重力G方向的夹角β的度数为 ( )
A.155° B.125° C.115° D.65°
6.如图,它是源于我国汉代数学家赵爽的弦图,它是由四个全等直角三角形与一个小正方形拼成的一个大正方形.若小正方形的面积为1,大正方形的面积为25,直角三角形中较小的锐角为α,则 cosα的值为 ( )
A. B.
C. D.
7.[2024·成都模拟]课外活动小组测量学校旗杆的高度,如图,当太阳光线与地面成30°角时,测得旗杆 AB在地面上的投影BC 长为24米,则旗杆AB的高度约是 米.(结果保留一位小数,
8.如图所示的衣架可以近似看成一个等腰三角形ABC,其中AB=AC,∠ABC=27°,BC=40 cm,则高 AD 为 cm.(参考数据:sin 27°≈0.45, cos 27°≈0.89,t an27°≈0.51)
9.如图,已知公路l上A,B两点之间的距离为20米,点 B在C的南偏西30°的方向上,A在C的南偏西60°方向上,则点 C到公路l的距离为 米.
10.[2024·贵州]综合与实践:小星学习解直角三角形知识后,结合光的折射规律进行了如下综合性学习.
【实验操作】
第一步:将长方体空水槽放置在水平桌面上,一束光线从水槽边沿 A 处投射到底部B 处,入射光线与水槽内壁AC的夹角为∠A;
第二步:向水槽注水,水面上升到 AC的中点E处时,停止注水.(直线 NN'为法线,AO为入射光线,OD为折射光线.)
【测量数据】
如图,点 A,B,C,D,E,F,O,N,N'在同一平面内,测得AC=20cm,∠A=45°,折射角∠DON=32°.
【问题解决】
根据以上实验操作和测量的数据,解答下列问题:
(1)求 BC的长.
(2)求 B,D 之间的距离.(结果精确到0.1 cm)
(参考数据:
B 掌握通性与通法
11.爬坡时坡面与水平面夹角为α,则每爬1m 耗能(1.025-cosα) J,若某人爬了 1 000 m,该坡角为30°,则他耗能(参考数据: 1.414) ( )
A.58 J B.159J C.1 025 J D.1 732 J
12.如图,已知点 B,D,C在同一直线的水平地面上,在点 C处测得建筑物AB 的顶端A 的仰角为α,在点 D 处测得建筑物AB 的顶端A 的仰角为β,若CD=a,则建筑物AB的高度为
( )
13.[2024·广州]如图1,在水平地面上,一辆小车用一根绕过定滑轮的绳子将物体竖直向上提起.起始位置示意图如图 2,此时测得点 A 到BC 所在直线的距离AC=3m,∠CAB=60°,停止位置示意图如图3,此时测得∠CDB=37°(点C,A,D在同一直线上,且直线 CD 与地面平行),图3中所有点在同一平面内.定滑轮半径忽略不计,运动过程中绳子总长不变.
(1)求 AB的长.
(2)求物体上升的高度CE.(结果精确到0.1m)(参考数据:
C感悟思维与素养
14.[2024·北京]中国的探月工程激发了同学们对太空的兴趣.某晚,淇淇在家透过窗户的最高点 P 恰好看到一颗星星,此时淇淇距窗户的水平距离BQ=4m ,仰角为α;淇淇向前走了3m后到达点 D,透过点 P 恰好看到月亮,仰角为β,如图,这是示意图.已知淇淇的眼睛与水平地面BQ的距离AB=CD=1.6m ,点 P 到 BQ 的距离PQ=2.6 m,AC 的延长线交 PQ 于点 E.(注:图中所有点均在同一平面内)
(1)求β的大小及 tanα的值.
(2)求CP 的长及sin∠APC的值.
1. B 2. B 3. B 4. A 5. C 6. D 7.13.9 8.10.2 9.10 10.(1)20cm (2)3. 8cm 11. B 12. D
13.(1)6m (2)2.7m
14.解:(1)由题意可得 PQ⊥AE,PQ=2.6m,AB=CD=EQ=1. 6m,AE=BQ=4m,AC=BD=3m,
∴CE=4-3=1(m),PE=2.6-1.6=1(m),∠CEP=90°.
∴CE=PE,∴β=∠PCE=45°;tanα=tan∠PAE=PE=
(2)∵CE=PE=1m,∠CEP=90°,∴CP= +1 = (m).如图,过点 C作CH⊥AP于H,
∵tan α= tan ∠PAE= 设CH= xm,则AH=4xm,
同课章节目录
