2025年四川省成都市中考数学 平移、旋转与轴对称的应用 专题讲座 课件(共26张PPT)
文档属性
| 名称 | 2025年四川省成都市中考数学 平移、旋转与轴对称的应用 专题讲座 课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-10 00:00:00 | ||
图片预览








文档简介
(共26张PPT)
《平移、旋转与轴对称的应用》专题讲座
汇报人:
时间:
目录
01
课标要求
02
中考分析
03
解决问题
04
试题展示
05
总结展望
课标要求
Part 1
理解轴对称、旋转、平移这三类基本的图形运动,知道三类运动的基本特征。同时掌握它们的基本性质。
知识理解方面:
能够在方格纸上进行简单图形的平移、旋转、轴对称操作,并能利用平移、旋转、轴对称进行添加辅助线把分散的条件集中在一起,从而解决一些数学问题。
技能掌握方面:
运用平移、旋转和轴对称的知识来认识、理解和表达现实世界中相应的现象,解决一些简单的实际问题。探索图形之间的变化关系(轴对称、平移、旋转及其组合),灵活运用这些变换的组合进行图案设计,培养学生的创新意识和审美能力。在解决几何问题时,能够根据需要合理地运用平移、旋转和轴对称的性质,进行图形的转化和分析,提高逻辑推理和解决问题的能力。
应用与综合方面
新课标对平移、旋转、轴对称要求:
数学思维方面
通过对平移、旋转、轴对称等图形变换的学习,发展学生的空间观念,让学生能够感知并描述图形的运动和变化规律,根据几何图形想象出所描述的实际物体。同时,培养学生的推理能力,学生要能够依据平移、旋转、轴对称的性质进行简单的推理和论证,理解命题的结构与联系,探索并表述论证过程,感悟数学的严谨性。。
中考分析
Part2
近五年成都市中考试题分析:
2020-2024年成都中考平移、旋转、轴对称考题占比分析 年份 A卷分值 B卷分值 合计 占比
平移 旋转 轴对称 平移 旋转 轴对称 2020 第4题3分 第27题10分 10 6.67%
2021 第4题3分 第27题10分 第24题4分 17 11.33%
2022 第23题4分 4 2.67%
2023 第12题4分 第22题4分 8 5.33%
2024 第18题第2小题3分 第14题4分,第18题第3小题4分 第26题12分 19 12.67%
平移、旋转、轴对称考查平均分为11.6分,占比约为总分的8%
解决问题
Part3
平移是指在平面内,将一个图形沿某一方向移动特定距离的几何变换。此过程不改变图形的形状与大小,仅改变其位置。理解平移的定义是掌握其应用及与其他变换(如旋转、轴对称)结合的基础。
平移的几何定义
平移的向量表示是通过向量的大小和方向来描述图形位置的变化。在平面直角坐标系中,利用向量可以精确地确定平移的距离与方向,为后续研究旋转和轴对称奠定基础,同时增强几何问题的代数化解决能力。
平移的向量表示
在平移变换中,图形的形状、大小及方向保持不变,这些即为平移的不变量。通过研究这些特性,我们可以更好地理解平移对空间结构的影响,并将其应用于实际问题解决中,如建筑设计和图像处理等领域。
平移的不变量
平移的定义与性质
利用平移的方法构造辅助线(等线段,有距离,辅助线想平移)
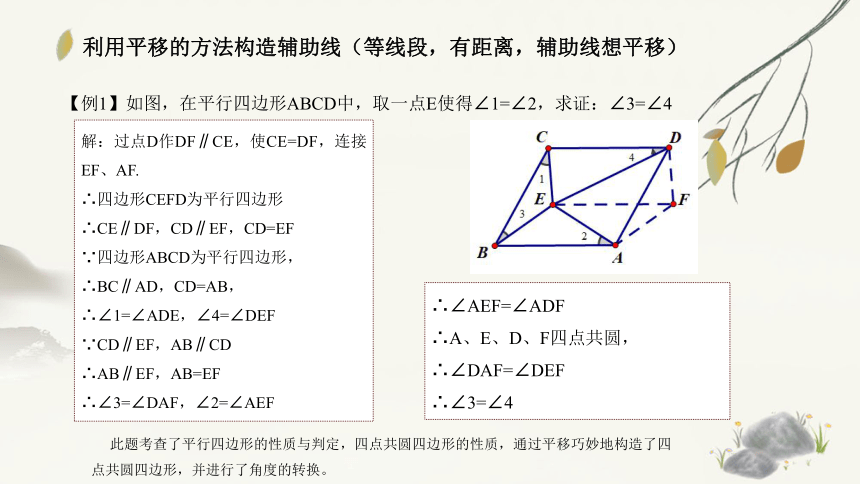
【例1】如图,在平行四边形ABCD中,取一点E使得∠1=∠2,求证:∠3=∠4
解:过点D作DF∥CE,使CE=DF,连接EF、AF.
∴四边形CEFD为平行四边形
∴CE∥DF,CD∥EF,CD=EF
∵四边形ABCD为平行四边形,
∴BC∥AD,CD=AB,
∴∠1=∠ADE,∠4=∠DEF
∵CD∥EF,AB∥CD
∴AB∥EF,AB=EF
∴∠3=∠DAF,∠2=∠AEF
∴∠AEF=∠ADF
∴A、E、D、F四点共圆,
∴∠DAF=∠DEF
∴∠3=∠4
此题考查了平行四边形的性质与判定,四点共圆四边形的性质,通过平移巧妙地构造了四点共圆四边形,并进行了角度的转换。
【例2】如图,∠DAB=∠DCB=15°,∠ADC=105°,CD=AB=4,求AD的长。
证明:过点C作CE∥AB,使CE=AB,连接AE、DE。
∴四边形AECB为平行四边形
∴AE=BC,AB=CE
∵AB=DC
∴AB=CE
∵∠ADC+∠DAB=∠B+∠DCB
∴∠B=15+105-15=105°
∵∠B+∠BCE=180°
∴∠BCE=75°
∴∠DCE=60°
∴三角形DCE为等边三角形
∴DE=4
∵∠BAE=∠BCE=75°
∴∠DAE=∠BAE+∠DAB=90°
∵∠ADE=∠ADC-∠EDC=45°
∴三角形ADE为等腰直角三角形
∴AD=
练一练:
在RT△ABC中,∠C=90°,点M是BC上一点,如果BM=AC,CM=AN,连接AN交AM于点P,求证:∠BPM=45°。
旋转的中心与角度是理解几何变换的关键。旋转中心作为固定点,决定了图形绕其转动的位置,而旋转角度则定义了转动的具体程度。通过明确这两者,可以精准描述图形在平面内的旋转变化,为后续复杂图形分析奠定基础。
旋转的中心与角度
旋转的方向性是理解几何变换的关键之一。顺时针与逆时针方向的判断,直接影响图形最终的位置和形态。通过明确旋转中心和角度,可以精准描述物体在平面内的转动变化,为后续复杂问题的解决奠定基础。
旋转的方向性
在旋转变换中,距离、角度和面积等几何属性保持不变。这些不变量是研究旋转对称性和图形性质的关键。掌握旋转的不变量,有助于深入理解图形在空间中的变化规律及其实际应用。
旋转的不变量
旋转的定义与性质
利用旋转的方法构造辅助线(等线段,共端点,辅助线用旋转)
【例3】如图,D是等边三角形ABC外一点,连接AD,BD,CD,已知BD=8,CD=3,则当线段 AD 的长度最小时,
①∠BDC= °:②AD 的最小值是 。
练一练:
(经典习题)如图,已知点P是等边△ABC内一点,PA=3,PB=4,PC=5求∠APB的度数.
轴对称是指图形沿某一直线折叠后两部分完全重合的特性,该直线称为对称轴。在几何中,掌握轴对称定义有助于分析图形性质及其变换规律,为后续研究平移与旋转奠定基础。
轴对称的几何定义
在轴对称图形中,对称轴是关键要素。它不仅是图形折叠后的重合线,还决定了图形的对称性质。通过确定对称轴的位置和数量,可以深入分析图形的几何特征及其应用,为后续研究奠定基础。
轴对称的对称轴
在轴对称变换中,距离、角度及面积等几何量保持不变。这些不变量是研究图形对称性的关键,它们帮助我们准确判断和描述轴对称关系,为解决实际问题提供理论依据。
轴对称的不变量
轴对称的定义与性质
利用轴对称作图进行转换,从而达到解决问题的方法:
如图,△ABC的边BC的垂直平分线DE交△ABC的外角平分线AD于点D,垂足为E,DF⊥AB于点F,且AB>AC,求证:BF=AC+AF
证明:连接BD、CD,作
DG⊥AC于G。
∵DE垂直平分BC,
∴BD=CD
∵AD平分∠BAG
∴∠DAF=∠DAG
∵DF⊥AB,DG⊥AC
∴∠DFA=∠DGA=90°
∵AD=AD
∴△ADG≌△ADF(AAS)
∴AG=AF
在RT△BDF与RT△CDG中
∴RT△BDF≌RT△CDG(HL)
∴BF=CG
∴BF=AC+AF
轴对称在图形变换中的应用
练一练:
如图,E、B、C三点在一条直线上,AD//EC,AD=BC,BD=EC:F为AE的中点,求/BFD的度数。
试题展示
Part 4
基本概念与应用
(1)(2020年第4题3分)在平面直角坐标系中,将点P(3,2)向下平移2个单位长度得到的点的坐标是( )
A.(3,0) B.(1,2) C.(5,2) D.(3,4)
(2)(2021年第4题3分)在平面直角坐标系xOy中,点M(﹣4,2)关于x轴对的点的坐标是( )
A.(﹣4,2) B.(4,2) C.(﹣4,﹣2) D.(4,﹣2)
(3)(2023年第12题4分)在平面直角坐标系xOy中,点P(5,﹣1)关于y轴对称的点的坐标是 : .
(4)(2024年第4题4分)在平面直角坐标系xOy中,点P(1,﹣4)关于原点对称的点的坐标是( )
A.(﹣1,﹣4) B.(﹣1,4) C.(1,4) D.(1,﹣4)
A
C
(-5,1)
B
平移、旋转与轴对称的综合应用
(1).(2020年27题10分)在矩形ABCD的CD边上取一点E,将△BCE沿BE翻折,使点C恰好落在AD边上点F处.
①如图1,若BC=2BA,求∠CBE的度数;
②如图2,当AB=5,且AF FD=10时,求BC的长;
③如图3,延长EF,与∠ABF的角平分线交于点M,BM交AD于点N,当NF=AN+FD时,求
的值.
解:①∵四边形ABCD是矩形,
∴∠C=90°,
∵将△BCE沿BE翻折,使点C恰好落在AD边上点F处,
∴BC=BF,∠FBE=∠EBC,∠C=∠BFE=90°,
∵BC=2AB,
∴BF=2AB,
∴∠AFB=30°,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠AFB=∠CBF=30°,
∴∠CBE=∠FBC=15°
②∵将△BCE沿BE翻折,使点C恰好落在AD边上点F处,
∴∠BFE=∠C=90°,CE=EF,
又∵矩形ABCD中,∠A=∠D=90°,
∴∠AFB+∠DFE=90°,∠DEF+∠DFE=90°,
∴∠AFB=∠DEF,
∴△FAB∽△EDF,
∴
∴AF DF=AB DE,
∵AF DF=10,AB=5,
∴DE=2,
∴EF=3,
∴CE=DC﹣DE=5﹣2=3,
∴DF= =
∴AF==2
∴BC=AD=AF+DF=3
③过点N作NG⊥BF于点G,
∵NF=AN+FD,
∴NF= AD= BC,
∵BC=BF,
∴NF= BF,
∵∠NFG=∠AFB,∠NGF=∠BAF=90°,
∴△NFG∽△BFA,
∴
设AN=x,
∵BN平分∠ABF,AN⊥AB,NG⊥BF,
∴AN=NG=x,AB=BG=2x,
设FG=y,则AF=2y,
∵AB2+AF2=BF2,
∴(2x)2+(2y)2=(2x+y)2,
解得y= x.
∴BF=BG+GF= .
壹
分析问题的关键点
分析问题时,需抓住图形变换的本质特征,如平移的向量、旋转中心与角度、对称轴位置等关键要素,结合具体条件进行推理,为后续解题奠定基础。这种方法能有效提升几何问题的解决效率。
贰
确定变换的顺序与方式
在解决几何变换问题时,明确平移、旋转与轴对称的顺序和方式至关重要。不同的变换顺序可能导致不同结果,需根据图形特征和目标位置精心设计变换步骤,确保准确还原或构造所需图形。
叁
验证结果的正确性
在验证结果的正确性时,需将变换后的图形与原图形进行对比,检查是否符合平移、旋转或轴对称的定义。通过反复推演和测量,确保每一步操作精准无误,从而提升解题的可靠性。
解题技巧与方法总结
总结与展望
Part 5
壹
几何变换的基本原理
几何变换是研究图形位置与形状变化的数学工具。平移改变图形位置而不影响其大小和形状,旋转围绕固定点改变方向,轴对称则生成镜像图形。这些基本原理为后续应用奠定了理论基础,帮助理解图形的运动规律及其特性。
贰
几何变换的实际意义
几何变换不仅是数学理论的基础,也在现实生活中有广泛的应用。平移、旋转与轴对称能够帮助我们理解物体的运动规律和空间结构,为解决实际问题提供有效方法,如建筑设计和图像处理等领域。
叁
几何变换的未来发展方向
几何变换在未来将深度融合人工智能与大数据,拓展在图像处理、虚拟现实等领域的应用,通过更高效的算法实现复杂变换,推动科技与艺术创新,为平移、旋转和轴对称带来全新可能性。
平移、旋转与轴对称的核心思想
壹
如何提高几何变换的理解能力
要提高几何变换的理解能力,需从直观感知入手,结合实例分析平移、旋转与轴对称的特性。通过动手操作和图形绘制,加深对变换规律的认识,并灵活运用到解题中,培养空间想象力和逻辑思维能力。
贰
如何培养几何变换的应用能力
培养几何变换的应用能力,需从实践出发,结合平移、旋转与轴对称解决实际问题。通过动手操作、图形分析和案例演练,学生可逐步掌握变换规律,提升空间想象与解决问题的能力。
叁
如何拓展几何变换的知识面
在拓展几何变换知识面时,可结合实际问题,如建筑设计中的对称美或导航系统中的旋转原理。通过跨学科应用,深化对平移、旋转与轴对称的理解,提升解决复杂几何问题的能力。这种方法有助于学生将理论与实践相结合,开阔思维。
学习方法与建议
感谢您的观看
《平移、旋转与轴对称的应用》专题讲座
汇报人:
时间:
目录
01
课标要求
02
中考分析
03
解决问题
04
试题展示
05
总结展望
课标要求
Part 1
理解轴对称、旋转、平移这三类基本的图形运动,知道三类运动的基本特征。同时掌握它们的基本性质。
知识理解方面:
能够在方格纸上进行简单图形的平移、旋转、轴对称操作,并能利用平移、旋转、轴对称进行添加辅助线把分散的条件集中在一起,从而解决一些数学问题。
技能掌握方面:
运用平移、旋转和轴对称的知识来认识、理解和表达现实世界中相应的现象,解决一些简单的实际问题。探索图形之间的变化关系(轴对称、平移、旋转及其组合),灵活运用这些变换的组合进行图案设计,培养学生的创新意识和审美能力。在解决几何问题时,能够根据需要合理地运用平移、旋转和轴对称的性质,进行图形的转化和分析,提高逻辑推理和解决问题的能力。
应用与综合方面
新课标对平移、旋转、轴对称要求:
数学思维方面
通过对平移、旋转、轴对称等图形变换的学习,发展学生的空间观念,让学生能够感知并描述图形的运动和变化规律,根据几何图形想象出所描述的实际物体。同时,培养学生的推理能力,学生要能够依据平移、旋转、轴对称的性质进行简单的推理和论证,理解命题的结构与联系,探索并表述论证过程,感悟数学的严谨性。。
中考分析
Part2
近五年成都市中考试题分析:
2020-2024年成都中考平移、旋转、轴对称考题占比分析 年份 A卷分值 B卷分值 合计 占比
平移 旋转 轴对称 平移 旋转 轴对称 2020 第4题3分 第27题10分 10 6.67%
2021 第4题3分 第27题10分 第24题4分 17 11.33%
2022 第23题4分 4 2.67%
2023 第12题4分 第22题4分 8 5.33%
2024 第18题第2小题3分 第14题4分,第18题第3小题4分 第26题12分 19 12.67%
平移、旋转、轴对称考查平均分为11.6分,占比约为总分的8%
解决问题
Part3
平移是指在平面内,将一个图形沿某一方向移动特定距离的几何变换。此过程不改变图形的形状与大小,仅改变其位置。理解平移的定义是掌握其应用及与其他变换(如旋转、轴对称)结合的基础。
平移的几何定义
平移的向量表示是通过向量的大小和方向来描述图形位置的变化。在平面直角坐标系中,利用向量可以精确地确定平移的距离与方向,为后续研究旋转和轴对称奠定基础,同时增强几何问题的代数化解决能力。
平移的向量表示
在平移变换中,图形的形状、大小及方向保持不变,这些即为平移的不变量。通过研究这些特性,我们可以更好地理解平移对空间结构的影响,并将其应用于实际问题解决中,如建筑设计和图像处理等领域。
平移的不变量
平移的定义与性质
利用平移的方法构造辅助线(等线段,有距离,辅助线想平移)
【例1】如图,在平行四边形ABCD中,取一点E使得∠1=∠2,求证:∠3=∠4
解:过点D作DF∥CE,使CE=DF,连接EF、AF.
∴四边形CEFD为平行四边形
∴CE∥DF,CD∥EF,CD=EF
∵四边形ABCD为平行四边形,
∴BC∥AD,CD=AB,
∴∠1=∠ADE,∠4=∠DEF
∵CD∥EF,AB∥CD
∴AB∥EF,AB=EF
∴∠3=∠DAF,∠2=∠AEF
∴∠AEF=∠ADF
∴A、E、D、F四点共圆,
∴∠DAF=∠DEF
∴∠3=∠4
此题考查了平行四边形的性质与判定,四点共圆四边形的性质,通过平移巧妙地构造了四点共圆四边形,并进行了角度的转换。
【例2】如图,∠DAB=∠DCB=15°,∠ADC=105°,CD=AB=4,求AD的长。
证明:过点C作CE∥AB,使CE=AB,连接AE、DE。
∴四边形AECB为平行四边形
∴AE=BC,AB=CE
∵AB=DC
∴AB=CE
∵∠ADC+∠DAB=∠B+∠DCB
∴∠B=15+105-15=105°
∵∠B+∠BCE=180°
∴∠BCE=75°
∴∠DCE=60°
∴三角形DCE为等边三角形
∴DE=4
∵∠BAE=∠BCE=75°
∴∠DAE=∠BAE+∠DAB=90°
∵∠ADE=∠ADC-∠EDC=45°
∴三角形ADE为等腰直角三角形
∴AD=
练一练:
在RT△ABC中,∠C=90°,点M是BC上一点,如果BM=AC,CM=AN,连接AN交AM于点P,求证:∠BPM=45°。
旋转的中心与角度是理解几何变换的关键。旋转中心作为固定点,决定了图形绕其转动的位置,而旋转角度则定义了转动的具体程度。通过明确这两者,可以精准描述图形在平面内的旋转变化,为后续复杂图形分析奠定基础。
旋转的中心与角度
旋转的方向性是理解几何变换的关键之一。顺时针与逆时针方向的判断,直接影响图形最终的位置和形态。通过明确旋转中心和角度,可以精准描述物体在平面内的转动变化,为后续复杂问题的解决奠定基础。
旋转的方向性
在旋转变换中,距离、角度和面积等几何属性保持不变。这些不变量是研究旋转对称性和图形性质的关键。掌握旋转的不变量,有助于深入理解图形在空间中的变化规律及其实际应用。
旋转的不变量
旋转的定义与性质
利用旋转的方法构造辅助线(等线段,共端点,辅助线用旋转)
【例3】如图,D是等边三角形ABC外一点,连接AD,BD,CD,已知BD=8,CD=3,则当线段 AD 的长度最小时,
①∠BDC= °:②AD 的最小值是 。
练一练:
(经典习题)如图,已知点P是等边△ABC内一点,PA=3,PB=4,PC=5求∠APB的度数.
轴对称是指图形沿某一直线折叠后两部分完全重合的特性,该直线称为对称轴。在几何中,掌握轴对称定义有助于分析图形性质及其变换规律,为后续研究平移与旋转奠定基础。
轴对称的几何定义
在轴对称图形中,对称轴是关键要素。它不仅是图形折叠后的重合线,还决定了图形的对称性质。通过确定对称轴的位置和数量,可以深入分析图形的几何特征及其应用,为后续研究奠定基础。
轴对称的对称轴
在轴对称变换中,距离、角度及面积等几何量保持不变。这些不变量是研究图形对称性的关键,它们帮助我们准确判断和描述轴对称关系,为解决实际问题提供理论依据。
轴对称的不变量
轴对称的定义与性质
利用轴对称作图进行转换,从而达到解决问题的方法:
如图,△ABC的边BC的垂直平分线DE交△ABC的外角平分线AD于点D,垂足为E,DF⊥AB于点F,且AB>AC,求证:BF=AC+AF
证明:连接BD、CD,作
DG⊥AC于G。
∵DE垂直平分BC,
∴BD=CD
∵AD平分∠BAG
∴∠DAF=∠DAG
∵DF⊥AB,DG⊥AC
∴∠DFA=∠DGA=90°
∵AD=AD
∴△ADG≌△ADF(AAS)
∴AG=AF
在RT△BDF与RT△CDG中
∴RT△BDF≌RT△CDG(HL)
∴BF=CG
∴BF=AC+AF
轴对称在图形变换中的应用
练一练:
如图,E、B、C三点在一条直线上,AD//EC,AD=BC,BD=EC:F为AE的中点,求/BFD的度数。
试题展示
Part 4
基本概念与应用
(1)(2020年第4题3分)在平面直角坐标系中,将点P(3,2)向下平移2个单位长度得到的点的坐标是( )
A.(3,0) B.(1,2) C.(5,2) D.(3,4)
(2)(2021年第4题3分)在平面直角坐标系xOy中,点M(﹣4,2)关于x轴对的点的坐标是( )
A.(﹣4,2) B.(4,2) C.(﹣4,﹣2) D.(4,﹣2)
(3)(2023年第12题4分)在平面直角坐标系xOy中,点P(5,﹣1)关于y轴对称的点的坐标是 : .
(4)(2024年第4题4分)在平面直角坐标系xOy中,点P(1,﹣4)关于原点对称的点的坐标是( )
A.(﹣1,﹣4) B.(﹣1,4) C.(1,4) D.(1,﹣4)
A
C
(-5,1)
B
平移、旋转与轴对称的综合应用
(1).(2020年27题10分)在矩形ABCD的CD边上取一点E,将△BCE沿BE翻折,使点C恰好落在AD边上点F处.
①如图1,若BC=2BA,求∠CBE的度数;
②如图2,当AB=5,且AF FD=10时,求BC的长;
③如图3,延长EF,与∠ABF的角平分线交于点M,BM交AD于点N,当NF=AN+FD时,求
的值.
解:①∵四边形ABCD是矩形,
∴∠C=90°,
∵将△BCE沿BE翻折,使点C恰好落在AD边上点F处,
∴BC=BF,∠FBE=∠EBC,∠C=∠BFE=90°,
∵BC=2AB,
∴BF=2AB,
∴∠AFB=30°,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠AFB=∠CBF=30°,
∴∠CBE=∠FBC=15°
②∵将△BCE沿BE翻折,使点C恰好落在AD边上点F处,
∴∠BFE=∠C=90°,CE=EF,
又∵矩形ABCD中,∠A=∠D=90°,
∴∠AFB+∠DFE=90°,∠DEF+∠DFE=90°,
∴∠AFB=∠DEF,
∴△FAB∽△EDF,
∴
∴AF DF=AB DE,
∵AF DF=10,AB=5,
∴DE=2,
∴EF=3,
∴CE=DC﹣DE=5﹣2=3,
∴DF= =
∴AF==2
∴BC=AD=AF+DF=3
③过点N作NG⊥BF于点G,
∵NF=AN+FD,
∴NF= AD= BC,
∵BC=BF,
∴NF= BF,
∵∠NFG=∠AFB,∠NGF=∠BAF=90°,
∴△NFG∽△BFA,
∴
设AN=x,
∵BN平分∠ABF,AN⊥AB,NG⊥BF,
∴AN=NG=x,AB=BG=2x,
设FG=y,则AF=2y,
∵AB2+AF2=BF2,
∴(2x)2+(2y)2=(2x+y)2,
解得y= x.
∴BF=BG+GF= .
壹
分析问题的关键点
分析问题时,需抓住图形变换的本质特征,如平移的向量、旋转中心与角度、对称轴位置等关键要素,结合具体条件进行推理,为后续解题奠定基础。这种方法能有效提升几何问题的解决效率。
贰
确定变换的顺序与方式
在解决几何变换问题时,明确平移、旋转与轴对称的顺序和方式至关重要。不同的变换顺序可能导致不同结果,需根据图形特征和目标位置精心设计变换步骤,确保准确还原或构造所需图形。
叁
验证结果的正确性
在验证结果的正确性时,需将变换后的图形与原图形进行对比,检查是否符合平移、旋转或轴对称的定义。通过反复推演和测量,确保每一步操作精准无误,从而提升解题的可靠性。
解题技巧与方法总结
总结与展望
Part 5
壹
几何变换的基本原理
几何变换是研究图形位置与形状变化的数学工具。平移改变图形位置而不影响其大小和形状,旋转围绕固定点改变方向,轴对称则生成镜像图形。这些基本原理为后续应用奠定了理论基础,帮助理解图形的运动规律及其特性。
贰
几何变换的实际意义
几何变换不仅是数学理论的基础,也在现实生活中有广泛的应用。平移、旋转与轴对称能够帮助我们理解物体的运动规律和空间结构,为解决实际问题提供有效方法,如建筑设计和图像处理等领域。
叁
几何变换的未来发展方向
几何变换在未来将深度融合人工智能与大数据,拓展在图像处理、虚拟现实等领域的应用,通过更高效的算法实现复杂变换,推动科技与艺术创新,为平移、旋转和轴对称带来全新可能性。
平移、旋转与轴对称的核心思想
壹
如何提高几何变换的理解能力
要提高几何变换的理解能力,需从直观感知入手,结合实例分析平移、旋转与轴对称的特性。通过动手操作和图形绘制,加深对变换规律的认识,并灵活运用到解题中,培养空间想象力和逻辑思维能力。
贰
如何培养几何变换的应用能力
培养几何变换的应用能力,需从实践出发,结合平移、旋转与轴对称解决实际问题。通过动手操作、图形分析和案例演练,学生可逐步掌握变换规律,提升空间想象与解决问题的能力。
叁
如何拓展几何变换的知识面
在拓展几何变换知识面时,可结合实际问题,如建筑设计中的对称美或导航系统中的旋转原理。通过跨学科应用,深化对平移、旋转与轴对称的理解,提升解决复杂几何问题的能力。这种方法有助于学生将理论与实践相结合,开阔思维。
学习方法与建议
感谢您的观看
同课章节目录
