人教版九年级数学下册 第二十九章 投影与视图 单元测试题(含答案)
文档属性
| 名称 | 人教版九年级数学下册 第二十九章 投影与视图 单元测试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-10 20:44:11 | ||
图片预览

文档简介
九年级数学下册人教版第二十九章《投影与视图》单元测试题
一、单选题
1.如图是一个由五个大小相同的正方体组成的立体图形,它的主视图是( )
A. B. C. D.
2.如图,日晷是我国古代的一种计时仪器,它由“晷面”和“晷针”组成.当太阳光照在日晷上时,晷针的影子就像钟表的指针一样慢慢地转动,晷针的影子指向晷面的某一位置,便可知道是白天的某一时间.晷针在晷面上形成的投影是( )
A.平行投影 B.既是平行投影又是中心投影
C.中心投影 D.无法确定
3.中国古代经典数学著作《孙子算经》有首歌谣:“今有竿不知其长,量得影长一丈五尺,立一标杆,长一尺五寸,影长五寸、问竿长几何?”其大意是:有一根竹竿不知道有多长,直立后量出它在太阳下的影子长一丈五尺,同时直立一根一尺五寸的小标杆(如图),它的影长五寸(备注:1丈尺,1尺寸),问竹竿长多少?若设竹竿长x尺,则可列方程为( )
A. B. C. D.
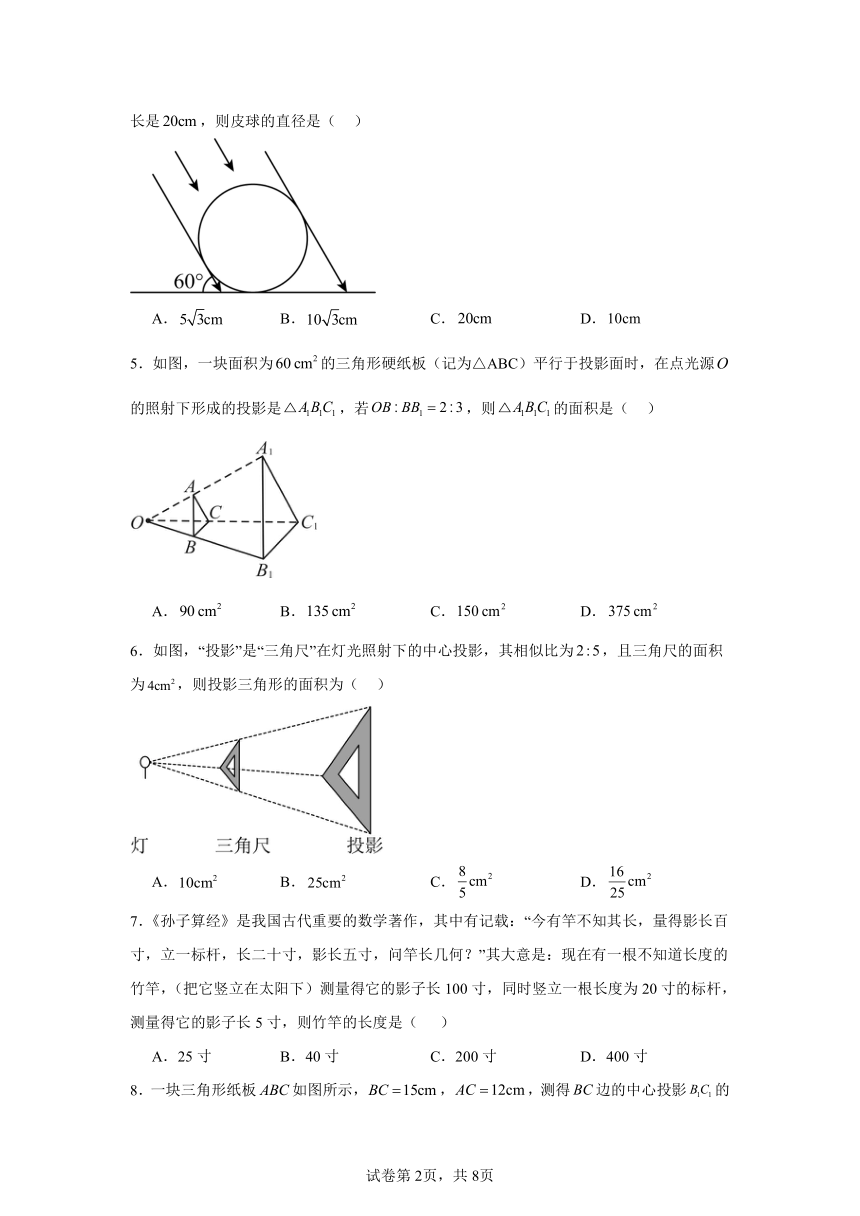
4.如图,太阳光线与地面成的角,照射在地面上的一只皮球上,皮球在地面上的投影长是,则皮球的直径是( )
A. B. C. D.
5.如图,一块面积为的三角形硬纸板(记为△ABC)平行于投影面时,在点光源的照射下形成的投影是,若,则的面积是( )
A. B. C. D.
6.如图,“投影”是“三角尺”在灯光照射下的中心投影,其相似比为,且三角尺的面积为,则投影三角形的面积为( )
A. B. C. D.
7.《孙子算经》是我国古代重要的数学著作,其中有记载:“今有竿不知其长,量得影长百寸,立一标杆,长二十寸,影长五寸,问竿长几何?”其大意是:现在有一根不知道长度的竹竿,(把它竖立在太阳下)测量得它的影子长100寸,同时竖立一根长度为20寸的标杆,测量得它的影子长5寸,则竹竿的长度是( )
A.25寸 B.40寸 C.200寸 D.400寸
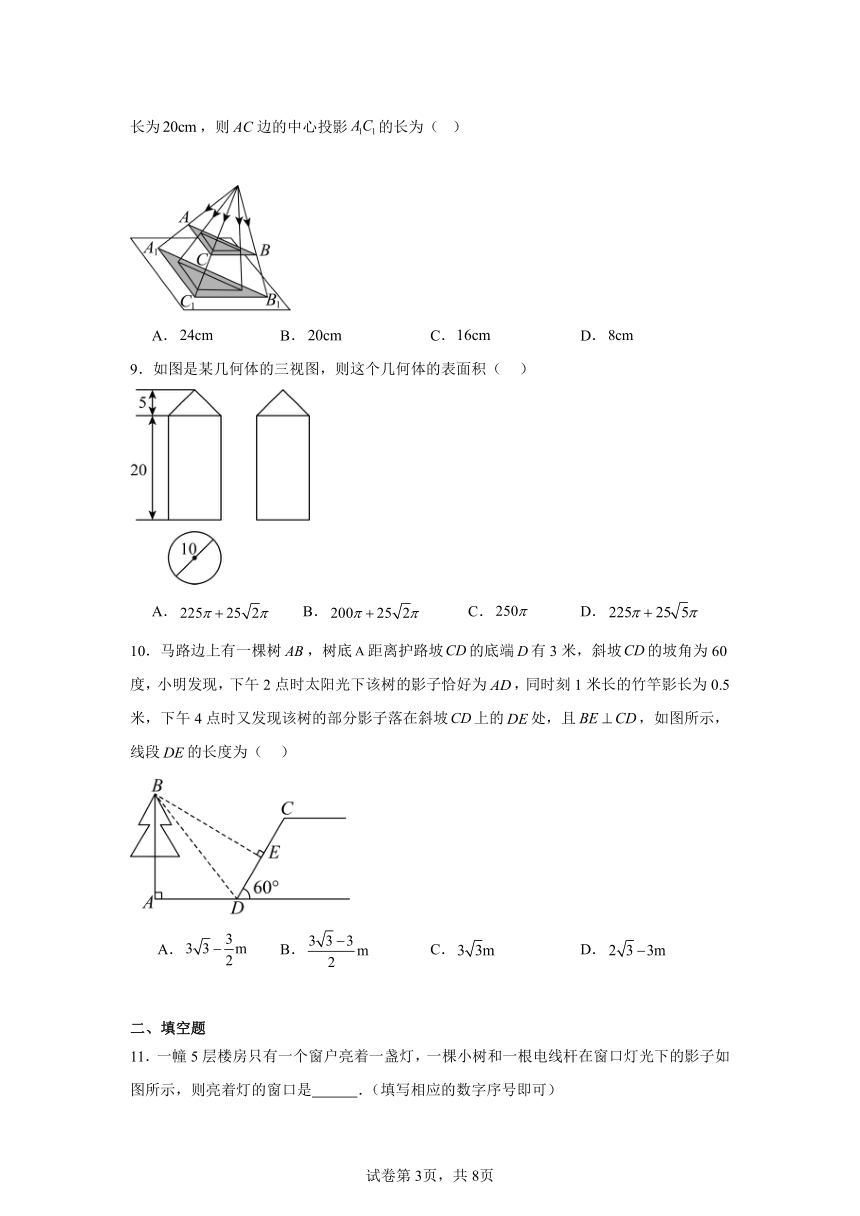
8.一块三角形纸板如图所示,,,测得边的中心投影的长为,则边的中心投影的长为( )
A. B. C. D.
9.如图是某几何体的三视图,则这个几何体的表面积( )
A. B. C. D.
10.马路边上有一棵树,树底距离护路坡的底端有3米,斜坡的坡角为60度,小明发现,下午2点时太阳光下该树的影子恰好为,同时刻1米长的竹竿影长为0.5米,下午4点时又发现该树的部分影子落在斜坡上的处,且,如图所示,线段的长度为( )
A. B. C. D.
二、填空题
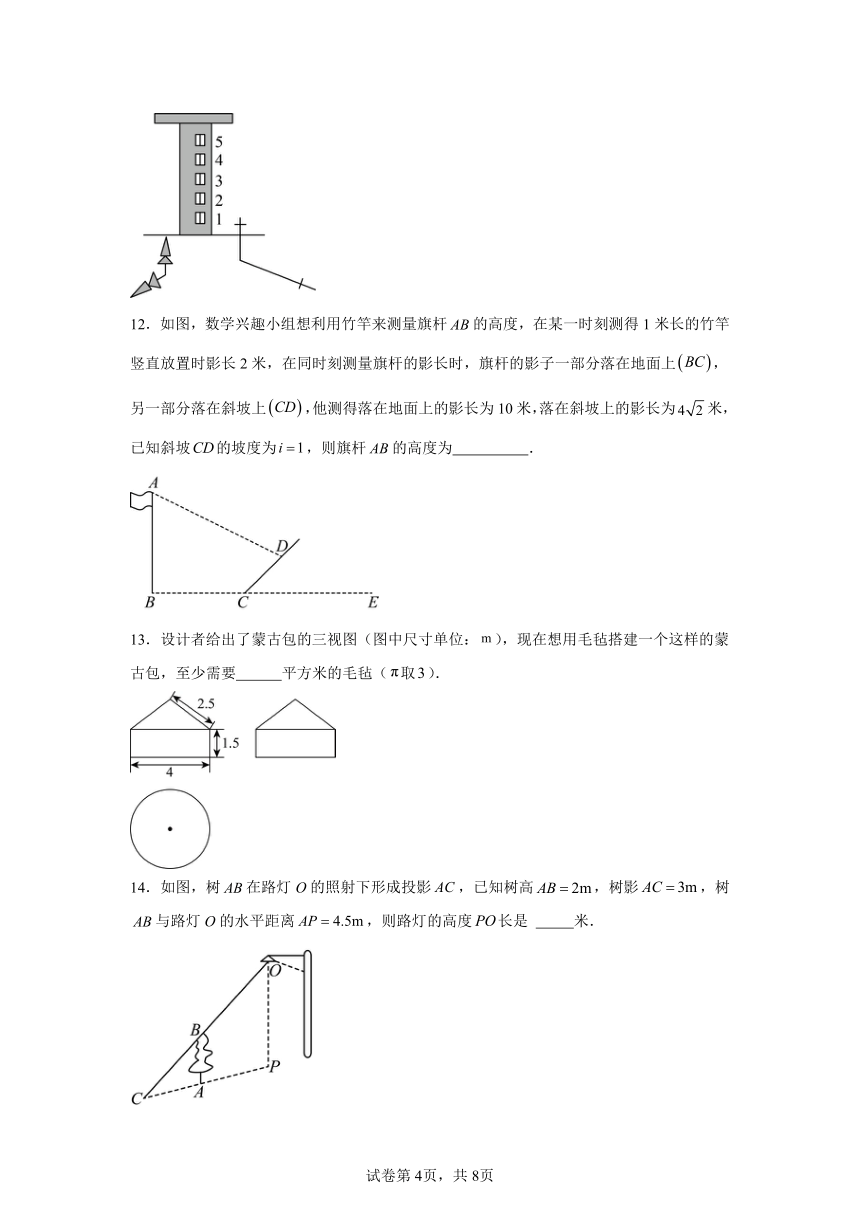
11.一幢5层楼房只有一个窗户亮着一盏灯,一棵小树和一根电线杆在窗口灯光下的影子如图所示,则亮着灯的窗口是 .(填写相应的数字序号即可)
12.如图,数学兴趣小组想利用竹竿来测量旗杆的高度,在某一时刻测得1米长的竹竿竖直放置时影长2米,在同时刻测量旗杆的影长时,旗杆的影子一部分落在地面上,另一部分落在斜坡上,他测得落在地面上的影长为10米,落在斜坡上的影长为米,已知斜坡的坡度为,则旗杆的高度为 .
13.设计者给出了蒙古包的三视图(图中尺寸单位:),现在想用毛毡搭建一个这样的蒙古包,至少需要 平方米的毛毡(取).
14.如图,树在路灯O的照射下形成投影,已知树高,树影,树与路灯O的水平距离,则路灯的高度长是 米.
三、解答题
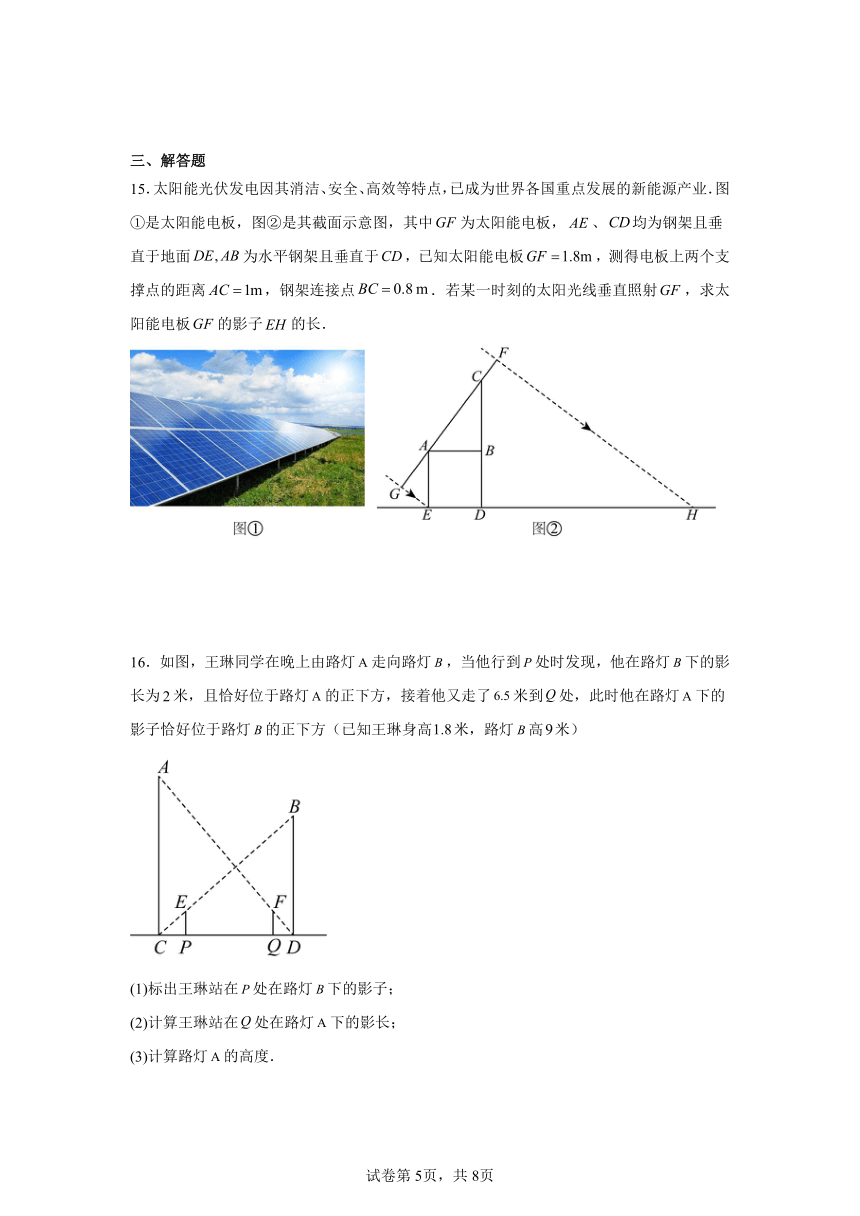
15.太阳能光伏发电因其消洁、安全、高效等特点,已成为世界各国重点发展的新能源产业.图①是太阳能电板,图②是其截面示意图,其中为太阳能电板,、均为钢架且垂直于地面为水平钢架且垂直于,已知太阳能电板,测得电板上两个支撑点的距离,钢架连接点.若某一时刻的太阳光线垂直照射,求太阳能电板的影子的长.
16.如图,王琳同学在晚上由路灯走向路灯,当他行到处时发现,他在路灯下的影长为米,且恰好位于路灯的正下方,接着他又走了米到处,此时他在路灯下的影子恰好位于路灯的正下方(已知王琳身高米,路灯高米)
(1)标出王琳站在处在路灯下的影子;
(2)计算王琳站在处在路灯下的影长;
(3)计算路灯的高度.
17.如图是由若干个完全相同的棱长为1的小正方体堆成的一个几何体.
(1)请在方格中分别画出它的主视图、左视图和俯视图;
(2)该几何体是由 个小正方体堆成的;
(3)若再添加n个小正方体,使新得到的几何体从正面和左面看到的平面图形不变,则n的最大值为 .
18.通常,路灯、台灯、手电筒……发出的光可以看成是从一个点发出的,在点光源的照射下,物体所产生的影称为中心投影.
(1)如图1,夜晚,小明从点A经过路灯C的正下方沿直线走到点B,他的影长y随他与点A之间的距离x的变化而变化,那么表示y与x之间函数关系的图像大致为_________;
A. B. C. D.
(2)如图2,小明为测河对岸的路灯杆的高度,在路灯A的灯光下,小明在点D处测得自己的影长,沿方向前进到达点F处测得自己的影长.已知小明的身高为,求路灯杆的高度.
19.如图所示的几何体是由5个大小相同的小正方体搭成.
(1)请在网格中画出这个几何体的主视图和左视图.
(2)在这个几何体中,当去掉一个小正方体______时,剩余部分的俯视图没有改变(填写图中小正方体的序号);如果在这个几何体上再添加一些相同的小正方体,并保持这个几何体的主视图和左视图不变,那么最多可以再添加______个小正方体.
20.用小立方块搭一个几何体,使它从正面、上面看到的形状图如图所示,从上面看到的形状图的小正方形中的字母表示在该位置小立方块的个数.试回答下列问题:
(1)a,d、f各表示几?
(2)这个几何体最少由几个小立方块搭成?最多呢?
(3)当,时,画出这个几何体从左面看到的形状图.
21.小彬做了探究物体投影规律的实验,并提出了一些数学问题请你解答:
(1)如图1,白天在阳光下,小彬将长度为2的木杆水平放置,此时木杆在水平地面上的影子为线段,并测量出光线与地面的夹角为.在同一时刻同一地点,将一根与长度相等的木杆直立于地面,请写出此时木杆在地面上影子的长度________;
(2)如图2,夜晚在路灯下,小彬仍将长度为2的木杆水平放置,此时木杆在水平地面上的影子为线段.
①请在图中画出表示路灯灯泡位置的点P;
②经测量木杆距离地面1,其影子的长为3,求路灯P距离地面的高度.
试卷第1页,共3页
试卷第1页,共3页
《九年级数学下册人教版第二十九章《投影与视图》单元测试题》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C A B B D B D C A A
11.3
12.11
13.
14.5
15.解:如图,过点作于,
由题意,得,,,,,
,,
四边形是矩形,
,,
.
在中,,
,
,
,
,
四边形是矩形,
,
.
,
,
.
,
,
.
在中,由勾股定理,
得,
,解得
答:太阳能电板的影子的长为.
16.(1)解:线段为王琳在站在处路灯下的影子;
(2)根据题意知:,,,,,,,
∴,,
∵,
∴,
∴,
∴,
解得:,
答:王琳站在处在路灯下的影长为米;
(3)由(2)知:,
∵,
∴,
∴,
∴,
解得:,
答:路灯的高度为米.
17.(1)解:主视图、左视图、俯视图依次是
;
(2)解:由图可知,该几何体是由8个小正方体堆成的,
故答案为:8;
(3)解:如图,加上6块,得到的几何体从正面和左面看到的平面图形不变.
∴n的最大值为6,
故答案为:6.
18.(1)解:等高的物体垂直地面时,在灯光下离点光源越近的物体,它的影子越短,离点光源越远的物体,它的影子越长, D符合题意,
故答案为:D;
(2)解:,
,,
,,
又,
,
,,,,
,
,,
,
解得:;
灯杆的高度为.
19.(1)解:如图所示:
(2)解:可画出俯视图为:
∴当去掉一个小正方体①时,剩余部分的俯视图没有改变.
保持这个几何体的主视图和左视图不变,可在第一层的前面第一行添加2个小正方体.
故答案为:①,2.
20.(1)解:由主视图可得,第1列小立方块的块数为2,第3列小立方块的块数为1,
故,,
(2)解:这个几何体最少由块小立方块搭成,
这个几何体最多由块小立方块搭成;
(3)解:如图所示:
21.(1)解:如图1,过作交于,
∴,即为木杆在地面上影子,
∴,
故答案为:;
(2)①解:由中心投影的性质作图,如图2,点即为所求;
②解:如图3,过作于,交于,则路灯P距离地面的高度为的长,
∵,
∴,,
∴,即,
解得,,
∴路灯P距离地面的高度为3.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.如图是一个由五个大小相同的正方体组成的立体图形,它的主视图是( )
A. B. C. D.
2.如图,日晷是我国古代的一种计时仪器,它由“晷面”和“晷针”组成.当太阳光照在日晷上时,晷针的影子就像钟表的指针一样慢慢地转动,晷针的影子指向晷面的某一位置,便可知道是白天的某一时间.晷针在晷面上形成的投影是( )
A.平行投影 B.既是平行投影又是中心投影
C.中心投影 D.无法确定
3.中国古代经典数学著作《孙子算经》有首歌谣:“今有竿不知其长,量得影长一丈五尺,立一标杆,长一尺五寸,影长五寸、问竿长几何?”其大意是:有一根竹竿不知道有多长,直立后量出它在太阳下的影子长一丈五尺,同时直立一根一尺五寸的小标杆(如图),它的影长五寸(备注:1丈尺,1尺寸),问竹竿长多少?若设竹竿长x尺,则可列方程为( )
A. B. C. D.
4.如图,太阳光线与地面成的角,照射在地面上的一只皮球上,皮球在地面上的投影长是,则皮球的直径是( )
A. B. C. D.
5.如图,一块面积为的三角形硬纸板(记为△ABC)平行于投影面时,在点光源的照射下形成的投影是,若,则的面积是( )
A. B. C. D.
6.如图,“投影”是“三角尺”在灯光照射下的中心投影,其相似比为,且三角尺的面积为,则投影三角形的面积为( )
A. B. C. D.
7.《孙子算经》是我国古代重要的数学著作,其中有记载:“今有竿不知其长,量得影长百寸,立一标杆,长二十寸,影长五寸,问竿长几何?”其大意是:现在有一根不知道长度的竹竿,(把它竖立在太阳下)测量得它的影子长100寸,同时竖立一根长度为20寸的标杆,测量得它的影子长5寸,则竹竿的长度是( )
A.25寸 B.40寸 C.200寸 D.400寸
8.一块三角形纸板如图所示,,,测得边的中心投影的长为,则边的中心投影的长为( )
A. B. C. D.
9.如图是某几何体的三视图,则这个几何体的表面积( )
A. B. C. D.
10.马路边上有一棵树,树底距离护路坡的底端有3米,斜坡的坡角为60度,小明发现,下午2点时太阳光下该树的影子恰好为,同时刻1米长的竹竿影长为0.5米,下午4点时又发现该树的部分影子落在斜坡上的处,且,如图所示,线段的长度为( )
A. B. C. D.
二、填空题
11.一幢5层楼房只有一个窗户亮着一盏灯,一棵小树和一根电线杆在窗口灯光下的影子如图所示,则亮着灯的窗口是 .(填写相应的数字序号即可)
12.如图,数学兴趣小组想利用竹竿来测量旗杆的高度,在某一时刻测得1米长的竹竿竖直放置时影长2米,在同时刻测量旗杆的影长时,旗杆的影子一部分落在地面上,另一部分落在斜坡上,他测得落在地面上的影长为10米,落在斜坡上的影长为米,已知斜坡的坡度为,则旗杆的高度为 .
13.设计者给出了蒙古包的三视图(图中尺寸单位:),现在想用毛毡搭建一个这样的蒙古包,至少需要 平方米的毛毡(取).
14.如图,树在路灯O的照射下形成投影,已知树高,树影,树与路灯O的水平距离,则路灯的高度长是 米.
三、解答题
15.太阳能光伏发电因其消洁、安全、高效等特点,已成为世界各国重点发展的新能源产业.图①是太阳能电板,图②是其截面示意图,其中为太阳能电板,、均为钢架且垂直于地面为水平钢架且垂直于,已知太阳能电板,测得电板上两个支撑点的距离,钢架连接点.若某一时刻的太阳光线垂直照射,求太阳能电板的影子的长.
16.如图,王琳同学在晚上由路灯走向路灯,当他行到处时发现,他在路灯下的影长为米,且恰好位于路灯的正下方,接着他又走了米到处,此时他在路灯下的影子恰好位于路灯的正下方(已知王琳身高米,路灯高米)
(1)标出王琳站在处在路灯下的影子;
(2)计算王琳站在处在路灯下的影长;
(3)计算路灯的高度.
17.如图是由若干个完全相同的棱长为1的小正方体堆成的一个几何体.
(1)请在方格中分别画出它的主视图、左视图和俯视图;
(2)该几何体是由 个小正方体堆成的;
(3)若再添加n个小正方体,使新得到的几何体从正面和左面看到的平面图形不变,则n的最大值为 .
18.通常,路灯、台灯、手电筒……发出的光可以看成是从一个点发出的,在点光源的照射下,物体所产生的影称为中心投影.
(1)如图1,夜晚,小明从点A经过路灯C的正下方沿直线走到点B,他的影长y随他与点A之间的距离x的变化而变化,那么表示y与x之间函数关系的图像大致为_________;
A. B. C. D.
(2)如图2,小明为测河对岸的路灯杆的高度,在路灯A的灯光下,小明在点D处测得自己的影长,沿方向前进到达点F处测得自己的影长.已知小明的身高为,求路灯杆的高度.
19.如图所示的几何体是由5个大小相同的小正方体搭成.
(1)请在网格中画出这个几何体的主视图和左视图.
(2)在这个几何体中,当去掉一个小正方体______时,剩余部分的俯视图没有改变(填写图中小正方体的序号);如果在这个几何体上再添加一些相同的小正方体,并保持这个几何体的主视图和左视图不变,那么最多可以再添加______个小正方体.
20.用小立方块搭一个几何体,使它从正面、上面看到的形状图如图所示,从上面看到的形状图的小正方形中的字母表示在该位置小立方块的个数.试回答下列问题:
(1)a,d、f各表示几?
(2)这个几何体最少由几个小立方块搭成?最多呢?
(3)当,时,画出这个几何体从左面看到的形状图.
21.小彬做了探究物体投影规律的实验,并提出了一些数学问题请你解答:
(1)如图1,白天在阳光下,小彬将长度为2的木杆水平放置,此时木杆在水平地面上的影子为线段,并测量出光线与地面的夹角为.在同一时刻同一地点,将一根与长度相等的木杆直立于地面,请写出此时木杆在地面上影子的长度________;
(2)如图2,夜晚在路灯下,小彬仍将长度为2的木杆水平放置,此时木杆在水平地面上的影子为线段.
①请在图中画出表示路灯灯泡位置的点P;
②经测量木杆距离地面1,其影子的长为3,求路灯P距离地面的高度.
试卷第1页,共3页
试卷第1页,共3页
《九年级数学下册人教版第二十九章《投影与视图》单元测试题》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C A B B D B D C A A
11.3
12.11
13.
14.5
15.解:如图,过点作于,
由题意,得,,,,,
,,
四边形是矩形,
,,
.
在中,,
,
,
,
,
四边形是矩形,
,
.
,
,
.
,
,
.
在中,由勾股定理,
得,
,解得
答:太阳能电板的影子的长为.
16.(1)解:线段为王琳在站在处路灯下的影子;
(2)根据题意知:,,,,,,,
∴,,
∵,
∴,
∴,
∴,
解得:,
答:王琳站在处在路灯下的影长为米;
(3)由(2)知:,
∵,
∴,
∴,
∴,
解得:,
答:路灯的高度为米.
17.(1)解:主视图、左视图、俯视图依次是
;
(2)解:由图可知,该几何体是由8个小正方体堆成的,
故答案为:8;
(3)解:如图,加上6块,得到的几何体从正面和左面看到的平面图形不变.
∴n的最大值为6,
故答案为:6.
18.(1)解:等高的物体垂直地面时,在灯光下离点光源越近的物体,它的影子越短,离点光源越远的物体,它的影子越长, D符合题意,
故答案为:D;
(2)解:,
,,
,,
又,
,
,,,,
,
,,
,
解得:;
灯杆的高度为.
19.(1)解:如图所示:
(2)解:可画出俯视图为:
∴当去掉一个小正方体①时,剩余部分的俯视图没有改变.
保持这个几何体的主视图和左视图不变,可在第一层的前面第一行添加2个小正方体.
故答案为:①,2.
20.(1)解:由主视图可得,第1列小立方块的块数为2,第3列小立方块的块数为1,
故,,
(2)解:这个几何体最少由块小立方块搭成,
这个几何体最多由块小立方块搭成;
(3)解:如图所示:
21.(1)解:如图1,过作交于,
∴,即为木杆在地面上影子,
∴,
故答案为:;
(2)①解:由中心投影的性质作图,如图2,点即为所求;
②解:如图3,过作于,交于,则路灯P距离地面的高度为的长,
∵,
∴,,
∴,即,
解得,,
∴路灯P距离地面的高度为3.
答案第1页,共2页
答案第1页,共2页
