第三章 概率的进一步认识 学情评估卷(含答案)北师大版数学九年级上册
文档属性
| 名称 | 第三章 概率的进一步认识 学情评估卷(含答案)北师大版数学九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 479.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-10 20:57:00 | ||
图片预览




文档简介
第三章 概率的进一步认识 学情评估卷
时间:120分钟 满分:120分
一、选择题(每题3分,共30分)
1.在“石头、剪刀、布”的游戏中,当你出“石头”时,对手与你打平的概率为( )
A. B. C. D.
2.[[2024北京中考]]不透明的袋子中装有一个红色小球和一个白色小球,除颜色外两个小球无其他差别.从中随机取出一个小球后,放回并摇匀,再从中随机取出一个小球,则两次都取到白色小球的概率为( )
A. B. C. D.
3.4件外观相同的产品中有2件不合格,现从中一次抽取2件进行检测,则1件产品合格,1件产品不合格的概率是( )
A. B. C. D.
4.[[2024晋中模拟]]“五一”假期,前来参观山西博物院的游客络绎不绝,在文创体验区,不少人手拿刻有特色文物的印章,将其印在自己精挑细选的明信片上.现有“晋侯鸟尊”“鸮卣”“兽形觥”“雁鱼铜灯”四枚特色文物的印章(除图案外,其他都相同),小乐从中随机抽取一枚印章(不放回),再从中随机抽取一枚印章,则小乐抽到的两枚印章的图案恰好是“晋侯鸟尊”和“兽形觥”的概率为( )
A. B. C. D.
5.如图所示的是四张背面相同的卡片,卡片正面写有常见的生活现象,现将所有卡片背面朝上洗匀,从中随机抽取两张,则这两张卡片正面恰好都是化学变化的概率是( )
A. B. C. D.
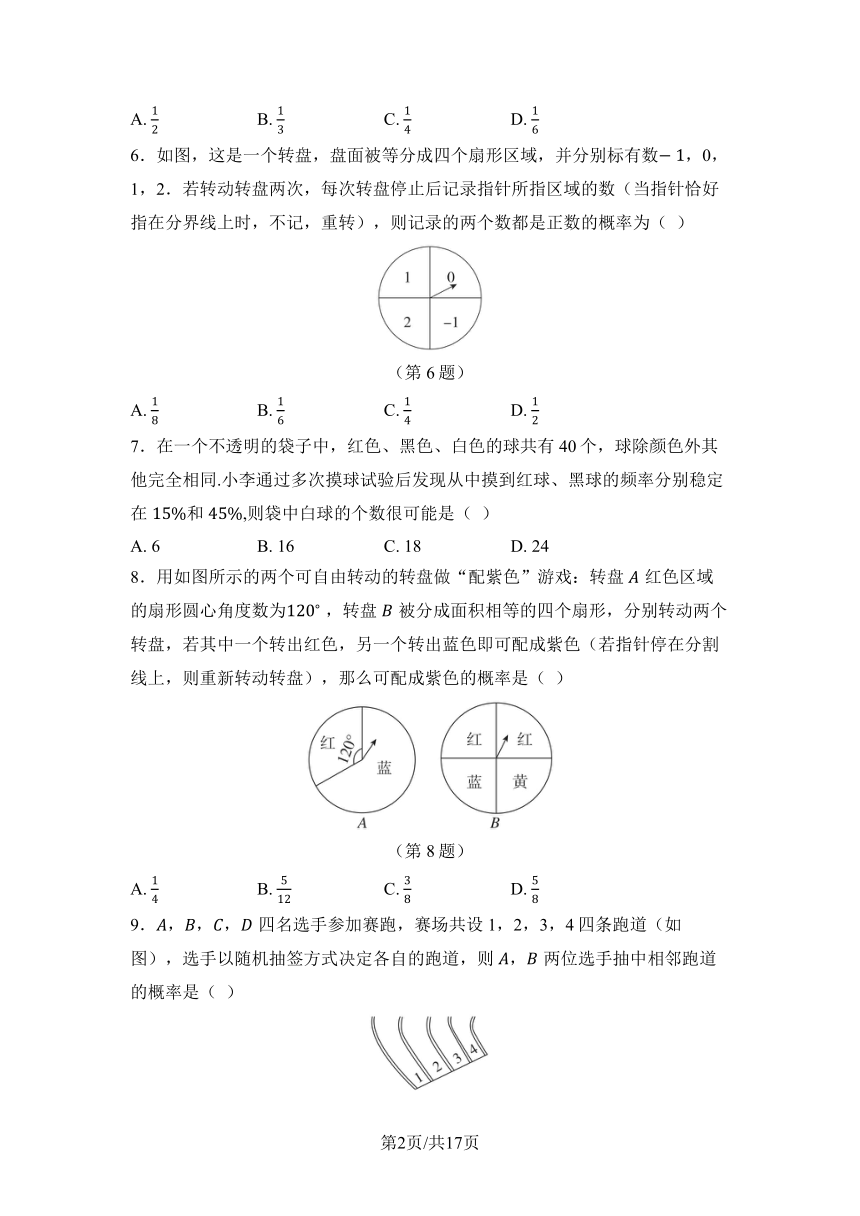
6.如图,这是一个转盘,盘面被等分成四个扇形区域,并分别标有数,0,1,2.若转动转盘两次,每次转盘停止后记录指针所指区域的数(当指针恰好指在分界线上时,不记,重转),则记录的两个数都是正数的概率为( )
(第6题)
A. B. C. D.
7.在一个不透明的袋子中,红色、黑色、白色的球共有40个,球除颜色外其他完全相同.小李通过多次摸球试验后发现从中摸到红球、黑球的频率分别稳定在和,则袋中白球的个数很可能是( )
A. 6 B. 16 C. 18 D. 24
8.用如图所示的两个可自由转动的转盘做“配紫色”游戏:转盘红色区域的扇形圆心角度数为 ,转盘被分成面积相等的四个扇形,分别转动两个转盘,若其中一个转出红色,另一个转出蓝色即可配成紫色(若指针停在分割线上,则重新转动转盘),那么可配成紫色的概率是( )
(第8题)
A. B. C. D.
9.,,,四名选手参加赛跑,赛场共设1,2,3,4四条跑道(如图),选手以随机抽签方式决定各自的跑道,则,两位选手抽中相邻跑道的概率是( )
(第9题)
A. B. C. D.
10.一枚质地均匀的正方体骰子的六个面上的数字分别是1,2,3,4,5,6.掷两次骰子,设其朝上的面上的两个数字之和除以4没有余数及余数分别是1,2,3的概率为,,,,则,,,中最大的是( )
A. B. C. D.
二、填空题(每题3分,共15分)
11.甲、乙两人分别从,,三个景区中随机选取一个景区前往游览,则他们恰好选择同一景区的概率为_ _ _ _ _ _ .
12.一只蚂蚁在如图所示的正方形地砖上爬行,蚂蚁停在阴影部分的概率为_ _ _ _ _ _ .
(第12题)
13.地理实践课上,活动小组的同学在一张面积为的长方形卡片上绘制了如图①所示的山西省地形图,他们想了解该地形图的面积,经研究采取了以下办法:将长方形卡片水平放置在地面上,在适当位置随机地朝长方形卡片内扔小球(球的大小忽略不计),并记录落在该地形图上的次数(球扔在地形图最外围的界线上或长方形卡片外不计入试验结果).他们将若干次有效试验结果绘制成了如图②所示的折线统计图,由此估计该地形图的面积为_ _ .
(第13题)
14.在数,0,1,2中任取两个数作为点的坐标,那么该点刚好在一次函数的图象上的概率是_ _ _ _ _ _ _ _ .
15.如图,有三类矩形(或正方形)卡片,其中甲同学持有,类卡片各一张,乙同学持有,类卡片各一张,丙同学持有,类卡片各一张,现随机选取两名同学手中的卡片共四张进行拼图,则能拼成一个正方形的概率是_ _ _ _ _ _ .
(第15题)
三、解答题(共75分)
16.[[2024镇江中考]](8分) 3张相同的卡片上分别写有中国二十四节气中的“小满”“芒种”“夏至”的字样,将卡片的背面朝上.
(1) 洗匀后,从中任意抽取1张卡片,抽到写有“小满”的卡片的概率为_ _ _ _ _ _ ;
(2) 洗匀后,从中任意抽取2张卡片,用画树状图或列表的方法,求抽到一张写有“芒种”,一张写有“夏至”的卡片的概率.
17.(8分)十一期间,甲、乙两人要去附近的景点游玩,甲从,两个景点中任意选择一个游玩,乙从,,三个景点中任意选择一个游玩.用列表或画树状图的方法列出所有可能的结果,并求甲、乙恰好游玩同一景点的概率.
18.(8分)某校为充分调动学生的积极性,在学校开展各项娱乐活动,丰富学生的课余生活,其中,语文组开展了以“说我身边的事”为主题的演讲比赛,共有5名同学获得一等奖,其中,七年级1名,八、九年级各2名.
(1) 从获得一等奖的5名同学中随机抽取1名参加区级比赛,则抽到八年级的同学的概率是_ _ _ _ _ _ ;
(2) 学校决定从获得一等奖的同学中任选2名同学参加社区组织的“说我身边的变化”演讲活动.请用列表或画树状图的方法求所选2名同学恰好是1名七年级同学和1名九年级同学的概率.
19.[[2025·运城期中]](8分) 游戏是生活中有趣味的社交活动,是人类终身不可缺少的伴侣,更是家庭欢乐的源泉.小刚父亲和小刚二叔玩一种游戏,游戏规则:两人只可以说出“木棒”“老虎”“公鸡”“小虫”中的任何一个,同时各说出一个后定胜负,其中“木棒”胜“老虎”、“老虎”胜“公鸡”、“公鸡”胜“小虫”、“小虫”胜“木棒”.其他情况,则为平局.例如,小刚父亲说“老虎”,小刚二叔说“公鸡”,则小刚父亲胜;又如,两人同时说“虫子”,则为平局;再如,一人说“公鸡”,一人说“木棒”,则为平局.
(1) 每一次小刚父亲说出“老虎”的概率是_ _ _ _ _ _ ;
(2) 如果用,,,分别表示小刚父亲说的“木棒”“老虎”“公鸡”“小虫”;用,,,分别表示小刚二叔说的“木棒”“老虎”“公鸡”“小虫”,那么某一次说出时小刚父亲胜小刚二叔的概率是多少?用列表法或画树状图法加以说明;
(3) 你认为这个游戏对小刚父亲和小刚二叔公平吗?为什么?
20.(8分)一个不透明的口袋中放着若干个红球和黑球,这两种球除了颜色之外没有其他任何区别,口袋中的球已经搅匀,闭眼从口袋中摸出一个球记下颜色后放回,经过很多次试验后发现摸到红球的频率逐渐稳定在.
(1) 估计摸到黑球的概率是_ _ _ _ _ _ ;
(2) 如果口袋中原有红球12个,又放入个黑球,再经过很多次试验后发现摸到黑球的频率逐渐稳定在,求的值.
21.(10分)一个不透明的袋子中装有4个质地、大小均相同的小球,这些小球分别标有数字2,3,4,.甲、乙两人每次同时从袋子中各随机摸出1个小球,并计算摸出的这2个小球上的数字之和,记录后都将小球放回袋子中搅匀,进行重复试验.试验数据如下表:
摸球总次数 20 30 60 90 120 180 240 330 450
“和为7”出现的频数 11 13 25 30 37 59 82 110 150
“和为7”出现的频率 0.550 0.433 0.417 0.333 0.308 0.328 0.342 0.333 0.333
解答下列问题:
(1) 如果试验继续进行下去,出现“和为7”的频率将稳定在它的概率附近,根据表中数据,估计出现“和为7”的概率是_ _ ;(保留两位小数)
(2) 当时,请用列表法或画树状图法计算“和为7”的概率.
22.(12分) 如图,的三个顶点及,,,,五个点分别位于正方形网格的格点上.
(1) 现以,,,,中的三个点为顶点画三角形,在所画的三角形中与不全等但面积相等的三角形是_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ ;(填一个三角形即可)
(2) 先从,两个点中任意取一个点,再从,,三个点中任意取两个不同的点,以所取得的这三个点为顶点画三角形,求所画三角形与面积相等的概率(用画树状图法或列表法求解).
23.(13分)学校为了解本校中考体育情况,随机抽取了部分学生的体育成绩进行统计分析,发现最低分为45分,且成绩为45分的学生占抽查人数的,现将抽查结果绘制成了如图所示的不完整的折线统计图,请根据图中信息,回答下列问题:
(1) 此次抽查的学生共名,抽查的学生体育成绩的中位数是_ _ 分,抽查的女生体育成绩的平均数是分;
(2) 补全折线统计图;
(3) 为了今后中考体育取得更好的成绩,学校决定分别从成绩为50分的男生和女生中各选一名参加“经验座谈会”,若成绩为50分的男、女生中各有两名体育特长生,请用列表或画树状图的方法求出所选的两名学生刚好都不是体育特长生的概率.
第三章 概率的进一步认识 学情评估卷
时间:120分钟 满分:120分
一、选择题(每题3分,共30分)
1.在“石头、剪刀、布”的游戏中,当你出“石头”时,对手与你打平的概率为( )
A. B. C. D.
【答案】B
2.[[2024北京中考]]不透明的袋子中装有一个红色小球和一个白色小球,除颜色外两个小球无其他差别.从中随机取出一个小球后,放回并摇匀,再从中随机取出一个小球,则两次都取到白色小球的概率为( )
A. B. C. D.
【答案】D
3.4件外观相同的产品中有2件不合格,现从中一次抽取2件进行检测,则1件产品合格,1件产品不合格的概率是( )
A. B. C. D.
【答案】D
4.[[2024晋中模拟]]“五一”假期,前来参观山西博物院的游客络绎不绝,在文创体验区,不少人手拿刻有特色文物的印章,将其印在自己精挑细选的明信片上.现有“晋侯鸟尊”“鸮卣”“兽形觥”“雁鱼铜灯”四枚特色文物的印章(除图案外,其他都相同),小乐从中随机抽取一枚印章(不放回),再从中随机抽取一枚印章,则小乐抽到的两枚印章的图案恰好是“晋侯鸟尊”和“兽形觥”的概率为( )
A. B. C. D.
【答案】A
5.如图所示的是四张背面相同的卡片,卡片正面写有常见的生活现象,现将所有卡片背面朝上洗匀,从中随机抽取两张,则这两张卡片正面恰好都是化学变化的概率是( )
A. B. C. D.
【答案】A
6.如图,这是一个转盘,盘面被等分成四个扇形区域,并分别标有数,0,1,2.若转动转盘两次,每次转盘停止后记录指针所指区域的数(当指针恰好指在分界线上时,不记,重转),则记录的两个数都是正数的概率为( )
(第6题)
A. B. C. D.
【答案】C
7.在一个不透明的袋子中,红色、黑色、白色的球共有40个,球除颜色外其他完全相同.小李通过多次摸球试验后发现从中摸到红球、黑球的频率分别稳定在和,则袋中白球的个数很可能是( )
A. 6 B. 16 C. 18 D. 24
【答案】B
8.用如图所示的两个可自由转动的转盘做“配紫色”游戏:转盘红色区域的扇形圆心角度数为 ,转盘被分成面积相等的四个扇形,分别转动两个转盘,若其中一个转出红色,另一个转出蓝色即可配成紫色(若指针停在分割线上,则重新转动转盘),那么可配成紫色的概率是( )
(第8题)
A. B. C. D.
【答案】B
9.,,,四名选手参加赛跑,赛场共设1,2,3,4四条跑道(如图),选手以随机抽签方式决定各自的跑道,则,两位选手抽中相邻跑道的概率是( )
(第9题)
A. B. C. D.
【答案】A
10.一枚质地均匀的正方体骰子的六个面上的数字分别是1,2,3,4,5,6.掷两次骰子,设其朝上的面上的两个数字之和除以4没有余数及余数分别是1,2,3的概率为,,,,则,,,中最大的是( )
A. B. C. D.
【答案】D
二、填空题(每题3分,共15分)
11.甲、乙两人分别从,,三个景区中随机选取一个景区前往游览,则他们恰好选择同一景区的概率为_ _ _ _ _ _ .
【答案】
12.一只蚂蚁在如图所示的正方形地砖上爬行,蚂蚁停在阴影部分的概率为_ _ _ _ _ _ .
(第12题)
【答案】
13.地理实践课上,活动小组的同学在一张面积为的长方形卡片上绘制了如图①所示的山西省地形图,他们想了解该地形图的面积,经研究采取了以下办法:将长方形卡片水平放置在地面上,在适当位置随机地朝长方形卡片内扔小球(球的大小忽略不计),并记录落在该地形图上的次数(球扔在地形图最外围的界线上或长方形卡片外不计入试验结果).他们将若干次有效试验结果绘制成了如图②所示的折线统计图,由此估计该地形图的面积为_ _ .
(第13题)
【答案】100
14.在数,0,1,2中任取两个数作为点的坐标,那么该点刚好在一次函数的图象上的概率是_ _ _ _ _ _ _ _ .
【答案】
15.如图,有三类矩形(或正方形)卡片,其中甲同学持有,类卡片各一张,乙同学持有,类卡片各一张,丙同学持有,类卡片各一张,现随机选取两名同学手中的卡片共四张进行拼图,则能拼成一个正方形的概率是_ _ _ _ _ _ .
(第15题)
【答案】
三、解答题(共75分)
16.[[2024镇江中考]](8分) 3张相同的卡片上分别写有中国二十四节气中的“小满”“芒种”“夏至”的字样,将卡片的背面朝上.
(1) 洗匀后,从中任意抽取1张卡片,抽到写有“小满”的卡片的概率为_ _ _ _ _ _ ;
(2) 洗匀后,从中任意抽取2张卡片,用画树状图或列表的方法,求抽到一张写有“芒种”,一张写有“夏至”的卡片的概率.
【答案】(1)
(2) 解:画树状图略.共有6种等可能的结果,其中抽到一张写有“芒种”,一张写有“夏至”的卡片的结果有2种, 抽到一张写有“芒种”,一张写有“夏至”的卡片的概率为.
17.(8分)十一期间,甲、乙两人要去附近的景点游玩,甲从,两个景点中任意选择一个游玩,乙从,,三个景点中任意选择一个游玩.用列表或画树状图的方法列出所有可能的结果,并求甲、乙恰好游玩同一景点的概率.
解:画树状图略.共有6种结果,且每种结果出现的可能性相同,其中甲、乙恰好游玩同一景点的结果有2种,所以甲、乙恰好游玩同一景点的概率为.
18.(8分)某校为充分调动学生的积极性,在学校开展各项娱乐活动,丰富学生的课余生活,其中,语文组开展了以“说我身边的事”为主题的演讲比赛,共有5名同学获得一等奖,其中,七年级1名,八、九年级各2名.
(1) 从获得一等奖的5名同学中随机抽取1名参加区级比赛,则抽到八年级的同学的概率是_ _ _ _ _ _ ;
(2) 学校决定从获得一等奖的同学中任选2名同学参加社区组织的“说我身边的变化”演讲活动.请用列表或画树状图的方法求所选2名同学恰好是1名七年级同学和1名九年级同学的概率.
【答案】(1)
(2) 解:画树状图略.共有20种等可能的结果,其中所选的2名同学恰好是1名七年级同学和1名九年级同学的结果有4种,则所选2名同学恰好是1名七年级同学和1名九年级同学的概率为.
19.[[2025·运城期中]](8分) 游戏是生活中有趣味的社交活动,是人类终身不可缺少的伴侣,更是家庭欢乐的源泉.小刚父亲和小刚二叔玩一种游戏,游戏规则:两人只可以说出“木棒”“老虎”“公鸡”“小虫”中的任何一个,同时各说出一个后定胜负,其中“木棒”胜“老虎”、“老虎”胜“公鸡”、“公鸡”胜“小虫”、“小虫”胜“木棒”.其他情况,则为平局.例如,小刚父亲说“老虎”,小刚二叔说“公鸡”,则小刚父亲胜;又如,两人同时说“虫子”,则为平局;再如,一人说“公鸡”,一人说“木棒”,则为平局.
(1) 每一次小刚父亲说出“老虎”的概率是_ _ _ _ _ _ ;
(2) 如果用,,,分别表示小刚父亲说的“木棒”“老虎”“公鸡”“小虫”;用,,,分别表示小刚二叔说的“木棒”“老虎”“公鸡”“小虫”,那么某一次说出时小刚父亲胜小刚二叔的概率是多少?用列表法或画树状图法加以说明;
(3) 你认为这个游戏对小刚父亲和小刚二叔公平吗?为什么?
【答案】(1)
(2) 解:列表略.共有16种等可能的结果,其中小刚父亲胜小刚二叔的结果有4种,
某一次说出时小刚父亲胜小刚二叔的概率为.
(3) 由(2)中表格可知某一次说出时小刚二叔胜小刚父亲的概率为,, 两人获胜的概率相等,这个游戏对小刚父亲和小刚二叔是公平的.
20.(8分)一个不透明的口袋中放着若干个红球和黑球,这两种球除了颜色之外没有其他任何区别,口袋中的球已经搅匀,闭眼从口袋中摸出一个球记下颜色后放回,经过很多次试验后发现摸到红球的频率逐渐稳定在.
(1) 估计摸到黑球的概率是_ _ _ _ _ _ ;
(2) 如果口袋中原有红球12个,又放入个黑球,再经过很多次试验后发现摸到黑球的频率逐渐稳定在,求的值.
【答案】(1)
(2) 解:设口袋中原有黑球个,根据题意得,
解得,经检验是原方程的根,且符合题意.
原有黑球18个.
根据题意得,解得,
经检验是原方程的根,且符合题意.的值是6.
21.(10分)一个不透明的袋子中装有4个质地、大小均相同的小球,这些小球分别标有数字2,3,4,.甲、乙两人每次同时从袋子中各随机摸出1个小球,并计算摸出的这2个小球上的数字之和,记录后都将小球放回袋子中搅匀,进行重复试验.试验数据如下表:
摸球总次数 20 30 60 90 120 180 240 330 450
“和为7”出现的频数 11 13 25 30 37 59 82 110 150
“和为7”出现的频率 0.550 0.433 0.417 0.333 0.308 0.328 0.342 0.333 0.333
解答下列问题:
(1) 如果试验继续进行下去,出现“和为7”的频率将稳定在它的概率附近,根据表中数据,估计出现“和为7”的概率是_ _ ;(保留两位小数)
(2) 当时,请用列表法或画树状图法计算“和为7”的概率.
【答案】(1) 0.33
(2) 解:当时,画树状图略.共有12种结果,且每种结果出现的可能性相同,其中“和为7”的结果有4种,所以“和为7”的概率为.
22.(12分) 如图,的三个顶点及,,,,五个点分别位于正方形网格的格点上.
(1) 现以,,,,中的三个点为顶点画三角形,在所画的三角形中与不全等但面积相等的三角形是_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ ;(填一个三角形即可)
(2) 先从,两个点中任意取一个点,再从,,三个点中任意取两个不同的点,以所取得的这三个点为顶点画三角形,求所画三角形与面积相等的概率(用画树状图法或列表法求解).
【答案】(1) (答案不唯一)
(2) 解:画树状图略.有,,,,,共6种等可能的结果,其中与面积相等的结果有,,,共3种,
所画三角形与面积相等的概率为.
23.(13分)学校为了解本校中考体育情况,随机抽取了部分学生的体育成绩进行统计分析,发现最低分为45分,且成绩为45分的学生占抽查人数的,现将抽查结果绘制成了如图所示的不完整的折线统计图,请根据图中信息,回答下列问题:
(1) 此次抽查的学生共名,抽查的学生体育成绩的中位数是_ _ 分,抽查的女生体育成绩的平均数是分;
(2) 补全折线统计图;
(3) 为了今后中考体育取得更好的成绩,学校决定分别从成绩为50分的男生和女生中各选一名参加“经验座谈会”,若成绩为50分的男、女生中各有两名体育特长生,请用列表或画树状图的方法求出所选的两名学生刚好都不是体育特长生的概率.
【答案】(1) 50;48.5;48
(2) 解:补全折线统计图如图.
(3) 设成绩为50分的男生分别为男1、男2、男3、男4,其中男1、男2是体育特长生,成绩为50分的女生分别为女1、女2、女3、女4、女5,其中女1、女2是体育特长生,
列表如下:
女1 女2 女3 女4 女5
男1 (男1,女1) (男1,女2) (男1,女3) (男1,女4) (男1,女5)
男2 (男2,女1) (男2,女2) (男2,女3) (男2,女4) (男2,女5)
男3 (男3,女1) (男3,女2) (男3,女3) (男3,女4) (男3,女5)
男4 (男4,女1) (男4,女2) (男4,女3) (男4,女4) (男4,女5)
由表可知,一共有20种结果,且每种结果出现的可能性相同,其中所选的两名学生都不是体育特长生的结果有6种,所以(所选的两名学生都不是体育特长生).
第页/共页
时间:120分钟 满分:120分
一、选择题(每题3分,共30分)
1.在“石头、剪刀、布”的游戏中,当你出“石头”时,对手与你打平的概率为( )
A. B. C. D.
2.[[2024北京中考]]不透明的袋子中装有一个红色小球和一个白色小球,除颜色外两个小球无其他差别.从中随机取出一个小球后,放回并摇匀,再从中随机取出一个小球,则两次都取到白色小球的概率为( )
A. B. C. D.
3.4件外观相同的产品中有2件不合格,现从中一次抽取2件进行检测,则1件产品合格,1件产品不合格的概率是( )
A. B. C. D.
4.[[2024晋中模拟]]“五一”假期,前来参观山西博物院的游客络绎不绝,在文创体验区,不少人手拿刻有特色文物的印章,将其印在自己精挑细选的明信片上.现有“晋侯鸟尊”“鸮卣”“兽形觥”“雁鱼铜灯”四枚特色文物的印章(除图案外,其他都相同),小乐从中随机抽取一枚印章(不放回),再从中随机抽取一枚印章,则小乐抽到的两枚印章的图案恰好是“晋侯鸟尊”和“兽形觥”的概率为( )
A. B. C. D.
5.如图所示的是四张背面相同的卡片,卡片正面写有常见的生活现象,现将所有卡片背面朝上洗匀,从中随机抽取两张,则这两张卡片正面恰好都是化学变化的概率是( )
A. B. C. D.
6.如图,这是一个转盘,盘面被等分成四个扇形区域,并分别标有数,0,1,2.若转动转盘两次,每次转盘停止后记录指针所指区域的数(当指针恰好指在分界线上时,不记,重转),则记录的两个数都是正数的概率为( )
(第6题)
A. B. C. D.
7.在一个不透明的袋子中,红色、黑色、白色的球共有40个,球除颜色外其他完全相同.小李通过多次摸球试验后发现从中摸到红球、黑球的频率分别稳定在和,则袋中白球的个数很可能是( )
A. 6 B. 16 C. 18 D. 24
8.用如图所示的两个可自由转动的转盘做“配紫色”游戏:转盘红色区域的扇形圆心角度数为 ,转盘被分成面积相等的四个扇形,分别转动两个转盘,若其中一个转出红色,另一个转出蓝色即可配成紫色(若指针停在分割线上,则重新转动转盘),那么可配成紫色的概率是( )
(第8题)
A. B. C. D.
9.,,,四名选手参加赛跑,赛场共设1,2,3,4四条跑道(如图),选手以随机抽签方式决定各自的跑道,则,两位选手抽中相邻跑道的概率是( )
(第9题)
A. B. C. D.
10.一枚质地均匀的正方体骰子的六个面上的数字分别是1,2,3,4,5,6.掷两次骰子,设其朝上的面上的两个数字之和除以4没有余数及余数分别是1,2,3的概率为,,,,则,,,中最大的是( )
A. B. C. D.
二、填空题(每题3分,共15分)
11.甲、乙两人分别从,,三个景区中随机选取一个景区前往游览,则他们恰好选择同一景区的概率为_ _ _ _ _ _ .
12.一只蚂蚁在如图所示的正方形地砖上爬行,蚂蚁停在阴影部分的概率为_ _ _ _ _ _ .
(第12题)
13.地理实践课上,活动小组的同学在一张面积为的长方形卡片上绘制了如图①所示的山西省地形图,他们想了解该地形图的面积,经研究采取了以下办法:将长方形卡片水平放置在地面上,在适当位置随机地朝长方形卡片内扔小球(球的大小忽略不计),并记录落在该地形图上的次数(球扔在地形图最外围的界线上或长方形卡片外不计入试验结果).他们将若干次有效试验结果绘制成了如图②所示的折线统计图,由此估计该地形图的面积为_ _ .
(第13题)
14.在数,0,1,2中任取两个数作为点的坐标,那么该点刚好在一次函数的图象上的概率是_ _ _ _ _ _ _ _ .
15.如图,有三类矩形(或正方形)卡片,其中甲同学持有,类卡片各一张,乙同学持有,类卡片各一张,丙同学持有,类卡片各一张,现随机选取两名同学手中的卡片共四张进行拼图,则能拼成一个正方形的概率是_ _ _ _ _ _ .
(第15题)
三、解答题(共75分)
16.[[2024镇江中考]](8分) 3张相同的卡片上分别写有中国二十四节气中的“小满”“芒种”“夏至”的字样,将卡片的背面朝上.
(1) 洗匀后,从中任意抽取1张卡片,抽到写有“小满”的卡片的概率为_ _ _ _ _ _ ;
(2) 洗匀后,从中任意抽取2张卡片,用画树状图或列表的方法,求抽到一张写有“芒种”,一张写有“夏至”的卡片的概率.
17.(8分)十一期间,甲、乙两人要去附近的景点游玩,甲从,两个景点中任意选择一个游玩,乙从,,三个景点中任意选择一个游玩.用列表或画树状图的方法列出所有可能的结果,并求甲、乙恰好游玩同一景点的概率.
18.(8分)某校为充分调动学生的积极性,在学校开展各项娱乐活动,丰富学生的课余生活,其中,语文组开展了以“说我身边的事”为主题的演讲比赛,共有5名同学获得一等奖,其中,七年级1名,八、九年级各2名.
(1) 从获得一等奖的5名同学中随机抽取1名参加区级比赛,则抽到八年级的同学的概率是_ _ _ _ _ _ ;
(2) 学校决定从获得一等奖的同学中任选2名同学参加社区组织的“说我身边的变化”演讲活动.请用列表或画树状图的方法求所选2名同学恰好是1名七年级同学和1名九年级同学的概率.
19.[[2025·运城期中]](8分) 游戏是生活中有趣味的社交活动,是人类终身不可缺少的伴侣,更是家庭欢乐的源泉.小刚父亲和小刚二叔玩一种游戏,游戏规则:两人只可以说出“木棒”“老虎”“公鸡”“小虫”中的任何一个,同时各说出一个后定胜负,其中“木棒”胜“老虎”、“老虎”胜“公鸡”、“公鸡”胜“小虫”、“小虫”胜“木棒”.其他情况,则为平局.例如,小刚父亲说“老虎”,小刚二叔说“公鸡”,则小刚父亲胜;又如,两人同时说“虫子”,则为平局;再如,一人说“公鸡”,一人说“木棒”,则为平局.
(1) 每一次小刚父亲说出“老虎”的概率是_ _ _ _ _ _ ;
(2) 如果用,,,分别表示小刚父亲说的“木棒”“老虎”“公鸡”“小虫”;用,,,分别表示小刚二叔说的“木棒”“老虎”“公鸡”“小虫”,那么某一次说出时小刚父亲胜小刚二叔的概率是多少?用列表法或画树状图法加以说明;
(3) 你认为这个游戏对小刚父亲和小刚二叔公平吗?为什么?
20.(8分)一个不透明的口袋中放着若干个红球和黑球,这两种球除了颜色之外没有其他任何区别,口袋中的球已经搅匀,闭眼从口袋中摸出一个球记下颜色后放回,经过很多次试验后发现摸到红球的频率逐渐稳定在.
(1) 估计摸到黑球的概率是_ _ _ _ _ _ ;
(2) 如果口袋中原有红球12个,又放入个黑球,再经过很多次试验后发现摸到黑球的频率逐渐稳定在,求的值.
21.(10分)一个不透明的袋子中装有4个质地、大小均相同的小球,这些小球分别标有数字2,3,4,.甲、乙两人每次同时从袋子中各随机摸出1个小球,并计算摸出的这2个小球上的数字之和,记录后都将小球放回袋子中搅匀,进行重复试验.试验数据如下表:
摸球总次数 20 30 60 90 120 180 240 330 450
“和为7”出现的频数 11 13 25 30 37 59 82 110 150
“和为7”出现的频率 0.550 0.433 0.417 0.333 0.308 0.328 0.342 0.333 0.333
解答下列问题:
(1) 如果试验继续进行下去,出现“和为7”的频率将稳定在它的概率附近,根据表中数据,估计出现“和为7”的概率是_ _ ;(保留两位小数)
(2) 当时,请用列表法或画树状图法计算“和为7”的概率.
22.(12分) 如图,的三个顶点及,,,,五个点分别位于正方形网格的格点上.
(1) 现以,,,,中的三个点为顶点画三角形,在所画的三角形中与不全等但面积相等的三角形是_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ ;(填一个三角形即可)
(2) 先从,两个点中任意取一个点,再从,,三个点中任意取两个不同的点,以所取得的这三个点为顶点画三角形,求所画三角形与面积相等的概率(用画树状图法或列表法求解).
23.(13分)学校为了解本校中考体育情况,随机抽取了部分学生的体育成绩进行统计分析,发现最低分为45分,且成绩为45分的学生占抽查人数的,现将抽查结果绘制成了如图所示的不完整的折线统计图,请根据图中信息,回答下列问题:
(1) 此次抽查的学生共名,抽查的学生体育成绩的中位数是_ _ 分,抽查的女生体育成绩的平均数是分;
(2) 补全折线统计图;
(3) 为了今后中考体育取得更好的成绩,学校决定分别从成绩为50分的男生和女生中各选一名参加“经验座谈会”,若成绩为50分的男、女生中各有两名体育特长生,请用列表或画树状图的方法求出所选的两名学生刚好都不是体育特长生的概率.
第三章 概率的进一步认识 学情评估卷
时间:120分钟 满分:120分
一、选择题(每题3分,共30分)
1.在“石头、剪刀、布”的游戏中,当你出“石头”时,对手与你打平的概率为( )
A. B. C. D.
【答案】B
2.[[2024北京中考]]不透明的袋子中装有一个红色小球和一个白色小球,除颜色外两个小球无其他差别.从中随机取出一个小球后,放回并摇匀,再从中随机取出一个小球,则两次都取到白色小球的概率为( )
A. B. C. D.
【答案】D
3.4件外观相同的产品中有2件不合格,现从中一次抽取2件进行检测,则1件产品合格,1件产品不合格的概率是( )
A. B. C. D.
【答案】D
4.[[2024晋中模拟]]“五一”假期,前来参观山西博物院的游客络绎不绝,在文创体验区,不少人手拿刻有特色文物的印章,将其印在自己精挑细选的明信片上.现有“晋侯鸟尊”“鸮卣”“兽形觥”“雁鱼铜灯”四枚特色文物的印章(除图案外,其他都相同),小乐从中随机抽取一枚印章(不放回),再从中随机抽取一枚印章,则小乐抽到的两枚印章的图案恰好是“晋侯鸟尊”和“兽形觥”的概率为( )
A. B. C. D.
【答案】A
5.如图所示的是四张背面相同的卡片,卡片正面写有常见的生活现象,现将所有卡片背面朝上洗匀,从中随机抽取两张,则这两张卡片正面恰好都是化学变化的概率是( )
A. B. C. D.
【答案】A
6.如图,这是一个转盘,盘面被等分成四个扇形区域,并分别标有数,0,1,2.若转动转盘两次,每次转盘停止后记录指针所指区域的数(当指针恰好指在分界线上时,不记,重转),则记录的两个数都是正数的概率为( )
(第6题)
A. B. C. D.
【答案】C
7.在一个不透明的袋子中,红色、黑色、白色的球共有40个,球除颜色外其他完全相同.小李通过多次摸球试验后发现从中摸到红球、黑球的频率分别稳定在和,则袋中白球的个数很可能是( )
A. 6 B. 16 C. 18 D. 24
【答案】B
8.用如图所示的两个可自由转动的转盘做“配紫色”游戏:转盘红色区域的扇形圆心角度数为 ,转盘被分成面积相等的四个扇形,分别转动两个转盘,若其中一个转出红色,另一个转出蓝色即可配成紫色(若指针停在分割线上,则重新转动转盘),那么可配成紫色的概率是( )
(第8题)
A. B. C. D.
【答案】B
9.,,,四名选手参加赛跑,赛场共设1,2,3,4四条跑道(如图),选手以随机抽签方式决定各自的跑道,则,两位选手抽中相邻跑道的概率是( )
(第9题)
A. B. C. D.
【答案】A
10.一枚质地均匀的正方体骰子的六个面上的数字分别是1,2,3,4,5,6.掷两次骰子,设其朝上的面上的两个数字之和除以4没有余数及余数分别是1,2,3的概率为,,,,则,,,中最大的是( )
A. B. C. D.
【答案】D
二、填空题(每题3分,共15分)
11.甲、乙两人分别从,,三个景区中随机选取一个景区前往游览,则他们恰好选择同一景区的概率为_ _ _ _ _ _ .
【答案】
12.一只蚂蚁在如图所示的正方形地砖上爬行,蚂蚁停在阴影部分的概率为_ _ _ _ _ _ .
(第12题)
【答案】
13.地理实践课上,活动小组的同学在一张面积为的长方形卡片上绘制了如图①所示的山西省地形图,他们想了解该地形图的面积,经研究采取了以下办法:将长方形卡片水平放置在地面上,在适当位置随机地朝长方形卡片内扔小球(球的大小忽略不计),并记录落在该地形图上的次数(球扔在地形图最外围的界线上或长方形卡片外不计入试验结果).他们将若干次有效试验结果绘制成了如图②所示的折线统计图,由此估计该地形图的面积为_ _ .
(第13题)
【答案】100
14.在数,0,1,2中任取两个数作为点的坐标,那么该点刚好在一次函数的图象上的概率是_ _ _ _ _ _ _ _ .
【答案】
15.如图,有三类矩形(或正方形)卡片,其中甲同学持有,类卡片各一张,乙同学持有,类卡片各一张,丙同学持有,类卡片各一张,现随机选取两名同学手中的卡片共四张进行拼图,则能拼成一个正方形的概率是_ _ _ _ _ _ .
(第15题)
【答案】
三、解答题(共75分)
16.[[2024镇江中考]](8分) 3张相同的卡片上分别写有中国二十四节气中的“小满”“芒种”“夏至”的字样,将卡片的背面朝上.
(1) 洗匀后,从中任意抽取1张卡片,抽到写有“小满”的卡片的概率为_ _ _ _ _ _ ;
(2) 洗匀后,从中任意抽取2张卡片,用画树状图或列表的方法,求抽到一张写有“芒种”,一张写有“夏至”的卡片的概率.
【答案】(1)
(2) 解:画树状图略.共有6种等可能的结果,其中抽到一张写有“芒种”,一张写有“夏至”的卡片的结果有2种, 抽到一张写有“芒种”,一张写有“夏至”的卡片的概率为.
17.(8分)十一期间,甲、乙两人要去附近的景点游玩,甲从,两个景点中任意选择一个游玩,乙从,,三个景点中任意选择一个游玩.用列表或画树状图的方法列出所有可能的结果,并求甲、乙恰好游玩同一景点的概率.
解:画树状图略.共有6种结果,且每种结果出现的可能性相同,其中甲、乙恰好游玩同一景点的结果有2种,所以甲、乙恰好游玩同一景点的概率为.
18.(8分)某校为充分调动学生的积极性,在学校开展各项娱乐活动,丰富学生的课余生活,其中,语文组开展了以“说我身边的事”为主题的演讲比赛,共有5名同学获得一等奖,其中,七年级1名,八、九年级各2名.
(1) 从获得一等奖的5名同学中随机抽取1名参加区级比赛,则抽到八年级的同学的概率是_ _ _ _ _ _ ;
(2) 学校决定从获得一等奖的同学中任选2名同学参加社区组织的“说我身边的变化”演讲活动.请用列表或画树状图的方法求所选2名同学恰好是1名七年级同学和1名九年级同学的概率.
【答案】(1)
(2) 解:画树状图略.共有20种等可能的结果,其中所选的2名同学恰好是1名七年级同学和1名九年级同学的结果有4种,则所选2名同学恰好是1名七年级同学和1名九年级同学的概率为.
19.[[2025·运城期中]](8分) 游戏是生活中有趣味的社交活动,是人类终身不可缺少的伴侣,更是家庭欢乐的源泉.小刚父亲和小刚二叔玩一种游戏,游戏规则:两人只可以说出“木棒”“老虎”“公鸡”“小虫”中的任何一个,同时各说出一个后定胜负,其中“木棒”胜“老虎”、“老虎”胜“公鸡”、“公鸡”胜“小虫”、“小虫”胜“木棒”.其他情况,则为平局.例如,小刚父亲说“老虎”,小刚二叔说“公鸡”,则小刚父亲胜;又如,两人同时说“虫子”,则为平局;再如,一人说“公鸡”,一人说“木棒”,则为平局.
(1) 每一次小刚父亲说出“老虎”的概率是_ _ _ _ _ _ ;
(2) 如果用,,,分别表示小刚父亲说的“木棒”“老虎”“公鸡”“小虫”;用,,,分别表示小刚二叔说的“木棒”“老虎”“公鸡”“小虫”,那么某一次说出时小刚父亲胜小刚二叔的概率是多少?用列表法或画树状图法加以说明;
(3) 你认为这个游戏对小刚父亲和小刚二叔公平吗?为什么?
【答案】(1)
(2) 解:列表略.共有16种等可能的结果,其中小刚父亲胜小刚二叔的结果有4种,
某一次说出时小刚父亲胜小刚二叔的概率为.
(3) 由(2)中表格可知某一次说出时小刚二叔胜小刚父亲的概率为,, 两人获胜的概率相等,这个游戏对小刚父亲和小刚二叔是公平的.
20.(8分)一个不透明的口袋中放着若干个红球和黑球,这两种球除了颜色之外没有其他任何区别,口袋中的球已经搅匀,闭眼从口袋中摸出一个球记下颜色后放回,经过很多次试验后发现摸到红球的频率逐渐稳定在.
(1) 估计摸到黑球的概率是_ _ _ _ _ _ ;
(2) 如果口袋中原有红球12个,又放入个黑球,再经过很多次试验后发现摸到黑球的频率逐渐稳定在,求的值.
【答案】(1)
(2) 解:设口袋中原有黑球个,根据题意得,
解得,经检验是原方程的根,且符合题意.
原有黑球18个.
根据题意得,解得,
经检验是原方程的根,且符合题意.的值是6.
21.(10分)一个不透明的袋子中装有4个质地、大小均相同的小球,这些小球分别标有数字2,3,4,.甲、乙两人每次同时从袋子中各随机摸出1个小球,并计算摸出的这2个小球上的数字之和,记录后都将小球放回袋子中搅匀,进行重复试验.试验数据如下表:
摸球总次数 20 30 60 90 120 180 240 330 450
“和为7”出现的频数 11 13 25 30 37 59 82 110 150
“和为7”出现的频率 0.550 0.433 0.417 0.333 0.308 0.328 0.342 0.333 0.333
解答下列问题:
(1) 如果试验继续进行下去,出现“和为7”的频率将稳定在它的概率附近,根据表中数据,估计出现“和为7”的概率是_ _ ;(保留两位小数)
(2) 当时,请用列表法或画树状图法计算“和为7”的概率.
【答案】(1) 0.33
(2) 解:当时,画树状图略.共有12种结果,且每种结果出现的可能性相同,其中“和为7”的结果有4种,所以“和为7”的概率为.
22.(12分) 如图,的三个顶点及,,,,五个点分别位于正方形网格的格点上.
(1) 现以,,,,中的三个点为顶点画三角形,在所画的三角形中与不全等但面积相等的三角形是_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ ;(填一个三角形即可)
(2) 先从,两个点中任意取一个点,再从,,三个点中任意取两个不同的点,以所取得的这三个点为顶点画三角形,求所画三角形与面积相等的概率(用画树状图法或列表法求解).
【答案】(1) (答案不唯一)
(2) 解:画树状图略.有,,,,,共6种等可能的结果,其中与面积相等的结果有,,,共3种,
所画三角形与面积相等的概率为.
23.(13分)学校为了解本校中考体育情况,随机抽取了部分学生的体育成绩进行统计分析,发现最低分为45分,且成绩为45分的学生占抽查人数的,现将抽查结果绘制成了如图所示的不完整的折线统计图,请根据图中信息,回答下列问题:
(1) 此次抽查的学生共名,抽查的学生体育成绩的中位数是_ _ 分,抽查的女生体育成绩的平均数是分;
(2) 补全折线统计图;
(3) 为了今后中考体育取得更好的成绩,学校决定分别从成绩为50分的男生和女生中各选一名参加“经验座谈会”,若成绩为50分的男、女生中各有两名体育特长生,请用列表或画树状图的方法求出所选的两名学生刚好都不是体育特长生的概率.
【答案】(1) 50;48.5;48
(2) 解:补全折线统计图如图.
(3) 设成绩为50分的男生分别为男1、男2、男3、男4,其中男1、男2是体育特长生,成绩为50分的女生分别为女1、女2、女3、女4、女5,其中女1、女2是体育特长生,
列表如下:
女1 女2 女3 女4 女5
男1 (男1,女1) (男1,女2) (男1,女3) (男1,女4) (男1,女5)
男2 (男2,女1) (男2,女2) (男2,女3) (男2,女4) (男2,女5)
男3 (男3,女1) (男3,女2) (男3,女3) (男3,女4) (男3,女5)
男4 (男4,女1) (男4,女2) (男4,女3) (男4,女4) (男4,女5)
由表可知,一共有20种结果,且每种结果出现的可能性相同,其中所选的两名学生都不是体育特长生的结果有6种,所以(所选的两名学生都不是体育特长生).
第页/共页
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
