北师大八下期中专题02 不等式组、方程组、一次函数(含解析)
文档属性
| 名称 | 北师大八下期中专题02 不等式组、方程组、一次函数(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 698.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-11 05:26:10 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
专题02 不等式组、方程组、一次函数
一、不等式与不等式组
1.如图,数轴上的点A与点B所表示的数分别为a,b,则下列不等式成立的是( )
A. B. C. D.
2.用甲乙两种原料配制成某种饮料,已知每千克的这两种原料的维生素C含量及购买这两种原料的价格如表所示:现配制这种饮料,要求至少含有4200单位的维生素C,且购买原料的费用不超过72元.设所需甲种原料,则可列不等式组为( )
原料 甲 乙
维生素 600单位 100单位
原料价格 8元 4元
A. B.
C. D.
3.若关于x的不等式组的解集是x>2,则m的取值范围是 .
4.解不等式组:,并写出该不等式组的整数解.
5.若,则下列不等式中正确的是( )
A. B. C. D.
6.已知点在第二象限,则的取值范围在数轴上表示正确的是( )
A. B.
C. D.
7.宝安凤凰山森林公园位于“宝安第一山”凤凰山脚下,公园树木丰茂,景色优美,所以小青想带她初三的表姐去游玩放松释放压力,计划15点10分从学校出发,已知两地相距5.1千米,她们跑步的平均速度为190米/分钟,步行的平均速度为80米/分钟,若她们要在16点之前到达,那么她们至少需要跑步多少分钟?设他跑步的时间为分钟,则列出的不等式为( )
A. B.
C. D.
8.2024年春晚,刘谦表演的扑克牌魔术“约瑟夫环”,是数学与神奇的完美结合,通过一定指令的操作,会得到一个数学规律.请依照下列定义,若,则的取值范围为 .
9.解不等式组.
10.若,则下列不等式变形错误的是( )
A. B. C. D.
11.2024年中央一号文件强调“强化农业科技支撑”,充分发挥科技生产力对企业和产业发展的作用,某镇计划引进无人机田间喷洒农药技术,无人机喷洒农药时,平均每亩地用药量比常规喷药壶用药量少10ml,无人机用药300ml喷洒的农田面积与常规喷药壶用药450ml喷洒的农田面积相同.
(1)求无人机喷洒农药时,平均每亩地的用药量 .
(2)该镇计划采购A,B两种型号喷药无人机共20台,已知A型号喷药无人机每台15000元,B型号喷药无人机每台20000元,若采购资金不超过360000元,则最少需采购A型号喷药无人机多少台?
12.已知关于x的不等式组有四个整数解,则m的取值范围是( )
A. B. C. D.
13.为推进全民健身设施建设,某体育中心准备改扩建一块运动场地.现有甲、乙两个工程队参与施工,具体信息如下:
信息—
工程队 每天施工面积(单位:) 每天施工费用(单位:元)
甲 3600
乙 x 2200
信息二
甲工程队施工所需天数与乙工程队施工所需天数相等.
(1)求x的值;
(2)该工程计划先由甲工程队单独施工若干天,再由乙工程队单独继续施工,两队共施工22天,且完成的施工面积不少于.该段时间内体育中心至少需要支付多少施工费用
14.当时,则( )
A. B. C. D.
15.不等式组的解集在数轴上表示为( )
A. B.
C. D.
16.关于的不等式有3个整数解,则的取值范围是( )
A. B. C. D.
17.解不等式组:
(1);
(2).
18.解不等式组:,并指出它的所有的非负整数解.
19.不等式的解集在数轴上表示正确的是( )
A. B.
C. D.
20.已知, 则下列各式成立的是( )
A. B. C. D.
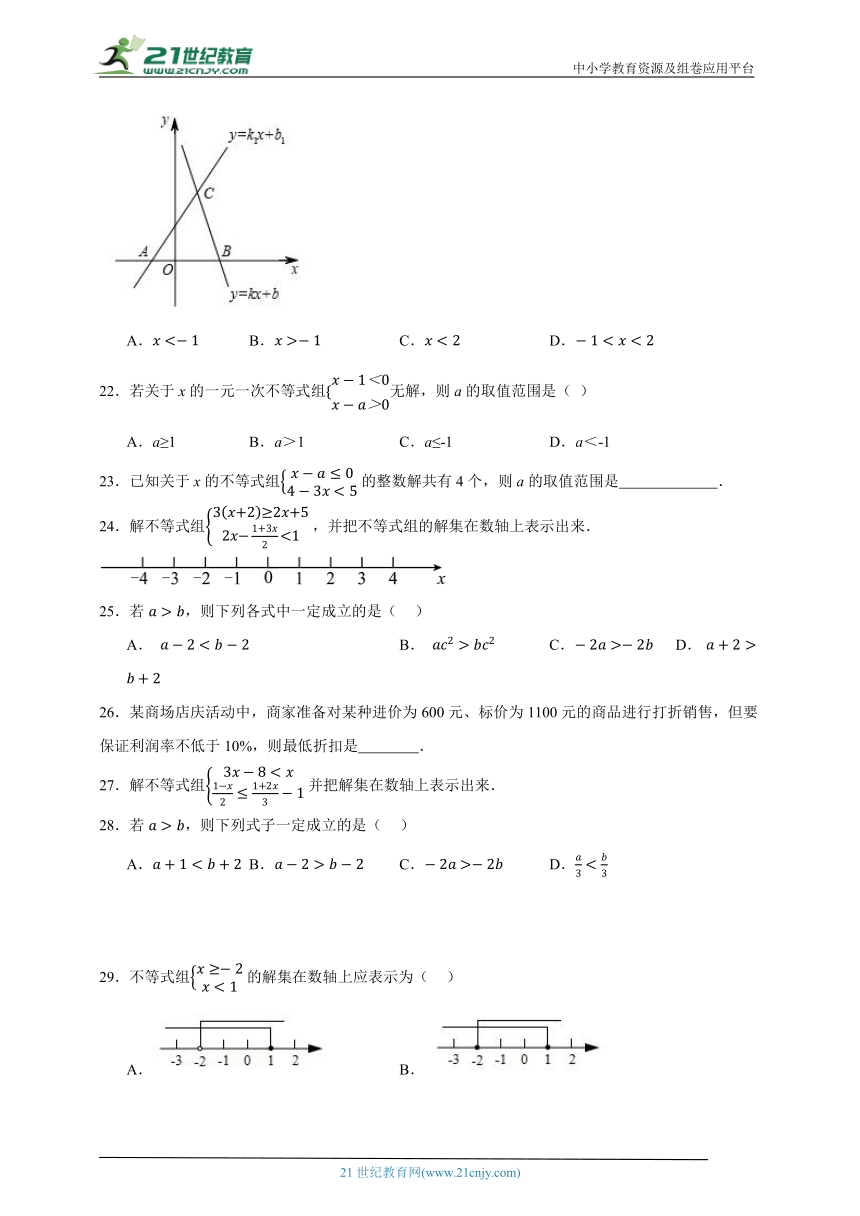
21.如图,一次函数和的图象分别与x轴交于点、,则关于x的不等式组的解集是( )
A. B. C. D.
22.若关于x的一元一次不等式组无解,则a的取值范围是( )
A.a≥1 B.a>1 C.a≤-1 D.a<-1
23.已知关于x的不等式组的整数解共有4个,则a的取值范围是 .
24.解不等式组,并把不等式组的解集在数轴上表示出来.
25.若,则下列各式中一定成立的是( )
A. B. C. D.
26.某商场店庆活动中,商家准备对某种进价为600元、标价为1100元的商品进行打折销售,但要保证利润率不低于10%,则最低折扣是 .
27.解不等式组并把解集在数轴上表示出来.
28.若,则下列式子一定成立的是( )
A. B. C. D.
29.不等式组的解集在数轴上应表示为( )
A. B.
C. D.
30.一次环保知识竞赛共有25道题,每一题答对得4分,答错或不答都扣1分,在这次竞赛中,小明被评为优秀(85分或85分以上),小明至少要答对多少道题?如果设小明答对了x道题,根据题意列式得( )
A.4x﹣1×(25﹣x)>85 B.4x+1×(25﹣x)≤85
C.4x﹣1×(25﹣x)≥85 D.4x+1×(25﹣x)>85
31.解不等式组,并把其解集表示在数轴上.
32.若,则下列不等关系一定成立的是( )
A. B. C. D.
33.定义:如果一元一次方程的解是一元一次不等式组的解,则称该一元一次方程为该不等式组的相伴方程,若方程,都是关于的不等式组的相伴方程,则的取值范围为 .
34.解不等式组:.
35.若,则下列式子中错误的是( )
A. B. C. D.
36.若关于的不等式组无解,则的取值范围是( )
A. B. C. D.
37.解不等式组:
(1); (2).
38.解不等式,并把解集在数轴上表示出来.
39.解不等式组并在数轴上表示它的解集
40.解不等式:
41.五一假期,两位老师计划带领若干学生去古镇参与社会实践,他们联系了报价均为每人200元的两家旅行社.经协商,甲旅行社的优惠条件是:两位老师全额收费,学生按六折收费;乙旅行社的优惠条件是:老师与学生都按照七折收费.
(1)设总人数为x人,选择甲旅行社时,所需费用为元,选择乙旅行社时,所需费用为元,请分别写出,与x之间的关系式.
(2)若学生人数不超过10人,为了减少花销,他们应该如何选择旅行社?
二、平面直角坐标系
42.如果点在平面直角坐标系的第三象限内,那么的取值范围在数轴上可表示为( )
A. B.
C. D.
三、一次函数
43.为丰富同学们阳光大课间活动,育才学校现决定增购两种体育器材:跳绳和毽子.已知跳绳的单价比毽子的单价多3元,用800元购买的跳绳数量和用500元购买的毽子数量相同.
(1)求跳绳和毽子的单价分别是多少元.
(2)恰逢店庆活动,体育用品店对这两种器材打折销售,其中跳绳以八折出售,毽子以七折出售.学校计划购买跳绳和毽子两种器材共600个,且要求跳绳的数量不少于毽子数量的3倍,请求出学校花钱最少的购买方案及最少花费.
44.如图,直线与直线的交点是,则不等式的解集是 .
45.如图,函数和的图象相交于点,则关于的x不等式的解集为 .
46.如图,直线:与直线:相交于点,则关于的不等式的解集为( )
A. B. C. D.
47.如图,一次函数y1=x+b与一次函数y2=kx+3的图象交于点P(1,2),则关于不等式x+bkx+3的解集是( )
A.x0 B.x0 C.x1 D.x1
48.如图,已知函数与函数的图像交于点P,则不等式的解集是 .
49.如图,一次函数和的图象相交于点,则关于的不等式的解集为
四、命题与证明
50.下列命题:①同旁内角互补,两直线平行;②若,则;③直角都相等;④相等的角是对顶角.它们的逆命题是真命题的个数是( )
A.4个 B.3个 C.2个 D.1个
五、二元一次方程组
51.某货运电梯限重标志显示,载重总质量禁止超过.现要用此货运电梯装运一批设备,每套设备由1个甲部件和2个乙部件组成.现已知2个甲部件和1个乙部件总质量为,3个甲部件和4个乙部件质量相同.
(1)请分别求出1个甲部件和1个乙部件的质量各是多少千克?
(2)每次装运都需要工人装卸,设备需要成套装运,现已知装卸工人总重量为,则货运电梯一次最多可装运多少套设备?
52.某校八年级为了丰富同学们的课余生活,决定举行一场校园义卖活动,小深和小圳都参加了这次活动,他们分别售卖类物品和类物品,若类卖了10件和类卖了20件一共可卖220元;若类卖了16件和类卖了30件一共可卖336元.
(1)请求出类物品和类物品每件的售价分别是多少元?
(2)为了鼓励更多同学参与,能筹到更多善款,学校决定设立奖励机制,如果两人合作筹集到善款总额不少于500元,则可获得电影票一张作为奖励.假设类和类一共卖了70件,则类至少要卖多少件,小深和小圳才能获得奖励?
53.美丽的滨海城市深圳,不仅阳光充沛,而且特色水果丰富,其中南山荔枝是广东省著名的荔枝品种,也是比较少能享有地理标志保护的荔枝,某经销商计划从南山购进糯米糍、桂味两种荔枝.已知购进糯米糍箱,桂味 箱,共需元;购进糯米糍箱,桂味箱,共需元.
(1)糯米糍、桂味每箱的价格分别是多少元?
(2)该经销商计划用不超过元购进糯米糍、桂味共箱,且糯米糍的箱数不超过桂味箱数的倍,共有多少不同的种进货方案?如果该经销商将 购进的荔枝按照糯米糍每箱元,桂味每箱元的价格全部售出,那么哪种进货方案获利最多?
54.为了迎接兔年的到来,广大市民纷纷开始购买兔年装饰物,某网店上架了“玉兔灯笼”和“玉兔摆件”这两款产品,已知10个“玉兔灯笼”和15个“玉兔摆件”的售价为2400元;30个“玉兔灯笼”和20个“玉兔摆件”的售价为5200元.
(1)每个“玉兔灯笼”和“玉兔摆件”的售价分别为多少元?
(2)已知“玉兔灯笼”和“玉兔摆件”的成本分别为80元/个和50元/个.进入2023年一月后,这两款产品持续热销,于是网店再购进了这两款产品共600个,其中“玉兔摆件”的数量不超过“玉兔灯笼”数量的2倍,且购进总价不超过37800元.为回馈新老客户,网店决定对“玉兔灯笼”降价10%后再销售,若一月份购进的这两款产品全部售出,则“玉兔灯笼”购进多少个时该网店当月销售利润最大?最大利润为多少?
55.某水果店经销甲、乙两种水果,两次购进水果的情况如下表所示:
进货批次 甲种水果质量 (单位:千克) 乙种水果质量 (单位:千克) 总费用 (单位:元)
第一次 60 40 1520
第二次 30 50 1360
(1)求甲、乙两种水果的进价;
(2)销售完前两次购进的水果后,该水果店决定回馈顾客,开展促销活动.第三次购进甲水果80千克,乙水果120千克.将其中的m千克甲种水果和3m千克乙种水果按进价销售,剩余的甲种水果以每千克17元、乙种水果以每千克30元的价格销售.若第三次购进的水果全部售出后,获得的最大利润不低于800元,求正整数m的最大值.
56.开学前夕,某书店计划购进A、B两种笔记本共350本,已知A种笔记本的进价为12/本,B种笔记本的进价为15元/本,共计4800元.
(1)请问购进了A种笔记本多少本?
(2)在销售过程中,A、B两种笔记本的标价分别为20元/本、25元/本.受疫情影响,两种笔记本按标价各卖出m本以后,该店进行促销活动,剩余的A种笔记本按标价的七折全部售出,剩余的B种笔记本按成本价清货,若两种笔记本的总利润不少于2348元,请求出m的最小值.
57.“人间烟火气,最抚凡人心.”在这喧嚣的世界里,地摊的存在,让人们感受到了那份朴实无华的温暖,也让城市多了一份生活的温度,某个体户购买了腊梅,百合两种鲜花摆摊销售,若购进腊梅5束,百合3束,需要114元;若购进腊梅8束,百合6束,需要204元.
(1)求腊梅,百合两种鲜花的进价分别是每束多少元?
(2)若每束腊梅的售价为20元,每束百合的售价为30元.结合市场需求,该个体户决定购进两种鲜花共80束,计划购买成本不超过1260元,且购进百合的数量不少于腊梅数量的,两种鲜花全部销售完时,求销售的最大利润及相应的进货方案.
58.俄乌战争仍在继续,人们对各种军用装备倍感兴趣,某商家购进坦克模型(记作A)和导弹(记作B)两种模型,若购进A种模型10件,B种模型5件,需要1000元;若购进A种模型4件,B种模型3件,需要550元.
(1)求购进A,B两种模型每件分别需多少元?
(2)若销售每件A种模型可获利润20元.每件B种模型可获利润30元.商店用1万元购进模型,且购进A种模型的数量不超过B种模型数量的8倍,设总盈利为W元,购买B种模型b件,请求出W关于b的函数关系式,并求出当b为何值时,销售利润最大,并求出最大值.
六、函数基础知识
59.结合所学研究函数的方法,我们研究函数性质及其应用,请根据下表信息,按要求完成下列各小题.
x … 0 1 2 3 4 …
y … m 0 2 n …
(1)______,______,______;
(2)请在平面直角坐标系中画出该函数的图象;
(3)判断下列关于该函数性质的说法是否正确(正确的打√,错误的打×);
①该函数图象是轴对称图形,它的对称轴为y轴.(______)
②当时,y随x的增大而减小;当时,y随x的增大而增大.(______)
(4)请在同一平面直角坐标系中再画出函数的图象,结合函数的图象,直接写出不等式的解集______.
参考答案
题号 1 2 5 6 7 10 12 14 15 16
答案 A C D D A D A D B C
题号 19 20 21 22 25 28 29 30 32 35
答案 A D D A D B D C A B
题号 36 42 46 47 50
答案 C D A C B
1.A
【分析】由图可知,,根据不等式的性质判断即可.
【详解】解:由图可知,,则有
A、,成立,本选项符合题意;
B、,原不等式不成立,本选项不符合题意;
C、,原不等式不成立,本选项不符合题意;
D、,原不等式不成立,本选项不符合题意;
故选:A.
【点睛】此题考查数轴和不等式的性质,通过数轴判断出,并掌握不等式的性质是解答本题的关键.
2.C
【分析】本题主要考查了列一元一次不等式组,理解题意、找准不等关系成为解题的关键.
设所需甲种原料的质量为,则需乙种原料.再根据不等关系“至少含有4200单位的维生素C”和“购买原料的费用不超过72元”列出不等式组即可.
【详解】解:设所需甲种原料的质量为,则需乙种原料.
根据题意,得:.
故选:C.
3.m≤2
【分析】根据不等式组的解集,可判断m与2的大小.
【详解】解:因为不等式组的解集是x>2,根据同大取较大原则可知:m<2,
当m=2时,不等式组的解集也是x>2,
所以m≤2.
故答案为:m≤2.
【点睛】本题考查了一元一次不等式组的解法,熟练掌握一元一次不等式组的解法是解答本题的关键.先分别解两个不等式,求出它们的解集,再求两个不等式解集的公共部分.不等式组解集的确定方法是:同大取大,同小取小,大小小大取中间,大大小小无解.
4.不等式的解集为,整数解为,,,0
【分析】先求出两个一元一次不等式的解集,然后求出不等式组的解集,最后找出其中的整数即可
【详解】解:
解不等式①:,解得,
解不等式②:,得,解得
∴不等式的解集为,
∴不等式组的整数解为,,,0.
【点睛】本题考查了一元一次不等式组的解法,熟练掌握一元一次不等式组的解法是解答本题的关键.先分别解两个不等式,求出它们的解集,再求两个不等式解集的公共部分.不等式组解集的确定方法是:同大取大,同小取小,大小小大取中间,大大小小无解.
5.D
【分析】本题考查不等式的性质,根据条件,运用不等式的性质逐项验证即可得到答案,熟记不等式的三个性质是解决问题的关键.
【详解】解:A、由于,则,故错误,不符合题意;
B、由于,则,故错误,不符合题意;
C、由于,则,故错误,不符合题意;
D、由于,则,故正确,符合题意;
故选:D.
6.D
【分析】根据第二象限内点的特征,列出一元一次不等式组,解不等式组,即可求解,
本题考查了,点的坐标,求一元一次不等式组的解集,在数轴上表示不等式的解集,解题的关键是:熟练掌握相关知识点.
【详解】解:∵点在第二象限,
∴,解得:,
故选:.
7.A
【分析】根据“步行时间步行速度跑步时间跑步速度”列不等式即可.本题主要考查由实际问题抽象出一元一次不等式,解题的关键是根据题意确定其中蕴含的不等关系.
【详解】解:∵计划15点10分从学校出发,要在16点之前到达
∴总时间为分钟
设他跑步的时间为分钟,则他步行时间为分钟,
根据题意,得:,
故选:A.
8./
【分析】本题主要考查了解不等式,根据题干提供的信息,得出,解不等式即可.
【详解】解:∵,
∴,
∴,
解得:,
故答案为:.
9..
【分析】本题考查的是解一元一次不等式组.分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小找不到确定不等式组的解集.
【详解】解:解不等式①,得:,
解不等式②,得:,
则不等式组的解集为.
10.D
【分析】根据不等式的基本性质逐一进行判断即可.
【详解】解:A、∵,
∴,故正确,不合题意;
B、∵,
∴,故正确,不合题意;
C、∵,
∴,故正确,不合题意;
D、∵,
∴,
∴,故错误,符合题意;
故选:D.
【点睛】本题考查不等式的性质:(1)不等式两边加(或减)同一个数(或式子),不等号的方向不变.(2)不等式两边乘(或除以)同一个正数,不等号的方向不变(3)不等式两边乘(或除以)同一个负数,不等号的方向改变.
11.(1)无人机喷洒农药时,平均每亩地的用药量为20ml;
(2)最少需采购A型号喷药无人机8台.
【分析】本题考查了分式方程的应用以及一元一次不等式的应用,解题的关键是:(1)找准等量关系,正确列出分式方程;(2)根据各数量之间的关系,正确列出一元一次不等式.
(1)设无人机喷洒农药时,平均每亩地的用药量为xml, 则用常规喷药壶喷洒农药时,平均每亩地的用药量为ml,根据无人机用药300ml 喷洒的农田面积与 常规喷药壶用药450ml 喷洒的农田面积相同,可列出关于x 的分式方程,解之经检验后,
即可得出结论;
(2)设采购m 台 A 型号喷药无人机,利用总价 =单价×数量,结合总价不超过360000元,可列出关于m的一元一次不等式,解之取其中的最小值,即可得出结论.
【详解】(1)解:设无人机喷洒农药时,平均每亩地的用药量为 ,则用常规喷药壶喷洒农药时,平均每亩地的用药量为,
根据题意得:,
解得:,
经检验,是所列方程的解,且符合题意.
答:无人机喷洒农药时,平均每亩地的用药量为;
(2)解:设采购台型号喷药无人机,则采购台型号喷药无人机,
根据题意得:,
解得:,
的最小值为8.
答:最少需采购型号喷药无人机8台.
12.A
【分析】本题主要考查不等式组的整数解问题,根据不等式组的整数解的个数得出关于的不等式组是解题的关键.解不等式组的两个不等式,根据其整数解的个数得出,解之可得.
【详解】解:解不等式,得:,
解不等式,得:,
不等式组有4个整数解,
,
解得:.
故选:A
13.(1)x的值为600
(2)该段时间内体育中心至少需要支付施工费用56800元
【分析】(1)根据题意甲工程队施工所需天数与乙工程队施工所需天数相等列出分式方程解方程即可;
(2)设甲工程队先单独施工天,体育中心共支付施工费用元,根据先由甲工程队单独施工若干天,再由乙工程队单独继续施工,两队共施工22天,且完成的施工面积不少于列出不等式即可得到答案.
【详解】(1)解:由题意列方程,得.
方程两边乘,得.
解得.
检验:当时,.
所以,原分式方程的解为.
答:x的值为600.
(2)解:设甲工程队先单独施工天,体育中心共支付施工费用元.
则.
,
.
1400>0,
随的增大而增大.
当时,取得最小值,最小值为56800.
答:该段时间内体育中心至少需要支付施工费用56800元.
【点睛】本题主要考查了分式方程的应用,一元一次不等式的应用以及一次函数的应用,熟练掌握知识点是解题的关键.
14.D
【分析】本题考查了不等式的性质,熟练掌握不等式的性质是解答本题的关键.根据不等式的性质可判断A,B,D;利用特殊值可判断C.
【详解】解:A.∵,∴,故不正确;
B.∵,∴,故不正确;
C.当时,满足,但,故不正确;
D.∵,∴,正确;
故选D.
15.B
【分析】分别求出每一个不等式的解集,根据“大于向右,小于向左,包括端点用实心,不包括端点用空心”的原则即可得答案.
【详解】解:,
解不等式2x 1≤5,得:x≤3,
解不等式8 4x<0,得:x>2,
故不等式组的解集为:2<x≤3,
故选:B.
【点睛】本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟悉在数轴上表示不等式解集的原则“大于向右,小于向左,包括端点用实心,不包括端点用空心”是解题的关键.
16.C
【分析】根据不等式的整数解只有0,1,2,即可得出实数a的取值范围.
【详解】解:∵不等式有3个整数解,
∴这3个整数解为0,1,2,
∴实数a的取值范围是
故选C
【点睛】本题考查一元一次不等式组的整数解,解题的关键是明确题意,会解一元一次不等式组.
17.(1)
(2)
【分析】本题主要考查了解一元一次不等式:
(1)先去括号,再移项合并同类项,即可求解;
(2)先取分母,再去括号,然后移项合并同类项,即可求解.
【详解】(1)解:
去括号得:
移项合并同类项得:
解得:;
(2)解:
去分母得:
去括号得:
解得:.
18.;非负整数解为:0,1.
【分析】本题考查了一元一次不等式组的解法,熟练掌握一元一次不等式组的解法是解答本题的关键.先分别解两个不等式,求出它们的解集,再求两个不等式解集的公共部分即可得到不等式组的解集,然后找出非负整数解即可.
【详解】解:由①得:,
由②得:,
∴不等式组的解集为,
满足的非负整数解为:0,1
19.A
【分析】本题考查的是解一元一次不等式,利用数轴表示不等式的解集.先求出不等式的解集,再在数轴上表示出来不等式的解集即可,注意大于小于用空心,大于等于小于等于用实心,大于大于等于开口向右,小于小于等于开口向左.
【详解】解:,
,
数轴上表示为:,
故选:A.
20.D
【分析】本题考查了不等式的性质,注意不等式的两边都乘或除以一个负数,不等号的方向改变.根据不等式的性质逐一判断即可解题.
【详解】解:A、,当时,,故本选项不符合题意;
B、,,故本选项不符合题意;
C、,,故本选项不符合题意;
D、,,故本选项符合题意;
故选:D.
21.D
【分析】根据图象可知y=k1x+b1>0的解集和y=kx+b>0的解集,即可确定不等式组的解集.
【详解】解:一次函数和的图象分别与x轴交于点、,
根据图象可知,的解集为:,的解集为:,
∴不等式组的解集是,
故选:D.
【点睛】本题考查了一次函数与一元一次不等式的关系,熟练掌握一次函数的图象是解题的关键.
22.A
【详解】解:解得,,
∵无解,
∴a≥1.
故选A.
23.
【分析】先求出不等式组的解集,根据一元一次不等式组有四个整数解进行分析,即可得到答案.
【详解】解:,
解不等式①,得:,
解不等式②,得:,
∵关于的不等式组的整数解共有4个,
则这四个整数解为:0,1,2,3,
当时,不等式组的整数解为:0,1,2,3,
∴.
故答案为:.
【点睛】本题考查了解一元一次不等式组的知识;解题的关键是正确求得一元一次不等式组的解集.
24.,数轴见解析
【分析】分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小找不到确定不等式组的解集.
【详解】解:,
解不等式①,得:,
解不等式②,得:,
则不等式组的解集为,
将不等式组的解集表示在数轴上如下:
【点睛】本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.
25.D
【分析】本题考查了不等式的性质,理解不等式的性质是解题的关键.
根据不等式的性质逐项判定即可求解.
【详解】解:A、∵,
∴,故此选项不符合题意;
B、∵,,
∴,故此选项不符合题意;
C、∵,
∴,故此选项不符合题意;
D、∵,
∴,故此选项符合题意;
故选:D.
26.6折.
【分析】利润率不低于10%,即利润要大于或等于:600×10%元,设打x折,则售价是110x元.根据利润率不低于10%就可以列出不等式,求出x的范围.
【详解】设可以打x折,
1100×﹣600≥600×10%,
解得x≥6,即最低折扣是6折.
故答案为6折.
【点睛】此题考查了一元一次不等式组的应用,正确理解利润率的含义,理解利润=进价×利润率是解题的关键.
27.不等式组的解集为:,图见解析;
【分析】先分别求出各不等式的解集,再求出其公共解集,并在数轴上表示出来即可.
【详解】,
解不等式①得.
解不等式②得.
∴原不等式组的解集为:.
在数轴上表示如图:
【点睛】本题考查的是在数轴上表示一元一次不等式组的解集,在解答此类题目时要注意实心圆点与空心圆点的区别,这是此题的易错点.
28.B
【分析】根据不等式的性质依次分析判断.
【详解】解:∵,∴a+1>b+1,故选项A不符合题意;
∵,∴,故选项B符合题意;
∵,∴-2a<-2b,故选项C不符合题意;
∵,∴,故选项D不符合题意;
故选:B.
【点睛】此题考查了不等式的性质:不等式两边同时加上或减去同一个整式,不等号方向不变;不等式两边同时乘或除以同一个不为0的整正数,不等号方向不变;不等式两边同时乘或除以同一个不为0的负数,不等号方向改变.
29.D
【分析】根据不等式“大于小的,小于大的取中间”即可求得解集.
【详解】解:由题意可知,不等式的解集为,
只有选项D符合题意要求,
故选:D.
【点睛】本题考查了解一元一次不等式(组),在数轴上表示不等式组的解集等知识点,注意:在数轴上表示不等式组的解集时,包括该点时用实心,不包括该点时用空心.
30.C
【分析】根据题意可以列出相应的不等式,从而可以解答本题.
【详解】解:由题意可得,
4x-1×(25-x)≥85,
故选C.
【点睛】本题考查由实际问题抽象出一元一次不等式,解答本题的关键是明确题意,列出相应的不等式.
31.解集为,数轴见解析
【分析】本题考查解一元一次不等式组、在数轴上表示不等式组的解集,分别解出两个不等式的解集,并表示在数轴上,再找到公共解集即可求解,熟知:同大取大,同小取小,大小小大中间找,大大小小找不到的原则是解题的关键.
【详解】解:解不等式,得:,
解不等式,得:,
则不等式组的解集为,
将不等式组的解集表示在数轴上如下:
32.A
【分析】本题考查不等式的性质,根据不等式的性质逐项验证即可得到答案,熟记不等式性质是解决问题的关键.
【详解】解:A、由不等式的性质可知,当时,则,不等关系一定成立,符合题意;
B、由不等式的性质可知,当时,则,原不等关系不成立,不符合题意;
C、由不等式的性质可知,当,且时,则,原不等关系不一定成立,不符合题意;
D、由不等式的性质可知,当,且时,则,原不等关系不一定成立,不符合题意;
故选:A.
33.
【分析】解方程求出两个方程的解,再解不等式组得出,根据,均是不等式组的解可得关于m的不等式组,解之可得.
【详解】解:解方程,得:,
解方程,得:,
由,得:,
由,得:,
∵,均是不等式组的解,
∴且,
∴.
故答案为:.
【点睛】本题考查的是新定义问题,涉及解一元一次方程,解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.
34.
【分析】本题考查的是解一元一次不等式组,分别求出各不等式的解集,再求出其公共解集即可.熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.
【详解】
解不等式①,得:
解不等式②,得
故不等式组的解集为:.
35.B
【分析】根据不等式的性质可进行求解.
【详解】解:由可知:
A、,正确,故不符合题意;
B、,原不等式错误,故符合题意;
C、,正确,故不符合题意;
D、,正确,故不符合题意;
故选B.
【点睛】本题主要考查不等式的性质,熟练掌握不等式的性质是解题的关键.
36.C
【分析】先依次求出不等式的解集,再根据不等式组无解进行求解.
【详解】解:解不等式组,得,
∵该不等式组无解,
∴.
故选:C.
【点睛】此题主要考查不等式组无解的情况,解题的关键是熟知不等式组的解集.
37.(1)﹣1<x≤3
(2)﹣6<x≤1
【分析】(1)分别解出各个不等式,再求公共解集即可;
(2)解出每个不等式,再求公共解集.
【详解】(1)解: ,
解不等式①得x>﹣1,
解不等式②得x≤3,
∴不等式组的解集为﹣1<x≤3.
(2)解:,
解不等式①得x>﹣6,
解不等式②得x≤1,
∴不等式组的解集为﹣6<x≤1.
【点睛】本题考查解一元一次不等式组,解题的关键是掌握取不等式公共解集的方法.
38.,图见解析
【分析】先去括号,再移项、合并同类项、最后系数化为1即可,再在数轴上把解集表示出来.
【详解】解:去括号得,,
去括号得,,
合并同类项得,,
系数化为1得,,
解集在数轴上表示为:
【点睛】本题考查了解一元一次不等式以及在数轴上表示不等式的解集,是基础知识要熟练掌握.
39.;数轴见解析
【分析】本题考查了解一元一次不等式组,在数轴上表示不等式的解集.按照解一元一次不等式组的步骤进行计算,即可解答.
【详解】解:,
解不等式①得:,
解不等式②得:,
原不等式组的解集为:,
该不等式组的解集在数轴上表示如图所示:
40.
【分析】本题考查的是解一元一次不等式.去分母,移项、合并同类项,系数化为1即可.
【详解】解:,
去分母,得,
移项,得,
合并同类项,得,
系数化1,得.
41.(1);
(2)当总人数少于8人,选择乙旅行社花销较少;总人数为8人,两个旅行社花销相同;总人数超过8人不超过12人,甲旅行社花销较少.
【分析】本题考查一次函数的应用.分类探讨选择花销较少的旅行社是解决本题的难点.
(1)甲旅行社所需费用两位老师的费用学生人数;乙旅行社所需费用总人数,把相关数值代入后化简即可;
(2)分别算出,,时对应的的值,即可根据人数判断出花销较少的旅行社.
【详解】(1)解:;
;
(2)解:①.
.
解得:;
②.
.
解得:;
③.
.
解得:,
学生人数不超过10人,老师有2人,
.
答:当总人数少于8人,选择乙旅行社花销较少;总人数为8人,两个旅行社花销相同;总人数超过8人不超过12人,甲旅行社花销较少.
42.D
【分析】根据点的位置得出不等式组,求出不等式组的解集,即可得出选项.
【详解】解:∵在平面直角坐标系的第三象限内,
∴,
解得:,
在数轴上表示为:
故选D.
【点睛】本题考查了点坐标特点、一元一次不等式组、在数轴上表示不等式组的解集等知识点,能求出不等式组的解集是解此题的关键.
43.(1)跳绳的单价为8元,毽子的单价为5元
(2)购买450个跳绳,150个毽子时,总费用最少为3405元
【分析】(1)设毽子的单价为元,根据用800元购买的跳绳数量和用500元购买的毽子数量相同列出方程,解之即可;
(2)设购买跳绳m个,则购买毽子个,根据题意列出不等式组进行求解,设学校购买跳绳和毽子两种器材共花元,求出一次函数解析式,根据一次函数的性质,求最小值即可.
【详解】(1)解:设毽子的单价为元,则跳绳的单价为元,
依题意,得:,解得:,
经检验,是原方程的解,且符合题意,
.
答:跳绳的单价为8元,毽子的单价为5元.
(2)设购买跳绳m个,
由题意可得:,
解得:,
设学校购买跳绳和毽子两种器材共花元,
则,
∵,
∴随的增大而增大,
∴当时,最小,且为,
∴当学校购买450个跳绳,150个毽子时,总费用最少为3405元.
【点睛】本题考查分式方程的应用,一元一次不等式的应用,以及利用一次函数解决最值问题.根据题意,准确的列出分式方程和一次函数表达式是解题的关键.
44.
【分析】结合图像,根据交点及解答即可.
【详解】解:直线与直线的交点是,
不等式的解集为,
故答案为:.
【点睛】此题考查了利用一次函数交点求不等式的解集,正确理解一次函数的交点与不等式的关系是解题的关键.
45.
【分析】此题考查了一次函数与一元一次不等式的关系,关键是求出A点坐标以及利用数形结合的思想.先利用待定系数法求出A点坐标,结合图象写出不等式的解集即可.
【详解】解:将点代入得,,
解得,,
所以点A的坐标为,
由图可知,不等式的解集为.
故答案为:.
46.A
【分析】首先将已知点的坐标代入直线求得的值,然后观察函数图象得到在点的左边,直线都在直线的下方,据此求解.
【详解】解:直线与直线相交于点,
,
解得:,
观察图象可知:关于的不等式的解集为,
故选:A.
【点睛】本题考查了一次函数与一元一次不等式,根据函数图象,比较函数值的大小,确定对应的自变量的取值范围,解此题需要有数形结合的思想.
47.C
【分析】观察函数图象得到当x>1时,函数的图象都在的图象上方,所以关于x的不等式x+b>kx+3的解集为x>1.
【详解】解:当x>1时,函数的图象都在的图象上方,
则x+b>kx+3,
即不等式x+b>kx+3的解集为x>1.
故选:C.
【点睛】本题考查了一次函数与一元一次不等式:从函数图象的角度看,就是由函数的图像在平面直角坐标系内的高低位置来确定自变量的取值范围,掌握数型结合是解题的关键.
48.
【分析】观察图像可得当时,函数的图像位于函数的图像的下方,即可求解.
【详解】解:观察图像得:当时,函数的图像位于函数的图像的下方,
∴不等式的解集是.
故答案为:
【点睛】本题主要考查了一次函数与一元一次不等式的关系,利用数形结合思想解答是解题的关键.
49.
【分析】本题考查了一次函数图象的交点与不等式的解集、一次函数的性质,先求出点的坐标,再根据图象即可得出答案.
【详解】解:将代入得:,
解得:,
,
由图象可得:关于的不等式的解集为,
故答案为:.
50.B
【分析】先写出命题的逆命题,再对逆命题的真假进行判断即可.
【详解】①同旁内角互补,两直线平行的逆命题是两直线平行,同旁内角互补,是真命题;
②若,则的逆命题是若,则,是真命题;
③直角都相等的逆命题是相等的角是直角,是假命题;
④相等的角是对顶角的逆命题是对顶角是相等的角,是真命题;
它们的逆命题是真命题的个数是3个.
故选:B.
【点睛】本题考查了逆命题的判定,平行线的性质,绝对值的意义,直角和对顶角的概念,理解相关性质是关键.
51.(1)1个甲部件的质量是,1个甲部件的质量是
(2)货运电梯一次最多可装运7套设备
【分析】(1)本题考查二元一次方程解决实际应用问题,根据题意找到等量关系式列方程组求解即可得到答案;
(2)本题考查不等式的应用,根据载重总质量禁止超过列不等式求解即可得到答案;
【详解】(1)解:设1个甲部件的质量是,1个甲部件的质量是,
根据题意得:,解得:.
答:1个甲部件的质量是,1个甲部件的质量是;
(2)解:设货运电梯一次可装运m套设备,
根据题意得:,解得:,
又∵m为正整数,
∴m的最大值为7.
答:货运电梯一次最多可装运7套设备.
52.(1)A类物品每件的售价是6元,B类物品每件的售价是8元
(2)B类物品至少要卖40件,小深和小圳才能获得奖励
【分析】本题考查了二元一次方程组的应用以及一元一次不等式的应用,解题的关键是:(1)找准等量关系,正确列出二元一次方程组;(2)根据各数量之间的关系,正确列出一元一次不等式.
(1)设A类物品每件的售价是x元,B类物品每件的售价是y元,根据“A类卖了10件和B类卖了20件一共可卖220元;A类卖了16件和B类卖了30件一共可卖336元”,列出关于x,y的二元一次方程组求解即可;
(2)设B类物品卖了m件,则A类物品卖了件,利用总价=单价×数量,结合总价不少于500元,可列出关于m的一元一次不等式,解之取其中的最小值,即可得出结论.
【详解】(1)设A类物品每件的售价是x元,B类物品每件的售价是y元,
根据题意得:,
解得:.
答:A类物品每件的售价是6元,B类物品每件的售价是8元;
(2)设B类物品卖了m件,则A类物品卖了件,
根据题意得:,
解得:,
∴m的最小值为40.
答:B类物品至少要卖40件,小深和小圳才能获得奖励.
53.(1)糯米糍每箱的价格是元,桂味每箱的价格是元;
(2)购进糯米糍箱,桂味箱时,获利最多.
【分析】本题考查了一次函数的应用、二元一次方程组的应用,一元一次不等式组的应用,找准等量关系,正确列出二元一次方程组是解题的关键.
(1)设糯米糍每箱的价格是元,桂味每箱的价格是元,根据题意列出二元一次方程组,解方程组,即可求解;
(2)设糯米糍有箱,则桂味有箱,据题意列出一元一次不等式组,解不等式组得出,设利润为,进而根据一次函数的性质,即可求解.
【详解】(1)解:(1)设糯米糍每箱的价格是元,桂味每箱的价格是元,
根据题意得:
解得:
答:糯米糍每箱的价格是元,桂味每箱的价格是元;
(2)设糯米糍有箱,则桂味有箱,
由题意可得:
解得:
为正整数,
共有 种方案,
设利润为,则
获利随的增加而减小
当时,获利最多,
购进糯米糍箱,桂味箱时,获利最多
54.(1)每个“玉兔灯笼”的售价为元,每个 “玉兔摆件”的售价为元.
(2)“玉兔灯笼”购进个,所获得的利润最大,最大利润为元.
【分析】(1)设每个“玉兔灯笼”的售价为元,每个 “玉兔摆件”的售价为元,再根据10个“玉兔灯笼”和15个“玉兔摆件”的售价为2400元;30个“玉兔灯笼”和20个“玉兔摆件”的售价为5200元,建立方程组,可得答案;
(2)设当月销售利润为元,“玉兔灯笼”购进个,则“玉兔摆件”购进个,再根据总利润等于两种商品的利润之和建立一次函数关系式,再根据一次函数的性质解决问题即可.
【详解】(1)解:设每个“玉兔灯笼”的售价为元,每个 “玉兔摆件”的售价为元,则
,解得:,
答:每个“玉兔灯笼”的售价为元,每个 “玉兔摆件”的售价为元.
(2)设当月销售利润为元,“玉兔灯笼”购进个,则“玉兔摆件”购进个,
∴
,
又∵,
解得:,
∵,
∴随的增大而减小,
∴当时,取得最大值,
此时;
∴“玉兔灯笼”购进个,所获得的利润最大,最大利润为元.
【点睛】本题考查的是二元一次方程组的应用,一元一次不等式组的应用,一次函数的应用,确定相等关系与不等关系建立方程,函数关系式或不等式组是解本题的关键.
55.(1)甲种水果的进价为每千克12元,乙种水果的进价为每千克20元.
(2)22.
【分析】(1)设甲种水果的进价为每千克a元,乙种水果的进价为每千克b元.根据题意列二元一次方程组求解即可.
(2)根据甲水果的利润+以水果的利润800,列不等式,求出m的值,再取m的最大整数值即可.
本题考查了列二元一次方程组和一元一次不等式解应用题,正确的列出方程组和不等式是解题的关键.
【详解】(1)设甲种水果的进价为每千克a元,乙种水果的进价为每千克b元.
根据题意,得,
解方程组,得,
答:甲种水果的进价为每千克12元,乙种水果的进价为每千克20元.
(2)水果店第三次获得的利润为
.
根据题意,得.
解这个不等式,得.
正整数m的最大值为22.
56.(1)150本
(2)128
【分析】本题主要考查了二一元一次方程的应用以及一元一次不等式的应用,理解题意,弄清数量关系是解题关键.
(1)设购进了种文件夹个,则购进了种文件夹y个,根据题意列出二一元一次方程并求解,即可获得答案;
(2)根据题意,列出关于的一元一次不等式并求解,即可获得答案.
【详解】(1)解:设购进了A种笔记本x本,购进了种笔记本y本,
由题意得:,
解得:,
答:购进了A种笔记本150本,购进了B种笔记本200本;
(2)解:由题意得:,
解得:,
答:m的最小值为128.
57.(1)腊梅的进价是12元/束,百合的进价是18元/束;
(2)当购进腊梅30束,百合50束时,销售利润最大,销售的最大利润为840元.
【分析】本题主要考查二元一次方程组的应用,一次函数,一元一次不等式组的应用,熟练掌握利润与进购量之间的数量关系是解决问题的关键.
(1)设腊梅的进价是x元/束,百合的进价是y元/束,根据题意列出方程组求解即可;
(2)设购进腊梅m束,则购进百合束,根据题意列出不等式组求出,然后表示出总利润,然后利用一次函数的性质求解即可.
【详解】(1)设腊梅的进价是x元/束,百合的进价是y元/束,
根据题意得:,
解得:.
答:腊梅的进价是12元/束,百合的进价是18元/束;
(2)设购进腊梅m束,则购进百合束,
根据题意得:,
解得:,
设购进的两种鲜花全部销售完后获得的总利润为w元,
则,
即,
∵,
∴w随m的增大而减小,
∴当时,w取得最大值,(元),
此时(束).
答:当购进腊梅30束,百合50束时,销售的最大利润为840元.
58.(1)A、B两种模型每件分别需要25元,150元
(2),购进A模型226件,B模型29件利润最大为5390元
【分析】(1)设购进A,B两种模型每件分别需要x元,y元,列方程组求解即可.
(2)设购买A种模型a件,购买B种模型b件,由题意列出方程组,求出b的范围,再列出W与b的函数关系式,求最值即可.
【详解】(1)设购进A、B两种模型每件分别需要x元,y元,由题意得:
解得
答:A、B两种模型每件分别需要25元,150元.
(2)设购买A种模型a件,B种模型b件,
,
解得
则购买A种模型为件,即件,
则,即
∵,
∴当b取最小值时总利润最大,由(2)得,b为整数,
∴当时,,
∴购进A模型226件,B模型29件利润最大为5390元
【点睛】本题考查了二元一次方程组的应用,一次函数的应用,一元一次不等式组的应用,找准数量关系,正确列出方程组,函数关系式,不等式组是解题的关键.
59.(1),,
(2)见解析
(3)①√;②√
(4)见解析,
【分析】本题考查的是一次函数的图象和性质,一次函数与一元一次不等式,利用描点法画出函数图象,并结合函数图象解题是关键.
(1)把代入,根据待定系数法即可求得,将和分别代入函数即可求解出;
(2)利用描点法画出图象;
(3)观察图象即可判断;
(4)求得交点坐标,根据图象即可求得结论.
【详解】(1)∵函数的图象经过点,
∴,
解得,
∴这个函数的表达式是;
∴当时,,
当时,,
∴,,;
(2)函数的图象如图所示:
(3)①该函数图象是轴对称图形,它的对称轴为y轴.正确;
②当时,y随x的增大而减小;当时,y随x的增大而增大,正确;
故答案为:√;√;
(4)在同一平面直角坐标系中画出直线与函数的图象,如图
把代入,得,
解得,
根据图象可知,不等式的解集是.
故答案为:.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
专题02 不等式组、方程组、一次函数
一、不等式与不等式组
1.如图,数轴上的点A与点B所表示的数分别为a,b,则下列不等式成立的是( )
A. B. C. D.
2.用甲乙两种原料配制成某种饮料,已知每千克的这两种原料的维生素C含量及购买这两种原料的价格如表所示:现配制这种饮料,要求至少含有4200单位的维生素C,且购买原料的费用不超过72元.设所需甲种原料,则可列不等式组为( )
原料 甲 乙
维生素 600单位 100单位
原料价格 8元 4元
A. B.
C. D.
3.若关于x的不等式组的解集是x>2,则m的取值范围是 .
4.解不等式组:,并写出该不等式组的整数解.
5.若,则下列不等式中正确的是( )
A. B. C. D.
6.已知点在第二象限,则的取值范围在数轴上表示正确的是( )
A. B.
C. D.
7.宝安凤凰山森林公园位于“宝安第一山”凤凰山脚下,公园树木丰茂,景色优美,所以小青想带她初三的表姐去游玩放松释放压力,计划15点10分从学校出发,已知两地相距5.1千米,她们跑步的平均速度为190米/分钟,步行的平均速度为80米/分钟,若她们要在16点之前到达,那么她们至少需要跑步多少分钟?设他跑步的时间为分钟,则列出的不等式为( )
A. B.
C. D.
8.2024年春晚,刘谦表演的扑克牌魔术“约瑟夫环”,是数学与神奇的完美结合,通过一定指令的操作,会得到一个数学规律.请依照下列定义,若,则的取值范围为 .
9.解不等式组.
10.若,则下列不等式变形错误的是( )
A. B. C. D.
11.2024年中央一号文件强调“强化农业科技支撑”,充分发挥科技生产力对企业和产业发展的作用,某镇计划引进无人机田间喷洒农药技术,无人机喷洒农药时,平均每亩地用药量比常规喷药壶用药量少10ml,无人机用药300ml喷洒的农田面积与常规喷药壶用药450ml喷洒的农田面积相同.
(1)求无人机喷洒农药时,平均每亩地的用药量 .
(2)该镇计划采购A,B两种型号喷药无人机共20台,已知A型号喷药无人机每台15000元,B型号喷药无人机每台20000元,若采购资金不超过360000元,则最少需采购A型号喷药无人机多少台?
12.已知关于x的不等式组有四个整数解,则m的取值范围是( )
A. B. C. D.
13.为推进全民健身设施建设,某体育中心准备改扩建一块运动场地.现有甲、乙两个工程队参与施工,具体信息如下:
信息—
工程队 每天施工面积(单位:) 每天施工费用(单位:元)
甲 3600
乙 x 2200
信息二
甲工程队施工所需天数与乙工程队施工所需天数相等.
(1)求x的值;
(2)该工程计划先由甲工程队单独施工若干天,再由乙工程队单独继续施工,两队共施工22天,且完成的施工面积不少于.该段时间内体育中心至少需要支付多少施工费用
14.当时,则( )
A. B. C. D.
15.不等式组的解集在数轴上表示为( )
A. B.
C. D.
16.关于的不等式有3个整数解,则的取值范围是( )
A. B. C. D.
17.解不等式组:
(1);
(2).
18.解不等式组:,并指出它的所有的非负整数解.
19.不等式的解集在数轴上表示正确的是( )
A. B.
C. D.
20.已知, 则下列各式成立的是( )
A. B. C. D.
21.如图,一次函数和的图象分别与x轴交于点、,则关于x的不等式组的解集是( )
A. B. C. D.
22.若关于x的一元一次不等式组无解,则a的取值范围是( )
A.a≥1 B.a>1 C.a≤-1 D.a<-1
23.已知关于x的不等式组的整数解共有4个,则a的取值范围是 .
24.解不等式组,并把不等式组的解集在数轴上表示出来.
25.若,则下列各式中一定成立的是( )
A. B. C. D.
26.某商场店庆活动中,商家准备对某种进价为600元、标价为1100元的商品进行打折销售,但要保证利润率不低于10%,则最低折扣是 .
27.解不等式组并把解集在数轴上表示出来.
28.若,则下列式子一定成立的是( )
A. B. C. D.
29.不等式组的解集在数轴上应表示为( )
A. B.
C. D.
30.一次环保知识竞赛共有25道题,每一题答对得4分,答错或不答都扣1分,在这次竞赛中,小明被评为优秀(85分或85分以上),小明至少要答对多少道题?如果设小明答对了x道题,根据题意列式得( )
A.4x﹣1×(25﹣x)>85 B.4x+1×(25﹣x)≤85
C.4x﹣1×(25﹣x)≥85 D.4x+1×(25﹣x)>85
31.解不等式组,并把其解集表示在数轴上.
32.若,则下列不等关系一定成立的是( )
A. B. C. D.
33.定义:如果一元一次方程的解是一元一次不等式组的解,则称该一元一次方程为该不等式组的相伴方程,若方程,都是关于的不等式组的相伴方程,则的取值范围为 .
34.解不等式组:.
35.若,则下列式子中错误的是( )
A. B. C. D.
36.若关于的不等式组无解,则的取值范围是( )
A. B. C. D.
37.解不等式组:
(1); (2).
38.解不等式,并把解集在数轴上表示出来.
39.解不等式组并在数轴上表示它的解集
40.解不等式:
41.五一假期,两位老师计划带领若干学生去古镇参与社会实践,他们联系了报价均为每人200元的两家旅行社.经协商,甲旅行社的优惠条件是:两位老师全额收费,学生按六折收费;乙旅行社的优惠条件是:老师与学生都按照七折收费.
(1)设总人数为x人,选择甲旅行社时,所需费用为元,选择乙旅行社时,所需费用为元,请分别写出,与x之间的关系式.
(2)若学生人数不超过10人,为了减少花销,他们应该如何选择旅行社?
二、平面直角坐标系
42.如果点在平面直角坐标系的第三象限内,那么的取值范围在数轴上可表示为( )
A. B.
C. D.
三、一次函数
43.为丰富同学们阳光大课间活动,育才学校现决定增购两种体育器材:跳绳和毽子.已知跳绳的单价比毽子的单价多3元,用800元购买的跳绳数量和用500元购买的毽子数量相同.
(1)求跳绳和毽子的单价分别是多少元.
(2)恰逢店庆活动,体育用品店对这两种器材打折销售,其中跳绳以八折出售,毽子以七折出售.学校计划购买跳绳和毽子两种器材共600个,且要求跳绳的数量不少于毽子数量的3倍,请求出学校花钱最少的购买方案及最少花费.
44.如图,直线与直线的交点是,则不等式的解集是 .
45.如图,函数和的图象相交于点,则关于的x不等式的解集为 .
46.如图,直线:与直线:相交于点,则关于的不等式的解集为( )
A. B. C. D.
47.如图,一次函数y1=x+b与一次函数y2=kx+3的图象交于点P(1,2),则关于不等式x+bkx+3的解集是( )
A.x0 B.x0 C.x1 D.x1
48.如图,已知函数与函数的图像交于点P,则不等式的解集是 .
49.如图,一次函数和的图象相交于点,则关于的不等式的解集为
四、命题与证明
50.下列命题:①同旁内角互补,两直线平行;②若,则;③直角都相等;④相等的角是对顶角.它们的逆命题是真命题的个数是( )
A.4个 B.3个 C.2个 D.1个
五、二元一次方程组
51.某货运电梯限重标志显示,载重总质量禁止超过.现要用此货运电梯装运一批设备,每套设备由1个甲部件和2个乙部件组成.现已知2个甲部件和1个乙部件总质量为,3个甲部件和4个乙部件质量相同.
(1)请分别求出1个甲部件和1个乙部件的质量各是多少千克?
(2)每次装运都需要工人装卸,设备需要成套装运,现已知装卸工人总重量为,则货运电梯一次最多可装运多少套设备?
52.某校八年级为了丰富同学们的课余生活,决定举行一场校园义卖活动,小深和小圳都参加了这次活动,他们分别售卖类物品和类物品,若类卖了10件和类卖了20件一共可卖220元;若类卖了16件和类卖了30件一共可卖336元.
(1)请求出类物品和类物品每件的售价分别是多少元?
(2)为了鼓励更多同学参与,能筹到更多善款,学校决定设立奖励机制,如果两人合作筹集到善款总额不少于500元,则可获得电影票一张作为奖励.假设类和类一共卖了70件,则类至少要卖多少件,小深和小圳才能获得奖励?
53.美丽的滨海城市深圳,不仅阳光充沛,而且特色水果丰富,其中南山荔枝是广东省著名的荔枝品种,也是比较少能享有地理标志保护的荔枝,某经销商计划从南山购进糯米糍、桂味两种荔枝.已知购进糯米糍箱,桂味 箱,共需元;购进糯米糍箱,桂味箱,共需元.
(1)糯米糍、桂味每箱的价格分别是多少元?
(2)该经销商计划用不超过元购进糯米糍、桂味共箱,且糯米糍的箱数不超过桂味箱数的倍,共有多少不同的种进货方案?如果该经销商将 购进的荔枝按照糯米糍每箱元,桂味每箱元的价格全部售出,那么哪种进货方案获利最多?
54.为了迎接兔年的到来,广大市民纷纷开始购买兔年装饰物,某网店上架了“玉兔灯笼”和“玉兔摆件”这两款产品,已知10个“玉兔灯笼”和15个“玉兔摆件”的售价为2400元;30个“玉兔灯笼”和20个“玉兔摆件”的售价为5200元.
(1)每个“玉兔灯笼”和“玉兔摆件”的售价分别为多少元?
(2)已知“玉兔灯笼”和“玉兔摆件”的成本分别为80元/个和50元/个.进入2023年一月后,这两款产品持续热销,于是网店再购进了这两款产品共600个,其中“玉兔摆件”的数量不超过“玉兔灯笼”数量的2倍,且购进总价不超过37800元.为回馈新老客户,网店决定对“玉兔灯笼”降价10%后再销售,若一月份购进的这两款产品全部售出,则“玉兔灯笼”购进多少个时该网店当月销售利润最大?最大利润为多少?
55.某水果店经销甲、乙两种水果,两次购进水果的情况如下表所示:
进货批次 甲种水果质量 (单位:千克) 乙种水果质量 (单位:千克) 总费用 (单位:元)
第一次 60 40 1520
第二次 30 50 1360
(1)求甲、乙两种水果的进价;
(2)销售完前两次购进的水果后,该水果店决定回馈顾客,开展促销活动.第三次购进甲水果80千克,乙水果120千克.将其中的m千克甲种水果和3m千克乙种水果按进价销售,剩余的甲种水果以每千克17元、乙种水果以每千克30元的价格销售.若第三次购进的水果全部售出后,获得的最大利润不低于800元,求正整数m的最大值.
56.开学前夕,某书店计划购进A、B两种笔记本共350本,已知A种笔记本的进价为12/本,B种笔记本的进价为15元/本,共计4800元.
(1)请问购进了A种笔记本多少本?
(2)在销售过程中,A、B两种笔记本的标价分别为20元/本、25元/本.受疫情影响,两种笔记本按标价各卖出m本以后,该店进行促销活动,剩余的A种笔记本按标价的七折全部售出,剩余的B种笔记本按成本价清货,若两种笔记本的总利润不少于2348元,请求出m的最小值.
57.“人间烟火气,最抚凡人心.”在这喧嚣的世界里,地摊的存在,让人们感受到了那份朴实无华的温暖,也让城市多了一份生活的温度,某个体户购买了腊梅,百合两种鲜花摆摊销售,若购进腊梅5束,百合3束,需要114元;若购进腊梅8束,百合6束,需要204元.
(1)求腊梅,百合两种鲜花的进价分别是每束多少元?
(2)若每束腊梅的售价为20元,每束百合的售价为30元.结合市场需求,该个体户决定购进两种鲜花共80束,计划购买成本不超过1260元,且购进百合的数量不少于腊梅数量的,两种鲜花全部销售完时,求销售的最大利润及相应的进货方案.
58.俄乌战争仍在继续,人们对各种军用装备倍感兴趣,某商家购进坦克模型(记作A)和导弹(记作B)两种模型,若购进A种模型10件,B种模型5件,需要1000元;若购进A种模型4件,B种模型3件,需要550元.
(1)求购进A,B两种模型每件分别需多少元?
(2)若销售每件A种模型可获利润20元.每件B种模型可获利润30元.商店用1万元购进模型,且购进A种模型的数量不超过B种模型数量的8倍,设总盈利为W元,购买B种模型b件,请求出W关于b的函数关系式,并求出当b为何值时,销售利润最大,并求出最大值.
六、函数基础知识
59.结合所学研究函数的方法,我们研究函数性质及其应用,请根据下表信息,按要求完成下列各小题.
x … 0 1 2 3 4 …
y … m 0 2 n …
(1)______,______,______;
(2)请在平面直角坐标系中画出该函数的图象;
(3)判断下列关于该函数性质的说法是否正确(正确的打√,错误的打×);
①该函数图象是轴对称图形,它的对称轴为y轴.(______)
②当时,y随x的增大而减小;当时,y随x的增大而增大.(______)
(4)请在同一平面直角坐标系中再画出函数的图象,结合函数的图象,直接写出不等式的解集______.
参考答案
题号 1 2 5 6 7 10 12 14 15 16
答案 A C D D A D A D B C
题号 19 20 21 22 25 28 29 30 32 35
答案 A D D A D B D C A B
题号 36 42 46 47 50
答案 C D A C B
1.A
【分析】由图可知,,根据不等式的性质判断即可.
【详解】解:由图可知,,则有
A、,成立,本选项符合题意;
B、,原不等式不成立,本选项不符合题意;
C、,原不等式不成立,本选项不符合题意;
D、,原不等式不成立,本选项不符合题意;
故选:A.
【点睛】此题考查数轴和不等式的性质,通过数轴判断出,并掌握不等式的性质是解答本题的关键.
2.C
【分析】本题主要考查了列一元一次不等式组,理解题意、找准不等关系成为解题的关键.
设所需甲种原料的质量为,则需乙种原料.再根据不等关系“至少含有4200单位的维生素C”和“购买原料的费用不超过72元”列出不等式组即可.
【详解】解:设所需甲种原料的质量为,则需乙种原料.
根据题意,得:.
故选:C.
3.m≤2
【分析】根据不等式组的解集,可判断m与2的大小.
【详解】解:因为不等式组的解集是x>2,根据同大取较大原则可知:m<2,
当m=2时,不等式组的解集也是x>2,
所以m≤2.
故答案为:m≤2.
【点睛】本题考查了一元一次不等式组的解法,熟练掌握一元一次不等式组的解法是解答本题的关键.先分别解两个不等式,求出它们的解集,再求两个不等式解集的公共部分.不等式组解集的确定方法是:同大取大,同小取小,大小小大取中间,大大小小无解.
4.不等式的解集为,整数解为,,,0
【分析】先求出两个一元一次不等式的解集,然后求出不等式组的解集,最后找出其中的整数即可
【详解】解:
解不等式①:,解得,
解不等式②:,得,解得
∴不等式的解集为,
∴不等式组的整数解为,,,0.
【点睛】本题考查了一元一次不等式组的解法,熟练掌握一元一次不等式组的解法是解答本题的关键.先分别解两个不等式,求出它们的解集,再求两个不等式解集的公共部分.不等式组解集的确定方法是:同大取大,同小取小,大小小大取中间,大大小小无解.
5.D
【分析】本题考查不等式的性质,根据条件,运用不等式的性质逐项验证即可得到答案,熟记不等式的三个性质是解决问题的关键.
【详解】解:A、由于,则,故错误,不符合题意;
B、由于,则,故错误,不符合题意;
C、由于,则,故错误,不符合题意;
D、由于,则,故正确,符合题意;
故选:D.
6.D
【分析】根据第二象限内点的特征,列出一元一次不等式组,解不等式组,即可求解,
本题考查了,点的坐标,求一元一次不等式组的解集,在数轴上表示不等式的解集,解题的关键是:熟练掌握相关知识点.
【详解】解:∵点在第二象限,
∴,解得:,
故选:.
7.A
【分析】根据“步行时间步行速度跑步时间跑步速度”列不等式即可.本题主要考查由实际问题抽象出一元一次不等式,解题的关键是根据题意确定其中蕴含的不等关系.
【详解】解:∵计划15点10分从学校出发,要在16点之前到达
∴总时间为分钟
设他跑步的时间为分钟,则他步行时间为分钟,
根据题意,得:,
故选:A.
8./
【分析】本题主要考查了解不等式,根据题干提供的信息,得出,解不等式即可.
【详解】解:∵,
∴,
∴,
解得:,
故答案为:.
9..
【分析】本题考查的是解一元一次不等式组.分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小找不到确定不等式组的解集.
【详解】解:解不等式①,得:,
解不等式②,得:,
则不等式组的解集为.
10.D
【分析】根据不等式的基本性质逐一进行判断即可.
【详解】解:A、∵,
∴,故正确,不合题意;
B、∵,
∴,故正确,不合题意;
C、∵,
∴,故正确,不合题意;
D、∵,
∴,
∴,故错误,符合题意;
故选:D.
【点睛】本题考查不等式的性质:(1)不等式两边加(或减)同一个数(或式子),不等号的方向不变.(2)不等式两边乘(或除以)同一个正数,不等号的方向不变(3)不等式两边乘(或除以)同一个负数,不等号的方向改变.
11.(1)无人机喷洒农药时,平均每亩地的用药量为20ml;
(2)最少需采购A型号喷药无人机8台.
【分析】本题考查了分式方程的应用以及一元一次不等式的应用,解题的关键是:(1)找准等量关系,正确列出分式方程;(2)根据各数量之间的关系,正确列出一元一次不等式.
(1)设无人机喷洒农药时,平均每亩地的用药量为xml, 则用常规喷药壶喷洒农药时,平均每亩地的用药量为ml,根据无人机用药300ml 喷洒的农田面积与 常规喷药壶用药450ml 喷洒的农田面积相同,可列出关于x 的分式方程,解之经检验后,
即可得出结论;
(2)设采购m 台 A 型号喷药无人机,利用总价 =单价×数量,结合总价不超过360000元,可列出关于m的一元一次不等式,解之取其中的最小值,即可得出结论.
【详解】(1)解:设无人机喷洒农药时,平均每亩地的用药量为 ,则用常规喷药壶喷洒农药时,平均每亩地的用药量为,
根据题意得:,
解得:,
经检验,是所列方程的解,且符合题意.
答:无人机喷洒农药时,平均每亩地的用药量为;
(2)解:设采购台型号喷药无人机,则采购台型号喷药无人机,
根据题意得:,
解得:,
的最小值为8.
答:最少需采购型号喷药无人机8台.
12.A
【分析】本题主要考查不等式组的整数解问题,根据不等式组的整数解的个数得出关于的不等式组是解题的关键.解不等式组的两个不等式,根据其整数解的个数得出,解之可得.
【详解】解:解不等式,得:,
解不等式,得:,
不等式组有4个整数解,
,
解得:.
故选:A
13.(1)x的值为600
(2)该段时间内体育中心至少需要支付施工费用56800元
【分析】(1)根据题意甲工程队施工所需天数与乙工程队施工所需天数相等列出分式方程解方程即可;
(2)设甲工程队先单独施工天,体育中心共支付施工费用元,根据先由甲工程队单独施工若干天,再由乙工程队单独继续施工,两队共施工22天,且完成的施工面积不少于列出不等式即可得到答案.
【详解】(1)解:由题意列方程,得.
方程两边乘,得.
解得.
检验:当时,.
所以,原分式方程的解为.
答:x的值为600.
(2)解:设甲工程队先单独施工天,体育中心共支付施工费用元.
则.
,
.
1400>0,
随的增大而增大.
当时,取得最小值,最小值为56800.
答:该段时间内体育中心至少需要支付施工费用56800元.
【点睛】本题主要考查了分式方程的应用,一元一次不等式的应用以及一次函数的应用,熟练掌握知识点是解题的关键.
14.D
【分析】本题考查了不等式的性质,熟练掌握不等式的性质是解答本题的关键.根据不等式的性质可判断A,B,D;利用特殊值可判断C.
【详解】解:A.∵,∴,故不正确;
B.∵,∴,故不正确;
C.当时,满足,但,故不正确;
D.∵,∴,正确;
故选D.
15.B
【分析】分别求出每一个不等式的解集,根据“大于向右,小于向左,包括端点用实心,不包括端点用空心”的原则即可得答案.
【详解】解:,
解不等式2x 1≤5,得:x≤3,
解不等式8 4x<0,得:x>2,
故不等式组的解集为:2<x≤3,
故选:B.
【点睛】本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟悉在数轴上表示不等式解集的原则“大于向右,小于向左,包括端点用实心,不包括端点用空心”是解题的关键.
16.C
【分析】根据不等式的整数解只有0,1,2,即可得出实数a的取值范围.
【详解】解:∵不等式有3个整数解,
∴这3个整数解为0,1,2,
∴实数a的取值范围是
故选C
【点睛】本题考查一元一次不等式组的整数解,解题的关键是明确题意,会解一元一次不等式组.
17.(1)
(2)
【分析】本题主要考查了解一元一次不等式:
(1)先去括号,再移项合并同类项,即可求解;
(2)先取分母,再去括号,然后移项合并同类项,即可求解.
【详解】(1)解:
去括号得:
移项合并同类项得:
解得:;
(2)解:
去分母得:
去括号得:
解得:.
18.;非负整数解为:0,1.
【分析】本题考查了一元一次不等式组的解法,熟练掌握一元一次不等式组的解法是解答本题的关键.先分别解两个不等式,求出它们的解集,再求两个不等式解集的公共部分即可得到不等式组的解集,然后找出非负整数解即可.
【详解】解:由①得:,
由②得:,
∴不等式组的解集为,
满足的非负整数解为:0,1
19.A
【分析】本题考查的是解一元一次不等式,利用数轴表示不等式的解集.先求出不等式的解集,再在数轴上表示出来不等式的解集即可,注意大于小于用空心,大于等于小于等于用实心,大于大于等于开口向右,小于小于等于开口向左.
【详解】解:,
,
数轴上表示为:,
故选:A.
20.D
【分析】本题考查了不等式的性质,注意不等式的两边都乘或除以一个负数,不等号的方向改变.根据不等式的性质逐一判断即可解题.
【详解】解:A、,当时,,故本选项不符合题意;
B、,,故本选项不符合题意;
C、,,故本选项不符合题意;
D、,,故本选项符合题意;
故选:D.
21.D
【分析】根据图象可知y=k1x+b1>0的解集和y=kx+b>0的解集,即可确定不等式组的解集.
【详解】解:一次函数和的图象分别与x轴交于点、,
根据图象可知,的解集为:,的解集为:,
∴不等式组的解集是,
故选:D.
【点睛】本题考查了一次函数与一元一次不等式的关系,熟练掌握一次函数的图象是解题的关键.
22.A
【详解】解:解得,,
∵无解,
∴a≥1.
故选A.
23.
【分析】先求出不等式组的解集,根据一元一次不等式组有四个整数解进行分析,即可得到答案.
【详解】解:,
解不等式①,得:,
解不等式②,得:,
∵关于的不等式组的整数解共有4个,
则这四个整数解为:0,1,2,3,
当时,不等式组的整数解为:0,1,2,3,
∴.
故答案为:.
【点睛】本题考查了解一元一次不等式组的知识;解题的关键是正确求得一元一次不等式组的解集.
24.,数轴见解析
【分析】分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小找不到确定不等式组的解集.
【详解】解:,
解不等式①,得:,
解不等式②,得:,
则不等式组的解集为,
将不等式组的解集表示在数轴上如下:
【点睛】本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.
25.D
【分析】本题考查了不等式的性质,理解不等式的性质是解题的关键.
根据不等式的性质逐项判定即可求解.
【详解】解:A、∵,
∴,故此选项不符合题意;
B、∵,,
∴,故此选项不符合题意;
C、∵,
∴,故此选项不符合题意;
D、∵,
∴,故此选项符合题意;
故选:D.
26.6折.
【分析】利润率不低于10%,即利润要大于或等于:600×10%元,设打x折,则售价是110x元.根据利润率不低于10%就可以列出不等式,求出x的范围.
【详解】设可以打x折,
1100×﹣600≥600×10%,
解得x≥6,即最低折扣是6折.
故答案为6折.
【点睛】此题考查了一元一次不等式组的应用,正确理解利润率的含义,理解利润=进价×利润率是解题的关键.
27.不等式组的解集为:,图见解析;
【分析】先分别求出各不等式的解集,再求出其公共解集,并在数轴上表示出来即可.
【详解】,
解不等式①得.
解不等式②得.
∴原不等式组的解集为:.
在数轴上表示如图:
【点睛】本题考查的是在数轴上表示一元一次不等式组的解集,在解答此类题目时要注意实心圆点与空心圆点的区别,这是此题的易错点.
28.B
【分析】根据不等式的性质依次分析判断.
【详解】解:∵,∴a+1>b+1,故选项A不符合题意;
∵,∴,故选项B符合题意;
∵,∴-2a<-2b,故选项C不符合题意;
∵,∴,故选项D不符合题意;
故选:B.
【点睛】此题考查了不等式的性质:不等式两边同时加上或减去同一个整式,不等号方向不变;不等式两边同时乘或除以同一个不为0的整正数,不等号方向不变;不等式两边同时乘或除以同一个不为0的负数,不等号方向改变.
29.D
【分析】根据不等式“大于小的,小于大的取中间”即可求得解集.
【详解】解:由题意可知,不等式的解集为,
只有选项D符合题意要求,
故选:D.
【点睛】本题考查了解一元一次不等式(组),在数轴上表示不等式组的解集等知识点,注意:在数轴上表示不等式组的解集时,包括该点时用实心,不包括该点时用空心.
30.C
【分析】根据题意可以列出相应的不等式,从而可以解答本题.
【详解】解:由题意可得,
4x-1×(25-x)≥85,
故选C.
【点睛】本题考查由实际问题抽象出一元一次不等式,解答本题的关键是明确题意,列出相应的不等式.
31.解集为,数轴见解析
【分析】本题考查解一元一次不等式组、在数轴上表示不等式组的解集,分别解出两个不等式的解集,并表示在数轴上,再找到公共解集即可求解,熟知:同大取大,同小取小,大小小大中间找,大大小小找不到的原则是解题的关键.
【详解】解:解不等式,得:,
解不等式,得:,
则不等式组的解集为,
将不等式组的解集表示在数轴上如下:
32.A
【分析】本题考查不等式的性质,根据不等式的性质逐项验证即可得到答案,熟记不等式性质是解决问题的关键.
【详解】解:A、由不等式的性质可知,当时,则,不等关系一定成立,符合题意;
B、由不等式的性质可知,当时,则,原不等关系不成立,不符合题意;
C、由不等式的性质可知,当,且时,则,原不等关系不一定成立,不符合题意;
D、由不等式的性质可知,当,且时,则,原不等关系不一定成立,不符合题意;
故选:A.
33.
【分析】解方程求出两个方程的解,再解不等式组得出,根据,均是不等式组的解可得关于m的不等式组,解之可得.
【详解】解:解方程,得:,
解方程,得:,
由,得:,
由,得:,
∵,均是不等式组的解,
∴且,
∴.
故答案为:.
【点睛】本题考查的是新定义问题,涉及解一元一次方程,解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.
34.
【分析】本题考查的是解一元一次不等式组,分别求出各不等式的解集,再求出其公共解集即可.熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.
【详解】
解不等式①,得:
解不等式②,得
故不等式组的解集为:.
35.B
【分析】根据不等式的性质可进行求解.
【详解】解:由可知:
A、,正确,故不符合题意;
B、,原不等式错误,故符合题意;
C、,正确,故不符合题意;
D、,正确,故不符合题意;
故选B.
【点睛】本题主要考查不等式的性质,熟练掌握不等式的性质是解题的关键.
36.C
【分析】先依次求出不等式的解集,再根据不等式组无解进行求解.
【详解】解:解不等式组,得,
∵该不等式组无解,
∴.
故选:C.
【点睛】此题主要考查不等式组无解的情况,解题的关键是熟知不等式组的解集.
37.(1)﹣1<x≤3
(2)﹣6<x≤1
【分析】(1)分别解出各个不等式,再求公共解集即可;
(2)解出每个不等式,再求公共解集.
【详解】(1)解: ,
解不等式①得x>﹣1,
解不等式②得x≤3,
∴不等式组的解集为﹣1<x≤3.
(2)解:,
解不等式①得x>﹣6,
解不等式②得x≤1,
∴不等式组的解集为﹣6<x≤1.
【点睛】本题考查解一元一次不等式组,解题的关键是掌握取不等式公共解集的方法.
38.,图见解析
【分析】先去括号,再移项、合并同类项、最后系数化为1即可,再在数轴上把解集表示出来.
【详解】解:去括号得,,
去括号得,,
合并同类项得,,
系数化为1得,,
解集在数轴上表示为:
【点睛】本题考查了解一元一次不等式以及在数轴上表示不等式的解集,是基础知识要熟练掌握.
39.;数轴见解析
【分析】本题考查了解一元一次不等式组,在数轴上表示不等式的解集.按照解一元一次不等式组的步骤进行计算,即可解答.
【详解】解:,
解不等式①得:,
解不等式②得:,
原不等式组的解集为:,
该不等式组的解集在数轴上表示如图所示:
40.
【分析】本题考查的是解一元一次不等式.去分母,移项、合并同类项,系数化为1即可.
【详解】解:,
去分母,得,
移项,得,
合并同类项,得,
系数化1,得.
41.(1);
(2)当总人数少于8人,选择乙旅行社花销较少;总人数为8人,两个旅行社花销相同;总人数超过8人不超过12人,甲旅行社花销较少.
【分析】本题考查一次函数的应用.分类探讨选择花销较少的旅行社是解决本题的难点.
(1)甲旅行社所需费用两位老师的费用学生人数;乙旅行社所需费用总人数,把相关数值代入后化简即可;
(2)分别算出,,时对应的的值,即可根据人数判断出花销较少的旅行社.
【详解】(1)解:;
;
(2)解:①.
.
解得:;
②.
.
解得:;
③.
.
解得:,
学生人数不超过10人,老师有2人,
.
答:当总人数少于8人,选择乙旅行社花销较少;总人数为8人,两个旅行社花销相同;总人数超过8人不超过12人,甲旅行社花销较少.
42.D
【分析】根据点的位置得出不等式组,求出不等式组的解集,即可得出选项.
【详解】解:∵在平面直角坐标系的第三象限内,
∴,
解得:,
在数轴上表示为:
故选D.
【点睛】本题考查了点坐标特点、一元一次不等式组、在数轴上表示不等式组的解集等知识点,能求出不等式组的解集是解此题的关键.
43.(1)跳绳的单价为8元,毽子的单价为5元
(2)购买450个跳绳,150个毽子时,总费用最少为3405元
【分析】(1)设毽子的单价为元,根据用800元购买的跳绳数量和用500元购买的毽子数量相同列出方程,解之即可;
(2)设购买跳绳m个,则购买毽子个,根据题意列出不等式组进行求解,设学校购买跳绳和毽子两种器材共花元,求出一次函数解析式,根据一次函数的性质,求最小值即可.
【详解】(1)解:设毽子的单价为元,则跳绳的单价为元,
依题意,得:,解得:,
经检验,是原方程的解,且符合题意,
.
答:跳绳的单价为8元,毽子的单价为5元.
(2)设购买跳绳m个,
由题意可得:,
解得:,
设学校购买跳绳和毽子两种器材共花元,
则,
∵,
∴随的增大而增大,
∴当时,最小,且为,
∴当学校购买450个跳绳,150个毽子时,总费用最少为3405元.
【点睛】本题考查分式方程的应用,一元一次不等式的应用,以及利用一次函数解决最值问题.根据题意,准确的列出分式方程和一次函数表达式是解题的关键.
44.
【分析】结合图像,根据交点及解答即可.
【详解】解:直线与直线的交点是,
不等式的解集为,
故答案为:.
【点睛】此题考查了利用一次函数交点求不等式的解集,正确理解一次函数的交点与不等式的关系是解题的关键.
45.
【分析】此题考查了一次函数与一元一次不等式的关系,关键是求出A点坐标以及利用数形结合的思想.先利用待定系数法求出A点坐标,结合图象写出不等式的解集即可.
【详解】解:将点代入得,,
解得,,
所以点A的坐标为,
由图可知,不等式的解集为.
故答案为:.
46.A
【分析】首先将已知点的坐标代入直线求得的值,然后观察函数图象得到在点的左边,直线都在直线的下方,据此求解.
【详解】解:直线与直线相交于点,
,
解得:,
观察图象可知:关于的不等式的解集为,
故选:A.
【点睛】本题考查了一次函数与一元一次不等式,根据函数图象,比较函数值的大小,确定对应的自变量的取值范围,解此题需要有数形结合的思想.
47.C
【分析】观察函数图象得到当x>1时,函数的图象都在的图象上方,所以关于x的不等式x+b>kx+3的解集为x>1.
【详解】解:当x>1时,函数的图象都在的图象上方,
则x+b>kx+3,
即不等式x+b>kx+3的解集为x>1.
故选:C.
【点睛】本题考查了一次函数与一元一次不等式:从函数图象的角度看,就是由函数的图像在平面直角坐标系内的高低位置来确定自变量的取值范围,掌握数型结合是解题的关键.
48.
【分析】观察图像可得当时,函数的图像位于函数的图像的下方,即可求解.
【详解】解:观察图像得:当时,函数的图像位于函数的图像的下方,
∴不等式的解集是.
故答案为:
【点睛】本题主要考查了一次函数与一元一次不等式的关系,利用数形结合思想解答是解题的关键.
49.
【分析】本题考查了一次函数图象的交点与不等式的解集、一次函数的性质,先求出点的坐标,再根据图象即可得出答案.
【详解】解:将代入得:,
解得:,
,
由图象可得:关于的不等式的解集为,
故答案为:.
50.B
【分析】先写出命题的逆命题,再对逆命题的真假进行判断即可.
【详解】①同旁内角互补,两直线平行的逆命题是两直线平行,同旁内角互补,是真命题;
②若,则的逆命题是若,则,是真命题;
③直角都相等的逆命题是相等的角是直角,是假命题;
④相等的角是对顶角的逆命题是对顶角是相等的角,是真命题;
它们的逆命题是真命题的个数是3个.
故选:B.
【点睛】本题考查了逆命题的判定,平行线的性质,绝对值的意义,直角和对顶角的概念,理解相关性质是关键.
51.(1)1个甲部件的质量是,1个甲部件的质量是
(2)货运电梯一次最多可装运7套设备
【分析】(1)本题考查二元一次方程解决实际应用问题,根据题意找到等量关系式列方程组求解即可得到答案;
(2)本题考查不等式的应用,根据载重总质量禁止超过列不等式求解即可得到答案;
【详解】(1)解:设1个甲部件的质量是,1个甲部件的质量是,
根据题意得:,解得:.
答:1个甲部件的质量是,1个甲部件的质量是;
(2)解:设货运电梯一次可装运m套设备,
根据题意得:,解得:,
又∵m为正整数,
∴m的最大值为7.
答:货运电梯一次最多可装运7套设备.
52.(1)A类物品每件的售价是6元,B类物品每件的售价是8元
(2)B类物品至少要卖40件,小深和小圳才能获得奖励
【分析】本题考查了二元一次方程组的应用以及一元一次不等式的应用,解题的关键是:(1)找准等量关系,正确列出二元一次方程组;(2)根据各数量之间的关系,正确列出一元一次不等式.
(1)设A类物品每件的售价是x元,B类物品每件的售价是y元,根据“A类卖了10件和B类卖了20件一共可卖220元;A类卖了16件和B类卖了30件一共可卖336元”,列出关于x,y的二元一次方程组求解即可;
(2)设B类物品卖了m件,则A类物品卖了件,利用总价=单价×数量,结合总价不少于500元,可列出关于m的一元一次不等式,解之取其中的最小值,即可得出结论.
【详解】(1)设A类物品每件的售价是x元,B类物品每件的售价是y元,
根据题意得:,
解得:.
答:A类物品每件的售价是6元,B类物品每件的售价是8元;
(2)设B类物品卖了m件,则A类物品卖了件,
根据题意得:,
解得:,
∴m的最小值为40.
答:B类物品至少要卖40件,小深和小圳才能获得奖励.
53.(1)糯米糍每箱的价格是元,桂味每箱的价格是元;
(2)购进糯米糍箱,桂味箱时,获利最多.
【分析】本题考查了一次函数的应用、二元一次方程组的应用,一元一次不等式组的应用,找准等量关系,正确列出二元一次方程组是解题的关键.
(1)设糯米糍每箱的价格是元,桂味每箱的价格是元,根据题意列出二元一次方程组,解方程组,即可求解;
(2)设糯米糍有箱,则桂味有箱,据题意列出一元一次不等式组,解不等式组得出,设利润为,进而根据一次函数的性质,即可求解.
【详解】(1)解:(1)设糯米糍每箱的价格是元,桂味每箱的价格是元,
根据题意得:
解得:
答:糯米糍每箱的价格是元,桂味每箱的价格是元;
(2)设糯米糍有箱,则桂味有箱,
由题意可得:
解得:
为正整数,
共有 种方案,
设利润为,则
获利随的增加而减小
当时,获利最多,
购进糯米糍箱,桂味箱时,获利最多
54.(1)每个“玉兔灯笼”的售价为元,每个 “玉兔摆件”的售价为元.
(2)“玉兔灯笼”购进个,所获得的利润最大,最大利润为元.
【分析】(1)设每个“玉兔灯笼”的售价为元,每个 “玉兔摆件”的售价为元,再根据10个“玉兔灯笼”和15个“玉兔摆件”的售价为2400元;30个“玉兔灯笼”和20个“玉兔摆件”的售价为5200元,建立方程组,可得答案;
(2)设当月销售利润为元,“玉兔灯笼”购进个,则“玉兔摆件”购进个,再根据总利润等于两种商品的利润之和建立一次函数关系式,再根据一次函数的性质解决问题即可.
【详解】(1)解:设每个“玉兔灯笼”的售价为元,每个 “玉兔摆件”的售价为元,则
,解得:,
答:每个“玉兔灯笼”的售价为元,每个 “玉兔摆件”的售价为元.
(2)设当月销售利润为元,“玉兔灯笼”购进个,则“玉兔摆件”购进个,
∴
,
又∵,
解得:,
∵,
∴随的增大而减小,
∴当时,取得最大值,
此时;
∴“玉兔灯笼”购进个,所获得的利润最大,最大利润为元.
【点睛】本题考查的是二元一次方程组的应用,一元一次不等式组的应用,一次函数的应用,确定相等关系与不等关系建立方程,函数关系式或不等式组是解本题的关键.
55.(1)甲种水果的进价为每千克12元,乙种水果的进价为每千克20元.
(2)22.
【分析】(1)设甲种水果的进价为每千克a元,乙种水果的进价为每千克b元.根据题意列二元一次方程组求解即可.
(2)根据甲水果的利润+以水果的利润800,列不等式,求出m的值,再取m的最大整数值即可.
本题考查了列二元一次方程组和一元一次不等式解应用题,正确的列出方程组和不等式是解题的关键.
【详解】(1)设甲种水果的进价为每千克a元,乙种水果的进价为每千克b元.
根据题意,得,
解方程组,得,
答:甲种水果的进价为每千克12元,乙种水果的进价为每千克20元.
(2)水果店第三次获得的利润为
.
根据题意,得.
解这个不等式,得.
正整数m的最大值为22.
56.(1)150本
(2)128
【分析】本题主要考查了二一元一次方程的应用以及一元一次不等式的应用,理解题意,弄清数量关系是解题关键.
(1)设购进了种文件夹个,则购进了种文件夹y个,根据题意列出二一元一次方程并求解,即可获得答案;
(2)根据题意,列出关于的一元一次不等式并求解,即可获得答案.
【详解】(1)解:设购进了A种笔记本x本,购进了种笔记本y本,
由题意得:,
解得:,
答:购进了A种笔记本150本,购进了B种笔记本200本;
(2)解:由题意得:,
解得:,
答:m的最小值为128.
57.(1)腊梅的进价是12元/束,百合的进价是18元/束;
(2)当购进腊梅30束,百合50束时,销售利润最大,销售的最大利润为840元.
【分析】本题主要考查二元一次方程组的应用,一次函数,一元一次不等式组的应用,熟练掌握利润与进购量之间的数量关系是解决问题的关键.
(1)设腊梅的进价是x元/束,百合的进价是y元/束,根据题意列出方程组求解即可;
(2)设购进腊梅m束,则购进百合束,根据题意列出不等式组求出,然后表示出总利润,然后利用一次函数的性质求解即可.
【详解】(1)设腊梅的进价是x元/束,百合的进价是y元/束,
根据题意得:,
解得:.
答:腊梅的进价是12元/束,百合的进价是18元/束;
(2)设购进腊梅m束,则购进百合束,
根据题意得:,
解得:,
设购进的两种鲜花全部销售完后获得的总利润为w元,
则,
即,
∵,
∴w随m的增大而减小,
∴当时,w取得最大值,(元),
此时(束).
答:当购进腊梅30束,百合50束时,销售的最大利润为840元.
58.(1)A、B两种模型每件分别需要25元,150元
(2),购进A模型226件,B模型29件利润最大为5390元
【分析】(1)设购进A,B两种模型每件分别需要x元,y元,列方程组求解即可.
(2)设购买A种模型a件,购买B种模型b件,由题意列出方程组,求出b的范围,再列出W与b的函数关系式,求最值即可.
【详解】(1)设购进A、B两种模型每件分别需要x元,y元,由题意得:
解得
答:A、B两种模型每件分别需要25元,150元.
(2)设购买A种模型a件,B种模型b件,
,
解得
则购买A种模型为件,即件,
则,即
∵,
∴当b取最小值时总利润最大,由(2)得,b为整数,
∴当时,,
∴购进A模型226件,B模型29件利润最大为5390元
【点睛】本题考查了二元一次方程组的应用,一次函数的应用,一元一次不等式组的应用,找准数量关系,正确列出方程组,函数关系式,不等式组是解题的关键.
59.(1),,
(2)见解析
(3)①√;②√
(4)见解析,
【分析】本题考查的是一次函数的图象和性质,一次函数与一元一次不等式,利用描点法画出函数图象,并结合函数图象解题是关键.
(1)把代入,根据待定系数法即可求得,将和分别代入函数即可求解出;
(2)利用描点法画出图象;
(3)观察图象即可判断;
(4)求得交点坐标,根据图象即可求得结论.
【详解】(1)∵函数的图象经过点,
∴,
解得,
∴这个函数的表达式是;
∴当时,,
当时,,
∴,,;
(2)函数的图象如图所示:
(3)①该函数图象是轴对称图形,它的对称轴为y轴.正确;
②当时,y随x的增大而减小;当时,y随x的增大而增大,正确;
故答案为:√;√;
(4)在同一平面直角坐标系中画出直线与函数的图象,如图
把代入,得,
解得,
根据图象可知,不等式的解集是.
故答案为:.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
