北师大七下期中专题07 选填压轴训练(含解析)
文档属性
| 名称 | 北师大七下期中专题07 选填压轴训练(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-11 05:31:08 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
专题07 选填压轴训练
一、单选题
1.某种细菌每分钟可由1个分裂成2个,将1个细菌放在培养瓶中经过64分钟就能分裂满一瓶.若将4个这种细菌放入同一个培养瓶中,分裂满一瓶的时间是( )
A.16分钟 B.32分钟 C.52分钟 D.62分钟
2.如图1,图2,点C是上一点,利用尺规过点C作,下列说法错误的是( )
A.图1的原理是同位角相等,两直线平行
B.以点E为圆心,以为半径作弧,得到弧
C.图2的原理是两直线平行,内错角相等
D.以点C为圆心,以为半径作弧,得到弧
3.我国宋代数学家杨辉所著《详解九章算法》中记载了用如图所示的三角形解释了二项和的乘方展开式中的系数规律,我们把这种数字三角形叫做“杨辉三角”.请你利用杨辉三角,计算的展开式中,含项的系数是( )
A.1 B.5 C.16 D.80
4.如图,在长方形中,,,对角线,动点从点出发,沿运动,设点的运动路程为(),的面积为().若与的对应关系如图所示,则图中( )
A. B.1 C.3 D.4
5.如图,已知长方形纸片,点,在边上,点,在边上,分别沿,折叠,使点和点都落在点处,若,则的度数为( )
A. B. C. D.
6.如图,在中,延长至点F,使得,延长至点D,使得,延长至点E,使得,连接,若,则为( )
A.2 B.3 C.4 D.6
7.如图,在中,D是的中点,E是上的一点,且,与相交于点F,若的面积为1,则的面积为( )
A.8 B.10 C.12 D.14
8.现有甲、乙两个正方形纸片,将甲、乙并列放置后得到图,已知点为的中点,连结,.将乙纸片放到甲的内部得到图.已知甲、乙两个正方形边长之和为,图的阴影部分面积为,则图的阴影部分面积为( )
A. B. C. D.
9.如图,在中,,平分交于点平分交于点交于点.则下列说法正确的个数为( )
①;②,③若,则;④;⑤.
A.2个 B.3个 C.4个 D.5个
10.如图,AB//CD,OP⊥CD,OE平分∠BOC,OF⊥OE,∠OCD=50°.下列结论:①∠COE=65°;②OF平分∠AOC;③∠AOF=∠POE;④∠POC=2∠AOF.其中结论正确的个数是( )
A.1个 B.2个 C.3个 D.4个
11.三角形中,如果一个角是另一个角的3倍,这样的三角形我们称之为“灵动三角形”.例如,三个内角分别为的三角形是“灵动三角形”.如图,,在射线上找一点,过点作交于点,以为端点作射线,交线段于点(我们规定).①的度数为;②是“灵动三角形”;③若,则是“灵动三角形”;④当为“灵动三角形”时,为或.结论正确的有( )个.
A.1 B.2 C.3 D.4
12.为了保护视力,某公司推出了一款护眼台灯,其侧面示意图(台灯底座高度忽略不计)如图所示,其中,经测试发现,当时,台灯光线最佳.则此时的度数为( )
A. B. C. D.
13.我国南宋数学家杨辉所著的《详解九章算术》一书中,用图中的三角形解释二项式的展开式的各项系数,此三角形称为“杨辉三角”.根据图中的规律,若,则( )
A.64 B. C.56 D.
14.如图,光的反射活动课中,小铭同学将支架平面镜放置在水平桌面上,镜面的调节角的调节范围为,激光笔发出的光束射到平面镜上,若激光笔与水平天花板(直线)的夹角,则反射光束与天花板所形成的角不可能取到的度数为( )
A. B. C. D.
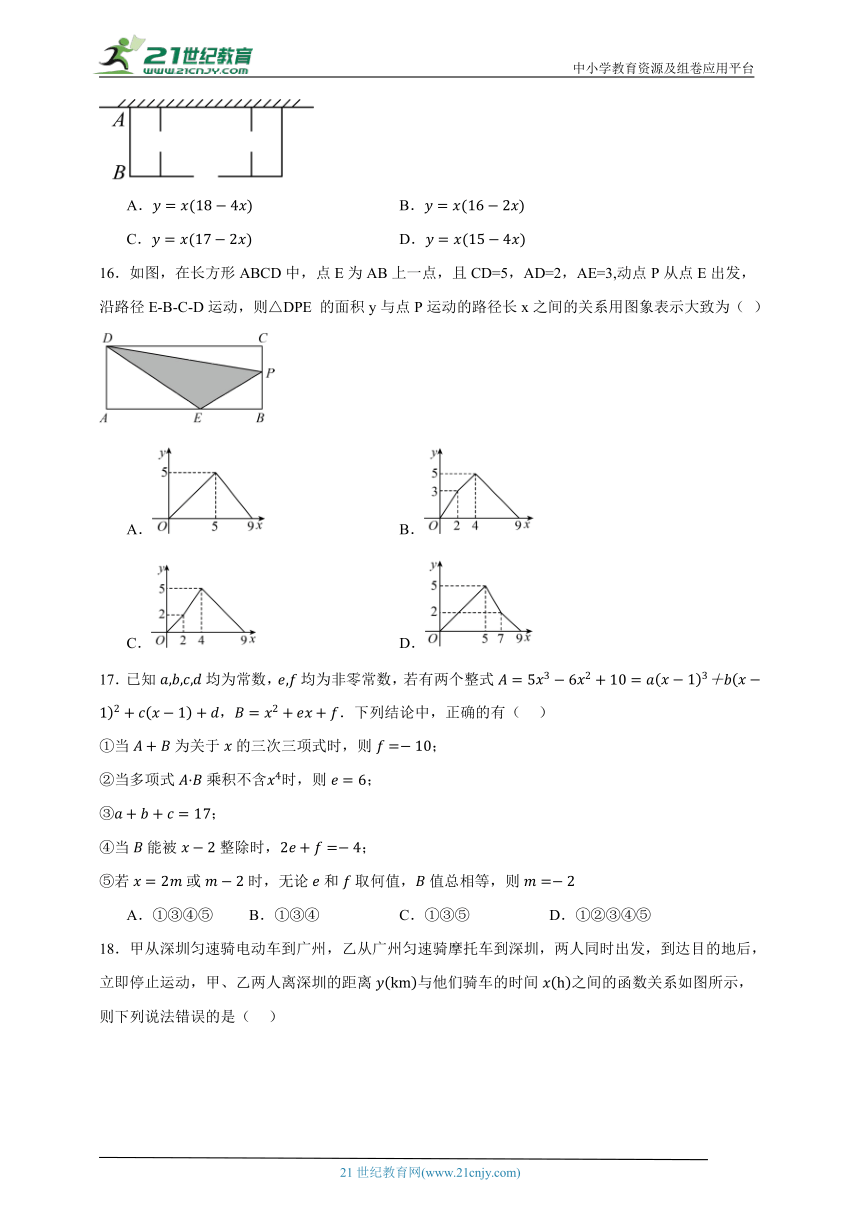
15.深高小学部饲养了两只萌萌的羊驼,建筑队在学校一边靠墙处,计划用15米长的铁栅栏围成三个相连的长方形羊驼草料仓库,仓库总面积为平方米,为方便取物,在各个仓库之间留出了1米宽的缺口作通道,在平行于墙的一边留下一个1米宽的缺口作小门,若设米,则关于x的函数关系式为( )
A. B.
C. D.
16.如图,在长方形ABCD中,点E为AB上一点,且CD=5,AD=2,AE=3,动点P从点E出发,沿路径E-B-C-D运动,则△DPE 的面积y与点P运动的路径长x之间的关系用图象表示大致为( )
A. B.
C. D.
17.已知均为常数,均为非零常数,若有两个整式,.下列结论中,正确的有( )
①当为关于的三次三项式时,则;
②当多项式乘积不含时,则;
③;
④当能被整除时,;
⑤若或时,无论和取何值,值总相等,则
A.①③④⑤ B.①③④ C.①③⑤ D.①②③④⑤
18.甲从深圳匀速骑电动车到广州,乙从广州匀速骑摩托车到深圳,两人同时出发,到达目的地后,立即停止运动,甲、乙两人离深圳的距离与他们骑车的时间之间的函数关系如图所示,则下列说法错误的是( )
A.深广两地的距离为 B.甲的速度为
C.乙的速度为 D.乙运动到达深圳
19.“抖空竹”经国务院批准列入第一批国家级非物质文化遗产名录,“裁竹成形腰鼓如,两端绳索弄徐徐.当风急转如流水,山寺闻钟韵有余.”就是对抖空竹的写照.某同学在研究“抖空竹”时有一个发现:他把它抽象成数学问题,如图所示,已知,,,则的度数是( )
A. B. C. D.
20.我国古代数学的许多创新和发展都位居世界前列,如南宋数学家杨辉(约13世纪)所著的《详解九章算术》一书中,用如图的三角形解释二项和(a+b)n的展开式的各项系数,此三角形称为“杨辉三角”.
根据“杨辉三角”请计算(a+b)20的展开式中第三项的系数为( )
A.2017 B.2016 C.191 D.190
21.方形纸带中,将纸带沿折叠成图2,再沿折叠成图3,则图3中度数是( )
A. B. C. D.
22.如图,将沿、翻折,顶点A,B均落在点O处,且与重合于线段,若,则的度数为( )
A. B. C. D.
二、填空题
23.如图,在长方形中 ,,点E,F是边,上的点,,且,分别以,为边在长方形外侧作正方形和,若长方形的面积为20,则图中阴影部分的面积和为
24.如图是长方形纸带,,将纸带沿折叠成图,再沿折叠成图,则图中的度数是 .
25.七巧板起源于我国先秦时期,古算书《周髀算经》中有关于正方形的分割术,经过历代演变而成七巧板.小深先用一副七巧板拼成了图1,图1的轮廓是一个边长为a的正方形,其中,小等腰直角三角板M的面积为,小深拿掉七巧板中的一块,又将剩下的六块拼成一个新的图形,其轮廓和M板的位置如图2所示,则图2的面积为 .
26.如图,已知,M为平行线之间一点,连接,N为上方一点,连接,E为延长线上一点,若分别平分,,则 .
27.某兴趣小组利用几何图形画出螳螂的简笔画,如图,已知,,,则 .
28.如图,中,,直线l经过点C且与边AB相交.动点P从点A出发沿路径向终点B运动;动点Q从点B出发沿路径向终点A运动.点P和点Q的速度分别为1cm/s和2cm/s,两点同时出发并开始计时,当点P到达终点B时计时结束.在某时刻分别过点P和点Q作于点E,于点F,设运动时间为t秒,与全等时,t为 s.(其中P、Q两点不重合)
29.如图,点在线段上,于,于.,且, ,点以的速度沿向终点运动,同时点以的速度从开始,在线段上往返运动(即沿运动),当点到达终点时,,同时停止运动.过,分别作的垂线,垂足为,.设运动时间为s,当以,,为顶点的三角形与全等时,的值为 .
30.将纸片沿折叠使点A落在点处,若,则的度数为 .
31.如图,在中,分别是的角平分线和高线,点 P在 的延长线上,交于点 Q,交于点 N,交于点 M,.下列结论:①;② ;③ ;④.其中正确的是 (填序号).
32.如图,中,,D是上一点,,以为边作等腰直角,当E恰好落在边上时,连接,则 .
33.如图所示,已知,平分,平分,点P是延长线上一点,且平分,设,,则α与β的数量关系是 .
34.如图:在△ABC中,∠ACB =90°,点D在边AB上,AD=AC,点E在BC边上,CE=BD,过点E作EF⊥CD交AB于点F,若AF=2,BC=8,则DF的长为
35.如图,△ABC中,D是AB的中点,且AE:CE=2:1,S△CEP=1,则△ABC=
36.在一个三角形中,如果一个角是另一个角的3倍,这样的三角形我们称之为“灵动三角形”.例如,三个内角分别为120°,40°,20°的三角形是“灵动三角形”.如图,∠MON=60°,在射线OM上找一点A,过点A作AB⊥OM交ON于点B,以A为端点作射线AD,交线段OB于点C(规定0°<∠OAC<60°).当△ABC为“灵动三角形”时,则∠OAC的度数为 .
37.如图,和中,,,,点D在边上,将 图中的绕点O按每秒15°的速度沿顺时针方向旋转一周,在旋转的过程中,在第 秒时,边恰好与边AB平行.
38.如图,在中,D、E、F分别为的中点,且,则的面积是 .
39.如图,在锐角三角形中,,,分别为的角平分线.,相交于点F,平分,已知,,的面积,求的面积 .
参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D C D C C A C C C C
题号 11 12 13 14 15 16 17 18 19 20
答案 C D B C A C A C D D
题号 21 22
答案 B A
1.D
【分析】本题考查有理数的乘方应用,数字类规律探究.根据细菌分裂的规律以及有理数乘方的计算方法分别进行计算即可.
【详解】解:将1个细菌放在培养瓶中,
第1分钟,细菌的个数为,
第2分钟,细菌的个数为,
第3分钟,细菌的个数为,
第4分钟,细菌的个数为,
……;
∴第n分钟,细菌的个数为;
∴第64分钟,细菌的个数为;
将4个细菌放在培养瓶中,
第1分钟,细菌的个数为,
第2分钟,细菌的个数为,
第3分钟,细菌的个数为,
第4分钟,细菌的个数为,
……;
∴第n分钟,细菌的个数为,
∴第62分钟,细菌的个数为;
故选:D.
2.C
【分析】本题主要考查平行线的判定与尺规作一个角等于已知角,解题的关键是熟练掌握平行线的判定方法.
根据平行线的判定及尺规作一个角等于已知角的方法逐一判断即可.
【详解】解:A.图1的作图是作,故原理是同位角相等,两直线平行,故本选项不符合题意;
B.以点E为圆心,以为半径作弧,得到弧,故本选项不符合题意;
C.图2的作图是作,原理是内错角相等,两直线平行,故本选项符合题意;
D.以点C为圆心,以为半径作弧,得到弧,故本选项不符合题意,
故选:C.
3.D
【分析】根据公式规律,写出展开式,计算即可,本题考查了规律探索,正确找到规律是解题的关键.
【详解】根据题意,得,
当时
,
含项的系数是,
故选D.
4.C
【分析】本题考查用图象表示变量的关系.根据题意,先求出当点在上运动时的面积即的值,再根据点沿运动到时的路程来求的值即可.
【详解】解:当点在上运动时,
由图知,点沿运动到时,路程为
.
故选:C.
5.C
【分析】首先根据平行线的性质得到,,然后由折叠的性质得到,,然后根据得到,最后利用三角形内角和定理求解即可.
【详解】解:∵
∴,
∵沿,折叠,使点和点都落在点处,
∴,
∴,
∵
∴
∴
∴.
故选:C.
6.A
【分析】本题考查了三角形的面积问题,等高且共底的三角形面积比是底边的比这个性质是解题的关键.先设的面积为,再根据底共线,高相等,面积的比等于底边的比,将其余各个三角形的面积表示出来,总面积为,解得的面积.
【详解】解:如图,连接、,设的面积为,
,
的面积为,的面积为,
,
的面积为,
,
的面积为,的面积为,的面积为,
,
,即的面积为2,
故选:A.
7.C
【分析】本题主要考查了三角形面积的有关计算,连接,先根据,求出,设,得出,
,,即可求出结果.
【详解】解:连接,
,
,
∴,
设,
,
,
,
∴,
,
,
,
,
∴,
.
故选:C.
8.C
【分析】设甲正方形边长为x,乙正方形边长为y,根据题意分别得到,,两式相加可得,在图1中利用两正方形面积之和减去两个三角形面积之和,代入计算可得阴影部分面积.
【详解】解:设甲正方形边长为x,乙正方形边长为y,
则AD=x,EF=y,AE=x+y=6,
∴,则,
∵H是AE中点,
∴AH=EH=3,
图2的阴影部分面积=,
∴,
∴,
∴图1中阴影部分面积=
=
=
=
=10,
故选:C.
【点睛】本题考查了完全平方公式的几何背景,解决本题的关键是利用完全平方公式,合理分析几何图形.
9.C
【分析】①根据三角形内角和定理可得可得,然后根据平分平分,可得,,再根据三角形内角和定理即可进行判断;
②当是的中线时,,进而可以进行判断;
③根据,证明为等边三角形,根据三线合一的性质进而可以进行判断;
④作的平分线交于点,可得,证明,,可得,进而可以判断;
⑤过作于点,由④知,为的角平分线,可得,所以可得,根据,进而可以进行判断.
【详解】解:①在中,,
∴,
∵平分平分,
∴,,
∴,故①正确;
②当是的中线时,,故②错误;
③∵,
∴为的中线,
∵为的角平分线,
∴,
∴为等边三角形,
∴,故③正确;
④如图,作的平分线交于点,
由①得,
∴,
∴,
∴,
∵,
∴,
∴,
∴,故④正确;
⑤过作,于点,
由④知,为的角平分线,
∴,
∴,
∵,
∴,故⑤正确.
综上所述:正确的有①③④⑤,共4个,
故选:C.
【点睛】本题考查了角平分线的定义以及性质,等边三角形的性质,等腰三角形的性质与判定,三角形全等的性质和判定,作辅助线,构建三角形全等是解题关键.
10.C
【分析】由于AB//CD,则∠AOC=∠OCD=50°,利用平角等于得到∠BOC=130°,再根据角平分线定义得到∠BOE=65°;利用OF⊥OE,可计算出∠COF=25°,则∠AOF=∠AOC-∠COF=25°,即OF平分∠AOC;利用同角的余角相等可得到∠AOF=∠POE;由∠POC=90°-∠AOC=40°,∠AOF=25°,可知④不正确.
【详解】解:∵AB//CD,
∴∠AOC=∠OCD=50°,
∴∠BOC=180°-50°=130°,
∵OE平分∠BOC,
∴∠BOE=∠COE=×130°=65°,故①正确;
∵OF⊥OE,
∴∠EOF=90°,
∴∠COF=∠EOF-∠COE=90°-65=25°,
∴∠AOF=∠AOC-∠COF=50°-25°=25°,
∴∠COF=∠AOF,
∴OF平分∠AOC,故②正确;
∵OP⊥CD,
∴∠CPO=90°,
∵AB//CD,
∴∠AOP=90°,
∴∠AOF+∠FOP=∠POE+∠FOP=90°,
∴∠AOF=∠POE,故③正确;
∵∠POC=90°-∠AOC=90°-50°=40°,∠AOF=25°,
∴∠POC≠2∠AOF,故④错误;
综上所述:正确的结论为①②③.
故选:C.
【点睛】本题考查了平行线的性质,角平分线的定义,余角的定义,根据平行线的性质求出∠AOC=50°是解决问题的关键.
11.C
【分析】本题考查了新定义问题,正确分类,灵活计算是解题的关键.
根据定义,逐一计算判定即可.
【详解】∵,,
∴,
故①正确;
∵,
∴是“灵动三角形”,
故②正确;
∵,
∴,,
∵,
∴是“灵动三角形”,
故③正确;
∵为“灵动三角形”, ,
∴或或或或或,
∵,
∴,舍去;
当时,
∴,
∴;
当时,
根据题意,得,
解得,
故,
当时,
根据题意,得,
解得,
∴不符合题意;
当时,
根据题意得:
∴
当时,
根据题意得:
∴,不符合题意;
综上所述,为或或
故④错误;
综上所述正确的有:①②③;
故选:C.
12.D
【分析】本题考查平行线的性质的判定.过作,得到,由,推出,由垂直的定义得到,由平行线的性质得出,即可求出结果.
【详解】解:过作,
∵,
∴,
,
,
,
,
,
.
故选:D.
13.B
【分析】本题考查了数字规律的探索,求出当和时的式子,相加即可求出结果.
【详解】解:当时,①,
当时,②,
①②得:,
.
故选:B.
14.C
【分析】本题主要考查了平行线的判定和性质.分两种情况:当时,当时,利用平行线的判定和性质求解即可.
【详解】解:当时,如图所示,过点G 作,
∵,
∴,
∴,
∴,
由反射定理可知,,
∴,
∴,
∴,
∴;
当时,如图所示,过点G 作,
同理可得,
∴,
∴,
∴,
∴,
∴,
综上所述,或,
∴反射光束与天花板所形成的角不可能取到的度数为,
故选C.
15.A
【分析】本题考查了根据实际问题列二次函数关系式,由铁栅栏的全长及的长,可得出平行于墙的一边长为米,再利用长方形的面积公式,即可找出y关于x的函数关系式.
【详解】解:铁栅栏的全长为15米,米,
平行于墙的一边长为米.
根据题意得:.
故选:A
16.C
【分析】求出BE的长,然后分①点P在BE上时,利用三角形的面积公式列式得到y与x的关系式,然后选择答案即可;②点P在BC上时,根据S△DPE=S梯形DEBC-S△DCP-S△BEP列式整理得到y与x的关系式;③点P在DC上时,利用三角形的面积公式列式得到y与x的函数关系.
【详解】解:∵在矩形DABC中,AD=2,DC=3,
∴BC=AD=2,AB=DC=5,
∵AE=3,
∴BE=AB-AE=5-3=2,
①点P在BE上时,,
∴y=x(0<x≤2),
②点P在BC上时,
S△DPE=S梯形DEBC-S△DCP-S△BEP
,
;
③点P在DC上时,△DPE的面积,
故选C.
【点睛】本题考查了动点问题函数图象,读懂题目信息,根据点P的位置的不同分三段列式求出y与x的关系式是解题的关键.
17.A
【分析】本题考查整式的运算,根据整式的加减法法则、整式的乘法法则、整式的除法法则进行计算,逐一判断即可解答.
【详解】
为关于的三次三项式,且为非零常数
,故①正确;
多项式乘积不含项
,故②错误;
当时,
当时,
,故③正确;
能被整除
设另一因式为
,故④正确;
当或时,无论和取何值,值总相等
,故⑤正确;
综上所述,正确的有:①③④⑤
故选:A.
18.C
【分析】本题考查了函数图象,解题的关键在于数形结合,从图象中获取正确的信息.根据图象可得深广两地的距离为,可判断A;再根据路程除以时间可求出甲的速度,可判断B;然后求出甲乙相遇的时间,可求出乙的速度,从而判断C,D.
【详解】解:由图象得:深广两地的距离为,故A正确,故不符合题意;
甲的速度为,故B正确,故不符合题意;
甲乙相遇的时间为,则乙的速度为,故C错误,故符合题意;
乙运动到达深圳所用时间为,故D正确,不符合题意;
故选:C
19.D
【分析】延长交于点,根据平行线的性质可得,再利用三角形外角的性质,可得.
【详解】解:如图,延长交于点,
,,
,
,
,
故选:D.
【点睛】本题考查了平行线的性质,三角形外角的性质,熟练掌握知识点,正确构造辅助线是解题的关键.
20.D
【详解】解:找规律发现(a+b)3的第三项系数为3=1+2;
(a+b)4的第三项系数为6=1+2+3;
(a+b)5的第三项系数为10=1+2+3+4;
不难发现(a+b)n的第三项系数为1+2+3+…+(n﹣2)+(n﹣1),
∴(a+b)20第三项系数为1+2+3+…+19=190,
故选 D.
21.B
【分析】本题考查了平行线的性质、图形的折叠,理解掌握翻折的特征是解题的关键.
由长方形得,,即,可得,由于折叠,图2中的,由于折叠,图3中的.
【详解】解:如图1,由长方形得,,即,
,
由于折叠,图2中的,
由于折叠,图3中的,
故选:B.
22.A
【分析】本题考查三角形内角和定理;由折叠的性质可得,,可得,由三角形内角和定理可得,即可求的度数.
【详解】解:将沿,翻折,顶点,均落在点处,
,,
,
,
,
,
,
,
故选:A.
23.41
【分析】本题考查了完全平方公式的应用,根据题意列式和掌握完全平方公式是解题的关键.根据题意得到,,利用完全平方公式推出,结合图中阴影部分的面积和为 即可解题.
【详解】解:在长方形中 ,,,
,
,,
,
,
长方形的面积为20,
,
,
,
图中阴影部分的面积和为 .
24./15度
【分析】本题主要考查折叠的性质及平行线的性质,熟练掌握折叠的性质及平行线的性质是解题的关键;由题意易得,,然后根据折叠的性质及角的和差关系可进行求解.
【详解】解:如图①,∵,,
∴,,
∴图②中的,
∴图③中的;
故答案为:.
25.7
【分析】本题考查七巧板,熟练掌握七巧板中各部分面积之间的关系,是解题的关键.
根据七巧板中,各部分的面积关系,利用割补法求出面积即可.
【详解】由图形可知:图1是由大正方形中,这七部分组成的,图2是由这六部分组成的,
∴图2的面积等于图1的面积减去正方形A的面积,
∵,小等腰直角三角板M的面积为,
即:图2的面积 ;
故答案为:7.
26.
【分析】如图所示,过点M作,过点N作,则,先由平行线的性质得到,再由角平分线的定义得到;再证明,,即可得到,由此即可得到答案.
【详解】解:如图所示,过点M作,过点N作,
∵,
∴,
∴,
∴,
∵分别平分,
∴,
∵,
∴,
∵,
∴,
∴
,
故答案为:.
【点睛】本题主要考查了平行线的性质与判定,角平分线的定义,熟知平行线的性质与判定条件是解题的关键.
27./20度
【分析】过点C作,先证明,然后根据平行线的性质求出,,最后利用角的和差关系求解即可.
【详解】解:过点C作,
∵,
∴,
∴,,
又,,
∴,,
∴.
故答案为:.
【点睛】本题考查了平行线的判定与性质,添加合适的辅助线是解题的关键.
28.或/2或12
【分析】点Q在上,点P在上以及点Q与A重合,这两种情况,根据全等三角形的性质列式计算.本题考查的是全等三角形的判定和性质、掌握全等三角形的对应边相等是解题的关键.
【详解】解:①如图1,Q在上,点P在上时,作
由题意得,,
∵,
∴
∵,
∴,
∴,
当时,
则,
即,
解得:;
②如图3,当点Q与A重合时,,则,
即,
解得:,
故答案为:2或12.
29.1或
【分析】本题主要考查全等三角形的性质,以,,为顶点的三角形与全等时,,分点沿运动和沿运动两种情况,根据列方程,即可求解.注意分情况讨论是解题的关键.
【详解】解:点P从运动到点C从用时间为:,
点从运动到点C从用时间为:,
点从运动到点C后,从点C返回,又运动了.
如图,
以,,为顶点的三角形与全等,
,
当点沿运动时,,
解得;
当点沿运动时,,
解得,,符合题意,
综上所述,的值为1或.
故答案为:1或.
30./度
【分析】先由折叠的性质得到,再由三角形外角的性质推出,据此求解即可.
【详解】解:由折叠的性质可知,
∵,
∴,
∵,
∴,
故答案为:.
【点睛】本题主要考查了折叠的性质,三角形外角的性质,熟知三角形一个外角的度数等于与其不相邻的两个内角度数之和是解题的关键.
31.①③④
【分析】本题考查了三角形内角和、全等三角形的判定和性质、垂线的定义等知识点,解题的关键熟知相关的定理和定义.
由高线的定义及对顶角相等可判断①正确;由角平分线定义、三角形内角和、高线可判断②错误;由三角形外角的性质可判断③正确;由全等三角形的判定和性质可推导④正确.
【详解】∵是高线,,
∴,又,
∴(同角的余角相等),故①正确;
由平分知,,
由是高线知,,
∴,
即,故②错误;
,故③正确;
∵,
∴
∴,
∴
故④正确.
因此正确的选项有①③④.
故答案为:①③④.
32.
【分析】过点作于点D,过点E,作于点M,利用勾股定理求出,先证明为等腰直角三角形,进而求出的长,再证明,进而求出的长,从而得出结果.
【详解】解:如图,过点作于点D,过点E,作于点M,
为等腰直角三角形,
,
,
,
,
,
为等腰直角三角形,
,
,
,,
,
,
,
,
,
故答案为:.
【点睛】本题考查了等腰三角形的判定与性质,三角形外角性质,相似三角形的判定与性质,勾股定理,熟练掌握相关性质定理,是解题关键.
33.
【分析】本题考查了平行线的性质、角平分线性质、三角形外角定理等知识,熟练掌握相应性质找到相等角是求解的关键.令交于,为外角,可证,为外角,可证,而,,则有,则可证:,则,即证.
【详解】解:令交于,为外角,
∵为外角,
∴,
∵平分,
∴,
∴,
∵为外角,
∴,
∵,
∴,
∴,
∴,
∴,
∵平分,
∴,
即: ;
故答案是:.
34.4
【分析】延长AC至点G,使AG=AB,延长EF、CA交于H,根据题意证明△CEH≌CGB,即可得到DF=AD-AF=AC-AH=CH-2AF=BC-2AF,即可求解.
【详解】设∠BCD=a,∵∠ACB=90°,∴∠ACD=90°-a,∵AD=AC,∴∠ADC=∠ACD=90°-a,∴∠CAB=2a,∴∠ABC=90°-2a,
∵EF⊥CD,∴∠DKF=90°,∴∠DFK=a,∴∠CEF=90°-a,
延长AC至点G,使AG=AB,连接BG,∴∠G=90°-a=∠CEF,
∵AC=AD,∴BD=CG=CE,
延长EF、CA交于H,
∴∠H=a=∠BFE=∠AFH,
∴AH=AF=2,
∵∠ACB=∠BCG=90°,CG=CE,∠G=∠CEF
∴△CEH≌CGB
∴BC=CH=8,
∴DF=AD-AF=AC-AH=CH-2AF=BC-2AF=4.
故填:4.
【点睛】此题主要考查全等三角形的判定与性质及等腰三角形的性质,解题的关键是根据题意作出辅助线进行求解.
35.12
【分析】连接AP,根据三角形中线的性质可得,,从而证出,然后求出,即可求出,结合图形即可求出结论.
【详解】解:连接AP,
∵D是AB的中点,
∴,,
∴,
∴,
∵AE:CE=2:1,,
∴
∴
∴,
∴,
∵AE:CE=2:1,
∴,
∴,
故答案为:12.
【点睛】此题考查的是三角形中线性质的应用,掌握三角形中线的性质是解题关键.
36.30°或52.5°
【分析】由于∠O=60°,∠ABC=30°,因此可分两种情况进行解答,即当∠ACB=3∠ABC,或∠ACB=3∠CAB时,根据三角形的内角和定理以及互为余角可得答案.
【详解】解:∵∠AB⊥OM,MON=60°,
∴∠ABC=90°﹣60°=30°,
当△ABC为“灵动三角形”时,有
①当∠ACB=3∠ABC时,
∠ACB=3×30°=90°,
∴∠OAC=90°﹣∠O=90°﹣60°=30°,
②当∠ACB=3∠CAB时,
4∠CAB+30°=180°,
∴∠CAB=37.5°,
∴∠OAC=90°﹣∠CAB=52.5°,
故答案为:30°或52.5°.
【点睛】本题考查的是三角形内角和定理、“灵动三角形”的概念,用分类讨论的思想解决问题是解本题的关键.
37.5或17
【分析】本题考查了平行线的性质,旋转变换的性质,以及三角形外角的性质,难点在于分情况讨论,作出图形更形象直观.分两种情况求解:①两三角形在点O的同侧时,②两三角形在点O的异侧时.
【详解】解:①两三角形在点O的同侧时,如图1,设与相交于点E,
∵,,
∴.
∵,
∴,
∵,
∴,
∴,
∵每秒旋转,
∴时间为秒;
②两三角形在点O的异侧时,如图2,延长与相交于点E,
∵,
∴,
∵,
∴,
∴,
∴旋转角为,
∵每秒旋转,
∴时间为秒;
综上所述,在第5或11秒时,边恰好与边平行.
故答案为5或17.
38.
【分析】根据三角形中线平分三角形面积进行求解即可.
【详解】解:∵,F是的中点,
∴,
∵E为的中点,
∴,
∵D是的中点,
∴,
故答案为:.
【点睛】本题主要考查了三角形中线的性质,熟知三角形中线平分三角形面积是解题的关键.
39.4
【分析】本题主要考查了三角形面积计算,三角形全等的判定和性质,角平分线的性质,三角形内角和定理应用,解题的关键是作出辅助线,熟练掌握三角形全等的判定方法.过点F作于点N,于点M,证明,得出,同理可得,得出,求出,得出,根据的面积,得出,求出,即可得出答案.
【详解】解:如图,过点F作于点N,于点M,
,,分别为的角平分线,
,,
∴,
,
∵平分,
,
在和中,
,
∴,
∴,
同理可得,
∴,
∴,
∵,,
∴,
∵的面积,
,
∴,
∴,
,
∴的面积,
故答案为:4.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
专题07 选填压轴训练
一、单选题
1.某种细菌每分钟可由1个分裂成2个,将1个细菌放在培养瓶中经过64分钟就能分裂满一瓶.若将4个这种细菌放入同一个培养瓶中,分裂满一瓶的时间是( )
A.16分钟 B.32分钟 C.52分钟 D.62分钟
2.如图1,图2,点C是上一点,利用尺规过点C作,下列说法错误的是( )
A.图1的原理是同位角相等,两直线平行
B.以点E为圆心,以为半径作弧,得到弧
C.图2的原理是两直线平行,内错角相等
D.以点C为圆心,以为半径作弧,得到弧
3.我国宋代数学家杨辉所著《详解九章算法》中记载了用如图所示的三角形解释了二项和的乘方展开式中的系数规律,我们把这种数字三角形叫做“杨辉三角”.请你利用杨辉三角,计算的展开式中,含项的系数是( )
A.1 B.5 C.16 D.80
4.如图,在长方形中,,,对角线,动点从点出发,沿运动,设点的运动路程为(),的面积为().若与的对应关系如图所示,则图中( )
A. B.1 C.3 D.4
5.如图,已知长方形纸片,点,在边上,点,在边上,分别沿,折叠,使点和点都落在点处,若,则的度数为( )
A. B. C. D.
6.如图,在中,延长至点F,使得,延长至点D,使得,延长至点E,使得,连接,若,则为( )
A.2 B.3 C.4 D.6
7.如图,在中,D是的中点,E是上的一点,且,与相交于点F,若的面积为1,则的面积为( )
A.8 B.10 C.12 D.14
8.现有甲、乙两个正方形纸片,将甲、乙并列放置后得到图,已知点为的中点,连结,.将乙纸片放到甲的内部得到图.已知甲、乙两个正方形边长之和为,图的阴影部分面积为,则图的阴影部分面积为( )
A. B. C. D.
9.如图,在中,,平分交于点平分交于点交于点.则下列说法正确的个数为( )
①;②,③若,则;④;⑤.
A.2个 B.3个 C.4个 D.5个
10.如图,AB//CD,OP⊥CD,OE平分∠BOC,OF⊥OE,∠OCD=50°.下列结论:①∠COE=65°;②OF平分∠AOC;③∠AOF=∠POE;④∠POC=2∠AOF.其中结论正确的个数是( )
A.1个 B.2个 C.3个 D.4个
11.三角形中,如果一个角是另一个角的3倍,这样的三角形我们称之为“灵动三角形”.例如,三个内角分别为的三角形是“灵动三角形”.如图,,在射线上找一点,过点作交于点,以为端点作射线,交线段于点(我们规定).①的度数为;②是“灵动三角形”;③若,则是“灵动三角形”;④当为“灵动三角形”时,为或.结论正确的有( )个.
A.1 B.2 C.3 D.4
12.为了保护视力,某公司推出了一款护眼台灯,其侧面示意图(台灯底座高度忽略不计)如图所示,其中,经测试发现,当时,台灯光线最佳.则此时的度数为( )
A. B. C. D.
13.我国南宋数学家杨辉所著的《详解九章算术》一书中,用图中的三角形解释二项式的展开式的各项系数,此三角形称为“杨辉三角”.根据图中的规律,若,则( )
A.64 B. C.56 D.
14.如图,光的反射活动课中,小铭同学将支架平面镜放置在水平桌面上,镜面的调节角的调节范围为,激光笔发出的光束射到平面镜上,若激光笔与水平天花板(直线)的夹角,则反射光束与天花板所形成的角不可能取到的度数为( )
A. B. C. D.
15.深高小学部饲养了两只萌萌的羊驼,建筑队在学校一边靠墙处,计划用15米长的铁栅栏围成三个相连的长方形羊驼草料仓库,仓库总面积为平方米,为方便取物,在各个仓库之间留出了1米宽的缺口作通道,在平行于墙的一边留下一个1米宽的缺口作小门,若设米,则关于x的函数关系式为( )
A. B.
C. D.
16.如图,在长方形ABCD中,点E为AB上一点,且CD=5,AD=2,AE=3,动点P从点E出发,沿路径E-B-C-D运动,则△DPE 的面积y与点P运动的路径长x之间的关系用图象表示大致为( )
A. B.
C. D.
17.已知均为常数,均为非零常数,若有两个整式,.下列结论中,正确的有( )
①当为关于的三次三项式时,则;
②当多项式乘积不含时,则;
③;
④当能被整除时,;
⑤若或时,无论和取何值,值总相等,则
A.①③④⑤ B.①③④ C.①③⑤ D.①②③④⑤
18.甲从深圳匀速骑电动车到广州,乙从广州匀速骑摩托车到深圳,两人同时出发,到达目的地后,立即停止运动,甲、乙两人离深圳的距离与他们骑车的时间之间的函数关系如图所示,则下列说法错误的是( )
A.深广两地的距离为 B.甲的速度为
C.乙的速度为 D.乙运动到达深圳
19.“抖空竹”经国务院批准列入第一批国家级非物质文化遗产名录,“裁竹成形腰鼓如,两端绳索弄徐徐.当风急转如流水,山寺闻钟韵有余.”就是对抖空竹的写照.某同学在研究“抖空竹”时有一个发现:他把它抽象成数学问题,如图所示,已知,,,则的度数是( )
A. B. C. D.
20.我国古代数学的许多创新和发展都位居世界前列,如南宋数学家杨辉(约13世纪)所著的《详解九章算术》一书中,用如图的三角形解释二项和(a+b)n的展开式的各项系数,此三角形称为“杨辉三角”.
根据“杨辉三角”请计算(a+b)20的展开式中第三项的系数为( )
A.2017 B.2016 C.191 D.190
21.方形纸带中,将纸带沿折叠成图2,再沿折叠成图3,则图3中度数是( )
A. B. C. D.
22.如图,将沿、翻折,顶点A,B均落在点O处,且与重合于线段,若,则的度数为( )
A. B. C. D.
二、填空题
23.如图,在长方形中 ,,点E,F是边,上的点,,且,分别以,为边在长方形外侧作正方形和,若长方形的面积为20,则图中阴影部分的面积和为
24.如图是长方形纸带,,将纸带沿折叠成图,再沿折叠成图,则图中的度数是 .
25.七巧板起源于我国先秦时期,古算书《周髀算经》中有关于正方形的分割术,经过历代演变而成七巧板.小深先用一副七巧板拼成了图1,图1的轮廓是一个边长为a的正方形,其中,小等腰直角三角板M的面积为,小深拿掉七巧板中的一块,又将剩下的六块拼成一个新的图形,其轮廓和M板的位置如图2所示,则图2的面积为 .
26.如图,已知,M为平行线之间一点,连接,N为上方一点,连接,E为延长线上一点,若分别平分,,则 .
27.某兴趣小组利用几何图形画出螳螂的简笔画,如图,已知,,,则 .
28.如图,中,,直线l经过点C且与边AB相交.动点P从点A出发沿路径向终点B运动;动点Q从点B出发沿路径向终点A运动.点P和点Q的速度分别为1cm/s和2cm/s,两点同时出发并开始计时,当点P到达终点B时计时结束.在某时刻分别过点P和点Q作于点E,于点F,设运动时间为t秒,与全等时,t为 s.(其中P、Q两点不重合)
29.如图,点在线段上,于,于.,且, ,点以的速度沿向终点运动,同时点以的速度从开始,在线段上往返运动(即沿运动),当点到达终点时,,同时停止运动.过,分别作的垂线,垂足为,.设运动时间为s,当以,,为顶点的三角形与全等时,的值为 .
30.将纸片沿折叠使点A落在点处,若,则的度数为 .
31.如图,在中,分别是的角平分线和高线,点 P在 的延长线上,交于点 Q,交于点 N,交于点 M,.下列结论:①;② ;③ ;④.其中正确的是 (填序号).
32.如图,中,,D是上一点,,以为边作等腰直角,当E恰好落在边上时,连接,则 .
33.如图所示,已知,平分,平分,点P是延长线上一点,且平分,设,,则α与β的数量关系是 .
34.如图:在△ABC中,∠ACB =90°,点D在边AB上,AD=AC,点E在BC边上,CE=BD,过点E作EF⊥CD交AB于点F,若AF=2,BC=8,则DF的长为
35.如图,△ABC中,D是AB的中点,且AE:CE=2:1,S△CEP=1,则△ABC=
36.在一个三角形中,如果一个角是另一个角的3倍,这样的三角形我们称之为“灵动三角形”.例如,三个内角分别为120°,40°,20°的三角形是“灵动三角形”.如图,∠MON=60°,在射线OM上找一点A,过点A作AB⊥OM交ON于点B,以A为端点作射线AD,交线段OB于点C(规定0°<∠OAC<60°).当△ABC为“灵动三角形”时,则∠OAC的度数为 .
37.如图,和中,,,,点D在边上,将 图中的绕点O按每秒15°的速度沿顺时针方向旋转一周,在旋转的过程中,在第 秒时,边恰好与边AB平行.
38.如图,在中,D、E、F分别为的中点,且,则的面积是 .
39.如图,在锐角三角形中,,,分别为的角平分线.,相交于点F,平分,已知,,的面积,求的面积 .
参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D C D C C A C C C C
题号 11 12 13 14 15 16 17 18 19 20
答案 C D B C A C A C D D
题号 21 22
答案 B A
1.D
【分析】本题考查有理数的乘方应用,数字类规律探究.根据细菌分裂的规律以及有理数乘方的计算方法分别进行计算即可.
【详解】解:将1个细菌放在培养瓶中,
第1分钟,细菌的个数为,
第2分钟,细菌的个数为,
第3分钟,细菌的个数为,
第4分钟,细菌的个数为,
……;
∴第n分钟,细菌的个数为;
∴第64分钟,细菌的个数为;
将4个细菌放在培养瓶中,
第1分钟,细菌的个数为,
第2分钟,细菌的个数为,
第3分钟,细菌的个数为,
第4分钟,细菌的个数为,
……;
∴第n分钟,细菌的个数为,
∴第62分钟,细菌的个数为;
故选:D.
2.C
【分析】本题主要考查平行线的判定与尺规作一个角等于已知角,解题的关键是熟练掌握平行线的判定方法.
根据平行线的判定及尺规作一个角等于已知角的方法逐一判断即可.
【详解】解:A.图1的作图是作,故原理是同位角相等,两直线平行,故本选项不符合题意;
B.以点E为圆心,以为半径作弧,得到弧,故本选项不符合题意;
C.图2的作图是作,原理是内错角相等,两直线平行,故本选项符合题意;
D.以点C为圆心,以为半径作弧,得到弧,故本选项不符合题意,
故选:C.
3.D
【分析】根据公式规律,写出展开式,计算即可,本题考查了规律探索,正确找到规律是解题的关键.
【详解】根据题意,得,
当时
,
含项的系数是,
故选D.
4.C
【分析】本题考查用图象表示变量的关系.根据题意,先求出当点在上运动时的面积即的值,再根据点沿运动到时的路程来求的值即可.
【详解】解:当点在上运动时,
由图知,点沿运动到时,路程为
.
故选:C.
5.C
【分析】首先根据平行线的性质得到,,然后由折叠的性质得到,,然后根据得到,最后利用三角形内角和定理求解即可.
【详解】解:∵
∴,
∵沿,折叠,使点和点都落在点处,
∴,
∴,
∵
∴
∴
∴.
故选:C.
6.A
【分析】本题考查了三角形的面积问题,等高且共底的三角形面积比是底边的比这个性质是解题的关键.先设的面积为,再根据底共线,高相等,面积的比等于底边的比,将其余各个三角形的面积表示出来,总面积为,解得的面积.
【详解】解:如图,连接、,设的面积为,
,
的面积为,的面积为,
,
的面积为,
,
的面积为,的面积为,的面积为,
,
,即的面积为2,
故选:A.
7.C
【分析】本题主要考查了三角形面积的有关计算,连接,先根据,求出,设,得出,
,,即可求出结果.
【详解】解:连接,
,
,
∴,
设,
,
,
,
∴,
,
,
,
,
∴,
.
故选:C.
8.C
【分析】设甲正方形边长为x,乙正方形边长为y,根据题意分别得到,,两式相加可得,在图1中利用两正方形面积之和减去两个三角形面积之和,代入计算可得阴影部分面积.
【详解】解:设甲正方形边长为x,乙正方形边长为y,
则AD=x,EF=y,AE=x+y=6,
∴,则,
∵H是AE中点,
∴AH=EH=3,
图2的阴影部分面积=,
∴,
∴,
∴图1中阴影部分面积=
=
=
=
=10,
故选:C.
【点睛】本题考查了完全平方公式的几何背景,解决本题的关键是利用完全平方公式,合理分析几何图形.
9.C
【分析】①根据三角形内角和定理可得可得,然后根据平分平分,可得,,再根据三角形内角和定理即可进行判断;
②当是的中线时,,进而可以进行判断;
③根据,证明为等边三角形,根据三线合一的性质进而可以进行判断;
④作的平分线交于点,可得,证明,,可得,进而可以判断;
⑤过作于点,由④知,为的角平分线,可得,所以可得,根据,进而可以进行判断.
【详解】解:①在中,,
∴,
∵平分平分,
∴,,
∴,故①正确;
②当是的中线时,,故②错误;
③∵,
∴为的中线,
∵为的角平分线,
∴,
∴为等边三角形,
∴,故③正确;
④如图,作的平分线交于点,
由①得,
∴,
∴,
∴,
∵,
∴,
∴,
∴,故④正确;
⑤过作,于点,
由④知,为的角平分线,
∴,
∴,
∵,
∴,故⑤正确.
综上所述:正确的有①③④⑤,共4个,
故选:C.
【点睛】本题考查了角平分线的定义以及性质,等边三角形的性质,等腰三角形的性质与判定,三角形全等的性质和判定,作辅助线,构建三角形全等是解题关键.
10.C
【分析】由于AB//CD,则∠AOC=∠OCD=50°,利用平角等于得到∠BOC=130°,再根据角平分线定义得到∠BOE=65°;利用OF⊥OE,可计算出∠COF=25°,则∠AOF=∠AOC-∠COF=25°,即OF平分∠AOC;利用同角的余角相等可得到∠AOF=∠POE;由∠POC=90°-∠AOC=40°,∠AOF=25°,可知④不正确.
【详解】解:∵AB//CD,
∴∠AOC=∠OCD=50°,
∴∠BOC=180°-50°=130°,
∵OE平分∠BOC,
∴∠BOE=∠COE=×130°=65°,故①正确;
∵OF⊥OE,
∴∠EOF=90°,
∴∠COF=∠EOF-∠COE=90°-65=25°,
∴∠AOF=∠AOC-∠COF=50°-25°=25°,
∴∠COF=∠AOF,
∴OF平分∠AOC,故②正确;
∵OP⊥CD,
∴∠CPO=90°,
∵AB//CD,
∴∠AOP=90°,
∴∠AOF+∠FOP=∠POE+∠FOP=90°,
∴∠AOF=∠POE,故③正确;
∵∠POC=90°-∠AOC=90°-50°=40°,∠AOF=25°,
∴∠POC≠2∠AOF,故④错误;
综上所述:正确的结论为①②③.
故选:C.
【点睛】本题考查了平行线的性质,角平分线的定义,余角的定义,根据平行线的性质求出∠AOC=50°是解决问题的关键.
11.C
【分析】本题考查了新定义问题,正确分类,灵活计算是解题的关键.
根据定义,逐一计算判定即可.
【详解】∵,,
∴,
故①正确;
∵,
∴是“灵动三角形”,
故②正确;
∵,
∴,,
∵,
∴是“灵动三角形”,
故③正确;
∵为“灵动三角形”, ,
∴或或或或或,
∵,
∴,舍去;
当时,
∴,
∴;
当时,
根据题意,得,
解得,
故,
当时,
根据题意,得,
解得,
∴不符合题意;
当时,
根据题意得:
∴
当时,
根据题意得:
∴,不符合题意;
综上所述,为或或
故④错误;
综上所述正确的有:①②③;
故选:C.
12.D
【分析】本题考查平行线的性质的判定.过作,得到,由,推出,由垂直的定义得到,由平行线的性质得出,即可求出结果.
【详解】解:过作,
∵,
∴,
,
,
,
,
,
.
故选:D.
13.B
【分析】本题考查了数字规律的探索,求出当和时的式子,相加即可求出结果.
【详解】解:当时,①,
当时,②,
①②得:,
.
故选:B.
14.C
【分析】本题主要考查了平行线的判定和性质.分两种情况:当时,当时,利用平行线的判定和性质求解即可.
【详解】解:当时,如图所示,过点G 作,
∵,
∴,
∴,
∴,
由反射定理可知,,
∴,
∴,
∴,
∴;
当时,如图所示,过点G 作,
同理可得,
∴,
∴,
∴,
∴,
∴,
综上所述,或,
∴反射光束与天花板所形成的角不可能取到的度数为,
故选C.
15.A
【分析】本题考查了根据实际问题列二次函数关系式,由铁栅栏的全长及的长,可得出平行于墙的一边长为米,再利用长方形的面积公式,即可找出y关于x的函数关系式.
【详解】解:铁栅栏的全长为15米,米,
平行于墙的一边长为米.
根据题意得:.
故选:A
16.C
【分析】求出BE的长,然后分①点P在BE上时,利用三角形的面积公式列式得到y与x的关系式,然后选择答案即可;②点P在BC上时,根据S△DPE=S梯形DEBC-S△DCP-S△BEP列式整理得到y与x的关系式;③点P在DC上时,利用三角形的面积公式列式得到y与x的函数关系.
【详解】解:∵在矩形DABC中,AD=2,DC=3,
∴BC=AD=2,AB=DC=5,
∵AE=3,
∴BE=AB-AE=5-3=2,
①点P在BE上时,,
∴y=x(0<x≤2),
②点P在BC上时,
S△DPE=S梯形DEBC-S△DCP-S△BEP
,
;
③点P在DC上时,△DPE的面积,
故选C.
【点睛】本题考查了动点问题函数图象,读懂题目信息,根据点P的位置的不同分三段列式求出y与x的关系式是解题的关键.
17.A
【分析】本题考查整式的运算,根据整式的加减法法则、整式的乘法法则、整式的除法法则进行计算,逐一判断即可解答.
【详解】
为关于的三次三项式,且为非零常数
,故①正确;
多项式乘积不含项
,故②错误;
当时,
当时,
,故③正确;
能被整除
设另一因式为
,故④正确;
当或时,无论和取何值,值总相等
,故⑤正确;
综上所述,正确的有:①③④⑤
故选:A.
18.C
【分析】本题考查了函数图象,解题的关键在于数形结合,从图象中获取正确的信息.根据图象可得深广两地的距离为,可判断A;再根据路程除以时间可求出甲的速度,可判断B;然后求出甲乙相遇的时间,可求出乙的速度,从而判断C,D.
【详解】解:由图象得:深广两地的距离为,故A正确,故不符合题意;
甲的速度为,故B正确,故不符合题意;
甲乙相遇的时间为,则乙的速度为,故C错误,故符合题意;
乙运动到达深圳所用时间为,故D正确,不符合题意;
故选:C
19.D
【分析】延长交于点,根据平行线的性质可得,再利用三角形外角的性质,可得.
【详解】解:如图,延长交于点,
,,
,
,
,
故选:D.
【点睛】本题考查了平行线的性质,三角形外角的性质,熟练掌握知识点,正确构造辅助线是解题的关键.
20.D
【详解】解:找规律发现(a+b)3的第三项系数为3=1+2;
(a+b)4的第三项系数为6=1+2+3;
(a+b)5的第三项系数为10=1+2+3+4;
不难发现(a+b)n的第三项系数为1+2+3+…+(n﹣2)+(n﹣1),
∴(a+b)20第三项系数为1+2+3+…+19=190,
故选 D.
21.B
【分析】本题考查了平行线的性质、图形的折叠,理解掌握翻折的特征是解题的关键.
由长方形得,,即,可得,由于折叠,图2中的,由于折叠,图3中的.
【详解】解:如图1,由长方形得,,即,
,
由于折叠,图2中的,
由于折叠,图3中的,
故选:B.
22.A
【分析】本题考查三角形内角和定理;由折叠的性质可得,,可得,由三角形内角和定理可得,即可求的度数.
【详解】解:将沿,翻折,顶点,均落在点处,
,,
,
,
,
,
,
,
故选:A.
23.41
【分析】本题考查了完全平方公式的应用,根据题意列式和掌握完全平方公式是解题的关键.根据题意得到,,利用完全平方公式推出,结合图中阴影部分的面积和为 即可解题.
【详解】解:在长方形中 ,,,
,
,,
,
,
长方形的面积为20,
,
,
,
图中阴影部分的面积和为 .
24./15度
【分析】本题主要考查折叠的性质及平行线的性质,熟练掌握折叠的性质及平行线的性质是解题的关键;由题意易得,,然后根据折叠的性质及角的和差关系可进行求解.
【详解】解:如图①,∵,,
∴,,
∴图②中的,
∴图③中的;
故答案为:.
25.7
【分析】本题考查七巧板,熟练掌握七巧板中各部分面积之间的关系,是解题的关键.
根据七巧板中,各部分的面积关系,利用割补法求出面积即可.
【详解】由图形可知:图1是由大正方形中,这七部分组成的,图2是由这六部分组成的,
∴图2的面积等于图1的面积减去正方形A的面积,
∵,小等腰直角三角板M的面积为,
即:图2的面积 ;
故答案为:7.
26.
【分析】如图所示,过点M作,过点N作,则,先由平行线的性质得到,再由角平分线的定义得到;再证明,,即可得到,由此即可得到答案.
【详解】解:如图所示,过点M作,过点N作,
∵,
∴,
∴,
∴,
∵分别平分,
∴,
∵,
∴,
∵,
∴,
∴
,
故答案为:.
【点睛】本题主要考查了平行线的性质与判定,角平分线的定义,熟知平行线的性质与判定条件是解题的关键.
27./20度
【分析】过点C作,先证明,然后根据平行线的性质求出,,最后利用角的和差关系求解即可.
【详解】解:过点C作,
∵,
∴,
∴,,
又,,
∴,,
∴.
故答案为:.
【点睛】本题考查了平行线的判定与性质,添加合适的辅助线是解题的关键.
28.或/2或12
【分析】点Q在上,点P在上以及点Q与A重合,这两种情况,根据全等三角形的性质列式计算.本题考查的是全等三角形的判定和性质、掌握全等三角形的对应边相等是解题的关键.
【详解】解:①如图1,Q在上,点P在上时,作
由题意得,,
∵,
∴
∵,
∴,
∴,
当时,
则,
即,
解得:;
②如图3,当点Q与A重合时,,则,
即,
解得:,
故答案为:2或12.
29.1或
【分析】本题主要考查全等三角形的性质,以,,为顶点的三角形与全等时,,分点沿运动和沿运动两种情况,根据列方程,即可求解.注意分情况讨论是解题的关键.
【详解】解:点P从运动到点C从用时间为:,
点从运动到点C从用时间为:,
点从运动到点C后,从点C返回,又运动了.
如图,
以,,为顶点的三角形与全等,
,
当点沿运动时,,
解得;
当点沿运动时,,
解得,,符合题意,
综上所述,的值为1或.
故答案为:1或.
30./度
【分析】先由折叠的性质得到,再由三角形外角的性质推出,据此求解即可.
【详解】解:由折叠的性质可知,
∵,
∴,
∵,
∴,
故答案为:.
【点睛】本题主要考查了折叠的性质,三角形外角的性质,熟知三角形一个外角的度数等于与其不相邻的两个内角度数之和是解题的关键.
31.①③④
【分析】本题考查了三角形内角和、全等三角形的判定和性质、垂线的定义等知识点,解题的关键熟知相关的定理和定义.
由高线的定义及对顶角相等可判断①正确;由角平分线定义、三角形内角和、高线可判断②错误;由三角形外角的性质可判断③正确;由全等三角形的判定和性质可推导④正确.
【详解】∵是高线,,
∴,又,
∴(同角的余角相等),故①正确;
由平分知,,
由是高线知,,
∴,
即,故②错误;
,故③正确;
∵,
∴
∴,
∴
故④正确.
因此正确的选项有①③④.
故答案为:①③④.
32.
【分析】过点作于点D,过点E,作于点M,利用勾股定理求出,先证明为等腰直角三角形,进而求出的长,再证明,进而求出的长,从而得出结果.
【详解】解:如图,过点作于点D,过点E,作于点M,
为等腰直角三角形,
,
,
,
,
,
为等腰直角三角形,
,
,
,,
,
,
,
,
,
故答案为:.
【点睛】本题考查了等腰三角形的判定与性质,三角形外角性质,相似三角形的判定与性质,勾股定理,熟练掌握相关性质定理,是解题关键.
33.
【分析】本题考查了平行线的性质、角平分线性质、三角形外角定理等知识,熟练掌握相应性质找到相等角是求解的关键.令交于,为外角,可证,为外角,可证,而,,则有,则可证:,则,即证.
【详解】解:令交于,为外角,
∵为外角,
∴,
∵平分,
∴,
∴,
∵为外角,
∴,
∵,
∴,
∴,
∴,
∴,
∵平分,
∴,
即: ;
故答案是:.
34.4
【分析】延长AC至点G,使AG=AB,延长EF、CA交于H,根据题意证明△CEH≌CGB,即可得到DF=AD-AF=AC-AH=CH-2AF=BC-2AF,即可求解.
【详解】设∠BCD=a,∵∠ACB=90°,∴∠ACD=90°-a,∵AD=AC,∴∠ADC=∠ACD=90°-a,∴∠CAB=2a,∴∠ABC=90°-2a,
∵EF⊥CD,∴∠DKF=90°,∴∠DFK=a,∴∠CEF=90°-a,
延长AC至点G,使AG=AB,连接BG,∴∠G=90°-a=∠CEF,
∵AC=AD,∴BD=CG=CE,
延长EF、CA交于H,
∴∠H=a=∠BFE=∠AFH,
∴AH=AF=2,
∵∠ACB=∠BCG=90°,CG=CE,∠G=∠CEF
∴△CEH≌CGB
∴BC=CH=8,
∴DF=AD-AF=AC-AH=CH-2AF=BC-2AF=4.
故填:4.
【点睛】此题主要考查全等三角形的判定与性质及等腰三角形的性质,解题的关键是根据题意作出辅助线进行求解.
35.12
【分析】连接AP,根据三角形中线的性质可得,,从而证出,然后求出,即可求出,结合图形即可求出结论.
【详解】解:连接AP,
∵D是AB的中点,
∴,,
∴,
∴,
∵AE:CE=2:1,,
∴
∴
∴,
∴,
∵AE:CE=2:1,
∴,
∴,
故答案为:12.
【点睛】此题考查的是三角形中线性质的应用,掌握三角形中线的性质是解题关键.
36.30°或52.5°
【分析】由于∠O=60°,∠ABC=30°,因此可分两种情况进行解答,即当∠ACB=3∠ABC,或∠ACB=3∠CAB时,根据三角形的内角和定理以及互为余角可得答案.
【详解】解:∵∠AB⊥OM,MON=60°,
∴∠ABC=90°﹣60°=30°,
当△ABC为“灵动三角形”时,有
①当∠ACB=3∠ABC时,
∠ACB=3×30°=90°,
∴∠OAC=90°﹣∠O=90°﹣60°=30°,
②当∠ACB=3∠CAB时,
4∠CAB+30°=180°,
∴∠CAB=37.5°,
∴∠OAC=90°﹣∠CAB=52.5°,
故答案为:30°或52.5°.
【点睛】本题考查的是三角形内角和定理、“灵动三角形”的概念,用分类讨论的思想解决问题是解本题的关键.
37.5或17
【分析】本题考查了平行线的性质,旋转变换的性质,以及三角形外角的性质,难点在于分情况讨论,作出图形更形象直观.分两种情况求解:①两三角形在点O的同侧时,②两三角形在点O的异侧时.
【详解】解:①两三角形在点O的同侧时,如图1,设与相交于点E,
∵,,
∴.
∵,
∴,
∵,
∴,
∴,
∵每秒旋转,
∴时间为秒;
②两三角形在点O的异侧时,如图2,延长与相交于点E,
∵,
∴,
∵,
∴,
∴,
∴旋转角为,
∵每秒旋转,
∴时间为秒;
综上所述,在第5或11秒时,边恰好与边平行.
故答案为5或17.
38.
【分析】根据三角形中线平分三角形面积进行求解即可.
【详解】解:∵,F是的中点,
∴,
∵E为的中点,
∴,
∵D是的中点,
∴,
故答案为:.
【点睛】本题主要考查了三角形中线的性质,熟知三角形中线平分三角形面积是解题的关键.
39.4
【分析】本题主要考查了三角形面积计算,三角形全等的判定和性质,角平分线的性质,三角形内角和定理应用,解题的关键是作出辅助线,熟练掌握三角形全等的判定方法.过点F作于点N,于点M,证明,得出,同理可得,得出,求出,得出,根据的面积,得出,求出,即可得出答案.
【详解】解:如图,过点F作于点N,于点M,
,,分别为的角平分线,
,,
∴,
,
∵平分,
,
在和中,
,
∴,
∴,
同理可得,
∴,
∴,
∵,,
∴,
∵的面积,
,
∴,
∴,
,
∴的面积,
故答案为:4.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
