北师大七下期中专题04 概率(含解析)
文档属性
| 名称 | 北师大七下期中专题04 概率(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 429.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-11 05:34:40 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
专题04 概率
一、单选题
1.抛掷一枚质地均匀的正方体骰子,骰子各面分别标有数字1、2、3、4、5、6,则出现朝上的数字小于3的概率是( )
A. B. C. D.
2.下列事件中,属于必然事件的是( )
A.任意购买一张电影票,座位号是偶数
B.梦到醒来会下雨,醒来后发现窗外在下雨
C.解锁手机,提示微信收到了新消息
D.随意掷一枚质地均匀的骰子,掷出的点数不超过6
3.对某品种的麦粒在相同条件下进行发芽试验,结果如下表所示:
试验的麦粒数n 200 500 1000 2000 5000
发芽的粒数m 191 473 954 1906 4748
发芽的频率 0.955 0.946 0.954 0.953 0.9496
根据上表,在这批麦粒中任取一粒,估计它能发芽的概率为( )
A.0.92 B.0.95 C.0.97 D.0.98
4.“某篮球运动员2次罚球,投中1个”所描述的事件是( )
A.必然事件 B.不可能事件 C.不确定事件 D.确定事件
5.下列成语所描述的事件中,属于必然事件的是( )
A.水涨船高 B.水中捞月 C.守株待兔 D.拔苗助长
6.下列事件中,属于必然事件的是( )
A.明天的最高气温将达35℃
B.任意购买一张动车票,座位刚好挨着窗口
C.掷两次质地均匀的骰子,其中有一次正面朝上
D.对顶角相等
7.毛泽东在《沁园春·雪》中提到五位历史名人:秦始皇、汉武帝、唐太宗、宋太祖、成吉思汗,小明将这五位名人简介分别写在五张完全相同的知识卡片上,小哲从中随机抽取一张,卡片上介绍的人物是唐朝出生的概率是( )
A. B. C. D.
二、填空题
8.李老师将1个黑球和若干个白球(球除颜色外其他均相同)放入一个不透明的口袋并搅拌均匀,让学生进行摸球试验,学生每次从中随机摸出一个球,记下颜色后放回.重复该试验,得到如下表所示的一组统计数据:
摸球的次数n 100 300 500 800 1000
摸到黑球的次数m 23 81 130 204 250
摸到黑球的频率 0.23 0.27 0.26 0.255 0.25
根据表中数据估计袋中白球有 个.
9.一个不透明的袋子里只装有红球、黄球,总共20个,这些球除颜色外形状大小都相同.芳芳每次摸球前先将袋子里的球摇匀,任意摸出一个球记下颜色后再放回袋子,通过多次重复试验发现,摸出红球的频率稳定在0.25左右,则袋子中红球大约有 个.
10.在单词(数学)中任意选择一个字母,选中的字母是元音字母的概率是 .
11.一个不透明的书箱中有4本《海底两万里》和2本《钢铁是怎样炼成的》,从书箱中任意拿出n本书,其中拿出的书中至少有一本《海底两万里》是一个必然事件,则n的最小值是 .
12.中国古代数学有着辉煌的成就,《周髀算经》《算学启蒙》《测圆海镜》《四元玉鉴》是我国古代数学的重要文献.某中学拟从这4部数学名著中选择1部作为校本课程“数学文化”的学习内容,恰好选中《算学启蒙》的概率是 .
13.如果小球在如图所示的地板上自由地滚动,并随机的停留在某块方砖上,那么它最终停留在阴影区域的概率是 .
三、解答题
14.某路口南北方向红绿灯的设置时间为:红灯30秒,绿灯若干秒,黄灯3秒.小明的爸爸随机地由南往北开车到达该路口.
(1)如果绿灯时长为70秒,那么他遇到绿灯的概率________遇到红灯的概率(填“”“”或“”);
(2)若他遇到红灯的概率为,求每次绿灯时长为多少秒?
15.一个不透明的袋中只装有白、红、黄三种颜色的球共40个,它们除颜色外都完全相同,其中白球个数是黄球个数的2倍多1个.已知从袋中随机摸出一个球是红球的概率是.
(1)从袋中随机摸出一个球是黄球是 事件(从“随机”、“必然”、“不可能”选一个填入);
(2)袋中有 个红球;
(3)求从袋中随机摸出一个球是黄球的概率.
16.如图,有一枚质地均匀的正二十面体形状的骰子,其中的1个面标有“1”,2个面标有“2”,3个面标有“3”,4个面标有“4”,5个面标有“5”,其余的面标有“6”,投掷这枚骰子一次,求下列事件的概率:
(1)向上一面的数字是6;
(2)向上一面的数字是2的倍数或3的倍数.
17.在一个不透明的盒子里装有黑、白两种颜色的球,这些球除颜色外都相同.小颖做摸球试验,搅匀后,她从盒子里随机摸出一只球记下颜色后,再把球放回盒子中,不断重复上述过程,下表是试验中的部分统计数据:
摸球的次数n 10 20 50 100 200 400 500 1000 2000
摸到白球的次数m 4 7 10 28 45 97 127 252 498
摸到白球的频率m 0.400 0.350 0.200 0.280 0.225 0.243 0.254 0.252 0.249
(1)小颖从盒子里随机摸出一只蓝球是 (填序号)
①必然事件 ②不可能事件 ③随机事件
(2)摸到白球的概率的估计值是 (精确到0.01);
(3)某小组进行“用频率估计概率”的试验,符合问题(2)中结果的试验最有可能的是 (填序号).
①投掷一枚均匀的硬币,落到桌面上恰好是正面朝上.
②在甲、乙、丙、丁四人中用抽签的方式产生一名幸运观众,正好抽到甲.
③掷一个质地均匀的正方体骰子(面的点数分别为1到6),落地时面朝上点数“小于3”.
(4)受上述摸球实验的启发,小刚为了估计边长为10的正方形二维码上黑色阴影部分的面积,他在纸片内随机掷点,经过大量实验,发现点落在黑色阴影的频率稳定在 0.65 左右,则据此估计此二维码黑色阴影部分的面积为 .
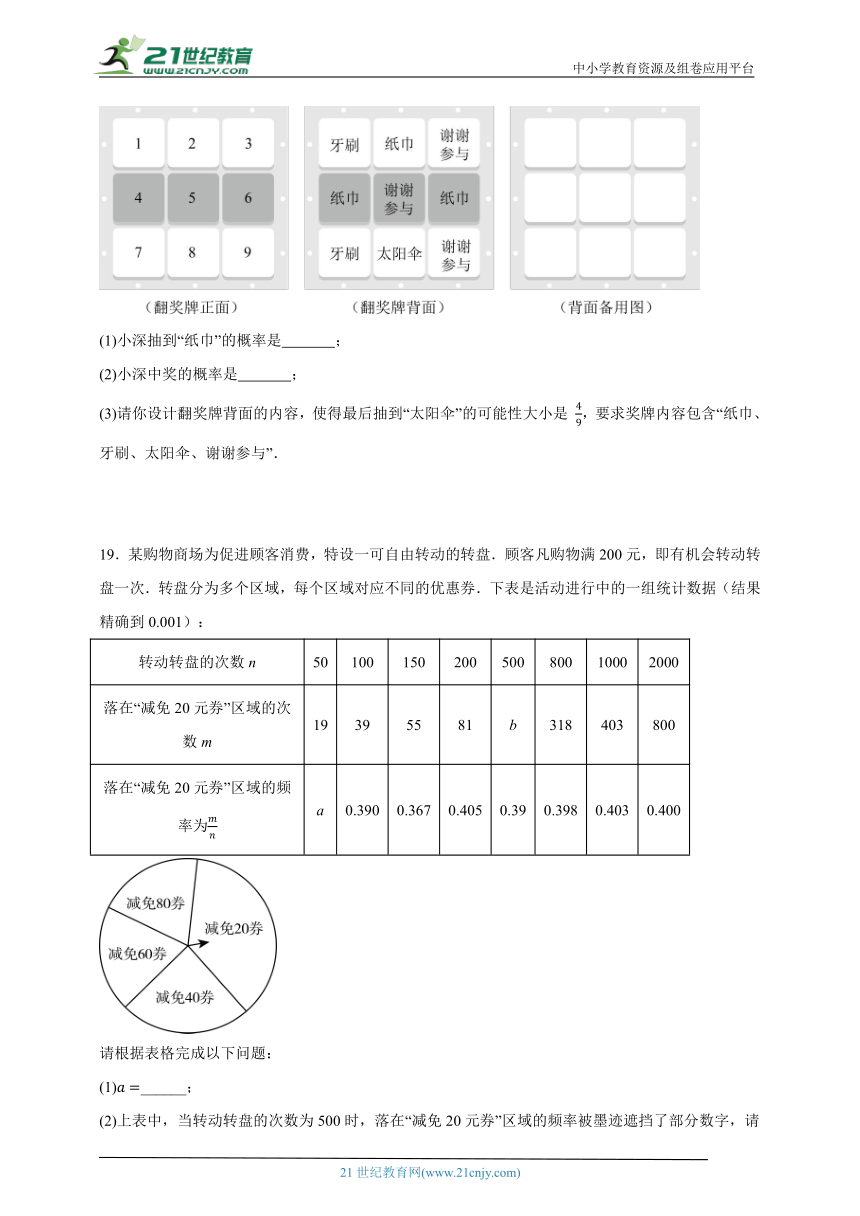
18.小深一家逛完超市后,凭小票参加一次抽奖活动,超市设置如下的翻奖牌,翻奖牌的正面、背面如下.如果小深只能抽奖一次,且抽到数字1至9的可能性一样,请解决下面的问题:
(1)小深抽到“纸巾”的概率是 ;
(2)小深中奖的概率是 ;
(3)请你设计翻奖牌背面的内容,使得最后抽到“太阳伞”的可能性大小是 ,要求奖牌内容包含“纸巾、牙刷、太阳伞、谢谢参与”.
19.某购物商场为促进顾客消费,特设一可自由转动的转盘.顾客凡购物满200元,即有机会转动转盘一次.转盘分为多个区域,每个区域对应不同的优惠券.下表是活动进行中的一组统计数据(结果精确到0.001):
转动转盘的次数n 50 100 150 200 500 800 1000 2000
落在“减免20元券”区域的次数m 19 39 55 81 b 318 403 800
落在“减免20元券”区域的频率为 a 0.390 0.367 0.405 0.39 0.398 0.403 0.400
请根据表格完成以下问题:
(1)______;
(2)上表中,当转动转盘的次数为500时,落在“减免20元券”区域的频率被墨迹遮挡了部分数字,请估计b的值是______(填写一个值);
(3)落在“减免20元券”区域的频率的变化有什么规律?
(4)请估计落在“减免20元券”区域的概率是______.
20.如图是计算机“扫雷”游戏的画面,在个小方格的雷区中,随机地埋藏着10颗地雷,每个小方格最多能埋藏1颗地雷.小明先点一个小方格,显示数字2,它表示围着数字2的8个方块中埋藏着2颗地雷(包含数字2的黑框区域记为A).
(1)小明如果踩在图中个小方格的任意一个小方格,则踩中地雷的概率是 .
(2)若小明在区域A内围着数字2的8个方块中任点一个,踩中地雷的概率是 .
(3)为了尽可能不踩中地雷,小明点完第一步之后,小明的第二步应踩在A区域内的小方格上还是应踩在A区域外的小方格上?并说明理由.
21.在一个不透明的盒子里装有除颜色外完全相同的红、白、黑三种颜色的球,共15个.其中红球3个,白球5个.
(1)从中任意摸出一个球,是红球的概率比是白球的概率______(填“大”或“小”);
(2)从中任意摸出一个球,是黑球的概率为_______;
(3)小明从盒子里取出m个黑球(其他颜色的球数量没有改变),使得从盒子里任意摸出一个球是红球的概率为,请求出m的值.
参考答案
题号 1 2 3 4 5 6 7
答案 B D B C A D B
1.B
【分析】用朝上的数字小于3的情况数除以总情况数即为所求的概率.
【详解】解:抛掷六个面上分别刻有的1,2,3,4,5,6的骰子有6种结果,其中朝上一面的数字小于3的有2种,
朝上一面的数字小于3的倍数概率是.
故选:B.
【点睛】本题考查了概率公式的应用,掌握概率等于所求情况数与总情况数之比是关键.
2.D
【分析】本题考查随机事件、必然事件,理解必然事件的意义是正确判断的前提,结合问题情境判断事件发生的可能性是正确解答的关键.根据必然事件的意义,结合具体的问题情境逐项进行判断即可.
【详解】解:A.任意购买一张电影票,座位号是偶数是随机事件,因此选项A不符合题意;
B.梦到醒来会下雨,醒来后发现窗外在下雨是随机事件,因此选项B不符合题意;
C.解锁手机,提示微信收到了新消息是随机事件,因此选项C不符合题意;
D.随意掷一枚质地均匀的骰子,掷出的点数不超过6是必然事件,因此选项D符合题意;
故选:D.
3.B
【分析】本题考查由频率估计概率,根据表格可知:随着实验麦粒数的增加,其发芽的频率稳定在0.95左右,据此解答.
【详解】解:由表格可得:随着实验麦粒数的增加,其发芽的频率稳定在0.95左右,
故选:B.
4.C
【分析】本题考查了事件的分类,正确理解必然事件、不可能事件、随机事件的概念是解决本题的关键.
必然事件指在一定条件下一定发生的事件;不可能事件是指在一定条件下,一定不发生的事件;不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件,据此判断即可.
【详解】篮球运动员2次罚球,可能投中篮筐,也可能投不中篮筐,投中1个.因此“篮球运动员2次罚球,投中1个”这一事件是不确定事件.
故选:C.
5.A
【分析】本题考查了事件的分类,解决本题需要正确理解必然事件、不可能事件、随机事件的概念.根据必然事件指在一定条件下,一定发生的事件;不可能事件是指在一定条件下,一定不发生的事件;不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件,对每一项进行分析即可.
【详解】解:A.水涨船高是必然事件,故符合题意;
B.水中捞月是不可能事件,故不符合题意;
C.守株待兔是随机事件,故不符合题意;
D.拔苗助长是不可能事件,故不符合题意;
故选A.
6.D
【分析】A、明天最高气温是随机的,故A选项错误;
B、任意买一张动车票,座位刚好挨着窗口是随机的,故B选项错误;
C、掷骰子两面有一次正面朝上是随机的,故C选项错误;
D、对顶角一定相等,所以是真命题,故D选项正确.
【详解】解:“对顶角相等”是真命题,发生的可能性为100%,
故选:D.
【点睛】本题的考点是随机事件.解决本题需要正确理解必然事件的概念:必然事件指在一定条件下一定发生的事件.
7.B
【分析】本题主要考查概率公式,熟练掌握简单概率的计算方法是解决本题的关键;
先找出唐朝出生的人物,然后依据概率公式计算即可.
【详解】解:在秦始皇、汉武帝、唐太宗、宋太祖、成吉思汗五人中,唐朝出生的只有唐太宗1人,
∴在上述5人中随机抽取一张,所有抽到的人物为唐朝出生的概率.
故选:B.
8.3
【分析】本题考查了利用频率估计概率、概率公式、分式方程的应用,熟练掌握利用频率估计概率的方法是解题关键.先根据利用频率估计概率可得从口袋中随机摸出一个球是黑球的概率约为,再利用概率公式建立方程,解方程即可得.
【详解】解:设袋中白球有个,
由表中数据估计从口袋中随机摸出一个球是黑球的概率约为,
则,
解得,
经检验,是所列分式方程的解,
所以根据表中数据估计袋中白球有3个,
故答案为:3.
9.5
【分析】设袋子中红球有x个,根据摸出红球的频率稳定在0.25左右列出关于x的方程,求出x的值,从而得出答案.
【详解】解:设袋子中红球有x个,
根据题意,得:
,
解得:,
∴袋子中红球的个数最有可能是5个,
故答案为:5.
【点睛】本题主要考查利用频率估计概率,大量重复试验时,事件发生的频率在某个固定位置左右摆动,并且摆动的幅度越来越小,根据这个频率稳定性定理,可以用频率的集中趋势来估计概率,这个固定的近似值就是这个事件的概率.
10.
【分析】本题考查了概率公式,根据总字母数量为11,元音字母的是,数量是4个,代入公式进行作答即可.
【详解】解:∵单词(数学),总字母数量为11个,元音字母的是,数量是4个
∴选中的字母是元音字母的概率是
故答案为:.
11.3
【分析】本题考查的是必然事件、不可能事件、随机事件的概念.必然事件指在一定条件下,一定发生的事件.不可能事件是指在一定条件下,一定不发生的事件,不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件.
【详解】解:从书箱中任意拿出n本书,其中拿出的书中至少有一本《海底两万里》是一个必然事件,
当时,拿出的书中至少有一本《海底两万里》是一个必然事件,
则n的最小值是3,
故答案为:3.
12.
【分析】根据概率计算公式进行求解即可.
【详解】解:∵一共有4本数学名著,每一本名著被抽到的概率相同,
∴从这4部数学名著中选择1部作为校本课程“数学文化”的学习内容,恰好选中《算学启蒙》的概率是,
故答案为:.
【点睛】本题主要考查了简单的概率计算,熟知概率计算公式是解题的关键.
13.
【分析】本题考查几何概率的求法:计算阴影区域的面积在总面积中占的比例,这个比例即事件发生的概率,得到阴影区域面积是关键.根据几何概率的求解方法,求得阴影区域的面积与总面积的比值即可求解.
【详解】解:由图可知,总面积为9个小正方形的面积,其中阴影区域的面积为3个小正方形的面积,则小球停留在阴影区域的概率是,
故答案为:.
14.(1)
(2)路口绿灯设置的时长为60秒
【分析】此题主要考查了概率的意义以及概率求法,一元一次方程的应用,正确理解概率的意义是解题关键.
(1)直接利用概率的意义得出遇到绿灯的概率大;
(2)设该路口绿灯设置的时长为x秒,由题意得:,求出绿灯时间即可.
【详解】(1)解:红灯30秒,
如果绿灯时长为70秒,那么他遇到绿灯的概率大于遇到红灯的概率,
故答案为:;
(2)设该路口绿灯设置的时长为x秒,由题意得:
,
解得.
答:路口绿灯设置的时长为60秒.
15.(1)随机
(2)24
(3)
【分析】本题考查根据概率公式求概率和求数量,一元一次方程的应用,掌握概率的计算公式是解题的关键.
(1)根据三类事件的定义判断即可;
(2)根据“从袋中随机摸出一个球是红球的概率是”,即可求出袋中红球的个数;
(3)先求出黄球的个数,从而求出概率即可.
【详解】(1)解:袋中有黄球也有其他球,从袋中随机摸出一个球是黄球是随机事件,
故答案是:随机;
(2)因为从袋中随机摸出一个球是红球的概率是,
所以袋中红球的个数是: (个),
故答案为:24;
(3)设黄球有x个,则白球有个,
根据题意得,
解得,
从袋中任摸一个球共有40种等可能得结果,其中摸出黄球有5种,
∴P(摸出黄球)=
答:摸出一个球是黄球的概率是.
16.(1)
(2)
【分析】本题主要考查了运用概率公式求概率,求出所有等可能结果数和满足题意的结果数成为解题的关键.
(1)先求出标“6”的面有5个,然后利用概率公式求解即可;
(2)先求数字是2的倍数或3的倍数有14个,然后利用概率公式求解即可.
【详解】(1)解:投掷质地均匀的正二十面体形状的骰子,一共有20个面,每个面出现的可能性相同.
向上一面的数字是6的共有5个面,
所以.
(2)解:向上一面的数字是2的倍数或3的倍数的数字是2、3、4、6,一共有种等可能结果,所以.
17.(1)②
(2)0.25
(3)②
(4)65
【分析】本题主要考查用频率估计概率,理解频率和概率之间的关系是解决问题的关键.
(1)根据事件的分类可得答案;
(2)用频率估计概率可得答案;
(3)分别求出试验①②③的概率可得答案;
(4)用正方形面积乘以点落在黑色阴影的频率即可.
【详解】(1)解:小颖从盒子里随机摸出一只蓝球是不可能事件,
故答案为:②;
(2)解:由表可知,摸球2000次时摸到白球的频率为0.249,
因此摸到白球的概率的估计值是0.25,
故答案为:0.25;
(3)解:①“投掷一枚均匀的硬币,落到桌面上恰好是正面朝上”的概率为.
②“在甲、乙、丙、丁四人中用抽签的方式产生一名幸运观众,正好抽到甲”的概率为.
③“掷一个质地均匀的正方体骰子(面的点数分别为1到6),落地时面朝上点数小于3”的概率为.
因此符合问题(2)中结果的试验最有可能的是②,
故答案为:②;
(4)解:,
估计此二维码黑色阴影部分的面积为65,
故答案为:65.
18.(1)
(2)
(3)4张写着太阳伞,其它的五张牌中纸巾1张、牙刷1张,谢谢参与3张(答案不唯一)
【分析】本题考查了概率公式,熟练掌握概率公式是解题的关键;
(1)用“纸巾”对应牌的数量除以牌的总数量即可;
(2)用“纸巾”、“牙刷”“太阳伞”、对应牌的数量和除以牌的总数量即可;
(3)根据题意,可知本题答案不唯一,只要九张牌中有四张写着太阳伞,其他的五张包含纸巾、牙刷、太阳伞、谢谢参与即可.
【详解】(1)解:由图可得,一共有9个方格,“纸巾”奖品占3个,
抽到“纸巾”奖品的可能性是:;
故答案为:;
(2)解:由图可得,一共有9个方格,“纸巾”奖品占3个,“牙刷”奖品占2个,“太阳伞”奖品占1个,“谢谢参与”奖品占3个,
小深中奖的概率是
故答案为:;
(3)解:设计九张牌中有4张写着太阳伞,其它的五张牌中纸巾、牙刷,各1张,谢谢参与3张.
19.(1)
(2)
(3)频率的变化稳定在附近
(4)
【分析】本题主要考查利用频率估计概率,大量重复实验时,事件发生的频率在某个固定位置左右摆动,并且摆动的幅度越来越小,根据这个频率稳定性定理,可以用频率的集中趋势来估计概率,这个固定的近似值就是这个事件的概率.
(1)根据频率频数总数,计算即可得出答案;
(2)由频数乘以频率即可得到答案;
(3)利用频率估计概率求解即可.
(4)由稳定的频率可得概率
【详解】(1)解:;
(2)解:;
(3)解:落在“减免20元券”区域的频率的变化稳定在附近;
(4)解:估计落在“减免20元券”区域的概率是
20.(1)
(2)
(3)小明的第二步应踩在A区域外的小方格上
【分析】本题考查了概率公式:概率=所求情况数与总情况数之比,熟记概率公式是解题的关.
(1)根据概率公式计算即可;
(2)根据概率公式计算即可;
(3)分别计算出小明点完第一步之后,小明的第二步踩在A区域内的小方格上踩中地雷的概率和小明点完第一步之后,小明的第二步踩在A区域外的小方格上踩中地雷的概率,再比较即可;
【详解】(1)解:根据题意,总共有个小方格,其中藏着10颗地雷,
故踩中地雷的概率,
故答案为:.
(2)解:在区域A内围着数字2的8个方块中任点一个,其中藏着2颗地雷,
故踩中地雷的概率,
故答案为:.
(3)解:小明点完第一步之后,小明的第二步踩在A区域内的小方格上踩中地雷的概率,
小明点完第一步之后,小明的第二步踩在A区域外的小方格上踩中地雷的概率,
∵,
故为了尽可能不踩中地雷,小明点完第一步之后,小明的第二步应踩在A区域外的小方格上.
21.(1)小
(2)
(3)
【分析】本题考查了简单事件的概率,清楚所有可能结果数及事件发生时的可能结果数是解题的关键.注意概率公式的变形运用.
(1)根据概率公式计算即可;
(2)根据概率公式计算即可;
(3)由红球的概率可求得盒子里的总球数,用15减去总球数即可得到要取出黑球的个数,即可求得m的值.
【详解】(1)解:∵红球的概率
白球的概率
∴红球的概率比是白球的概率小.
故答案为:小;
(2)黑球的概率为.
故答案为:;
(3)∵任意摸出一个球是红球的概率为
∴盒子中球的总量为:(个),
∴可以将盒子中的黑球拿出(个).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
专题04 概率
一、单选题
1.抛掷一枚质地均匀的正方体骰子,骰子各面分别标有数字1、2、3、4、5、6,则出现朝上的数字小于3的概率是( )
A. B. C. D.
2.下列事件中,属于必然事件的是( )
A.任意购买一张电影票,座位号是偶数
B.梦到醒来会下雨,醒来后发现窗外在下雨
C.解锁手机,提示微信收到了新消息
D.随意掷一枚质地均匀的骰子,掷出的点数不超过6
3.对某品种的麦粒在相同条件下进行发芽试验,结果如下表所示:
试验的麦粒数n 200 500 1000 2000 5000
发芽的粒数m 191 473 954 1906 4748
发芽的频率 0.955 0.946 0.954 0.953 0.9496
根据上表,在这批麦粒中任取一粒,估计它能发芽的概率为( )
A.0.92 B.0.95 C.0.97 D.0.98
4.“某篮球运动员2次罚球,投中1个”所描述的事件是( )
A.必然事件 B.不可能事件 C.不确定事件 D.确定事件
5.下列成语所描述的事件中,属于必然事件的是( )
A.水涨船高 B.水中捞月 C.守株待兔 D.拔苗助长
6.下列事件中,属于必然事件的是( )
A.明天的最高气温将达35℃
B.任意购买一张动车票,座位刚好挨着窗口
C.掷两次质地均匀的骰子,其中有一次正面朝上
D.对顶角相等
7.毛泽东在《沁园春·雪》中提到五位历史名人:秦始皇、汉武帝、唐太宗、宋太祖、成吉思汗,小明将这五位名人简介分别写在五张完全相同的知识卡片上,小哲从中随机抽取一张,卡片上介绍的人物是唐朝出生的概率是( )
A. B. C. D.
二、填空题
8.李老师将1个黑球和若干个白球(球除颜色外其他均相同)放入一个不透明的口袋并搅拌均匀,让学生进行摸球试验,学生每次从中随机摸出一个球,记下颜色后放回.重复该试验,得到如下表所示的一组统计数据:
摸球的次数n 100 300 500 800 1000
摸到黑球的次数m 23 81 130 204 250
摸到黑球的频率 0.23 0.27 0.26 0.255 0.25
根据表中数据估计袋中白球有 个.
9.一个不透明的袋子里只装有红球、黄球,总共20个,这些球除颜色外形状大小都相同.芳芳每次摸球前先将袋子里的球摇匀,任意摸出一个球记下颜色后再放回袋子,通过多次重复试验发现,摸出红球的频率稳定在0.25左右,则袋子中红球大约有 个.
10.在单词(数学)中任意选择一个字母,选中的字母是元音字母的概率是 .
11.一个不透明的书箱中有4本《海底两万里》和2本《钢铁是怎样炼成的》,从书箱中任意拿出n本书,其中拿出的书中至少有一本《海底两万里》是一个必然事件,则n的最小值是 .
12.中国古代数学有着辉煌的成就,《周髀算经》《算学启蒙》《测圆海镜》《四元玉鉴》是我国古代数学的重要文献.某中学拟从这4部数学名著中选择1部作为校本课程“数学文化”的学习内容,恰好选中《算学启蒙》的概率是 .
13.如果小球在如图所示的地板上自由地滚动,并随机的停留在某块方砖上,那么它最终停留在阴影区域的概率是 .
三、解答题
14.某路口南北方向红绿灯的设置时间为:红灯30秒,绿灯若干秒,黄灯3秒.小明的爸爸随机地由南往北开车到达该路口.
(1)如果绿灯时长为70秒,那么他遇到绿灯的概率________遇到红灯的概率(填“”“”或“”);
(2)若他遇到红灯的概率为,求每次绿灯时长为多少秒?
15.一个不透明的袋中只装有白、红、黄三种颜色的球共40个,它们除颜色外都完全相同,其中白球个数是黄球个数的2倍多1个.已知从袋中随机摸出一个球是红球的概率是.
(1)从袋中随机摸出一个球是黄球是 事件(从“随机”、“必然”、“不可能”选一个填入);
(2)袋中有 个红球;
(3)求从袋中随机摸出一个球是黄球的概率.
16.如图,有一枚质地均匀的正二十面体形状的骰子,其中的1个面标有“1”,2个面标有“2”,3个面标有“3”,4个面标有“4”,5个面标有“5”,其余的面标有“6”,投掷这枚骰子一次,求下列事件的概率:
(1)向上一面的数字是6;
(2)向上一面的数字是2的倍数或3的倍数.
17.在一个不透明的盒子里装有黑、白两种颜色的球,这些球除颜色外都相同.小颖做摸球试验,搅匀后,她从盒子里随机摸出一只球记下颜色后,再把球放回盒子中,不断重复上述过程,下表是试验中的部分统计数据:
摸球的次数n 10 20 50 100 200 400 500 1000 2000
摸到白球的次数m 4 7 10 28 45 97 127 252 498
摸到白球的频率m 0.400 0.350 0.200 0.280 0.225 0.243 0.254 0.252 0.249
(1)小颖从盒子里随机摸出一只蓝球是 (填序号)
①必然事件 ②不可能事件 ③随机事件
(2)摸到白球的概率的估计值是 (精确到0.01);
(3)某小组进行“用频率估计概率”的试验,符合问题(2)中结果的试验最有可能的是 (填序号).
①投掷一枚均匀的硬币,落到桌面上恰好是正面朝上.
②在甲、乙、丙、丁四人中用抽签的方式产生一名幸运观众,正好抽到甲.
③掷一个质地均匀的正方体骰子(面的点数分别为1到6),落地时面朝上点数“小于3”.
(4)受上述摸球实验的启发,小刚为了估计边长为10的正方形二维码上黑色阴影部分的面积,他在纸片内随机掷点,经过大量实验,发现点落在黑色阴影的频率稳定在 0.65 左右,则据此估计此二维码黑色阴影部分的面积为 .
18.小深一家逛完超市后,凭小票参加一次抽奖活动,超市设置如下的翻奖牌,翻奖牌的正面、背面如下.如果小深只能抽奖一次,且抽到数字1至9的可能性一样,请解决下面的问题:
(1)小深抽到“纸巾”的概率是 ;
(2)小深中奖的概率是 ;
(3)请你设计翻奖牌背面的内容,使得最后抽到“太阳伞”的可能性大小是 ,要求奖牌内容包含“纸巾、牙刷、太阳伞、谢谢参与”.
19.某购物商场为促进顾客消费,特设一可自由转动的转盘.顾客凡购物满200元,即有机会转动转盘一次.转盘分为多个区域,每个区域对应不同的优惠券.下表是活动进行中的一组统计数据(结果精确到0.001):
转动转盘的次数n 50 100 150 200 500 800 1000 2000
落在“减免20元券”区域的次数m 19 39 55 81 b 318 403 800
落在“减免20元券”区域的频率为 a 0.390 0.367 0.405 0.39 0.398 0.403 0.400
请根据表格完成以下问题:
(1)______;
(2)上表中,当转动转盘的次数为500时,落在“减免20元券”区域的频率被墨迹遮挡了部分数字,请估计b的值是______(填写一个值);
(3)落在“减免20元券”区域的频率的变化有什么规律?
(4)请估计落在“减免20元券”区域的概率是______.
20.如图是计算机“扫雷”游戏的画面,在个小方格的雷区中,随机地埋藏着10颗地雷,每个小方格最多能埋藏1颗地雷.小明先点一个小方格,显示数字2,它表示围着数字2的8个方块中埋藏着2颗地雷(包含数字2的黑框区域记为A).
(1)小明如果踩在图中个小方格的任意一个小方格,则踩中地雷的概率是 .
(2)若小明在区域A内围着数字2的8个方块中任点一个,踩中地雷的概率是 .
(3)为了尽可能不踩中地雷,小明点完第一步之后,小明的第二步应踩在A区域内的小方格上还是应踩在A区域外的小方格上?并说明理由.
21.在一个不透明的盒子里装有除颜色外完全相同的红、白、黑三种颜色的球,共15个.其中红球3个,白球5个.
(1)从中任意摸出一个球,是红球的概率比是白球的概率______(填“大”或“小”);
(2)从中任意摸出一个球,是黑球的概率为_______;
(3)小明从盒子里取出m个黑球(其他颜色的球数量没有改变),使得从盒子里任意摸出一个球是红球的概率为,请求出m的值.
参考答案
题号 1 2 3 4 5 6 7
答案 B D B C A D B
1.B
【分析】用朝上的数字小于3的情况数除以总情况数即为所求的概率.
【详解】解:抛掷六个面上分别刻有的1,2,3,4,5,6的骰子有6种结果,其中朝上一面的数字小于3的有2种,
朝上一面的数字小于3的倍数概率是.
故选:B.
【点睛】本题考查了概率公式的应用,掌握概率等于所求情况数与总情况数之比是关键.
2.D
【分析】本题考查随机事件、必然事件,理解必然事件的意义是正确判断的前提,结合问题情境判断事件发生的可能性是正确解答的关键.根据必然事件的意义,结合具体的问题情境逐项进行判断即可.
【详解】解:A.任意购买一张电影票,座位号是偶数是随机事件,因此选项A不符合题意;
B.梦到醒来会下雨,醒来后发现窗外在下雨是随机事件,因此选项B不符合题意;
C.解锁手机,提示微信收到了新消息是随机事件,因此选项C不符合题意;
D.随意掷一枚质地均匀的骰子,掷出的点数不超过6是必然事件,因此选项D符合题意;
故选:D.
3.B
【分析】本题考查由频率估计概率,根据表格可知:随着实验麦粒数的增加,其发芽的频率稳定在0.95左右,据此解答.
【详解】解:由表格可得:随着实验麦粒数的增加,其发芽的频率稳定在0.95左右,
故选:B.
4.C
【分析】本题考查了事件的分类,正确理解必然事件、不可能事件、随机事件的概念是解决本题的关键.
必然事件指在一定条件下一定发生的事件;不可能事件是指在一定条件下,一定不发生的事件;不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件,据此判断即可.
【详解】篮球运动员2次罚球,可能投中篮筐,也可能投不中篮筐,投中1个.因此“篮球运动员2次罚球,投中1个”这一事件是不确定事件.
故选:C.
5.A
【分析】本题考查了事件的分类,解决本题需要正确理解必然事件、不可能事件、随机事件的概念.根据必然事件指在一定条件下,一定发生的事件;不可能事件是指在一定条件下,一定不发生的事件;不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件,对每一项进行分析即可.
【详解】解:A.水涨船高是必然事件,故符合题意;
B.水中捞月是不可能事件,故不符合题意;
C.守株待兔是随机事件,故不符合题意;
D.拔苗助长是不可能事件,故不符合题意;
故选A.
6.D
【分析】A、明天最高气温是随机的,故A选项错误;
B、任意买一张动车票,座位刚好挨着窗口是随机的,故B选项错误;
C、掷骰子两面有一次正面朝上是随机的,故C选项错误;
D、对顶角一定相等,所以是真命题,故D选项正确.
【详解】解:“对顶角相等”是真命题,发生的可能性为100%,
故选:D.
【点睛】本题的考点是随机事件.解决本题需要正确理解必然事件的概念:必然事件指在一定条件下一定发生的事件.
7.B
【分析】本题主要考查概率公式,熟练掌握简单概率的计算方法是解决本题的关键;
先找出唐朝出生的人物,然后依据概率公式计算即可.
【详解】解:在秦始皇、汉武帝、唐太宗、宋太祖、成吉思汗五人中,唐朝出生的只有唐太宗1人,
∴在上述5人中随机抽取一张,所有抽到的人物为唐朝出生的概率.
故选:B.
8.3
【分析】本题考查了利用频率估计概率、概率公式、分式方程的应用,熟练掌握利用频率估计概率的方法是解题关键.先根据利用频率估计概率可得从口袋中随机摸出一个球是黑球的概率约为,再利用概率公式建立方程,解方程即可得.
【详解】解:设袋中白球有个,
由表中数据估计从口袋中随机摸出一个球是黑球的概率约为,
则,
解得,
经检验,是所列分式方程的解,
所以根据表中数据估计袋中白球有3个,
故答案为:3.
9.5
【分析】设袋子中红球有x个,根据摸出红球的频率稳定在0.25左右列出关于x的方程,求出x的值,从而得出答案.
【详解】解:设袋子中红球有x个,
根据题意,得:
,
解得:,
∴袋子中红球的个数最有可能是5个,
故答案为:5.
【点睛】本题主要考查利用频率估计概率,大量重复试验时,事件发生的频率在某个固定位置左右摆动,并且摆动的幅度越来越小,根据这个频率稳定性定理,可以用频率的集中趋势来估计概率,这个固定的近似值就是这个事件的概率.
10.
【分析】本题考查了概率公式,根据总字母数量为11,元音字母的是,数量是4个,代入公式进行作答即可.
【详解】解:∵单词(数学),总字母数量为11个,元音字母的是,数量是4个
∴选中的字母是元音字母的概率是
故答案为:.
11.3
【分析】本题考查的是必然事件、不可能事件、随机事件的概念.必然事件指在一定条件下,一定发生的事件.不可能事件是指在一定条件下,一定不发生的事件,不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件.
【详解】解:从书箱中任意拿出n本书,其中拿出的书中至少有一本《海底两万里》是一个必然事件,
当时,拿出的书中至少有一本《海底两万里》是一个必然事件,
则n的最小值是3,
故答案为:3.
12.
【分析】根据概率计算公式进行求解即可.
【详解】解:∵一共有4本数学名著,每一本名著被抽到的概率相同,
∴从这4部数学名著中选择1部作为校本课程“数学文化”的学习内容,恰好选中《算学启蒙》的概率是,
故答案为:.
【点睛】本题主要考查了简单的概率计算,熟知概率计算公式是解题的关键.
13.
【分析】本题考查几何概率的求法:计算阴影区域的面积在总面积中占的比例,这个比例即事件发生的概率,得到阴影区域面积是关键.根据几何概率的求解方法,求得阴影区域的面积与总面积的比值即可求解.
【详解】解:由图可知,总面积为9个小正方形的面积,其中阴影区域的面积为3个小正方形的面积,则小球停留在阴影区域的概率是,
故答案为:.
14.(1)
(2)路口绿灯设置的时长为60秒
【分析】此题主要考查了概率的意义以及概率求法,一元一次方程的应用,正确理解概率的意义是解题关键.
(1)直接利用概率的意义得出遇到绿灯的概率大;
(2)设该路口绿灯设置的时长为x秒,由题意得:,求出绿灯时间即可.
【详解】(1)解:红灯30秒,
如果绿灯时长为70秒,那么他遇到绿灯的概率大于遇到红灯的概率,
故答案为:;
(2)设该路口绿灯设置的时长为x秒,由题意得:
,
解得.
答:路口绿灯设置的时长为60秒.
15.(1)随机
(2)24
(3)
【分析】本题考查根据概率公式求概率和求数量,一元一次方程的应用,掌握概率的计算公式是解题的关键.
(1)根据三类事件的定义判断即可;
(2)根据“从袋中随机摸出一个球是红球的概率是”,即可求出袋中红球的个数;
(3)先求出黄球的个数,从而求出概率即可.
【详解】(1)解:袋中有黄球也有其他球,从袋中随机摸出一个球是黄球是随机事件,
故答案是:随机;
(2)因为从袋中随机摸出一个球是红球的概率是,
所以袋中红球的个数是: (个),
故答案为:24;
(3)设黄球有x个,则白球有个,
根据题意得,
解得,
从袋中任摸一个球共有40种等可能得结果,其中摸出黄球有5种,
∴P(摸出黄球)=
答:摸出一个球是黄球的概率是.
16.(1)
(2)
【分析】本题主要考查了运用概率公式求概率,求出所有等可能结果数和满足题意的结果数成为解题的关键.
(1)先求出标“6”的面有5个,然后利用概率公式求解即可;
(2)先求数字是2的倍数或3的倍数有14个,然后利用概率公式求解即可.
【详解】(1)解:投掷质地均匀的正二十面体形状的骰子,一共有20个面,每个面出现的可能性相同.
向上一面的数字是6的共有5个面,
所以.
(2)解:向上一面的数字是2的倍数或3的倍数的数字是2、3、4、6,一共有种等可能结果,所以.
17.(1)②
(2)0.25
(3)②
(4)65
【分析】本题主要考查用频率估计概率,理解频率和概率之间的关系是解决问题的关键.
(1)根据事件的分类可得答案;
(2)用频率估计概率可得答案;
(3)分别求出试验①②③的概率可得答案;
(4)用正方形面积乘以点落在黑色阴影的频率即可.
【详解】(1)解:小颖从盒子里随机摸出一只蓝球是不可能事件,
故答案为:②;
(2)解:由表可知,摸球2000次时摸到白球的频率为0.249,
因此摸到白球的概率的估计值是0.25,
故答案为:0.25;
(3)解:①“投掷一枚均匀的硬币,落到桌面上恰好是正面朝上”的概率为.
②“在甲、乙、丙、丁四人中用抽签的方式产生一名幸运观众,正好抽到甲”的概率为.
③“掷一个质地均匀的正方体骰子(面的点数分别为1到6),落地时面朝上点数小于3”的概率为.
因此符合问题(2)中结果的试验最有可能的是②,
故答案为:②;
(4)解:,
估计此二维码黑色阴影部分的面积为65,
故答案为:65.
18.(1)
(2)
(3)4张写着太阳伞,其它的五张牌中纸巾1张、牙刷1张,谢谢参与3张(答案不唯一)
【分析】本题考查了概率公式,熟练掌握概率公式是解题的关键;
(1)用“纸巾”对应牌的数量除以牌的总数量即可;
(2)用“纸巾”、“牙刷”“太阳伞”、对应牌的数量和除以牌的总数量即可;
(3)根据题意,可知本题答案不唯一,只要九张牌中有四张写着太阳伞,其他的五张包含纸巾、牙刷、太阳伞、谢谢参与即可.
【详解】(1)解:由图可得,一共有9个方格,“纸巾”奖品占3个,
抽到“纸巾”奖品的可能性是:;
故答案为:;
(2)解:由图可得,一共有9个方格,“纸巾”奖品占3个,“牙刷”奖品占2个,“太阳伞”奖品占1个,“谢谢参与”奖品占3个,
小深中奖的概率是
故答案为:;
(3)解:设计九张牌中有4张写着太阳伞,其它的五张牌中纸巾、牙刷,各1张,谢谢参与3张.
19.(1)
(2)
(3)频率的变化稳定在附近
(4)
【分析】本题主要考查利用频率估计概率,大量重复实验时,事件发生的频率在某个固定位置左右摆动,并且摆动的幅度越来越小,根据这个频率稳定性定理,可以用频率的集中趋势来估计概率,这个固定的近似值就是这个事件的概率.
(1)根据频率频数总数,计算即可得出答案;
(2)由频数乘以频率即可得到答案;
(3)利用频率估计概率求解即可.
(4)由稳定的频率可得概率
【详解】(1)解:;
(2)解:;
(3)解:落在“减免20元券”区域的频率的变化稳定在附近;
(4)解:估计落在“减免20元券”区域的概率是
20.(1)
(2)
(3)小明的第二步应踩在A区域外的小方格上
【分析】本题考查了概率公式:概率=所求情况数与总情况数之比,熟记概率公式是解题的关.
(1)根据概率公式计算即可;
(2)根据概率公式计算即可;
(3)分别计算出小明点完第一步之后,小明的第二步踩在A区域内的小方格上踩中地雷的概率和小明点完第一步之后,小明的第二步踩在A区域外的小方格上踩中地雷的概率,再比较即可;
【详解】(1)解:根据题意,总共有个小方格,其中藏着10颗地雷,
故踩中地雷的概率,
故答案为:.
(2)解:在区域A内围着数字2的8个方块中任点一个,其中藏着2颗地雷,
故踩中地雷的概率,
故答案为:.
(3)解:小明点完第一步之后,小明的第二步踩在A区域内的小方格上踩中地雷的概率,
小明点完第一步之后,小明的第二步踩在A区域外的小方格上踩中地雷的概率,
∵,
故为了尽可能不踩中地雷,小明点完第一步之后,小明的第二步应踩在A区域外的小方格上.
21.(1)小
(2)
(3)
【分析】本题考查了简单事件的概率,清楚所有可能结果数及事件发生时的可能结果数是解题的关键.注意概率公式的变形运用.
(1)根据概率公式计算即可;
(2)根据概率公式计算即可;
(3)由红球的概率可求得盒子里的总球数,用15减去总球数即可得到要取出黑球的个数,即可求得m的值.
【详解】(1)解:∵红球的概率
白球的概率
∴红球的概率比是白球的概率小.
故答案为:小;
(2)黑球的概率为.
故答案为:;
(3)∵任意摸出一个球是红球的概率为
∴盒子中球的总量为:(个),
∴可以将盒子中的黑球拿出(个).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
