北师大七下期中专题06 变量之间的关系(含解析)
文档属性
| 名称 | 北师大七下期中专题06 变量之间的关系(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 979.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-11 05:33:51 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
专题06 变量之间的关系
一、单选题
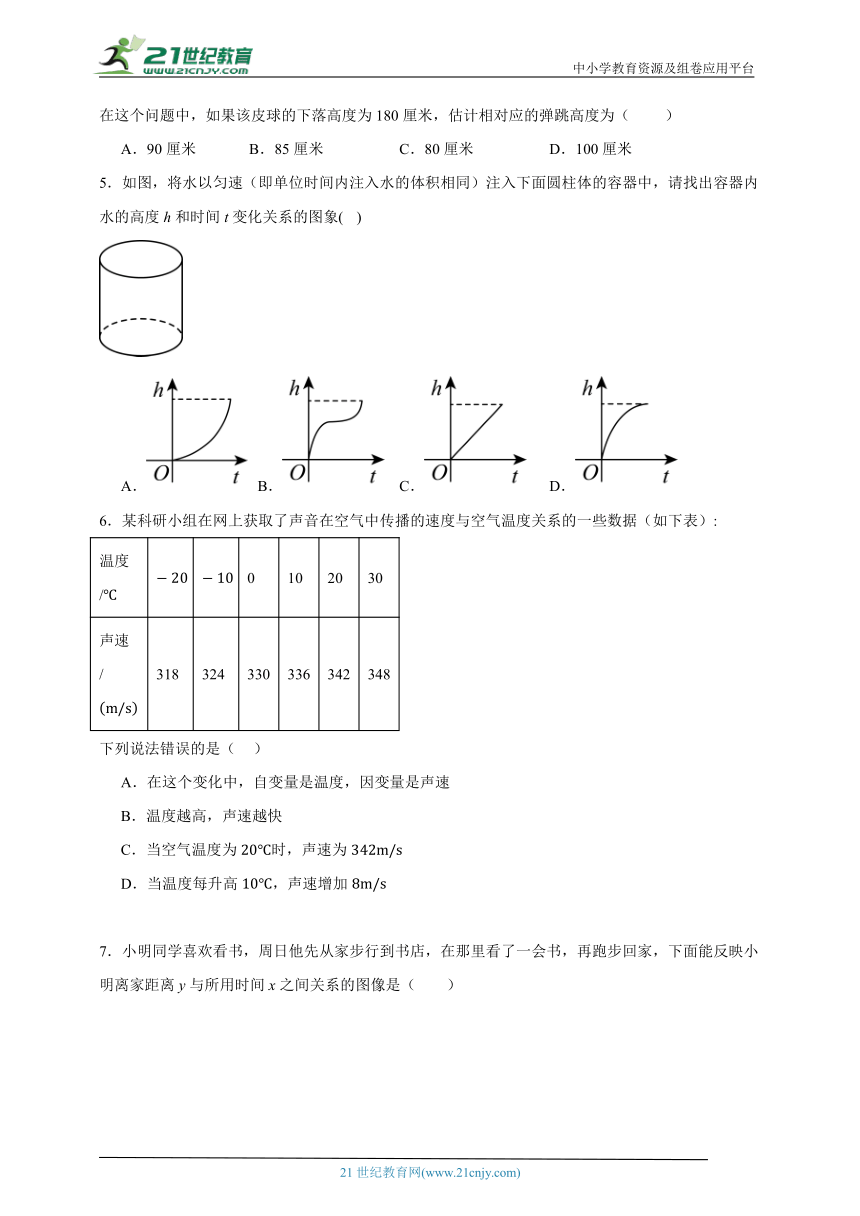
1.小华和小明是同班同学,也是邻居,某日早晨,小明7:40先出发去学校,走了一段后,在途中停下吃了早餐,后来发现上学时间快到了,就跑步到学校;小华离家后直接乘公共汽车到了学校,如图是他们从家到学校已走的路程(米)和所用时间(分钟)的关系图,则下列说法中错误的是( )
A.小明家和学校距离1200米 B.小华乘公共汽车的速度是240米/分
C.小华乘坐公共汽车后7:50与小明相遇D.小明从家到学校的平均速度为80米/分
2.弹簧挂上物体后会伸长,测得一弹簧的长度与所挂的物体的质量间有下面的关系:
0 1 2 3 4 5
10 11 12
下列说法错误的是( )
A.x与y都是变量,且x是自变量,y是因变量
B.弹簧不挂重物时的长度为
C.当时,物体质量每增加,弹簧长度y增加
D.当时,x与y满足的关系式是
3.如图,图象(折线)描述了一汽车在某一直线上的行驶过程中,汽车离出发地的距离(千米)和行驶时间(小时)之间的函数关系,根据图中提供的信息,给出下列说法,其中正确的说法是( )
A.汽车共行驶了120千米 B.汽车在整个行驶过程中平均速度为40千米
C.汽车返回时的速度为80千米/时 D.汽车自出发后小时至2小时之间速度不变
4.为了测试一种皮球的弹跳高度与下落高度之间的关系,通过试验得到下列一组数据(单位:厘米):
下落高度 40 50 80 100 150
弹跳高度 20 25 40 50 75
在这个问题中,如果该皮球的下落高度为180厘米,估计相对应的弹跳高度为( )
A.90厘米 B.85厘米 C.80厘米 D.100厘米
5.如图,将水以匀速(即单位时间内注入水的体积相同)注入下面圆柱体的容器中,请找出容器内水的高度h和时间t变化关系的图象( )
A. B. C. D.
6.某科研小组在网上获取了声音在空气中传播的速度与空气温度关系的一些数据(如下表):
温度/ 0 10 20 30
声速/ 318 324 330 336 342 348
下列说法错误的是( )
A.在这个变化中,自变量是温度,因变量是声速
B.温度越高,声速越快
C.当空气温度为时,声速为
D.当温度每升高,声速增加
7.小明同学喜欢看书,周日他先从家步行到书店,在那里看了一会书,再跑步回家,下面能反映小明离家距离y与所用时间x之间关系的图像是( )
A. B.
C. D.
8.下表是研究弹簧长度与所挂物体质量关系的实验表格:
所挂物体重量x(kg) 1 2 3 4 5
弹簧长度y(cm) 10 12 14 16 18
则弹簧不挂物体时的长度为( ).
A.4cm B.6cm C.8cm D.10cm
9.,两地相距,甲、乙两辆汽车匀速行驶从地出发到地,甲出发1小时后,乙出发沿同一路线行驶,设甲、乙两车相距,甲行驶的时间为,与的关系如图所示,下列说法中错误的( )
①甲车行驶的速度是,乙车行驶的速度是;
②甲出发后被乙追上;③甲比乙晩到;
④甲车行驶或,甲,乙两车相距;
A.序号① B.序号② C.序号③ D.序号④
10.某种商品的售价为每件150元,若按现售价的8折进行促销,设购买件需要元,则与间的函数表达式为( )
A. B. C. D.
11.甲、乙两车沿同一条路从A地出发匀速行驶至相距300km的B地,甲出发1小时后乙再出发,如图表示甲、乙两车离开A地的距离s(km)与乙出发的时间t(h)之间的关系,下列结论错误的是( )
A.甲车的速度是60km/h,乙车的速度是100km/h
B.a的值为60,b的值为4
C.甲、乙两车相遇时,两车距离A地150km
D.甲车出发2.3h后追上乙车
12.弹簧挂上物体后伸长,已知一弹簧的长度()与所挂物体的质量()之间的关系如下表:下列说法错误的是( )
物体的质量() 0 1 2 3 4 5
弹簧的长度() 10 15 20
A.在没挂物体时,弹簧的长度为
B.弹簧的长度随物体的质量的变化而变化,物体的质量是因变量,弹簧的长度是自变量
C.在弹簧能承受的范围内,所挂物体的质量每增加,弹簧的长度就增加
D.在弹簧能承受的范围内,当物体的质量为时,弹簧的长度为
13.如图,在长方形ABCD中,动点P从A出发,以一定的速度,沿方向运动到点A处停止(提示:当点P在AB上运动时,点P到DC的距离始终等于AD和BC).设点P运动的路程为x,的面积为y,如果y与x之间的关系如图所示,那么长方形ABCD的面积为( )
A.6 B.9 C.15 D.18
14.某市的出租车收费标准如下:3千米以内(包括3千米)收费8元,超过3千米后,每超过1千米就加收2元,若某人乘出租车行驶的距离为千米,则需付费用y元与x(千米)之间的关系式为( )
A. B. C. D.
15.一种手持烟花,这种烟花每隔0.5秒发射一发花弹,每一发花弹的飞行路径,爆炸时的高度均相同.皮皮小朋友发射出的第一发花弹的飞行高度h(米)随飞行时间t(秒)变化的规律如下表所示.下列对这一变化的过程说法正确的是( )
t/秒 0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 …
h/米 1.8 7.3 11.8 15.3 17.8 19.3 19.8 19.3 17.8 15.3 …
A.飞行时间t每增加0.5秒,飞行高度h就增加5.5米
B.飞行时间t每增加0.5秒,飞行高度h就减少5.5米
C.估计飞行时间t为5秒时,飞行高度h为11.8米
D.从0秒到2秒花弹飞行的高度是15米
16.甲从深圳匀速骑电动车到广州,乙从广州匀速骑摩托车到深圳,两人同时出发,到达目的地后,立即停止运动,甲、乙两人离深圳的距离与他们骑车的时间之间的函数关系如图所示,则下列说法错误的是( )
A.深广两地的距离为 B.甲的速度为
C.乙的速度为 D.乙运动到达深圳
17.如图,将一个圆柱形无盖小烧杯放置在一个圆柱形无盖大烧杯底部,杯底厚度忽略不计.已知大烧杯的底面半径是小烧杯的底面半径的2倍,现向小烧杯内匀速加水,当大烧杯内的水面高度与小烧杯顶部齐平时,就停止加水.在加水的过程中,小烧杯、大烧杯内水面的高度差随加水时间变化的图象可能是( )
A. B.
C. D.
18.如图(a)所示,长方形边上的一动点P从点B出发,沿B→C→D→A方向匀速运动至点A停止,已知点P的运动速度为,设点P的运动时间为t(s),的面积为,若y关于t的函数图象如图(b)所示,则长方形的周长为( ).
A.14cm B.28cm C.36cm D.48cm
二、填空题
19.随着气温下降,人们开始增添衣服,在这个问题中,自变量是 .
20.如图1,一个正方体铁块放置在圆柱形水槽内,现以一定的速度往水槽中注水,时注满水槽,水槽内水面的高度与注水时间之间的函数图像如图2所示.如果将正方体铁块取出,又经过 秒恰好将水槽注满.
21.甲、乙两人赛跑,路程s(m)与时间t(s)之间的关系如图所示,则下列说法正确的是 .(填序号)
(1)两人赛跑的路程是100m
(2)甲先到达终点
(3)甲跑的平均速度比乙跑的平均速度快0.5m/s
(4)乙跑的平均速度是8m/s
22.张大妈购进一批柚子,在集贸市场零售,已知卖出的柚子重量x(kg)与售价y(元)之间的关系如下表:
重量/kg 1 2 3 …
售价/元 1.2+0.1 2.4+0.1 3.6+0.1 …
根据表中数据可知,若卖出柚子10kg,则售价为 元.
23.如图所示的计算程序中,y与x之间的关系式是 .
24.深圳市出租车的收费标准是起步价10元(行程小于或等于2千米),超过2千米每增加1千米(不足1千米按1千米计算)加收元,小鸣从深圳市体育中心打车去深圳图书馆,百度地图显示行程约为千米,则出租车费约为 元.
25.某地市话的话费y(元)随着时间x(分钟)的变化而变化,收费标准为:
(1)通话时间在3分钟以内(包括3分钟)话费元;
(2)通话时间超过3分钟时,超过部分的话费按每分钟元计算.
在一次通话中,如果通话时间8分钟,那么话费y(元)为 (元).
26.我国首辆火星车正式被命名为:“祝融”,为应对极限温度环境,火星车使用的是新型隔温材料——纳米气凝胶,该材料导热率\与温度的关系如表:
温度
导热率
根据表格中两者的对应关系,若导热率为,则温度为 .
三、解答题
27.某新型品牌充电器给手机充电时充电速度是匀速的,一台手机屏幕画面显示初始电量为,其电量y(单位:%)与充电时间x(单位:h)为表格中几组对应值.根据以上信息,回答下列问题:充电时间
充电时间x(单位:h) 0 n
电量y(单位:%) 20 m 40 60 80
(1)______,______;
(2)该手机充电直至电量达到需要多久?
28.已知甲乙两地相距,一辆轿车从甲地出发往返于甲乙两地,一辆货车匀速沿同一条路线从乙地前往甲地,两车同时出发,经过后两车第一次相遇.轿车到达乙地后立即按原路返回,结果比货车早一个小时到达甲地.如图是两车距各自出发地的距离y()与货车行驶时间x(h)之间的函数图象,结合图象回答下列问题:
(1)图中a的值是______;
(2)求轿车到达乙地再返回甲地所花费的时间;
(3)轿车在返回甲地的过程中与货车相距,直接写出货车已经从乙地出发了多长时间?
29.如图,,两地相距50千米,甲于某日下午1时骑自行车从地出发骑往地,图中的折线和线段分别表示甲与乙所行驶的路程和时间的关系.根据图象回答下列问题:
(1)甲出发______小时,乙才开始出发;
(2)乙比甲早到______小时;
(3)甲从下午2时到5时的平均速度是______千米/小时;乙的平均速度是______千米/小时;
(4)请你根据图象上的数据,求乙出发后用多长时间就追上甲?
30.小明从家出发骑自行车去上学,当他以往常的速度骑了一段路后,突然想起要买文具,于是又折回到刚经过的文具店,买到文具后继续骑车去学校.如图是他本次上学所用的时间与离家的距离之间的关系图,根据图中提供的信息回答下列问题:
(1)小明家到学校的距离是____ 米,文具店到学校的距离是____米 ;
(2)小明在文具店停留了____分钟,本次上学途中,小明一共行驶了____米 ;
(3)观察图象,请编制一道新的问题并给出解答过程.
31.小明晚饭后外出散步,碰见同学,交谈一会,返回途中在读报栏看了一会报.如图是根据此情景画出的图象,请你回答下列问题:
(1)小明碰见同学后交谈了______分钟.
(2)读报栏离家______米.
(3)小明出发15分钟后离家______米.
(4)小明出发______分钟后离家500米.
32.某机动车出发前油箱内有油48L.行驶若干小时后,途中在加油站加油若干升.油箱中剩余油量与行驶时间之间的关系如图所示,根据图象回答下列问题.
(1)在这个变化过程中,____________是自变量,______________是因变量;
(2)机动车行驶___________小时后加油,中途加油__________L;
(3)如果加油站距目的地还有360km,车速为,要到达目的地,请判断油箱中的油是否够用,并说明理由.
33.如图反映的是小华从家里跑步去体育馆,在那里锻炼了一段时间后又走到文具店去买笔,然后散步回家,其中(分)表示时间,(千米)表示小华离家的距离.根据图象回答下列问题:
(1)体育馆距离小华家__________千米,小华在体育馆锻炼了__________分钟;
(2)体育馆距离文具店__________千米,小华在文具店买笔用了__________分钟;
(3)小华从家跑步到体育馆,从文具店散步回家的速度分别是多少千米/小时?
34.【问题背景】如图①,“漏刻”是我国古代一种利用水流计时的工具,古诗“金炉香尽漏声残,翦翦轻风阵阵寒”,描绘了“漏刻”不断漏水的情景.如图②,小明用甲、乙两个透明的竖直放置的容器和一根装有节流阀(控制水的流速)的软管,制作了类似“漏刻”的简易计时装置.
【实践操作】上午9:00,小明在甲容器里加满水,此时水面高度为,开始放水后,小明每隔记录一次甲容器中的水面高度,相关数据如表:
记录时间 9:00 9:10 9:20 9:30 9:40
流水时间 0 10 20 30 40
水面高度 30 29.5 29 28.5 28
【问题解决】
(1)下列图像可以大致反映水面高度随时间变化而变化的是__________.(填序号)
(2)由表中数据可知,流水时间每隔,甲容器中的水面高度下降__________,据此规律,10:10时水面高度应为__________.
(3)请你直接写出水面高度与流水时间的关系式__________.
35.自行车是很多同学家校往返的重要交通工具,如图,某款自行车每节链条的长度为,交叉重叠部分的圆的直径为.
(1)观察图形填写下表:
链条节数(节) 2 3 4
链条长度()
(2)如果节链条的总长度是,求与之间的关系式;
(3)晓明同学的同款自行车链条生锈断了,需要在淘宝网上采购并自行安装,该型号自行车的链条(安装前)由90节这样的链条组成,那么晓明需要购买该型号链条的总长度是多少?实际安装长度是多少?
36.甲骑电动车,乙骑自行车从深圳湾公园门口出发沿同一路线匀速游玩,设乙行驶的时间为,甲、乙两人距出发点的路程、关于x的函数图象如图①所示,甲、乙两人之间的路程差y关于x的函数图象如图②所示,请你解决以下问题:
(1)甲的速度是______km/h,乙的速度是______km/h;
(2)对比图①、图②可知______,______;
(3)乙出发多少时间,甲、乙两人路程差为7.5km?
37.某车间甲、乙两名工人分别同时开始生产同种试剂,图中的折线和折线表示他们一天生产试剂y(克)与生产时间t(小时)的关系,工人甲因机器故障停止生产了一段时间,修好机器后速度提高到每小时生产10克试剂,结果还提前一小时完成了任务,请你根据图中给出的信息解决下列问题:
(1)折线表示_________(填“甲”或“乙”)工人生产试剂与生产时间的关系,乙这一天共生产__________克试剂;
(2)工人乙起初每小时生产__________克试剂;
(3)求工人甲中间停下修机器所用时间为__________小时;
(4)请列式计算,甲、乙两名工人何时加工的试剂一样多?
38.在“看图说故事”活动中,某学习小组结合图象设计了一个问题情境.已知小亮所在学校的教学楼、图书馆、食堂依次在同一条直线上,图书馆离教学楼,食堂离教学楼.某日中午,小亮从教学楼出发,匀速走了(分钟)到图书馆;在图书馆停留借书后,匀速走了到食堂;在食堂停留吃完饭后,匀速走了返回教学楼.给出的图象反映了这个过程中小亮离教学楼的距离与离开教学楼的时间之间的对应关系.请根据相关信息,解答下列问题:
(1)图中自变量是________,因变量是________;小亮从教学楼到图书馆的速度为________,小亮从图书馆到食堂的速度为________;
(2)填表:
离开教学楼的时间/ 2 20 25 30
离教学楼的距离/ ________ 700 ________ ________
(3)当小亮离开教学楼的时间为________时,他离教学楼的距离为.
参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D B C A C D A C D C
题号 11 12 13 14 15 16 17 18
答案 D B D B C C C B
1.D
【分析】根据已知信息和函数图象的数据,依次解答每个选项.
【详解】解:由图象可知,小华和小明的家离学校1200米,故A正确;
根据图象,小华乘公共汽车,从出发到到达学校共用了(分钟),所以公共汽车的速度为(米/分),故B正确;
小明先出发8分钟然后停下来吃早餐,由图象可知在小明吃早餐的过程中,小华出发并与小明相遇然后超过小明,所以二人相遇所用的时间是(分钟),即7:50相遇,故C正确;
小明从家到学校的时间为20分钟,所以小明的平均速度为(米/分),故D错误.
故选:D.
【点睛】此题考查一次函数的实际应用,正确理解函数图象,掌握行程问题中时间、速度、路程之间的关系是解题的关键.
2.B
【分析】根据函数的定义,一次函数的解析式,k的意义,计算即可,本题考查了函数的定义,一次函数的解析式,熟练掌握待定系数法是解题的关键.
【详解】A. x与y都是变量,且x是自变量,y是因变量,正确;不符合题意;
B. 弹簧不挂重物时的长度为,错误,符合题意;
C. 当时,物体质量每增加,弹簧长度y增加,正确;不符合题意;
D. 当时,x与y满足的关系式是,正确;不符合题意;
故选B.
3.C
【分析】横轴代表时间,纵轴代表行驶的路程,利用图象判断相应的路程和时间,再结合速度路程时间,逐项分析,即可得到答案.
【详解】解:A、由图象可以看出,最远处到达距离出发地120千米处,但又返回原地,所以行驶的路程为240千米,原说法错误,不符合题意,选项错误;
B、平均速度总路程总时间,总路程为240千米,总时间为小时,所以平均速度为千米/时,原说法错误,不符合题意,选项错误;
C、汽车返回所用的时间是小时,则平均速度为:千米/时,原说法正确,符合题意,选项正确;
D、汽车自出发后1.5小时至2小时之间静止不动,原说法错误,不符合题意,选项错误;
故选:C.
【点睛】本题考查了利用函数的图象解决实际问题,解题关键是正确理解函数图象横纵坐标表示的意义,理解问题的过程,熟练掌握速度路程时间.
4.A
【分析】设弹跳高度为,下落高度为,根据题意和表格数据,可以得出,然后将下落高度为180厘米代入求解即可.
【详解】解:设弹跳高度为,下落高度为,
由表格数据可知,弹跳高度是下落高度的一半,即,
∴当时,.
故选:A.
【点睛】本题主要考查根据实际问题列一次函数的解析式,根据题意和表格数据得出正比例函数解析式是解题的关键.
5.C
【分析】先观察容器的形状,再分析水面上升的速度,据此选择合适的函数图像即可.
【详解】解:因为圆柱上下一样粗,所以水面上升的高度h随注水时间t的增大而匀速增大.
故选:C.
【点睛】本题主要考查函数图像的知识,根据h随t的变化情况判断相应的函数图像是解决本题的关键.
6.D
【分析】根据自变量、因变量的定义,以及声音在空气中传播的速度与空气温度关系逐一判断即可.
【详解】解:∵在这个变化中,自变量是温度,因变量是声速,
∴选项A说法正确,不符合题意;
∵根据数据表,可得温度越低,声速越慢,温度越高,声速越快,
∴选项B说法正确,不符合题意;
由列表可知,当空气温度为时,声速为,
∴选项C说法正确,不符合题意;
∵ , , , , ,
∴当温度每升高,声速增加,
∴选项D说法不正确,符合题意.
故选D.
【点睛】本题主要考查了自变量,因变量.熟练掌握自变量、因变量的定义是解题的关键.在一个变化过程种,如果有两个变量x和y,对于x的每一个确定的值,y都有唯一确定的值与其对应,那么x是自变量,y是因变量.
7.A
【分析】本题需要根据已知条件,确定出每一步的函数图像,再把函数图像结合起来即可得到答案.
【详解】解:∵小明从家步行到书店,
∴随着时间的增加离家的距离越来越远,
∵到达书店后,他在那里看了会书,
∴在书店的这段时间,他离家的距离不变,
又∵再跑步回家,
∴这段时间,他离家越来越近,而且跑步回家比步行到书店用的时间少,
∴能反映小明离家距离y与所用时间x之间关系的图像是A,
故选A.
【点睛】本题主要考查了函数图像的识别,解题的关键在于能够根据实际情况进行分析每一个过程.
8.C
【分析】根据表格数据,设弹簧长度y与所挂物体重量x的关系式为,进而求得关系式,令即可求得弹簧不挂物体时的长度.
【详解】设弹簧长度y与所挂物体重量x的关系式为,
将,分别代入得,
解得
即,
将,分别代入,符合关系式,
当时,则,
故选C.
【点睛】本题考查了变量与表格,函数关系式,找到关系式是解题的关键.
9.D
【分析】根据图象可得甲车行驶的速度是,再由甲先出发1h,乙出发3h后追上甲,可得到乙车行驶的速度是80km/h;根据图象可得当乙到达B地时,甲乙相距100km,从而得到甲比乙晚到h;然后分两种情况:当乙车在甲车前,且未到达B地时和当乙车到达B地后时甲,乙两车相距80km,进行求解判断即可.
【详解】解:由图可得,甲车行驶的速度是
根据图象可知:甲先出发1h,甲出发4h后被乙追上,
∴,
∴
即乙车行驶的速度是80km/h,故选项A,B正确;
由图可得,当乙到达B地时,甲乙相距100km,
∴甲比乙晚到h,故选项C正确;
由图可得,当乙车在甲车前,且未到达B地时,则,
解得:,
当乙车到达B地后时,,
解得:,
∴甲车行驶8h或h,甲,乙两车相距80km,故选项D错误.
故选:D.
【点睛】本题主要考查了函数的图象、能从函数图象的获取准确信息和灵活利用数形结合思想解答是解题的关键.
10.C
【分析】根据题意,列出一元一次方程,即可得到答案.
【详解】解:根据题意,得
;
∴与间的函数表达式为:;
故选:C.
【点睛】本题考查了一元一次方程的应用,解题的关键是熟练掌握题意,正确列出一元一次方程.
11.D
【分析】根据函数图象,列出关于a,b的方程,求出a,b的值,从而即可逐一判断各个选项.
【详解】解:根据图象可知,(300-a)÷b=(240-a)÷3=a÷1,
解得:a=60,b=4,
甲车的速度=60÷1=60km/h,乙车的速度=300÷3=100km/h,
故A,B正确,不符合题意;
∵60÷(100-60)=1.5,1.5×100=150km,
∴乙车出发1.5小时后追上甲车,甲、乙两车相遇时,两车距离A地150km,
故C正确,不符合题意,D错误,符合题意,
故选D.
【点睛】本题考查了一次函数的应用,理解函数图象以及分别求出甲、乙两人的速度是解题的关键.
12.B
【分析】根据表格得出函数的相关性质即可.
【详解】解:A.在没挂物体时,弹簧的长度为,根据图表,当质量时,,故此选项正确,不符合题意;
B、反映了所挂物体的质量和弹簧的长度之间的关系,所挂物体的质量是自变量;弹簧的长度是因变量,故此选项错误,符合题意;
C.在弹簧能承受的范围内,所挂物体的质量每增加,弹簧的长度就增加,故此选项正确,不符合题意;
D、由C中,,解得,在弹簧的弹性范围内,故此选项正确,不符合题意;
故选:B.
【点睛】题目主要考查函数的基本知识点,根据表格得出相关信息是解题关键.
13.D
【分析】根据题意结合图象得出AB、BC的长度,再求出面积即可.
【详解】由题意可知,当点P从点A运动到点B时,△PCD的面积为:,即△PCD的面积不变,则结合图象可知AB=6,
当点P从点B运动到点C时,△PCD的面积逐渐变小直到为0,
即结合图象可知BC=x-AB=9-6=3,
∴长方形ABCD的面积为:AB BC=6×3=18.
故选:D.
【点睛】本题考查了动点问题的函数图象,能根据图形得出正确信息是解此题的关键.
14.B
【分析】本题考查了函数关系式,解题的关键是对关系式进行化简,得到y与x的函数关系式.根据题意把x千米分成3千米和千米两部分,再根据单价乘里程表示出关系式,再化简即可.
【详解】解:当时,
,
故选:B.
15.C
【分析】本题考查函数的表示方法;能够通过表格观察自变量和因变量的变化情况是解题的关键.
根据表格数据分析通过表格观察随着时间的变化,飞行高度是先增加后减少,并且在3秒的两侧对称,从表格可以看到0秒到3秒的过程中,随着飞行时间的增加飞行高度增加,再逐项判断即可.
【详解】通过表格观察随着时间的变化,飞行高度是先增加后减少,并且在3秒的两侧对称,从表格可以看到0秒到3秒的过程中,随着飞行时间的增加飞行高度增加;
从3秒以后,随着飞行时间的增加,飞行高度减小;
因此,A与B选项不正确;
从表格看到飞行高度在3秒左右是对称的,所以C选项正确;
从0秒到2秒花弹飞行的高度是米,所以D不正确.
故选:C.
16.C
【分析】本题考查了函数图象,解题的关键在于数形结合,从图象中获取正确的信息.根据图象可得深广两地的距离为,可判断A;再根据路程除以时间可求出甲的速度,可判断B;然后求出甲乙相遇的时间,可求出乙的速度,从而判断C,D.
【详解】解:由图象得:深广两地的距离为,故A正确,故不符合题意;
甲的速度为,故B正确,故不符合题意;
甲乙相遇的时间为,则乙的速度为,故C错误,故符合题意;
乙运动到达深圳所用时间为,故D正确,不符合题意;
故选:C
17.C
【分析】本题考查了函数的图象.正确理解函数图象横纵坐标表示的意义,理解问题的过程,能够通过图象得到函数是随自变量的增大,知道函数值是增大还是减小.根据题意判断出小烧杯、大烧杯的液面高度随时间的变化情况即可.
【详解】解:大烧杯的底面半径是小烧杯的底面半径的2倍,
小烧杯的容积是大烧杯与小烧杯顶部齐平时下部容积的,
注满小烧杯的所需时间是大烧杯下部注水时间的,
小烧杯、大烧杯内水面的高度差随加水时间变化的图象可能是选项C.
故选:C
18.B
【分析】本题考查了动点问题的函数图象.根据的面积只与点P的位置有关,结合图2求出长方形的长和宽,再由长方形的周长公式计算即可.
【详解】解:根据题意得:动点P从点B出发,沿、、运动至点A停止,
当点P在点B,C之间运动时,根据运动速度为,可得,
的面积,
由图2得,当时,点P由B点到达点C处,
∴;
当点P运动到点C,D之间时,
的面积,保持不变,
由图2得,点P从点C运动到点D所用时间为,
∴,
∴长方形的周长:.
故选:B.
19.气温
【分析】本题考查函数的定义.设在某变化过程中有两个变量,如果对于在某一范围内的每一个确定的值,都有唯一确定的值与它对应,那么就称是的函数,叫做自变量.
【详解】解:根据题意,随着气温下降,人们开始增添衣服,在这个问题中,自变量是气温.
故答案为:气温.
20.4
【分析】根据函数图像可得正方体的棱长为10cm,同时可得水面上升从10cm到20cm,所用的时间为16秒,结合前12秒由于立方体的存在,导致水面上升速度加快了4秒可得答案.
【详解】解:由题意可得:12秒时,水槽内水面的高度为10cm,12秒后水槽内水面高度变化趋势改变,正方体的棱长为10cm;
没有立方体时,水面上升从10cm到20cm,所用的时间为:28-12=16秒
前12秒由于立方体的存在,导致水面上升速度加快了4秒
将正方体铁块取出, 又经过4秒恰好将此水槽注满.
故答案:4
【点睛】本题主要考查一次函数的图像及应用,根据函数图像读懂信息是解题的关键.
21.(1)(2)(4)
【分析】根据函数图象逐项分析判断即可求解.
【详解】解:(1)两人赛跑的路程是100m,故(1)正确;
(2)甲先到达终点,故(2)正确;
(3)甲跑的平均速度为 m/s,乙跑的平均速度为m/s,
甲跑的平均速度比乙跑的平均速度快m/s,故(3)不正确,
(4)乙跑的平均速度是8m/s,正确.
故答案为:(1)(2)(4).
【点睛】本题考查了函数图象,从函数图象获取信息是解题的关键.
22.12.1
【分析】根据表格求出的对应关系即可求解.
【详解】当时,,
当时,,
当时,,
,
当时,,
故答案为:12.1.
【点睛】本题考查了函数的表示方法,能够根据题意列出的表达式是解题关键.
23.
【分析】根据程序框图列出正确的关系式即可得解.
【详解】解:根据程序框图可得 ;
故答案为:.
【点睛】本题考查根据程序框图列关系式,解题的关键是按照运算顺序准确列出关系式.
24.
【分析】本题主要考查有理数的混合运算的应用,根据题意、正确列出算式是正确解答的前提.
根据题意、正确列出算式,然后再计算即可.
【详解】解:由题意可知:当时,出租车费约为.
故答案为:.
25.
【分析】本题主要考查了求函数值,根据所给的收费标准列式计算即可.
【详解】解:由题意得,,
故答案为:.
26.
【分析】根据表格中两个变量、的对应值以及变化规律可得答案.
【详解】解:根据题意,温度每增加,导热率增加,
所以当导热率为时,温度为.
故答案为:.
【点睛】本题考查函数及其表示方法,理解函数的意义以及变量之间的变化规律是正确解答的关键.
27.(1)30;1
(2)2小时
【分析】本题考查一次函数的应用,解题的关键是读懂题意,能正确识图.
(1)用待定系数法可得函数关系式,即可解答;
(2)根据,列方程求解即可.
【详解】(1)∵充电器给手机充电时充电速度是匀速的,
∴设其电量y与充电时间x对应的函数表达式为,
将代入得:
,
解得,
∴函数表达式为;
当时,,
当时,,,
故答案为:30;1;
(2)当时,,
解得,
故该手机充电直至电量达到需要2h.
28.(1)90
(2)7小时
(3)或
【分析】本题考查一次函数的应用,解题的关键是读懂题意,能正确识图.
(1)用待定系数法可得函数关系式,即可求解;
(2)根据两车同时出发,经过后两车第一次相遇,列方程求货车的速度即可解答.
(3)分两种情况分别计算即可;
【详解】(1)由图象知,,
设直线的解析式为,把代入得,,
解得,
∴直线的解析式为;
把代入,得,
故答案为:90;
(2)轿车的速度千米/小时,
∵两车同时出发,经过后两车第一次相遇,
设货车的速度为v千米/小时,
则,
解得,
故货车从乙地到甲地共用时小时,
∵轿车比货车早一个小时到达甲地,
∴轿车到达乙地再返回甲地所花费的时间小时.
(3)由(2)得,,
货车的速度千米/小时,
轿车在返回甲地的过程中所花费的时间小时,则返回甲地的过程中的速度千米/小时,
设轿车在返回甲地的过程中与货车相距时,货车已经从乙地出发了,
返回时当轿车在货车前时:
解得:,
返回时当货车在轿车前时:
解得:,
故轿车在返回甲地的过程中与货车相距时,货车已经从乙地出发了或.
29.(1)1;(2)2;(3)10;50;(4)0.5小时
【分析】(1)由图象横轴上的甲、乙出发时间即可解答;
(2)由甲、乙到达B的时间即可解答;
(3)根据速度=路程÷时间求解即可;
(4)设乙出发后x小时就追上甲,根据(3)中求得速度结合图象列方程求解即可.
【详解】解:(1)由图象知,甲下午1时出发,乙下午2时出发,
∴甲出发1小时,乙才开始出发,
故答案为:1;
(2)由图象知,甲下午5时到达B地,乙下午3时到达B地,
∴乙比甲早到2小时,
故答案为:2;
(3)根据图象,甲从下午2时到5时的平均速度是(50﹣20)÷(5﹣2)=10千米/小时,乙的平均速度是50÷(3﹣2)=50千米/小时,
故答案为:10;50;
(3)设乙出发后用小时就追上了甲,
根据题意,得,
解得
答:乙出发0.5小时就追上甲.
【点睛】本题考查函数的图象、一元一次方程的应用,解答的关键是正确获取图象上的有关信息解决问题.
30.(1),;
(2),;
(3)见解析.
【分析】()根据题意和函数图象即可求解;
()根据题意和函数图象即可求解;
()根据函数图象提出合理问题并解答即可;
本题考查了函数图象,看懂函数图象是解题的关键.
【详解】(1)解:由题意和函数图象可得,小明家到学校的距离是米,
文具店到学校的距离是米,
故答案为:,;
(2)解:由函数图象可得,小明在文具店停留了分钟,
本次上学途中,小明一共行驶了米,
故答案为:,;
(3)解:自编第三问:如图,若小明不买文具,以往常的速度去学校,需要花费多长时间?
小明往常的速度为米/分,
去学校需要花费的时间为分钟,
答:小明不买文具以往常的速度去学校需要分钟.
31.(1)10
(2)400
(3)600
(4)或
【分析】本题考查一次函数的应用,掌握速度、时间、路程三者之间的数量关系和待定系数法求函数关系式是解题的关键.
(1)观察图象直接作答即可;
(2)观察图象直接作答即可;
(3)根据“速度路程时间”求出当时小明的速度,再根据“路程速度时间”求出小明出发15分钟后离家的距离;
(4)分别根据“路程速度时间”和待定系数法求出和时的y与x的函数关系式,分别将代入,求出对应x的值即可.
【详解】(1)解:(分钟),
∴小明碰见同学后交谈了10分钟.
故答案为:10;
(2)根据图象可知,读报栏离家400米.
故答案为:400;
(3)当时,小明的速度为(米/分),
则小明出发15分钟后离家的距离为(米).
故答案为:600;
(4)当时,y与t的关系式为,
当时,解得;
当时,设y与t的关系式为(k、b为常数,且).
将坐标和代入,
得,
解得,
∴y与t的关系式为,当时,解得.
综上,小明出发或分钟后离家500米.
故答案为:或.
32.(1)行驶时间,剩余油量
(2),
(3)不够用,理由见解析
【分析】(1)根据函数的定义直接求解即可;
(2)根据函数图象直接求解即可;
(3)根据函数图象可知机动车的耗油量为,根据行驶时间乘以耗油量即可求解
【详解】(1)根据题意可知:行驶时间是自变量,剩余油量是因变量;
故答案为:行驶时间,剩余油量
(2)根据函数图象可知,机动车行驶小时后加油,中途加油
故答案为:,
(3)不够用.理由如下:
机动车的耗油量:,
行驶时间,需要油量,
故不够用.
【点睛】本题考查了函数的定义,函数图象,根据函数图象获取信息是解题的关键.
33.(1)2.5;15
(2)1;20
(3)小华从家跑步到体育场的速度为10千米/小时;小华从文具店散步回家的速度为千米/小时
【分析】本题考查了函数图象,正确理解函数图象横纵坐标表示的意义,理解问题的过程,就能够通过图象得到函数问题的相应解决.需注意计算单位的统一.
(1)根据观察函数图象的纵坐标,可得距离,观察函数图象的横坐标,可得时间;
(2)根据观察函数图象的横坐标,可得体育馆与文具店的距离,观察函数图象的横坐标,可得在文具店停留的时间;
(3)根据观察函数图象的纵坐标,可得路程,根据观察函数图象的横坐标,可得回家的时间,根据路程与时间的关系,可得答案.
【详解】(1)解:(1)由纵坐标看出体育馆距离小华家2.5千米,由横坐标看出小华在体育馆锻炼了15分钟;
故答案为:2.5;15.
(2)解:由纵坐标看出体育馆距离文具店(千米),由横坐标看出小华在文具店买笔用了(分).
故答案为:1;20.
(3)解:小华从家跑步到体育馆的速度为(千米小时),
小华从文具店散步回家的平均速度是(千米/小时).
答:小华从家跑步到体育场的速度为10千米/小时;小华从文具店散步回家的速度为千米/小时.
34.(1)②
(2),
(3)
【分析】本题考查了一次函数的应用,求一次函数解析式,判断一次函数图像,根据表格中的数据写出函数关系式,是解答本题的关键.
(1)由表格中的数据直接判断即可;
(2)由表格中的数据直接判断即可;
(3)根据(2),求出甲容器中水面每分钟下降的高度,再根据甲容器中的高度甲容器中开始的水面高度甲容器中水面高度每分钟下降的距离流水时间,即可写出函数关系式.
【详解】(1)解:由表格可知,水面高度随时间而降低,即该函数为减函数,而且流水时间不会小于0,水面高度流到最后,管口以下流不净,也就是y的值不会为零,
故答案为:②;
由表格数据可知,流水时间每隔,甲容器中的水面高度下降,
∵距离为,
(2)∴时水面高度应为,
故答案为:,;
(3)由(2)可知,甲容器中的水面高度每分钟下降,
,
故答案为:.
35.(1)
(2)
(3),
【分析】此题主要考查了函数关系式,根据题意得出节链条的长度与每节长度之间的关系是解决问题的关键.
(1)根据图形找出规律计算4节链条的长度即可;
(2)由(1)写出表示链条节数的一般式;
(3)根据(2)计算时,特别注意自行车上的链条为环形,在展直的基础上还要缩短.
【详解】(1)解:根据图形可得出:
2节链条的长度为:,
3节链条的长度为:,
4节链条的长度为:.
故答案为:;
(2)由(1)可得节链条长为:;
∴与之间的关系式为:;
(3)当.
故晓明需要购买该型号链条的总长度是;
因为自行车上的链条为环形,在展直的基础上还要缩短,
故这辆自行车链条的总长为厘米,
所以90节这样的链条总长度是117厘米.
36.(1)25,10
(2)10,1.5
(3)或
【分析】(1)根据题意和函数图象中的数据可以求得甲乙的速度;
(2)根据题意和图象中的数据,可以分别得到、的值;
(3)由图象可知甲乙相距有两种情况,然后分别计算两种情况下乙出发的时间即可解答本题.
【详解】(1)解:由图可得,
甲的速度为:,乙的速度为:,
故答案为:25,10;
(2)解:由图可得,
,
,
故答案为:10;1.5;
(3)解:由题意可得,
前,乙行驶的路程为:,
则甲、乙两人路程差为是在甲乙相遇之后,
设乙出发时,甲、乙两人路程差为,
,
解得,,
,得;
即乙出发或时,甲、乙两人路程差为.
【点睛】本题主要考查函数图象,解题的关键是由函数图象得到解题的信息.
37.(1)甲,40;
(2)2;
(3)3;
(4)3或.
【分析】本题考查了一次函数的应用,函数图象,明确题意,利用一次函数的性质和数形结合思想是解题的关键.
(1)根据题意结合图象可得答案;
(2)用“工作效率工作总量工作时间”可得答案;
(3)根据函数图象可以解答本题;
(4)根据函数图象和图象中的数据可以求得甲乙对应的函数解析式,从而可以解答本题.
【详解】(1)解:由题意可知,折线表示甲工人生产试剂与生产时间的关系,乙这一天共生产克试剂.
故答案为:甲;;
(2)解:乙起初每小时生产试剂:(克).
故答案为:;
(3)解:在生产过程中,甲因机器故障停止生产(小时),
(4)当时,乙对应的函数解析式为,
,
解得,
即当时,乙对应的函数解析式为,
设当,甲对应的函数解析式为,
,
解得,
即当,甲对应的函数解析式为,
令,得,
当时,得,
即当为或时,甲、乙两人生产的零件个数相等.
38.(1)小亮离开教学楼的时间,小亮离教学楼的距离,100,60
(2)200,820,1000
(3)或
【分析】(1)根据函数的定义,以及速度、路程、时间的关系即可求解;
(2)根据题意和函数图象,可以将表格补充完整;
(3)分两种情况,根据函数图象中的数据,求出当时,当时,小亮离教学楼的距离为时,求他离开教学楼的时间即可.
【详解】(1)解:图中自变量是小亮离开教学楼的时间,因变量是小亮离教学楼的距离;
小亮从教学楼到图书馆的速度为,
小亮从图书馆到食堂的速度为;
(2)解:当时,离教学楼的距离为,
当时,离教学楼的距离为,
在时,距离不变,都是,
故当时,离教学楼的距离为,
(3)解:小亮离教学楼的距离为时,
有两种情况,
①当时,
∵在前7分钟的速度为,
∴当小亮离教学楼的距离为时,他离开教学楼的时间为,
当时,
小亮离教学楼的距离为时,他离开教学楼的时间为,
∴当小亮离教学楼的距离为600m时,求他离开教学楼的时间或.
【点睛】本题考查一次函数的应用,解答本题的关键是明确题意,利用数形结合的思想解答.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
专题06 变量之间的关系
一、单选题
1.小华和小明是同班同学,也是邻居,某日早晨,小明7:40先出发去学校,走了一段后,在途中停下吃了早餐,后来发现上学时间快到了,就跑步到学校;小华离家后直接乘公共汽车到了学校,如图是他们从家到学校已走的路程(米)和所用时间(分钟)的关系图,则下列说法中错误的是( )
A.小明家和学校距离1200米 B.小华乘公共汽车的速度是240米/分
C.小华乘坐公共汽车后7:50与小明相遇D.小明从家到学校的平均速度为80米/分
2.弹簧挂上物体后会伸长,测得一弹簧的长度与所挂的物体的质量间有下面的关系:
0 1 2 3 4 5
10 11 12
下列说法错误的是( )
A.x与y都是变量,且x是自变量,y是因变量
B.弹簧不挂重物时的长度为
C.当时,物体质量每增加,弹簧长度y增加
D.当时,x与y满足的关系式是
3.如图,图象(折线)描述了一汽车在某一直线上的行驶过程中,汽车离出发地的距离(千米)和行驶时间(小时)之间的函数关系,根据图中提供的信息,给出下列说法,其中正确的说法是( )
A.汽车共行驶了120千米 B.汽车在整个行驶过程中平均速度为40千米
C.汽车返回时的速度为80千米/时 D.汽车自出发后小时至2小时之间速度不变
4.为了测试一种皮球的弹跳高度与下落高度之间的关系,通过试验得到下列一组数据(单位:厘米):
下落高度 40 50 80 100 150
弹跳高度 20 25 40 50 75
在这个问题中,如果该皮球的下落高度为180厘米,估计相对应的弹跳高度为( )
A.90厘米 B.85厘米 C.80厘米 D.100厘米
5.如图,将水以匀速(即单位时间内注入水的体积相同)注入下面圆柱体的容器中,请找出容器内水的高度h和时间t变化关系的图象( )
A. B. C. D.
6.某科研小组在网上获取了声音在空气中传播的速度与空气温度关系的一些数据(如下表):
温度/ 0 10 20 30
声速/ 318 324 330 336 342 348
下列说法错误的是( )
A.在这个变化中,自变量是温度,因变量是声速
B.温度越高,声速越快
C.当空气温度为时,声速为
D.当温度每升高,声速增加
7.小明同学喜欢看书,周日他先从家步行到书店,在那里看了一会书,再跑步回家,下面能反映小明离家距离y与所用时间x之间关系的图像是( )
A. B.
C. D.
8.下表是研究弹簧长度与所挂物体质量关系的实验表格:
所挂物体重量x(kg) 1 2 3 4 5
弹簧长度y(cm) 10 12 14 16 18
则弹簧不挂物体时的长度为( ).
A.4cm B.6cm C.8cm D.10cm
9.,两地相距,甲、乙两辆汽车匀速行驶从地出发到地,甲出发1小时后,乙出发沿同一路线行驶,设甲、乙两车相距,甲行驶的时间为,与的关系如图所示,下列说法中错误的( )
①甲车行驶的速度是,乙车行驶的速度是;
②甲出发后被乙追上;③甲比乙晩到;
④甲车行驶或,甲,乙两车相距;
A.序号① B.序号② C.序号③ D.序号④
10.某种商品的售价为每件150元,若按现售价的8折进行促销,设购买件需要元,则与间的函数表达式为( )
A. B. C. D.
11.甲、乙两车沿同一条路从A地出发匀速行驶至相距300km的B地,甲出发1小时后乙再出发,如图表示甲、乙两车离开A地的距离s(km)与乙出发的时间t(h)之间的关系,下列结论错误的是( )
A.甲车的速度是60km/h,乙车的速度是100km/h
B.a的值为60,b的值为4
C.甲、乙两车相遇时,两车距离A地150km
D.甲车出发2.3h后追上乙车
12.弹簧挂上物体后伸长,已知一弹簧的长度()与所挂物体的质量()之间的关系如下表:下列说法错误的是( )
物体的质量() 0 1 2 3 4 5
弹簧的长度() 10 15 20
A.在没挂物体时,弹簧的长度为
B.弹簧的长度随物体的质量的变化而变化,物体的质量是因变量,弹簧的长度是自变量
C.在弹簧能承受的范围内,所挂物体的质量每增加,弹簧的长度就增加
D.在弹簧能承受的范围内,当物体的质量为时,弹簧的长度为
13.如图,在长方形ABCD中,动点P从A出发,以一定的速度,沿方向运动到点A处停止(提示:当点P在AB上运动时,点P到DC的距离始终等于AD和BC).设点P运动的路程为x,的面积为y,如果y与x之间的关系如图所示,那么长方形ABCD的面积为( )
A.6 B.9 C.15 D.18
14.某市的出租车收费标准如下:3千米以内(包括3千米)收费8元,超过3千米后,每超过1千米就加收2元,若某人乘出租车行驶的距离为千米,则需付费用y元与x(千米)之间的关系式为( )
A. B. C. D.
15.一种手持烟花,这种烟花每隔0.5秒发射一发花弹,每一发花弹的飞行路径,爆炸时的高度均相同.皮皮小朋友发射出的第一发花弹的飞行高度h(米)随飞行时间t(秒)变化的规律如下表所示.下列对这一变化的过程说法正确的是( )
t/秒 0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 …
h/米 1.8 7.3 11.8 15.3 17.8 19.3 19.8 19.3 17.8 15.3 …
A.飞行时间t每增加0.5秒,飞行高度h就增加5.5米
B.飞行时间t每增加0.5秒,飞行高度h就减少5.5米
C.估计飞行时间t为5秒时,飞行高度h为11.8米
D.从0秒到2秒花弹飞行的高度是15米
16.甲从深圳匀速骑电动车到广州,乙从广州匀速骑摩托车到深圳,两人同时出发,到达目的地后,立即停止运动,甲、乙两人离深圳的距离与他们骑车的时间之间的函数关系如图所示,则下列说法错误的是( )
A.深广两地的距离为 B.甲的速度为
C.乙的速度为 D.乙运动到达深圳
17.如图,将一个圆柱形无盖小烧杯放置在一个圆柱形无盖大烧杯底部,杯底厚度忽略不计.已知大烧杯的底面半径是小烧杯的底面半径的2倍,现向小烧杯内匀速加水,当大烧杯内的水面高度与小烧杯顶部齐平时,就停止加水.在加水的过程中,小烧杯、大烧杯内水面的高度差随加水时间变化的图象可能是( )
A. B.
C. D.
18.如图(a)所示,长方形边上的一动点P从点B出发,沿B→C→D→A方向匀速运动至点A停止,已知点P的运动速度为,设点P的运动时间为t(s),的面积为,若y关于t的函数图象如图(b)所示,则长方形的周长为( ).
A.14cm B.28cm C.36cm D.48cm
二、填空题
19.随着气温下降,人们开始增添衣服,在这个问题中,自变量是 .
20.如图1,一个正方体铁块放置在圆柱形水槽内,现以一定的速度往水槽中注水,时注满水槽,水槽内水面的高度与注水时间之间的函数图像如图2所示.如果将正方体铁块取出,又经过 秒恰好将水槽注满.
21.甲、乙两人赛跑,路程s(m)与时间t(s)之间的关系如图所示,则下列说法正确的是 .(填序号)
(1)两人赛跑的路程是100m
(2)甲先到达终点
(3)甲跑的平均速度比乙跑的平均速度快0.5m/s
(4)乙跑的平均速度是8m/s
22.张大妈购进一批柚子,在集贸市场零售,已知卖出的柚子重量x(kg)与售价y(元)之间的关系如下表:
重量/kg 1 2 3 …
售价/元 1.2+0.1 2.4+0.1 3.6+0.1 …
根据表中数据可知,若卖出柚子10kg,则售价为 元.
23.如图所示的计算程序中,y与x之间的关系式是 .
24.深圳市出租车的收费标准是起步价10元(行程小于或等于2千米),超过2千米每增加1千米(不足1千米按1千米计算)加收元,小鸣从深圳市体育中心打车去深圳图书馆,百度地图显示行程约为千米,则出租车费约为 元.
25.某地市话的话费y(元)随着时间x(分钟)的变化而变化,收费标准为:
(1)通话时间在3分钟以内(包括3分钟)话费元;
(2)通话时间超过3分钟时,超过部分的话费按每分钟元计算.
在一次通话中,如果通话时间8分钟,那么话费y(元)为 (元).
26.我国首辆火星车正式被命名为:“祝融”,为应对极限温度环境,火星车使用的是新型隔温材料——纳米气凝胶,该材料导热率\与温度的关系如表:
温度
导热率
根据表格中两者的对应关系,若导热率为,则温度为 .
三、解答题
27.某新型品牌充电器给手机充电时充电速度是匀速的,一台手机屏幕画面显示初始电量为,其电量y(单位:%)与充电时间x(单位:h)为表格中几组对应值.根据以上信息,回答下列问题:充电时间
充电时间x(单位:h) 0 n
电量y(单位:%) 20 m 40 60 80
(1)______,______;
(2)该手机充电直至电量达到需要多久?
28.已知甲乙两地相距,一辆轿车从甲地出发往返于甲乙两地,一辆货车匀速沿同一条路线从乙地前往甲地,两车同时出发,经过后两车第一次相遇.轿车到达乙地后立即按原路返回,结果比货车早一个小时到达甲地.如图是两车距各自出发地的距离y()与货车行驶时间x(h)之间的函数图象,结合图象回答下列问题:
(1)图中a的值是______;
(2)求轿车到达乙地再返回甲地所花费的时间;
(3)轿车在返回甲地的过程中与货车相距,直接写出货车已经从乙地出发了多长时间?
29.如图,,两地相距50千米,甲于某日下午1时骑自行车从地出发骑往地,图中的折线和线段分别表示甲与乙所行驶的路程和时间的关系.根据图象回答下列问题:
(1)甲出发______小时,乙才开始出发;
(2)乙比甲早到______小时;
(3)甲从下午2时到5时的平均速度是______千米/小时;乙的平均速度是______千米/小时;
(4)请你根据图象上的数据,求乙出发后用多长时间就追上甲?
30.小明从家出发骑自行车去上学,当他以往常的速度骑了一段路后,突然想起要买文具,于是又折回到刚经过的文具店,买到文具后继续骑车去学校.如图是他本次上学所用的时间与离家的距离之间的关系图,根据图中提供的信息回答下列问题:
(1)小明家到学校的距离是____ 米,文具店到学校的距离是____米 ;
(2)小明在文具店停留了____分钟,本次上学途中,小明一共行驶了____米 ;
(3)观察图象,请编制一道新的问题并给出解答过程.
31.小明晚饭后外出散步,碰见同学,交谈一会,返回途中在读报栏看了一会报.如图是根据此情景画出的图象,请你回答下列问题:
(1)小明碰见同学后交谈了______分钟.
(2)读报栏离家______米.
(3)小明出发15分钟后离家______米.
(4)小明出发______分钟后离家500米.
32.某机动车出发前油箱内有油48L.行驶若干小时后,途中在加油站加油若干升.油箱中剩余油量与行驶时间之间的关系如图所示,根据图象回答下列问题.
(1)在这个变化过程中,____________是自变量,______________是因变量;
(2)机动车行驶___________小时后加油,中途加油__________L;
(3)如果加油站距目的地还有360km,车速为,要到达目的地,请判断油箱中的油是否够用,并说明理由.
33.如图反映的是小华从家里跑步去体育馆,在那里锻炼了一段时间后又走到文具店去买笔,然后散步回家,其中(分)表示时间,(千米)表示小华离家的距离.根据图象回答下列问题:
(1)体育馆距离小华家__________千米,小华在体育馆锻炼了__________分钟;
(2)体育馆距离文具店__________千米,小华在文具店买笔用了__________分钟;
(3)小华从家跑步到体育馆,从文具店散步回家的速度分别是多少千米/小时?
34.【问题背景】如图①,“漏刻”是我国古代一种利用水流计时的工具,古诗“金炉香尽漏声残,翦翦轻风阵阵寒”,描绘了“漏刻”不断漏水的情景.如图②,小明用甲、乙两个透明的竖直放置的容器和一根装有节流阀(控制水的流速)的软管,制作了类似“漏刻”的简易计时装置.
【实践操作】上午9:00,小明在甲容器里加满水,此时水面高度为,开始放水后,小明每隔记录一次甲容器中的水面高度,相关数据如表:
记录时间 9:00 9:10 9:20 9:30 9:40
流水时间 0 10 20 30 40
水面高度 30 29.5 29 28.5 28
【问题解决】
(1)下列图像可以大致反映水面高度随时间变化而变化的是__________.(填序号)
(2)由表中数据可知,流水时间每隔,甲容器中的水面高度下降__________,据此规律,10:10时水面高度应为__________.
(3)请你直接写出水面高度与流水时间的关系式__________.
35.自行车是很多同学家校往返的重要交通工具,如图,某款自行车每节链条的长度为,交叉重叠部分的圆的直径为.
(1)观察图形填写下表:
链条节数(节) 2 3 4
链条长度()
(2)如果节链条的总长度是,求与之间的关系式;
(3)晓明同学的同款自行车链条生锈断了,需要在淘宝网上采购并自行安装,该型号自行车的链条(安装前)由90节这样的链条组成,那么晓明需要购买该型号链条的总长度是多少?实际安装长度是多少?
36.甲骑电动车,乙骑自行车从深圳湾公园门口出发沿同一路线匀速游玩,设乙行驶的时间为,甲、乙两人距出发点的路程、关于x的函数图象如图①所示,甲、乙两人之间的路程差y关于x的函数图象如图②所示,请你解决以下问题:
(1)甲的速度是______km/h,乙的速度是______km/h;
(2)对比图①、图②可知______,______;
(3)乙出发多少时间,甲、乙两人路程差为7.5km?
37.某车间甲、乙两名工人分别同时开始生产同种试剂,图中的折线和折线表示他们一天生产试剂y(克)与生产时间t(小时)的关系,工人甲因机器故障停止生产了一段时间,修好机器后速度提高到每小时生产10克试剂,结果还提前一小时完成了任务,请你根据图中给出的信息解决下列问题:
(1)折线表示_________(填“甲”或“乙”)工人生产试剂与生产时间的关系,乙这一天共生产__________克试剂;
(2)工人乙起初每小时生产__________克试剂;
(3)求工人甲中间停下修机器所用时间为__________小时;
(4)请列式计算,甲、乙两名工人何时加工的试剂一样多?
38.在“看图说故事”活动中,某学习小组结合图象设计了一个问题情境.已知小亮所在学校的教学楼、图书馆、食堂依次在同一条直线上,图书馆离教学楼,食堂离教学楼.某日中午,小亮从教学楼出发,匀速走了(分钟)到图书馆;在图书馆停留借书后,匀速走了到食堂;在食堂停留吃完饭后,匀速走了返回教学楼.给出的图象反映了这个过程中小亮离教学楼的距离与离开教学楼的时间之间的对应关系.请根据相关信息,解答下列问题:
(1)图中自变量是________,因变量是________;小亮从教学楼到图书馆的速度为________,小亮从图书馆到食堂的速度为________;
(2)填表:
离开教学楼的时间/ 2 20 25 30
离教学楼的距离/ ________ 700 ________ ________
(3)当小亮离开教学楼的时间为________时,他离教学楼的距离为.
参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D B C A C D A C D C
题号 11 12 13 14 15 16 17 18
答案 D B D B C C C B
1.D
【分析】根据已知信息和函数图象的数据,依次解答每个选项.
【详解】解:由图象可知,小华和小明的家离学校1200米,故A正确;
根据图象,小华乘公共汽车,从出发到到达学校共用了(分钟),所以公共汽车的速度为(米/分),故B正确;
小明先出发8分钟然后停下来吃早餐,由图象可知在小明吃早餐的过程中,小华出发并与小明相遇然后超过小明,所以二人相遇所用的时间是(分钟),即7:50相遇,故C正确;
小明从家到学校的时间为20分钟,所以小明的平均速度为(米/分),故D错误.
故选:D.
【点睛】此题考查一次函数的实际应用,正确理解函数图象,掌握行程问题中时间、速度、路程之间的关系是解题的关键.
2.B
【分析】根据函数的定义,一次函数的解析式,k的意义,计算即可,本题考查了函数的定义,一次函数的解析式,熟练掌握待定系数法是解题的关键.
【详解】A. x与y都是变量,且x是自变量,y是因变量,正确;不符合题意;
B. 弹簧不挂重物时的长度为,错误,符合题意;
C. 当时,物体质量每增加,弹簧长度y增加,正确;不符合题意;
D. 当时,x与y满足的关系式是,正确;不符合题意;
故选B.
3.C
【分析】横轴代表时间,纵轴代表行驶的路程,利用图象判断相应的路程和时间,再结合速度路程时间,逐项分析,即可得到答案.
【详解】解:A、由图象可以看出,最远处到达距离出发地120千米处,但又返回原地,所以行驶的路程为240千米,原说法错误,不符合题意,选项错误;
B、平均速度总路程总时间,总路程为240千米,总时间为小时,所以平均速度为千米/时,原说法错误,不符合题意,选项错误;
C、汽车返回所用的时间是小时,则平均速度为:千米/时,原说法正确,符合题意,选项正确;
D、汽车自出发后1.5小时至2小时之间静止不动,原说法错误,不符合题意,选项错误;
故选:C.
【点睛】本题考查了利用函数的图象解决实际问题,解题关键是正确理解函数图象横纵坐标表示的意义,理解问题的过程,熟练掌握速度路程时间.
4.A
【分析】设弹跳高度为,下落高度为,根据题意和表格数据,可以得出,然后将下落高度为180厘米代入求解即可.
【详解】解:设弹跳高度为,下落高度为,
由表格数据可知,弹跳高度是下落高度的一半,即,
∴当时,.
故选:A.
【点睛】本题主要考查根据实际问题列一次函数的解析式,根据题意和表格数据得出正比例函数解析式是解题的关键.
5.C
【分析】先观察容器的形状,再分析水面上升的速度,据此选择合适的函数图像即可.
【详解】解:因为圆柱上下一样粗,所以水面上升的高度h随注水时间t的增大而匀速增大.
故选:C.
【点睛】本题主要考查函数图像的知识,根据h随t的变化情况判断相应的函数图像是解决本题的关键.
6.D
【分析】根据自变量、因变量的定义,以及声音在空气中传播的速度与空气温度关系逐一判断即可.
【详解】解:∵在这个变化中,自变量是温度,因变量是声速,
∴选项A说法正确,不符合题意;
∵根据数据表,可得温度越低,声速越慢,温度越高,声速越快,
∴选项B说法正确,不符合题意;
由列表可知,当空气温度为时,声速为,
∴选项C说法正确,不符合题意;
∵ , , , , ,
∴当温度每升高,声速增加,
∴选项D说法不正确,符合题意.
故选D.
【点睛】本题主要考查了自变量,因变量.熟练掌握自变量、因变量的定义是解题的关键.在一个变化过程种,如果有两个变量x和y,对于x的每一个确定的值,y都有唯一确定的值与其对应,那么x是自变量,y是因变量.
7.A
【分析】本题需要根据已知条件,确定出每一步的函数图像,再把函数图像结合起来即可得到答案.
【详解】解:∵小明从家步行到书店,
∴随着时间的增加离家的距离越来越远,
∵到达书店后,他在那里看了会书,
∴在书店的这段时间,他离家的距离不变,
又∵再跑步回家,
∴这段时间,他离家越来越近,而且跑步回家比步行到书店用的时间少,
∴能反映小明离家距离y与所用时间x之间关系的图像是A,
故选A.
【点睛】本题主要考查了函数图像的识别,解题的关键在于能够根据实际情况进行分析每一个过程.
8.C
【分析】根据表格数据,设弹簧长度y与所挂物体重量x的关系式为,进而求得关系式,令即可求得弹簧不挂物体时的长度.
【详解】设弹簧长度y与所挂物体重量x的关系式为,
将,分别代入得,
解得
即,
将,分别代入,符合关系式,
当时,则,
故选C.
【点睛】本题考查了变量与表格,函数关系式,找到关系式是解题的关键.
9.D
【分析】根据图象可得甲车行驶的速度是,再由甲先出发1h,乙出发3h后追上甲,可得到乙车行驶的速度是80km/h;根据图象可得当乙到达B地时,甲乙相距100km,从而得到甲比乙晚到h;然后分两种情况:当乙车在甲车前,且未到达B地时和当乙车到达B地后时甲,乙两车相距80km,进行求解判断即可.
【详解】解:由图可得,甲车行驶的速度是
根据图象可知:甲先出发1h,甲出发4h后被乙追上,
∴,
∴
即乙车行驶的速度是80km/h,故选项A,B正确;
由图可得,当乙到达B地时,甲乙相距100km,
∴甲比乙晚到h,故选项C正确;
由图可得,当乙车在甲车前,且未到达B地时,则,
解得:,
当乙车到达B地后时,,
解得:,
∴甲车行驶8h或h,甲,乙两车相距80km,故选项D错误.
故选:D.
【点睛】本题主要考查了函数的图象、能从函数图象的获取准确信息和灵活利用数形结合思想解答是解题的关键.
10.C
【分析】根据题意,列出一元一次方程,即可得到答案.
【详解】解:根据题意,得
;
∴与间的函数表达式为:;
故选:C.
【点睛】本题考查了一元一次方程的应用,解题的关键是熟练掌握题意,正确列出一元一次方程.
11.D
【分析】根据函数图象,列出关于a,b的方程,求出a,b的值,从而即可逐一判断各个选项.
【详解】解:根据图象可知,(300-a)÷b=(240-a)÷3=a÷1,
解得:a=60,b=4,
甲车的速度=60÷1=60km/h,乙车的速度=300÷3=100km/h,
故A,B正确,不符合题意;
∵60÷(100-60)=1.5,1.5×100=150km,
∴乙车出发1.5小时后追上甲车,甲、乙两车相遇时,两车距离A地150km,
故C正确,不符合题意,D错误,符合题意,
故选D.
【点睛】本题考查了一次函数的应用,理解函数图象以及分别求出甲、乙两人的速度是解题的关键.
12.B
【分析】根据表格得出函数的相关性质即可.
【详解】解:A.在没挂物体时,弹簧的长度为,根据图表,当质量时,,故此选项正确,不符合题意;
B、反映了所挂物体的质量和弹簧的长度之间的关系,所挂物体的质量是自变量;弹簧的长度是因变量,故此选项错误,符合题意;
C.在弹簧能承受的范围内,所挂物体的质量每增加,弹簧的长度就增加,故此选项正确,不符合题意;
D、由C中,,解得,在弹簧的弹性范围内,故此选项正确,不符合题意;
故选:B.
【点睛】题目主要考查函数的基本知识点,根据表格得出相关信息是解题关键.
13.D
【分析】根据题意结合图象得出AB、BC的长度,再求出面积即可.
【详解】由题意可知,当点P从点A运动到点B时,△PCD的面积为:,即△PCD的面积不变,则结合图象可知AB=6,
当点P从点B运动到点C时,△PCD的面积逐渐变小直到为0,
即结合图象可知BC=x-AB=9-6=3,
∴长方形ABCD的面积为:AB BC=6×3=18.
故选:D.
【点睛】本题考查了动点问题的函数图象,能根据图形得出正确信息是解此题的关键.
14.B
【分析】本题考查了函数关系式,解题的关键是对关系式进行化简,得到y与x的函数关系式.根据题意把x千米分成3千米和千米两部分,再根据单价乘里程表示出关系式,再化简即可.
【详解】解:当时,
,
故选:B.
15.C
【分析】本题考查函数的表示方法;能够通过表格观察自变量和因变量的变化情况是解题的关键.
根据表格数据分析通过表格观察随着时间的变化,飞行高度是先增加后减少,并且在3秒的两侧对称,从表格可以看到0秒到3秒的过程中,随着飞行时间的增加飞行高度增加,再逐项判断即可.
【详解】通过表格观察随着时间的变化,飞行高度是先增加后减少,并且在3秒的两侧对称,从表格可以看到0秒到3秒的过程中,随着飞行时间的增加飞行高度增加;
从3秒以后,随着飞行时间的增加,飞行高度减小;
因此,A与B选项不正确;
从表格看到飞行高度在3秒左右是对称的,所以C选项正确;
从0秒到2秒花弹飞行的高度是米,所以D不正确.
故选:C.
16.C
【分析】本题考查了函数图象,解题的关键在于数形结合,从图象中获取正确的信息.根据图象可得深广两地的距离为,可判断A;再根据路程除以时间可求出甲的速度,可判断B;然后求出甲乙相遇的时间,可求出乙的速度,从而判断C,D.
【详解】解:由图象得:深广两地的距离为,故A正确,故不符合题意;
甲的速度为,故B正确,故不符合题意;
甲乙相遇的时间为,则乙的速度为,故C错误,故符合题意;
乙运动到达深圳所用时间为,故D正确,不符合题意;
故选:C
17.C
【分析】本题考查了函数的图象.正确理解函数图象横纵坐标表示的意义,理解问题的过程,能够通过图象得到函数是随自变量的增大,知道函数值是增大还是减小.根据题意判断出小烧杯、大烧杯的液面高度随时间的变化情况即可.
【详解】解:大烧杯的底面半径是小烧杯的底面半径的2倍,
小烧杯的容积是大烧杯与小烧杯顶部齐平时下部容积的,
注满小烧杯的所需时间是大烧杯下部注水时间的,
小烧杯、大烧杯内水面的高度差随加水时间变化的图象可能是选项C.
故选:C
18.B
【分析】本题考查了动点问题的函数图象.根据的面积只与点P的位置有关,结合图2求出长方形的长和宽,再由长方形的周长公式计算即可.
【详解】解:根据题意得:动点P从点B出发,沿、、运动至点A停止,
当点P在点B,C之间运动时,根据运动速度为,可得,
的面积,
由图2得,当时,点P由B点到达点C处,
∴;
当点P运动到点C,D之间时,
的面积,保持不变,
由图2得,点P从点C运动到点D所用时间为,
∴,
∴长方形的周长:.
故选:B.
19.气温
【分析】本题考查函数的定义.设在某变化过程中有两个变量,如果对于在某一范围内的每一个确定的值,都有唯一确定的值与它对应,那么就称是的函数,叫做自变量.
【详解】解:根据题意,随着气温下降,人们开始增添衣服,在这个问题中,自变量是气温.
故答案为:气温.
20.4
【分析】根据函数图像可得正方体的棱长为10cm,同时可得水面上升从10cm到20cm,所用的时间为16秒,结合前12秒由于立方体的存在,导致水面上升速度加快了4秒可得答案.
【详解】解:由题意可得:12秒时,水槽内水面的高度为10cm,12秒后水槽内水面高度变化趋势改变,正方体的棱长为10cm;
没有立方体时,水面上升从10cm到20cm,所用的时间为:28-12=16秒
前12秒由于立方体的存在,导致水面上升速度加快了4秒
将正方体铁块取出, 又经过4秒恰好将此水槽注满.
故答案:4
【点睛】本题主要考查一次函数的图像及应用,根据函数图像读懂信息是解题的关键.
21.(1)(2)(4)
【分析】根据函数图象逐项分析判断即可求解.
【详解】解:(1)两人赛跑的路程是100m,故(1)正确;
(2)甲先到达终点,故(2)正确;
(3)甲跑的平均速度为 m/s,乙跑的平均速度为m/s,
甲跑的平均速度比乙跑的平均速度快m/s,故(3)不正确,
(4)乙跑的平均速度是8m/s,正确.
故答案为:(1)(2)(4).
【点睛】本题考查了函数图象,从函数图象获取信息是解题的关键.
22.12.1
【分析】根据表格求出的对应关系即可求解.
【详解】当时,,
当时,,
当时,,
,
当时,,
故答案为:12.1.
【点睛】本题考查了函数的表示方法,能够根据题意列出的表达式是解题关键.
23.
【分析】根据程序框图列出正确的关系式即可得解.
【详解】解:根据程序框图可得 ;
故答案为:.
【点睛】本题考查根据程序框图列关系式,解题的关键是按照运算顺序准确列出关系式.
24.
【分析】本题主要考查有理数的混合运算的应用,根据题意、正确列出算式是正确解答的前提.
根据题意、正确列出算式,然后再计算即可.
【详解】解:由题意可知:当时,出租车费约为.
故答案为:.
25.
【分析】本题主要考查了求函数值,根据所给的收费标准列式计算即可.
【详解】解:由题意得,,
故答案为:.
26.
【分析】根据表格中两个变量、的对应值以及变化规律可得答案.
【详解】解:根据题意,温度每增加,导热率增加,
所以当导热率为时,温度为.
故答案为:.
【点睛】本题考查函数及其表示方法,理解函数的意义以及变量之间的变化规律是正确解答的关键.
27.(1)30;1
(2)2小时
【分析】本题考查一次函数的应用,解题的关键是读懂题意,能正确识图.
(1)用待定系数法可得函数关系式,即可解答;
(2)根据,列方程求解即可.
【详解】(1)∵充电器给手机充电时充电速度是匀速的,
∴设其电量y与充电时间x对应的函数表达式为,
将代入得:
,
解得,
∴函数表达式为;
当时,,
当时,,,
故答案为:30;1;
(2)当时,,
解得,
故该手机充电直至电量达到需要2h.
28.(1)90
(2)7小时
(3)或
【分析】本题考查一次函数的应用,解题的关键是读懂题意,能正确识图.
(1)用待定系数法可得函数关系式,即可求解;
(2)根据两车同时出发,经过后两车第一次相遇,列方程求货车的速度即可解答.
(3)分两种情况分别计算即可;
【详解】(1)由图象知,,
设直线的解析式为,把代入得,,
解得,
∴直线的解析式为;
把代入,得,
故答案为:90;
(2)轿车的速度千米/小时,
∵两车同时出发,经过后两车第一次相遇,
设货车的速度为v千米/小时,
则,
解得,
故货车从乙地到甲地共用时小时,
∵轿车比货车早一个小时到达甲地,
∴轿车到达乙地再返回甲地所花费的时间小时.
(3)由(2)得,,
货车的速度千米/小时,
轿车在返回甲地的过程中所花费的时间小时,则返回甲地的过程中的速度千米/小时,
设轿车在返回甲地的过程中与货车相距时,货车已经从乙地出发了,
返回时当轿车在货车前时:
解得:,
返回时当货车在轿车前时:
解得:,
故轿车在返回甲地的过程中与货车相距时,货车已经从乙地出发了或.
29.(1)1;(2)2;(3)10;50;(4)0.5小时
【分析】(1)由图象横轴上的甲、乙出发时间即可解答;
(2)由甲、乙到达B的时间即可解答;
(3)根据速度=路程÷时间求解即可;
(4)设乙出发后x小时就追上甲,根据(3)中求得速度结合图象列方程求解即可.
【详解】解:(1)由图象知,甲下午1时出发,乙下午2时出发,
∴甲出发1小时,乙才开始出发,
故答案为:1;
(2)由图象知,甲下午5时到达B地,乙下午3时到达B地,
∴乙比甲早到2小时,
故答案为:2;
(3)根据图象,甲从下午2时到5时的平均速度是(50﹣20)÷(5﹣2)=10千米/小时,乙的平均速度是50÷(3﹣2)=50千米/小时,
故答案为:10;50;
(3)设乙出发后用小时就追上了甲,
根据题意,得,
解得
答:乙出发0.5小时就追上甲.
【点睛】本题考查函数的图象、一元一次方程的应用,解答的关键是正确获取图象上的有关信息解决问题.
30.(1),;
(2),;
(3)见解析.
【分析】()根据题意和函数图象即可求解;
()根据题意和函数图象即可求解;
()根据函数图象提出合理问题并解答即可;
本题考查了函数图象,看懂函数图象是解题的关键.
【详解】(1)解:由题意和函数图象可得,小明家到学校的距离是米,
文具店到学校的距离是米,
故答案为:,;
(2)解:由函数图象可得,小明在文具店停留了分钟,
本次上学途中,小明一共行驶了米,
故答案为:,;
(3)解:自编第三问:如图,若小明不买文具,以往常的速度去学校,需要花费多长时间?
小明往常的速度为米/分,
去学校需要花费的时间为分钟,
答:小明不买文具以往常的速度去学校需要分钟.
31.(1)10
(2)400
(3)600
(4)或
【分析】本题考查一次函数的应用,掌握速度、时间、路程三者之间的数量关系和待定系数法求函数关系式是解题的关键.
(1)观察图象直接作答即可;
(2)观察图象直接作答即可;
(3)根据“速度路程时间”求出当时小明的速度,再根据“路程速度时间”求出小明出发15分钟后离家的距离;
(4)分别根据“路程速度时间”和待定系数法求出和时的y与x的函数关系式,分别将代入,求出对应x的值即可.
【详解】(1)解:(分钟),
∴小明碰见同学后交谈了10分钟.
故答案为:10;
(2)根据图象可知,读报栏离家400米.
故答案为:400;
(3)当时,小明的速度为(米/分),
则小明出发15分钟后离家的距离为(米).
故答案为:600;
(4)当时,y与t的关系式为,
当时,解得;
当时,设y与t的关系式为(k、b为常数,且).
将坐标和代入,
得,
解得,
∴y与t的关系式为,当时,解得.
综上,小明出发或分钟后离家500米.
故答案为:或.
32.(1)行驶时间,剩余油量
(2),
(3)不够用,理由见解析
【分析】(1)根据函数的定义直接求解即可;
(2)根据函数图象直接求解即可;
(3)根据函数图象可知机动车的耗油量为,根据行驶时间乘以耗油量即可求解
【详解】(1)根据题意可知:行驶时间是自变量,剩余油量是因变量;
故答案为:行驶时间,剩余油量
(2)根据函数图象可知,机动车行驶小时后加油,中途加油
故答案为:,
(3)不够用.理由如下:
机动车的耗油量:,
行驶时间,需要油量,
故不够用.
【点睛】本题考查了函数的定义,函数图象,根据函数图象获取信息是解题的关键.
33.(1)2.5;15
(2)1;20
(3)小华从家跑步到体育场的速度为10千米/小时;小华从文具店散步回家的速度为千米/小时
【分析】本题考查了函数图象,正确理解函数图象横纵坐标表示的意义,理解问题的过程,就能够通过图象得到函数问题的相应解决.需注意计算单位的统一.
(1)根据观察函数图象的纵坐标,可得距离,观察函数图象的横坐标,可得时间;
(2)根据观察函数图象的横坐标,可得体育馆与文具店的距离,观察函数图象的横坐标,可得在文具店停留的时间;
(3)根据观察函数图象的纵坐标,可得路程,根据观察函数图象的横坐标,可得回家的时间,根据路程与时间的关系,可得答案.
【详解】(1)解:(1)由纵坐标看出体育馆距离小华家2.5千米,由横坐标看出小华在体育馆锻炼了15分钟;
故答案为:2.5;15.
(2)解:由纵坐标看出体育馆距离文具店(千米),由横坐标看出小华在文具店买笔用了(分).
故答案为:1;20.
(3)解:小华从家跑步到体育馆的速度为(千米小时),
小华从文具店散步回家的平均速度是(千米/小时).
答:小华从家跑步到体育场的速度为10千米/小时;小华从文具店散步回家的速度为千米/小时.
34.(1)②
(2),
(3)
【分析】本题考查了一次函数的应用,求一次函数解析式,判断一次函数图像,根据表格中的数据写出函数关系式,是解答本题的关键.
(1)由表格中的数据直接判断即可;
(2)由表格中的数据直接判断即可;
(3)根据(2),求出甲容器中水面每分钟下降的高度,再根据甲容器中的高度甲容器中开始的水面高度甲容器中水面高度每分钟下降的距离流水时间,即可写出函数关系式.
【详解】(1)解:由表格可知,水面高度随时间而降低,即该函数为减函数,而且流水时间不会小于0,水面高度流到最后,管口以下流不净,也就是y的值不会为零,
故答案为:②;
由表格数据可知,流水时间每隔,甲容器中的水面高度下降,
∵距离为,
(2)∴时水面高度应为,
故答案为:,;
(3)由(2)可知,甲容器中的水面高度每分钟下降,
,
故答案为:.
35.(1)
(2)
(3),
【分析】此题主要考查了函数关系式,根据题意得出节链条的长度与每节长度之间的关系是解决问题的关键.
(1)根据图形找出规律计算4节链条的长度即可;
(2)由(1)写出表示链条节数的一般式;
(3)根据(2)计算时,特别注意自行车上的链条为环形,在展直的基础上还要缩短.
【详解】(1)解:根据图形可得出:
2节链条的长度为:,
3节链条的长度为:,
4节链条的长度为:.
故答案为:;
(2)由(1)可得节链条长为:;
∴与之间的关系式为:;
(3)当.
故晓明需要购买该型号链条的总长度是;
因为自行车上的链条为环形,在展直的基础上还要缩短,
故这辆自行车链条的总长为厘米,
所以90节这样的链条总长度是117厘米.
36.(1)25,10
(2)10,1.5
(3)或
【分析】(1)根据题意和函数图象中的数据可以求得甲乙的速度;
(2)根据题意和图象中的数据,可以分别得到、的值;
(3)由图象可知甲乙相距有两种情况,然后分别计算两种情况下乙出发的时间即可解答本题.
【详解】(1)解:由图可得,
甲的速度为:,乙的速度为:,
故答案为:25,10;
(2)解:由图可得,
,
,
故答案为:10;1.5;
(3)解:由题意可得,
前,乙行驶的路程为:,
则甲、乙两人路程差为是在甲乙相遇之后,
设乙出发时,甲、乙两人路程差为,
,
解得,,
,得;
即乙出发或时,甲、乙两人路程差为.
【点睛】本题主要考查函数图象,解题的关键是由函数图象得到解题的信息.
37.(1)甲,40;
(2)2;
(3)3;
(4)3或.
【分析】本题考查了一次函数的应用,函数图象,明确题意,利用一次函数的性质和数形结合思想是解题的关键.
(1)根据题意结合图象可得答案;
(2)用“工作效率工作总量工作时间”可得答案;
(3)根据函数图象可以解答本题;
(4)根据函数图象和图象中的数据可以求得甲乙对应的函数解析式,从而可以解答本题.
【详解】(1)解:由题意可知,折线表示甲工人生产试剂与生产时间的关系,乙这一天共生产克试剂.
故答案为:甲;;
(2)解:乙起初每小时生产试剂:(克).
故答案为:;
(3)解:在生产过程中,甲因机器故障停止生产(小时),
(4)当时,乙对应的函数解析式为,
,
解得,
即当时,乙对应的函数解析式为,
设当,甲对应的函数解析式为,
,
解得,
即当,甲对应的函数解析式为,
令,得,
当时,得,
即当为或时,甲、乙两人生产的零件个数相等.
38.(1)小亮离开教学楼的时间,小亮离教学楼的距离,100,60
(2)200,820,1000
(3)或
【分析】(1)根据函数的定义,以及速度、路程、时间的关系即可求解;
(2)根据题意和函数图象,可以将表格补充完整;
(3)分两种情况,根据函数图象中的数据,求出当时,当时,小亮离教学楼的距离为时,求他离开教学楼的时间即可.
【详解】(1)解:图中自变量是小亮离开教学楼的时间,因变量是小亮离教学楼的距离;
小亮从教学楼到图书馆的速度为,
小亮从图书馆到食堂的速度为;
(2)解:当时,离教学楼的距离为,
当时,离教学楼的距离为,
在时,距离不变,都是,
故当时,离教学楼的距离为,
(3)解:小亮离教学楼的距离为时,
有两种情况,
①当时,
∵在前7分钟的速度为,
∴当小亮离教学楼的距离为时,他离开教学楼的时间为,
当时,
小亮离教学楼的距离为时,他离开教学楼的时间为,
∴当小亮离教学楼的距离为600m时,求他离开教学楼的时间或.
【点睛】本题考查一次函数的应用,解答本题的关键是明确题意,利用数形结合的思想解答.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
