数学(提升卷02)-2024-2025学年六年级数学下学期期中素养测评(北京版)(含解析)
文档属性
| 名称 | 数学(提升卷02)-2024-2025学年六年级数学下学期期中素养测评(北京版)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 295.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北京版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-11 05:43:52 | ||
图片预览




文档简介
保密★启用前
2024-2025学年六年级数学下学期期中素养测评(北京版)
【学易金卷·提升卷02】
考试分数:100分;考试时间:90分钟
注意事项:
1.答题前,填写好自己的姓名、班级、考号等信息,请写在答题卡规定的位置上。
2.选择题、判断题必须使用2B铅笔填涂答案,非选择、判断题必须使用黑色墨迹签字笔或钢笔答题,请将答案填写在答题卡规定的位置上。
3.所有题目必须在答题卡上作答,在试卷上作答无效。
4.考试结束后将试卷和答题卡一并交回。
一、选择题(共10分)
1.下面四句话中,正确的一句是( )
A.北京某天的气温是﹣3℃至8℃,这天的温差是5℃
B.圆锥的体积一定,底面半径和高成反比例
C.2、3、8、5、2、6、7、2这八个数的中位数是3.5
2.表示两个比相等的式子叫作( )。
A.等式 B.比例 C.方程
3.将直角三角形ABC的AB轴旋转一周,得到的圆锥体积是V,那么V=( ).
A.12π B.25π C.36π D.48π
4.甲、乙是两个成反比例的量,当甲减少20%时,乙( )。
A.增加20% B.减少20% C.增加25% D.减少25%
5.如果a和b成反比例,b和c成反比例,那么a和c( )。(a、b、c均不为0)
A.成正比例 B.成反比例 C.不成比例
二、填空题(共17分)
6.把2∶0.75化成最简单的整数比是( ).
7.圆锥的底面是一个( ),侧面是一个( )。从圆锥的顶点到底面圆心的距离是圆锥的( )。
8.如表,如果x和y成正比例关系,“?”处应填( );如果x和y成反比例关系,“?”处应填( )。
x 3 ?
y 12 24
9.0.75=18÷( )( )∶44=( )%。
10.甲数的和乙数的相等,甲和乙数的最简整数比是( ):( ).
11.一个圆柱形水桶的直径是4分米,放在地上,它的占地面积为( ).
12.出油率一定,香油质量与芝麻质量成( )比例.
13.在比例尺为1:2000000的这个地图上,量得北京到郑州的距离是32厘米;把它画在比例尺为的地图上.应画( )厘米.
14.如图,一根长2米的圆柱形木料,截去一半后,剩下的圆柱形木料的表面积比原来减少了62.8平方分米,原来圆柱形木料的底面积是( )平方分米,体积是( )立方分米。
15.一个数与比它小4的数的比值,化简后是 ,你知道这个数是( )吗?
16.一个圆柱(如图),过底面圆心沿高切开后,表面积会增加60平方厘米,已知圆柱的高是5厘米,那么这个圆柱的表面积是( )平方厘米。(取3.14)
三、判断题(共6分)
17.3:4和 ∶可以组成比例. ( )
18.一个圆柱体有无数条高。( )
19.a∶b=2∶5,那么a一定等于2。( )
20.若A的等于B的(A、B均不为0),则A∶B=4∶5. ( )
21.下面题中的两个量是不是成反比例?
平行四边形的面积一定,底和高。 ( )
22.一个圆锥的底面半径和高相等,过顶点和直径把这个圆锥切开,切面一定是等腰直角三角形。( )
四、计算题(共14分)
23.直接写出得数。(共8分)
= ×0.36= ×1×= =
= 16÷= 0.8∶= ∶=
24.解方程。(共6分)
五、作图题(共3分)
25.按3∶1的比画出下面长方形放大后的图形;再按照1∶2的比画出下面平行四边形缩小后的图形。
六、解答题(共50分)
26.榨油厂用100千克黄豆可以榨出13千克油,照这样计算,用5吨黄豆可以榨出多少吨油?
27.一个长方形的长8厘米,宽4厘米,以长方形的长为轴旋转一周得到一个立体图形,这个立体图形的底面积、侧面积各是多少?
28.用一张长12.56分米、宽5分米的长方形铁皮做一个圆柱体水桶的侧面。
(1)如果要使这个水桶的容积最大,那么它的高应是多少分米?
(2)再配一个底做成无盖的圆柱体水桶,至少还需要多少平方分米的铁皮?
29.一个圆锥形沙堆,底面周长是12.56米,高6米,将这些沙铺在宽10米的道路上铺4厘米厚,可以铺多少米长?
30.在如图所示的方格纸上画几个边长各不相同的正方形.
根据画出的正方形,把下表填写完整.
边长/cm 5 2
周长/cm 20 8
(2)正方形的周长与边长成正比例吗?为什么?
31.一间房子要用方砖铺地,用边长是4分米的方砖,需用96块,如果改用面积是20平方分米的方砖,需用多少块?(用比例解)
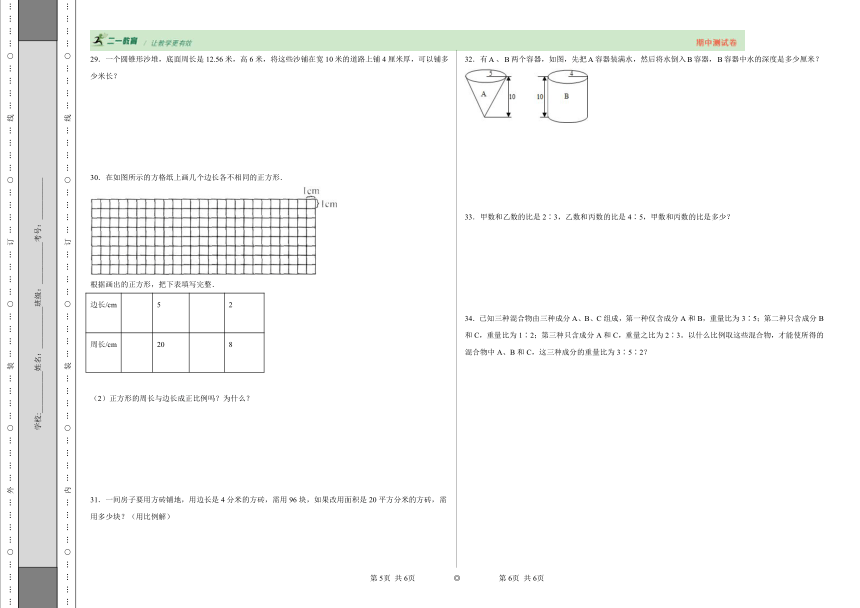
32.有、两个容器,如图,先把容器装满水,然后将水倒入容器,容器中水的深度是多少厘米?
33.甲数和乙数的比是2∶3,乙数和丙数的比是4∶5,甲数和丙数的比是多少?
34.已知三种混合物由三种成分A、B、C组成,第一种仅含成分A和B,重量比为3∶5;第二种只含成分B和C,重量比为1∶2;第三种只含成分A和C,重量之比为2∶3。以什么比例取这些混合物,才能使所得的混合物中A、B和C,这三种成分的重量比为3∶5∶2?
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
) (
学校:___________姓名:___________班级:___________考号:___________
) (
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
第1页 共4页 ◎ 第2页 共4页
第1页 共4页 ◎ 第2页 共4页
参考答案:
1.B
【详解】试题分析:(1)用最高气温减去最低气温,求出这天的温差是多少即可.
(2)根据圆锥的体积公式,判断出底面半径和高的乘积一定,所以圆锥的体积一定,底面半径和高成反比例,据此解答即可.
(3)根据中位数的求法判断即可.
解答:解:(1)因为8﹣(﹣3)=11(℃),
所以这天的温差是11℃,
所以选项A不正确.
(2)因为圆锥的体积=底面积×高÷3,
所以圆锥的体积一定时,底面半径和高的乘积一定,
所以圆锥的体积一定,底面半径和高成反比例,
所以选项B正确.
(3)2、3、8、5、2、6、7、2这八个数的中位数是:
(3+5)÷2=8÷2=4,
所以选项C不正确.
故选B.
点评:此题主要考查了正、负数的运算,辨别成正比例的量和成反比例的量的方法,以及中位数的含义和求法,要熟练掌握.
2.B
【解析】表示两个比相等的式子叫作比例,根据比例的定义直接选择。
【详解】表示两个比相等的式子叫作比例;
故答案选:B。
【点睛】本题考查的是比例的定义,构成比例的基本条件是两个比的比值相等。
3.A
【详解】根据圆锥的展开图特点可知,将直角三角形ABC以AB为轴旋转一周,得到的是一个底面半径为3,高为4的圆锥,由此利用圆锥的体积公式即可解答问题
解答:×π×3 ×4=×π×9×4=12π
4.C
【分析】甲和乙是两个成反比例的量,那么它们的乘积一定,即符合xy=k(一定),当甲减少20%时,可知乙一定是增加了,又(1-20%)x=x,由于k一定,所以这里的y得变为y,进而确定乙是增加了25%;
【详解】1-20%=,1÷=
(5-4)÷4=25%
故答案为:C
【点睛】此题考查正反比例意义的运用,解题时要明确成正比例的两个量是比值一定,成反比例的两个量是乘积一定。
5.A
6.8:3
【详解】试题分析:
点评:把0.75化为4分之三更简单些.
7. 圆 曲面 高
【详解】圆锥的底面是一个圆,侧面是一个曲面。从圆锥的顶点到底面圆心的距离是圆锥的高。
8. 6 1.5
【分析】如果x和y成正比例关系,则它们的比值一定,则3∶12=?∶24,据此求出?的值;如果x和y成反比例关系,则它们的乘积一定,则3×12=?×24,据此求出?的值。
【详解】3∶12=?∶24
解:12×?=3×24
?=6;
3×12=?×24
解:?×24=36
?=1.5
【点睛】明确两个相关联的量,如果比值一定则成正比例关系,如果乘积一定,则成反比例关系。
9. 24 33 75
【分析】把0.75化成分数并化简是,根据分数与除法的关系,再根据商不变的性质被除数、除数都乘6就是;根据比与分数的关系,再根据比的基本性质比的前、后项都乘11就是;把0.75的小数点向右移动两位添上百分号就是。
【详解】
故答案为:24;33;75
【点睛】此题主要是考查除法、小数、百分数、比之间的关系及转化,利用它们之间的关系和性质进行转化即可。
10.20,21.
【详解】试题分析:根据甲数的和乙数的相等,知道甲数×=乙数×,设乙数是1,即可表示出甲数,列式解答即可.
解:设乙数是1,
则甲数为:1×÷=,
甲数:乙数,
=:1,
=20:21;
点评:解答此题可以用假设法,还可以根据比例基本性质的逆运算进行解答.
11.12.56平方分米
【详解】试题分析:根据题干分析可得,此题就是求这个底面直径为4分米的底面圆的面积,据此利用圆的面积公式计算即可解答.
解:3.14×(4÷2)2,
=3.14×4,
=12.56(平方分米),
答:占地面积是12.56平方分米.
故答案为12.56平方分米.
点评:明确圆柱的占地面积就是圆柱的底面圆的面积,是解决本题的关键.
12.正.
【详解】试题分析:判断两种量成不成比例,成什么比例,就看这两种量是否是①相关联;②一种量变化,另一种量也随着变化,变化方向相同或相反;③对应的比值或乘积一定;如果这两种量相关联的量都是变量,且对应的比值一定,就成正比例;如果两种量相关联的量都是变量,且对应的乘积一定,就成反比例;如果是其它的量一定或乘积、比值不一定,就不成比例.
解:因为香油质量:芝麻质量=出油率(一定),是对应的比值一定,
所以香油质量与芝麻质量成正比例;
点评:此题属于根据正、反比例的意义,辨识两种相关联的量成不成比例,成什么比例,就看这两种量是否都是变量,且对应的比值一定,或是对应的乘积一定,再做出判断.
13.20
【详解】先求甲、乙两地间的实际距离,根据“图上距离÷比例尺=实际距离”,带入数值,计算出甲、乙两地间的实际距离,进而根据“实际距离×比例尺=图上距离”解答即可.
14. 3.14 62.8
【分析】减少的表面积就是截去一半圆柱的侧面积,根据底面周长=侧面积÷高,底面面积=(底面周长÷π÷2)2×π,体积=底面积×高,代入数据计算即可。
【详解】2÷2=1(米)
1米=10分米
62.8÷10÷3.14÷2
=6.28÷3.14÷2
=1(分米)
3.14×12=3.14(平方分米)
2米=20分米
3.14×20=62.8(立方分米)
【点睛】这是一道关于圆柱的题目,根据圆柱的侧面积和体积公式、圆的周长和面积公式解答。
15.16
16.150.72
【分析】将圆柱过底面圆心沿高切开,表面积增加了2个面,增加的2个面是长方形,这个长方形的长是底面直径,宽是圆柱的高。根据增加的表面积和圆柱的高,可以求出圆柱的底面直径和半径,然后再根据表面积公式求出圆柱的表面积。
【详解】底面半径是:(厘米)
表面积是:
(厘米)
【点睛】本题考查圆柱的表面积,弄清楚切开后表面积增加的是哪个部分是解决此题的关键。
17.错
【详解】判断两个比能不能组成比例,要看它们的比值是不是相等.
18.√
【分析】根据圆柱的高的概念圆柱两个底面之间的距离叫做圆柱的高,判断即可。
【详解】一个圆柱体有无数条高。
故答案为:√
【点睛】牢记圆柱有无数条高,圆锥只有一条高。
19.×
【分析】根据比例的意义∶表示两个比相等的式子,叫做比例;可知∶2∶5的比值是0.4(或),因为a、b都不知道具体的数值,只要a∶b=0.4即可,所以a的取值不固定;进而判断即可。
【详解】2∶5的比值是0.4(或 );
因为a、b都不知道具体的数值,只要a∶b=0.4即可,如∶当b=10,a=4;当b=15时,a=6;
故答案为错误。
【点睛】解答此类题的关键是∶理解比例的意义,能够灵活运用比例的意义解答实际问题。
20.√
【详解】略
21.底和高成反比例。因为底×高=平行四边形的面积(一定)。
【分析】根据平行四边形的面积公式判断出底和高的商(比值)一定还是乘积一定,如果商(比值)一定就成正比例,如果乘积一定就成反比例,否则不成比例。
【详解】略
22.√
【分析】圆锥纵切面是一个三角形,三角形的底是圆锥底面直径,三角形高是圆锥的高,如果圆锥的底面半径和高相等,纵切面如图,切面是一个等腰直角三角形。
【详解】根据分析,一个圆锥的底面半径和高相等,过顶点和直径把这个圆锥切开,切面一定是等腰直角三角形,说法正确。
故答案为:√
【点睛】关键是熟悉圆锥特征,想清楚纵切面和圆锥之间的关系。
23.2;0.14;1;
;20;1.6;
【详解】略
24.x=;x=;x=
【分析】第一题先计算3×0.9,将其转化为2x+2.7=24.7,再左右两边同时减去2.7,将其转化为2x=22,再左右两边同时除以2即可;
第二题根据比例的基本性质可知,再左右两边同时除以即可;
第三题左右两边同时乘0.25,将其转化为,再左右两边同时除以即可。
【详解】2x+3×0.9=24.7
解:2x+2.7=24.7
2x+2.7-2.7=24.7-2.7
2x=22
2x÷2=22÷2
x=11
解:
x=
解:
x=
25.见详解
【分析】根据图形放大与缩小的意义,把长方形的长和宽均扩大到原来的3倍,所得到的长方形就是原长方形按3:1放大后的图形.同理,把平行四边形的边长均缩小到原来的,对应角大小不变,所到得的平行四边形就是原平行四边形按1:2缩小后的图形。
【详解】3:1的比画出长方形放大后的图形(图中1所示),按1:2的比画出平行四边形缩小后的图形(图中2所示)。
【点睛】图形放大或缩小的倍数是指对应边放大或缩小的倍数,对应角大小不变;即图形放大或缩小后只是大小变了,形状不变。
26.x=0.65吨
【详解】略
27.50.24;200.96
【详解】试题分析:根据题意,以长方形的长为轴旋转一周得到一个以8厘米为高、4厘米为底面半径的圆柱体,圆柱体的底面积=πr2,圆柱的侧面积=底面周长×高,将数据代入公式进行计算即可得到答案.
解:立体图形的底面积为:3.14×42=50.24(平方厘米),
立体图形的侧面积为:3.14×4×2×8
=12.56×2×8,
=25.12×8,
=200.96(平方厘米),
答:这个立体图形的底面积是50.24平方厘米,侧面积是200.96平方厘米.
【点评】解答此题的关键是确定长方形旋转一周后得到的是什么样的立体图形,然后再根据公式进行计算即可.
28.(1)5分米;(2)12.56平方分米
【分析】(1)要想使容积最大,应让底面积尽量大,用长边做底面周长;
(2)根据底面周长求出底面半径,再根据圆的面积公式求出底面积即可。
【详解】(1)答:高应是5分米。
(2)12.56÷3.14÷2=2(分米)
3.14×2=12.56(平方分米)
答:至少还需要12.56平方分米的铁皮。
【点睛】本题考查了圆柱的特征和容积。
29.可以铺62.8米长.
【详解】试题分析:要求用这堆沙子铺多少米长,先求得沙堆的体积,沙堆的形状是圆锥形的,利用圆锥的体积计算公式求得体积,进一步再求铺多少米长,问题得解.
解答:解:4厘米=0.04米,
沙堆的体积:
×3.14×(12.56÷3.14÷2)2×6,
=×3.14×22×6,
=3.14×4×2,
=25.12(立方米);
可以铺:
25.12÷(10×0.04),
=25.12÷0.4,
=62.8(米);
答:可以铺62.8米长.
点评:此题主要考查圆锥的体积计算公式:V=πr2h,以及解决实际问题的能力.
30.
边长/cm 6 5 3 2
周长/cm 24 20 12 8
成正比例.
【详解】试题分析:(1)先确定出正方形的边长,进而依据正方形的特征,即可画出符合要求的正方形;
(2)依据正方形的周长C=4a,代入数据即可求解;
(3)依据正比例的意义,即如果两个相关联量的比值一定,则这两个相关联的量成正比例,据此即可判断.
解:(1)据分析画图如下:
;
(2)6×4=24(厘米),
5×4=20(厘米),
3×4=12(厘米),
(3),
因为正方形的周长与边长的比值一定,
所以正方形的周长与边长成正比例.
点评:此题主要考查正方形的特征、周长的计算方法、以及正比例的意义.
31.需要77块
【详解】试题分析:根据一间房子的面积一定,方砖的面积与方砖的块数成反比例,由此列出比例解答即可.
解答:解:设需要x块,
20×x=4×4×96
20x=1536
x≈77
答:需要77块.
点评:解答解答此题的关键是,根据题意,先判断哪两种相关联的量成何比例,即两个量的乘积一定则成反比例,两个量的比值一定则成正比例;解答时注意此题的4分米是边长不是面积.
32.厘米
【分析】先利用圆锥的容积公式求出水的体积,再把这些水倒入圆柱容器中,利用圆柱的体积公式求出水的高度。
【详解】
(厘米)
答:容器中水的深度是厘米。
故答案为:厘米
【点睛】此题考查了圆锥与圆柱的体积公式的灵活应用。
33.8∶15
【分析】在甲乙两数的比中,乙数是3份,在乙丙两数的比中,乙数是4份,求出3和4的最小公倍数,根据比的基本性质,将两个比统一成乙数是12份的比,再写出甲丙两数的比即可。
【详解】3×4=12
甲乙两数的比:2∶3=8∶12
乙丙两数的比:4∶5=12∶15
甲∶丙=8∶15
答:甲数和丙数的比是8∶15。
【点睛】本题考查了统一比,比的前项和后项同时乘或除以相同的数(0除外),比值不变。
34.20∶6∶3
【分析】第一种混合物中A、B重量比与最终混合物的A、B重量比相同,均为3∶5。所以,先将第二种、第三种混合物的A、B重量比调整到3∶5,再将第二种、第三种混合物中A、B与第一种混合物中A、B视为单一物质D,然后求出新配成的物质中D∶C的比。最终确定三种混合物的重量比。
【详解】D∶C=(3+5)∶2=4∶1;
第二种混合物不含A,B的含量为,第三种混合物不含B,A的含量为,所以倍第三种混合物含A为3,倍第二种混合物含B为5,即第二种、第三种混合物的重量比为2∶1;于是此时含有C:,即C∶D=29∶(45-29)=29∶16,而最终混合物中C∶D=1∶4=29∶116,所以第一种混合物的质量与后两种混合质量和之比为(116-16)∶45=20∶9,所以三种混合物的重量比为20∶6∶3。
答:三种混合物的比为20∶6∶3。
【点睛】本题主要考查了比的应用,关键是要认真分析题意,找出题目中的数量关系进行解答。
答案第1页,共2页
答案第1页,共2页
2024-2025学年六年级数学下学期期中素养测评(北京版)
【学易金卷·提升卷02】
考试分数:100分;考试时间:90分钟
注意事项:
1.答题前,填写好自己的姓名、班级、考号等信息,请写在答题卡规定的位置上。
2.选择题、判断题必须使用2B铅笔填涂答案,非选择、判断题必须使用黑色墨迹签字笔或钢笔答题,请将答案填写在答题卡规定的位置上。
3.所有题目必须在答题卡上作答,在试卷上作答无效。
4.考试结束后将试卷和答题卡一并交回。
一、选择题(共10分)
1.下面四句话中,正确的一句是( )
A.北京某天的气温是﹣3℃至8℃,这天的温差是5℃
B.圆锥的体积一定,底面半径和高成反比例
C.2、3、8、5、2、6、7、2这八个数的中位数是3.5
2.表示两个比相等的式子叫作( )。
A.等式 B.比例 C.方程
3.将直角三角形ABC的AB轴旋转一周,得到的圆锥体积是V,那么V=( ).
A.12π B.25π C.36π D.48π
4.甲、乙是两个成反比例的量,当甲减少20%时,乙( )。
A.增加20% B.减少20% C.增加25% D.减少25%
5.如果a和b成反比例,b和c成反比例,那么a和c( )。(a、b、c均不为0)
A.成正比例 B.成反比例 C.不成比例
二、填空题(共17分)
6.把2∶0.75化成最简单的整数比是( ).
7.圆锥的底面是一个( ),侧面是一个( )。从圆锥的顶点到底面圆心的距离是圆锥的( )。
8.如表,如果x和y成正比例关系,“?”处应填( );如果x和y成反比例关系,“?”处应填( )。
x 3 ?
y 12 24
9.0.75=18÷( )( )∶44=( )%。
10.甲数的和乙数的相等,甲和乙数的最简整数比是( ):( ).
11.一个圆柱形水桶的直径是4分米,放在地上,它的占地面积为( ).
12.出油率一定,香油质量与芝麻质量成( )比例.
13.在比例尺为1:2000000的这个地图上,量得北京到郑州的距离是32厘米;把它画在比例尺为的地图上.应画( )厘米.
14.如图,一根长2米的圆柱形木料,截去一半后,剩下的圆柱形木料的表面积比原来减少了62.8平方分米,原来圆柱形木料的底面积是( )平方分米,体积是( )立方分米。
15.一个数与比它小4的数的比值,化简后是 ,你知道这个数是( )吗?
16.一个圆柱(如图),过底面圆心沿高切开后,表面积会增加60平方厘米,已知圆柱的高是5厘米,那么这个圆柱的表面积是( )平方厘米。(取3.14)
三、判断题(共6分)
17.3:4和 ∶可以组成比例. ( )
18.一个圆柱体有无数条高。( )
19.a∶b=2∶5,那么a一定等于2。( )
20.若A的等于B的(A、B均不为0),则A∶B=4∶5. ( )
21.下面题中的两个量是不是成反比例?
平行四边形的面积一定,底和高。 ( )
22.一个圆锥的底面半径和高相等,过顶点和直径把这个圆锥切开,切面一定是等腰直角三角形。( )
四、计算题(共14分)
23.直接写出得数。(共8分)
= ×0.36= ×1×= =
= 16÷= 0.8∶= ∶=
24.解方程。(共6分)
五、作图题(共3分)
25.按3∶1的比画出下面长方形放大后的图形;再按照1∶2的比画出下面平行四边形缩小后的图形。
六、解答题(共50分)
26.榨油厂用100千克黄豆可以榨出13千克油,照这样计算,用5吨黄豆可以榨出多少吨油?
27.一个长方形的长8厘米,宽4厘米,以长方形的长为轴旋转一周得到一个立体图形,这个立体图形的底面积、侧面积各是多少?
28.用一张长12.56分米、宽5分米的长方形铁皮做一个圆柱体水桶的侧面。
(1)如果要使这个水桶的容积最大,那么它的高应是多少分米?
(2)再配一个底做成无盖的圆柱体水桶,至少还需要多少平方分米的铁皮?
29.一个圆锥形沙堆,底面周长是12.56米,高6米,将这些沙铺在宽10米的道路上铺4厘米厚,可以铺多少米长?
30.在如图所示的方格纸上画几个边长各不相同的正方形.
根据画出的正方形,把下表填写完整.
边长/cm 5 2
周长/cm 20 8
(2)正方形的周长与边长成正比例吗?为什么?
31.一间房子要用方砖铺地,用边长是4分米的方砖,需用96块,如果改用面积是20平方分米的方砖,需用多少块?(用比例解)
32.有、两个容器,如图,先把容器装满水,然后将水倒入容器,容器中水的深度是多少厘米?
33.甲数和乙数的比是2∶3,乙数和丙数的比是4∶5,甲数和丙数的比是多少?
34.已知三种混合物由三种成分A、B、C组成,第一种仅含成分A和B,重量比为3∶5;第二种只含成分B和C,重量比为1∶2;第三种只含成分A和C,重量之比为2∶3。以什么比例取这些混合物,才能使所得的混合物中A、B和C,这三种成分的重量比为3∶5∶2?
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
) (
学校:___________姓名:___________班级:___________考号:___________
) (
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
第1页 共4页 ◎ 第2页 共4页
第1页 共4页 ◎ 第2页 共4页
参考答案:
1.B
【详解】试题分析:(1)用最高气温减去最低气温,求出这天的温差是多少即可.
(2)根据圆锥的体积公式,判断出底面半径和高的乘积一定,所以圆锥的体积一定,底面半径和高成反比例,据此解答即可.
(3)根据中位数的求法判断即可.
解答:解:(1)因为8﹣(﹣3)=11(℃),
所以这天的温差是11℃,
所以选项A不正确.
(2)因为圆锥的体积=底面积×高÷3,
所以圆锥的体积一定时,底面半径和高的乘积一定,
所以圆锥的体积一定,底面半径和高成反比例,
所以选项B正确.
(3)2、3、8、5、2、6、7、2这八个数的中位数是:
(3+5)÷2=8÷2=4,
所以选项C不正确.
故选B.
点评:此题主要考查了正、负数的运算,辨别成正比例的量和成反比例的量的方法,以及中位数的含义和求法,要熟练掌握.
2.B
【解析】表示两个比相等的式子叫作比例,根据比例的定义直接选择。
【详解】表示两个比相等的式子叫作比例;
故答案选:B。
【点睛】本题考查的是比例的定义,构成比例的基本条件是两个比的比值相等。
3.A
【详解】根据圆锥的展开图特点可知,将直角三角形ABC以AB为轴旋转一周,得到的是一个底面半径为3,高为4的圆锥,由此利用圆锥的体积公式即可解答问题
解答:×π×3 ×4=×π×9×4=12π
4.C
【分析】甲和乙是两个成反比例的量,那么它们的乘积一定,即符合xy=k(一定),当甲减少20%时,可知乙一定是增加了,又(1-20%)x=x,由于k一定,所以这里的y得变为y,进而确定乙是增加了25%;
【详解】1-20%=,1÷=
(5-4)÷4=25%
故答案为:C
【点睛】此题考查正反比例意义的运用,解题时要明确成正比例的两个量是比值一定,成反比例的两个量是乘积一定。
5.A
6.8:3
【详解】试题分析:
点评:把0.75化为4分之三更简单些.
7. 圆 曲面 高
【详解】圆锥的底面是一个圆,侧面是一个曲面。从圆锥的顶点到底面圆心的距离是圆锥的高。
8. 6 1.5
【分析】如果x和y成正比例关系,则它们的比值一定,则3∶12=?∶24,据此求出?的值;如果x和y成反比例关系,则它们的乘积一定,则3×12=?×24,据此求出?的值。
【详解】3∶12=?∶24
解:12×?=3×24
?=6;
3×12=?×24
解:?×24=36
?=1.5
【点睛】明确两个相关联的量,如果比值一定则成正比例关系,如果乘积一定,则成反比例关系。
9. 24 33 75
【分析】把0.75化成分数并化简是,根据分数与除法的关系,再根据商不变的性质被除数、除数都乘6就是;根据比与分数的关系,再根据比的基本性质比的前、后项都乘11就是;把0.75的小数点向右移动两位添上百分号就是。
【详解】
故答案为:24;33;75
【点睛】此题主要是考查除法、小数、百分数、比之间的关系及转化,利用它们之间的关系和性质进行转化即可。
10.20,21.
【详解】试题分析:根据甲数的和乙数的相等,知道甲数×=乙数×,设乙数是1,即可表示出甲数,列式解答即可.
解:设乙数是1,
则甲数为:1×÷=,
甲数:乙数,
=:1,
=20:21;
点评:解答此题可以用假设法,还可以根据比例基本性质的逆运算进行解答.
11.12.56平方分米
【详解】试题分析:根据题干分析可得,此题就是求这个底面直径为4分米的底面圆的面积,据此利用圆的面积公式计算即可解答.
解:3.14×(4÷2)2,
=3.14×4,
=12.56(平方分米),
答:占地面积是12.56平方分米.
故答案为12.56平方分米.
点评:明确圆柱的占地面积就是圆柱的底面圆的面积,是解决本题的关键.
12.正.
【详解】试题分析:判断两种量成不成比例,成什么比例,就看这两种量是否是①相关联;②一种量变化,另一种量也随着变化,变化方向相同或相反;③对应的比值或乘积一定;如果这两种量相关联的量都是变量,且对应的比值一定,就成正比例;如果两种量相关联的量都是变量,且对应的乘积一定,就成反比例;如果是其它的量一定或乘积、比值不一定,就不成比例.
解:因为香油质量:芝麻质量=出油率(一定),是对应的比值一定,
所以香油质量与芝麻质量成正比例;
点评:此题属于根据正、反比例的意义,辨识两种相关联的量成不成比例,成什么比例,就看这两种量是否都是变量,且对应的比值一定,或是对应的乘积一定,再做出判断.
13.20
【详解】先求甲、乙两地间的实际距离,根据“图上距离÷比例尺=实际距离”,带入数值,计算出甲、乙两地间的实际距离,进而根据“实际距离×比例尺=图上距离”解答即可.
14. 3.14 62.8
【分析】减少的表面积就是截去一半圆柱的侧面积,根据底面周长=侧面积÷高,底面面积=(底面周长÷π÷2)2×π,体积=底面积×高,代入数据计算即可。
【详解】2÷2=1(米)
1米=10分米
62.8÷10÷3.14÷2
=6.28÷3.14÷2
=1(分米)
3.14×12=3.14(平方分米)
2米=20分米
3.14×20=62.8(立方分米)
【点睛】这是一道关于圆柱的题目,根据圆柱的侧面积和体积公式、圆的周长和面积公式解答。
15.16
16.150.72
【分析】将圆柱过底面圆心沿高切开,表面积增加了2个面,增加的2个面是长方形,这个长方形的长是底面直径,宽是圆柱的高。根据增加的表面积和圆柱的高,可以求出圆柱的底面直径和半径,然后再根据表面积公式求出圆柱的表面积。
【详解】底面半径是:(厘米)
表面积是:
(厘米)
【点睛】本题考查圆柱的表面积,弄清楚切开后表面积增加的是哪个部分是解决此题的关键。
17.错
【详解】判断两个比能不能组成比例,要看它们的比值是不是相等.
18.√
【分析】根据圆柱的高的概念圆柱两个底面之间的距离叫做圆柱的高,判断即可。
【详解】一个圆柱体有无数条高。
故答案为:√
【点睛】牢记圆柱有无数条高,圆锥只有一条高。
19.×
【分析】根据比例的意义∶表示两个比相等的式子,叫做比例;可知∶2∶5的比值是0.4(或),因为a、b都不知道具体的数值,只要a∶b=0.4即可,所以a的取值不固定;进而判断即可。
【详解】2∶5的比值是0.4(或 );
因为a、b都不知道具体的数值,只要a∶b=0.4即可,如∶当b=10,a=4;当b=15时,a=6;
故答案为错误。
【点睛】解答此类题的关键是∶理解比例的意义,能够灵活运用比例的意义解答实际问题。
20.√
【详解】略
21.底和高成反比例。因为底×高=平行四边形的面积(一定)。
【分析】根据平行四边形的面积公式判断出底和高的商(比值)一定还是乘积一定,如果商(比值)一定就成正比例,如果乘积一定就成反比例,否则不成比例。
【详解】略
22.√
【分析】圆锥纵切面是一个三角形,三角形的底是圆锥底面直径,三角形高是圆锥的高,如果圆锥的底面半径和高相等,纵切面如图,切面是一个等腰直角三角形。
【详解】根据分析,一个圆锥的底面半径和高相等,过顶点和直径把这个圆锥切开,切面一定是等腰直角三角形,说法正确。
故答案为:√
【点睛】关键是熟悉圆锥特征,想清楚纵切面和圆锥之间的关系。
23.2;0.14;1;
;20;1.6;
【详解】略
24.x=;x=;x=
【分析】第一题先计算3×0.9,将其转化为2x+2.7=24.7,再左右两边同时减去2.7,将其转化为2x=22,再左右两边同时除以2即可;
第二题根据比例的基本性质可知,再左右两边同时除以即可;
第三题左右两边同时乘0.25,将其转化为,再左右两边同时除以即可。
【详解】2x+3×0.9=24.7
解:2x+2.7=24.7
2x+2.7-2.7=24.7-2.7
2x=22
2x÷2=22÷2
x=11
解:
x=
解:
x=
25.见详解
【分析】根据图形放大与缩小的意义,把长方形的长和宽均扩大到原来的3倍,所得到的长方形就是原长方形按3:1放大后的图形.同理,把平行四边形的边长均缩小到原来的,对应角大小不变,所到得的平行四边形就是原平行四边形按1:2缩小后的图形。
【详解】3:1的比画出长方形放大后的图形(图中1所示),按1:2的比画出平行四边形缩小后的图形(图中2所示)。
【点睛】图形放大或缩小的倍数是指对应边放大或缩小的倍数,对应角大小不变;即图形放大或缩小后只是大小变了,形状不变。
26.x=0.65吨
【详解】略
27.50.24;200.96
【详解】试题分析:根据题意,以长方形的长为轴旋转一周得到一个以8厘米为高、4厘米为底面半径的圆柱体,圆柱体的底面积=πr2,圆柱的侧面积=底面周长×高,将数据代入公式进行计算即可得到答案.
解:立体图形的底面积为:3.14×42=50.24(平方厘米),
立体图形的侧面积为:3.14×4×2×8
=12.56×2×8,
=25.12×8,
=200.96(平方厘米),
答:这个立体图形的底面积是50.24平方厘米,侧面积是200.96平方厘米.
【点评】解答此题的关键是确定长方形旋转一周后得到的是什么样的立体图形,然后再根据公式进行计算即可.
28.(1)5分米;(2)12.56平方分米
【分析】(1)要想使容积最大,应让底面积尽量大,用长边做底面周长;
(2)根据底面周长求出底面半径,再根据圆的面积公式求出底面积即可。
【详解】(1)答:高应是5分米。
(2)12.56÷3.14÷2=2(分米)
3.14×2=12.56(平方分米)
答:至少还需要12.56平方分米的铁皮。
【点睛】本题考查了圆柱的特征和容积。
29.可以铺62.8米长.
【详解】试题分析:要求用这堆沙子铺多少米长,先求得沙堆的体积,沙堆的形状是圆锥形的,利用圆锥的体积计算公式求得体积,进一步再求铺多少米长,问题得解.
解答:解:4厘米=0.04米,
沙堆的体积:
×3.14×(12.56÷3.14÷2)2×6,
=×3.14×22×6,
=3.14×4×2,
=25.12(立方米);
可以铺:
25.12÷(10×0.04),
=25.12÷0.4,
=62.8(米);
答:可以铺62.8米长.
点评:此题主要考查圆锥的体积计算公式:V=πr2h,以及解决实际问题的能力.
30.
边长/cm 6 5 3 2
周长/cm 24 20 12 8
成正比例.
【详解】试题分析:(1)先确定出正方形的边长,进而依据正方形的特征,即可画出符合要求的正方形;
(2)依据正方形的周长C=4a,代入数据即可求解;
(3)依据正比例的意义,即如果两个相关联量的比值一定,则这两个相关联的量成正比例,据此即可判断.
解:(1)据分析画图如下:
;
(2)6×4=24(厘米),
5×4=20(厘米),
3×4=12(厘米),
(3),
因为正方形的周长与边长的比值一定,
所以正方形的周长与边长成正比例.
点评:此题主要考查正方形的特征、周长的计算方法、以及正比例的意义.
31.需要77块
【详解】试题分析:根据一间房子的面积一定,方砖的面积与方砖的块数成反比例,由此列出比例解答即可.
解答:解:设需要x块,
20×x=4×4×96
20x=1536
x≈77
答:需要77块.
点评:解答解答此题的关键是,根据题意,先判断哪两种相关联的量成何比例,即两个量的乘积一定则成反比例,两个量的比值一定则成正比例;解答时注意此题的4分米是边长不是面积.
32.厘米
【分析】先利用圆锥的容积公式求出水的体积,再把这些水倒入圆柱容器中,利用圆柱的体积公式求出水的高度。
【详解】
(厘米)
答:容器中水的深度是厘米。
故答案为:厘米
【点睛】此题考查了圆锥与圆柱的体积公式的灵活应用。
33.8∶15
【分析】在甲乙两数的比中,乙数是3份,在乙丙两数的比中,乙数是4份,求出3和4的最小公倍数,根据比的基本性质,将两个比统一成乙数是12份的比,再写出甲丙两数的比即可。
【详解】3×4=12
甲乙两数的比:2∶3=8∶12
乙丙两数的比:4∶5=12∶15
甲∶丙=8∶15
答:甲数和丙数的比是8∶15。
【点睛】本题考查了统一比,比的前项和后项同时乘或除以相同的数(0除外),比值不变。
34.20∶6∶3
【分析】第一种混合物中A、B重量比与最终混合物的A、B重量比相同,均为3∶5。所以,先将第二种、第三种混合物的A、B重量比调整到3∶5,再将第二种、第三种混合物中A、B与第一种混合物中A、B视为单一物质D,然后求出新配成的物质中D∶C的比。最终确定三种混合物的重量比。
【详解】D∶C=(3+5)∶2=4∶1;
第二种混合物不含A,B的含量为,第三种混合物不含B,A的含量为,所以倍第三种混合物含A为3,倍第二种混合物含B为5,即第二种、第三种混合物的重量比为2∶1;于是此时含有C:,即C∶D=29∶(45-29)=29∶16,而最终混合物中C∶D=1∶4=29∶116,所以第一种混合物的质量与后两种混合质量和之比为(116-16)∶45=20∶9,所以三种混合物的重量比为20∶6∶3。
答:三种混合物的比为20∶6∶3。
【点睛】本题主要考查了比的应用,关键是要认真分析题意,找出题目中的数量关系进行解答。
答案第1页,共2页
答案第1页,共2页
同课章节目录
