2025年九年级数学中考二轮复习专题相似三角形之一线三等角模型(含答案)
文档属性
| 名称 | 2025年九年级数学中考二轮复习专题相似三角形之一线三等角模型(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 966.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-11 05:42:08 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2025年九年级数学中考二轮复习专题相似三角形之一线三等角模型
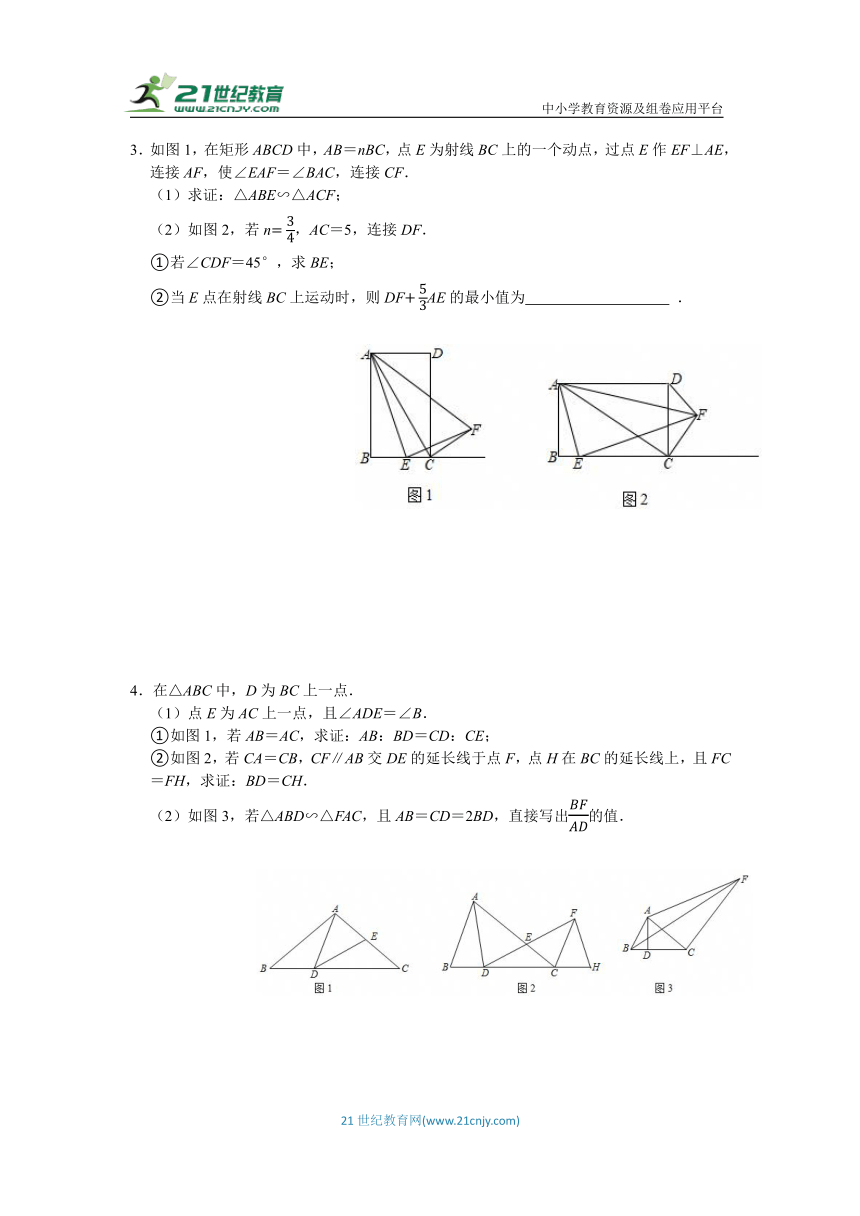
1.在△ABC中,点D为BC上一点,点E为AC上一点,且∠ADE=∠B
(1)如图1,若AB=AC,求证:;
(2)如图2,若AD=AE,求证:;
(3)在(2)的条件下,若∠DAC=90°,且CE=4,sin,直接写出线段AB的长.
2.如图,在△ABC中,AB=AC=5,BC=6,点D是BC边长的动点(不与B,C重合),点E是AC上的某点并且满足∠ADE=∠C.
(1)求证:△ABD∽△DCE;
(2)若BD的长为x,请用含x的代数式表示AE的长;
(3)当(2)中的AE最短时,求△ADE的面积.
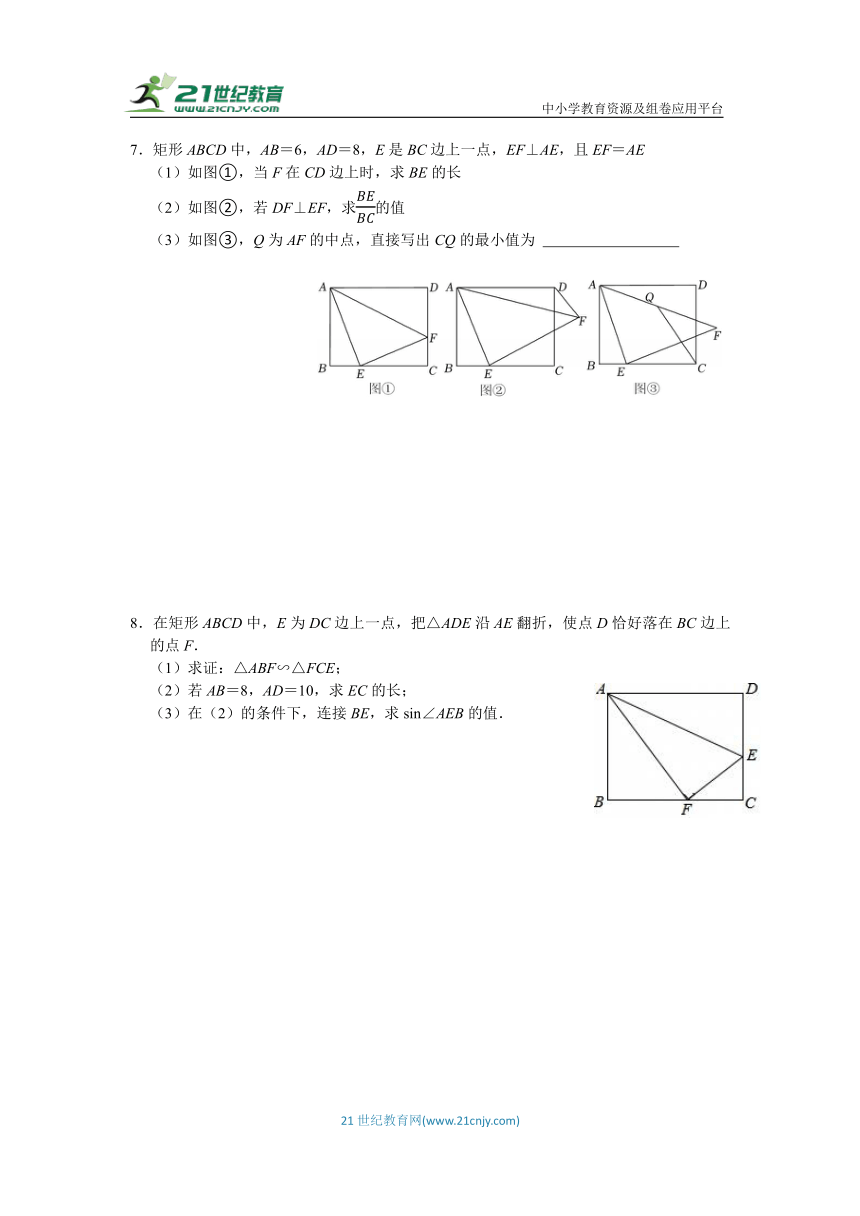
3.如图1,在矩形ABCD中,AB=nBC,点E为射线BC上的一个动点,过点E作EF⊥AE,连接AF,使∠EAF=∠BAC,连接CF.
(1)求证:△ABE∽△ACF;
(2)如图2,若n,AC=5,连接DF.
①若∠CDF=45°,求BE;
②当E点在射线BC上运动时,则DFAE的最小值为 .
4.在△ABC中,D为BC上一点.
(1)点E为AC上一点,且∠ADE=∠B.
①如图1,若AB=AC,求证:AB:BD=CD:CE;
②如图2,若CA=CB,CF∥AB交DE的延长线于点F,点H在BC的延长线上,且FC=FH,求证:BD=CH.
(2)如图3,若△ABD∽△FAC,且AB=CD=2BD,直接写出的值.
5.在△ABC中,AB=AC,点D在底边BC上,∠EDF的两边分别交AB、AC所在直线于E,F两点,∠EDF=2∠ABC,BD=nCD.
(1)如图1,若∠ABC=45°,n=1,求证:DE=DF;
(2)如图2,求的值(含n的式子表示):
(3)如图3,连接EF,若tan∠B=1,EF∥BC,且,直接写出n的值为 .
6.在△ABC中,点P为边BC上一点,∠APD=∠B,PD交边AC于点D.
(1)若△ABC为等边三角形.
①如图1,求证:;
②如图2,点E在边AC上,BE交AP于点F,且∠AFE=60°,AF=6PF,求的值;
(2)如图3,若∠APD=45°,且∠PAD=90°,AB=2,CD,直接写出△APC的面积 .
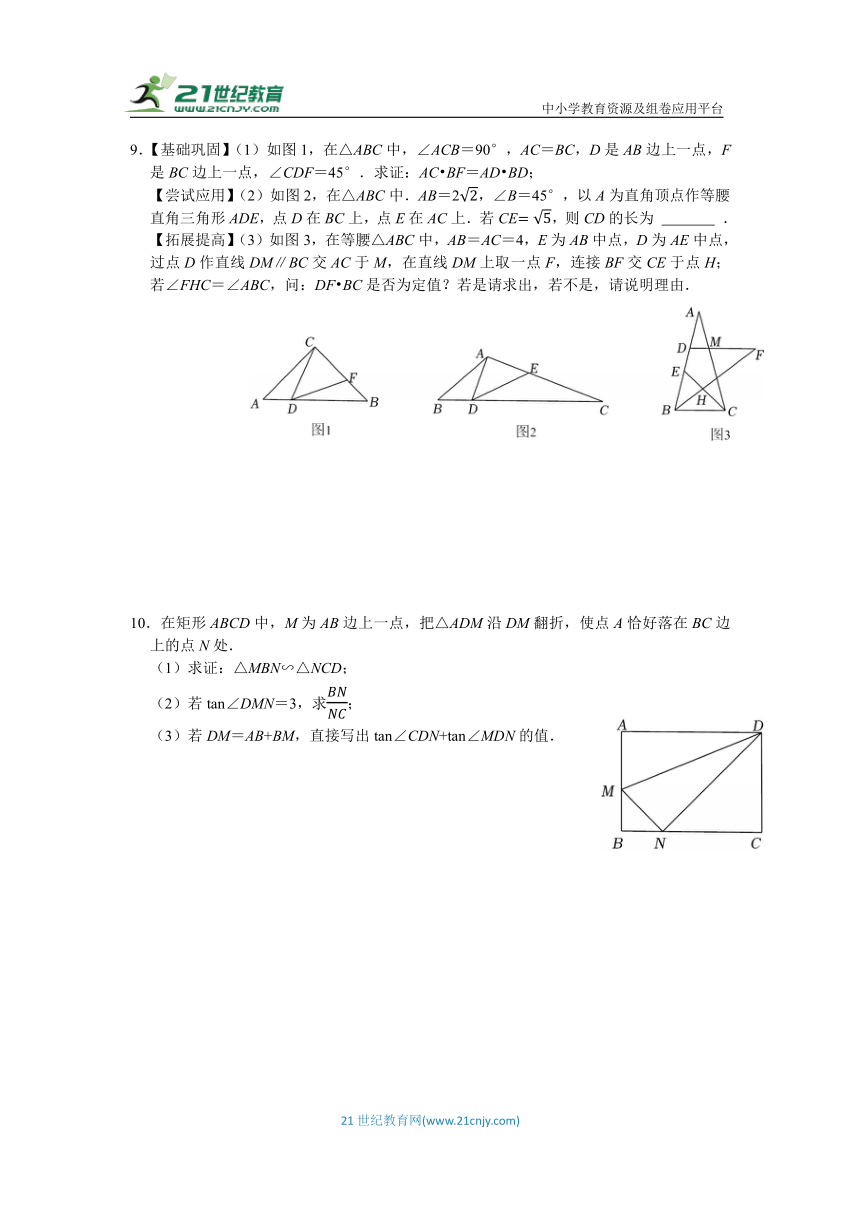
7.矩形ABCD中,AB=6,AD=8,E是BC边上一点,EF⊥AE,且EF=AE
(1)如图①,当F在CD边上时,求BE的长
(2)如图②,若DF⊥EF,求的值
(3)如图③,Q为AF的中点,直接写出CQ的最小值为
8.在矩形ABCD中,E为DC边上一点,把△ADE沿AE翻折,使点D恰好落在BC边上的点F.
(1)求证:△ABF∽△FCE;
(2)若AB=8,AD=10,求EC的长;
(3)在(2)的条件下,连接BE,求sin∠AEB的值.
9.【基础巩固】(1)如图1,在△ABC中,∠ACB=90°,AC=BC,D是AB边上一点,F是BC边上一点,∠CDF=45°.求证:AC BF=AD BD;
【尝试应用】(2)如图2,在△ABC中.AB=2,∠B=45°,以A为直角顶点作等腰直角三角形ADE,点D在BC上,点E在AC上.若CE,则CD的长为 .
【拓展提高】(3)如图3,在等腰△ABC中,AB=AC=4,E为AB中点,D为AE中点,过点D作直线DM∥BC交AC于M,在直线DM上取一点F,连接BF交CE于点H;若∠FHC=∠ABC,问:DF BC是否为定值?若是请求出,若不是,请说明理由.
10.在矩形ABCD中,M为AB边上一点,把△ADM沿DM翻折,使点A恰好落在BC边上的点N处.
(1)求证:△MBN∽△NCD;
(2)若tan∠DMN=3,求;
(3)若DM=AB+BM,直接写出tan∠CDN+tan∠MDN的值.
11.如图1,矩形ABCD中,AB=nAD,点E,F分别在边AB,AD上且不与A,B,D重合,∠AEF=∠BCE.
(1)求证:△AEF∽△BCE;
(2)如图2,若G为EF中点,GH⊥CD,D是垂足,若EF=EC,GH=GE,求n的值;
(3)在(2)的条件下,在线段BC上找一点Q,使得△HGQ是等腰三角形,求CQ:CE.
12.△ABC中,∠ABC=45°,D是BC边上一点,E是AC边上一点,∠ADE=45°.
(1)如图1,若∠ACB=45°,求证:△ABD∽△DCE;
(2)①如图2,若AD⊥AC,AE=CE,求证:CD=5BD;
②如图3,若AD⊥AC,CE=3BD=3,则CD的长度为 .
13.如图,在△ABC中,点D、E分别在边BC、AC上的点,且∠ADE=∠B.
(1)如图1,若∠B=∠C,求证:AB CE=BD CD;
(2)若AB=8,BC=10,∠B=2∠C.
①如图2,当AD=DE时,求BD的长;
②如图3,当BD=CE时,直接写出BD的长是 .
14.问题情境
如图1,在正方形ABCD中,E是BC的中点,F是CD上一点,且AE⊥EF.则①∠BAE=∠CEF;②△AEF∽△ABE(结论不需要证明).
初步探究
(1)如图2,在矩形ABCD中,E是BC的中点,EF⊥AE与直线CD交于点F.请证明:①∠BAE=∠CEF;②△AEF∽△ABE.
结论运用
(2)在(1)的条件下,
①如图3,当AB=2,AD平分∠EAF时,求AF的长;
②如图4,若EF与矩形外角∠DCC′的平分线交于点G,当A,D,G在同一条直线上时,请直接写出的值.
15.在矩形ABCD中,点E,F分别在边AD,BC上,将矩形ABCD沿EF折叠,使点A的对应点P落在边CD上,点B的对应点为点G,PG交BC于点H.
(1)如图1,求证:△DEP∽△CPH;
(2)如图2,当P为CD的中点,AB=2,AD=3时,求GH的长;
(3)如图3,连接BG,当P,H分别为CD,BC的中点时,探究BG与AB的数量关系,并说明理由.
参考答案
1.【解答】(1)证明:如图1中,
∵AB=AC,
∴∠B=∠C,
∵∠ADC=∠B+∠DAB=∠ADE+∠EDC,∠ADE=∠B,
∴∠EDC=∠BAD,
∴△ABD∽△DCE,
∴,
∴.
(2)证明:如图2中,作CH∥AD交DE的延长线于H.
∵AD=AE,
∴∠ADE=∠AED,
∵AD∥CH,
∴∠H=∠ADE,
∵∠AED=∠CEH,
∴∠H=∠CEH,
∴CE=CH,
∵∠ADE=∠B,∠ADE=∠H,
∴∠B=∠H,
∵∠HDC=∠BAD,
∴△BAD∽△HDC,
∴,
∴,
∴.
(3)解:如图3中,作CH∥AD交DE的延长线于H,作CG⊥EH于G.
∵∠DAC=90°,AD=AE,
∴∠ADE=∠AED=∠H=∠CEH=45°,
∴EC=CH=4,∠ECH=90°,
∵CG⊥EH,
∴EH=4,EG=CG=GH=2,
∵sin∠CDE,
∴CD=2,DG4,
∴DE=EG=2,DH=6,
∴AD=DE=2,
∵△BAD∽△HDC,
∴,
∴,
∴AB.
2.【解答】解:(1)∵AB=AC,
∴∠B=∠C,
∵∠ADC=∠ADE+∠EDC=∠B+∠BAD,
∵∠ADE=∠C,
∴∠BAD=∠CDE,
∴△ABD∽△DCE.
(2)∵△ABD∽△DCE,
∴,
∴,
∴CEx(6﹣x),
∴AE=5x(6﹣x)x2x+5.
(3)∵AEx2x+5(x﹣3)2,
∵0,
∴x=3时,AE的值最小,此时BD=CD=3,
∵AB=AC,
∴AD⊥BC,
∴AD4,
∴S△ADCAD×CD=6,
∵此时AE,EC=5,
∴AE:EC=16:9,
∴S△ADE=6.
3.【解答】(1)证明:∵四边形ABCD是矩形,
∴∠B=90°,
∵EF⊥AE,
∴∠AEF=∠B=90°,
∵∠EAF=∠BAC,
∴△ABC∽AEF,
∴∠ACB=∠AFE,
∴A,E,C,F四点共圆,
∴∠ACF=∠AEF=90°,
∴∠ACF=∠ABE,
∵BAC=∠EAF,
∴∠BAE=∠CAF,
∴△ABE∽△ACF.
(2)①解:如图2中,过点F作FH⊥CD于H.
∵Rt△ABC中,∠B=90°,AC=5,ABBC,
∴可以假设AB=3k,BC=4k,
则有(3k)2+(4k)2=5,
∴k=1,
∴AB=3,BC=4,
∵△ABE∽△ACF,
∴∠ACF=∠B=90°,,设BE=3m,则CF=5m,
∵∠BCD=∠ACF=90°,
∴∠DCF=∠ACB,
∵FH⊥CD,
∴∠FHC=∠B=90°,
∴△CHF∽△CBA,
∴,
∴,
∴CH=4m,FH=3m,
∵∠CDF=45°,∠DHF=90°,
∴∠DFH=∠HDF=45°,
∴DH=FH=3m,
∴CD=CH+DH=7m=3,
∴m,
∴BE=3m.
②如图3中,延长AC到A′,使得CA′=CA,连接A′D,A′F,过点A′作A′H⊥DC交DC的延长线于H.
∵△ABE∽△ACF,
∴∠B=∠ACF=90°,,
∴AFAE,CF⊥AC,
∴A,A′关于CF对称,
∴DFAE=DF+AF=DF+FA′≥A′D,
∴当D,F,A′共线时,DFAE的值最小,最小值为线段DA′的长,
∵AC=CA′,∠ACD=∠A′CH,∠ADC=∠H=90°,
∴△ADC≌△A′HC(AAS),
∴AD=A′H=4,DC=CH=3,
∴DH=6,
∴DA′2,
∴DFAE的最小值为2.
故答案为2.
4.【解答】(1)①证明:如图1.∵AB=AC,
∴∠B=∠C,
∵∠ADE=∠B,
∴∠BAD=180°﹣∠B﹣∠ADB=180°﹣∠ADE﹣∠ADB=∠CDE,
∴△ABD∽△DCE,
∴,
∴.
②证明:如图2,连结AF.
∵CF∥AB,
∴∠FCE=∠CAB,
∵CA=CB,
∴∠CAB=∠B=∠ADE,
∴∠ADE=∠FCE,
∵∠AED=∠FEC,
∴△ADE∽△FCE,
∴,
∴,
∵∠AEF=∠DFC,
∴△AEF∽△DEC,
∴∠FAC=∠FDH;
∵FC=FH,
∴∠FCH=∠H,
∵∠FCH=∠B=∠CAB=∠ACF,
∴∠ACF=∠H,
∴△ACF≌△DHF(AAS),
∴CA=HD,
∴CB=HD,
∴CB﹣CD=HD﹣CD,
∴BD=CH.
(2)如图3,作∠AFE=∠CAB,FE交BA的延长线于点E,设BD=a,则AB=CD=2a,BC=3a.
∵△ABD∽△FAC,
∴,
∴2;
∵∠ABC=∠FAC,∠ABC+∠CAB+∠ACB=180°,
∴∠FAC+∠CAB+∠ACB=180°,
∵∠FAC+∠CAB+∠FAE=180°,
∴∠FAE=∠ACB,
∴△EFA∽△BAC,
∴,
∴EF=2AB=4a,AE=2BC=6a,
∴BE=2a+6a=8a;
∵2,
∴,
∴,
∵∠E=∠ABD,
∴△BEF∽△ABD,
∴4.
5.【解答】(1)证明:如图1中,连接AD.
∵AB=AC,
∴∠ABC=∠C=45°,
∵BD=nCD,n=1,
∴BD=CD,
∴AD⊥BC,∠DAC=∠DAB=45°,AD=DB=DC,
∵∠EDF=2∠ABC=90°,
∴∠BDA=∠EDF=90°,
∴∠BDE=∠ADF,
∵∠B=∠DAF,BD=AD,
∴△BDE≌△ADF(ASA),
∴DE=DF.
(2)解:在射线BA上取一点T,使得DB=DT.
∵DB=DT,
∴∠B=∠T,
∴∠TDC=∠B+∠T=2∠B,
∵∠EDF=2∠B,
∴∠EDF=∠TDC,
∴∠EDT=∠FDC,
∵∠BAC+2∠B=180°,
∴∠BAC+∠EDF=180°,
∴∠TED+∠AFD=180°,
∵∠DFC+∠AFD=180°,
∴∠TED=∠DFC,
∴△TED∽△FDC,
∴n.
(3)如图3中,作ET⊥BC于T,FH⊥BC于H.
∵EF∥BC,ET∥FH,
∴四边形EFHT是平行四边形,
∵∠ETH=90°,
∴四边形EFHT是矩形,
∴ET=FH,EF=TH,
∵EF:BC=5:8,设EF=5k,BC=8k,则TH=5k,
∵tanB=1,
∴∠B=∠C=45°,
∵∠ETB=∠FHC=90°,
∴ET=BT=FH=CH=1.5k,设DT=x,则DH=5k﹣x,
∵∠EDF=2∠B=90°,∠ETD=∠FHD=90°,
∴∠EDT+∠FDH=90°,∠TED+∠EDT=90°,
∴∠TED=∠FDH,
∴△ETD∽△DHF,
∴,
∴,
∴5kx﹣x2=2.25k2,
解得x=0.5k或4.5k,
∴BD=2k或6k,
∴BD:DC=2k:6k=1:3或BD:DC=6k:2k=3:1.
∴n=3或.
6.【解答】(1)①证明:在△ABP中,∠B+∠BAP+∠APB=180°,
∵∠APD=∠B=∠C,
∴∠APD+∠BAP+∠APB=180°,
∵∠APB+∠APD+∠CPD=180°,
∴∠BAP=∠CPD,
∴△ABP∽△PCD,
∴;
②解:∵△ABC是等边三角形,
∴AB=AC,∠BAC=60°,
延长BE至点M,使FM=AF,连接AM,CM.
∵∠AFE=60°,
∴△AFM为等边三角形,
∴AF=AM,∠FAM=60°=∠BAC,
∴∠BAC﹣∠CAP=∠FAM﹣∠CAP,
∴△ABF≌△ACM(SAS),
∴BF=CM,∠AFB=∠AMC=120°,
∵∠AMF=60°,
∴∠BMC=120°﹣60°=60°,
∴∠BMC=∠AFM,
∴FP∥CM,
∴△BPF∽△BCM,
∴,
∵AF=6PF,
∴设PF=a,AF=6a,则FM=6a.设BF=x,则CM=x,
∴,
∴x=3a或x=﹣2a(舍),
∴;
(2)面积为5,
解:过D作∠DNP=45°,
在△ABP中,∠B+∠BAP+∠APB=180°,
∵∠B=∠APD,
∴∠APD+∠BAP+∠APB=180°,
∵∠APB+∠APD+∠DPN=180°,
∴∠BAP=∠DPN,
∴△ABP∽△PND,
∵∠APD=45°,∠PAD=90°,
∴∠ADP=90°﹣∠APD=45°,
∴AP=AD,
∴△APD为等腰直角三角形,
∴,
∴PN=4,
∵∠APB=∠PDN,
∴∠DPC+∠APD=∠CDN+∠ADP,
∴∠DPC=∠CDN,
∴△CDN∽△CPD,
∴,
∴CN=1,
∴PC=1+4=5,
在Rt△APD中,由勾股定理可得AP,
∴AD,
∴S5,
故答案为:5.
7.【解答】解:(1)在矩形ABCD中,∠B=∠C=90°,BC=AD=8,CD=AB=6,
∴∠BAE+∠AEB=90°,
∴EF⊥AE,
∴∠AEB+∠CEF=90°,
∴∠BAE=∠CEF,
∵EF=AE,
在△ABE和△ECF中,
,
∴△ABE≌△ECF(AAS),
∴CE=AB=6,
∴BE=BC﹣CE=8﹣6=2;
(2)如图,延长EC,DF交于点P,
∵DF⊥EF,EF⊥AE,
∴AE∥DF,
在矩形ABCD中,AD∥BC,
∴四边形AEPD是平行四边形,
∴PE=AD=8,
∴S AEPD=PE CD=AE EF即8×6=AE2,
∴AE2=48,
在Rt△ABE中,BE2,
∴;
(3)如图,连接BQ,EQ,过点Q作QT⊥BQ交BC的延长线于点T,
∵△AEF是等腰直角三角形,Q是AF的中点,
∴∠AQE=∠AQB+∠BQE=90°,AQ=EQ,
∵BQ⊥QT,
∴∠BQT=∠BQE+∠EQT=90°,
∴∠AQB=∠EQT,
∵∠ABC=90°,∠AQE=90°,
∴∠BAQ+∠BEQ=360°﹣90°﹣90°=180°,
∵∠BEQ+∠QET=180°,
∴∠BAQ=∠QET,
∴△ABQ≌△ETQ(ASA),
∴∠ABQ=∠QTB,BQ=TQ,
∴∠QBT=∠QTB,
∴∠ABQ=∠QBT,
即点Q在∠ABC的角平分线上,
∴当CQ⊥BQ时,CQ取最小值,此时点T与点C重合,
∴△BCQ为等腰直角三角形,
∴CQ=BQ4,
故答案为4.
8.【解答】(1)证明:∵四边形ABCD是矩形,
∴∠B=∠C=∠D=90°,
∴∠BAF+∠AFB=90°,
由折叠知,∠AFE=∠D=90°,
∴∠AFB+∠CFE=90°,
∴∠BAF=∠CFE,
∵∠B=∠C,
∴△ABF∽△FCE;
(2)解:∵四边形ABCD是矩形,
∴∠B=∠C=90°,BC=AD=10,CD=AB=8,DE=EF,
由折叠知,AF=AD=10,
在Rt△ABF中,AB=8,
根据勾股定理得,BF=6,
∴CF=BC﹣BF=4,
设CE=x,则DE=CD﹣CE=8﹣x,
∴EF=8﹣x,
在Rt△ECF中,根据勾股定理得,CF2+CE2=EF2,
∴42+x2=(8﹣x)2,
∴x=3,
即EC的长为3;
(3)解:如图,
过点A作AH⊥BE于H,则∠AHE=90°,
由(2)知,CE=3,∴DE=5,
在Rt△BCE中,根据勾股定理得,BE,
∴S△ABEBE AHAB AD,
∴AH,
在Rt△ADE中,根据勾股定理得,AE5,
在RtAHE中,sin∠AEB.
9.【解答】(1)证明:∵∠ABC=90°,AC=BC,
∴∠A=∠B=45°,
∵∠A+∠ACD=∠CDF+∠BDF,∠A=∠CDF=45°,
∴∠ACD=∠BDF,
∴△ACD∽△BDF,
∴,
∴AC BF=AD BD;
(2)解:如图,过点E作EF与CD交于点F,使∠EFD=45°,
∵∠B=∠ADE=45°,
∴∠BAD=∠EDF,
∴△ABD∽△DFE,
∴,
∵DEAD,AB=2,
∴DFAB=4,
∵∠EFD=45°,∠ADE=45°,
∴∠EFC=∠DEC=135°,
∴△EFC∽△DEC,
∴,
∵EC,
∴EC2=FC CD=FC×(4+FC),
∴5=FC×(4+FC),
∴FC=1,
∴CD=5,
故答案为:5;
(3)解:是,理由如下:
如图,延长FD,CE交于点G,
∵AB=AC,DM∥BC,
∴∠ADM=∠AMD,
又∵∠ABC=∠FHC,
∴∠ABF+∠FBC=∠FBC+∠ECB,
∴∠ABF=∠ECB,
∴∠BDM=∠CMD,
又∵DF∥BC,
∴∠G=∠ECB,∠G=∠ABF,
∴△GMC∽△BDF,
∴,
∴DF GM=MC DB=3×3=9,
又∵GD∥BC,DE=1,BE=2,
∴△GED∽△CEB,
∴,
同理,
∴GM=GD+DM,
∴DF,
∴DF BC=12,
∴DF BC是定值12.
10.【解答】(1)证明:∵四边形ABCD是矩形,
∴∠A=∠B=∠C=90°,
由翻折知,∠A=∠MND=90°,
∴∠MNB+∠DNC=90°,∠MNB+∠BMN=90°,
∴∠BMN=∠DNC,
∴△MBN∽△NCD;
(2)解:∵tan∠DMN=3,
设AM=MN=a,BM=b,AB=CD=a+b,AD=DN=BC=3a,
∵△MBN∽△NCD,
∴,
∴CN=3BM=3b,BN=BC﹣CN=3(a﹣b),CD=2BN,
∴a+b=9(a﹣b),
∴,
∴;
(3)解:∵△MBN∽△NCD,
∴,
∴tan∠CDN+tan∠MDN,
设AB=CD=a,BC=AD=b,AM=x,
∴DM=AB+BM=a+(a﹣x)=2a﹣x,
∵AD=DN=b,AM=MN=x,∠A=∠B=∠C=90°,
∴CN,BN,
∵AM2+AD2=DM2,
∴x2+b2=(2a﹣x)2,
∴a,
∵△MBN∽△NCD,
∴,
∴,
∴a,
∴,
整理得:16a4﹣24a2b2+9b4=0,
∴(4a2﹣3b2)2=0,
∴,
∴tan∠CDN+tan∠MDN.
11.【解答】解:(1)∵四边形ABCD是矩形,
∴∠A=∠B=90°,
又∵∠AEF=∠BCE,
∴△AEF∽△BCE;
(2)延长HG交AE于点P,
在△AEF与△BCE中,
∴△AEF≌△BCE(AAS)
设BC=AE=y,
则BE=AF=(n﹣1)y,PEAEy
∴由题意知:GE=GF=GH,
∴由中位线的性质可知:GPAFy,
∴GE=GH=yyy,
∴Rt△PGE中,由勾股定理可知:()2=()2+()2,
解得n;
(3)由(2)知ABAD,即,
设AB=7x,AD=4x,
则AE=BC=4x,BE=AB﹣AE=3x,PEAE=2x,
∴BP=5x,
∴EF=EC5x,
∵点G是EF中点,且GH=GE,∠A=90°,
∴GE=GF=GHx,
作GH的垂直平分线,垂足为M,交BC于点Q,
则四边形HMQC是矩形,
∴CQ=HMGHx,
此时△HGQ是等腰三角形,
∴.
12.【解答】(1)证明:∵∠ABC+∠BAD=∠ADC,
∴∠ABC+∠BAD=∠ADE+∠CDE,
∵ABC=45°,∠ADE=45°,
∴∠ABC=∠ADE,
∴∠BAD=∠CDE,又∠ABC=∠ACB=45°,
∴△ABD∽△DCE;
(2)①证明:如图2,过点D作DF⊥BC交AB于点F,
设AE=CE=a,则AC=AE+CE=2a,
∵AD⊥AC,∠ADE=45°,
∴AD=AE=a,
∴在Rt△ACD中,CDa,
∵DF⊥BC,
∴∠BDF=90°,又∠ABC=45°,∠AFD=∠ABC+∠BDF,
∴∠AFD=135°,
同理∠DEC=135°,
∴∠AFD=∠DEC,又由(1)知∠BAD=∠CDE,
∴△ADF∽△DCE,
∴,即,
∴DFa,又CDa
∴CD=5DF,
∵∠FDB=90°,∠ABC=45°,
∴BD=DF,
∴CD=5BD;
②解:如图3,过D作DG⊥BC交AB于点G,则BD=DG=1,
设AD=x,则AC=x+3,DEx,
由①可知,△ADG∽△DCE,
∴,即,
解得,CD=3x,
在Rt△ACD中,AD2+AC2=CD2,即x2+(x+3)2=(3x)2,
解得,x1,x2(舍去),
则CD=3x,
故答案为:.
13.【解答】解:(1)在△ABD中,∠B+∠ADB+∠BAD=180°,
∵∠ADE=∠B,
∴∠ADE+∠ADB+∠BAD=180°,
∴∠BDE+∠BAD=180°,
∵∠BDE+∠CDE=180°,
∴∠BAD=∠CDE,
又∠B=∠C,
∴△ABD∽△DCE,
∴,
∴AB CE=BD CD;
(2)①如图1,作CE的垂直平分线交DC于F,
∴EF=FC,
∴∠EFD=2∠C,
∵∠B=2∠C,
∴∠B=∠EFD,
又∵AD=DE,
∴△ABD≌△DFE(AAS),
∴BD=EF=FC,DF=AB,
∵AB=8,BC=10,
∴BC=BD+DF+FC=BD+AB+BD,
∴10=BD+8+BD,
∴BD=1;
②如图2,延长CB到G,使BG=AB=8,
则∠G=∠C,
∴AG=AC,
作AH⊥BC于H,
∴GH=HC(BG+BC)=9,
∴BH=GH﹣BG=1,
在Rt△ABH中,根据勾股定理得,AH,
在Rt△ACH中,根据勾股定理得,AC12,
∴cos∠C,
作EC中垂线NP交BC于N,EC于P,
则设BD=EC=x,PCx,
∴NCx,
∴△ABD∽△DNE,
∴,
∴,
解得x,
经检验,x是方式方程的解,且满足题意,
∴BD,
故答案为.
14.【解答】(1)证明:①∵四边形ABCD是矩形,EF⊥AE与直线CD交于点F,
∴∠B=∠C=90°,∠AEF=90°,
∴∠BAE+∠AEB=∠AEB+∠CEF,
∴∠BAE=∠CEF;
②∵EF⊥AE与直线CD交于点F,
∴∠AEF=∠B=∠C=90°,
∵由①得∠BAE=∠CEF,
∴△ABE∽△ECF,
∴,
在矩形ABCD中,E是BC的中点,
设AB=x、BE=CE=y、AE=a,
∵,
∴,
∴,
∴,,
∴且∠AEF=∠B=90°,
∴△AEF∽△ABE;
(2)解:①∵AD平分∠EAF,
∴∠FAD=∠DAE,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠DAE=∠AEB,
∴∠FAD=∠AEB,
∵∠FDA=∠B=90°,
∴△ABE∽△FDA,
设BE=EC=x,则AD=2x,
∴,
∴∠AFE=30°,
由(1)得△AEF∽△ABE,
∴∠AFE=∠AEB,
∴∠AFE=∠AEB=30°,
∴AE=2AB=4,
∴,
∴AF=8.
②;理由如下:
∵∠ECF=∠GDF=90°,∠CFE=∠DFG,
∴△ECF∽△GDF,
设AB=CD=x,BE=EC=y,
∵CG平分∠DCC′,
∴∠DCG=∠GCC′=45°,
∵AG∥BC′,
∴∠DGC=∠GCC′=45°,
∴DG=DC=x,
∴.
∵由(1)得△ABE∽△ECF,
∴,
∴,
∴,,
∵,
∴,
∴,
∴xy=x2﹣y2,
∴,
设,
∴t=1﹣t2,
解得:,(t2<0,舍去),
∴.
15.【解答】(1)证明:如图,
∵四边形ABCD是矩形,
∴∠A=∠D=∠C=90°,
∴∠1+∠3=90°,
∵E,F分别在AD,BC上,将四边形ABFE沿EF翻折,使A的对称点P落在DC上,
∴∠EPH=∠A=90°,
∴∠1+∠2=90°,
∴∠3=∠2,
∴△EDP∽△PCH;
(2)解:∵四边形ABCD是矩形,
∴CD=AB=2,AD=BC=3,∠A=∠D=∠C=90°,
∵P为CD中点,
∴DP=CP1,
设EP=AE=x,
∴ED=AD﹣x=3﹣x,
在Rt△EDP中,EP2=ED2+DP2,
即x2=(3﹣x)2+1,
解得x,
∴EP=AP=x,
∴ED=AD﹣AE,
∵△EDP∽△PCH,
∴,即,
∴PH,
∵PG=AB=2,
∴GH=PG﹣PH.
(3)解:如图,延长AB,PG交于一点M,连接AP,
∵E,F分别在AD,BC上,将四边形ABFE沿EF翻折,使A的对称点P落在CD上,
∴AP⊥EF,BG⊥直线EF,
∴BG∥AP,
∵AE=EP,
∴∠EAP=∠EPA,
∴∠BAP=∠GPA,
∴△MAP是等腰三角形,
∴MA=MP,
∵P为CD中点,
∴设DP=CP=y,
∴AB=PG=CD=2y,
∵H为BC中点,
∴BH=CH,
∵∠BHM=∠CHP,∠CBM=∠PCH,
∴△MBH≌△PCH(ASA),
∴BM=CP=y,HM=HP,
∴MP=MA=MB+AB=3y,
∴HPPMy,
在Rt△PCH中,CHy,
∴BC=2CHy,
∴AD=BCy,
在Rt△APD中,APy,
∵BG∥AP,
∴△BMG∽△AMP,
∴,
∴BGy,
∴,
∴ABBG.
21世纪教育网(www.21cnjy.com)
2025年九年级数学中考二轮复习专题相似三角形之一线三等角模型
1.在△ABC中,点D为BC上一点,点E为AC上一点,且∠ADE=∠B
(1)如图1,若AB=AC,求证:;
(2)如图2,若AD=AE,求证:;
(3)在(2)的条件下,若∠DAC=90°,且CE=4,sin,直接写出线段AB的长.
2.如图,在△ABC中,AB=AC=5,BC=6,点D是BC边长的动点(不与B,C重合),点E是AC上的某点并且满足∠ADE=∠C.
(1)求证:△ABD∽△DCE;
(2)若BD的长为x,请用含x的代数式表示AE的长;
(3)当(2)中的AE最短时,求△ADE的面积.
3.如图1,在矩形ABCD中,AB=nBC,点E为射线BC上的一个动点,过点E作EF⊥AE,连接AF,使∠EAF=∠BAC,连接CF.
(1)求证:△ABE∽△ACF;
(2)如图2,若n,AC=5,连接DF.
①若∠CDF=45°,求BE;
②当E点在射线BC上运动时,则DFAE的最小值为 .
4.在△ABC中,D为BC上一点.
(1)点E为AC上一点,且∠ADE=∠B.
①如图1,若AB=AC,求证:AB:BD=CD:CE;
②如图2,若CA=CB,CF∥AB交DE的延长线于点F,点H在BC的延长线上,且FC=FH,求证:BD=CH.
(2)如图3,若△ABD∽△FAC,且AB=CD=2BD,直接写出的值.
5.在△ABC中,AB=AC,点D在底边BC上,∠EDF的两边分别交AB、AC所在直线于E,F两点,∠EDF=2∠ABC,BD=nCD.
(1)如图1,若∠ABC=45°,n=1,求证:DE=DF;
(2)如图2,求的值(含n的式子表示):
(3)如图3,连接EF,若tan∠B=1,EF∥BC,且,直接写出n的值为 .
6.在△ABC中,点P为边BC上一点,∠APD=∠B,PD交边AC于点D.
(1)若△ABC为等边三角形.
①如图1,求证:;
②如图2,点E在边AC上,BE交AP于点F,且∠AFE=60°,AF=6PF,求的值;
(2)如图3,若∠APD=45°,且∠PAD=90°,AB=2,CD,直接写出△APC的面积 .
7.矩形ABCD中,AB=6,AD=8,E是BC边上一点,EF⊥AE,且EF=AE
(1)如图①,当F在CD边上时,求BE的长
(2)如图②,若DF⊥EF,求的值
(3)如图③,Q为AF的中点,直接写出CQ的最小值为
8.在矩形ABCD中,E为DC边上一点,把△ADE沿AE翻折,使点D恰好落在BC边上的点F.
(1)求证:△ABF∽△FCE;
(2)若AB=8,AD=10,求EC的长;
(3)在(2)的条件下,连接BE,求sin∠AEB的值.
9.【基础巩固】(1)如图1,在△ABC中,∠ACB=90°,AC=BC,D是AB边上一点,F是BC边上一点,∠CDF=45°.求证:AC BF=AD BD;
【尝试应用】(2)如图2,在△ABC中.AB=2,∠B=45°,以A为直角顶点作等腰直角三角形ADE,点D在BC上,点E在AC上.若CE,则CD的长为 .
【拓展提高】(3)如图3,在等腰△ABC中,AB=AC=4,E为AB中点,D为AE中点,过点D作直线DM∥BC交AC于M,在直线DM上取一点F,连接BF交CE于点H;若∠FHC=∠ABC,问:DF BC是否为定值?若是请求出,若不是,请说明理由.
10.在矩形ABCD中,M为AB边上一点,把△ADM沿DM翻折,使点A恰好落在BC边上的点N处.
(1)求证:△MBN∽△NCD;
(2)若tan∠DMN=3,求;
(3)若DM=AB+BM,直接写出tan∠CDN+tan∠MDN的值.
11.如图1,矩形ABCD中,AB=nAD,点E,F分别在边AB,AD上且不与A,B,D重合,∠AEF=∠BCE.
(1)求证:△AEF∽△BCE;
(2)如图2,若G为EF中点,GH⊥CD,D是垂足,若EF=EC,GH=GE,求n的值;
(3)在(2)的条件下,在线段BC上找一点Q,使得△HGQ是等腰三角形,求CQ:CE.
12.△ABC中,∠ABC=45°,D是BC边上一点,E是AC边上一点,∠ADE=45°.
(1)如图1,若∠ACB=45°,求证:△ABD∽△DCE;
(2)①如图2,若AD⊥AC,AE=CE,求证:CD=5BD;
②如图3,若AD⊥AC,CE=3BD=3,则CD的长度为 .
13.如图,在△ABC中,点D、E分别在边BC、AC上的点,且∠ADE=∠B.
(1)如图1,若∠B=∠C,求证:AB CE=BD CD;
(2)若AB=8,BC=10,∠B=2∠C.
①如图2,当AD=DE时,求BD的长;
②如图3,当BD=CE时,直接写出BD的长是 .
14.问题情境
如图1,在正方形ABCD中,E是BC的中点,F是CD上一点,且AE⊥EF.则①∠BAE=∠CEF;②△AEF∽△ABE(结论不需要证明).
初步探究
(1)如图2,在矩形ABCD中,E是BC的中点,EF⊥AE与直线CD交于点F.请证明:①∠BAE=∠CEF;②△AEF∽△ABE.
结论运用
(2)在(1)的条件下,
①如图3,当AB=2,AD平分∠EAF时,求AF的长;
②如图4,若EF与矩形外角∠DCC′的平分线交于点G,当A,D,G在同一条直线上时,请直接写出的值.
15.在矩形ABCD中,点E,F分别在边AD,BC上,将矩形ABCD沿EF折叠,使点A的对应点P落在边CD上,点B的对应点为点G,PG交BC于点H.
(1)如图1,求证:△DEP∽△CPH;
(2)如图2,当P为CD的中点,AB=2,AD=3时,求GH的长;
(3)如图3,连接BG,当P,H分别为CD,BC的中点时,探究BG与AB的数量关系,并说明理由.
参考答案
1.【解答】(1)证明:如图1中,
∵AB=AC,
∴∠B=∠C,
∵∠ADC=∠B+∠DAB=∠ADE+∠EDC,∠ADE=∠B,
∴∠EDC=∠BAD,
∴△ABD∽△DCE,
∴,
∴.
(2)证明:如图2中,作CH∥AD交DE的延长线于H.
∵AD=AE,
∴∠ADE=∠AED,
∵AD∥CH,
∴∠H=∠ADE,
∵∠AED=∠CEH,
∴∠H=∠CEH,
∴CE=CH,
∵∠ADE=∠B,∠ADE=∠H,
∴∠B=∠H,
∵∠HDC=∠BAD,
∴△BAD∽△HDC,
∴,
∴,
∴.
(3)解:如图3中,作CH∥AD交DE的延长线于H,作CG⊥EH于G.
∵∠DAC=90°,AD=AE,
∴∠ADE=∠AED=∠H=∠CEH=45°,
∴EC=CH=4,∠ECH=90°,
∵CG⊥EH,
∴EH=4,EG=CG=GH=2,
∵sin∠CDE,
∴CD=2,DG4,
∴DE=EG=2,DH=6,
∴AD=DE=2,
∵△BAD∽△HDC,
∴,
∴,
∴AB.
2.【解答】解:(1)∵AB=AC,
∴∠B=∠C,
∵∠ADC=∠ADE+∠EDC=∠B+∠BAD,
∵∠ADE=∠C,
∴∠BAD=∠CDE,
∴△ABD∽△DCE.
(2)∵△ABD∽△DCE,
∴,
∴,
∴CEx(6﹣x),
∴AE=5x(6﹣x)x2x+5.
(3)∵AEx2x+5(x﹣3)2,
∵0,
∴x=3时,AE的值最小,此时BD=CD=3,
∵AB=AC,
∴AD⊥BC,
∴AD4,
∴S△ADCAD×CD=6,
∵此时AE,EC=5,
∴AE:EC=16:9,
∴S△ADE=6.
3.【解答】(1)证明:∵四边形ABCD是矩形,
∴∠B=90°,
∵EF⊥AE,
∴∠AEF=∠B=90°,
∵∠EAF=∠BAC,
∴△ABC∽AEF,
∴∠ACB=∠AFE,
∴A,E,C,F四点共圆,
∴∠ACF=∠AEF=90°,
∴∠ACF=∠ABE,
∵BAC=∠EAF,
∴∠BAE=∠CAF,
∴△ABE∽△ACF.
(2)①解:如图2中,过点F作FH⊥CD于H.
∵Rt△ABC中,∠B=90°,AC=5,ABBC,
∴可以假设AB=3k,BC=4k,
则有(3k)2+(4k)2=5,
∴k=1,
∴AB=3,BC=4,
∵△ABE∽△ACF,
∴∠ACF=∠B=90°,,设BE=3m,则CF=5m,
∵∠BCD=∠ACF=90°,
∴∠DCF=∠ACB,
∵FH⊥CD,
∴∠FHC=∠B=90°,
∴△CHF∽△CBA,
∴,
∴,
∴CH=4m,FH=3m,
∵∠CDF=45°,∠DHF=90°,
∴∠DFH=∠HDF=45°,
∴DH=FH=3m,
∴CD=CH+DH=7m=3,
∴m,
∴BE=3m.
②如图3中,延长AC到A′,使得CA′=CA,连接A′D,A′F,过点A′作A′H⊥DC交DC的延长线于H.
∵△ABE∽△ACF,
∴∠B=∠ACF=90°,,
∴AFAE,CF⊥AC,
∴A,A′关于CF对称,
∴DFAE=DF+AF=DF+FA′≥A′D,
∴当D,F,A′共线时,DFAE的值最小,最小值为线段DA′的长,
∵AC=CA′,∠ACD=∠A′CH,∠ADC=∠H=90°,
∴△ADC≌△A′HC(AAS),
∴AD=A′H=4,DC=CH=3,
∴DH=6,
∴DA′2,
∴DFAE的最小值为2.
故答案为2.
4.【解答】(1)①证明:如图1.∵AB=AC,
∴∠B=∠C,
∵∠ADE=∠B,
∴∠BAD=180°﹣∠B﹣∠ADB=180°﹣∠ADE﹣∠ADB=∠CDE,
∴△ABD∽△DCE,
∴,
∴.
②证明:如图2,连结AF.
∵CF∥AB,
∴∠FCE=∠CAB,
∵CA=CB,
∴∠CAB=∠B=∠ADE,
∴∠ADE=∠FCE,
∵∠AED=∠FEC,
∴△ADE∽△FCE,
∴,
∴,
∵∠AEF=∠DFC,
∴△AEF∽△DEC,
∴∠FAC=∠FDH;
∵FC=FH,
∴∠FCH=∠H,
∵∠FCH=∠B=∠CAB=∠ACF,
∴∠ACF=∠H,
∴△ACF≌△DHF(AAS),
∴CA=HD,
∴CB=HD,
∴CB﹣CD=HD﹣CD,
∴BD=CH.
(2)如图3,作∠AFE=∠CAB,FE交BA的延长线于点E,设BD=a,则AB=CD=2a,BC=3a.
∵△ABD∽△FAC,
∴,
∴2;
∵∠ABC=∠FAC,∠ABC+∠CAB+∠ACB=180°,
∴∠FAC+∠CAB+∠ACB=180°,
∵∠FAC+∠CAB+∠FAE=180°,
∴∠FAE=∠ACB,
∴△EFA∽△BAC,
∴,
∴EF=2AB=4a,AE=2BC=6a,
∴BE=2a+6a=8a;
∵2,
∴,
∴,
∵∠E=∠ABD,
∴△BEF∽△ABD,
∴4.
5.【解答】(1)证明:如图1中,连接AD.
∵AB=AC,
∴∠ABC=∠C=45°,
∵BD=nCD,n=1,
∴BD=CD,
∴AD⊥BC,∠DAC=∠DAB=45°,AD=DB=DC,
∵∠EDF=2∠ABC=90°,
∴∠BDA=∠EDF=90°,
∴∠BDE=∠ADF,
∵∠B=∠DAF,BD=AD,
∴△BDE≌△ADF(ASA),
∴DE=DF.
(2)解:在射线BA上取一点T,使得DB=DT.
∵DB=DT,
∴∠B=∠T,
∴∠TDC=∠B+∠T=2∠B,
∵∠EDF=2∠B,
∴∠EDF=∠TDC,
∴∠EDT=∠FDC,
∵∠BAC+2∠B=180°,
∴∠BAC+∠EDF=180°,
∴∠TED+∠AFD=180°,
∵∠DFC+∠AFD=180°,
∴∠TED=∠DFC,
∴△TED∽△FDC,
∴n.
(3)如图3中,作ET⊥BC于T,FH⊥BC于H.
∵EF∥BC,ET∥FH,
∴四边形EFHT是平行四边形,
∵∠ETH=90°,
∴四边形EFHT是矩形,
∴ET=FH,EF=TH,
∵EF:BC=5:8,设EF=5k,BC=8k,则TH=5k,
∵tanB=1,
∴∠B=∠C=45°,
∵∠ETB=∠FHC=90°,
∴ET=BT=FH=CH=1.5k,设DT=x,则DH=5k﹣x,
∵∠EDF=2∠B=90°,∠ETD=∠FHD=90°,
∴∠EDT+∠FDH=90°,∠TED+∠EDT=90°,
∴∠TED=∠FDH,
∴△ETD∽△DHF,
∴,
∴,
∴5kx﹣x2=2.25k2,
解得x=0.5k或4.5k,
∴BD=2k或6k,
∴BD:DC=2k:6k=1:3或BD:DC=6k:2k=3:1.
∴n=3或.
6.【解答】(1)①证明:在△ABP中,∠B+∠BAP+∠APB=180°,
∵∠APD=∠B=∠C,
∴∠APD+∠BAP+∠APB=180°,
∵∠APB+∠APD+∠CPD=180°,
∴∠BAP=∠CPD,
∴△ABP∽△PCD,
∴;
②解:∵△ABC是等边三角形,
∴AB=AC,∠BAC=60°,
延长BE至点M,使FM=AF,连接AM,CM.
∵∠AFE=60°,
∴△AFM为等边三角形,
∴AF=AM,∠FAM=60°=∠BAC,
∴∠BAC﹣∠CAP=∠FAM﹣∠CAP,
∴△ABF≌△ACM(SAS),
∴BF=CM,∠AFB=∠AMC=120°,
∵∠AMF=60°,
∴∠BMC=120°﹣60°=60°,
∴∠BMC=∠AFM,
∴FP∥CM,
∴△BPF∽△BCM,
∴,
∵AF=6PF,
∴设PF=a,AF=6a,则FM=6a.设BF=x,则CM=x,
∴,
∴x=3a或x=﹣2a(舍),
∴;
(2)面积为5,
解:过D作∠DNP=45°,
在△ABP中,∠B+∠BAP+∠APB=180°,
∵∠B=∠APD,
∴∠APD+∠BAP+∠APB=180°,
∵∠APB+∠APD+∠DPN=180°,
∴∠BAP=∠DPN,
∴△ABP∽△PND,
∵∠APD=45°,∠PAD=90°,
∴∠ADP=90°﹣∠APD=45°,
∴AP=AD,
∴△APD为等腰直角三角形,
∴,
∴PN=4,
∵∠APB=∠PDN,
∴∠DPC+∠APD=∠CDN+∠ADP,
∴∠DPC=∠CDN,
∴△CDN∽△CPD,
∴,
∴CN=1,
∴PC=1+4=5,
在Rt△APD中,由勾股定理可得AP,
∴AD,
∴S5,
故答案为:5.
7.【解答】解:(1)在矩形ABCD中,∠B=∠C=90°,BC=AD=8,CD=AB=6,
∴∠BAE+∠AEB=90°,
∴EF⊥AE,
∴∠AEB+∠CEF=90°,
∴∠BAE=∠CEF,
∵EF=AE,
在△ABE和△ECF中,
,
∴△ABE≌△ECF(AAS),
∴CE=AB=6,
∴BE=BC﹣CE=8﹣6=2;
(2)如图,延长EC,DF交于点P,
∵DF⊥EF,EF⊥AE,
∴AE∥DF,
在矩形ABCD中,AD∥BC,
∴四边形AEPD是平行四边形,
∴PE=AD=8,
∴S AEPD=PE CD=AE EF即8×6=AE2,
∴AE2=48,
在Rt△ABE中,BE2,
∴;
(3)如图,连接BQ,EQ,过点Q作QT⊥BQ交BC的延长线于点T,
∵△AEF是等腰直角三角形,Q是AF的中点,
∴∠AQE=∠AQB+∠BQE=90°,AQ=EQ,
∵BQ⊥QT,
∴∠BQT=∠BQE+∠EQT=90°,
∴∠AQB=∠EQT,
∵∠ABC=90°,∠AQE=90°,
∴∠BAQ+∠BEQ=360°﹣90°﹣90°=180°,
∵∠BEQ+∠QET=180°,
∴∠BAQ=∠QET,
∴△ABQ≌△ETQ(ASA),
∴∠ABQ=∠QTB,BQ=TQ,
∴∠QBT=∠QTB,
∴∠ABQ=∠QBT,
即点Q在∠ABC的角平分线上,
∴当CQ⊥BQ时,CQ取最小值,此时点T与点C重合,
∴△BCQ为等腰直角三角形,
∴CQ=BQ4,
故答案为4.
8.【解答】(1)证明:∵四边形ABCD是矩形,
∴∠B=∠C=∠D=90°,
∴∠BAF+∠AFB=90°,
由折叠知,∠AFE=∠D=90°,
∴∠AFB+∠CFE=90°,
∴∠BAF=∠CFE,
∵∠B=∠C,
∴△ABF∽△FCE;
(2)解:∵四边形ABCD是矩形,
∴∠B=∠C=90°,BC=AD=10,CD=AB=8,DE=EF,
由折叠知,AF=AD=10,
在Rt△ABF中,AB=8,
根据勾股定理得,BF=6,
∴CF=BC﹣BF=4,
设CE=x,则DE=CD﹣CE=8﹣x,
∴EF=8﹣x,
在Rt△ECF中,根据勾股定理得,CF2+CE2=EF2,
∴42+x2=(8﹣x)2,
∴x=3,
即EC的长为3;
(3)解:如图,
过点A作AH⊥BE于H,则∠AHE=90°,
由(2)知,CE=3,∴DE=5,
在Rt△BCE中,根据勾股定理得,BE,
∴S△ABEBE AHAB AD,
∴AH,
在Rt△ADE中,根据勾股定理得,AE5,
在RtAHE中,sin∠AEB.
9.【解答】(1)证明:∵∠ABC=90°,AC=BC,
∴∠A=∠B=45°,
∵∠A+∠ACD=∠CDF+∠BDF,∠A=∠CDF=45°,
∴∠ACD=∠BDF,
∴△ACD∽△BDF,
∴,
∴AC BF=AD BD;
(2)解:如图,过点E作EF与CD交于点F,使∠EFD=45°,
∵∠B=∠ADE=45°,
∴∠BAD=∠EDF,
∴△ABD∽△DFE,
∴,
∵DEAD,AB=2,
∴DFAB=4,
∵∠EFD=45°,∠ADE=45°,
∴∠EFC=∠DEC=135°,
∴△EFC∽△DEC,
∴,
∵EC,
∴EC2=FC CD=FC×(4+FC),
∴5=FC×(4+FC),
∴FC=1,
∴CD=5,
故答案为:5;
(3)解:是,理由如下:
如图,延长FD,CE交于点G,
∵AB=AC,DM∥BC,
∴∠ADM=∠AMD,
又∵∠ABC=∠FHC,
∴∠ABF+∠FBC=∠FBC+∠ECB,
∴∠ABF=∠ECB,
∴∠BDM=∠CMD,
又∵DF∥BC,
∴∠G=∠ECB,∠G=∠ABF,
∴△GMC∽△BDF,
∴,
∴DF GM=MC DB=3×3=9,
又∵GD∥BC,DE=1,BE=2,
∴△GED∽△CEB,
∴,
同理,
∴GM=GD+DM,
∴DF,
∴DF BC=12,
∴DF BC是定值12.
10.【解答】(1)证明:∵四边形ABCD是矩形,
∴∠A=∠B=∠C=90°,
由翻折知,∠A=∠MND=90°,
∴∠MNB+∠DNC=90°,∠MNB+∠BMN=90°,
∴∠BMN=∠DNC,
∴△MBN∽△NCD;
(2)解:∵tan∠DMN=3,
设AM=MN=a,BM=b,AB=CD=a+b,AD=DN=BC=3a,
∵△MBN∽△NCD,
∴,
∴CN=3BM=3b,BN=BC﹣CN=3(a﹣b),CD=2BN,
∴a+b=9(a﹣b),
∴,
∴;
(3)解:∵△MBN∽△NCD,
∴,
∴tan∠CDN+tan∠MDN,
设AB=CD=a,BC=AD=b,AM=x,
∴DM=AB+BM=a+(a﹣x)=2a﹣x,
∵AD=DN=b,AM=MN=x,∠A=∠B=∠C=90°,
∴CN,BN,
∵AM2+AD2=DM2,
∴x2+b2=(2a﹣x)2,
∴a,
∵△MBN∽△NCD,
∴,
∴,
∴a,
∴,
整理得:16a4﹣24a2b2+9b4=0,
∴(4a2﹣3b2)2=0,
∴,
∴tan∠CDN+tan∠MDN.
11.【解答】解:(1)∵四边形ABCD是矩形,
∴∠A=∠B=90°,
又∵∠AEF=∠BCE,
∴△AEF∽△BCE;
(2)延长HG交AE于点P,
在△AEF与△BCE中,
∴△AEF≌△BCE(AAS)
设BC=AE=y,
则BE=AF=(n﹣1)y,PEAEy
∴由题意知:GE=GF=GH,
∴由中位线的性质可知:GPAFy,
∴GE=GH=yyy,
∴Rt△PGE中,由勾股定理可知:()2=()2+()2,
解得n;
(3)由(2)知ABAD,即,
设AB=7x,AD=4x,
则AE=BC=4x,BE=AB﹣AE=3x,PEAE=2x,
∴BP=5x,
∴EF=EC5x,
∵点G是EF中点,且GH=GE,∠A=90°,
∴GE=GF=GHx,
作GH的垂直平分线,垂足为M,交BC于点Q,
则四边形HMQC是矩形,
∴CQ=HMGHx,
此时△HGQ是等腰三角形,
∴.
12.【解答】(1)证明:∵∠ABC+∠BAD=∠ADC,
∴∠ABC+∠BAD=∠ADE+∠CDE,
∵ABC=45°,∠ADE=45°,
∴∠ABC=∠ADE,
∴∠BAD=∠CDE,又∠ABC=∠ACB=45°,
∴△ABD∽△DCE;
(2)①证明:如图2,过点D作DF⊥BC交AB于点F,
设AE=CE=a,则AC=AE+CE=2a,
∵AD⊥AC,∠ADE=45°,
∴AD=AE=a,
∴在Rt△ACD中,CDa,
∵DF⊥BC,
∴∠BDF=90°,又∠ABC=45°,∠AFD=∠ABC+∠BDF,
∴∠AFD=135°,
同理∠DEC=135°,
∴∠AFD=∠DEC,又由(1)知∠BAD=∠CDE,
∴△ADF∽△DCE,
∴,即,
∴DFa,又CDa
∴CD=5DF,
∵∠FDB=90°,∠ABC=45°,
∴BD=DF,
∴CD=5BD;
②解:如图3,过D作DG⊥BC交AB于点G,则BD=DG=1,
设AD=x,则AC=x+3,DEx,
由①可知,△ADG∽△DCE,
∴,即,
解得,CD=3x,
在Rt△ACD中,AD2+AC2=CD2,即x2+(x+3)2=(3x)2,
解得,x1,x2(舍去),
则CD=3x,
故答案为:.
13.【解答】解:(1)在△ABD中,∠B+∠ADB+∠BAD=180°,
∵∠ADE=∠B,
∴∠ADE+∠ADB+∠BAD=180°,
∴∠BDE+∠BAD=180°,
∵∠BDE+∠CDE=180°,
∴∠BAD=∠CDE,
又∠B=∠C,
∴△ABD∽△DCE,
∴,
∴AB CE=BD CD;
(2)①如图1,作CE的垂直平分线交DC于F,
∴EF=FC,
∴∠EFD=2∠C,
∵∠B=2∠C,
∴∠B=∠EFD,
又∵AD=DE,
∴△ABD≌△DFE(AAS),
∴BD=EF=FC,DF=AB,
∵AB=8,BC=10,
∴BC=BD+DF+FC=BD+AB+BD,
∴10=BD+8+BD,
∴BD=1;
②如图2,延长CB到G,使BG=AB=8,
则∠G=∠C,
∴AG=AC,
作AH⊥BC于H,
∴GH=HC(BG+BC)=9,
∴BH=GH﹣BG=1,
在Rt△ABH中,根据勾股定理得,AH,
在Rt△ACH中,根据勾股定理得,AC12,
∴cos∠C,
作EC中垂线NP交BC于N,EC于P,
则设BD=EC=x,PCx,
∴NCx,
∴△ABD∽△DNE,
∴,
∴,
解得x,
经检验,x是方式方程的解,且满足题意,
∴BD,
故答案为.
14.【解答】(1)证明:①∵四边形ABCD是矩形,EF⊥AE与直线CD交于点F,
∴∠B=∠C=90°,∠AEF=90°,
∴∠BAE+∠AEB=∠AEB+∠CEF,
∴∠BAE=∠CEF;
②∵EF⊥AE与直线CD交于点F,
∴∠AEF=∠B=∠C=90°,
∵由①得∠BAE=∠CEF,
∴△ABE∽△ECF,
∴,
在矩形ABCD中,E是BC的中点,
设AB=x、BE=CE=y、AE=a,
∵,
∴,
∴,
∴,,
∴且∠AEF=∠B=90°,
∴△AEF∽△ABE;
(2)解:①∵AD平分∠EAF,
∴∠FAD=∠DAE,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠DAE=∠AEB,
∴∠FAD=∠AEB,
∵∠FDA=∠B=90°,
∴△ABE∽△FDA,
设BE=EC=x,则AD=2x,
∴,
∴∠AFE=30°,
由(1)得△AEF∽△ABE,
∴∠AFE=∠AEB,
∴∠AFE=∠AEB=30°,
∴AE=2AB=4,
∴,
∴AF=8.
②;理由如下:
∵∠ECF=∠GDF=90°,∠CFE=∠DFG,
∴△ECF∽△GDF,
设AB=CD=x,BE=EC=y,
∵CG平分∠DCC′,
∴∠DCG=∠GCC′=45°,
∵AG∥BC′,
∴∠DGC=∠GCC′=45°,
∴DG=DC=x,
∴.
∵由(1)得△ABE∽△ECF,
∴,
∴,
∴,,
∵,
∴,
∴,
∴xy=x2﹣y2,
∴,
设,
∴t=1﹣t2,
解得:,(t2<0,舍去),
∴.
15.【解答】(1)证明:如图,
∵四边形ABCD是矩形,
∴∠A=∠D=∠C=90°,
∴∠1+∠3=90°,
∵E,F分别在AD,BC上,将四边形ABFE沿EF翻折,使A的对称点P落在DC上,
∴∠EPH=∠A=90°,
∴∠1+∠2=90°,
∴∠3=∠2,
∴△EDP∽△PCH;
(2)解:∵四边形ABCD是矩形,
∴CD=AB=2,AD=BC=3,∠A=∠D=∠C=90°,
∵P为CD中点,
∴DP=CP1,
设EP=AE=x,
∴ED=AD﹣x=3﹣x,
在Rt△EDP中,EP2=ED2+DP2,
即x2=(3﹣x)2+1,
解得x,
∴EP=AP=x,
∴ED=AD﹣AE,
∵△EDP∽△PCH,
∴,即,
∴PH,
∵PG=AB=2,
∴GH=PG﹣PH.
(3)解:如图,延长AB,PG交于一点M,连接AP,
∵E,F分别在AD,BC上,将四边形ABFE沿EF翻折,使A的对称点P落在CD上,
∴AP⊥EF,BG⊥直线EF,
∴BG∥AP,
∵AE=EP,
∴∠EAP=∠EPA,
∴∠BAP=∠GPA,
∴△MAP是等腰三角形,
∴MA=MP,
∵P为CD中点,
∴设DP=CP=y,
∴AB=PG=CD=2y,
∵H为BC中点,
∴BH=CH,
∵∠BHM=∠CHP,∠CBM=∠PCH,
∴△MBH≌△PCH(ASA),
∴BM=CP=y,HM=HP,
∴MP=MA=MB+AB=3y,
∴HPPMy,
在Rt△PCH中,CHy,
∴BC=2CHy,
∴AD=BCy,
在Rt△APD中,APy,
∵BG∥AP,
∴△BMG∽△AMP,
∴,
∴BGy,
∴,
∴ABBG.
21世纪教育网(www.21cnjy.com)
同课章节目录
