2025年九年级数学中考二轮复习专题四边形中的十字架模型与相似三角形综合问题(含答案)
文档属性
| 名称 | 2025年九年级数学中考二轮复习专题四边形中的十字架模型与相似三角形综合问题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-11 05:40:46 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2025年九年级数学中考二轮复习专题四边形中的十字架模型与相似三角形综合问题
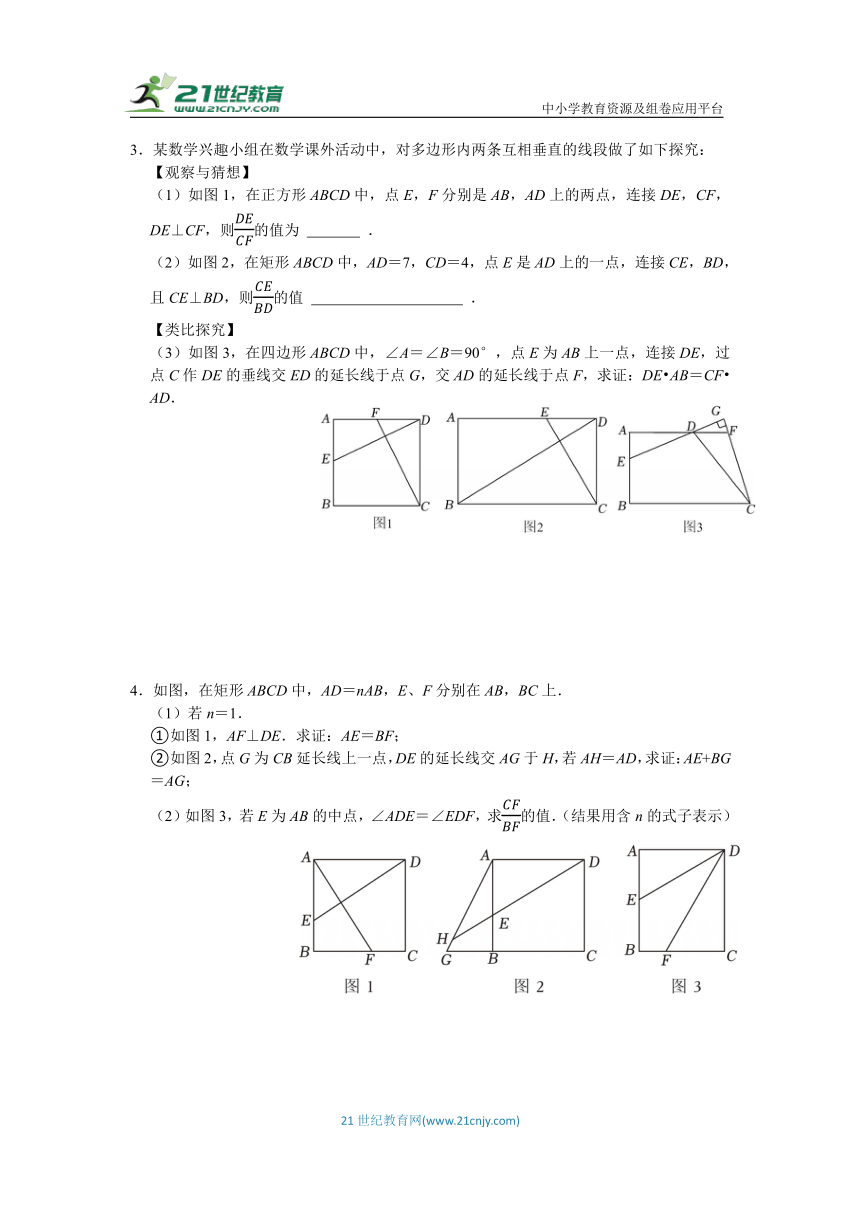
1.在正方形ABCD中,点H,E,F分别在边AB,BC,CD上,AE⊥HF于点G.
(1)如图1,求证:AE=HF;
(2)如图2,延长FH,交CB的延长线于M,连接AC,交HF于N.若MB=BE,EC=2BE,求的值;
(3)如图3,若AB=2,BH=DF,将线段HF绕点F顺时针旋转90°至线段MF,连接AM,则线段AM的最小值为 .
2.小王在学习人教版课本第二十七章后,进一步开展探究活动:如图1,在正方形ABCD中,点E是AB边上的一个动点(点E与点A,B不重合),连接CE,过点B作BF⊥CE于点G,交AD于点F.
(1)(探究1)如图1,很容易发现线段BF与CE之间的数量关系,请写出这个关系式,并加以证明.
(2)(探究2)如图2,当点E运动到AB中点时,连接DG,求证:DC=DG;
(3)(探究3)如图2,在(2)的条件下,求证:∠FGD=∠GCB;
(4)(探究4)如图3,在(2)的条件下,过点C作CM⊥DG于点H,分别交AD,BF于点M,N,求的值.
3.某数学兴趣小组在数学课外活动中,对多边形内两条互相垂直的线段做了如下探究:
【观察与猜想】
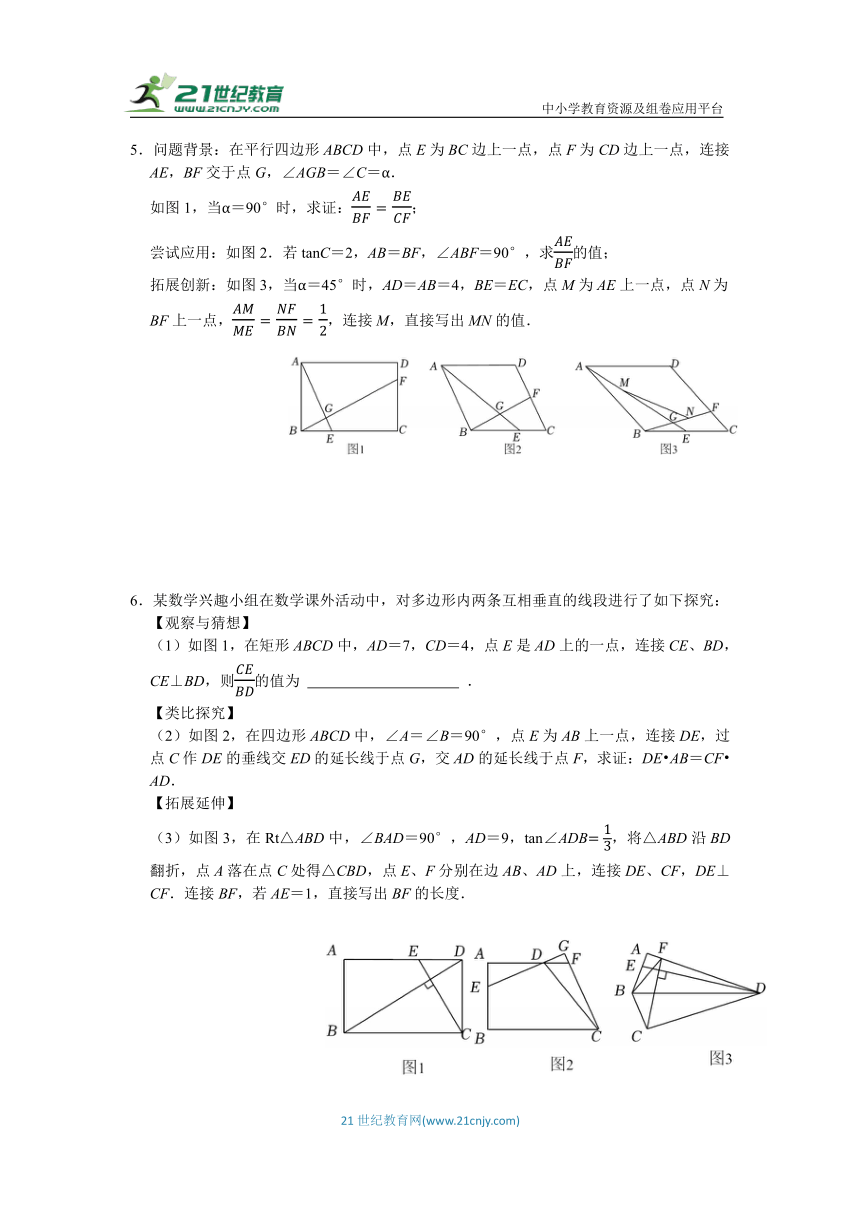
(1)如图1,在正方形ABCD中,点E,F分别是AB,AD上的两点,连接DE,CF,DE⊥CF,则的值为 .
(2)如图2,在矩形ABCD中,AD=7,CD=4,点E是AD上的一点,连接CE,BD,且CE⊥BD,则的值 .
【类比探究】
(3)如图3,在四边形ABCD中,∠A=∠B=90°,点E为AB上一点,连接DE,过点C作DE的垂线交ED的延长线于点G,交AD的延长线于点F,求证:DE AB=CF AD.
4.如图,在矩形ABCD中,AD=nAB,E、F分别在AB,BC上.
(1)若n=1.
①如图1,AF⊥DE.求证:AE=BF;
②如图2,点G为CB延长线上一点,DE的延长线交AG于H,若AH=AD,求证:AE+BG=AG;
(2)如图3,若E为AB的中点,∠ADE=∠EDF,求的值.(结果用含n的式子表示)
5.问题背景:在平行四边形ABCD中,点E为BC边上一点,点F为CD边上一点,连接AE,BF交于点G,∠AGB=∠C=α.
如图1,当α=90°时,求证:;
尝试应用:如图2.若tanC=2,AB=BF,∠ABF=90°,求的值;
拓展创新:如图3,当α=45°时,AD=AB=4,BE=EC,点M为AE上一点,点N为BF上一点,,连接M,直接写出MN的值.
6.某数学兴趣小组在数学课外活动中,对多边形内两条互相垂直的线段进行了如下探究:
【观察与猜想】
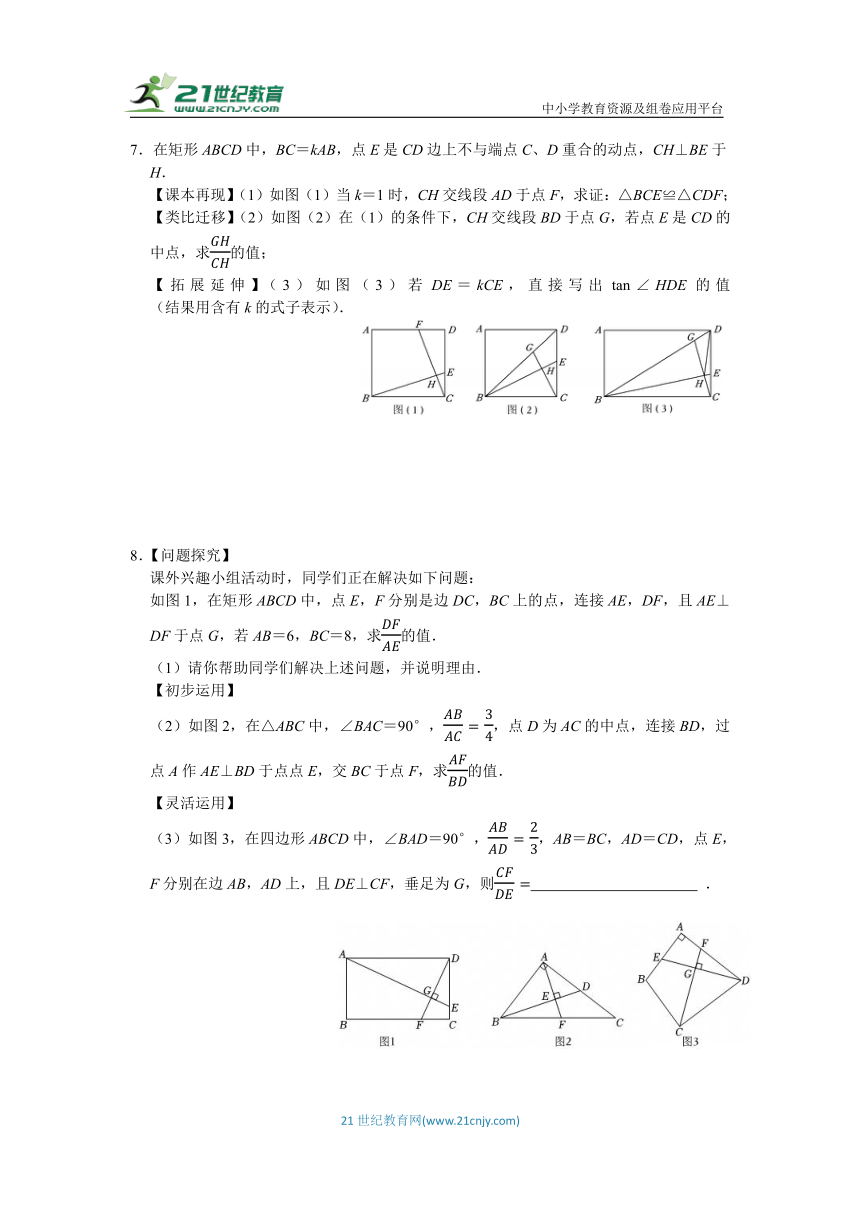
(1)如图1,在矩形ABCD中,AD=7,CD=4,点E是AD上的一点,连接CE、BD,CE⊥BD,则的值为 .
【类比探究】
(2)如图2,在四边形ABCD中,∠A=∠B=90°,点E为AB上一点,连接DE,过点C作DE的垂线交ED的延长线于点G,交AD的延长线于点F,求证:DE AB=CF AD.
【拓展延伸】
(3)如图3,在Rt△ABD中,∠BAD=90°,AD=9,tan∠ADB,将△ABD沿BD翻折,点A落在点C处得△CBD,点E、F分别在边AB、AD上,连接DE、CF,DE⊥CF.连接BF,若AE=1,直接写出BF的长度.
7.在矩形ABCD中,BC=kAB,点E是CD边上不与端点C、D重合的动点,CH⊥BE于H.
【课本再现】(1)如图(1)当k=1时,CH交线段AD于点F,求证:△BCE≌△CDF;
【类比迁移】(2)如图(2)在(1)的条件下,CH交线段BD于点G,若点E是CD的中点,求的值;
【拓展延伸】(3)如图(3)若DE=kCE,直接写出tan∠HDE的值 (结果用含有k的式子表示).
8.【问题探究】
课外兴趣小组活动时,同学们正在解决如下问题:
如图1,在矩形ABCD中,点E,F分别是边DC,BC上的点,连接AE,DF,且AE⊥DF于点G,若AB=6,BC=8,求的值.
(1)请你帮助同学们解决上述问题,并说明理由.
【初步运用】
(2)如图2,在△ABC中,∠BAC=90°,,点D为AC的中点,连接BD,过点A作AE⊥BD于点点E,交BC于点F,求的值.
【灵活运用】
(3)如图3,在四边形ABCD中,∠BAD=90°,,AB=BC,AD=CD,点E,F分别在边AB,AD上,且DE⊥CF,垂足为G,则 .
9.综合与探究
问题背景:如图3,四边形ABCD是矩形,AB=mBC,点G、H、E分别是线段AD、BC、AB上的动点,连接GH,过点E作GH的垂线交线段CD于点F(只考虑F在CD上的情况)
(1)①如图1,当点G运动到A点,点E运动到B点时,若AB=6,BH=2,m=2,则的值为 (直接写答案)
②如图2,当点G不与A点重合,点E运动到B点时,若m=2,试求的值.
问题探究:(2)如图3,当G不与A重合,E不与B重合时,用含m的式子表示的值.
问题拓展:(3)如图4,将背景问题中的矩形改成已知“在四边形GBCF中,∠C=90°,,,GH⊥BF,则的值为 .(直接写答案).
10.(1)问题提出如图(1),在正方形ABCD中,E为AD中点,BF⊥CE,求的值;
(2)问题探究如图(2),在等腰Rt△ABC中,点E为AB的中点,BF⊥CE,求的值.
11.如图1,在Rt△ABC中,∠BAC=90°,D为边AB上一点,∠ACD=∠B.
(1)求证:AC2=AD AB;
(2)如图2,过点A作AM⊥CD于M,交BC于点E,若AB=4AD,求的值;
(3)如图,N为CD延长线上一点,连接BN,且∠NBD=2∠ACD,若,直接写出的值(用含n的代数式表示).
12.问题背景:如图(1),在矩形ABCD中,过C作CE⊥BD于F,交AD于E,图中与△ABD相似的三角形有多个,试写出其中一个三角形并证明.
尝试运用:如图(2),在四边形ABCD中,∠A=∠B=90°,点E为AB上一点,过点E作EF⊥CD交CD的延长线于点F,交AD于点G,求证:EG AB=CD AG.
拓展创新:如图(3),在四边形ABCD中,∠BAD=∠BCD=90°,BA=BC=1,DA=DC=3,点E,F分别在边AB,AD上,连接DE,CF.若DE⊥CF,求的值.
13.(1)[问题探究]如图1,在正方形ABCD中,点E、F、G、H分别在线段AB、BC、CD、DM上,且EG⊥FH.试猜想的值,并证明你的猜想.
(2)[知识迁移]如图2,在矩形ABCD中,AB=m,BC=n,点E、F、G、H分别在线段AB、BC、CD、DA上,且EG⊥FH.则求的值(用含m,n的式子表示).
(3)[拓展应用]如图3,在四边形ABCD中,∠DAB=90°,∠ABC=60°,AB=BC,点E、F分别在线段AB、AD上,且CE⊥BF.则 .
14.【问题探究】如图1,正方形ABCD中,点F、G分别在边BC、CD上,且AF⊥BG于点P,求证AF=BG;
【知识迁移】如图2,矩形ABCD中,AB=m,BC=n,点E、F、G、H分别在边AB、BC、CD、AD上,且EG⊥FH于点P.求的值;
【拓展应用】如图3,在四边形ABCD中,∠ABC=90°,∠BDC=120°,DB=DC,点E、F分别在线段AB、BC上,且CE⊥DF于点P.请直接写出的值.
15.在△ABC中,∠BAC=90°,E、F分别在BC、AB边上.
(1)如图1,EF⊥AB,求证:;
(2)点D在AC边上,AE⊥DF,且m.
①如图2,若,求m的值;
②如图3,若∠C=2∠ADF,m,直接写出的值.
参考答案
1.【解答】(1)证明:如图1中,作HM⊥CD于M.
∴四边形ABC都是正方形,
∴∠B=∠C=∠CMH=90°,AB=BC,
∴四边形BCMH是矩形,
∴HM=BC=AB,
∵AE⊥HF,
∴∠AGH=∠AHM=90°,
∴∠BAE+∠AHG=90°,∠AHG+∠FHM=90°,
∴∠BAE=∠FHM,∵∠B=∠HMF=90°,
∴△ABE≌△HMF(ASA),
∴AE=HF.
(2)解:如图2中,
∵EC=2BE,不妨设BE=BM=a,EC=2a,则AB=BC=CD=3a,CM=4a,
∴tan∠BAE,
∵ABE=∠MGE=90°,
∴∠BAE+∠AEB=90°,∠M+∠AEB=90°,
∴∠M=∠BAE,
∴tan,
∴BHa,CFa,
∴AH=AB﹣BH=3aaa,
∴CF∥AH,
∴△ANH∽△CNF,
∴2.
(3)解:如图3中,延长BA到N,使得AN=AD,作MJ⊥AN于J,交CD的延长线于K,作FQ⊥AB于Q,则四边形BCFQ,四边形ADKJ都是矩形,△FQH≌△FKM(AAS).
∴QH=KM,DF=AQ=BH,
∵KJ=AD=AB,
∴JM=AQ+BH=2AQ,
∵FK=FQ=JQ=AD=AN,
∴AQ=JN,
∴JM=2JN,
∴tan∠N2,
∴点M的运动轨迹是射线NM,∠N是的定值,作AP⊥MN于P,
根据垂线段最短可知:当AM与AP重合时,AM的值最小,
∵tan∠N2,设NP=x,AP=2x,
在Rt△APN中,则有22=x2+4x2,
解得x(负根已经舍弃),
∴PA=2x,
∴AM的最小值为.
2.【解答】(1)解:BF=CE,理由如下:
∵四边形ABCD是正方形,
∴AB=BC,∠FAB=∠EBC=90°,
∴∠ECB+∠CEB=90°,
∵BF⊥CE,
∴∠FBA+∠CEB=90°,
∴∠FBA=∠ECB,
在△FBA和△ECB中,
,
∴△FBA≌△ECB(ASA),
∴BF=CE;
(2)证明:如图2,过点D作DK⊥CE于K,
设AB=CD=BC=2a,
∵点E是AB的中点,
∴,
∴,
在Rt△CEB中,根据面积相等,得BG CE=CB EB,
∴,
∴,
∵∠DCE+∠BCE=90°,∠CBF+∠BCE=90°,
∴∠DCE=∠CBF,
又∵CD=BC,∠CKD=∠BGC=90°,
∴△CKD≌△BGC(AAS),
∴,
∴,
∵DK=DK,∠CKD=∠GKD=90°,
∴△DGK≌△DCK(SAS),
∴CD=GD;
(3)证明:∵DK⊥CE,BF⊥CE,
∴DK∥BF,即DK∥GF,
∴∠GDK=∠FGD,
由(2)知△DGK≌△DCK,
∴∠CDK=∠GDK,
∴∠CDK=∠FGD,
由(2)知△CKD≌△BGC,
∴∠CDK=∠BCG,
∴∠FGD=∠GCB,
(4)解:如图3,过点D作DQ⊥CE于Q,
∵,
∴,
在Rt△CQD中,CD=2a,
∴,
∵∠MDH+∠HDC=90°,∠HCD+∠HDC=90°,
∴∠MDH=∠HCD,
∴△CHD∽△DHM,
∴,
∴,
在Rt△CHG中,,,
∴,
∵∠MGH+∠CGH=90°,∠HCG+∠CGH=90°,
∴∠CGH=∠CNG,
∴△GHN∽△CHG,
∴,
∴,
∴,
∴.
3.【解答】(1)解:设DE与CF的交点为G,
∵四边形ABCD是正方形,
∴∠A=∠FDC=90°,AD=CD,
∵DE⊥CF,
∴∠DGF=90°,
∴∠ADE+∠CFD=90°,
∠ADE+∠AED=90°,
∴∠CFD=∠AED,
在△AED与△DFC中,
,
∴△AED≌△DFC(AAS),
∴DE=CF,
∴,
故答案为:1;
(2)解:如图,设DB与CE交于点G,
∵四边形ABCD是矩形,
∴∠A=∠EDC=90°,
∵CE⊥BD,
∴∠DGC=90°,
∴∠CDG+∠ECD=90°,
∠ADB+∠CDG=90°,
∴∠ECD=∠ADB,
∵∠CDE=∠A,
∴△DEC∽△ABD,
∴,
故答案为:;
(3)证明:如图,过点C作CH⊥AF交AF的延长线于点H,
∵CG⊥EG,
∴∠G=∠H=∠A=∠B=90°,
∴四边形ABCH为矩形,
∴AB=CH,
∠FCH+∠CFH=∠DFG+∠FDG=90°,
∴∠FCH=∠FDG=∠ADE,∠A=∠H=90°,
∴△AED∽△HFC,
∴,
∴,
∴DE AB=CF AD.
4.【解答】(1)①证明:∵四边形ABCD是矩形,AD=nAB,n=1,
∴四边形ABCD是正方形,
∴AD=AB,∠DAB=90°=∠ABC,
∴∠DAF+∠BAF=90°,
∵AF⊥DE,
∴∠DAF+∠ADE=90°,
∴∠ADE=∠BAF,
而AD=AB,∠DAE=∠ABF=90°,
∴△ADE≌△BAF(ASA),
∴AE=BF;
②过点A作AF⊥HD交BC于点F,如图:
由(1)可知:AE=BF,
∵AH=AD,AF⊥HD,
∴∠HAF=∠DAF,
∵AD∥BC,
∴∠DAF=∠AFG,
∴∠HAF=∠AFG,
∴AG=GF,
∵GF=GB+BF,
∴AG=GB+BF=GB+AE;
(3)过点E作EH⊥DF于H,连接EF,如图:
∵E为AB的中点,
∴AE=BEAB,
∵∠ADE=∠EDF,EA⊥AD,EH⊥DF,
∴AE=EH,AD=DH=nAB,
∴BE=EH,而EF=EF,
∴Rt△BEF≌Rt△HEF(HL),
∴BF=FH,
设BF=x=FH,则FC=BC﹣BF=nAB﹣x,
∵DF2=FC2+CD2,
∴(nAB+x)2=(nAB﹣x)2+AB2,
∴xBF,
∴FC=nAB﹣xAB,
∴4n2﹣1.
5.【解答】问题背景:
证明:∵在平行四边形ABCD中,∠AGB=∠C=α=90°,
∴四边形ABCD是矩形,
∴∠ABG+∠BAG=∠ABG+∠CBG=90°,
∴∠BAG=∠CBG,
∵∠ABF=∠C=90°,
∴Rt△ABE∽Rt△BCF,
∴;
尝试应用:
解:延长AE、DC交于点P,
∵AB∥CD,
∴∠BFC=∠ABF=90°,
在Rt△BCF中,设CF=m,
∵tanC2,
∴BF=2m=AB,
∵∠AGB=∠C=α,
∴在Rt△ABG中,tan∠AGB=tan∠C2,
∴BG=m=FG,AGm,
∵AB∥CD,
∴∠BAG=∠P,∠ABG=∠PFG,
∴△ABG≌△PFG(AAS),
∴AG=PGm,AB=PF=2m,
∴PC=m,
∵AB∥DC,
∴△ABG≌△PFG(AAS),
∴2,
∴AEAPm,
∴;
拓展创新:
延长BM交AD于点P,过E作EQ⊥AB,交AB延长线于点Q,过F作FH⊥BC于点H,延长HF、AD 交于点K,连接PF,
∵AD∥BC,
∴△APM∽△EBM,
∴,
∵BE=EC=2,
∴AP=1,PD=3,
∵,
∴MN∥PF,MNPF,
∵∠AGB=∠C=45°=∠CBQ,∠ABG=∠CFB,
∴Rt△BEQ是等腰直角三角形,BQ=EQ,∠BAE=∠CBF,
在等腰直角三角形Rt△CFH中,设CH=FH=x,则CFx,
∴tan∠BAE,tan∠CBF,
∴,
解得:x=22,
∴CF=4﹣2,DF=2,
∴DK=FK=2,PK=5,
在Rt△PFK中,由勾股定理得:PF,
∴MNPF.
故MN的值为.
6.【解答】(1)解:如图,设DB与CE交于点G,
∵四边形ABCD是矩形,
∴∠A=∠EDC=90°,
∵CE⊥BD,
∴∠DGC=90°,
∴∠CDG+∠ECD=90°,∠ADB+∠CDG=90°,
∴∠ECD=∠ADB,
∵∠CDE=∠A,
∴△DEC∽△ABD,
∴,
故答案为:;
(2)证明:如图,过点C作CH⊥AF交AF的延长线于点H,
∵CG⊥EG,
∴∠G=∠H=∠A=∠B=90°,
∴四边形ABCH为矩形,
∴AB=CH,∠FCH+∠CFH=∠DFG+∠FDG=90°,
∴∠FCH=∠FDG=∠ADE,∠A=∠H=90°,
∴△DEA∽△CFH,
∴,
∴,
∴DE AB=CF AD;
(3)解:如图,连接AC交BD于点H,则AH⊥BD,
∵AD=9,tan∠ADB,
∴AB=3,
由勾股定理得,BD=3,
由面积法知,AH,
∵将△ABD沿BD翻折,点A落在点C处得△CBD,
∴AC=2AH,
∵CF⊥DE,
∴∠ACF=∠BDE,
∵∠HAD=∠ABD,
∴△ACF∽△BDE,
∴,
∵AE=1,
∴BE=2,
∴AF,
∴BF.
7.【解答】(1)证明:当k=1时,BC=AB,
∴矩形ABCD是正方形,
∴BC=CD,∠BCD=∠D=90°,
∵CH⊥BE,
∴∠BHC=90°,
∴∠1+∠2=∠2+∠3=90°,
∴∠1=∠3,
在△BCE和△CDF中
.
∴△BCE≌△CDF(ASA);
(2)解:延长CH,交AD于点F,由(1)可知:△BCE≌△CDF,
∴CE=DF,BE=CF.
∵点E是CD中点,
∴CD=2CE,
∴BC=2CE=2DF,
∴tan,
∴tan∠3,
设EH=a,则CH=2a,BH=4a,
∴BE=BH+EH=5a,
∴CF=BE=5a,
∵AD∥BC,
∴△GFD∽△GCB,
∴
∴,
∴;
(3)解:∵DE=kCE,
∴CD=DE+CE=(k+1)CE,
∴CE=k+1CD,
∵BC=kAB=kCD,
∴tan,
∵∠1=∠3,
∴tan∠3,
设EH=1,HC=k(k+1),BH=k2(k+1)2
∴BE=k2(k+1)2+1,
∵△BCE∽△CDF.
∴
∴FHk(k+1),
∴tan,
∵F、H、E、D四点共圆,
∴tan∠HDE.
故答案为:.
8.【解答】解:(1)∵四边形ABCD是矩形,且AB=6,BC=8,
∴∠C=∠ADE=90°,AB=CD=6,BC=AD=8,
∴∠ADG+∠FDC=90°,
∵AE⊥DF,
∴∠AGD=90°,
∴∠DAG+∠ADG=90°,
∴∠DAG=∠FDC,
∴△DCF∽△ADE,
∴.
(2)过点B作CB的垂线,过点D作BC的垂线,垂足为K,过点A作BC的平行线,分别交两条垂线于G、H,如图:
则四边形GBKH为矩形,
∵D为AC的中点,
∵∠AHD=∠CKD=90°,∠ADH=∠CDK,
∴△ADH≌△CDK(AAS),
∴DH=DK,
∵∠BAD=90°,
∴∠GAB+∠HAD=90°,
∵∠GAB+∠GBA=90°,
∴∠HAD=∠GBA,
∵∠G=∠AHD=90°,
∴△AHD∽△BGA,
∴,
∵,
∴,
设DH=2y,则BG=4y,
∴,
由(1)知:,
∴.
(3)过C作CN⊥AD于N,CM⊥AB交AB的延长线于点M,如图3:
∵∠BAD=90°,即AB⊥AD,
∴∠A=∠M=∠CNA=90°,
∴四边形AMCN是矩形,
∴AM=CN,AN=CM,
在△BAD和△BCD中,
,
∵△BAD≌△BCD(SSS),
∴∠BCD=∠A=90°,
∴∠ABC+∠ADC=180°,
∵∠ABC+∠CBM=180°,
∴∠MBC=∠ADC,
∵∠CND=∠M=90°,
∴△BCM∽△DCN,
∵,
∴,
设BM=2y,AB=BC=2x,则DN=3y,AD=CD=3x,
∴CN=2x+2y,
在Rt△CND中,由勾股定理得:DN2+CN2=CD2,
∴(3y)2+(2x+2y)2=(3x)2,
解得:或x=﹣y(舍去),
∴,
故答案为:.
9.【解答】解:(1)①∵矩形ABCD,
∴∠ABC=∠BCD=90°,
∴∠BAH+∠AHB=90°,
∵AH⊥BF,
∴∠CBF+∠AHB=90°,
∴∠BAH=∠CBF,
∴△ABH∽△BCF,
∴,
∵AB=mBC,m=2,
∴,
故答案为:2;
②如图,过A作AT∥GH交BC于T,
∵GH⊥BF,
∴AT⊥BF,
∵矩形ABCD,
∴AD∥BC,
∴四边形ATHG是平行四边形,
∴AT=GH,
由①可得,
∴;
(2)如图,过A作AT∥GH交BC于T,
∵GH⊥EF,
∴AT⊥EF,
同理可得AT=GH,
过B作BK∥EF交CD于K,
同理可得四边形BEFK为平行四边形,
∴BK=EF,BK⊥AT,
由①可得,
∴;
(3)如图,过G作BC的平行线交CF的延长线于D,过B作BC的垂线交DG于A,
∵∠C=90°,
∴∠ABC=90°,∠ADC=180°﹣90°=90°,∠AGB=∠GBC,
∴四边形ABCD为矩形,
∴∠A=90°,
∵,
∴,
设AB=9x,则BG=10x,
∵,
∴,
∵GH⊥BF,
结合(1)的结论可得,
故答案为:.
10.【解答】(1)证明:∵四边形ABCD是正方形,
∴BC=CD=AD,∠D=∠BCF=90°,
∴∠DCE+∠BCE=90°,
∵BF⊥CE,
∴∠BGC=90°,
∴∠BCE+∠CBG=90°,
∴∠DCE=∠CBG,
∴△DCE≌△CBF(ASA),
∴DE=CF,
∵E为AD中点,
∴AE=DE,
∴CF=DF,
∴;
(2)解:过点A作AD∥BC,CD∥AB,则四边形ABCD是正方形,
∵E为AB的中点.
由(1)可知M为AD的中点,
∵AD∥BC,
∴△AMF∽△CBF,
∴,
设BE=AE=x,
∴AC=2x,CEx,
∴CFx,
∵,
∴BGx,
∴CGx,
∴FGx,
∴.
11.【解答】(1)证明:∵∠ACD=∠B,∠A=∠A,
∴△ACD∽△ABC,
∴,
∴AC2=AD AB;
(2)解:过E点作EF⊥AB,交CD的延长线于F点,
∵AB=4AD,
∴设AD=m,AB=4m,
∴AC=2m,
∵∠EAB+∠EAC=90°=∠EAC+∠ACD,
∴∠EAB=∠ACD=∠B,
∴EA=EB,∠EAC=∠C,
∴EA=EC=EB,
∵EF⊥AB,CA⊥AB,
∴EF∥AC,
∴BG=AG=2m,GE=m,
∴DG=DA=m,
∵∠GDF=∠ADC,∠FGD=∠CAD=90°,
∴△FGD≌△CAD(ASA),
∴∠F=∠ACD,FG=AC=2m,
∴EF=3m,
∵∠FME=∠CMA,
∴△FME∽△CMA,
∴.
(3)解:作BF⊥NC于F,作AE⊥NC交BC于E,交NC于M;
设DM=x,
∵∠ACD+∠CAM=∠CAM+∠MAD=90°,
∴∠ACD=∠MAD,
∴tan∠ACD=tan∠MAD,
即:,
∴AM=nx,AM2=DM MC,
即n2x2=x MC,
∴MC=n2x,
∵∠ACD=∠MAD,∠ACD=∠ABC,
∴∠MAD=∠ABC,
∴BE=AE,
又∵∠CAE+∠EAB=∠ACB+∠ABC,
∴∠CAE=∠ACB,
∴CE=AE,
∴BE=CE,
∴E为BC中点,
又BF⊥NC,AE⊥NC,
∴BE∥AE,
在Rt△BCF中,EM为中位线,
∴MF=MC,
∴MF=n2x,
∴FD=(n2﹣1)x,
∵∠NBD=2∠ACD,
而∠ACD=∠DAM,
∴∠NBD=2∠DAM,
而由BF∥AM可得,∠DAM=∠FBD,
∴∠NBD=2∠FBD,
∴BF为∠NBD的角平分线,
又BF⊥ND,
∴BF为△NBD的中线,BN=BD,
∴ND=2DF=2(n2﹣1)x,
∴.
12.【解答】问题背景:解:△EFD∽△CFB,证明如下:
∵四边形ABCD是矩形,
∴AD∥BC,
∴△EFD∽△CFB;
尝试运用:证明:如图(2),过点A作AH∥CD,交BC于点H,
则∠AHB=∠C,
∵∠BAD=∠B=90°,
∴∠BAD+∠B=180°,
∴AD∥BC,
∴四边形ADCH是平行四边形,∠GDF=∠C,
∴AH=CD,
∵EF⊥CD,
∴∠GFD=90°,
∵∠BAD=90°=∠GFD,∠AGE=∠DGF,
∴∠AEG=∠GDF,
∴∠AEG=∠C=∠AHB,
又∵∠GAE=∠B,
∴△AEG∽△BHA.
∴AG:AB=EG:AH.
∴AG:AB=EG:CD,
∴EG AB=CD AG;
拓展创新:解:如图(3),过点C作CG⊥AD于点G,连接AC、BD交于点H,
∵BA=BC,DA=DC,
∴BD垂直平分AC,
∴∠AHD=90°,AH=CH,
∵CF⊥DE,CG⊥AD,
∴∠FCG+∠CFG=∠CFG+∠ADE=90°,
∴∠FCG=∠ADE,
∵∠BAD=∠CGF=90°,
∴△DEA∽△CFG,
∴,
在Rt△ADB中,tan∠ADB,
∴tan∠ADH,
设AH=a,则DH=3a,
∵AH2+DH2=AD2,
∴a2+(3a)2=32,
解得:a(负值已舍去),
∴AH,DH,
∴AC=2AH,
∵S△ADCAC DHAD CG,
∴AC DH=AD CG,
即3CG,
∴CG,
∴.
13.【解答】解:(1)1,理由如下:
如图1,过点A作AM∥HF交BC于点M,作AN∥EG交CD的延长线于点N,
∵四边形ABCD是正方形,
∴AB∥CD,AD∥BC,AB=AD,∠ABM=∠BAD=∠ADN=90°,
∴AM=HF,AN=EG,
∵EG⊥FH,
∴∠NAM=90°,
∴∠BAM=∠DAN,
在△ABM和△ADN中,∠BAM=∠DAN,AB=AD,∠ABM=∠ADN,
∴△ABM≌△ADN(ASA),
∴AM=AN,即EG=FH,
∴1;
(2)如图2,过点A作AM∥HF交BC于点M,作AN∥EG交CD的延长线于点N,
∴AM=HF,AN=EG,
在长方形ABCD中,BC=AD,∠ABM=∠BAD=∠ADN=90°,
∵EG⊥FH,
∴∠NAM=90°,
∴∠BAM=∠DAN,
∴△ABM∽△ADN,
∴,
∵AB=m,BC=AD=n,
∴;
(3)如图3,过点C作CM⊥AB于点M,CE交BF于点O.
∵CM⊥AB,
∴∠CME=90°,
∴∠ECM+∠CEM=90°,
∵CE⊥BF,
∴∠BOE=90°,
∴∠CEM+∠ABF=90°,
∴∠ECM=∠ABF,
又∠FAB=∠EMC=90°,
∴△CME∽△BAF,
∴,
∵AB=BC,∠ABC=60°,
∴sin60°,
故答案为:.
14.【解答】(1)证明:∵四边形ABCD是正方形,
∴∠ABC=∠C=90°,AB=BC,∠2+∠ABP=90°,
∵AF⊥BG,
∴∠1+∠ABP=90°,
∴∠1=∠2,
在△ABF和△BCG中,
,
∴△ABF≌△BCG(ASA),
∴AF=BG;
(2)解:作EM⊥DC于点M,作HN⊥BC于点N,
则EM∥AD∥BC,HN∥AB∥DC,
∴EM⊥HN,EM=AD=BC,HN=AB=DC,
又∵EG⊥HF,
∴∠GEM=∠FHN,
∴Rt△EMG∽Rt△HNF,
∴,
即;
(3)解:过点D作DH⊥BC于点H,交CE于点M,
则∠DHF=∠ABC=90°,
∴∠CMH+∠BCE=90°,
∵CE⊥DF,
∴∠PDM+∠PMD=90°,
∵∠PMD=∠CMH,
∴∠BCE=∠PDM,
∴△CBE∽△DHF,
∴,
∵BD=CD,∠BDC=120°,
∴∠DCH=30°,BC=2CH,
在Rt△CHD中,∠CHD=90°,
∴tan30°,
∴CHDH,
∴BC=2DH,
∴2.
15.【解答】(1)证明:如图1中,
∵EF⊥AB,∠A=90°,
∴∠EFB=∠A=90°,
∵∠B=∠B,
∴△BFE∽△BAC,
∴.
(2)①解:如图2中,过点E作EM⊥AB于M,连接DM.
由(1)可知:,
∴,
∵m,
∴m,
∴CD=EM,
∵∠EMB=∠BAC=90°,
∴EM∥CD,
∴四边形ECDM是平行四边形,
∴DM∥BC,
∴,
∵AE⊥DF,
∴∠EAM+∠AFD=90°,
∵∠AFD+∠ADF=90°,
∴∠EAM=∠ADF,
∵∠AME=∠DAF=90°,
∴△AFD∽△MEA,
∴,设AD=2m,AM=3m,
∴DMm,
∴.
②解:过点E作EM⊥AB于M,连接DM,过点F作FH⊥DM于H.
由①可知,四边形ECDM是平行四边形,
∴DM∥BC,
∴m,设AD=3k,DM=5k,则AM=4k,
∵∠C=2∠ADF,∠C=∠ADM,
∴∠ADF=∠FDM,
∵FA⊥AD,FH⊥DM,
∴∠DAF=∠DHF=90°,
∵DF=DF,
∴△DFA≌△DFH(AAS),
∴AF=FH,AD=DH=3k,设AF=FH=y,
∴MH=DM﹣DH=2k,
在Rt△FMH中,∵FM2=FH2+MH2,
∴(4k﹣y)2=y2+(2k)2,
解得yk,
∴AFk,
∴DFk,
由①可知,,
∴,
∴AE=2k,
∴.
21世纪教育网(www.21cnjy.com)
2025年九年级数学中考二轮复习专题四边形中的十字架模型与相似三角形综合问题
1.在正方形ABCD中,点H,E,F分别在边AB,BC,CD上,AE⊥HF于点G.
(1)如图1,求证:AE=HF;
(2)如图2,延长FH,交CB的延长线于M,连接AC,交HF于N.若MB=BE,EC=2BE,求的值;
(3)如图3,若AB=2,BH=DF,将线段HF绕点F顺时针旋转90°至线段MF,连接AM,则线段AM的最小值为 .
2.小王在学习人教版课本第二十七章后,进一步开展探究活动:如图1,在正方形ABCD中,点E是AB边上的一个动点(点E与点A,B不重合),连接CE,过点B作BF⊥CE于点G,交AD于点F.
(1)(探究1)如图1,很容易发现线段BF与CE之间的数量关系,请写出这个关系式,并加以证明.
(2)(探究2)如图2,当点E运动到AB中点时,连接DG,求证:DC=DG;
(3)(探究3)如图2,在(2)的条件下,求证:∠FGD=∠GCB;
(4)(探究4)如图3,在(2)的条件下,过点C作CM⊥DG于点H,分别交AD,BF于点M,N,求的值.
3.某数学兴趣小组在数学课外活动中,对多边形内两条互相垂直的线段做了如下探究:
【观察与猜想】
(1)如图1,在正方形ABCD中,点E,F分别是AB,AD上的两点,连接DE,CF,DE⊥CF,则的值为 .
(2)如图2,在矩形ABCD中,AD=7,CD=4,点E是AD上的一点,连接CE,BD,且CE⊥BD,则的值 .
【类比探究】
(3)如图3,在四边形ABCD中,∠A=∠B=90°,点E为AB上一点,连接DE,过点C作DE的垂线交ED的延长线于点G,交AD的延长线于点F,求证:DE AB=CF AD.
4.如图,在矩形ABCD中,AD=nAB,E、F分别在AB,BC上.
(1)若n=1.
①如图1,AF⊥DE.求证:AE=BF;
②如图2,点G为CB延长线上一点,DE的延长线交AG于H,若AH=AD,求证:AE+BG=AG;
(2)如图3,若E为AB的中点,∠ADE=∠EDF,求的值.(结果用含n的式子表示)
5.问题背景:在平行四边形ABCD中,点E为BC边上一点,点F为CD边上一点,连接AE,BF交于点G,∠AGB=∠C=α.
如图1,当α=90°时,求证:;
尝试应用:如图2.若tanC=2,AB=BF,∠ABF=90°,求的值;
拓展创新:如图3,当α=45°时,AD=AB=4,BE=EC,点M为AE上一点,点N为BF上一点,,连接M,直接写出MN的值.
6.某数学兴趣小组在数学课外活动中,对多边形内两条互相垂直的线段进行了如下探究:
【观察与猜想】
(1)如图1,在矩形ABCD中,AD=7,CD=4,点E是AD上的一点,连接CE、BD,CE⊥BD,则的值为 .
【类比探究】
(2)如图2,在四边形ABCD中,∠A=∠B=90°,点E为AB上一点,连接DE,过点C作DE的垂线交ED的延长线于点G,交AD的延长线于点F,求证:DE AB=CF AD.
【拓展延伸】
(3)如图3,在Rt△ABD中,∠BAD=90°,AD=9,tan∠ADB,将△ABD沿BD翻折,点A落在点C处得△CBD,点E、F分别在边AB、AD上,连接DE、CF,DE⊥CF.连接BF,若AE=1,直接写出BF的长度.
7.在矩形ABCD中,BC=kAB,点E是CD边上不与端点C、D重合的动点,CH⊥BE于H.
【课本再现】(1)如图(1)当k=1时,CH交线段AD于点F,求证:△BCE≌△CDF;
【类比迁移】(2)如图(2)在(1)的条件下,CH交线段BD于点G,若点E是CD的中点,求的值;
【拓展延伸】(3)如图(3)若DE=kCE,直接写出tan∠HDE的值 (结果用含有k的式子表示).
8.【问题探究】
课外兴趣小组活动时,同学们正在解决如下问题:
如图1,在矩形ABCD中,点E,F分别是边DC,BC上的点,连接AE,DF,且AE⊥DF于点G,若AB=6,BC=8,求的值.
(1)请你帮助同学们解决上述问题,并说明理由.
【初步运用】
(2)如图2,在△ABC中,∠BAC=90°,,点D为AC的中点,连接BD,过点A作AE⊥BD于点点E,交BC于点F,求的值.
【灵活运用】
(3)如图3,在四边形ABCD中,∠BAD=90°,,AB=BC,AD=CD,点E,F分别在边AB,AD上,且DE⊥CF,垂足为G,则 .
9.综合与探究
问题背景:如图3,四边形ABCD是矩形,AB=mBC,点G、H、E分别是线段AD、BC、AB上的动点,连接GH,过点E作GH的垂线交线段CD于点F(只考虑F在CD上的情况)
(1)①如图1,当点G运动到A点,点E运动到B点时,若AB=6,BH=2,m=2,则的值为 (直接写答案)
②如图2,当点G不与A点重合,点E运动到B点时,若m=2,试求的值.
问题探究:(2)如图3,当G不与A重合,E不与B重合时,用含m的式子表示的值.
问题拓展:(3)如图4,将背景问题中的矩形改成已知“在四边形GBCF中,∠C=90°,,,GH⊥BF,则的值为 .(直接写答案).
10.(1)问题提出如图(1),在正方形ABCD中,E为AD中点,BF⊥CE,求的值;
(2)问题探究如图(2),在等腰Rt△ABC中,点E为AB的中点,BF⊥CE,求的值.
11.如图1,在Rt△ABC中,∠BAC=90°,D为边AB上一点,∠ACD=∠B.
(1)求证:AC2=AD AB;
(2)如图2,过点A作AM⊥CD于M,交BC于点E,若AB=4AD,求的值;
(3)如图,N为CD延长线上一点,连接BN,且∠NBD=2∠ACD,若,直接写出的值(用含n的代数式表示).
12.问题背景:如图(1),在矩形ABCD中,过C作CE⊥BD于F,交AD于E,图中与△ABD相似的三角形有多个,试写出其中一个三角形并证明.
尝试运用:如图(2),在四边形ABCD中,∠A=∠B=90°,点E为AB上一点,过点E作EF⊥CD交CD的延长线于点F,交AD于点G,求证:EG AB=CD AG.
拓展创新:如图(3),在四边形ABCD中,∠BAD=∠BCD=90°,BA=BC=1,DA=DC=3,点E,F分别在边AB,AD上,连接DE,CF.若DE⊥CF,求的值.
13.(1)[问题探究]如图1,在正方形ABCD中,点E、F、G、H分别在线段AB、BC、CD、DM上,且EG⊥FH.试猜想的值,并证明你的猜想.
(2)[知识迁移]如图2,在矩形ABCD中,AB=m,BC=n,点E、F、G、H分别在线段AB、BC、CD、DA上,且EG⊥FH.则求的值(用含m,n的式子表示).
(3)[拓展应用]如图3,在四边形ABCD中,∠DAB=90°,∠ABC=60°,AB=BC,点E、F分别在线段AB、AD上,且CE⊥BF.则 .
14.【问题探究】如图1,正方形ABCD中,点F、G分别在边BC、CD上,且AF⊥BG于点P,求证AF=BG;
【知识迁移】如图2,矩形ABCD中,AB=m,BC=n,点E、F、G、H分别在边AB、BC、CD、AD上,且EG⊥FH于点P.求的值;
【拓展应用】如图3,在四边形ABCD中,∠ABC=90°,∠BDC=120°,DB=DC,点E、F分别在线段AB、BC上,且CE⊥DF于点P.请直接写出的值.
15.在△ABC中,∠BAC=90°,E、F分别在BC、AB边上.
(1)如图1,EF⊥AB,求证:;
(2)点D在AC边上,AE⊥DF,且m.
①如图2,若,求m的值;
②如图3,若∠C=2∠ADF,m,直接写出的值.
参考答案
1.【解答】(1)证明:如图1中,作HM⊥CD于M.
∴四边形ABC都是正方形,
∴∠B=∠C=∠CMH=90°,AB=BC,
∴四边形BCMH是矩形,
∴HM=BC=AB,
∵AE⊥HF,
∴∠AGH=∠AHM=90°,
∴∠BAE+∠AHG=90°,∠AHG+∠FHM=90°,
∴∠BAE=∠FHM,∵∠B=∠HMF=90°,
∴△ABE≌△HMF(ASA),
∴AE=HF.
(2)解:如图2中,
∵EC=2BE,不妨设BE=BM=a,EC=2a,则AB=BC=CD=3a,CM=4a,
∴tan∠BAE,
∵ABE=∠MGE=90°,
∴∠BAE+∠AEB=90°,∠M+∠AEB=90°,
∴∠M=∠BAE,
∴tan,
∴BHa,CFa,
∴AH=AB﹣BH=3aaa,
∴CF∥AH,
∴△ANH∽△CNF,
∴2.
(3)解:如图3中,延长BA到N,使得AN=AD,作MJ⊥AN于J,交CD的延长线于K,作FQ⊥AB于Q,则四边形BCFQ,四边形ADKJ都是矩形,△FQH≌△FKM(AAS).
∴QH=KM,DF=AQ=BH,
∵KJ=AD=AB,
∴JM=AQ+BH=2AQ,
∵FK=FQ=JQ=AD=AN,
∴AQ=JN,
∴JM=2JN,
∴tan∠N2,
∴点M的运动轨迹是射线NM,∠N是的定值,作AP⊥MN于P,
根据垂线段最短可知:当AM与AP重合时,AM的值最小,
∵tan∠N2,设NP=x,AP=2x,
在Rt△APN中,则有22=x2+4x2,
解得x(负根已经舍弃),
∴PA=2x,
∴AM的最小值为.
2.【解答】(1)解:BF=CE,理由如下:
∵四边形ABCD是正方形,
∴AB=BC,∠FAB=∠EBC=90°,
∴∠ECB+∠CEB=90°,
∵BF⊥CE,
∴∠FBA+∠CEB=90°,
∴∠FBA=∠ECB,
在△FBA和△ECB中,
,
∴△FBA≌△ECB(ASA),
∴BF=CE;
(2)证明:如图2,过点D作DK⊥CE于K,
设AB=CD=BC=2a,
∵点E是AB的中点,
∴,
∴,
在Rt△CEB中,根据面积相等,得BG CE=CB EB,
∴,
∴,
∵∠DCE+∠BCE=90°,∠CBF+∠BCE=90°,
∴∠DCE=∠CBF,
又∵CD=BC,∠CKD=∠BGC=90°,
∴△CKD≌△BGC(AAS),
∴,
∴,
∵DK=DK,∠CKD=∠GKD=90°,
∴△DGK≌△DCK(SAS),
∴CD=GD;
(3)证明:∵DK⊥CE,BF⊥CE,
∴DK∥BF,即DK∥GF,
∴∠GDK=∠FGD,
由(2)知△DGK≌△DCK,
∴∠CDK=∠GDK,
∴∠CDK=∠FGD,
由(2)知△CKD≌△BGC,
∴∠CDK=∠BCG,
∴∠FGD=∠GCB,
(4)解:如图3,过点D作DQ⊥CE于Q,
∵,
∴,
在Rt△CQD中,CD=2a,
∴,
∵∠MDH+∠HDC=90°,∠HCD+∠HDC=90°,
∴∠MDH=∠HCD,
∴△CHD∽△DHM,
∴,
∴,
在Rt△CHG中,,,
∴,
∵∠MGH+∠CGH=90°,∠HCG+∠CGH=90°,
∴∠CGH=∠CNG,
∴△GHN∽△CHG,
∴,
∴,
∴,
∴.
3.【解答】(1)解:设DE与CF的交点为G,
∵四边形ABCD是正方形,
∴∠A=∠FDC=90°,AD=CD,
∵DE⊥CF,
∴∠DGF=90°,
∴∠ADE+∠CFD=90°,
∠ADE+∠AED=90°,
∴∠CFD=∠AED,
在△AED与△DFC中,
,
∴△AED≌△DFC(AAS),
∴DE=CF,
∴,
故答案为:1;
(2)解:如图,设DB与CE交于点G,
∵四边形ABCD是矩形,
∴∠A=∠EDC=90°,
∵CE⊥BD,
∴∠DGC=90°,
∴∠CDG+∠ECD=90°,
∠ADB+∠CDG=90°,
∴∠ECD=∠ADB,
∵∠CDE=∠A,
∴△DEC∽△ABD,
∴,
故答案为:;
(3)证明:如图,过点C作CH⊥AF交AF的延长线于点H,
∵CG⊥EG,
∴∠G=∠H=∠A=∠B=90°,
∴四边形ABCH为矩形,
∴AB=CH,
∠FCH+∠CFH=∠DFG+∠FDG=90°,
∴∠FCH=∠FDG=∠ADE,∠A=∠H=90°,
∴△AED∽△HFC,
∴,
∴,
∴DE AB=CF AD.
4.【解答】(1)①证明:∵四边形ABCD是矩形,AD=nAB,n=1,
∴四边形ABCD是正方形,
∴AD=AB,∠DAB=90°=∠ABC,
∴∠DAF+∠BAF=90°,
∵AF⊥DE,
∴∠DAF+∠ADE=90°,
∴∠ADE=∠BAF,
而AD=AB,∠DAE=∠ABF=90°,
∴△ADE≌△BAF(ASA),
∴AE=BF;
②过点A作AF⊥HD交BC于点F,如图:
由(1)可知:AE=BF,
∵AH=AD,AF⊥HD,
∴∠HAF=∠DAF,
∵AD∥BC,
∴∠DAF=∠AFG,
∴∠HAF=∠AFG,
∴AG=GF,
∵GF=GB+BF,
∴AG=GB+BF=GB+AE;
(3)过点E作EH⊥DF于H,连接EF,如图:
∵E为AB的中点,
∴AE=BEAB,
∵∠ADE=∠EDF,EA⊥AD,EH⊥DF,
∴AE=EH,AD=DH=nAB,
∴BE=EH,而EF=EF,
∴Rt△BEF≌Rt△HEF(HL),
∴BF=FH,
设BF=x=FH,则FC=BC﹣BF=nAB﹣x,
∵DF2=FC2+CD2,
∴(nAB+x)2=(nAB﹣x)2+AB2,
∴xBF,
∴FC=nAB﹣xAB,
∴4n2﹣1.
5.【解答】问题背景:
证明:∵在平行四边形ABCD中,∠AGB=∠C=α=90°,
∴四边形ABCD是矩形,
∴∠ABG+∠BAG=∠ABG+∠CBG=90°,
∴∠BAG=∠CBG,
∵∠ABF=∠C=90°,
∴Rt△ABE∽Rt△BCF,
∴;
尝试应用:
解:延长AE、DC交于点P,
∵AB∥CD,
∴∠BFC=∠ABF=90°,
在Rt△BCF中,设CF=m,
∵tanC2,
∴BF=2m=AB,
∵∠AGB=∠C=α,
∴在Rt△ABG中,tan∠AGB=tan∠C2,
∴BG=m=FG,AGm,
∵AB∥CD,
∴∠BAG=∠P,∠ABG=∠PFG,
∴△ABG≌△PFG(AAS),
∴AG=PGm,AB=PF=2m,
∴PC=m,
∵AB∥DC,
∴△ABG≌△PFG(AAS),
∴2,
∴AEAPm,
∴;
拓展创新:
延长BM交AD于点P,过E作EQ⊥AB,交AB延长线于点Q,过F作FH⊥BC于点H,延长HF、AD 交于点K,连接PF,
∵AD∥BC,
∴△APM∽△EBM,
∴,
∵BE=EC=2,
∴AP=1,PD=3,
∵,
∴MN∥PF,MNPF,
∵∠AGB=∠C=45°=∠CBQ,∠ABG=∠CFB,
∴Rt△BEQ是等腰直角三角形,BQ=EQ,∠BAE=∠CBF,
在等腰直角三角形Rt△CFH中,设CH=FH=x,则CFx,
∴tan∠BAE,tan∠CBF,
∴,
解得:x=22,
∴CF=4﹣2,DF=2,
∴DK=FK=2,PK=5,
在Rt△PFK中,由勾股定理得:PF,
∴MNPF.
故MN的值为.
6.【解答】(1)解:如图,设DB与CE交于点G,
∵四边形ABCD是矩形,
∴∠A=∠EDC=90°,
∵CE⊥BD,
∴∠DGC=90°,
∴∠CDG+∠ECD=90°,∠ADB+∠CDG=90°,
∴∠ECD=∠ADB,
∵∠CDE=∠A,
∴△DEC∽△ABD,
∴,
故答案为:;
(2)证明:如图,过点C作CH⊥AF交AF的延长线于点H,
∵CG⊥EG,
∴∠G=∠H=∠A=∠B=90°,
∴四边形ABCH为矩形,
∴AB=CH,∠FCH+∠CFH=∠DFG+∠FDG=90°,
∴∠FCH=∠FDG=∠ADE,∠A=∠H=90°,
∴△DEA∽△CFH,
∴,
∴,
∴DE AB=CF AD;
(3)解:如图,连接AC交BD于点H,则AH⊥BD,
∵AD=9,tan∠ADB,
∴AB=3,
由勾股定理得,BD=3,
由面积法知,AH,
∵将△ABD沿BD翻折,点A落在点C处得△CBD,
∴AC=2AH,
∵CF⊥DE,
∴∠ACF=∠BDE,
∵∠HAD=∠ABD,
∴△ACF∽△BDE,
∴,
∵AE=1,
∴BE=2,
∴AF,
∴BF.
7.【解答】(1)证明:当k=1时,BC=AB,
∴矩形ABCD是正方形,
∴BC=CD,∠BCD=∠D=90°,
∵CH⊥BE,
∴∠BHC=90°,
∴∠1+∠2=∠2+∠3=90°,
∴∠1=∠3,
在△BCE和△CDF中
.
∴△BCE≌△CDF(ASA);
(2)解:延长CH,交AD于点F,由(1)可知:△BCE≌△CDF,
∴CE=DF,BE=CF.
∵点E是CD中点,
∴CD=2CE,
∴BC=2CE=2DF,
∴tan,
∴tan∠3,
设EH=a,则CH=2a,BH=4a,
∴BE=BH+EH=5a,
∴CF=BE=5a,
∵AD∥BC,
∴△GFD∽△GCB,
∴
∴,
∴;
(3)解:∵DE=kCE,
∴CD=DE+CE=(k+1)CE,
∴CE=k+1CD,
∵BC=kAB=kCD,
∴tan,
∵∠1=∠3,
∴tan∠3,
设EH=1,HC=k(k+1),BH=k2(k+1)2
∴BE=k2(k+1)2+1,
∵△BCE∽△CDF.
∴
∴FHk(k+1),
∴tan,
∵F、H、E、D四点共圆,
∴tan∠HDE.
故答案为:.
8.【解答】解:(1)∵四边形ABCD是矩形,且AB=6,BC=8,
∴∠C=∠ADE=90°,AB=CD=6,BC=AD=8,
∴∠ADG+∠FDC=90°,
∵AE⊥DF,
∴∠AGD=90°,
∴∠DAG+∠ADG=90°,
∴∠DAG=∠FDC,
∴△DCF∽△ADE,
∴.
(2)过点B作CB的垂线,过点D作BC的垂线,垂足为K,过点A作BC的平行线,分别交两条垂线于G、H,如图:
则四边形GBKH为矩形,
∵D为AC的中点,
∵∠AHD=∠CKD=90°,∠ADH=∠CDK,
∴△ADH≌△CDK(AAS),
∴DH=DK,
∵∠BAD=90°,
∴∠GAB+∠HAD=90°,
∵∠GAB+∠GBA=90°,
∴∠HAD=∠GBA,
∵∠G=∠AHD=90°,
∴△AHD∽△BGA,
∴,
∵,
∴,
设DH=2y,则BG=4y,
∴,
由(1)知:,
∴.
(3)过C作CN⊥AD于N,CM⊥AB交AB的延长线于点M,如图3:
∵∠BAD=90°,即AB⊥AD,
∴∠A=∠M=∠CNA=90°,
∴四边形AMCN是矩形,
∴AM=CN,AN=CM,
在△BAD和△BCD中,
,
∵△BAD≌△BCD(SSS),
∴∠BCD=∠A=90°,
∴∠ABC+∠ADC=180°,
∵∠ABC+∠CBM=180°,
∴∠MBC=∠ADC,
∵∠CND=∠M=90°,
∴△BCM∽△DCN,
∵,
∴,
设BM=2y,AB=BC=2x,则DN=3y,AD=CD=3x,
∴CN=2x+2y,
在Rt△CND中,由勾股定理得:DN2+CN2=CD2,
∴(3y)2+(2x+2y)2=(3x)2,
解得:或x=﹣y(舍去),
∴,
故答案为:.
9.【解答】解:(1)①∵矩形ABCD,
∴∠ABC=∠BCD=90°,
∴∠BAH+∠AHB=90°,
∵AH⊥BF,
∴∠CBF+∠AHB=90°,
∴∠BAH=∠CBF,
∴△ABH∽△BCF,
∴,
∵AB=mBC,m=2,
∴,
故答案为:2;
②如图,过A作AT∥GH交BC于T,
∵GH⊥BF,
∴AT⊥BF,
∵矩形ABCD,
∴AD∥BC,
∴四边形ATHG是平行四边形,
∴AT=GH,
由①可得,
∴;
(2)如图,过A作AT∥GH交BC于T,
∵GH⊥EF,
∴AT⊥EF,
同理可得AT=GH,
过B作BK∥EF交CD于K,
同理可得四边形BEFK为平行四边形,
∴BK=EF,BK⊥AT,
由①可得,
∴;
(3)如图,过G作BC的平行线交CF的延长线于D,过B作BC的垂线交DG于A,
∵∠C=90°,
∴∠ABC=90°,∠ADC=180°﹣90°=90°,∠AGB=∠GBC,
∴四边形ABCD为矩形,
∴∠A=90°,
∵,
∴,
设AB=9x,则BG=10x,
∵,
∴,
∵GH⊥BF,
结合(1)的结论可得,
故答案为:.
10.【解答】(1)证明:∵四边形ABCD是正方形,
∴BC=CD=AD,∠D=∠BCF=90°,
∴∠DCE+∠BCE=90°,
∵BF⊥CE,
∴∠BGC=90°,
∴∠BCE+∠CBG=90°,
∴∠DCE=∠CBG,
∴△DCE≌△CBF(ASA),
∴DE=CF,
∵E为AD中点,
∴AE=DE,
∴CF=DF,
∴;
(2)解:过点A作AD∥BC,CD∥AB,则四边形ABCD是正方形,
∵E为AB的中点.
由(1)可知M为AD的中点,
∵AD∥BC,
∴△AMF∽△CBF,
∴,
设BE=AE=x,
∴AC=2x,CEx,
∴CFx,
∵,
∴BGx,
∴CGx,
∴FGx,
∴.
11.【解答】(1)证明:∵∠ACD=∠B,∠A=∠A,
∴△ACD∽△ABC,
∴,
∴AC2=AD AB;
(2)解:过E点作EF⊥AB,交CD的延长线于F点,
∵AB=4AD,
∴设AD=m,AB=4m,
∴AC=2m,
∵∠EAB+∠EAC=90°=∠EAC+∠ACD,
∴∠EAB=∠ACD=∠B,
∴EA=EB,∠EAC=∠C,
∴EA=EC=EB,
∵EF⊥AB,CA⊥AB,
∴EF∥AC,
∴BG=AG=2m,GE=m,
∴DG=DA=m,
∵∠GDF=∠ADC,∠FGD=∠CAD=90°,
∴△FGD≌△CAD(ASA),
∴∠F=∠ACD,FG=AC=2m,
∴EF=3m,
∵∠FME=∠CMA,
∴△FME∽△CMA,
∴.
(3)解:作BF⊥NC于F,作AE⊥NC交BC于E,交NC于M;
设DM=x,
∵∠ACD+∠CAM=∠CAM+∠MAD=90°,
∴∠ACD=∠MAD,
∴tan∠ACD=tan∠MAD,
即:,
∴AM=nx,AM2=DM MC,
即n2x2=x MC,
∴MC=n2x,
∵∠ACD=∠MAD,∠ACD=∠ABC,
∴∠MAD=∠ABC,
∴BE=AE,
又∵∠CAE+∠EAB=∠ACB+∠ABC,
∴∠CAE=∠ACB,
∴CE=AE,
∴BE=CE,
∴E为BC中点,
又BF⊥NC,AE⊥NC,
∴BE∥AE,
在Rt△BCF中,EM为中位线,
∴MF=MC,
∴MF=n2x,
∴FD=(n2﹣1)x,
∵∠NBD=2∠ACD,
而∠ACD=∠DAM,
∴∠NBD=2∠DAM,
而由BF∥AM可得,∠DAM=∠FBD,
∴∠NBD=2∠FBD,
∴BF为∠NBD的角平分线,
又BF⊥ND,
∴BF为△NBD的中线,BN=BD,
∴ND=2DF=2(n2﹣1)x,
∴.
12.【解答】问题背景:解:△EFD∽△CFB,证明如下:
∵四边形ABCD是矩形,
∴AD∥BC,
∴△EFD∽△CFB;
尝试运用:证明:如图(2),过点A作AH∥CD,交BC于点H,
则∠AHB=∠C,
∵∠BAD=∠B=90°,
∴∠BAD+∠B=180°,
∴AD∥BC,
∴四边形ADCH是平行四边形,∠GDF=∠C,
∴AH=CD,
∵EF⊥CD,
∴∠GFD=90°,
∵∠BAD=90°=∠GFD,∠AGE=∠DGF,
∴∠AEG=∠GDF,
∴∠AEG=∠C=∠AHB,
又∵∠GAE=∠B,
∴△AEG∽△BHA.
∴AG:AB=EG:AH.
∴AG:AB=EG:CD,
∴EG AB=CD AG;
拓展创新:解:如图(3),过点C作CG⊥AD于点G,连接AC、BD交于点H,
∵BA=BC,DA=DC,
∴BD垂直平分AC,
∴∠AHD=90°,AH=CH,
∵CF⊥DE,CG⊥AD,
∴∠FCG+∠CFG=∠CFG+∠ADE=90°,
∴∠FCG=∠ADE,
∵∠BAD=∠CGF=90°,
∴△DEA∽△CFG,
∴,
在Rt△ADB中,tan∠ADB,
∴tan∠ADH,
设AH=a,则DH=3a,
∵AH2+DH2=AD2,
∴a2+(3a)2=32,
解得:a(负值已舍去),
∴AH,DH,
∴AC=2AH,
∵S△ADCAC DHAD CG,
∴AC DH=AD CG,
即3CG,
∴CG,
∴.
13.【解答】解:(1)1,理由如下:
如图1,过点A作AM∥HF交BC于点M,作AN∥EG交CD的延长线于点N,
∵四边形ABCD是正方形,
∴AB∥CD,AD∥BC,AB=AD,∠ABM=∠BAD=∠ADN=90°,
∴AM=HF,AN=EG,
∵EG⊥FH,
∴∠NAM=90°,
∴∠BAM=∠DAN,
在△ABM和△ADN中,∠BAM=∠DAN,AB=AD,∠ABM=∠ADN,
∴△ABM≌△ADN(ASA),
∴AM=AN,即EG=FH,
∴1;
(2)如图2,过点A作AM∥HF交BC于点M,作AN∥EG交CD的延长线于点N,
∴AM=HF,AN=EG,
在长方形ABCD中,BC=AD,∠ABM=∠BAD=∠ADN=90°,
∵EG⊥FH,
∴∠NAM=90°,
∴∠BAM=∠DAN,
∴△ABM∽△ADN,
∴,
∵AB=m,BC=AD=n,
∴;
(3)如图3,过点C作CM⊥AB于点M,CE交BF于点O.
∵CM⊥AB,
∴∠CME=90°,
∴∠ECM+∠CEM=90°,
∵CE⊥BF,
∴∠BOE=90°,
∴∠CEM+∠ABF=90°,
∴∠ECM=∠ABF,
又∠FAB=∠EMC=90°,
∴△CME∽△BAF,
∴,
∵AB=BC,∠ABC=60°,
∴sin60°,
故答案为:.
14.【解答】(1)证明:∵四边形ABCD是正方形,
∴∠ABC=∠C=90°,AB=BC,∠2+∠ABP=90°,
∵AF⊥BG,
∴∠1+∠ABP=90°,
∴∠1=∠2,
在△ABF和△BCG中,
,
∴△ABF≌△BCG(ASA),
∴AF=BG;
(2)解:作EM⊥DC于点M,作HN⊥BC于点N,
则EM∥AD∥BC,HN∥AB∥DC,
∴EM⊥HN,EM=AD=BC,HN=AB=DC,
又∵EG⊥HF,
∴∠GEM=∠FHN,
∴Rt△EMG∽Rt△HNF,
∴,
即;
(3)解:过点D作DH⊥BC于点H,交CE于点M,
则∠DHF=∠ABC=90°,
∴∠CMH+∠BCE=90°,
∵CE⊥DF,
∴∠PDM+∠PMD=90°,
∵∠PMD=∠CMH,
∴∠BCE=∠PDM,
∴△CBE∽△DHF,
∴,
∵BD=CD,∠BDC=120°,
∴∠DCH=30°,BC=2CH,
在Rt△CHD中,∠CHD=90°,
∴tan30°,
∴CHDH,
∴BC=2DH,
∴2.
15.【解答】(1)证明:如图1中,
∵EF⊥AB,∠A=90°,
∴∠EFB=∠A=90°,
∵∠B=∠B,
∴△BFE∽△BAC,
∴.
(2)①解:如图2中,过点E作EM⊥AB于M,连接DM.
由(1)可知:,
∴,
∵m,
∴m,
∴CD=EM,
∵∠EMB=∠BAC=90°,
∴EM∥CD,
∴四边形ECDM是平行四边形,
∴DM∥BC,
∴,
∵AE⊥DF,
∴∠EAM+∠AFD=90°,
∵∠AFD+∠ADF=90°,
∴∠EAM=∠ADF,
∵∠AME=∠DAF=90°,
∴△AFD∽△MEA,
∴,设AD=2m,AM=3m,
∴DMm,
∴.
②解:过点E作EM⊥AB于M,连接DM,过点F作FH⊥DM于H.
由①可知,四边形ECDM是平行四边形,
∴DM∥BC,
∴m,设AD=3k,DM=5k,则AM=4k,
∵∠C=2∠ADF,∠C=∠ADM,
∴∠ADF=∠FDM,
∵FA⊥AD,FH⊥DM,
∴∠DAF=∠DHF=90°,
∵DF=DF,
∴△DFA≌△DFH(AAS),
∴AF=FH,AD=DH=3k,设AF=FH=y,
∴MH=DM﹣DH=2k,
在Rt△FMH中,∵FM2=FH2+MH2,
∴(4k﹣y)2=y2+(2k)2,
解得yk,
∴AFk,
∴DFk,
由①可知,,
∴,
∴AE=2k,
∴.
21世纪教育网(www.21cnjy.com)
同课章节目录
