2025年九年级数学中考三轮冲刺训练正方形中的相似三角形综合问题(含答案)
文档属性
| 名称 | 2025年九年级数学中考三轮冲刺训练正方形中的相似三角形综合问题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-11 05:47:27 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2025年九年级数学中考三轮冲刺训练正方形中的相似三角形综合问题
1.如图,E,F是正方形ABCD边AB,BC上点,∠EDF=45°.
(1)在图(1)中,延长BC至点G,使CG=AE,并连接DG,求证:△ADE≌△CDG;
(2)在图(2)中,若∠BFE=45°,求tan∠ADE值;
(3)在图(1)中,连接AC分别交DE,DF于点M,N,求的值.
2.如图,在正方形ABCD中,点E在边AD上,连接CE,将四边形ABCE沿直线CE折叠,点A、B的对应点分别为点N、M,AD的延长线分别与MN、CM延长线交于点F、G.
(1)如图①,求证:EG=CG;
(2)如图②,若F为MN的中点,求证:∠MDN=90°;
(3)如图③,在(2)的条件下,连接ND并延长,分别交CE、BC于点P、Q,求的值.
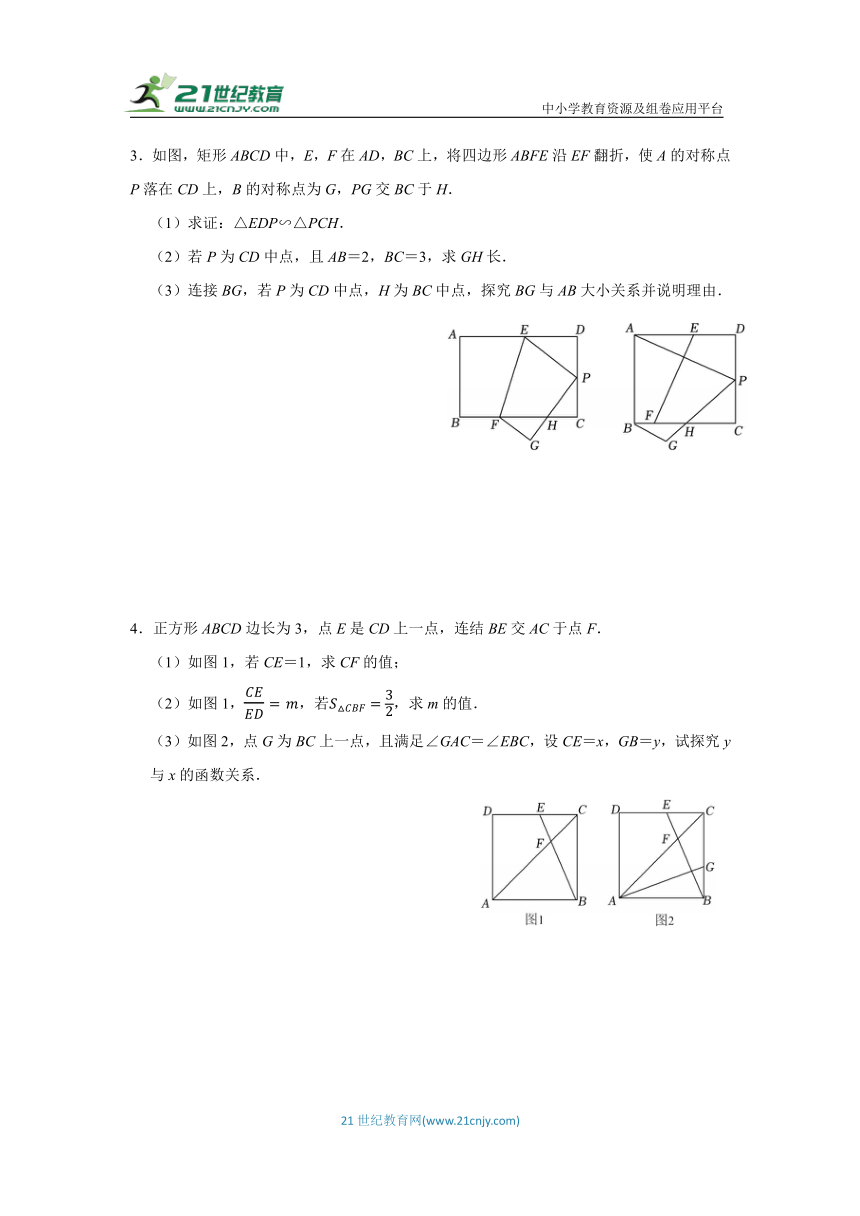
3.如图,矩形ABCD中,E,F在AD,BC上,将四边形ABFE沿EF翻折,使A的对称点P落在CD上,B的对称点为G,PG交BC于H.
(1)求证:△EDP∽△PCH.
(2)若P为CD中点,且AB=2,BC=3,求GH长.
(3)连接BG,若P为CD中点,H为BC中点,探究BG与AB大小关系并说明理由.
4.正方形ABCD边长为3,点E是CD上一点,连结BE交AC于点F.
(1)如图1,若CE=1,求CF的值;
(2)如图1,,若,求m的值.
(3)如图2,点G为BC上一点,且满足∠GAC=∠EBC,设CE=x,GB=y,试探究y与x的函数关系.
5.在正方形ABCD,E,F分别是射线BC,CD上的点,AE⊥BF于点G.如图,若点E是BC边上的点.延长BF交AD的延长线于点H,连结CH.
(1)求证:△BEF∽△BCH;
(2)连结ED,若AB=4,BE=3,直接写出tan∠BHC的值 ;
(3)延长BF交射线AD于点H,连结CG,CH,若,求的值(用含k的代数式表示).
6.(1)如图1,四边形ABCD是正方形,△BEF是等腰直角三角形,∠BFE=90°.
①求证:△BDE∽△BCF;②线段DE与CF的数量关系是 ;
(2)将图1中的△BEF绕点B顺时针旋转,当旋转到点F在DE的延长线上时,EF与BC相交于点G,
①如图2,当点G是BC的中点时,若,求线段CF的长;
②如图3,当点G不是BC的中点时,设DE的中点为H,连接AH,判断线段AH,FH的关系,并说明理由.
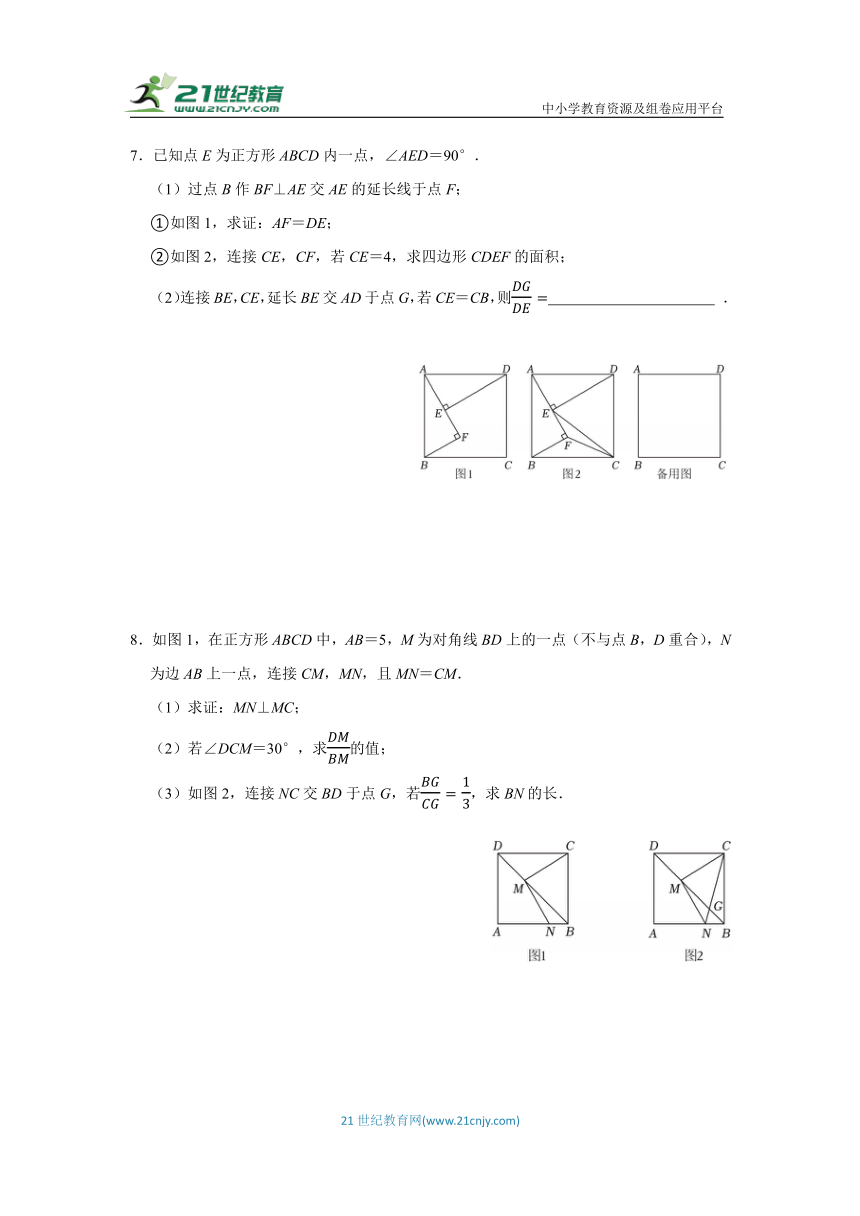
7.已知点E为正方形ABCD内一点,∠AED=90°.
(1)过点B作BF⊥AE交AE的延长线于点F;
①如图1,求证:AF=DE;
②如图2,连接CE,CF,若CE=4,求四边形CDEF的面积;
(2)连接BE,CE,延长BE交AD于点G,若CE=CB,则 .
8.如图1,在正方形ABCD中,AB=5,M为对角线BD上的一点(不与点B,D重合),N为边AB上一点,连接CM,MN,且MN=CM.
(1)求证:MN⊥MC;
(2)若∠DCM=30°,求的值;
(3)如图2,连接NC交BD于点G,若,求BN的长.
9.定义:有一组邻边垂直且对角线相等的四边形称为垂等四边形.
(1)写出一个已学的特殊平行四边形中是垂等四边形的是 ;
(2)如图1,在正方形ABCD中,点E,F,G分别在AD,AB,BC上,四边形DEFG是垂等四边形,且∠EFG=90°,AF=CG.
①求证:EG=DG;
②若BC=n BG,求n的值;
(3)如图2,在Rt△ABC中,,,以AB为对角线,作垂等四边形ACBD.过点D作CB的延长线的垂线,垂足为E,且△ACB与△DBE相似,求四边形ACBD的面积.
10.如图,在正方形ABCD中,E,F分别是边AD,AB上的点,连接CE,EF,CF.
(1)若正方形ABCD的边长为2,E是AD的中点.
①如图1,当∠FEC=90°时,求证:△AEF∽△DCE;
②如图2,当tan∠FCE时,求AF的长;
(2)如图3,延长CF,DA交于点G,当GE=DE,sin∠FCE时,求证:AE=AF.
11.如图,E为平面内一点,以正方形ABCD的顶点A为旋转中心,将线段AE顺时针旋转90°得到线段AF,连接BF.
(1)如图(1),当点E在边CD上时,求证:DE=BF;
(2)如图(2),当点E在对角线BD上时,连接EF,若AB=4,BE=3DE,求EF的长;
(3)如图(3),当点E在线段DF上时,连接CF,若BE=3DE,直接写出的值.
12.如图,正方形ABCD的边长是3,E为CD上一动点,将△ADE绕点A顺时针旋转90°至△ABF(点D的对应点为点B),连接EF.
(1)如图1,当DE=1时,直接写出EF的长是 ;
(2)如图2,连接BD交EF于点M,
①求证:M为EF的中点;
②直接写出的值是 .
(3)如图3,将△ADE沿AE翻折至△AQE,点D的对应点为点Q,延长EQ交BC于点P,在点E运动过程中,FP的最小值是 .
13.如图,四边形ABCD是正方形,E是边BC的中点,∠AEF=90°,且EF交正方形外角的平分线CF于点F.
(1)求证:AE=EF;
(2)连接AC,则的值为 ;
(3)连接AF,设AF与CD交于点H,连接EH,探究BE,EH,DH之间的关系.
14.已知:正方形ABCD中,点E是对角线AC上一点△FBE和△ABE关于直线BE对称,点F是点A的对称点,
(1)如图,BF,AC相交于G,求证:CG EG=BG FG;
(2)当BF∥AC时,求的值;
(3)直线BF,BE分别与边CD,AD交于点P,Q,当DP=2CP时,求的值.
15.如图,在正方形ABCD中,E,F分别是边BC,CD上的一点,BE=DF,连接AE,AF.
(1)求证:AE=AF;
(2)如图,连接BF交AE于点G,连接DG,若BF⊥AE,求的值;
(3)如图,过点F作FM⊥AE于点M,若EM=2,FM=5,直接写出AB的长.
参考答案
1.【解答】(1)证明:如图1,延长BC至点G,使CG=AE,并连接DG,
∵四边形ABCD是正方形,
∴AD=CD,∠A=∠DCG=90°,
又∵CG=AE,
∴△ADE≌△CDG(SAS);
(2)解:如图2,截取AH=AE,
∴∠AEH=∠AHE=45°,
∵四边形ABCD是正方形,
∴∠A=∠B=∠C=∠ADC=90°,AD=DC=AB=BC,
又∵∠BFE=45°,
∴BE=BF,
∴AB﹣BE=BC﹣BF,即AE=CF,
∴△ADE≌△DCF(SAS),
又∵∠EDF=45°,
∴,
∴DE=DF,
∴,
∴∠HED=180°﹣∠AEH﹣∠DEF﹣∠BEF=22.5°,
∴∠HED=∠ADE,
∴HE=DH,
设AE=x,
则在Rt△AHE中,AE2+AH2=HE2,
∴,
∴;
(3)如图3,延长BC至点G,使CG=AE,并连接DG,连接AC分别交DE,DF于点M,N,连接EN.
由(1)可知△ADE≌△CDG,
∴DE=DG,∠ADE=∠CDG,
∵四边形ABCD是正方形,∠EDF=45°,
∴∠ADE+∠CDF=90°﹣∠EDF=45°,
∴∠GDF=∠CDF+∠CDG=45°,
∴∠GDF=∠EDF,
又∵DF=DF,
∴△DEF≌△DFG(SAS),
∴∠DFE=∠DFC,
又∵∠MDN=∠EAN=45°,
∴A、E、N、D四点共圆,
∴∠DEN=∠DAC=45°,
∴∠DEF=∠DCE,
∴△DEN∽△DAC,
∴△END为等腰直角三角形,
∴,
又∵∠FCN=∠EDF=45°,∠DMN=∠CMF(对顶角相等),
∴△CNF∽△DNM.
∴∠DMN=∠DFC,
∴∠DFE=∠DMN,
又∵∠DEF=∠DEF,
∴△DFE∽△DNM.
∴.
2.【解答】(1)证明:∵四边形ABCD是正方形,
∴AD∥BC,
∴∠GEC=∠BCE,
∵四边形ABCE沿直线CE折叠,
∴∠BCE=∠GCE,
∴∠GEC=∠GCE,
∴EG=CG;
(2)证明:如图1,
连接CF,
∵四边形ABCD是正方形,
∴∠B=∠ADC=∠CDF=90°,BC=CD,
∵四边形ABCE沿直线CE折叠,
∴CM=BC,∠CMF=∠B=90°,
∴∠CMF=∠CDDF=90°,CM=CD,
∵CF=CF,
∴△CMF≌△CDF(HL),
∴DF=FM,
∴∠FDM=∠FMD,
∵F是MN的中点,
∴FN=FM,
∴FN=FD,
∴∠FNF=∠FDN,
∵∠FMD+∠FND+(∠FDN+∠FDM)=180°,
∴2∠FDN+2∠FDM=180°,
∴∠FDN+∠FDM=90°,
∴∠MDN=90°;
(3)解:如图2,连接CF,交DM于O,
设DF=FN=FM=a,则CD=CM=BC=MN=2a,
设FG=x,
∵∠GMF=∠CDG=90°,∠G=∠G,
∴△GMF∽△GDC,
∴,
∴CG=2FG=2x,
∴DG=x+a,CG=2x,CD=2a,
在Rt△CDG中,CD2+DG2=CG2,
∴(2a)2+(x+a)2=(2x)2,
∴x=﹣a(舍去)或xa,
∴CG=2xa,DG=x+aa,
由(1)知,EG=CGa,
∴DE=EG﹣DGaaa,
∵CM=CD,DF=FM,
∴DM⊥CF,
∴∠FOM=90°,
由(2)知,∠MDN=90°,
∴∠MDN=∠FOM,
∴CF∥DQ,
∵DF∥CB,
∴四边形DQCF是平行四边形,
∴CQ=DF=a,
∴.
3.【解答】(1)证明:如图,
∵四边形ABCD是矩形,
∴∠A=∠D=∠C=90°,
∴∠1+∠3=90°,
∵E,F分别在AD,BC上,将四边形ABFE沿EF翻折,使A的对称点P落在DC上,
∴∠EPH=∠A=90°,
∴∠1+∠2=90°,
∴∠3=∠2,
∴△EDP∽△PCH;
(2)解:∵四边形ABCD是矩形,
∴CD=AB=2,AD=BC=3,∠A=∠D=∠C=90°,
∵P为CD中点,
∴,
设EP=AP=x,
∴ED=AD﹣x=3﹣x,
在Rt△EDP中,EP2=ED2+DP2,
即x2=(3﹣x)2+1,
解得,
∴,
∴,
∵△EDP∽△PCH,
∴,
∴,
解得,
∵PG=AB=2,
∴;
(3)解:如图,延长AB,PG交于一点M,连接AP,
∵E,F分别在AD,BC上,将四边形ABFE沿EF翻折,使A的对称点P落在CD上,
∴AP⊥EF,BG⊥直线EF,
∴BG∥AP,
∵AE=EP,
∴∠EAP=∠EPA,
∴∠BAP=∠GPA,
∴△MAP是等腰三角形,
∴MA=MP,
∵P为CD中点,
∴设DP=CP=y,
∴AB=PG=CD=2y,
∵H为BC中点,
∴BH=CH,
∵∠BHM=∠CHP,∠CBM=∠PCH,
∴△MBH≌△PCH(ASA),
∴BM=CP=y,HM=HP,
∴MP=MA=MB+AB=3y,
∴,
在Rt△PCH中,,
∴,
∴,
在Rt△APD中,,
∵BG∥AP,
∴△BMG∽△MAP,
∴,
∴,
∴,
∴.
4.【解答】解:(1)由题意得:AB∥CE,AB=BC=3,
∴,
∴,
即:,
解得:;
(2)∵,
∴,
∴,
由(1)可得:,
∴,
∴,
∵,,
∴,
解得:m=1;
(3)由(1)得:,
即:,
解得:,
∵∠GAC=∠EBC,∠ACG=∠BCF,
∴△ACG∽△BCF,
∴,
即:,
∴,
整理得:,
∵y≥0,
∴9﹣3x≥0,x≤3,
又x≥0,
∴0≤x≤3,
故:(0≤x≤3).
5.【解答】.(1)证明:如图1,
∵四边形ABCD是正方形,且AE⊥BF,
∴∠BAE+∠ABF=90°,∠ABF+∠FBC=90°,
∴∠BAE=∠FBC,
∵∠ABE=∠BCF=90°,AB=BC,
∴△ABE≌△BCF(ASA),
∴BE=CF,
∴;
∵四边形ABCD是正方形,
∴AD∥BC,
∴,
∴,
又∵∠FBE=∠HBC,
∴△BEF∽△BCH;
(2)解:∵AB=4,BE=3,
在Rt△ABE 中,AE5,
如图2,过点C作CK⊥BH交于点K,
∵△ABE≌△BCF,
∴∠BAE=∠KBC,
∵∠ABE=∠BKC,
∴△ABE∽△BKC,
∴,
∵AB=BC=4,
∴BK,KC,
∵cos∠ABH=cos∠AEB,
∴BH,
∴KH=HB﹣BK,
∴tan∠BHC,
故答案为;
(3)分两种情况:
①点E在线段BC上,如图3,
由(1)得△ABE≌△BCF,
∴∠AEB=∠BFC,则∠GEC=∠HFC,
∴BE=CF,则CE=DF,
∵AH∥BC,
∴∠AHB=∠HBC,
∵∠BGE=∠HDF=90°,
∴△BGE∽△HDF,
∴,
∴,
∵∠GEC=∠HFC,
∴△GEC∽△CFH,
∴k,
设CE=DF=a,则FH=ak,
在Rt△DHF中,DH=a,
∵∠HDF=∠DCB,∠DFH=∠BFC,
∴△DFH∽△CFB,
设BC=CD=1,则CF=1﹣a,
∴,
∴a=1,
∴BE,
∴;
②点E在点C右侧,如图4,
同(1)可证得△ABE≌△BCF,
∴∠AEB=∠BFC,
∴BE=CF,则CE=DF,
∵∠FDH=∠EBG=90°,
∴△BGE∽△HDF,
∴,
∴,
∵∠GEC=∠HFC,
∴△GEC∽△CFH,
∴k,
设CE=DF=a,则FH=ak,
在Rt△DHF中,DH=a,
∵∠HDF=∠DCB,∠DFH=∠BFC,
∴△DFH∽△CFB,
设BC=CD=1,则CF=1+a,
∴,
∴a,
∴BE,
∴1,
综上所述,1或1.
6.【解答】解:(1)①∵四边形ABCD是正方形,
∴,
∵△BEF是等腰直角三角形,∠BFE=90°,
∴,
∴,∠CBD=∠EBF=45°,
∴∠DBE=∠CBF,
∴△BDE∽△BCF;
②∵△BDE∽△BCF,
∴,
∴,
故答案为:;
(2)①∵四边形ABCD是正方形,
∴,∠DCG=∠BFG=90°,
∵点G是BC的中点,
∴,
在Rt△CDG中,由勾股定理得,
∵∠DGC=∠BGF,
∴△DGC∽△BGF,
∴,即,
∴BF=2,
∴EF=BF=2,
在Rt△BFG中,由勾股定理得,
∴EG=EF﹣FG=1,
∴DE=DG﹣EG=4,
∴;
②AH=FH,AH⊥FH,理由如下:
如图所示,连接AF,AE,
∵∠BFD=∠BAD=90°,
∴∠BFD+∠BAD=180°
∴A、B、F、D四点共圆,
∴∠AFB=∠ADB=45°,∠AFD=∠ABD=45°,
∴AF平分∠BFE,
∵△BEF是等腰直角三角形,
∴AF垂直平分BE,
∴AE=AB,
由正方形的性质可得AB=AD,
∴AD=AE,
∵点H为DE的中点,
∴AH⊥DE,
∴△AHF是等腰直角三角形,
∴AH=HF,AH⊥HF.
7.【解答】(1)①证明:如图,
∵四边形ABCD是正方形,
∴∠1+∠2=∠BAD=90°,AB=AD,
∵∠AED=90°,
∴∠2+∠3=90°,
∴∠3=∠1,
∵BF⊥AE,
∴∠F=∠AED=90°,
∴△ABF≌△DAE(AAS),
∴AF=DE;
②解:如图:过C作CH⊥ED.
∵四边形ABCD是正方形,
∴∠4+∠5=∠ADC=90°,DC=AD,
∵CH⊥ED,
∴∠6+∠5=90°,
∴∠6=∠4,
∵∠DHC=∠AED=90°,
∴△CDH≌△DAE(AAS),
即△CDH≌△ABF,
∴设EH=x,HD=y,ED=HC=AF=x+y,
∴AE=HD=y,EF=AF﹣AE=(x+y)﹣y=x,
在Rt△EHC中,EC2=EH2+CH2=x2+(x+y)2=2x2+2xy+y2=16,
∴,
∴四边形CDEF的面积
=8;
(2)解:如图所示:延长AE交BC于点M.
∵点E为正方形ABCD内一点,∠AED=90°,
∴点E的轨迹为以AD的中点为圆心,的长为半径,且在正方形ABCD内,
∵CE=CB,
∴点E的轨迹为以点C为圆心,BC的长为半径,且在正方形ABCD内,
即点E的位置如图所示:
过C作CH⊥ED,
∵四边形ABCD是正方形,
∴∠4+∠5=∠ADC=90°,DC=AD,
∵CB=CE,CB=DC,
∴CE=CD,
∵CH⊥ED,
∴∠6+∠5=90°,
∴∠6=∠4,
∵∠DHC=∠AED=90°,
∴△CDH≌△DAE(AAS),
∵CE=CB,
∴,
则设AE=x,ED=2x,
∴,
∴,
∵∠BAM+∠DAM=∠DAM+∠ADE=90°,
∴∠BAM=∠ADE,
∴,
∴,
∴,
在Rt△ABM中,,
∴,
∵AD∥BC,
∴△AEG∽△MEB,
∴,
即,
∴,
∴.
8.【解答】(1)证明:如图1.1,连接AM,
∵四边形ABCD是正方形,
∴MA=MC,∠MAN=∠MCF,
∵MN=MC,
∴MA=MN,
∴∠MAN=∠MNA,
∴∠MNA=∠MCF,
∴∠MNA+∠BNM=∠MCF+∠BNM=180°,
∵∠ABC=90°,
∴∠CMN=90°,
即MN⊥MC;
(2)解:如图1,过点M作ME⊥CD于点E,MF⊥BC于点F,
∴四边形MFCE是矩形,
∴EC=MF,
∵∠CBD=∠CDB=45°,
设DE=ME=a,则DMa,
∵∠DCM=30°,
∴CE=MFa,BMa,
∴;
(3)解:由(2)知△CMN是等腰直角三角形,
∴∠MCN=45°,
又∵∠ABD=45°,
∴∠MCG=∠NBG,
又∵∠CGM=∠BGN,
∴△BGN∽△CGM,
∴,
又∵CM=NM,,
∴,
设BN=x,则CM=MN=3x,
∴CN=3x,
∵BC=AB=5,BN2+BC2=CN2,
∴x2+52,
∴x或(舍去),
∴BN.
9.【解答】(1)解:矩形有一组邻边垂直且对角线相等,故矩形的垂等四边形.
故答案为:矩形;
(2)①证明:∵四边形ABCD为正方形,
∴AD=CD,∠A=∠C.
又∵AF=CG,
∴△ADF≌△CDG(SAS),
∴DF=DG.
∵四边形DEFG是垂等四边形,
∴EG=DF,
∴EG=DG.
②解:如图1,过点G作GH⊥AD,垂足为H,
∴四边形CDHG为矩形,
∴CG=DH.
由①知EG=DG,
∴DH=EH.
由题意知∠A=∠B=90°,AB=BC=CD=AD,AF=CG,
∴AB﹣AF=BC﹣CG,
即BF=BG,
∴△BFG为等腰直角三角形,
∴∠GFB=45°.
又∵∠EFG=90°,
∴∠EFA=180°﹣90°﹣45°=45°,
∴△AEF为等腰直角三角形,
∴AE=AF=CG,
∴AE=EH=DH,
∴BC=3AE,BG=2AE.
∵BC=n BG,
∴.
∵BC=nBG,
∴;
(3)如图2,过点D作 DF⊥AC,垂足为F,
∵四边形CEDF 为矩形,,
∴AC=2CB.
在Rt△ABC中,,
∴AC2+BC2=AB2,即 (2BC)2+CB2=20,
∴AC=4,BC=2,
∵四边形ACBD为垂等四边形,
∴.
①当△ACB∽△BED时,,
设 DE=x,则 BE=2x,
∴CE=2+2x.
在 Rt△CDE中,根据勾股定理得,CE2+DE2=CD2,
即 (2+2x)2+x2=20
解得 , (舍去),
∴,,
∴;
5,
②当△ACB∽△DEB 时,,
设 BE=y,则 DE=2y,
∴CE=2+y.
∴(2+y)2+(2y)2=20
解得 , (舍去),
∴,,
∴S四边形ACBD=S△ACD+S△DCB
,
综上所述,四边形ACBD的面积为或 .
10.【解答】(1)①证明:如图1中,∵四边形ABCD是正方形,
∴∠A=∠D=90°,
∵∠CEF=90°,
∴∠AEF+∠CED=90°,∠ECD+∠CED=90°,
∴∠AEF=∠ECD,
∴△AEF∽△DCE;
②解:如图2中,延长DA交CF的延长线于点G,过点G作GH⊥CE交CE的延长线于点H.
∵∠H=∠D=90°,∠GEH=∠CED,
∴△GEH∽△CED,
∴,
∵CD=2,AE=ED=1,
∴GH=2HE,
设EH=m,GH=2m.
∵CE,
∴CH=m,
∵tan∠ECF,
∴,
∴m,
∴EH,GH,
∴EG,
∴AG=EG﹣AE1,DG=EG+DE1,
∵AF∥CD,
∴,
∴,
∴AF;
(3)证明:如图3中,过点G作GH⊥CE交CE的延长线于点H.
设AD=CD=a,GE=DE=t,EH=x,GH=y,CE=n,
∵∠H=∠D=90°,∠GEH=∠CED,
∴△GEH∽△CED,
∴
∴,
∴x,y,
在Rt△CGH中,sin∠ECF,
∴CG=3GH,CH=2GH,
∴,
∴2y=x+n,
∴2n,
∴2at=t2+n2,
在Rt△CDE中,n2=t2+a2,
∴2at=2t2+a2,
∴at,
∵AF∥CD,
∴,
∴,
∴AFaa﹣t,
∵AE=a﹣t,
∴AE=AF.
解法二:设AE=x,则DE=EG=1﹣x,DG=2﹣2x,
∴S△CDE=S△CEG,
∴(1﹣x)×1 ,
解得x=1(负根已经舍去),
∴AE=1,
由AF:CD=AG:DG,可得AF:1=(1):,
∴AF=1.
∴AE=AF.
11.【解答】(1)证明:∵将线段AE顺时针旋转90°得到线段AF,
∴AE=AF,∠EAF=90°,
∵四边形ABCD为正方形,
∴∠BAD=90°,AD=AB,
∴∠DAE=∠BAF,
∴△DAE≌△BAF(SAS),
则DE=BF.
(2)解:同(1)可证△DAE≌△BAF(SAS),
∴∠ADE=∠ABF,DE=BF,
∵点E在对角线BD上,
∴∠ADE=∠ABF=∠ABD=45°,
∴∠EBF=90°,
∵AB=AD=4,
∴,
∵BE=3DE,
∴,,
∴,
在Rt△EBF中,由勾股定理得,EF2=BF2+BE2=2+18=20,
则.
(3)解:延长FD至M,使ED=DM,连接MC,如图,
同(1)可证△DAE≌△BAF,则BF=DE=DM,∠ABF=∠ADE,
设∠ADE=α,则∠CDE=90°﹣α,
∴∠CDM=180°﹣∠EDC=90°+α,∠FBC=∠ABC+∠ABF=90°+α,
∵四边形ABCD为正方形,
∴DC=BC,
在△FBC和△MDC中,
,
∴△FBC≌△MDC(SAS),
∴FC=MC,∠FCB=∠MCD,
则∠FCM=∠DCF+∠DCM=∠DCF+∠BCF=90°,
故△FCM为等腰直角三角形,
在四边形BCDF中,∠FBC=90°+α,∠CDE=90°﹣α,则∠BFD=90°,
∴△BFE为直角三角形,
设DE=x,
∵BE=3DE,
∴BE=3x,
∴,
则,
∵,
∴,
则.
12.【解答】(1)解:∵四边形ABCD是正方形,
∴∠D=90°,
∴AE,
∵△ADE绕点A顺时针旋转90°至△ABF,
∴∠EAF=90°,AF=AE,
∴EFAE2,
故答案为:2;
(2)①证明;如图1,
连接AM,
设AE与BD交于点O,
∵四边形ABCD是正方形,
∴∠BDC=∠ADB=45°,
∵∠EAF=90°,AE=AF,
∴∠AEF=∠AFE=45°,
∴∠ADB=∠AEF,
∵∠AOD=∠EOM,
∴△AOD∽△MOE,
∴,
∵∠AOM=∠DOE,
∴△AOM∽△DOE,
∴∠EAM=∠BDC=45°,
∵AF=AE,
∴点M是EF的中点;
②解:如图2,
取CF的中点,连接MW,
∵点M是EF的中点,
∴MW∥CE,MWCE,
∴∠MWB=∠C=90°,
∵四边形ABCD是正方形,
∴∠CBD=45°,
∴BMMW,
∴BMCE,
∴,
故答案为:;
(3)解:如图3,
连接AP,作△APF的外接圆O,连接OA,作OV⊥BC于V,
设⊙O的半径为r,
∵△ADE沿AE翻折至△AQE,
∴AQ=AD=AB,∠AQP=∠AQE=∠D=∠ABC=90°,∠DAE=∠QAE,
∵AP=AP,
∴Rt△ABP≌Rt△APQ(HL),
∴∠BAP=∠QAP,
∵∠BAD=90°,
∴∠DAE+∠BAP=45°,
∵∠DAE=∠BAF,
∴∠BAF+∠BAP=45°,
∴∠PAF=45°,
∴∠POF=90°,
∴OVr,PFr,
∵AO+OV≥AB,
∴rr≥3,
∴r≥6﹣3,
∴当A、O、V共线时,r最小,最小值为:6﹣3,
此时PF最小值为:(6﹣3)=66,
故答案为:6.
13.【解答】解:(1)证明:如图所示,取AB的中点M,并连接ME,
∴AM=BM,
∵E是边BC的中点,
∴BE=CE,
∵四边形ABCD是正方形,
∴AM=BM=BE=CE,
∵∠AEF=90°,∠B=90°,
∴∠MAE+∠AEB=90°,∠CEF+∠AEB=90°,
∴∠MAE=∠CEB,
∵BM=BE,∠B=90°
∴∠BME=45°,∠AME=135°,
∵正方形外角的平分线为CF,
∴∠ECF=90°+45°=135°,
∴∠AME=∠ECF,
在△AME和△ECF中,
,
∴△AME≌△ECF(ASA),
∴AE=EF;
(2)解:如图所示,连接AC,
∵点M,E分别为AB,BC的中点,
∴ME为△ABC的中位线,
∴AC=2ME,
由(1)得△AME≌△ECF,
∴ME=CF,
∴AC=2CF,
∴,
故答案为:;
(3)解:EH=BE+DH,理由如下:
如图所示,延长CB至点N,使得BN=DH,连接AN,
由正方形基本性质得:∠ABN=∠ADH=90°,AB=AD,
∴△ABN≌△ADH(SAS),
∴AN=AH,∠DAH=∠BAN,
由(1)知,AE=EF,且∠AEF=90°,
∴∠EAF=∠EFA=45°,
∴∠DAH+∠BAE=∠BAD﹣∠EAF=90°﹣45°=45°,
∴∠NAE=∠BAN+∠BAE=45°,即:∠NAE=∠HAE=45°,
在△NAE和△HAE中,
,
∴△NAE≌△HAE(SAS),
∴EN=EH,
∵EN=BE+BN,BN=DH,
∴EN=BE+DH,
∴EH=BE+DH.
14.【解答】(1)证明:∵正方形ABCD,对角线AC,
∴∠BAC=∠BCA=45°,
∵△FBE和△ABE关于直线BE对称,
∴△FBE≌△ABE,
∴∠BFE=∠BAE,
∵∠FGE=∠CGB,
∴△FGE∽△CGB,
∴,
∴CG EG=BG FG.
(2)解:∵△FBE和△ABE关于直线BE对称,
∴△FBE≌△ABE,
∴FB=AB,FE=AE,∠FBE=∠ABE,
∵BF∥AC,
∴∠AEB=∠FBE,
∴∠ABE=∠AEB,
∴AB=AE,
∴AB=AE=BF=FE,
∵正方形ABCD,
∴AB=BC,∠ABC=90°,
设AB=x,则AE=x,
∴AC,
∴CE=AC﹣AE=()x,
∴.
(3)解:如图,延长CD,BQ交于点H,
设CP=x,则DP=2CP=2x,
∴CD=3x,
∵正方形ABCD,
∴BC=CD=AB=3x,AB∥CD,
在Rt△BCP中,BP,
∵∠H=∠HBA,
∴,
∵△FBE和△ABE关于直线BE对称,
∴△FBE≌△ABE,
∴∠HBA=∠HBP,
∴∠H=∠HBP,
∴PH=PB,
∴HD=PH﹣PD=()x,
∴,
∴.
15.【解答】(1)证明:∵四边形ABCD是正方形,
∴AD=AB,∠ADF=∠ABE=90°,
又∵BE=DF,
∴△ABE≌△ADF(SAS),
∴AE=AF.
(2)解:∵BF⊥AE,
∴∠BGE=90°,
∵四边形ABCD是正方形,
∴BC=AB,∠C=∠ABC=90°,
∴∠GEB+∠GBE=90°=∠GEB+∠EAB,
∴∠CBF=∠BAE,
∴△ABE≌△BCF(ASA),
∴CF=BE,
∴CF=DF,即点F为CD中点,
如图所示,取AB中点H,连接DH交AG于P,
∴,
∵AB=DA,∠ABE=∠DAH=90°,
∴△ABE≌△DAH(SAS),
∴∠BAE=∠ADH,
∵∠BAE+∠DAE=90°,
∴∠ADP+∠DAE=90°,
∴∠DPA=90°,即DH⊥AE,
∴DH∥BF;
取AG中点Q,连接HQ,则HQ是△ABG的中位线,
∴HQ∥BG,
∴由平行线的唯一性可知点Q与点P重合,
∴AP=GP,
∴DH垂直平分AG,
∴DA=DG,
∴.
答:的值为1.
(3)解:连接EF,如图,
设AM=x,则AF=AE=x+2,
在Rt△AFM中,AF2=AM2+FM2,
∴(x+2)2=x2+52,
解得,
∴,,
在Rt△EFM中,,
∵DF=BE,CD=BC,
∴CF=CE,
∴△CEF 是等腰直角三角形,
∴,
设BE=y,则,
在Rt△ABE中,AE2=AB2+BE2,
∴,
整理得,
解得y或(舍去),
∴.
答:AB的长为.
21世纪教育网(www.21cnjy.com)
2025年九年级数学中考三轮冲刺训练正方形中的相似三角形综合问题
1.如图,E,F是正方形ABCD边AB,BC上点,∠EDF=45°.
(1)在图(1)中,延长BC至点G,使CG=AE,并连接DG,求证:△ADE≌△CDG;
(2)在图(2)中,若∠BFE=45°,求tan∠ADE值;
(3)在图(1)中,连接AC分别交DE,DF于点M,N,求的值.
2.如图,在正方形ABCD中,点E在边AD上,连接CE,将四边形ABCE沿直线CE折叠,点A、B的对应点分别为点N、M,AD的延长线分别与MN、CM延长线交于点F、G.
(1)如图①,求证:EG=CG;
(2)如图②,若F为MN的中点,求证:∠MDN=90°;
(3)如图③,在(2)的条件下,连接ND并延长,分别交CE、BC于点P、Q,求的值.
3.如图,矩形ABCD中,E,F在AD,BC上,将四边形ABFE沿EF翻折,使A的对称点P落在CD上,B的对称点为G,PG交BC于H.
(1)求证:△EDP∽△PCH.
(2)若P为CD中点,且AB=2,BC=3,求GH长.
(3)连接BG,若P为CD中点,H为BC中点,探究BG与AB大小关系并说明理由.
4.正方形ABCD边长为3,点E是CD上一点,连结BE交AC于点F.
(1)如图1,若CE=1,求CF的值;
(2)如图1,,若,求m的值.
(3)如图2,点G为BC上一点,且满足∠GAC=∠EBC,设CE=x,GB=y,试探究y与x的函数关系.
5.在正方形ABCD,E,F分别是射线BC,CD上的点,AE⊥BF于点G.如图,若点E是BC边上的点.延长BF交AD的延长线于点H,连结CH.
(1)求证:△BEF∽△BCH;
(2)连结ED,若AB=4,BE=3,直接写出tan∠BHC的值 ;
(3)延长BF交射线AD于点H,连结CG,CH,若,求的值(用含k的代数式表示).
6.(1)如图1,四边形ABCD是正方形,△BEF是等腰直角三角形,∠BFE=90°.
①求证:△BDE∽△BCF;②线段DE与CF的数量关系是 ;
(2)将图1中的△BEF绕点B顺时针旋转,当旋转到点F在DE的延长线上时,EF与BC相交于点G,
①如图2,当点G是BC的中点时,若,求线段CF的长;
②如图3,当点G不是BC的中点时,设DE的中点为H,连接AH,判断线段AH,FH的关系,并说明理由.
7.已知点E为正方形ABCD内一点,∠AED=90°.
(1)过点B作BF⊥AE交AE的延长线于点F;
①如图1,求证:AF=DE;
②如图2,连接CE,CF,若CE=4,求四边形CDEF的面积;
(2)连接BE,CE,延长BE交AD于点G,若CE=CB,则 .
8.如图1,在正方形ABCD中,AB=5,M为对角线BD上的一点(不与点B,D重合),N为边AB上一点,连接CM,MN,且MN=CM.
(1)求证:MN⊥MC;
(2)若∠DCM=30°,求的值;
(3)如图2,连接NC交BD于点G,若,求BN的长.
9.定义:有一组邻边垂直且对角线相等的四边形称为垂等四边形.
(1)写出一个已学的特殊平行四边形中是垂等四边形的是 ;
(2)如图1,在正方形ABCD中,点E,F,G分别在AD,AB,BC上,四边形DEFG是垂等四边形,且∠EFG=90°,AF=CG.
①求证:EG=DG;
②若BC=n BG,求n的值;
(3)如图2,在Rt△ABC中,,,以AB为对角线,作垂等四边形ACBD.过点D作CB的延长线的垂线,垂足为E,且△ACB与△DBE相似,求四边形ACBD的面积.
10.如图,在正方形ABCD中,E,F分别是边AD,AB上的点,连接CE,EF,CF.
(1)若正方形ABCD的边长为2,E是AD的中点.
①如图1,当∠FEC=90°时,求证:△AEF∽△DCE;
②如图2,当tan∠FCE时,求AF的长;
(2)如图3,延长CF,DA交于点G,当GE=DE,sin∠FCE时,求证:AE=AF.
11.如图,E为平面内一点,以正方形ABCD的顶点A为旋转中心,将线段AE顺时针旋转90°得到线段AF,连接BF.
(1)如图(1),当点E在边CD上时,求证:DE=BF;
(2)如图(2),当点E在对角线BD上时,连接EF,若AB=4,BE=3DE,求EF的长;
(3)如图(3),当点E在线段DF上时,连接CF,若BE=3DE,直接写出的值.
12.如图,正方形ABCD的边长是3,E为CD上一动点,将△ADE绕点A顺时针旋转90°至△ABF(点D的对应点为点B),连接EF.
(1)如图1,当DE=1时,直接写出EF的长是 ;
(2)如图2,连接BD交EF于点M,
①求证:M为EF的中点;
②直接写出的值是 .
(3)如图3,将△ADE沿AE翻折至△AQE,点D的对应点为点Q,延长EQ交BC于点P,在点E运动过程中,FP的最小值是 .
13.如图,四边形ABCD是正方形,E是边BC的中点,∠AEF=90°,且EF交正方形外角的平分线CF于点F.
(1)求证:AE=EF;
(2)连接AC,则的值为 ;
(3)连接AF,设AF与CD交于点H,连接EH,探究BE,EH,DH之间的关系.
14.已知:正方形ABCD中,点E是对角线AC上一点△FBE和△ABE关于直线BE对称,点F是点A的对称点,
(1)如图,BF,AC相交于G,求证:CG EG=BG FG;
(2)当BF∥AC时,求的值;
(3)直线BF,BE分别与边CD,AD交于点P,Q,当DP=2CP时,求的值.
15.如图,在正方形ABCD中,E,F分别是边BC,CD上的一点,BE=DF,连接AE,AF.
(1)求证:AE=AF;
(2)如图,连接BF交AE于点G,连接DG,若BF⊥AE,求的值;
(3)如图,过点F作FM⊥AE于点M,若EM=2,FM=5,直接写出AB的长.
参考答案
1.【解答】(1)证明:如图1,延长BC至点G,使CG=AE,并连接DG,
∵四边形ABCD是正方形,
∴AD=CD,∠A=∠DCG=90°,
又∵CG=AE,
∴△ADE≌△CDG(SAS);
(2)解:如图2,截取AH=AE,
∴∠AEH=∠AHE=45°,
∵四边形ABCD是正方形,
∴∠A=∠B=∠C=∠ADC=90°,AD=DC=AB=BC,
又∵∠BFE=45°,
∴BE=BF,
∴AB﹣BE=BC﹣BF,即AE=CF,
∴△ADE≌△DCF(SAS),
又∵∠EDF=45°,
∴,
∴DE=DF,
∴,
∴∠HED=180°﹣∠AEH﹣∠DEF﹣∠BEF=22.5°,
∴∠HED=∠ADE,
∴HE=DH,
设AE=x,
则在Rt△AHE中,AE2+AH2=HE2,
∴,
∴;
(3)如图3,延长BC至点G,使CG=AE,并连接DG,连接AC分别交DE,DF于点M,N,连接EN.
由(1)可知△ADE≌△CDG,
∴DE=DG,∠ADE=∠CDG,
∵四边形ABCD是正方形,∠EDF=45°,
∴∠ADE+∠CDF=90°﹣∠EDF=45°,
∴∠GDF=∠CDF+∠CDG=45°,
∴∠GDF=∠EDF,
又∵DF=DF,
∴△DEF≌△DFG(SAS),
∴∠DFE=∠DFC,
又∵∠MDN=∠EAN=45°,
∴A、E、N、D四点共圆,
∴∠DEN=∠DAC=45°,
∴∠DEF=∠DCE,
∴△DEN∽△DAC,
∴△END为等腰直角三角形,
∴,
又∵∠FCN=∠EDF=45°,∠DMN=∠CMF(对顶角相等),
∴△CNF∽△DNM.
∴∠DMN=∠DFC,
∴∠DFE=∠DMN,
又∵∠DEF=∠DEF,
∴△DFE∽△DNM.
∴.
2.【解答】(1)证明:∵四边形ABCD是正方形,
∴AD∥BC,
∴∠GEC=∠BCE,
∵四边形ABCE沿直线CE折叠,
∴∠BCE=∠GCE,
∴∠GEC=∠GCE,
∴EG=CG;
(2)证明:如图1,
连接CF,
∵四边形ABCD是正方形,
∴∠B=∠ADC=∠CDF=90°,BC=CD,
∵四边形ABCE沿直线CE折叠,
∴CM=BC,∠CMF=∠B=90°,
∴∠CMF=∠CDDF=90°,CM=CD,
∵CF=CF,
∴△CMF≌△CDF(HL),
∴DF=FM,
∴∠FDM=∠FMD,
∵F是MN的中点,
∴FN=FM,
∴FN=FD,
∴∠FNF=∠FDN,
∵∠FMD+∠FND+(∠FDN+∠FDM)=180°,
∴2∠FDN+2∠FDM=180°,
∴∠FDN+∠FDM=90°,
∴∠MDN=90°;
(3)解:如图2,连接CF,交DM于O,
设DF=FN=FM=a,则CD=CM=BC=MN=2a,
设FG=x,
∵∠GMF=∠CDG=90°,∠G=∠G,
∴△GMF∽△GDC,
∴,
∴CG=2FG=2x,
∴DG=x+a,CG=2x,CD=2a,
在Rt△CDG中,CD2+DG2=CG2,
∴(2a)2+(x+a)2=(2x)2,
∴x=﹣a(舍去)或xa,
∴CG=2xa,DG=x+aa,
由(1)知,EG=CGa,
∴DE=EG﹣DGaaa,
∵CM=CD,DF=FM,
∴DM⊥CF,
∴∠FOM=90°,
由(2)知,∠MDN=90°,
∴∠MDN=∠FOM,
∴CF∥DQ,
∵DF∥CB,
∴四边形DQCF是平行四边形,
∴CQ=DF=a,
∴.
3.【解答】(1)证明:如图,
∵四边形ABCD是矩形,
∴∠A=∠D=∠C=90°,
∴∠1+∠3=90°,
∵E,F分别在AD,BC上,将四边形ABFE沿EF翻折,使A的对称点P落在DC上,
∴∠EPH=∠A=90°,
∴∠1+∠2=90°,
∴∠3=∠2,
∴△EDP∽△PCH;
(2)解:∵四边形ABCD是矩形,
∴CD=AB=2,AD=BC=3,∠A=∠D=∠C=90°,
∵P为CD中点,
∴,
设EP=AP=x,
∴ED=AD﹣x=3﹣x,
在Rt△EDP中,EP2=ED2+DP2,
即x2=(3﹣x)2+1,
解得,
∴,
∴,
∵△EDP∽△PCH,
∴,
∴,
解得,
∵PG=AB=2,
∴;
(3)解:如图,延长AB,PG交于一点M,连接AP,
∵E,F分别在AD,BC上,将四边形ABFE沿EF翻折,使A的对称点P落在CD上,
∴AP⊥EF,BG⊥直线EF,
∴BG∥AP,
∵AE=EP,
∴∠EAP=∠EPA,
∴∠BAP=∠GPA,
∴△MAP是等腰三角形,
∴MA=MP,
∵P为CD中点,
∴设DP=CP=y,
∴AB=PG=CD=2y,
∵H为BC中点,
∴BH=CH,
∵∠BHM=∠CHP,∠CBM=∠PCH,
∴△MBH≌△PCH(ASA),
∴BM=CP=y,HM=HP,
∴MP=MA=MB+AB=3y,
∴,
在Rt△PCH中,,
∴,
∴,
在Rt△APD中,,
∵BG∥AP,
∴△BMG∽△MAP,
∴,
∴,
∴,
∴.
4.【解答】解:(1)由题意得:AB∥CE,AB=BC=3,
∴,
∴,
即:,
解得:;
(2)∵,
∴,
∴,
由(1)可得:,
∴,
∴,
∵,,
∴,
解得:m=1;
(3)由(1)得:,
即:,
解得:,
∵∠GAC=∠EBC,∠ACG=∠BCF,
∴△ACG∽△BCF,
∴,
即:,
∴,
整理得:,
∵y≥0,
∴9﹣3x≥0,x≤3,
又x≥0,
∴0≤x≤3,
故:(0≤x≤3).
5.【解答】.(1)证明:如图1,
∵四边形ABCD是正方形,且AE⊥BF,
∴∠BAE+∠ABF=90°,∠ABF+∠FBC=90°,
∴∠BAE=∠FBC,
∵∠ABE=∠BCF=90°,AB=BC,
∴△ABE≌△BCF(ASA),
∴BE=CF,
∴;
∵四边形ABCD是正方形,
∴AD∥BC,
∴,
∴,
又∵∠FBE=∠HBC,
∴△BEF∽△BCH;
(2)解:∵AB=4,BE=3,
在Rt△ABE 中,AE5,
如图2,过点C作CK⊥BH交于点K,
∵△ABE≌△BCF,
∴∠BAE=∠KBC,
∵∠ABE=∠BKC,
∴△ABE∽△BKC,
∴,
∵AB=BC=4,
∴BK,KC,
∵cos∠ABH=cos∠AEB,
∴BH,
∴KH=HB﹣BK,
∴tan∠BHC,
故答案为;
(3)分两种情况:
①点E在线段BC上,如图3,
由(1)得△ABE≌△BCF,
∴∠AEB=∠BFC,则∠GEC=∠HFC,
∴BE=CF,则CE=DF,
∵AH∥BC,
∴∠AHB=∠HBC,
∵∠BGE=∠HDF=90°,
∴△BGE∽△HDF,
∴,
∴,
∵∠GEC=∠HFC,
∴△GEC∽△CFH,
∴k,
设CE=DF=a,则FH=ak,
在Rt△DHF中,DH=a,
∵∠HDF=∠DCB,∠DFH=∠BFC,
∴△DFH∽△CFB,
设BC=CD=1,则CF=1﹣a,
∴,
∴a=1,
∴BE,
∴;
②点E在点C右侧,如图4,
同(1)可证得△ABE≌△BCF,
∴∠AEB=∠BFC,
∴BE=CF,则CE=DF,
∵∠FDH=∠EBG=90°,
∴△BGE∽△HDF,
∴,
∴,
∵∠GEC=∠HFC,
∴△GEC∽△CFH,
∴k,
设CE=DF=a,则FH=ak,
在Rt△DHF中,DH=a,
∵∠HDF=∠DCB,∠DFH=∠BFC,
∴△DFH∽△CFB,
设BC=CD=1,则CF=1+a,
∴,
∴a,
∴BE,
∴1,
综上所述,1或1.
6.【解答】解:(1)①∵四边形ABCD是正方形,
∴,
∵△BEF是等腰直角三角形,∠BFE=90°,
∴,
∴,∠CBD=∠EBF=45°,
∴∠DBE=∠CBF,
∴△BDE∽△BCF;
②∵△BDE∽△BCF,
∴,
∴,
故答案为:;
(2)①∵四边形ABCD是正方形,
∴,∠DCG=∠BFG=90°,
∵点G是BC的中点,
∴,
在Rt△CDG中,由勾股定理得,
∵∠DGC=∠BGF,
∴△DGC∽△BGF,
∴,即,
∴BF=2,
∴EF=BF=2,
在Rt△BFG中,由勾股定理得,
∴EG=EF﹣FG=1,
∴DE=DG﹣EG=4,
∴;
②AH=FH,AH⊥FH,理由如下:
如图所示,连接AF,AE,
∵∠BFD=∠BAD=90°,
∴∠BFD+∠BAD=180°
∴A、B、F、D四点共圆,
∴∠AFB=∠ADB=45°,∠AFD=∠ABD=45°,
∴AF平分∠BFE,
∵△BEF是等腰直角三角形,
∴AF垂直平分BE,
∴AE=AB,
由正方形的性质可得AB=AD,
∴AD=AE,
∵点H为DE的中点,
∴AH⊥DE,
∴△AHF是等腰直角三角形,
∴AH=HF,AH⊥HF.
7.【解答】(1)①证明:如图,
∵四边形ABCD是正方形,
∴∠1+∠2=∠BAD=90°,AB=AD,
∵∠AED=90°,
∴∠2+∠3=90°,
∴∠3=∠1,
∵BF⊥AE,
∴∠F=∠AED=90°,
∴△ABF≌△DAE(AAS),
∴AF=DE;
②解:如图:过C作CH⊥ED.
∵四边形ABCD是正方形,
∴∠4+∠5=∠ADC=90°,DC=AD,
∵CH⊥ED,
∴∠6+∠5=90°,
∴∠6=∠4,
∵∠DHC=∠AED=90°,
∴△CDH≌△DAE(AAS),
即△CDH≌△ABF,
∴设EH=x,HD=y,ED=HC=AF=x+y,
∴AE=HD=y,EF=AF﹣AE=(x+y)﹣y=x,
在Rt△EHC中,EC2=EH2+CH2=x2+(x+y)2=2x2+2xy+y2=16,
∴,
∴四边形CDEF的面积
=8;
(2)解:如图所示:延长AE交BC于点M.
∵点E为正方形ABCD内一点,∠AED=90°,
∴点E的轨迹为以AD的中点为圆心,的长为半径,且在正方形ABCD内,
∵CE=CB,
∴点E的轨迹为以点C为圆心,BC的长为半径,且在正方形ABCD内,
即点E的位置如图所示:
过C作CH⊥ED,
∵四边形ABCD是正方形,
∴∠4+∠5=∠ADC=90°,DC=AD,
∵CB=CE,CB=DC,
∴CE=CD,
∵CH⊥ED,
∴∠6+∠5=90°,
∴∠6=∠4,
∵∠DHC=∠AED=90°,
∴△CDH≌△DAE(AAS),
∵CE=CB,
∴,
则设AE=x,ED=2x,
∴,
∴,
∵∠BAM+∠DAM=∠DAM+∠ADE=90°,
∴∠BAM=∠ADE,
∴,
∴,
∴,
在Rt△ABM中,,
∴,
∵AD∥BC,
∴△AEG∽△MEB,
∴,
即,
∴,
∴.
8.【解答】(1)证明:如图1.1,连接AM,
∵四边形ABCD是正方形,
∴MA=MC,∠MAN=∠MCF,
∵MN=MC,
∴MA=MN,
∴∠MAN=∠MNA,
∴∠MNA=∠MCF,
∴∠MNA+∠BNM=∠MCF+∠BNM=180°,
∵∠ABC=90°,
∴∠CMN=90°,
即MN⊥MC;
(2)解:如图1,过点M作ME⊥CD于点E,MF⊥BC于点F,
∴四边形MFCE是矩形,
∴EC=MF,
∵∠CBD=∠CDB=45°,
设DE=ME=a,则DMa,
∵∠DCM=30°,
∴CE=MFa,BMa,
∴;
(3)解:由(2)知△CMN是等腰直角三角形,
∴∠MCN=45°,
又∵∠ABD=45°,
∴∠MCG=∠NBG,
又∵∠CGM=∠BGN,
∴△BGN∽△CGM,
∴,
又∵CM=NM,,
∴,
设BN=x,则CM=MN=3x,
∴CN=3x,
∵BC=AB=5,BN2+BC2=CN2,
∴x2+52,
∴x或(舍去),
∴BN.
9.【解答】(1)解:矩形有一组邻边垂直且对角线相等,故矩形的垂等四边形.
故答案为:矩形;
(2)①证明:∵四边形ABCD为正方形,
∴AD=CD,∠A=∠C.
又∵AF=CG,
∴△ADF≌△CDG(SAS),
∴DF=DG.
∵四边形DEFG是垂等四边形,
∴EG=DF,
∴EG=DG.
②解:如图1,过点G作GH⊥AD,垂足为H,
∴四边形CDHG为矩形,
∴CG=DH.
由①知EG=DG,
∴DH=EH.
由题意知∠A=∠B=90°,AB=BC=CD=AD,AF=CG,
∴AB﹣AF=BC﹣CG,
即BF=BG,
∴△BFG为等腰直角三角形,
∴∠GFB=45°.
又∵∠EFG=90°,
∴∠EFA=180°﹣90°﹣45°=45°,
∴△AEF为等腰直角三角形,
∴AE=AF=CG,
∴AE=EH=DH,
∴BC=3AE,BG=2AE.
∵BC=n BG,
∴.
∵BC=nBG,
∴;
(3)如图2,过点D作 DF⊥AC,垂足为F,
∵四边形CEDF 为矩形,,
∴AC=2CB.
在Rt△ABC中,,
∴AC2+BC2=AB2,即 (2BC)2+CB2=20,
∴AC=4,BC=2,
∵四边形ACBD为垂等四边形,
∴.
①当△ACB∽△BED时,,
设 DE=x,则 BE=2x,
∴CE=2+2x.
在 Rt△CDE中,根据勾股定理得,CE2+DE2=CD2,
即 (2+2x)2+x2=20
解得 , (舍去),
∴,,
∴;
5,
②当△ACB∽△DEB 时,,
设 BE=y,则 DE=2y,
∴CE=2+y.
∴(2+y)2+(2y)2=20
解得 , (舍去),
∴,,
∴S四边形ACBD=S△ACD+S△DCB
,
综上所述,四边形ACBD的面积为或 .
10.【解答】(1)①证明:如图1中,∵四边形ABCD是正方形,
∴∠A=∠D=90°,
∵∠CEF=90°,
∴∠AEF+∠CED=90°,∠ECD+∠CED=90°,
∴∠AEF=∠ECD,
∴△AEF∽△DCE;
②解:如图2中,延长DA交CF的延长线于点G,过点G作GH⊥CE交CE的延长线于点H.
∵∠H=∠D=90°,∠GEH=∠CED,
∴△GEH∽△CED,
∴,
∵CD=2,AE=ED=1,
∴GH=2HE,
设EH=m,GH=2m.
∵CE,
∴CH=m,
∵tan∠ECF,
∴,
∴m,
∴EH,GH,
∴EG,
∴AG=EG﹣AE1,DG=EG+DE1,
∵AF∥CD,
∴,
∴,
∴AF;
(3)证明:如图3中,过点G作GH⊥CE交CE的延长线于点H.
设AD=CD=a,GE=DE=t,EH=x,GH=y,CE=n,
∵∠H=∠D=90°,∠GEH=∠CED,
∴△GEH∽△CED,
∴
∴,
∴x,y,
在Rt△CGH中,sin∠ECF,
∴CG=3GH,CH=2GH,
∴,
∴2y=x+n,
∴2n,
∴2at=t2+n2,
在Rt△CDE中,n2=t2+a2,
∴2at=2t2+a2,
∴at,
∵AF∥CD,
∴,
∴,
∴AFaa﹣t,
∵AE=a﹣t,
∴AE=AF.
解法二:设AE=x,则DE=EG=1﹣x,DG=2﹣2x,
∴S△CDE=S△CEG,
∴(1﹣x)×1 ,
解得x=1(负根已经舍去),
∴AE=1,
由AF:CD=AG:DG,可得AF:1=(1):,
∴AF=1.
∴AE=AF.
11.【解答】(1)证明:∵将线段AE顺时针旋转90°得到线段AF,
∴AE=AF,∠EAF=90°,
∵四边形ABCD为正方形,
∴∠BAD=90°,AD=AB,
∴∠DAE=∠BAF,
∴△DAE≌△BAF(SAS),
则DE=BF.
(2)解:同(1)可证△DAE≌△BAF(SAS),
∴∠ADE=∠ABF,DE=BF,
∵点E在对角线BD上,
∴∠ADE=∠ABF=∠ABD=45°,
∴∠EBF=90°,
∵AB=AD=4,
∴,
∵BE=3DE,
∴,,
∴,
在Rt△EBF中,由勾股定理得,EF2=BF2+BE2=2+18=20,
则.
(3)解:延长FD至M,使ED=DM,连接MC,如图,
同(1)可证△DAE≌△BAF,则BF=DE=DM,∠ABF=∠ADE,
设∠ADE=α,则∠CDE=90°﹣α,
∴∠CDM=180°﹣∠EDC=90°+α,∠FBC=∠ABC+∠ABF=90°+α,
∵四边形ABCD为正方形,
∴DC=BC,
在△FBC和△MDC中,
,
∴△FBC≌△MDC(SAS),
∴FC=MC,∠FCB=∠MCD,
则∠FCM=∠DCF+∠DCM=∠DCF+∠BCF=90°,
故△FCM为等腰直角三角形,
在四边形BCDF中,∠FBC=90°+α,∠CDE=90°﹣α,则∠BFD=90°,
∴△BFE为直角三角形,
设DE=x,
∵BE=3DE,
∴BE=3x,
∴,
则,
∵,
∴,
则.
12.【解答】(1)解:∵四边形ABCD是正方形,
∴∠D=90°,
∴AE,
∵△ADE绕点A顺时针旋转90°至△ABF,
∴∠EAF=90°,AF=AE,
∴EFAE2,
故答案为:2;
(2)①证明;如图1,
连接AM,
设AE与BD交于点O,
∵四边形ABCD是正方形,
∴∠BDC=∠ADB=45°,
∵∠EAF=90°,AE=AF,
∴∠AEF=∠AFE=45°,
∴∠ADB=∠AEF,
∵∠AOD=∠EOM,
∴△AOD∽△MOE,
∴,
∵∠AOM=∠DOE,
∴△AOM∽△DOE,
∴∠EAM=∠BDC=45°,
∵AF=AE,
∴点M是EF的中点;
②解:如图2,
取CF的中点,连接MW,
∵点M是EF的中点,
∴MW∥CE,MWCE,
∴∠MWB=∠C=90°,
∵四边形ABCD是正方形,
∴∠CBD=45°,
∴BMMW,
∴BMCE,
∴,
故答案为:;
(3)解:如图3,
连接AP,作△APF的外接圆O,连接OA,作OV⊥BC于V,
设⊙O的半径为r,
∵△ADE沿AE翻折至△AQE,
∴AQ=AD=AB,∠AQP=∠AQE=∠D=∠ABC=90°,∠DAE=∠QAE,
∵AP=AP,
∴Rt△ABP≌Rt△APQ(HL),
∴∠BAP=∠QAP,
∵∠BAD=90°,
∴∠DAE+∠BAP=45°,
∵∠DAE=∠BAF,
∴∠BAF+∠BAP=45°,
∴∠PAF=45°,
∴∠POF=90°,
∴OVr,PFr,
∵AO+OV≥AB,
∴rr≥3,
∴r≥6﹣3,
∴当A、O、V共线时,r最小,最小值为:6﹣3,
此时PF最小值为:(6﹣3)=66,
故答案为:6.
13.【解答】解:(1)证明:如图所示,取AB的中点M,并连接ME,
∴AM=BM,
∵E是边BC的中点,
∴BE=CE,
∵四边形ABCD是正方形,
∴AM=BM=BE=CE,
∵∠AEF=90°,∠B=90°,
∴∠MAE+∠AEB=90°,∠CEF+∠AEB=90°,
∴∠MAE=∠CEB,
∵BM=BE,∠B=90°
∴∠BME=45°,∠AME=135°,
∵正方形外角的平分线为CF,
∴∠ECF=90°+45°=135°,
∴∠AME=∠ECF,
在△AME和△ECF中,
,
∴△AME≌△ECF(ASA),
∴AE=EF;
(2)解:如图所示,连接AC,
∵点M,E分别为AB,BC的中点,
∴ME为△ABC的中位线,
∴AC=2ME,
由(1)得△AME≌△ECF,
∴ME=CF,
∴AC=2CF,
∴,
故答案为:;
(3)解:EH=BE+DH,理由如下:
如图所示,延长CB至点N,使得BN=DH,连接AN,
由正方形基本性质得:∠ABN=∠ADH=90°,AB=AD,
∴△ABN≌△ADH(SAS),
∴AN=AH,∠DAH=∠BAN,
由(1)知,AE=EF,且∠AEF=90°,
∴∠EAF=∠EFA=45°,
∴∠DAH+∠BAE=∠BAD﹣∠EAF=90°﹣45°=45°,
∴∠NAE=∠BAN+∠BAE=45°,即:∠NAE=∠HAE=45°,
在△NAE和△HAE中,
,
∴△NAE≌△HAE(SAS),
∴EN=EH,
∵EN=BE+BN,BN=DH,
∴EN=BE+DH,
∴EH=BE+DH.
14.【解答】(1)证明:∵正方形ABCD,对角线AC,
∴∠BAC=∠BCA=45°,
∵△FBE和△ABE关于直线BE对称,
∴△FBE≌△ABE,
∴∠BFE=∠BAE,
∵∠FGE=∠CGB,
∴△FGE∽△CGB,
∴,
∴CG EG=BG FG.
(2)解:∵△FBE和△ABE关于直线BE对称,
∴△FBE≌△ABE,
∴FB=AB,FE=AE,∠FBE=∠ABE,
∵BF∥AC,
∴∠AEB=∠FBE,
∴∠ABE=∠AEB,
∴AB=AE,
∴AB=AE=BF=FE,
∵正方形ABCD,
∴AB=BC,∠ABC=90°,
设AB=x,则AE=x,
∴AC,
∴CE=AC﹣AE=()x,
∴.
(3)解:如图,延长CD,BQ交于点H,
设CP=x,则DP=2CP=2x,
∴CD=3x,
∵正方形ABCD,
∴BC=CD=AB=3x,AB∥CD,
在Rt△BCP中,BP,
∵∠H=∠HBA,
∴,
∵△FBE和△ABE关于直线BE对称,
∴△FBE≌△ABE,
∴∠HBA=∠HBP,
∴∠H=∠HBP,
∴PH=PB,
∴HD=PH﹣PD=()x,
∴,
∴.
15.【解答】(1)证明:∵四边形ABCD是正方形,
∴AD=AB,∠ADF=∠ABE=90°,
又∵BE=DF,
∴△ABE≌△ADF(SAS),
∴AE=AF.
(2)解:∵BF⊥AE,
∴∠BGE=90°,
∵四边形ABCD是正方形,
∴BC=AB,∠C=∠ABC=90°,
∴∠GEB+∠GBE=90°=∠GEB+∠EAB,
∴∠CBF=∠BAE,
∴△ABE≌△BCF(ASA),
∴CF=BE,
∴CF=DF,即点F为CD中点,
如图所示,取AB中点H,连接DH交AG于P,
∴,
∵AB=DA,∠ABE=∠DAH=90°,
∴△ABE≌△DAH(SAS),
∴∠BAE=∠ADH,
∵∠BAE+∠DAE=90°,
∴∠ADP+∠DAE=90°,
∴∠DPA=90°,即DH⊥AE,
∴DH∥BF;
取AG中点Q,连接HQ,则HQ是△ABG的中位线,
∴HQ∥BG,
∴由平行线的唯一性可知点Q与点P重合,
∴AP=GP,
∴DH垂直平分AG,
∴DA=DG,
∴.
答:的值为1.
(3)解:连接EF,如图,
设AM=x,则AF=AE=x+2,
在Rt△AFM中,AF2=AM2+FM2,
∴(x+2)2=x2+52,
解得,
∴,,
在Rt△EFM中,,
∵DF=BE,CD=BC,
∴CF=CE,
∴△CEF 是等腰直角三角形,
∴,
设BE=y,则,
在Rt△ABE中,AE2=AB2+BE2,
∴,
整理得,
解得y或(舍去),
∴.
答:AB的长为.
21世纪教育网(www.21cnjy.com)
同课章节目录
