2025年九年级数学中考二轮专题复习二次函数中的角度问题(含答案)
文档属性
| 名称 | 2025年九年级数学中考二轮专题复习二次函数中的角度问题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-11 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2025年九年级数学中考二轮专题复习二次函数中的角度问题
1.如图,二次函数y=﹣x2+bx+c的图象与x轴交于A,B两点,与y轴交于点C.点A的坐标为(﹣3,0),且OA=OC.
(1)求抛物线的解析式;
(2)若P为y轴上的一个动点,连接PB,则的最小值为 .
(3)连接BC,M是抛物线上的一点,且满足∠MAB=2∠OCB,求点M的坐标.
2.如图,二次函数y=ax2﹣6ax+c(a<0)的图象与x轴的负半轴和正半轴分别交于A,B两点,与y轴交于点C,顶点为P,对称轴交x轴于点D,点Q是抛物线对称轴上一动点,直线BQ交y轴于点E,且5EQ=3BQ.
(1)请直接写出A,B两点的坐标:A ,B ;
(2)当顶点P与点Q关于x轴对称时,S△QCE.
①求此时抛物线的函数表达式;
②在抛物线的对称轴上存在点F,使∠BEF=2∠OBE,请直接写出点F的坐标.
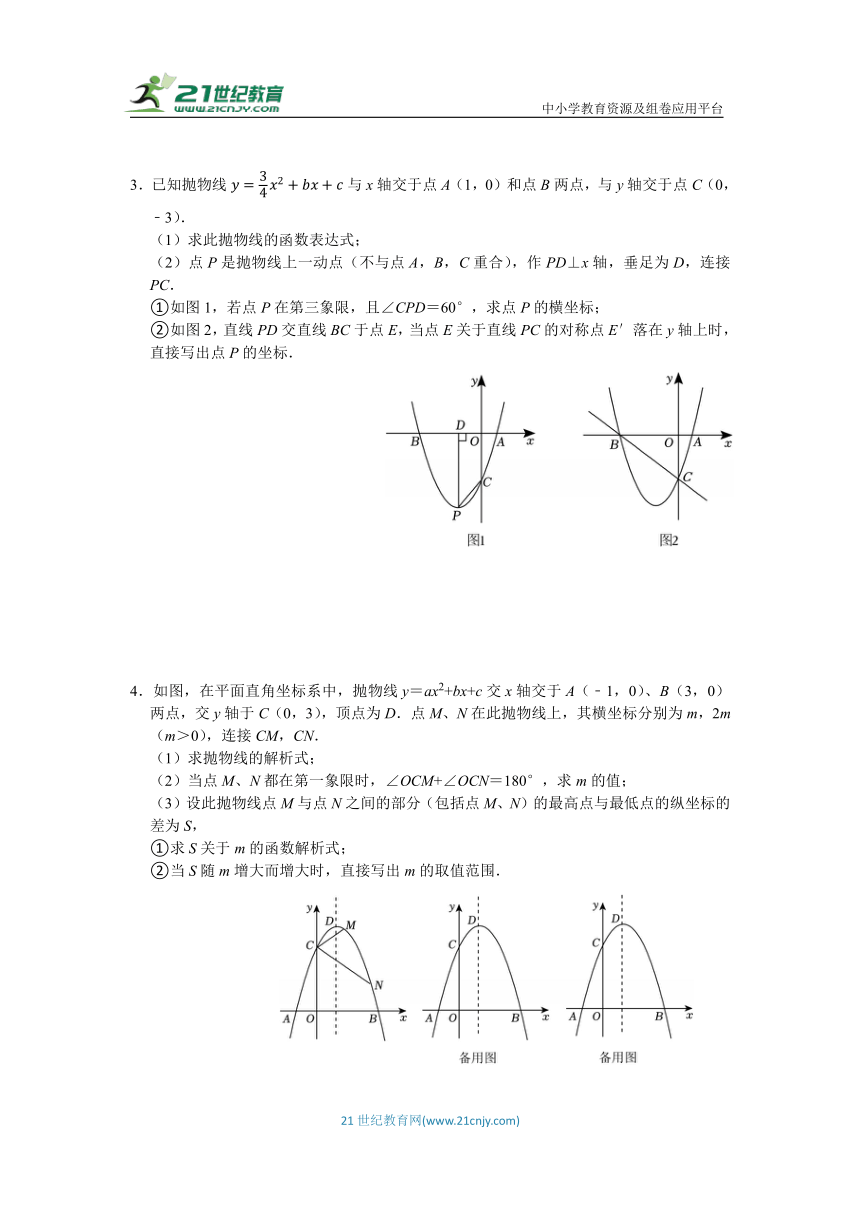
3.已知抛物线与x轴交于点A(1,0)和点B两点,与y轴交于点C(0,﹣3).
(1)求此抛物线的函数表达式;
(2)点P是抛物线上一动点(不与点A,B,C重合),作PD⊥x轴,垂足为D,连接PC.
①如图1,若点P在第三象限,且∠CPD=60°,求点P的横坐标;
②如图2,直线PD交直线BC于点E,当点E关于直线PC的对称点E′落在y轴上时,直接写出点P的坐标.
4.如图,在平面直角坐标系中,抛物线y=ax2+bx+c交x轴交于A(﹣1,0)、B(3,0)两点,交y轴于C(0,3),顶点为D.点M、N在此抛物线上,其横坐标分别为m,2m(m>0),连接CM,CN.
(1)求抛物线的解析式;
(2)当点M、N都在第一象限时,∠OCM+∠OCN=180°,求m的值;
(3)设此抛物线点M与点N之间的部分(包括点M、N)的最高点与最低点的纵坐标的差为S,
①求S关于m的函数解析式;
②当S随m增大而增大时,直接写出m的取值范围.
5.在平面直角坐标系中,抛物线y=x2﹣2x﹣3与x轴交于点A和点B,与y轴交于点C,顶点为D.
(1)请直接写出A、B、D三点坐标.
(2)如图1,点M是第四象限内抛物线上的一点,过点M作x轴的垂线,交直线BC于点N,求线段MN长度的最大值;
(3)如图2,若点P在抛物线上且满足∠PCB=∠CBD,求点P的坐标.
6.如图,在平面直角坐标系中,抛物线过A,B,C三点,点A(﹣1,0),点B(4,0),点C在y轴的正半轴上,连接AC,BC,AC⊥BC,点D在抛物线的对称轴上,其纵坐标为,连接BD,CD,并延长CD交抛物线于点E,连接BE.
(1)求抛物线的函数解析式;
(2)求△BCE的面积;
(3)若点K在抛物线上,且满足∠BDK=∠CBD,求点K的坐标.
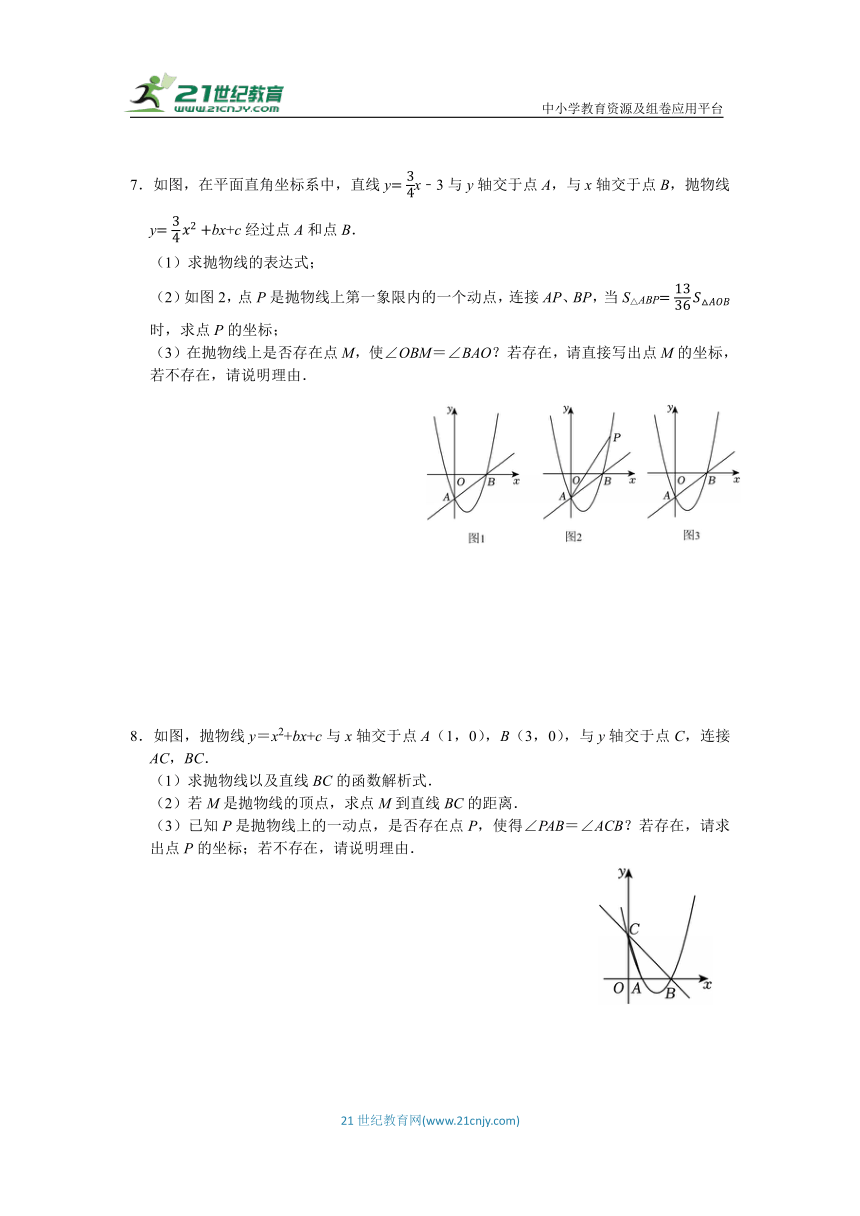
7.如图,在平面直角坐标系中,直线yx﹣3与y轴交于点A,与x轴交于点B,抛物线ybx+c经过点A和点B.
(1)求抛物线的表达式;
(2)如图2,点P是抛物线上第一象限内的一个动点,连接AP、BP,当S△ABP时,求点P的坐标;
(3)在抛物线上是否存在点M,使∠OBM=∠BAO?若存在,请直接写出点M的坐标,若不存在,请说明理由.
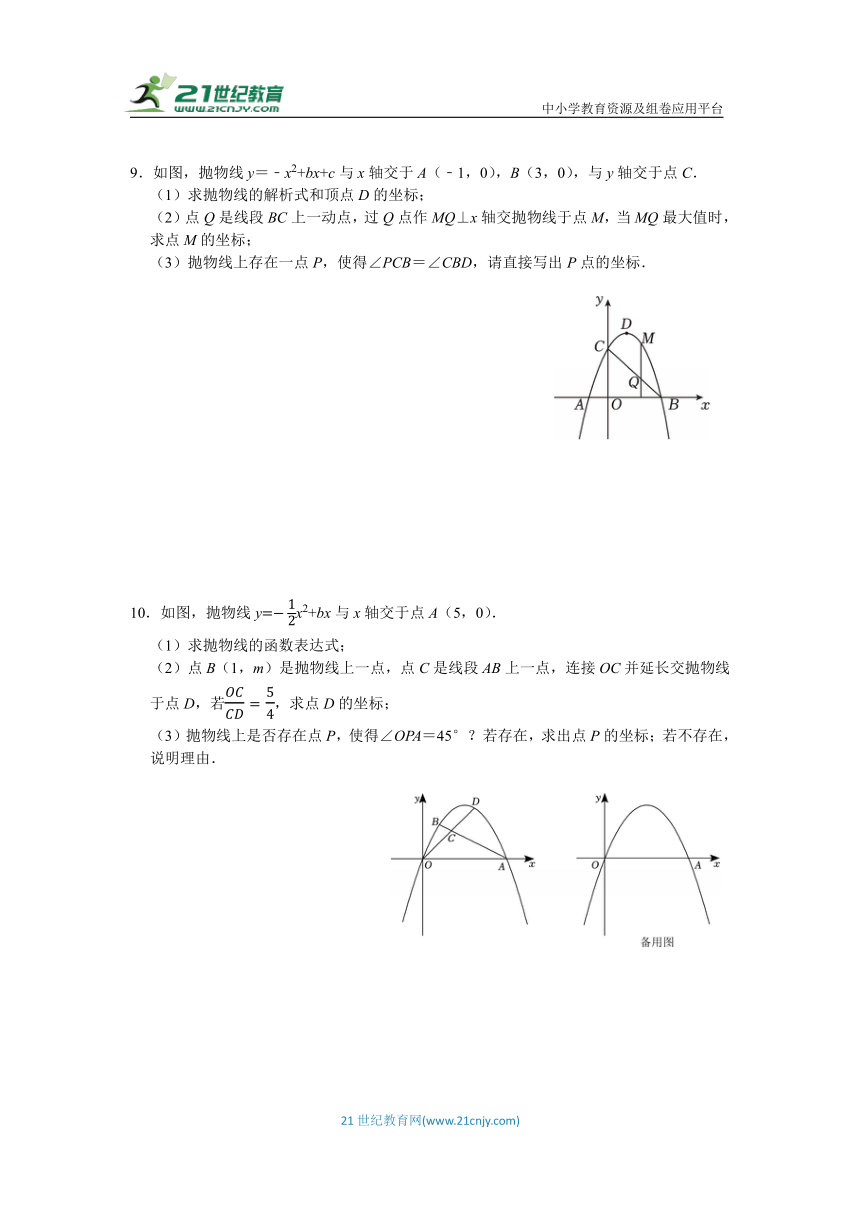
8.如图,抛物线y=x2+bx+c与x轴交于点A(1,0),B(3,0),与y轴交于点C,连接AC,BC.
(1)求抛物线以及直线BC的函数解析式.
(2)若M是抛物线的顶点,求点M到直线BC的距离.
(3)已知P是抛物线上的一动点,是否存在点P,使得∠PAB=∠ACB?若存在,请求出点P的坐标;若不存在,请说明理由.
9.如图,抛物线y=﹣x2+bx+c与x轴交于A(﹣1,0),B(3,0),与y轴交于点C.
(1)求抛物线的解析式和顶点D的坐标;
(2)点Q是线段BC上一动点,过Q点作MQ⊥x轴交抛物线于点M,当MQ最大值时,求点M的坐标;
(3)抛物线上存在一点P,使得∠PCB=∠CBD,请直接写出P点的坐标.
10.如图,抛物线yx2+bx与x轴交于点A(5,0).
(1)求抛物线的函数表达式;
(2)点B(1,m)是抛物线上一点,点C是线段AB上一点,连接OC并延长交抛物线于点D,若,求点D的坐标;
(3)抛物线上是否存在点P,使得∠OPA=45°?若存在,求出点P的坐标;若不存在,说明理由.
11.如图,抛物线与x轴交于A、C两点(点A在点C的右侧),与y轴交于点B,且OA=OB.
(1)求抛物线的表达式;
(2)点P在抛物线上,当∠PBA+∠CBO=45°时,求点P的横坐标.
12.如图,在平面直角坐标系中,抛物线与y轴交于点A,与x轴的正半轴交于点B.
(1)求△AOB的面积;
(2)点P是直线AB下方抛物线上一点,过点P作y轴的平行线,交AB于点E,过点P作AB的垂线,垂足为点F,求EF的最大值及此时点P的坐标;
(3)在抛物线上是否存在点Q,使∠OBQ=∠BAO?若存在,请直接写出点Q的坐标,若不存在,请说明理由.
13.如图,抛物线y=﹣x2+bx+c经过点A(﹣4,0)、B(1,0),交y轴于点C(0,4),点P是抛物线上一动点.
(1)求该抛物线的函数表达式;
(2)当点P的坐标为(﹣2,6)时,求四边形AOCP的面积;
(3)若∠PBA=45°,求点P的坐标.
14.如图,已知抛物线y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣1,0)和点B(3,0),与y轴交于点C(0,﹣3).
(1)求二次函数的表达式;
(2)如图,点M是直线BC下方的二次函数图象上的一个动点,过点M作MH⊥x轴于点H,交BC于点N,求线段MN最大时点M的坐标;
(3)在(2)的条件下,该抛物线上是否存在点Q,使得∠QCB=∠CBM.若存在,请直接写出点Q的坐标;若不存在,请说明理由.
15.如图所示,直线y=﹣x+n与x轴交于点A(3,0),与y轴交于点B,抛物线y=﹣x2+bx+c经过A、B两点,与x轴的另一个交点为点C.
(1)求抛物线的解析式;
(2)点E(m,0)是x轴正半轴上一动点,过点E作ED⊥x轴于点E,交直线AB于点D,交抛物线于点P,连结PB,BC.
①当点E在线段OA上时,若△PBD与△ABC相似,求点E的坐标;
②若∠PBD+∠CBO=45°,求出m的值.
参考答案
1.【解答】解:(1)二次函数y=﹣x2+bx+c的图象与x轴交于A,B两点,与y轴交于点C.点A的坐标为(﹣3,0),且OA=OC,
∴OA=OC=3,
∴C(0,3),
将点A,点C的坐标分别代入y=﹣x2+bx+c得:
,
解得,
∴抛物线的解析式为y=﹣x2﹣2x+3;
(2)P为y轴上的一个动点,如图1,过P作PH⊥AC于H,过B作BH′⊥AC于H′,
∵OA=OC,∠AOC=90°,
∴∠OAC=∠OCA=45°,
∴,
∴,
当B、P、H共线且BH⊥AC时取等号,此时H与H′重合,最小值为BH′的长,
∵二次函数y=﹣x2﹣2x+3的图象与x轴交于A,B两点,
当y=0时,得:y=﹣x2﹣2x+3=0,
解得x1=﹣3,x2=1,
∴B(1,0),
∴OB=1,
在Rt△ABH′中,AB=OA+OB=4,∠OAC=45°,∠AH′B=90°,
∴,
即的最小值为,
故答案为:2;
(3)在OC上截取CD=BD,连接BD,如图2,
则∠OCB=∠CBD,
∴∠ODB=∠OCB+∠CBD=2∠OCB=∠MAB,
设CD=BD=t,则OD=OC﹣CD=3﹣t,
在Rt△BOD中,由勾股定理得:OD2+OB2=BD2,
∴(3﹣t)2+12=t2,
解得,
∴,
∴,
设M(m,﹣m2﹣2m+3),
当点M在x轴的上方时,如图2,过M作MN⊥x轴于点N,
则MN=﹣m2﹣2m+3,AN=m+3,
由得,
解得或m=﹣3(舍去),
∴,
∴;
当点M在x轴的下方时,如图3,过M作MN⊥x轴于点N,
则MN=m2+2m﹣3,AN=m+3,
由得,
解得或m=﹣3,
∴,
∴,
综上所述,满足条件的点M的坐标为或.
2.【解答】解:(1)y=ax2﹣6ax+c=a(x﹣3)2﹣9a+c,
∴抛物线对称轴是:直线x=3,
∴OD=3,
如图1所示,
∵DQ∥y轴,则OD:BD=EQ:BQ,
∵5EQ=3BQ,
∴EQ:BQ=3:5=OD:BD,
则BD=5,
∴B(8,0),
由对称性得:A(﹣2,0),
故答案为:(﹣2,0),(8,0);
(2)①如图1,
将点A(﹣2,0)代入二次函数y=ax2﹣6ax+c中得:4a+12a+c=0,
∴c=﹣16a,
∵y=ax2﹣6ax+c=a(x﹣3)2﹣9a+c,
∴P(3,﹣9a+c),
∵顶点P与点Q关于x轴对称,
∴Q(3,9a﹣c),即Q(3,25a),
∵S△QCE.
∴,
∴EC,
由点B、Q的坐标得,直线BQ的表达式为:y=﹣5ax+40a,
∴E(0,40a),
∵C(0,c),即(0,﹣16a),
∴﹣16a﹣40a,
解得:a=﹣0.1,
∴c=﹣16×(﹣0.1),
∴此时抛物线的函数表达式为:yx2x;
②如图2,当点F在BE的下方时,连接PB,
∵顶点P与点Q关于x轴对称,
∴∠PBD=∠QBD,
∵∠BEF=2∠OBE,
∴∠BEF=∠PBQ,
∴PB∥EF,
由①知:a=﹣0.1
∴P(3,2.5),
同理得:PB的解析式为:yx+4,
∴设EF的解析式为:yx+n,
∵E(0,﹣4),
∴n=﹣4,
则F(3,);
②如图:
当点F在BE的上方时,连接DE,
设F(3,m),
∵D(3,0),
∴BD=5,
∵D(3,0)E(0,﹣4),OD=3,OE=4,
由勾股定理得ED=5,
∴DE=BD,
∴∠DEB=∠OBE,
∵∠FEB=2∠OBE,
∴∠FEB=2∠DEB,
∴EQ:EF=DQ:FD,
∵BE4,
又∵5EQ=3BQ,
∴EQBQ,
∴EQ+BQ=BE,
∴EQ,
∵DQ=2.5,
FD=m,
则EQ:EF=DQ:FD,
∴EFm,
过F作FD⊥y轴,垂足为N,
在直角三角形中,EF,
∴m,
解得m或(舍去),
综上所述,F(3,)或F(3,).
3.【解答】解:(1)已知抛物线与x轴交于点A(1,0)和点B两点,与y轴交于点C(0,﹣3),将点A,点C的坐标代入得:
,
解得:,
∴抛物线的函数表达式为;
(2)①PD⊥x轴,垂足为D,如图1,设直线PC交x轴于E,
∴∠OCE=∠CPD=60°,
∵∠COE=90°,
∴∠CEO=90°﹣∠ECO=30°,
∴CE=2OC=6,
∴,
∴点,
∴直线PC的解析式为,
由得:,x2=0(舍去),
即点P的横坐标为;
②点P的坐标为或.理由如下:
如图2,
令,
解得x1=﹣4,x2=1,
∴B(﹣4,0),
设直线BC的解析式为y=mx+n,将点B(﹣4,0)、C(0,﹣3)代入得:
,
解得:,
∴直线BC的解析式为,
设点,
分以下两种情况:
点P在第三象限时,作EF⊥y轴于F,
∵点E与E′关于PC对称,
∴∠ECP=∠E′PC,CE=CE′,
∵PE∥y轴,
∴∠EPC=∠PCE′,
∴∠ECP=∠EPC,
∴PE=CE,
∴PE=CE′,
∴四边形PECE′为平行四边形,
∴ PECE′为菱形,
∴CE=PE,
∵EF∥OA,
∴,,
∴,
∴,
∵,
∴,
∴m1=0(舍去),,
∴;
当点P在第二象限时,
同理可得:,
解得:m3=0(舍去),,
∴;
综上所述,点P的坐标为或.
4.【解答】解:(1)∵抛物线y=ax2+bx+c交x轴交于A(﹣1,0)、B(3,0)两点,交y轴于C(0,3),
∴,
解得,
∴抛物线的解析式为y=﹣x2+2x+3;
(2)过M作ME⊥OC于E,过N作NF⊥OC于F,则∠MEC=∠NFC=90°,
∵点M、N都在第一象限,M、N在此抛物线上,其横坐标分别为m,2m,
∴ME=m,OE=﹣m2+2m+3,NF=2m,OF=﹣4m2+4m+3,
∴EF=3m2﹣2m,
∵∠OCM+∠OCN=180°,∠OCM+∠ECM=180°,
∴∠OCN=∠ECM,
又∵∠MEC=∠NFC=90°,
∴△MEC∽△NFC,
∴,
∴,
∵C(0,3),
∴OC=3,
∵OC=OF+CF,
∴,
解得,
∴m的值为;
(3)①∵y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴顶点为D(1,4),
∵点M、N在此抛物线上,其横坐标分别为m,2m(m>0),
∴M(m,﹣m2+2m+3),N(2m,﹣4m2+4m+3),
如图2,
当点M、N都在顶点D左侧时,,M为最低点,N为最高点,
则S=﹣4m2+4m+3﹣(﹣m2+2m+3)=﹣3m2+2m;
如图3,
当点M在点D左侧,N在顶点D右侧时,,M为最低点,D为最高点,
则S=4﹣(﹣m2+2m+3)=m2﹣2m+1;
如图4,
当点M在点D左侧,N在顶点D右侧时,,N为最低点,D为最高点,
则S=4﹣(﹣4m2+4m+3)=4m2﹣4m+1;
如图5,
当点M、N都在顶点D右侧时,m>1,N为最低点,M为最高点,
则S=﹣m2+2m+3﹣(﹣4m2+4m+3)=3m2﹣2m;
综上所述,;
②m的取值范围为或;理由如下:
当S=﹣3m2+2m时,抛物线的对称轴为直线,
∵﹣3<0,
∴当时,S随m增大而增大,
又∵,
∴;
当S=m2﹣2m+1时,抛物线的对称轴为直线m=1,
∵1>0,
∴当m>1时,S随m增大而增大,
∵,
∴此种情况不存在;
当S=4m2﹣4m+1时,抛物线的对称轴为直线,
∵4>0,
∴当时,S随m增大而增大,
∵,
∴;
当S=3m2﹣2m时,抛物线的对称轴为直线,
∵3>0,
∴当,S随m增大而增大,
∵m>1,
∴m>1;
综上,当S随m增大而增大时,m的取值范围为或.
5.【解答】解:(1)点A的坐标为(﹣1,0),点B的坐标为(3,0),点D的坐标为(1,﹣4);理由如下:
∵在平面直角坐标系中,抛物线y=x2﹣2x﹣3与x轴交于点A和点B,与y轴交于点C,
当y=0时,得x2﹣2x﹣3=0,
解得:x=﹣1或x=3,
当x=0时,得y=﹣3,
∴A(﹣1,0),B(3,0),C(0,﹣3),
∵抛物线y=x2﹣2x﹣3=(x﹣1)2﹣4,
∴D(1,﹣4),
∴点A的坐标为(﹣1,0),点B的坐标为(3,0),点D的坐标为(1,﹣4);
(2)设ME⊥x轴于点E,设M(m,m2﹣2m﹣3),如图1,
设直线BC的解析式为y=kBCx+bBC,将点B,点C的坐标代入得:
,
解得:,
∴直线BC的解析式为y=x﹣3,
∵过点M作x轴的垂线,交直线BC于点N,
∴N(m,m﹣3),
∴,
∵﹣1<0,
∴当时,线段MN的长度取得最大值,此时最大值为;
(3)设直线BD的解析式为y=kBDx+bBD,将点B,点D的坐标代入得:
,
解得:,
∴直线BD的解析式为y=2x﹣6,
①如图2,
∵∠PCB=∠CBD,
∴PC∥BD,
设直线PC的解析式为y=2x+bPC,将点C的坐标代入得:bPC=﹣3,
∴直线PC的解析式为y=2x﹣3,
联立,
解得:或,
此时点P的坐标为(4,5);
②如图3,设CP交BD于点G,作射线OG交BC于点F,
∵∠PCB=∠CBD,
∴GC=GB,
∵B(3,0),C(0,﹣3),
∴OC=OB=3,
∴OG垂直平分BC,
∴点F是BC的中点,
∴点F的坐标是,即,
设直线OG的解析式为y=kOGx,过点,
∴,
∴kOG=﹣1,
∴直线OG的解析式为y=﹣x,
∵直线OG:y=﹣x与直线BD:y=2x﹣6交于点G,
联立,
解得:,
∴G(2,﹣2),
设直线CG的解析式为y=kCGx+bCG,将点C,点G的坐标代入得:
,
解得:,
∴直线CG的解析式为,
联立,
解得:或,
此时点P的坐标为;
综上所述,点P的坐标为(4,5)或.
6.【解答】解:(1)∵AC⊥BC,
故∠ACO+∠OCB=90°,
∵∠OCB+∠CBO=90°,
∴∠ACO=∠OCB,
∴tan∠ACO=tan∠OCB,即OA:CO=OC:BO,
则OC2=AO OB=4,则CO=2,即c=2,
则抛物线的表达式为:y=a(x+1)(x﹣4)=a(x2﹣3x﹣4),
则﹣4a=2,则a,
故抛物线的表达式为:yx2x+2;
(2)由抛物线的表达式知,其对称轴为直线x,则点D(,),
由点C、D的坐标得,直线CD的表达式为:yx+2,
联立上式和抛物线的表达式得:x+2x2x+2,
解得:x=0(舍去)或,则点E(,),
由点B、C的坐标得,直线BC的表达式为:yx+2,
作EH∥y轴交CB于点H,则点H(,),则DH,
则△BCE的面积EH×OB;
(3)当点K在BC的左侧时,
设DK交BC于点H,
∵∠BDK=∠CBD,则HD=HB,
设点H(m,m+2),
则(m)2+(m+2)2=(m﹣4)2+(m+2)2,
解得:x,则点H(,),
由点D、H的坐标得,直线DH的表达式为:y=﹣2(x),
联立上式和抛物线的表达式得:﹣2(x)x2x+2,
解得:x(不合题意的值已舍去),
即点K(,);
当点K在BC的右侧时,
∵∠BDK=∠CBD,则DK∥BC,
则直线DK的表达式为:y(x),
联立上式和抛物线的表达式得:(x)x2x+2,
解得:x(不合题意的值已舍去),
则点K(,),
综上,点K的坐标为:(,)或(,).
7.【解答】解:(1)∵直线yx﹣3与y轴交于点A,与x轴交于点B,
当x=0时,y=﹣3,
当y=0时,x﹣3=0,解得:x=4,
∴A(0,﹣3),B(4,0),
把A(0,﹣3),B(4,0)代入ybx+c,
得,
解得:,
∴抛物线的表达式为yx﹣3;
(2)设P(t,t2t﹣3),过点P作PE∥y轴,交直线AB于点E,如图,
则E(t,t﹣3),
∴PEt2t﹣3﹣(t﹣3)t2﹣3t,
∵A(0,﹣3),B(4,0),
∴S△AOBOA×OB3×4=6,
S△ABP=S△APE﹣S△BPE(t2﹣3t)×[t﹣(t﹣4)]t2﹣6t,
∵S△ABP,
∴36S△ABP=13S△AOB,
即36(t2﹣6t)=13×6,
解得:t1(舍去),t2,
此时yP()23,
∴点P的坐标为(,);
(3)设直线BM交y轴于点N,
∵∠AOB=∠BON=90°,∠OBM=∠BAO,
∴△ABO∽△BNO,
∴,即,
∴ON,
∴N1(0,),N2(0,),
∴直线BM的解析式为yx或yx,
联立得或,
解得:,(舍去),,
∴点M的坐标为(,)或(,).
8.【解答】解:(1)将点A(1,0),B(3,0)代入y=x2+bx+c,
得
解得
∴抛物线的函数解析式为y=x2﹣4x+3,
令x=0,解得y=3,
∴点C(0,3).
设直线BC的函数解析式为y=kx+3,
将点B的坐标代入上式得:0=3k+3,则k=﹣1,
则BC的表达式为:y=﹣x+3;
(2)由抛物线的表达式知,点M(2,﹣1),
作MH∥y轴交CB于点H,作MT⊥BC于点T,
当x=2时,y=﹣x+3=1,
则点H(2,1),
则∠MHT=∠OCB=45°,
则MH=2,
则MT=MH cos45°;
(3)存在,理由:
作AN⊥CB于点N,
在△ABC中,OB=OC,则∠CBA=45°,
由点A、B、C的坐标得,BC=3,AB=2,
则NBABAN,则CN=BC﹣BN=2,
则tan∠ACB,
∵∠PAB=∠ACB,则tan∠PAB=tan∠ACB,
则PA的表达式为:y=±(x﹣1),
联立上式和抛物线的表达式得:(x﹣1)=x2﹣4x+3或(x﹣1)=x2﹣4x+3,
解得:x或,
则点P(,)或(,).
9.【解答】解:(1)由题意得:y=﹣(x+1)(x﹣3)=﹣x2+2x+3,
则点D(1,4);
(2)由抛物线的表达式知,点C(0,3),
由点B、C的坐标得,直线BC的表达式为:y=﹣x+3,
设点M(x,﹣x2+2x+3),则点Q(x,﹣x+3),
则MQ=﹣x2+2x+3﹣(﹣x+3)=﹣(x)2,
当MQ取得最大值时,x,则点M(,);
(3)当点P在BC左侧时,
∵∠PCB=∠CBD,则PC∥BD,
由B、D的坐标得,直线BD的表达式为:y=﹣2(x﹣3),
则直线PC的表达式为:y=﹣2x+3,
联立上式和抛物线的表达式得:﹣2x+3=﹣x2+2x+3,
解得:x=0(舍去)或4,即点P(4,﹣5),
当点P在BC的右侧时,
同理可得,直线PC的表达式为:yx+3,
联立上式和抛物线的表达式得:x+3=﹣x2+2x+3,
解得:x=0(舍去)或2.5,即点P(,),
综上,P(4,﹣5)或(,).
10.【解答】解:(1)由已知得25+b×5=0,b,
∴yx2x.
(2)作CE⊥OA于E,DF⊥OA于F.
当x=1时,
m121=2,
点B坐标为(1,2).
设AB解析式为:y=kx+b,
,
解得.
∴y.
∵,
∴.
∵CE⊥OA于E,DF⊥OA于F,
∴CE∥DF,
∴,
设E点坐标为(m,0),
∴点C坐标为(m,),
点F坐标为(m,0),
点D坐标为(m,).
∵点D在抛物线上,
∴(m)2m,
∴9m2﹣30m+25=0,
m1=m2.
∴点D坐标为(3,3).
(3)作过O、P、A三点的圆M,连接OM,AM,PM,作MN⊥OA于N,
∵∠OPA=45°,
∴∠AMO=90°,
∵OM=AM,OA=5,
又∵MN⊥OA,
∴ON=AN=MN=2.5,
∴点M坐标为(2.5,﹣2.5),
∴AM=OM,
∴PM,
设点P坐标为(x,y),
∴(x﹣2.5)2+(y+2,5)2=()2,
∴x2﹣5x+y2+5y=0,
∵yx2x.
∴y2+3y=0,
∴y1=0,(不合题意舍去),y2=﹣3.
∴y=﹣3,
∴﹣3x2x,
∴x1=﹣1,x2=6,
∴点P坐标为(﹣1,﹣3)或(6,﹣3).
11.【解答】解:(1)当x=0时,y=﹣4,
∴点B的坐标为(0,﹣4),OB=4,
∵OA=OB,
∴OA=4,
∴A(4,0),
将点A的坐标(4,0)代入抛物线中得:
4b﹣4=0,
∴b,
∴抛物线的表达式为:yx2x﹣4;
(2)当y=0时,x2x﹣4=0,
解得:x1=4,x2=﹣3,
∴C(﹣3,0),
分两种情况:
①如图1,在OA上取一点C',使OC=OC'=3,作射线BC'交抛物线于点P,
∴∠CBO=∠C'BO,
∵OA=OB,∠AOB=90°,
∴△AOB是等腰直角三角形,
∴∠ABO=45°,
∴∠PBA+∠C'BO=∠CBO+∠PBA=45°,点P满足条件,
∵点B的坐标为(0,﹣4),
∴设BP的解析式为:y=kx﹣4,
把点C'的坐标为(3,0)代入得:3k﹣4=0,
∴k,
∴BP的解析式为:yx﹣4,
∴x2x﹣4x﹣4,
解得:x1=0(舍),x2=5,
∴点P的横坐标为5;
②如图2,当BC⊥BP时,∠CBO+∠PBA=90°﹣45°=45°,点P满足条件,
过点P作PM⊥OB于M,
∴∠PBM+∠CBO=∠CBO+∠BCO=90°,
∴∠PBM=∠BCO,
∴tan∠PBM=tan∠BCO,
∴,
设点P的坐标为(t,t2t﹣4),
∴,
∴t1=0(舍),t2,
∴点P的横坐标为;
综上,点P的横坐标为5或.
12.【解答】解:(1)抛物线与y轴交于点A,与x轴的正半轴交于点B.
由知,
当x=0时,y=﹣3,
∴A(0,﹣3),
∴OA=3,
当y=0时,,
整理得:(x﹣4)(x+1)=0,
∴x1=4,x2=﹣1,
∴B(4,0),
∴OB=4,
∴.
(2)设AB解析式为y=kx+b,把A,B代入得:
,
解得:,
∴,
设,则,
∴,
又∵PE∥y轴,
∴∠PEF=∠OAB,
又∵PF⊥AB1
∴∠PFE=∠BOA=90°,
∴△PEF∽△BAO,
∴,
在Rt△AOB中,
,
∴,
∴,
∴当m=2时,EF有最大值为,
∴P的纵坐标:,
∴.
(3)设,过Q点作QP⊥x轴,垂足为P,
∵在Rt△AOB中,,
而∠OAB=∠OBQ,
∴,
在Rt△BPQ中,,
∴,
①当Q点在x轴下方时,,
解得:,a2=4(不合题意,舍去),
∴,
∴,
②当Q点在x轴上方时,,
解得:,a2=4(不合题意,舍去),
∴,
∴,
∴或.
13.【解答】解:(1)将点B(1,0)代入y=﹣x2+bx+4,
得﹣1+b+4=0,
解得b=﹣3,
∴抛物线解析式为y=﹣x2﹣3x+4;
(2)如图所示,过点P作PT⊥AB于T,
∵P(﹣2,6),A(﹣4,0),C(0,4),
∴OA=4,OT=2,OC=4 PT=6,
∴AT=2,
∴S四边形AOCP=S△APT+S梯形OCPT
=16;
(3)如图所示,取H1(﹣4,5),连接AH1,BH1,
∵A(﹣4,0)、B(1,0),H1(﹣4,5),
∴AH1=5,AB=5,AH1⊥AB,
∴∠ABH1=45°,
∴线段BH1与抛物线的交点P1即为所求;
设直线BH1的解析式为y=kx+b1,
∴,
∴,
∴直线BH1的解析式为y=﹣x+1,
联立,解得或(舍去),
∴P1(﹣3,4);
如图所示,取H2(﹣4,﹣5),连接AH2,BH2,
同理可得∠ABH2=45°,
∴直线BH2与抛物线的交点P2即为所求;
同理可知直线BH2的解析式为y=x﹣1,
联立,
解得或(舍去),
∴P2(﹣5,﹣6);
综上所述,符合题意的点P的坐标为(﹣3,4)或(﹣5,﹣6).
14.【解答】解:(1)将点A(﹣1,0),B(3,0),C(0,﹣3)代入y=ax2+bx+c,
得:,解得:,
∴二次函数的表达式为:y=x2﹣2x﹣3,
(2)设直线BC的解析式为:y=k1x+b1,
将B(3,0),C(0,﹣3)代入y=k1x+b1,
得:,解得:,
∴直线BC的解析式为:y=x﹣3,
设点M的横坐标为t,
∵点M在BC下方的二次函数图象上,
∴点M的纵坐标为:t2﹣2t﹣3,
∵MH⊥x轴交BC于点N,
∴点N的横坐标为t,
∴点N的纵坐标为:t﹣3,
∴,
∴当时,MN为最大,
当时,,
∴点M的坐标为.
(3)存在,点Q的坐标为或.
理由如下:
设直线BM的解析式为:y=k2x+b2,
将点B(3,0),M(3/2,﹣15/4)代入y=k2x+b2,
得:,解得:,
∴直线BM的解析式为:,
当∠QCB=∠CBM时,有以下两种情况:
①当点Q在直线BC上方时,
∵∠QCB=∠CBM,
∴CQ∥BM,
设直线CQ的解析式为:y=k3x+b3,
则,b3=﹣3,
∴直线CQ的解析式为:,
解方程组,得:,,
∴点Q的坐标为;
②当点Q在直线BC的下方时,
设CQ与BM交于点R,连接OR,
∵∠QCB=∠CBM,
∴RB=RC,
又点A(﹣1,0),C(0,﹣3),
∴OB=OC=3,
∴OR为BC的垂直平分线,且为∠BOC的平分线,
由(2)知:点N的横坐标为,
∴,
∴,
∴H为OB的中点,
∵NH∥OC,
∴点N为BC的中点,
∴OR经过点N,
∵OR为∠BOC的平分线,
∴直线OR的解析式为:y=﹣x,
解方程组,得:,
∴点R的坐标为,
设直线CR的解析式为:y=k4x+b4,
将C(0,﹣3),代入y=k4x+b4,
得:,解得:,
∴直线CR的解析式为:,
解方程组,得:,,
∴点Q的坐标为.
综上所述:点Q的坐标为或.
15.【解答】解:(1)直线y=﹣x+n与x轴交于点A(3,0),与y轴交于点B,将点A的坐标代入得:
﹣3+n=0,
解得:n=3,
故y=﹣x+3,
当x=0时,y=3,
∴B(0,3),
抛物线y=﹣x2+bx+c经过A、B两点,把点A,点B的坐标代入得:
,
解得,
∴抛物线的解析式的为:y=﹣x2+2x+3.
(2)①∵y=﹣x2+2x+3,
令y=0,则﹣x2+2x+3=0,
解得:x=﹣1或3,
∴C(﹣1,0),
又∵OA=OB=3,
∴∠OAB=45°,AC=4,,
又∵PE⊥x轴,
∴∠PEA=90°,
∴∠OAB=∠ADE=45°,
∴∠PDB=∠BAC=45°,
∵E(m,0),
∴P(m,﹣m2+2m+3),D(m,﹣m+3),
∴,
当△PDB∽△BAC,即时,,
解得:m=0(舍去)或,
故;
当△PDB∽△CAB,即时,,
解得:m=0(舍去)或,
故,
综上所述,或.
②∵点C(﹣1,0),B(0,3),
设直线CB的解析式为y=kx+3,
则0=﹣k+3,
解得:k=3,
∴直线CB的解析式为y=3x+3,
当点P在x轴上方时,如图1,连接BC,延长BP交x轴于N,
∵∠PBD+∠CBO=45°,∠BAO=∠PBD+∠BNO=45°,
∴∠CBO=∠BNO,
∵∠BOC=∠BON=90°,
∴△BCO∽△NBO,
∴,
∴ON=9,
∴N(9,0),
设直线BP的解析式为:y=ax+3,则0=9a+3,
解得:,
∴直线BP的解析式为:,
∴,
解得:(舍去);
当点P在x轴下方时,如图2:
∵∠OBA=45°,∠PBD+∠CBO=45°,
∴∠CBO=∠FBO,
∵OB=OB,∠COB=∠BOF,
∴△BOF≌△BOC(ASA),
∴OC=OF=1,
∴F(1,0),
设直线BP的解析式为:y=k′x+3,则0=k′+3,
解得:k′=﹣3,
∴直线BP的解析式为y=﹣3x+3,
∴﹣3m+3=﹣m2+2m+3,
解得:m=5,m=0(舍去);
综上所述,m的值为:或5.
21世纪教育网(www.21cnjy.com)
2025年九年级数学中考二轮专题复习二次函数中的角度问题
1.如图,二次函数y=﹣x2+bx+c的图象与x轴交于A,B两点,与y轴交于点C.点A的坐标为(﹣3,0),且OA=OC.
(1)求抛物线的解析式;
(2)若P为y轴上的一个动点,连接PB,则的最小值为 .
(3)连接BC,M是抛物线上的一点,且满足∠MAB=2∠OCB,求点M的坐标.
2.如图,二次函数y=ax2﹣6ax+c(a<0)的图象与x轴的负半轴和正半轴分别交于A,B两点,与y轴交于点C,顶点为P,对称轴交x轴于点D,点Q是抛物线对称轴上一动点,直线BQ交y轴于点E,且5EQ=3BQ.
(1)请直接写出A,B两点的坐标:A ,B ;
(2)当顶点P与点Q关于x轴对称时,S△QCE.
①求此时抛物线的函数表达式;
②在抛物线的对称轴上存在点F,使∠BEF=2∠OBE,请直接写出点F的坐标.
3.已知抛物线与x轴交于点A(1,0)和点B两点,与y轴交于点C(0,﹣3).
(1)求此抛物线的函数表达式;
(2)点P是抛物线上一动点(不与点A,B,C重合),作PD⊥x轴,垂足为D,连接PC.
①如图1,若点P在第三象限,且∠CPD=60°,求点P的横坐标;
②如图2,直线PD交直线BC于点E,当点E关于直线PC的对称点E′落在y轴上时,直接写出点P的坐标.
4.如图,在平面直角坐标系中,抛物线y=ax2+bx+c交x轴交于A(﹣1,0)、B(3,0)两点,交y轴于C(0,3),顶点为D.点M、N在此抛物线上,其横坐标分别为m,2m(m>0),连接CM,CN.
(1)求抛物线的解析式;
(2)当点M、N都在第一象限时,∠OCM+∠OCN=180°,求m的值;
(3)设此抛物线点M与点N之间的部分(包括点M、N)的最高点与最低点的纵坐标的差为S,
①求S关于m的函数解析式;
②当S随m增大而增大时,直接写出m的取值范围.
5.在平面直角坐标系中,抛物线y=x2﹣2x﹣3与x轴交于点A和点B,与y轴交于点C,顶点为D.
(1)请直接写出A、B、D三点坐标.
(2)如图1,点M是第四象限内抛物线上的一点,过点M作x轴的垂线,交直线BC于点N,求线段MN长度的最大值;
(3)如图2,若点P在抛物线上且满足∠PCB=∠CBD,求点P的坐标.
6.如图,在平面直角坐标系中,抛物线过A,B,C三点,点A(﹣1,0),点B(4,0),点C在y轴的正半轴上,连接AC,BC,AC⊥BC,点D在抛物线的对称轴上,其纵坐标为,连接BD,CD,并延长CD交抛物线于点E,连接BE.
(1)求抛物线的函数解析式;
(2)求△BCE的面积;
(3)若点K在抛物线上,且满足∠BDK=∠CBD,求点K的坐标.
7.如图,在平面直角坐标系中,直线yx﹣3与y轴交于点A,与x轴交于点B,抛物线ybx+c经过点A和点B.
(1)求抛物线的表达式;
(2)如图2,点P是抛物线上第一象限内的一个动点,连接AP、BP,当S△ABP时,求点P的坐标;
(3)在抛物线上是否存在点M,使∠OBM=∠BAO?若存在,请直接写出点M的坐标,若不存在,请说明理由.
8.如图,抛物线y=x2+bx+c与x轴交于点A(1,0),B(3,0),与y轴交于点C,连接AC,BC.
(1)求抛物线以及直线BC的函数解析式.
(2)若M是抛物线的顶点,求点M到直线BC的距离.
(3)已知P是抛物线上的一动点,是否存在点P,使得∠PAB=∠ACB?若存在,请求出点P的坐标;若不存在,请说明理由.
9.如图,抛物线y=﹣x2+bx+c与x轴交于A(﹣1,0),B(3,0),与y轴交于点C.
(1)求抛物线的解析式和顶点D的坐标;
(2)点Q是线段BC上一动点,过Q点作MQ⊥x轴交抛物线于点M,当MQ最大值时,求点M的坐标;
(3)抛物线上存在一点P,使得∠PCB=∠CBD,请直接写出P点的坐标.
10.如图,抛物线yx2+bx与x轴交于点A(5,0).
(1)求抛物线的函数表达式;
(2)点B(1,m)是抛物线上一点,点C是线段AB上一点,连接OC并延长交抛物线于点D,若,求点D的坐标;
(3)抛物线上是否存在点P,使得∠OPA=45°?若存在,求出点P的坐标;若不存在,说明理由.
11.如图,抛物线与x轴交于A、C两点(点A在点C的右侧),与y轴交于点B,且OA=OB.
(1)求抛物线的表达式;
(2)点P在抛物线上,当∠PBA+∠CBO=45°时,求点P的横坐标.
12.如图,在平面直角坐标系中,抛物线与y轴交于点A,与x轴的正半轴交于点B.
(1)求△AOB的面积;
(2)点P是直线AB下方抛物线上一点,过点P作y轴的平行线,交AB于点E,过点P作AB的垂线,垂足为点F,求EF的最大值及此时点P的坐标;
(3)在抛物线上是否存在点Q,使∠OBQ=∠BAO?若存在,请直接写出点Q的坐标,若不存在,请说明理由.
13.如图,抛物线y=﹣x2+bx+c经过点A(﹣4,0)、B(1,0),交y轴于点C(0,4),点P是抛物线上一动点.
(1)求该抛物线的函数表达式;
(2)当点P的坐标为(﹣2,6)时,求四边形AOCP的面积;
(3)若∠PBA=45°,求点P的坐标.
14.如图,已知抛物线y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣1,0)和点B(3,0),与y轴交于点C(0,﹣3).
(1)求二次函数的表达式;
(2)如图,点M是直线BC下方的二次函数图象上的一个动点,过点M作MH⊥x轴于点H,交BC于点N,求线段MN最大时点M的坐标;
(3)在(2)的条件下,该抛物线上是否存在点Q,使得∠QCB=∠CBM.若存在,请直接写出点Q的坐标;若不存在,请说明理由.
15.如图所示,直线y=﹣x+n与x轴交于点A(3,0),与y轴交于点B,抛物线y=﹣x2+bx+c经过A、B两点,与x轴的另一个交点为点C.
(1)求抛物线的解析式;
(2)点E(m,0)是x轴正半轴上一动点,过点E作ED⊥x轴于点E,交直线AB于点D,交抛物线于点P,连结PB,BC.
①当点E在线段OA上时,若△PBD与△ABC相似,求点E的坐标;
②若∠PBD+∠CBO=45°,求出m的值.
参考答案
1.【解答】解:(1)二次函数y=﹣x2+bx+c的图象与x轴交于A,B两点,与y轴交于点C.点A的坐标为(﹣3,0),且OA=OC,
∴OA=OC=3,
∴C(0,3),
将点A,点C的坐标分别代入y=﹣x2+bx+c得:
,
解得,
∴抛物线的解析式为y=﹣x2﹣2x+3;
(2)P为y轴上的一个动点,如图1,过P作PH⊥AC于H,过B作BH′⊥AC于H′,
∵OA=OC,∠AOC=90°,
∴∠OAC=∠OCA=45°,
∴,
∴,
当B、P、H共线且BH⊥AC时取等号,此时H与H′重合,最小值为BH′的长,
∵二次函数y=﹣x2﹣2x+3的图象与x轴交于A,B两点,
当y=0时,得:y=﹣x2﹣2x+3=0,
解得x1=﹣3,x2=1,
∴B(1,0),
∴OB=1,
在Rt△ABH′中,AB=OA+OB=4,∠OAC=45°,∠AH′B=90°,
∴,
即的最小值为,
故答案为:2;
(3)在OC上截取CD=BD,连接BD,如图2,
则∠OCB=∠CBD,
∴∠ODB=∠OCB+∠CBD=2∠OCB=∠MAB,
设CD=BD=t,则OD=OC﹣CD=3﹣t,
在Rt△BOD中,由勾股定理得:OD2+OB2=BD2,
∴(3﹣t)2+12=t2,
解得,
∴,
∴,
设M(m,﹣m2﹣2m+3),
当点M在x轴的上方时,如图2,过M作MN⊥x轴于点N,
则MN=﹣m2﹣2m+3,AN=m+3,
由得,
解得或m=﹣3(舍去),
∴,
∴;
当点M在x轴的下方时,如图3,过M作MN⊥x轴于点N,
则MN=m2+2m﹣3,AN=m+3,
由得,
解得或m=﹣3,
∴,
∴,
综上所述,满足条件的点M的坐标为或.
2.【解答】解:(1)y=ax2﹣6ax+c=a(x﹣3)2﹣9a+c,
∴抛物线对称轴是:直线x=3,
∴OD=3,
如图1所示,
∵DQ∥y轴,则OD:BD=EQ:BQ,
∵5EQ=3BQ,
∴EQ:BQ=3:5=OD:BD,
则BD=5,
∴B(8,0),
由对称性得:A(﹣2,0),
故答案为:(﹣2,0),(8,0);
(2)①如图1,
将点A(﹣2,0)代入二次函数y=ax2﹣6ax+c中得:4a+12a+c=0,
∴c=﹣16a,
∵y=ax2﹣6ax+c=a(x﹣3)2﹣9a+c,
∴P(3,﹣9a+c),
∵顶点P与点Q关于x轴对称,
∴Q(3,9a﹣c),即Q(3,25a),
∵S△QCE.
∴,
∴EC,
由点B、Q的坐标得,直线BQ的表达式为:y=﹣5ax+40a,
∴E(0,40a),
∵C(0,c),即(0,﹣16a),
∴﹣16a﹣40a,
解得:a=﹣0.1,
∴c=﹣16×(﹣0.1),
∴此时抛物线的函数表达式为:yx2x;
②如图2,当点F在BE的下方时,连接PB,
∵顶点P与点Q关于x轴对称,
∴∠PBD=∠QBD,
∵∠BEF=2∠OBE,
∴∠BEF=∠PBQ,
∴PB∥EF,
由①知:a=﹣0.1
∴P(3,2.5),
同理得:PB的解析式为:yx+4,
∴设EF的解析式为:yx+n,
∵E(0,﹣4),
∴n=﹣4,
则F(3,);
②如图:
当点F在BE的上方时,连接DE,
设F(3,m),
∵D(3,0),
∴BD=5,
∵D(3,0)E(0,﹣4),OD=3,OE=4,
由勾股定理得ED=5,
∴DE=BD,
∴∠DEB=∠OBE,
∵∠FEB=2∠OBE,
∴∠FEB=2∠DEB,
∴EQ:EF=DQ:FD,
∵BE4,
又∵5EQ=3BQ,
∴EQBQ,
∴EQ+BQ=BE,
∴EQ,
∵DQ=2.5,
FD=m,
则EQ:EF=DQ:FD,
∴EFm,
过F作FD⊥y轴,垂足为N,
在直角三角形中,EF,
∴m,
解得m或(舍去),
综上所述,F(3,)或F(3,).
3.【解答】解:(1)已知抛物线与x轴交于点A(1,0)和点B两点,与y轴交于点C(0,﹣3),将点A,点C的坐标代入得:
,
解得:,
∴抛物线的函数表达式为;
(2)①PD⊥x轴,垂足为D,如图1,设直线PC交x轴于E,
∴∠OCE=∠CPD=60°,
∵∠COE=90°,
∴∠CEO=90°﹣∠ECO=30°,
∴CE=2OC=6,
∴,
∴点,
∴直线PC的解析式为,
由得:,x2=0(舍去),
即点P的横坐标为;
②点P的坐标为或.理由如下:
如图2,
令,
解得x1=﹣4,x2=1,
∴B(﹣4,0),
设直线BC的解析式为y=mx+n,将点B(﹣4,0)、C(0,﹣3)代入得:
,
解得:,
∴直线BC的解析式为,
设点,
分以下两种情况:
点P在第三象限时,作EF⊥y轴于F,
∵点E与E′关于PC对称,
∴∠ECP=∠E′PC,CE=CE′,
∵PE∥y轴,
∴∠EPC=∠PCE′,
∴∠ECP=∠EPC,
∴PE=CE,
∴PE=CE′,
∴四边形PECE′为平行四边形,
∴ PECE′为菱形,
∴CE=PE,
∵EF∥OA,
∴,,
∴,
∴,
∵,
∴,
∴m1=0(舍去),,
∴;
当点P在第二象限时,
同理可得:,
解得:m3=0(舍去),,
∴;
综上所述,点P的坐标为或.
4.【解答】解:(1)∵抛物线y=ax2+bx+c交x轴交于A(﹣1,0)、B(3,0)两点,交y轴于C(0,3),
∴,
解得,
∴抛物线的解析式为y=﹣x2+2x+3;
(2)过M作ME⊥OC于E,过N作NF⊥OC于F,则∠MEC=∠NFC=90°,
∵点M、N都在第一象限,M、N在此抛物线上,其横坐标分别为m,2m,
∴ME=m,OE=﹣m2+2m+3,NF=2m,OF=﹣4m2+4m+3,
∴EF=3m2﹣2m,
∵∠OCM+∠OCN=180°,∠OCM+∠ECM=180°,
∴∠OCN=∠ECM,
又∵∠MEC=∠NFC=90°,
∴△MEC∽△NFC,
∴,
∴,
∵C(0,3),
∴OC=3,
∵OC=OF+CF,
∴,
解得,
∴m的值为;
(3)①∵y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴顶点为D(1,4),
∵点M、N在此抛物线上,其横坐标分别为m,2m(m>0),
∴M(m,﹣m2+2m+3),N(2m,﹣4m2+4m+3),
如图2,
当点M、N都在顶点D左侧时,,M为最低点,N为最高点,
则S=﹣4m2+4m+3﹣(﹣m2+2m+3)=﹣3m2+2m;
如图3,
当点M在点D左侧,N在顶点D右侧时,,M为最低点,D为最高点,
则S=4﹣(﹣m2+2m+3)=m2﹣2m+1;
如图4,
当点M在点D左侧,N在顶点D右侧时,,N为最低点,D为最高点,
则S=4﹣(﹣4m2+4m+3)=4m2﹣4m+1;
如图5,
当点M、N都在顶点D右侧时,m>1,N为最低点,M为最高点,
则S=﹣m2+2m+3﹣(﹣4m2+4m+3)=3m2﹣2m;
综上所述,;
②m的取值范围为或;理由如下:
当S=﹣3m2+2m时,抛物线的对称轴为直线,
∵﹣3<0,
∴当时,S随m增大而增大,
又∵,
∴;
当S=m2﹣2m+1时,抛物线的对称轴为直线m=1,
∵1>0,
∴当m>1时,S随m增大而增大,
∵,
∴此种情况不存在;
当S=4m2﹣4m+1时,抛物线的对称轴为直线,
∵4>0,
∴当时,S随m增大而增大,
∵,
∴;
当S=3m2﹣2m时,抛物线的对称轴为直线,
∵3>0,
∴当,S随m增大而增大,
∵m>1,
∴m>1;
综上,当S随m增大而增大时,m的取值范围为或.
5.【解答】解:(1)点A的坐标为(﹣1,0),点B的坐标为(3,0),点D的坐标为(1,﹣4);理由如下:
∵在平面直角坐标系中,抛物线y=x2﹣2x﹣3与x轴交于点A和点B,与y轴交于点C,
当y=0时,得x2﹣2x﹣3=0,
解得:x=﹣1或x=3,
当x=0时,得y=﹣3,
∴A(﹣1,0),B(3,0),C(0,﹣3),
∵抛物线y=x2﹣2x﹣3=(x﹣1)2﹣4,
∴D(1,﹣4),
∴点A的坐标为(﹣1,0),点B的坐标为(3,0),点D的坐标为(1,﹣4);
(2)设ME⊥x轴于点E,设M(m,m2﹣2m﹣3),如图1,
设直线BC的解析式为y=kBCx+bBC,将点B,点C的坐标代入得:
,
解得:,
∴直线BC的解析式为y=x﹣3,
∵过点M作x轴的垂线,交直线BC于点N,
∴N(m,m﹣3),
∴,
∵﹣1<0,
∴当时,线段MN的长度取得最大值,此时最大值为;
(3)设直线BD的解析式为y=kBDx+bBD,将点B,点D的坐标代入得:
,
解得:,
∴直线BD的解析式为y=2x﹣6,
①如图2,
∵∠PCB=∠CBD,
∴PC∥BD,
设直线PC的解析式为y=2x+bPC,将点C的坐标代入得:bPC=﹣3,
∴直线PC的解析式为y=2x﹣3,
联立,
解得:或,
此时点P的坐标为(4,5);
②如图3,设CP交BD于点G,作射线OG交BC于点F,
∵∠PCB=∠CBD,
∴GC=GB,
∵B(3,0),C(0,﹣3),
∴OC=OB=3,
∴OG垂直平分BC,
∴点F是BC的中点,
∴点F的坐标是,即,
设直线OG的解析式为y=kOGx,过点,
∴,
∴kOG=﹣1,
∴直线OG的解析式为y=﹣x,
∵直线OG:y=﹣x与直线BD:y=2x﹣6交于点G,
联立,
解得:,
∴G(2,﹣2),
设直线CG的解析式为y=kCGx+bCG,将点C,点G的坐标代入得:
,
解得:,
∴直线CG的解析式为,
联立,
解得:或,
此时点P的坐标为;
综上所述,点P的坐标为(4,5)或.
6.【解答】解:(1)∵AC⊥BC,
故∠ACO+∠OCB=90°,
∵∠OCB+∠CBO=90°,
∴∠ACO=∠OCB,
∴tan∠ACO=tan∠OCB,即OA:CO=OC:BO,
则OC2=AO OB=4,则CO=2,即c=2,
则抛物线的表达式为:y=a(x+1)(x﹣4)=a(x2﹣3x﹣4),
则﹣4a=2,则a,
故抛物线的表达式为:yx2x+2;
(2)由抛物线的表达式知,其对称轴为直线x,则点D(,),
由点C、D的坐标得,直线CD的表达式为:yx+2,
联立上式和抛物线的表达式得:x+2x2x+2,
解得:x=0(舍去)或,则点E(,),
由点B、C的坐标得,直线BC的表达式为:yx+2,
作EH∥y轴交CB于点H,则点H(,),则DH,
则△BCE的面积EH×OB;
(3)当点K在BC的左侧时,
设DK交BC于点H,
∵∠BDK=∠CBD,则HD=HB,
设点H(m,m+2),
则(m)2+(m+2)2=(m﹣4)2+(m+2)2,
解得:x,则点H(,),
由点D、H的坐标得,直线DH的表达式为:y=﹣2(x),
联立上式和抛物线的表达式得:﹣2(x)x2x+2,
解得:x(不合题意的值已舍去),
即点K(,);
当点K在BC的右侧时,
∵∠BDK=∠CBD,则DK∥BC,
则直线DK的表达式为:y(x),
联立上式和抛物线的表达式得:(x)x2x+2,
解得:x(不合题意的值已舍去),
则点K(,),
综上,点K的坐标为:(,)或(,).
7.【解答】解:(1)∵直线yx﹣3与y轴交于点A,与x轴交于点B,
当x=0时,y=﹣3,
当y=0时,x﹣3=0,解得:x=4,
∴A(0,﹣3),B(4,0),
把A(0,﹣3),B(4,0)代入ybx+c,
得,
解得:,
∴抛物线的表达式为yx﹣3;
(2)设P(t,t2t﹣3),过点P作PE∥y轴,交直线AB于点E,如图,
则E(t,t﹣3),
∴PEt2t﹣3﹣(t﹣3)t2﹣3t,
∵A(0,﹣3),B(4,0),
∴S△AOBOA×OB3×4=6,
S△ABP=S△APE﹣S△BPE(t2﹣3t)×[t﹣(t﹣4)]t2﹣6t,
∵S△ABP,
∴36S△ABP=13S△AOB,
即36(t2﹣6t)=13×6,
解得:t1(舍去),t2,
此时yP()23,
∴点P的坐标为(,);
(3)设直线BM交y轴于点N,
∵∠AOB=∠BON=90°,∠OBM=∠BAO,
∴△ABO∽△BNO,
∴,即,
∴ON,
∴N1(0,),N2(0,),
∴直线BM的解析式为yx或yx,
联立得或,
解得:,(舍去),,
∴点M的坐标为(,)或(,).
8.【解答】解:(1)将点A(1,0),B(3,0)代入y=x2+bx+c,
得
解得
∴抛物线的函数解析式为y=x2﹣4x+3,
令x=0,解得y=3,
∴点C(0,3).
设直线BC的函数解析式为y=kx+3,
将点B的坐标代入上式得:0=3k+3,则k=﹣1,
则BC的表达式为:y=﹣x+3;
(2)由抛物线的表达式知,点M(2,﹣1),
作MH∥y轴交CB于点H,作MT⊥BC于点T,
当x=2时,y=﹣x+3=1,
则点H(2,1),
则∠MHT=∠OCB=45°,
则MH=2,
则MT=MH cos45°;
(3)存在,理由:
作AN⊥CB于点N,
在△ABC中,OB=OC,则∠CBA=45°,
由点A、B、C的坐标得,BC=3,AB=2,
则NBABAN,则CN=BC﹣BN=2,
则tan∠ACB,
∵∠PAB=∠ACB,则tan∠PAB=tan∠ACB,
则PA的表达式为:y=±(x﹣1),
联立上式和抛物线的表达式得:(x﹣1)=x2﹣4x+3或(x﹣1)=x2﹣4x+3,
解得:x或,
则点P(,)或(,).
9.【解答】解:(1)由题意得:y=﹣(x+1)(x﹣3)=﹣x2+2x+3,
则点D(1,4);
(2)由抛物线的表达式知,点C(0,3),
由点B、C的坐标得,直线BC的表达式为:y=﹣x+3,
设点M(x,﹣x2+2x+3),则点Q(x,﹣x+3),
则MQ=﹣x2+2x+3﹣(﹣x+3)=﹣(x)2,
当MQ取得最大值时,x,则点M(,);
(3)当点P在BC左侧时,
∵∠PCB=∠CBD,则PC∥BD,
由B、D的坐标得,直线BD的表达式为:y=﹣2(x﹣3),
则直线PC的表达式为:y=﹣2x+3,
联立上式和抛物线的表达式得:﹣2x+3=﹣x2+2x+3,
解得:x=0(舍去)或4,即点P(4,﹣5),
当点P在BC的右侧时,
同理可得,直线PC的表达式为:yx+3,
联立上式和抛物线的表达式得:x+3=﹣x2+2x+3,
解得:x=0(舍去)或2.5,即点P(,),
综上,P(4,﹣5)或(,).
10.【解答】解:(1)由已知得25+b×5=0,b,
∴yx2x.
(2)作CE⊥OA于E,DF⊥OA于F.
当x=1时,
m121=2,
点B坐标为(1,2).
设AB解析式为:y=kx+b,
,
解得.
∴y.
∵,
∴.
∵CE⊥OA于E,DF⊥OA于F,
∴CE∥DF,
∴,
设E点坐标为(m,0),
∴点C坐标为(m,),
点F坐标为(m,0),
点D坐标为(m,).
∵点D在抛物线上,
∴(m)2m,
∴9m2﹣30m+25=0,
m1=m2.
∴点D坐标为(3,3).
(3)作过O、P、A三点的圆M,连接OM,AM,PM,作MN⊥OA于N,
∵∠OPA=45°,
∴∠AMO=90°,
∵OM=AM,OA=5,
又∵MN⊥OA,
∴ON=AN=MN=2.5,
∴点M坐标为(2.5,﹣2.5),
∴AM=OM,
∴PM,
设点P坐标为(x,y),
∴(x﹣2.5)2+(y+2,5)2=()2,
∴x2﹣5x+y2+5y=0,
∵yx2x.
∴y2+3y=0,
∴y1=0,(不合题意舍去),y2=﹣3.
∴y=﹣3,
∴﹣3x2x,
∴x1=﹣1,x2=6,
∴点P坐标为(﹣1,﹣3)或(6,﹣3).
11.【解答】解:(1)当x=0时,y=﹣4,
∴点B的坐标为(0,﹣4),OB=4,
∵OA=OB,
∴OA=4,
∴A(4,0),
将点A的坐标(4,0)代入抛物线中得:
4b﹣4=0,
∴b,
∴抛物线的表达式为:yx2x﹣4;
(2)当y=0时,x2x﹣4=0,
解得:x1=4,x2=﹣3,
∴C(﹣3,0),
分两种情况:
①如图1,在OA上取一点C',使OC=OC'=3,作射线BC'交抛物线于点P,
∴∠CBO=∠C'BO,
∵OA=OB,∠AOB=90°,
∴△AOB是等腰直角三角形,
∴∠ABO=45°,
∴∠PBA+∠C'BO=∠CBO+∠PBA=45°,点P满足条件,
∵点B的坐标为(0,﹣4),
∴设BP的解析式为:y=kx﹣4,
把点C'的坐标为(3,0)代入得:3k﹣4=0,
∴k,
∴BP的解析式为:yx﹣4,
∴x2x﹣4x﹣4,
解得:x1=0(舍),x2=5,
∴点P的横坐标为5;
②如图2,当BC⊥BP时,∠CBO+∠PBA=90°﹣45°=45°,点P满足条件,
过点P作PM⊥OB于M,
∴∠PBM+∠CBO=∠CBO+∠BCO=90°,
∴∠PBM=∠BCO,
∴tan∠PBM=tan∠BCO,
∴,
设点P的坐标为(t,t2t﹣4),
∴,
∴t1=0(舍),t2,
∴点P的横坐标为;
综上,点P的横坐标为5或.
12.【解答】解:(1)抛物线与y轴交于点A,与x轴的正半轴交于点B.
由知,
当x=0时,y=﹣3,
∴A(0,﹣3),
∴OA=3,
当y=0时,,
整理得:(x﹣4)(x+1)=0,
∴x1=4,x2=﹣1,
∴B(4,0),
∴OB=4,
∴.
(2)设AB解析式为y=kx+b,把A,B代入得:
,
解得:,
∴,
设,则,
∴,
又∵PE∥y轴,
∴∠PEF=∠OAB,
又∵PF⊥AB1
∴∠PFE=∠BOA=90°,
∴△PEF∽△BAO,
∴,
在Rt△AOB中,
,
∴,
∴,
∴当m=2时,EF有最大值为,
∴P的纵坐标:,
∴.
(3)设,过Q点作QP⊥x轴,垂足为P,
∵在Rt△AOB中,,
而∠OAB=∠OBQ,
∴,
在Rt△BPQ中,,
∴,
①当Q点在x轴下方时,,
解得:,a2=4(不合题意,舍去),
∴,
∴,
②当Q点在x轴上方时,,
解得:,a2=4(不合题意,舍去),
∴,
∴,
∴或.
13.【解答】解:(1)将点B(1,0)代入y=﹣x2+bx+4,
得﹣1+b+4=0,
解得b=﹣3,
∴抛物线解析式为y=﹣x2﹣3x+4;
(2)如图所示,过点P作PT⊥AB于T,
∵P(﹣2,6),A(﹣4,0),C(0,4),
∴OA=4,OT=2,OC=4 PT=6,
∴AT=2,
∴S四边形AOCP=S△APT+S梯形OCPT
=16;
(3)如图所示,取H1(﹣4,5),连接AH1,BH1,
∵A(﹣4,0)、B(1,0),H1(﹣4,5),
∴AH1=5,AB=5,AH1⊥AB,
∴∠ABH1=45°,
∴线段BH1与抛物线的交点P1即为所求;
设直线BH1的解析式为y=kx+b1,
∴,
∴,
∴直线BH1的解析式为y=﹣x+1,
联立,解得或(舍去),
∴P1(﹣3,4);
如图所示,取H2(﹣4,﹣5),连接AH2,BH2,
同理可得∠ABH2=45°,
∴直线BH2与抛物线的交点P2即为所求;
同理可知直线BH2的解析式为y=x﹣1,
联立,
解得或(舍去),
∴P2(﹣5,﹣6);
综上所述,符合题意的点P的坐标为(﹣3,4)或(﹣5,﹣6).
14.【解答】解:(1)将点A(﹣1,0),B(3,0),C(0,﹣3)代入y=ax2+bx+c,
得:,解得:,
∴二次函数的表达式为:y=x2﹣2x﹣3,
(2)设直线BC的解析式为:y=k1x+b1,
将B(3,0),C(0,﹣3)代入y=k1x+b1,
得:,解得:,
∴直线BC的解析式为:y=x﹣3,
设点M的横坐标为t,
∵点M在BC下方的二次函数图象上,
∴点M的纵坐标为:t2﹣2t﹣3,
∵MH⊥x轴交BC于点N,
∴点N的横坐标为t,
∴点N的纵坐标为:t﹣3,
∴,
∴当时,MN为最大,
当时,,
∴点M的坐标为.
(3)存在,点Q的坐标为或.
理由如下:
设直线BM的解析式为:y=k2x+b2,
将点B(3,0),M(3/2,﹣15/4)代入y=k2x+b2,
得:,解得:,
∴直线BM的解析式为:,
当∠QCB=∠CBM时,有以下两种情况:
①当点Q在直线BC上方时,
∵∠QCB=∠CBM,
∴CQ∥BM,
设直线CQ的解析式为:y=k3x+b3,
则,b3=﹣3,
∴直线CQ的解析式为:,
解方程组,得:,,
∴点Q的坐标为;
②当点Q在直线BC的下方时,
设CQ与BM交于点R,连接OR,
∵∠QCB=∠CBM,
∴RB=RC,
又点A(﹣1,0),C(0,﹣3),
∴OB=OC=3,
∴OR为BC的垂直平分线,且为∠BOC的平分线,
由(2)知:点N的横坐标为,
∴,
∴,
∴H为OB的中点,
∵NH∥OC,
∴点N为BC的中点,
∴OR经过点N,
∵OR为∠BOC的平分线,
∴直线OR的解析式为:y=﹣x,
解方程组,得:,
∴点R的坐标为,
设直线CR的解析式为:y=k4x+b4,
将C(0,﹣3),代入y=k4x+b4,
得:,解得:,
∴直线CR的解析式为:,
解方程组,得:,,
∴点Q的坐标为.
综上所述:点Q的坐标为或.
15.【解答】解:(1)直线y=﹣x+n与x轴交于点A(3,0),与y轴交于点B,将点A的坐标代入得:
﹣3+n=0,
解得:n=3,
故y=﹣x+3,
当x=0时,y=3,
∴B(0,3),
抛物线y=﹣x2+bx+c经过A、B两点,把点A,点B的坐标代入得:
,
解得,
∴抛物线的解析式的为:y=﹣x2+2x+3.
(2)①∵y=﹣x2+2x+3,
令y=0,则﹣x2+2x+3=0,
解得:x=﹣1或3,
∴C(﹣1,0),
又∵OA=OB=3,
∴∠OAB=45°,AC=4,,
又∵PE⊥x轴,
∴∠PEA=90°,
∴∠OAB=∠ADE=45°,
∴∠PDB=∠BAC=45°,
∵E(m,0),
∴P(m,﹣m2+2m+3),D(m,﹣m+3),
∴,
当△PDB∽△BAC,即时,,
解得:m=0(舍去)或,
故;
当△PDB∽△CAB,即时,,
解得:m=0(舍去)或,
故,
综上所述,或.
②∵点C(﹣1,0),B(0,3),
设直线CB的解析式为y=kx+3,
则0=﹣k+3,
解得:k=3,
∴直线CB的解析式为y=3x+3,
当点P在x轴上方时,如图1,连接BC,延长BP交x轴于N,
∵∠PBD+∠CBO=45°,∠BAO=∠PBD+∠BNO=45°,
∴∠CBO=∠BNO,
∵∠BOC=∠BON=90°,
∴△BCO∽△NBO,
∴,
∴ON=9,
∴N(9,0),
设直线BP的解析式为:y=ax+3,则0=9a+3,
解得:,
∴直线BP的解析式为:,
∴,
解得:(舍去);
当点P在x轴下方时,如图2:
∵∠OBA=45°,∠PBD+∠CBO=45°,
∴∠CBO=∠FBO,
∵OB=OB,∠COB=∠BOF,
∴△BOF≌△BOC(ASA),
∴OC=OF=1,
∴F(1,0),
设直线BP的解析式为:y=k′x+3,则0=k′+3,
解得:k′=﹣3,
∴直线BP的解析式为y=﹣3x+3,
∴﹣3m+3=﹣m2+2m+3,
解得:m=5,m=0(舍去);
综上所述,m的值为:或5.
21世纪教育网(www.21cnjy.com)
同课章节目录
