2024-2025年人教版六年级下册数学第三单元圆柱与圆锥图形计算题专题训练(含解析)
文档属性
| 名称 | 2024-2025年人教版六年级下册数学第三单元圆柱与圆锥图形计算题专题训练(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 605.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-11 06:02:25 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
2024-2025年人教版六年级下册数学第三单元圆柱与圆锥图形计算题专题训练
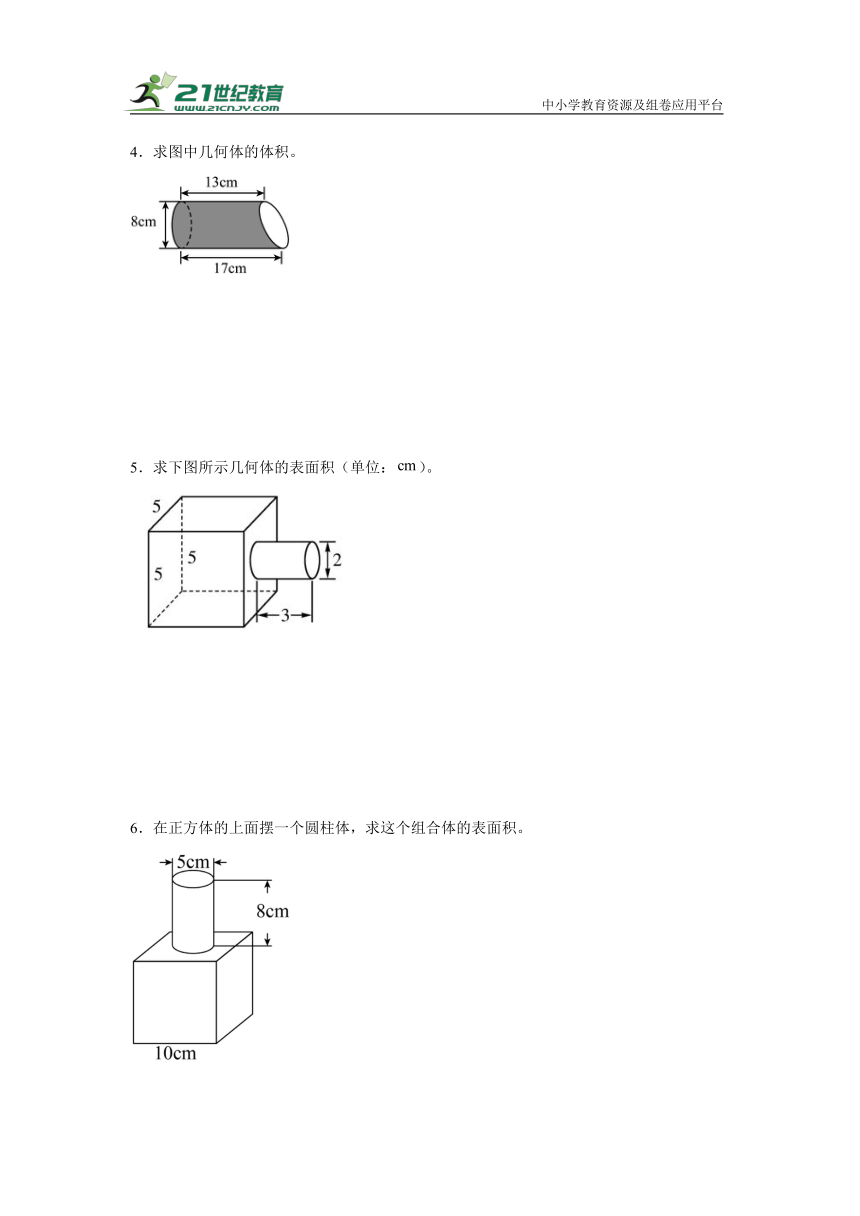
1.求圆锥的体积。
2.计算下图的表面积。
3.求旋转所成图形的体积。
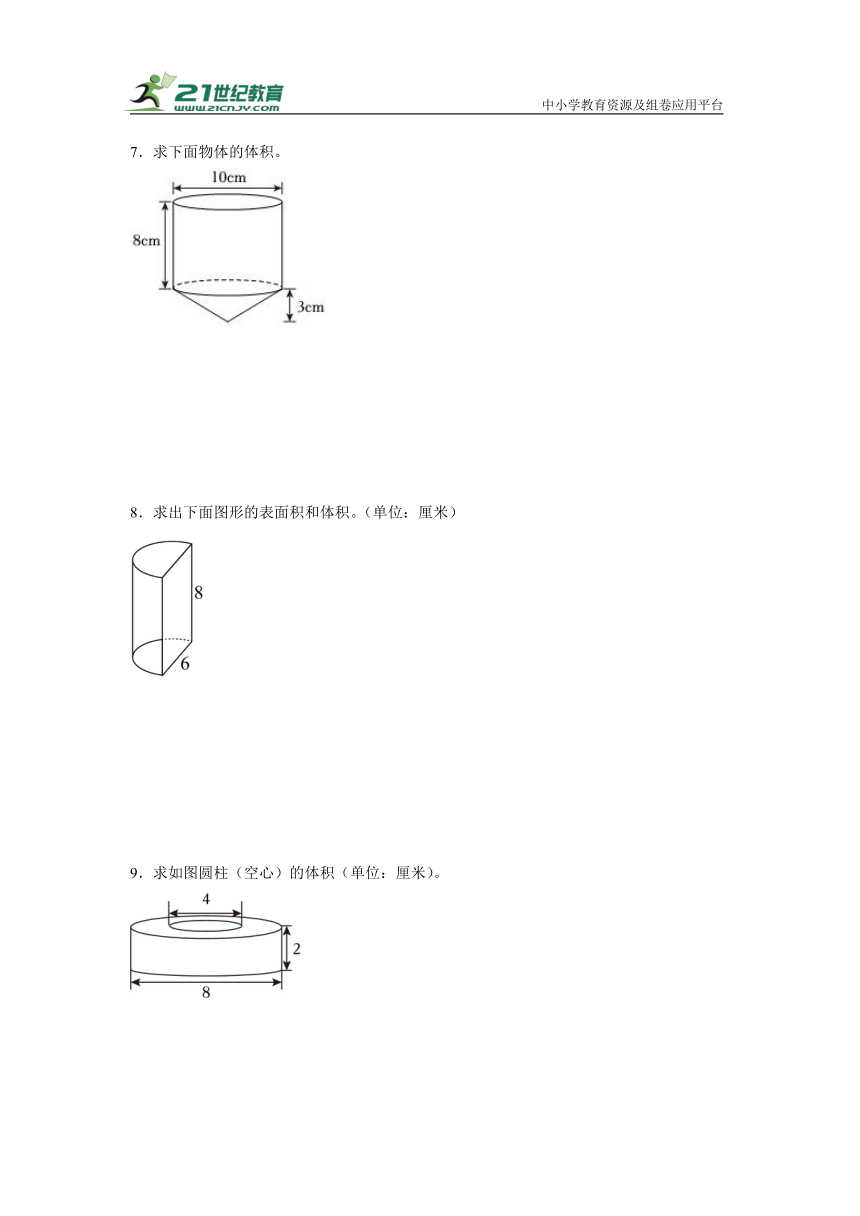
4.求图中几何体的体积。
5.求下图所示几何体的表面积(单位:)。
6.在正方体的上面摆一个圆柱体,求这个组合体的表面积。
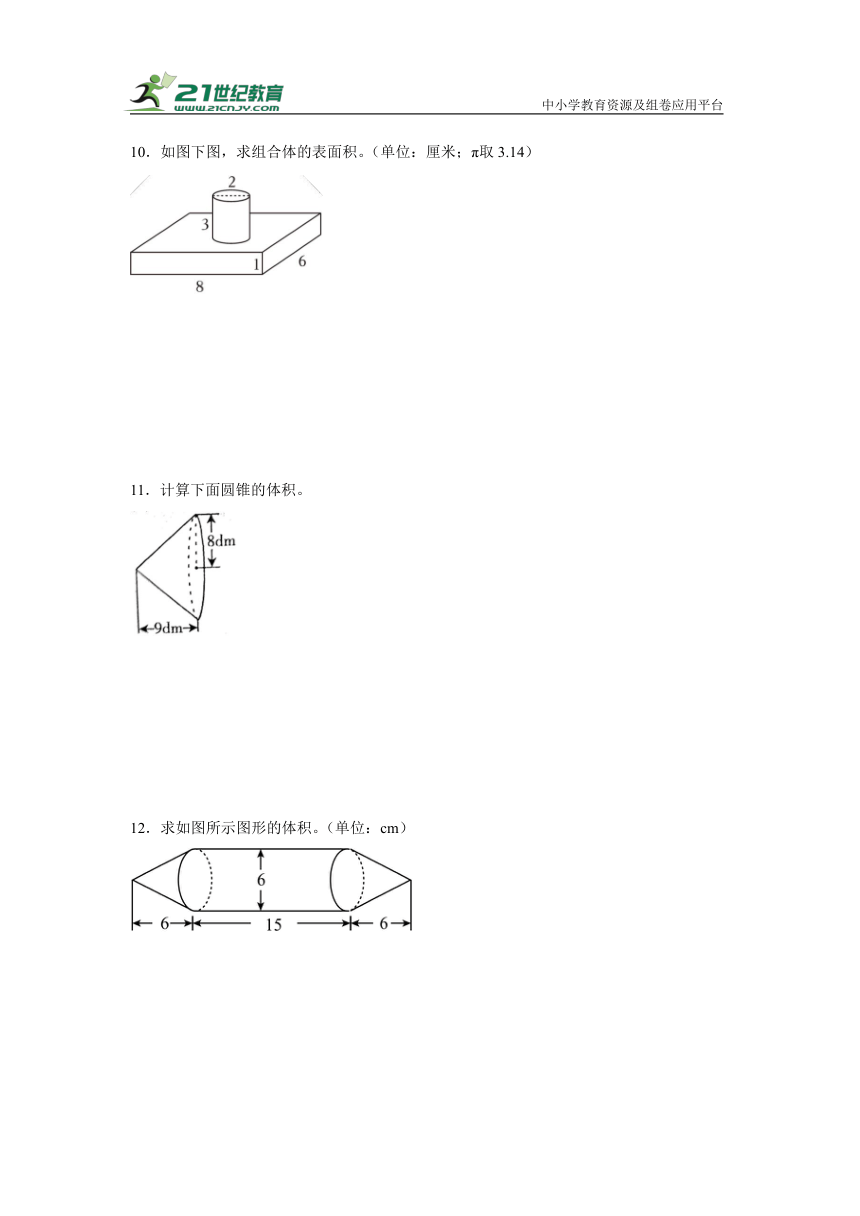
7.求下面物体的体积。
8.求出下面图形的表面积和体积。(单位:厘米)
9.求如图圆柱(空心)的体积(单位:厘米)。
10.如图下图,求组合体的表面积。(单位:厘米;π取3.14)
11.计算下面圆锥的体积。
12.求如图所示图形的体积。(单位:cm)
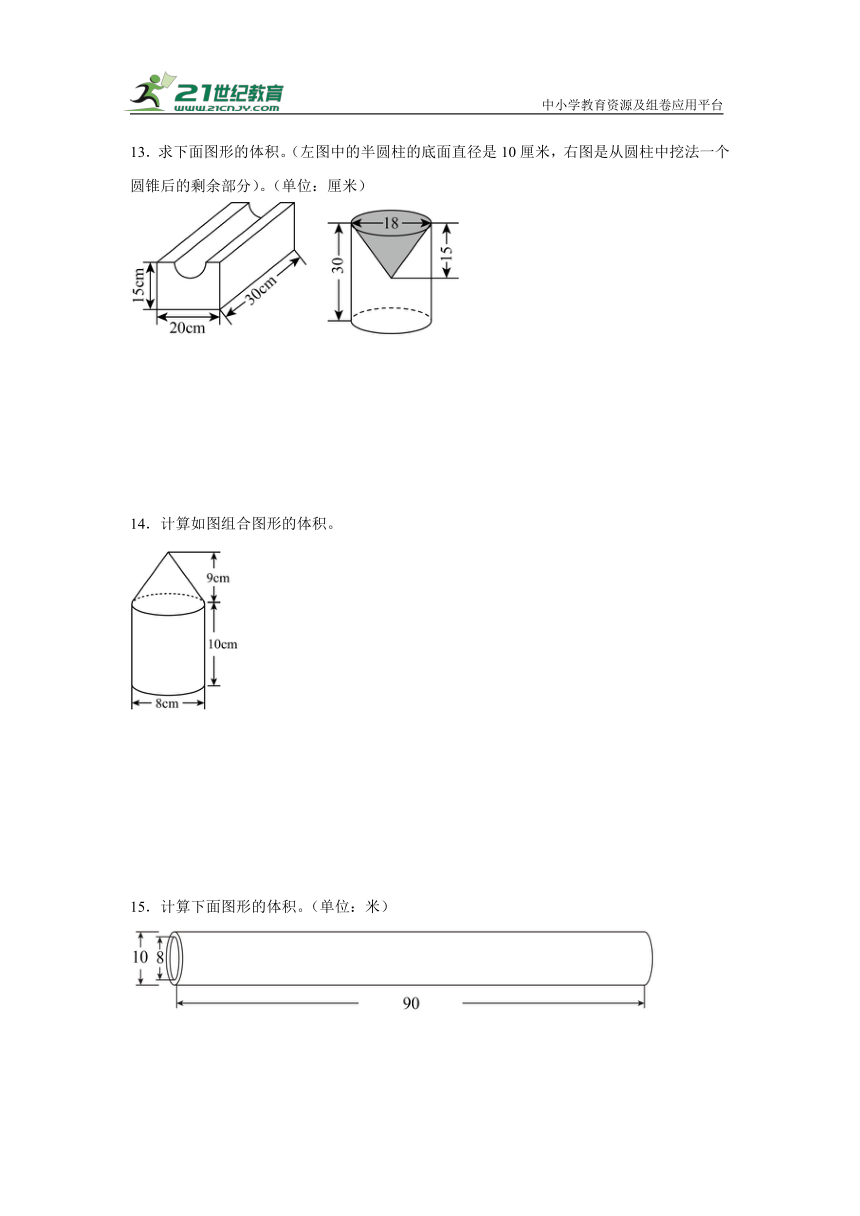
13.求下面图形的体积。(左图中的半圆柱的底面直径是10厘米,右图是从圆柱中挖法一个圆锥后的剩余部分)。(单位:厘米)
14.计算如图组合图形的体积。
15.计算下面图形的体积。(单位:米)
16.求下面图形的表面积。
17.从圆柱形木块上挖掉一个圆锥形木块,求剩下部分的体积。
18.计算下图的体积。(单位:厘米)
19.求下面立体图形的体积。
20.计算下面图形的表面积和体积。
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
《2024-2025年人教版六年级下册数学第三单元圆柱与圆锥图形计算题专题训练》参考答案
1.251.2cm3
【分析】已知圆锥的底面半径是4cm,圆锥的高是15cm,根据圆锥的体积=,代入相应数值计算,据此解答。
【详解】
(cm3)
2.653.12cm2
【分析】观察图形可知,小圆柱和大圆柱有重合的部分,把小圆柱的上底面向下平移,补给大圆柱的上底面;这样大圆柱的表面积是侧面积和2个底面积之和,而小圆柱只需计算侧面积即可;所以组合图形的表面积=大圆柱的侧面积+大圆柱的2个底面积+小圆柱的侧面积;根据公式S侧=πdh,S底=πr2,代入数据计算求解。
【详解】3.14×14×5+3.14×(14÷2)2×2+3.14×8×5
=3.14×14×5+3.14×72×2+3.14×8×5
=3.14×14×5+3.14×49×2+3.14×8×5
=219.8+307.72+125.6
=653.12(cm2)
组合图形的表面积是653.12cm2。
3.37.68cm3
【分析】以一个直角三角形的一条直角边所在的直线为轴旋转一周,那么这条直角边是圆锥的高,另一条直角边是圆锥的底面半径,根据圆锥的体积公式V=πr2h,代入数据计算即可求出旋转所成图形的体积。
【详解】×3.14×32×4
=×3.14×9×4
=37.68(cm3)
旋转所成图形的体积是37.68cm3。
4.753.6cm3
【分析】由图可知:可以把这个几何体看作直径为8cm,高为(13+17)cm圆柱的一半,利用圆柱的体积V=πr2h即可求得上图的体积。
【详解】3.14×(8÷2)2×(13+17)÷2
=3.14×42×30÷2
=3.14×16×30÷2
=50.24×30÷2
=1507.2÷2
=753.6(cm3)
几何体的体积是753.6cm3。
5.168.84
【分析】观察图形可知,图形的表面积等于正方体表面积与圆柱侧面积之和,再根据正方体的表面积=棱长×棱长×6,圆柱侧面积=底面周长×高,进行解答即可。
【详解】正方体表面积:
(cm2)
圆柱侧面积:
(cm2)
几何体表面积:
6.725.6cm2
【分析】由于圆柱和正方体摆在一起,会减少两个接触面的面积,所以组合体的表面积等于棱长是10cm的正方体的表面积加上直径是5cm,高是8cm的圆柱的侧面积;根据正方体表面积公式:表面积=棱长×棱长×6,圆柱的侧面积公式:侧面积=底面周长×高,代入数据,即可解答。
【详解】10×10×6+3.14×5×8
=100×6+15.7×8
=600+125.6
=725.6(cm2)
7.706.5cm3
【分析】根据题意可知,底面半径是(10÷2)cm,根据圆柱的体积公式:V=πr2h和圆锥的体积公式:V=πr2h,分别代入数据求出圆柱和圆锥的体积,再相加即可。
【详解】
(cm3)
这个立体图形的体积是706.5cm3。
8.151.62平方厘米;113.04立方厘米
【分析】观察图形可知,图形的表面积=圆柱表面积÷2+长方形的面积,图形的体积=圆柱的体积÷2,根据圆柱的表面积公式,长方形的面积公式,圆柱的体积公式,代入数据计算即可。
【详解】(厘米)
(平方厘米)
(立方厘米)
图形的表面积是151.62平方厘米,体积是113.04立方厘米。
9.75.36立方厘米
【分析】从图意可知,空心圆柱的体积=大圆柱体积-小圆柱体积。根据圆柱的体积=底面积×高,代入数据即可求解。
【详解】(8÷2)2×3.14×2-(4÷2)2×3.14×2
=42×3.14×2-22×3.14×2
=16×3.14×2-4×3.14×2
=100.48-25.12
=75.36(立方厘米)
圆柱(空心)的体积是75.36立方厘米。
10.142.84平方厘米
【分析】观察图形可知,组合体的表面积等于长方体的表面积加上圆柱体的侧面积,根据长方体的表面积公式:,圆柱体的侧面积公式:,代入数据计算即可。
【详解】
(平方厘米)
即组合体的表面积是142.84平方厘米。
11.602.88dm3
【分析】根据圆锥的体积V=πr2h,代入数据解答即可。
【详解】3.14×82×9×
=3.14×64×9×
=200.96×9×
=1808.64×
=602.88(dm3)
圆锥的体积是602.88dm3。
12.536.94 cm
【分析】根据图示,图形的体积等于两个圆锥的体积加圆柱的体积,圆锥的体积=×底面积×高,圆柱的体积=底面积×高,圆锥和圆柱的底面半径为(6÷2),圆锥的高为6,圆柱的高为15,代入数据计算即可。
【详解】×3.14×(6÷2)2×6×2+3.14×(6÷2)2×15
=3.14×36+3.14×135
=113.04+423.9
=536.94(cm )
13.7822.5立方厘米;6358.5立方厘米
【分析】观察第一个图形,是从一个长方体中截取了一个半圆柱,图形的体积=长方体的体积-半圆柱的体积,根据“V长方体=abh”“V圆柱=πr2h”,代入数据即可解答;
观察第二个图形可知:剩余部分的体积是圆柱与圆锥的体积之差,根据圆柱的体积:V=Sh,圆锥的体积公式:V=Sh,把数据分别代入公式解答即可。
【详解】第一个图形的体积:
30×20×15-3.14×(10÷2)2×30÷2
=30×20×15-3.14×25×30÷2
=600×15-78.5×30÷2
=9000-2355÷2
=9000-1177.5
=7822.5(立方厘米)
它的体积是7822.5立方厘米。
第二个图形的体积:
3.14×()2×30-×3.14×()2×15
=3.14×92×30-×3.14×92×15
=3.14×81×30-×3.14×81×15
=3.14×81×30-3.14×81×5
=254.34×30-254.34×5
=7630.2-1271.7
=6358.5(立方厘米)
它的体积是6358.5立方厘米。
14.653.12立方厘米
【分析】由图可知,组合图形可分为两部分:圆锥和圆柱,所以组合图形的体积是圆锥体积和圆柱体积之和。圆锥的底面直径是8厘米,则底面半径为4厘米,高是9厘米,代入圆锥体积公式即可求出圆锥体积。圆柱底面直径是8厘米,则底面半径为4厘米,高是10厘米,代入圆柱体积公式即可求出圆柱体积,最后将圆锥体积和圆柱体积相加即可。
【详解】圆锥体积:
×9×3.14×(8÷2)2
=3×3.14×16
=9.42×16
=150.72(立方厘米)
圆柱体积:
3.14×(8÷2)2×10
=3.14×16×10
=50.24×10
=502.4(立方厘米)
502.4+150.72=653.12(立方厘米)
即组合图形的体积是653.12立方厘米。
15.2543.4立方米
【分析】圆柱体积=底面积×高,据此先分别求出大圆柱和小圆柱的体积,再相减即可得出题中图形的体积。
【详解】3.14×(10÷2)2×90-3.14×(8÷2)2×90
=3.14×52×90-3.14×42×90
=7065-4521.6
=2543.4(立方米)
所以,这个图形的体积是2543.4立方米。
16.675.36
【详解】由于正方体里面挖出一个圆柱,正方体的上面减少了一个圆柱的底面的面积,多了一个圆柱,会增加一个圆柱的底面积以及一个圆柱的侧面积,所以组合体的表面积=正方体的表方面积+圆柱的侧面积。利用正方体表面积=棱长×棱长×6,圆柱的侧面积=计算后再相加。据此解答。
【点睛】
=
=
图形的表面积是675.36。
17.100.48立方分米
【分析】求剩下木料的体积,就是底面直径是4分米,高是10分米的圆柱的体积减去底面直径是4分米,高是6分米的圆锥的体积;根据圆柱的体积=底面积×高;圆锥的体积=底面积×高×,代入数据,即可解答。
【详解】3.14×(4÷2)2×10-3.14×(4÷2)2×6×
=3.14×4×10-3.14×4×6×
=12.56×10-12.56×6×
=125.6-75.36×
=125.6-25.12
=100.48(立方分米)
剩下部分的体积100.48立方分米。
18.2607.5立方厘米
【分析】观察题意可知,立体图形的体积相当于长方体的体积减去圆柱的体积,长方体的长30厘米、宽5厘米、高20厘米,根据长方体的体积=长×宽×高,用30×5×20即可求长方体的体积;圆柱的底面直径是10厘米,高是5厘米,根据圆柱的体积公式:V=πr2h,用3.14×(10÷2)2×5即可求出圆柱的体积,据此求出立体图形的体积。
【详解】30×5×20=3000(立方厘米)
3.14×(10÷2)2×5
=3.14×52×5
=3.14×25×5
=392.5(立方厘米)
3000-392.5=2607.5(立方厘米)
立体图形的体积是2607.5立方厘米。
19.7638.5立方厘米
【分析】图中立体图形的体积等于圆锥体体积加上长方体体积,根据圆锥体的体积,长方体的体积=长×宽×高,即可算出图中立体图形的体积。
【详解】圆锥体体积:
(立方厘米)
长方体体积:
(立方厘米)
图中立体图形的体积:6358.5+1280=7638.5(立方厘米)
20.表面积:188.4cm2;体积:178.98 cm3
【分析】观察图形可知,该立体图形的表面积等于下方圆柱的表面积加上上方圆柱的侧面积,根据圆柱的表面积公式:S=2πr2+πdh,圆柱的侧面积公式:S=πdh,据此代入数值进行计算即可;该立体图形的体积等于下方圆柱的体积加上上方圆柱的体积,再根据圆柱的体积公式:V=πr2h,据此进行计算即可。
【详解】表面积:
=
=
=188.4(cm2)
体积:
=
=
=178.98(cm3)
中小学教育资源及组卷应用平台
2024-2025年人教版六年级下册数学第三单元圆柱与圆锥图形计算题专题训练
1.求圆锥的体积。
2.计算下图的表面积。
3.求旋转所成图形的体积。
4.求图中几何体的体积。
5.求下图所示几何体的表面积(单位:)。
6.在正方体的上面摆一个圆柱体,求这个组合体的表面积。
7.求下面物体的体积。
8.求出下面图形的表面积和体积。(单位:厘米)
9.求如图圆柱(空心)的体积(单位:厘米)。
10.如图下图,求组合体的表面积。(单位:厘米;π取3.14)
11.计算下面圆锥的体积。
12.求如图所示图形的体积。(单位:cm)
13.求下面图形的体积。(左图中的半圆柱的底面直径是10厘米,右图是从圆柱中挖法一个圆锥后的剩余部分)。(单位:厘米)
14.计算如图组合图形的体积。
15.计算下面图形的体积。(单位:米)
16.求下面图形的表面积。
17.从圆柱形木块上挖掉一个圆锥形木块,求剩下部分的体积。
18.计算下图的体积。(单位:厘米)
19.求下面立体图形的体积。
20.计算下面图形的表面积和体积。
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
《2024-2025年人教版六年级下册数学第三单元圆柱与圆锥图形计算题专题训练》参考答案
1.251.2cm3
【分析】已知圆锥的底面半径是4cm,圆锥的高是15cm,根据圆锥的体积=,代入相应数值计算,据此解答。
【详解】
(cm3)
2.653.12cm2
【分析】观察图形可知,小圆柱和大圆柱有重合的部分,把小圆柱的上底面向下平移,补给大圆柱的上底面;这样大圆柱的表面积是侧面积和2个底面积之和,而小圆柱只需计算侧面积即可;所以组合图形的表面积=大圆柱的侧面积+大圆柱的2个底面积+小圆柱的侧面积;根据公式S侧=πdh,S底=πr2,代入数据计算求解。
【详解】3.14×14×5+3.14×(14÷2)2×2+3.14×8×5
=3.14×14×5+3.14×72×2+3.14×8×5
=3.14×14×5+3.14×49×2+3.14×8×5
=219.8+307.72+125.6
=653.12(cm2)
组合图形的表面积是653.12cm2。
3.37.68cm3
【分析】以一个直角三角形的一条直角边所在的直线为轴旋转一周,那么这条直角边是圆锥的高,另一条直角边是圆锥的底面半径,根据圆锥的体积公式V=πr2h,代入数据计算即可求出旋转所成图形的体积。
【详解】×3.14×32×4
=×3.14×9×4
=37.68(cm3)
旋转所成图形的体积是37.68cm3。
4.753.6cm3
【分析】由图可知:可以把这个几何体看作直径为8cm,高为(13+17)cm圆柱的一半,利用圆柱的体积V=πr2h即可求得上图的体积。
【详解】3.14×(8÷2)2×(13+17)÷2
=3.14×42×30÷2
=3.14×16×30÷2
=50.24×30÷2
=1507.2÷2
=753.6(cm3)
几何体的体积是753.6cm3。
5.168.84
【分析】观察图形可知,图形的表面积等于正方体表面积与圆柱侧面积之和,再根据正方体的表面积=棱长×棱长×6,圆柱侧面积=底面周长×高,进行解答即可。
【详解】正方体表面积:
(cm2)
圆柱侧面积:
(cm2)
几何体表面积:
6.725.6cm2
【分析】由于圆柱和正方体摆在一起,会减少两个接触面的面积,所以组合体的表面积等于棱长是10cm的正方体的表面积加上直径是5cm,高是8cm的圆柱的侧面积;根据正方体表面积公式:表面积=棱长×棱长×6,圆柱的侧面积公式:侧面积=底面周长×高,代入数据,即可解答。
【详解】10×10×6+3.14×5×8
=100×6+15.7×8
=600+125.6
=725.6(cm2)
7.706.5cm3
【分析】根据题意可知,底面半径是(10÷2)cm,根据圆柱的体积公式:V=πr2h和圆锥的体积公式:V=πr2h,分别代入数据求出圆柱和圆锥的体积,再相加即可。
【详解】
(cm3)
这个立体图形的体积是706.5cm3。
8.151.62平方厘米;113.04立方厘米
【分析】观察图形可知,图形的表面积=圆柱表面积÷2+长方形的面积,图形的体积=圆柱的体积÷2,根据圆柱的表面积公式,长方形的面积公式,圆柱的体积公式,代入数据计算即可。
【详解】(厘米)
(平方厘米)
(立方厘米)
图形的表面积是151.62平方厘米,体积是113.04立方厘米。
9.75.36立方厘米
【分析】从图意可知,空心圆柱的体积=大圆柱体积-小圆柱体积。根据圆柱的体积=底面积×高,代入数据即可求解。
【详解】(8÷2)2×3.14×2-(4÷2)2×3.14×2
=42×3.14×2-22×3.14×2
=16×3.14×2-4×3.14×2
=100.48-25.12
=75.36(立方厘米)
圆柱(空心)的体积是75.36立方厘米。
10.142.84平方厘米
【分析】观察图形可知,组合体的表面积等于长方体的表面积加上圆柱体的侧面积,根据长方体的表面积公式:,圆柱体的侧面积公式:,代入数据计算即可。
【详解】
(平方厘米)
即组合体的表面积是142.84平方厘米。
11.602.88dm3
【分析】根据圆锥的体积V=πr2h,代入数据解答即可。
【详解】3.14×82×9×
=3.14×64×9×
=200.96×9×
=1808.64×
=602.88(dm3)
圆锥的体积是602.88dm3。
12.536.94 cm
【分析】根据图示,图形的体积等于两个圆锥的体积加圆柱的体积,圆锥的体积=×底面积×高,圆柱的体积=底面积×高,圆锥和圆柱的底面半径为(6÷2),圆锥的高为6,圆柱的高为15,代入数据计算即可。
【详解】×3.14×(6÷2)2×6×2+3.14×(6÷2)2×15
=3.14×36+3.14×135
=113.04+423.9
=536.94(cm )
13.7822.5立方厘米;6358.5立方厘米
【分析】观察第一个图形,是从一个长方体中截取了一个半圆柱,图形的体积=长方体的体积-半圆柱的体积,根据“V长方体=abh”“V圆柱=πr2h”,代入数据即可解答;
观察第二个图形可知:剩余部分的体积是圆柱与圆锥的体积之差,根据圆柱的体积:V=Sh,圆锥的体积公式:V=Sh,把数据分别代入公式解答即可。
【详解】第一个图形的体积:
30×20×15-3.14×(10÷2)2×30÷2
=30×20×15-3.14×25×30÷2
=600×15-78.5×30÷2
=9000-2355÷2
=9000-1177.5
=7822.5(立方厘米)
它的体积是7822.5立方厘米。
第二个图形的体积:
3.14×()2×30-×3.14×()2×15
=3.14×92×30-×3.14×92×15
=3.14×81×30-×3.14×81×15
=3.14×81×30-3.14×81×5
=254.34×30-254.34×5
=7630.2-1271.7
=6358.5(立方厘米)
它的体积是6358.5立方厘米。
14.653.12立方厘米
【分析】由图可知,组合图形可分为两部分:圆锥和圆柱,所以组合图形的体积是圆锥体积和圆柱体积之和。圆锥的底面直径是8厘米,则底面半径为4厘米,高是9厘米,代入圆锥体积公式即可求出圆锥体积。圆柱底面直径是8厘米,则底面半径为4厘米,高是10厘米,代入圆柱体积公式即可求出圆柱体积,最后将圆锥体积和圆柱体积相加即可。
【详解】圆锥体积:
×9×3.14×(8÷2)2
=3×3.14×16
=9.42×16
=150.72(立方厘米)
圆柱体积:
3.14×(8÷2)2×10
=3.14×16×10
=50.24×10
=502.4(立方厘米)
502.4+150.72=653.12(立方厘米)
即组合图形的体积是653.12立方厘米。
15.2543.4立方米
【分析】圆柱体积=底面积×高,据此先分别求出大圆柱和小圆柱的体积,再相减即可得出题中图形的体积。
【详解】3.14×(10÷2)2×90-3.14×(8÷2)2×90
=3.14×52×90-3.14×42×90
=7065-4521.6
=2543.4(立方米)
所以,这个图形的体积是2543.4立方米。
16.675.36
【详解】由于正方体里面挖出一个圆柱,正方体的上面减少了一个圆柱的底面的面积,多了一个圆柱,会增加一个圆柱的底面积以及一个圆柱的侧面积,所以组合体的表面积=正方体的表方面积+圆柱的侧面积。利用正方体表面积=棱长×棱长×6,圆柱的侧面积=计算后再相加。据此解答。
【点睛】
=
=
图形的表面积是675.36。
17.100.48立方分米
【分析】求剩下木料的体积,就是底面直径是4分米,高是10分米的圆柱的体积减去底面直径是4分米,高是6分米的圆锥的体积;根据圆柱的体积=底面积×高;圆锥的体积=底面积×高×,代入数据,即可解答。
【详解】3.14×(4÷2)2×10-3.14×(4÷2)2×6×
=3.14×4×10-3.14×4×6×
=12.56×10-12.56×6×
=125.6-75.36×
=125.6-25.12
=100.48(立方分米)
剩下部分的体积100.48立方分米。
18.2607.5立方厘米
【分析】观察题意可知,立体图形的体积相当于长方体的体积减去圆柱的体积,长方体的长30厘米、宽5厘米、高20厘米,根据长方体的体积=长×宽×高,用30×5×20即可求长方体的体积;圆柱的底面直径是10厘米,高是5厘米,根据圆柱的体积公式:V=πr2h,用3.14×(10÷2)2×5即可求出圆柱的体积,据此求出立体图形的体积。
【详解】30×5×20=3000(立方厘米)
3.14×(10÷2)2×5
=3.14×52×5
=3.14×25×5
=392.5(立方厘米)
3000-392.5=2607.5(立方厘米)
立体图形的体积是2607.5立方厘米。
19.7638.5立方厘米
【分析】图中立体图形的体积等于圆锥体体积加上长方体体积,根据圆锥体的体积,长方体的体积=长×宽×高,即可算出图中立体图形的体积。
【详解】圆锥体体积:
(立方厘米)
长方体体积:
(立方厘米)
图中立体图形的体积:6358.5+1280=7638.5(立方厘米)
20.表面积:188.4cm2;体积:178.98 cm3
【分析】观察图形可知,该立体图形的表面积等于下方圆柱的表面积加上上方圆柱的侧面积,根据圆柱的表面积公式:S=2πr2+πdh,圆柱的侧面积公式:S=πdh,据此代入数值进行计算即可;该立体图形的体积等于下方圆柱的体积加上上方圆柱的体积,再根据圆柱的体积公式:V=πr2h,据此进行计算即可。
【详解】表面积:
=
=
=188.4(cm2)
体积:
=
=
=178.98(cm3)
