23.3实践与探索-根与系数的关系
文档属性
| 名称 | 23.3实践与探索-根与系数的关系 |  | |
| 格式 | rar | ||
| 文件大小 | 701.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-12-25 21:21:00 | ||
图片预览





文档简介
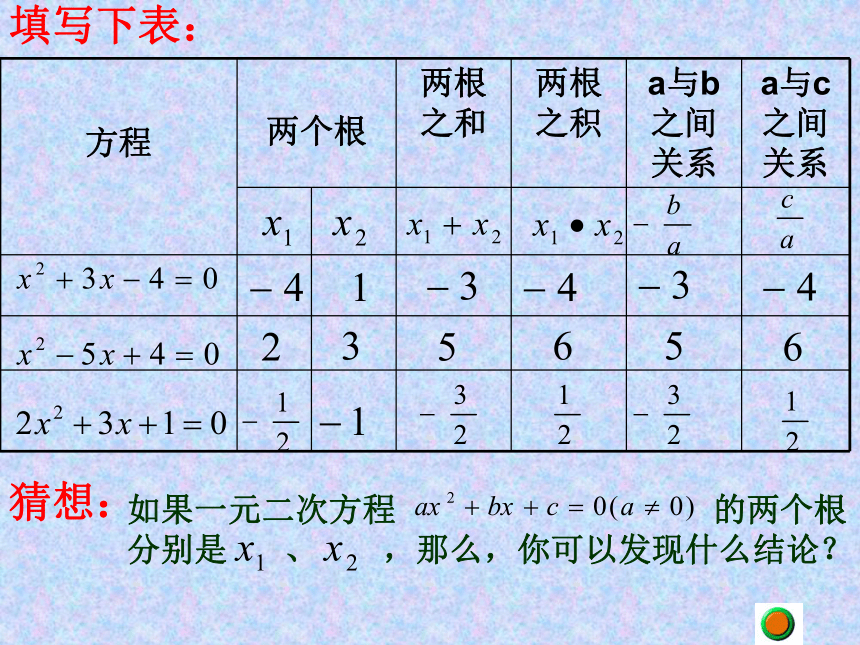
课件13张PPT。华师版九年级《数学》上第23章 《一元二次方程》根与系数的关系泌阳县付庄乡中心校1.一元二次方程的一般形式是什么?3.一元二次方程的的解的情况怎样确定?2.一元二次方程的求根公式是什么?填写下表:猜想:如果一元二次方程 的两个根
分别是 、 ,那么,你可以发现什么结论? 如果一元二次方程
的两个根分别是 、 ,那么:这就是一元二次方程根与系数的关系,也叫韦达定理。已知:如果一元二次方程
的两个根分别是 、 。求证: 韦达(1540——1603)是法国数学家,最早发现代数
方程的根与系数之间有这种关系,因此,人们把这个关系
称为韦达定理。韦达最重要的贡献是对代数学的推进,他
最早系统地引入代数符号,推进了方程论的发展。韦达用
“分析”这个词来概括当时代数的内容和方法。他创设了大
量的代数符号,用字母代替未知数,系统阐述并改良了三、
四次方程的解法,著有《分析方法入门》、《论方程的识
别与订正》等多部著作。1.3.2.4.5.例1.
不解方程,求方程 的
两根的平方和、倒数和。例2.
已知方程 的
两根为 、 , 且 ,求
k的值。运用根与系数的关系解题 2.方程 的两根互为倒数,求k的值。想看答案吗? 1. 已知方程5x2+kx-6=0的一个根是2,求它的另一个根及k的值. 想看答案吗? 1. 已知方程 的一个根是2,求它的另一个根及k的值. 解:设方程 的两个根
分别是 、 ,其中 。
所以:
即:
由于
得:k=—7
答:方程的另一个根是 ,k=—7
解:设方程的两根分别为 和 ,
则:
而方程的两根互为倒数
即:
所以:
得: 2.方程 的两根互
为倒数,求k的值。 2.应用一元二次方程的根与系数关系时,
首先要把已知方程化成一般形式. 3.应用一元二次方程的根与系数关系时,
要特别注意,方程有实根的条件,即在初
中代数里,当且仅当 时,才
能应用根与系数的关系. 1.一元二次方程根与系数的关系是什么?总结归纳 请同学们在课后通过以下几道题检测
自己对本节知识的掌握情况:
P36 第6题
P38 第11、12题
886
分别是 、 ,那么,你可以发现什么结论? 如果一元二次方程
的两个根分别是 、 ,那么:这就是一元二次方程根与系数的关系,也叫韦达定理。已知:如果一元二次方程
的两个根分别是 、 。求证: 韦达(1540——1603)是法国数学家,最早发现代数
方程的根与系数之间有这种关系,因此,人们把这个关系
称为韦达定理。韦达最重要的贡献是对代数学的推进,他
最早系统地引入代数符号,推进了方程论的发展。韦达用
“分析”这个词来概括当时代数的内容和方法。他创设了大
量的代数符号,用字母代替未知数,系统阐述并改良了三、
四次方程的解法,著有《分析方法入门》、《论方程的识
别与订正》等多部著作。1.3.2.4.5.例1.
不解方程,求方程 的
两根的平方和、倒数和。例2.
已知方程 的
两根为 、 , 且 ,求
k的值。运用根与系数的关系解题 2.方程 的两根互为倒数,求k的值。想看答案吗? 1. 已知方程5x2+kx-6=0的一个根是2,求它的另一个根及k的值. 想看答案吗? 1. 已知方程 的一个根是2,求它的另一个根及k的值. 解:设方程 的两个根
分别是 、 ,其中 。
所以:
即:
由于
得:k=—7
答:方程的另一个根是 ,k=—7
解:设方程的两根分别为 和 ,
则:
而方程的两根互为倒数
即:
所以:
得: 2.方程 的两根互
为倒数,求k的值。 2.应用一元二次方程的根与系数关系时,
首先要把已知方程化成一般形式. 3.应用一元二次方程的根与系数关系时,
要特别注意,方程有实根的条件,即在初
中代数里,当且仅当 时,才
能应用根与系数的关系. 1.一元二次方程根与系数的关系是什么?总结归纳 请同学们在课后通过以下几道题检测
自己对本节知识的掌握情况:
P36 第6题
P38 第11、12题
886
