人教版九年级数学上册 24.3 正多边形和圆 课时练习(含答案)
文档属性
| 名称 | 人教版九年级数学上册 24.3 正多边形和圆 课时练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-11 15:19:46 | ||
图片预览

文档简介
九年级数学上册第二十四章第3节《正多边形和圆》课时练习
一、单选题
1.如图,正五边形内接于,为弧上的一点(点不与点重合),则的度数为( )
A. B. C. D.
2.如图,在正五边形中,经过,两点的分别与,相切于点,,连接,,则( )
A. B. C. D.
3.如图,螺母的外围可以看作是正六边形,已知这个正六边形的半径是2,则它的面积是( )
A. B.12 C. D.24
4.刘徽在《九章算术注》中首创“割圆术”,利用圆的内接正多边形来确定圆周率,开创了中国数学发展史上圆周率研究的新纪元.某同学在学习“割圆术”的过程中,作了一个如图所示的圆内接正八边形.若的半径为2,则这个圆内接正八边形的面积为( )
A. B. C. D.
5.刘徽在《九章算术注》中首创“割圆术”,利用圆的内接正多边形来确定圆周率.如图,内部多边形为的内接正十二边形,若的半径为2,则这个圆内接正十二边形的面积为( )
A.1 B. C.12 D.
6.我国魏晋时期数学家刘徽在《九章算术注》中提到了著名的“割圆术”,“割圆术”孕育了微积分思想,他用这种思想得到了圆周率的近似值为3.1416.如图,⊙的半径为1,运用“割圆术”,以圆内接正六边形面积近似估计⊙的面积,可得的估计值为( )
A. B. C. D.
7.如图,正六边形内接于为的中点,连接,,四边形的面积为,正六边形剩余部分的面积为,则( )
A.6 B.4 C.3 D.2
8.正六边形蜂巢的建筑结构密合度最高、用材最少、空间最大、也最为坚固.如图,某蜂巢的房孔是边长为6的正六边形,若的内接正六边形为正六边形,则的长为( )
A. B. C. D.6
二、填空题
9.李师傅要在木板上开一个小孔,使其恰好能穿过一个正六边形的螺母,如图所示,若圆孔的周长等于,则正六边形螺母的边长为 .
10.如图,正八边形内接于,连接,则 .
11.如图,正六边形的边长为,以为圆心,得,连接,则图中阴影部分的面积为 .
12.如图,为正六边形的一条对角线,于点,连接,若正六边形的边长为2,则的长为 .
13.生活中常见的螺母横截面外轮廓大多数都是正六边形,将如图①所示的螺母横截面抽象成几何图形如图②所示,正六边形的中心与中间圆的圆心重合于点O处,连接交于点H,若中间圆的半径为9,正六边形的半径为15,则的长为 .
三、解答题
14.如图,正方形内接于是的中点,连接.
(1)求证:;
(2)求证:;
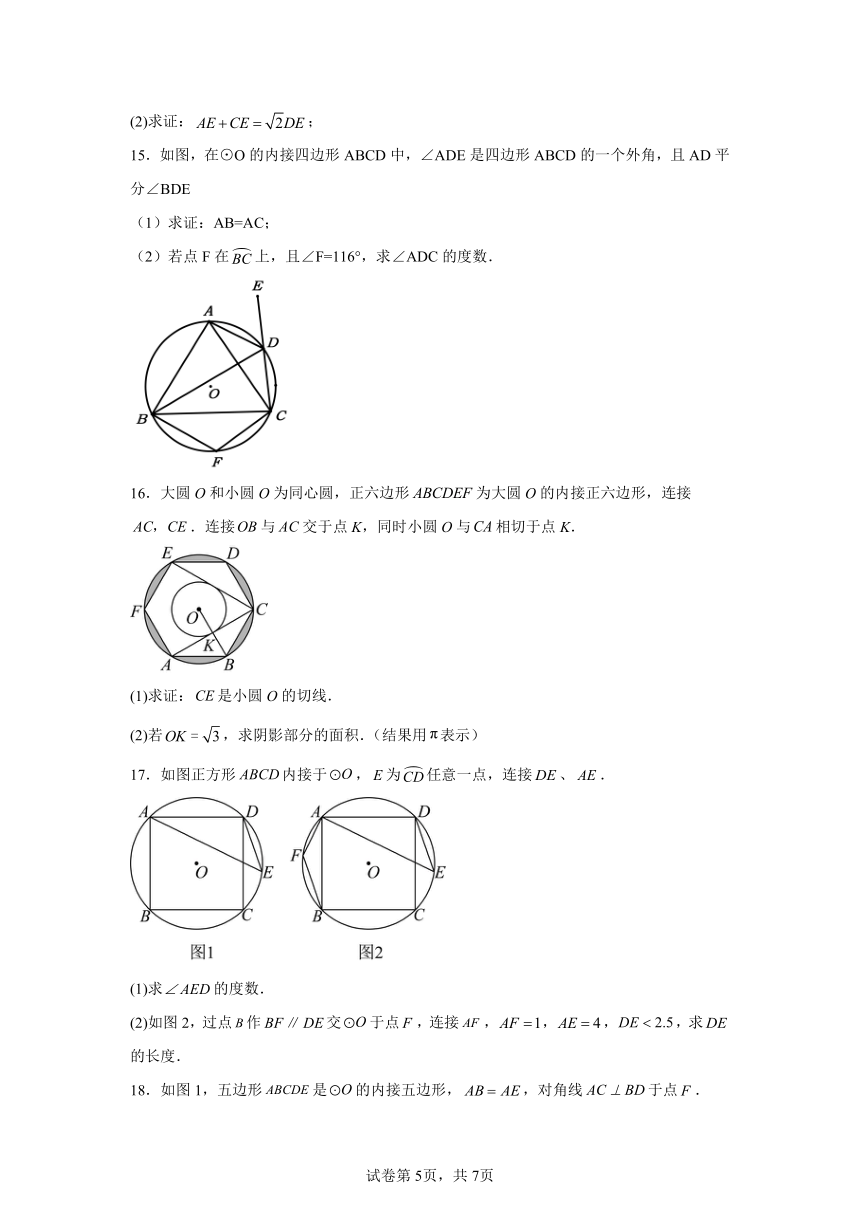
15.如图,在⊙O的内接四边形ABCD中,∠ADE是四边形ABCD的一个外角,且AD平分∠BDE
(1)求证:AB=AC;
(2)若点F在上,且∠F=116°,求∠ADC的度数.
16.大圆O和小圆O为同心圆,正六边形为大圆O的内接正六边形,连接.连接与交于点K,同时小圆O与相切于点K.
(1)求证:是小圆O的切线.
(2)若,求阴影部分的面积.(结果用表示)
17.如图正方形内接于,为任意一点,连接、.
(1)求的度数.
(2)如图2,过点作交于点,连接,,,,求的长度.
18.如图1,五边形是的内接五边形,,对角线于点.
(1)①若,则_______;
②猜想和的数量关系,并证明;
(2)如图2,当经过圆心时,若,,求;
(3)作于点,求的值.
19.【给出问题】如图1,正方形内接于,是的中点,连接,.求证:;
【深入思考】如图2,正方形内接于,点为上任意一点,连接、、,请探究、、三者之间有何数量关系,并给予证明.
【拓展应用】如图3,若四边形是矩形,点为边上一点,,,,试求矩形的面积.
20.【给出问题】:已知:是正方形的外接圆,点P在上(除A、B外),试求的度数.
【分析问题】:善于思考的小明在分析上述题目后,有了以圆为工具来解决问题的思路.用圆来画出准确的示意图就能顺利解题了,在此基础上进一步探索就有了新发现.请善于思考的你帮助解答以下问题:
(1)①尺规作图,在中作出内接正方形(保留痕迹,不写作法).
②原题中 .
【深入思考】:
(2)【问题】如图1,若四边形是的内接正方形,点P为弧上一动点,连接,请探究三者之间或者三者之间有何数量关系,并给予证明.
(3)【拓展】如图2,若六边形是的内接正六边形,点P为弧上一动点,请探究三者之间有何数量关系: (不写证明过程).
(4)【应用】如图3,若四边形是矩形,点P为边上一点,,,,试求矩形的面积.
试卷第1页,共3页
试卷第1页,共3页
《九年级数学上册第二十四章第3节《正多边形和圆》课时练习》参考答案
题号 1 2 3 4 5 6 7 8
答案 A B A B C B C C
9.3
10.90
11.
12.
13.6
14.(1)证明:∵四边形是正方形,
∴,
∴.
∵是的中点,
∴,
∴,
∴.
(2)解:连接,过点作交的延长线于.
∵四边形是正方形,
∴.
∵,
∴,
∴.
∵,
∴.
在△ADE和△CDF中,
,
∴,
∴,
∴,
即.
15.解:(1)∵AD平分∠BDE,
∴∠ADB=∠ADE,
∵四边形ABCD内接于圆O,
∴∠ADE=∠ABC,
∴∠ADB=∠ABC,
∴AB=AC;
(2)∵∠F=116°,
∴∠BAC=180°-116°=64°,
∵AB=AC,
∴∠ABC=∠ACB=(180°-64°)÷2=58°,
∴∠ADC=180°-58°=122°.
16.(1)证明:如图所示,连接,设交于H,
∵正六边形为大圆O的内接正六边形,
∴,
∴,
又∵,
∴垂直平分,
∴,
∵小圆O与相切于点K,
∴,
又∵,
∴,
∴,
∴点H在小圆O上,
又∵,
∴是小圆O的切线;
(2)解:∵正六边形为大圆O的内接正六边形,
∴,
∴是等边三角形,
∵小圆O与相切于点K,
∴,
∴,
∴,
∴,
∴,
∴.
17.(1)解:如图1中,连接、.
四边形是正方形,
,
;
(2)解:如图2中,连接,,,,作于.
∵,,
,,
,
,,
,
,
,
,
,
,
,
,
,
设,
在中,,
,
解得或(舍弃),
.
18.(1)①解:如图,连接,
,
,
,
,
,
;
故答案为:;
②,
证明:如图,连接,
,
,
,
,
,
,
,
,
即;
(2)解:如图,连接、,连接交于点,
在中,,
设,则,
在中,,
,
解得:,
,,,
,,
垂直平分,
,,
设,则,
在中,,
在中,,
解得:,
,
,
为的直径,
,
在中,;
(3)解:如图,连接、、、,过点作于点,
,
,
,
,,
,
,
,
,
,
,即,
在和中,
,
,
,
,,
,
,
.
19.[给出问题]证明:四边形是正方形,
,
是的中点,
;
[深入思考] ,理由如下,
过点作交于点,取圆心,连接,,
,
,
,
,
,
,,
在和中,
,
,
,即
[拓展应用] 解:以为边,作正方形,连接,,,,作正方形的外接圆,则圆心在上,
,,
点在上,
,,
,,
,
,
设,则,,
在中,,
在中,,
在中,,
解得:(负值舍去)
,
矩形的面积.
20.解:(1)①如图所示,作直径的垂直平分线交于点A,C,则四边形是正方形;
②如图所示,
,
故答案为:.
(2),证明如下:
如图,过点C作交于E,
∵,
∴,
∵,
∴,
又∵,
∴(ASA),
∴,
∴是等腰直角三角形,
∴,
即,
如图所示,过点C作交于F,
同理可得是等腰直角三角形,,
∴,;
(3),
如图,过点B,作,在上截取,连接,
∵,,
在和中,
,
∴(),
∴,
∴,
又∵,
∴,
∴,
∴.
(4)如图,以为边,作正方形,连接,,
根据(1)可得P在上,则,
∴,
设,则,,
在中,,
在中,,
在 中,,
∴,
解得 (负值舍去),
∴,
∴矩形的面积为.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.如图,正五边形内接于,为弧上的一点(点不与点重合),则的度数为( )
A. B. C. D.
2.如图,在正五边形中,经过,两点的分别与,相切于点,,连接,,则( )
A. B. C. D.
3.如图,螺母的外围可以看作是正六边形,已知这个正六边形的半径是2,则它的面积是( )
A. B.12 C. D.24
4.刘徽在《九章算术注》中首创“割圆术”,利用圆的内接正多边形来确定圆周率,开创了中国数学发展史上圆周率研究的新纪元.某同学在学习“割圆术”的过程中,作了一个如图所示的圆内接正八边形.若的半径为2,则这个圆内接正八边形的面积为( )
A. B. C. D.
5.刘徽在《九章算术注》中首创“割圆术”,利用圆的内接正多边形来确定圆周率.如图,内部多边形为的内接正十二边形,若的半径为2,则这个圆内接正十二边形的面积为( )
A.1 B. C.12 D.
6.我国魏晋时期数学家刘徽在《九章算术注》中提到了著名的“割圆术”,“割圆术”孕育了微积分思想,他用这种思想得到了圆周率的近似值为3.1416.如图,⊙的半径为1,运用“割圆术”,以圆内接正六边形面积近似估计⊙的面积,可得的估计值为( )
A. B. C. D.
7.如图,正六边形内接于为的中点,连接,,四边形的面积为,正六边形剩余部分的面积为,则( )
A.6 B.4 C.3 D.2
8.正六边形蜂巢的建筑结构密合度最高、用材最少、空间最大、也最为坚固.如图,某蜂巢的房孔是边长为6的正六边形,若的内接正六边形为正六边形,则的长为( )
A. B. C. D.6
二、填空题
9.李师傅要在木板上开一个小孔,使其恰好能穿过一个正六边形的螺母,如图所示,若圆孔的周长等于,则正六边形螺母的边长为 .
10.如图,正八边形内接于,连接,则 .
11.如图,正六边形的边长为,以为圆心,得,连接,则图中阴影部分的面积为 .
12.如图,为正六边形的一条对角线,于点,连接,若正六边形的边长为2,则的长为 .
13.生活中常见的螺母横截面外轮廓大多数都是正六边形,将如图①所示的螺母横截面抽象成几何图形如图②所示,正六边形的中心与中间圆的圆心重合于点O处,连接交于点H,若中间圆的半径为9,正六边形的半径为15,则的长为 .
三、解答题
14.如图,正方形内接于是的中点,连接.
(1)求证:;
(2)求证:;
15.如图,在⊙O的内接四边形ABCD中,∠ADE是四边形ABCD的一个外角,且AD平分∠BDE
(1)求证:AB=AC;
(2)若点F在上,且∠F=116°,求∠ADC的度数.
16.大圆O和小圆O为同心圆,正六边形为大圆O的内接正六边形,连接.连接与交于点K,同时小圆O与相切于点K.
(1)求证:是小圆O的切线.
(2)若,求阴影部分的面积.(结果用表示)
17.如图正方形内接于,为任意一点,连接、.
(1)求的度数.
(2)如图2,过点作交于点,连接,,,,求的长度.
18.如图1,五边形是的内接五边形,,对角线于点.
(1)①若,则_______;
②猜想和的数量关系,并证明;
(2)如图2,当经过圆心时,若,,求;
(3)作于点,求的值.
19.【给出问题】如图1,正方形内接于,是的中点,连接,.求证:;
【深入思考】如图2,正方形内接于,点为上任意一点,连接、、,请探究、、三者之间有何数量关系,并给予证明.
【拓展应用】如图3,若四边形是矩形,点为边上一点,,,,试求矩形的面积.
20.【给出问题】:已知:是正方形的外接圆,点P在上(除A、B外),试求的度数.
【分析问题】:善于思考的小明在分析上述题目后,有了以圆为工具来解决问题的思路.用圆来画出准确的示意图就能顺利解题了,在此基础上进一步探索就有了新发现.请善于思考的你帮助解答以下问题:
(1)①尺规作图,在中作出内接正方形(保留痕迹,不写作法).
②原题中 .
【深入思考】:
(2)【问题】如图1,若四边形是的内接正方形,点P为弧上一动点,连接,请探究三者之间或者三者之间有何数量关系,并给予证明.
(3)【拓展】如图2,若六边形是的内接正六边形,点P为弧上一动点,请探究三者之间有何数量关系: (不写证明过程).
(4)【应用】如图3,若四边形是矩形,点P为边上一点,,,,试求矩形的面积.
试卷第1页,共3页
试卷第1页,共3页
《九年级数学上册第二十四章第3节《正多边形和圆》课时练习》参考答案
题号 1 2 3 4 5 6 7 8
答案 A B A B C B C C
9.3
10.90
11.
12.
13.6
14.(1)证明:∵四边形是正方形,
∴,
∴.
∵是的中点,
∴,
∴,
∴.
(2)解:连接,过点作交的延长线于.
∵四边形是正方形,
∴.
∵,
∴,
∴.
∵,
∴.
在△ADE和△CDF中,
,
∴,
∴,
∴,
即.
15.解:(1)∵AD平分∠BDE,
∴∠ADB=∠ADE,
∵四边形ABCD内接于圆O,
∴∠ADE=∠ABC,
∴∠ADB=∠ABC,
∴AB=AC;
(2)∵∠F=116°,
∴∠BAC=180°-116°=64°,
∵AB=AC,
∴∠ABC=∠ACB=(180°-64°)÷2=58°,
∴∠ADC=180°-58°=122°.
16.(1)证明:如图所示,连接,设交于H,
∵正六边形为大圆O的内接正六边形,
∴,
∴,
又∵,
∴垂直平分,
∴,
∵小圆O与相切于点K,
∴,
又∵,
∴,
∴,
∴点H在小圆O上,
又∵,
∴是小圆O的切线;
(2)解:∵正六边形为大圆O的内接正六边形,
∴,
∴是等边三角形,
∵小圆O与相切于点K,
∴,
∴,
∴,
∴,
∴,
∴.
17.(1)解:如图1中,连接、.
四边形是正方形,
,
;
(2)解:如图2中,连接,,,,作于.
∵,,
,,
,
,,
,
,
,
,
,
,
,
,
,
设,
在中,,
,
解得或(舍弃),
.
18.(1)①解:如图,连接,
,
,
,
,
,
;
故答案为:;
②,
证明:如图,连接,
,
,
,
,
,
,
,
,
即;
(2)解:如图,连接、,连接交于点,
在中,,
设,则,
在中,,
,
解得:,
,,,
,,
垂直平分,
,,
设,则,
在中,,
在中,,
解得:,
,
,
为的直径,
,
在中,;
(3)解:如图,连接、、、,过点作于点,
,
,
,
,,
,
,
,
,
,
,即,
在和中,
,
,
,
,,
,
,
.
19.[给出问题]证明:四边形是正方形,
,
是的中点,
;
[深入思考] ,理由如下,
过点作交于点,取圆心,连接,,
,
,
,
,
,
,,
在和中,
,
,
,即
[拓展应用] 解:以为边,作正方形,连接,,,,作正方形的外接圆,则圆心在上,
,,
点在上,
,,
,,
,
,
设,则,,
在中,,
在中,,
在中,,
解得:(负值舍去)
,
矩形的面积.
20.解:(1)①如图所示,作直径的垂直平分线交于点A,C,则四边形是正方形;
②如图所示,
,
故答案为:.
(2),证明如下:
如图,过点C作交于E,
∵,
∴,
∵,
∴,
又∵,
∴(ASA),
∴,
∴是等腰直角三角形,
∴,
即,
如图所示,过点C作交于F,
同理可得是等腰直角三角形,,
∴,;
(3),
如图,过点B,作,在上截取,连接,
∵,,
在和中,
,
∴(),
∴,
∴,
又∵,
∴,
∴,
∴.
(4)如图,以为边,作正方形,连接,,
根据(1)可得P在上,则,
∴,
设,则,,
在中,,
在中,,
在 中,,
∴,
解得 (负值舍去),
∴,
∴矩形的面积为.
答案第1页,共2页
答案第1页,共2页
同课章节目录
