2025年浙江省中考数学一轮复习专题检测 专题25 与圆有关的计算(含解析)
文档属性
| 名称 | 2025年浙江省中考数学一轮复习专题检测 专题25 与圆有关的计算(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-11 13:26:50 | ||
图片预览

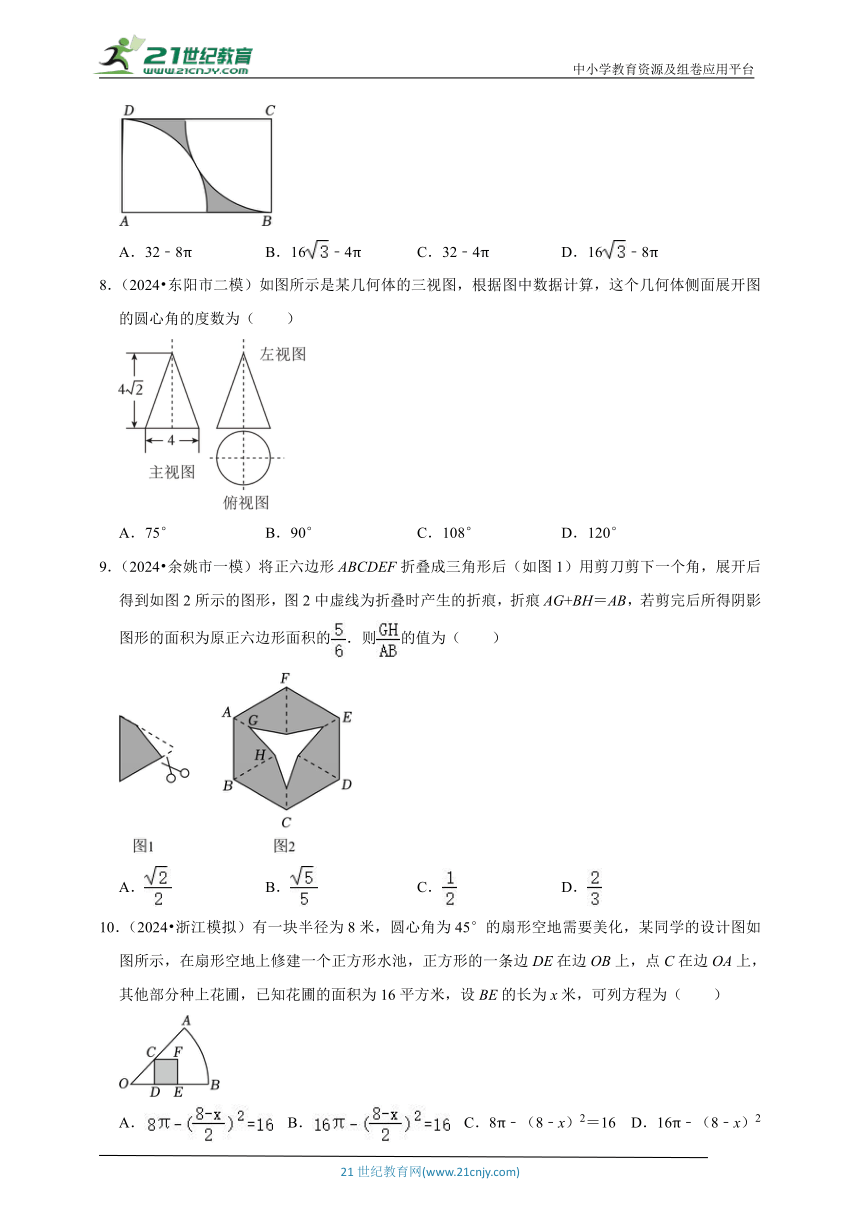


文档简介
中小学教育资源及组卷应用平台
专题25 与圆有关的计算
一.选择题
1.(2024 安徽)若扇形AOB的半径为6,∠AOB=120°,则的长为( )
A.2π B.3π C.4π D.6π
2.(2025 柳州二模)已知扇形的半径为3,圆心角为120°,则这个扇形的面积为( )
A.9π B.6π C.3π D.2π
3.(2024 甘孜州)如图,正六边形ABCDEF内接于⊙O,OA=1,则AB的长为( )
A.2 B. C.1 D.
4.(2024 南京模拟)一个圆锥的侧面积是12π,它的底面半径是3,则它的母线长等于( )
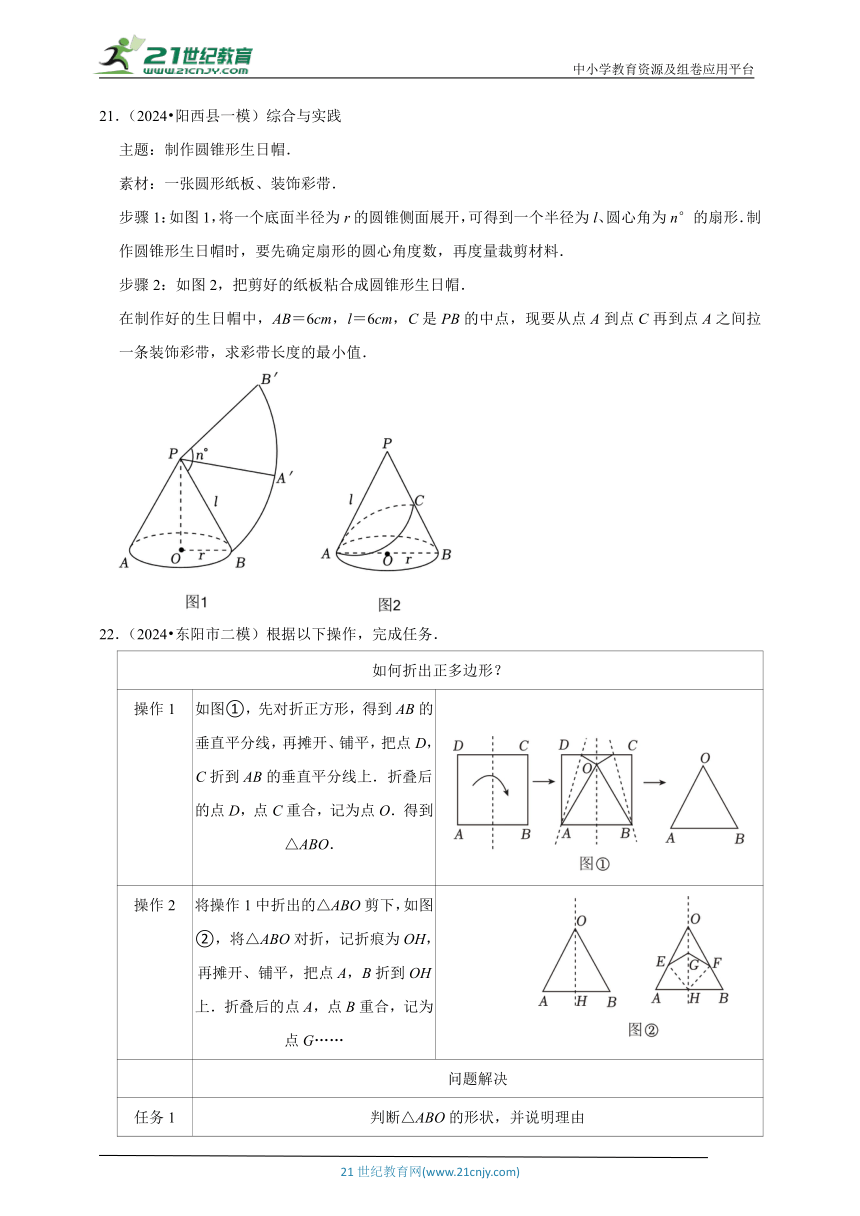
A.2 B.3 C.4 D.6
5.(2025 无为市一模)如图,在矩形ABCD中,AB=3,AD=6,以点A为圆心,AD为半径的弧交BC于点E,则阴影部分的扇形面积是( )
A. B.π C.2π D.3π
6.(2024 广安)如图,在等腰三角形ABC中,AB=AC=10,∠C=70°,以AB为直径作半圆,与AC,BC分别相交于点D,E,则的长度为( )
A. B. C. D.
7.(2024 重庆)如图,在矩形ABCD中,分别以点A和C为圆心,AD长为半径画弧,两弧有且仅有一个公共点.若AD=4,则图中阴影部分的面积为( )
A.32﹣8π B.16﹣4π C.32﹣4π D.16﹣8π
8.(2024 东阳市二模)如图所示是某几何体的三视图,根据图中数据计算,这个几何体侧面展开图的圆心角的度数为( )
A.75° B.90° C.108° D.120°
9.(2024 余姚市一模)将正六边形ABCDEF折叠成三角形后(如图1)用剪刀剪下一个角,展开后得到如图2所示的图形,图2中虚线为折叠时产生的折痕,折痕AG+BH=AB,若剪完后所得阴影图形的面积为原正六边形面积的.则的值为( )
A. B. C. D.
10.(2024 浙江模拟)有一块半径为8米,圆心角为45°的扇形空地需要美化,某同学的设计图如图所示,在扇形空地上修建一个正方形水池,正方形的一条边DE在边OB上,点C在边OA上,其他部分种上花圃,已知花圃的面积为16平方米,设BE的长为x米,可列方程为( )
A. B. C.8π﹣(8﹣x)2=16 D.16π﹣(8﹣x)2=16
二.填空题
11.(2025 泗阳县一模)若扇形的圆心角为120°,半径为3,则它的弧长为 .
12.(2024 盐城)已知圆锥的底面半径为4,母线长为5,该圆锥的侧面积为 .
13.(2024 润州区二模)如图,物理实验中利用一个半径为6cm的定滑轮提起砝码,小明向下拉动绳子一端,使得定滑轮逆时针转动了120°,此时砝码被提起了 cm.(结果保留π)
14.(2024 宁波模拟)将一张半径为13cm的扇形纸片卷成一个圆锥形桶(不重叠,无缝隙),通过测量,知该圆锥形桶高为12cm,则扇形纸片的面积为 cm2(结果保留π).
15.(2024 钱塘区一模)如图,分别以等边△ABC的顶点A,B,C为圆心,以AB长为半径画弧,我们把这三条弧组成的封闭图形叫做莱洛三角形.若莱洛三角形的周长为2π,则莱洛三角形的面积为 .
16.(2025 定兴县一模)如图,两个边长相等的正六边形的公共边为BD,点A,B,C在同一直线上,点O1,O2分别为两个正六边形的中心.则tan∠O2AC的值为 .
17.(2025 盐城一模)公元前四世纪,希腊哲学家、科学史家欧德莫斯曾研究过对数学发展有重要影响的如下问题:如图,AB为⊙O的直径,过圆心O作OC⊥AB,交⊙O于点C,以C为圆心,CA为半径作,若S阴=4cm2,则S△ABC= cm2.
三.解答题
18.(2024 垦利区三模)已知:如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,∠AOC=60°,AC=2.
(1)求弦CD的长;
(2)求图中阴影部分的面积.
19.(2024 亳州二模)如图,在△ABC中,AB=AC=6cm,∠BAC=45°,以AB为直径作半圆,交BC于点D,交AC于点E.
(1)求线段CE的长;
(2)求弧DE的长.
20.(2024 上海模拟)如图,正五边形ABCDE内接于⊙O,连结AC,BD交于点F.
(1)求证:AB=AF.
(2)若⊙O的半径为10,求正五边形ABCDE的面积(结果精确到0.1,参考数据:sin36°≈0.59,cos36°≈0.81,tan36°≈0.73).
21.(2024 阳西县一模)综合与实践
主题:制作圆锥形生日帽.
素材:一张圆形纸板、装饰彩带.
步骤1:如图1,将一个底面半径为r的圆锥侧面展开,可得到一个半径为l、圆心角为n°的扇形.制作圆锥形生日帽时,要先确定扇形的圆心角度数,再度量裁剪材料.
步骤2:如图2,把剪好的纸板粘合成圆锥形生日帽.
在制作好的生日帽中,AB=6cm,l=6cm,C是PB的中点,现要从点A到点C再到点A之间拉一条装饰彩带,求彩带长度的最小值.
22.(2024 东阳市二模)根据以下操作,完成任务.
如何折出正多边形?
操作1 如图①,先对折正方形,得到AB的垂直平分线,再摊开、铺平,把点D,C折到AB的垂直平分线上.折叠后的点D,点C重合,记为点O.得到△ABO.
操作2 将操作1中折出的△ABO剪下,如图②,将△ABO对折,记折痕为OH,再摊开、铺平,把点A,B折到OH上.折叠后的点A,点B重合,记为点G……
问题解决
任务1 判断△ABO的形状,并说明理由
任务2 某数学学科小组在操作2的基础上继续折叠,提供了以下三种方案: 方案①:将纸片沿EF向上折叠,使得点H落在点P处. 方案②:将∠OEG对折,使得角两边EO与EG重合,折痕交OH于点P. 方案③:将纸片向左上方折叠,使得点E与点H重合,折叠后的点F落在点P处. 以上方案中折出的四边形EHFP为正方形的是 .(填写序号)
任务3 求操作1中的正方形ABCD与操作2中所折出的正方形EHFP的面积之比.
答案与解析
一.选择题
1.(2024 安徽)若扇形AOB的半径为6,∠AOB=120°,则的长为( )
A.2π B.3π C.4π D.6π
【点拨】利用弧长计算公式计算即可.
【解析】解:=,
故选:C.
【点睛】本题考查了弧长的计算,掌握弧长计算公式是解题的关键.
2.(2025 柳州二模)已知扇形的半径为3,圆心角为120°,则这个扇形的面积为( )
A.9π B.6π C.3π D.2π
【点拨】直接代入扇形的面积公式即可得出答案.
【解析】解:S扇形==3π.
故选:C.
【点睛】本题考查了扇形的面积公式,属于基础题,解答本题的关键是熟练掌握扇形的面积公式:S=.
3.(2024 甘孜州)如图,正六边形ABCDEF内接于⊙O,OA=1,则AB的长为( )
A.2 B. C.1 D.
【点拨】由正六边形ABCDEF内接于⊙O,求得∠AOB=60°,则△AOB是等边三角形,所以AB=OA=1,于是得到问题的答案.
【解析】解:∵正六边形ABCDEF内接于⊙O,
∴∠AOB=×360°=60°,
∵OA=OB,
∴△AOB是等边三角形,
∴AB=OA=1,
故选:C.
【点睛】此题重点考查正多边形的半径及中心角的定义、等边三角形的判定等知识,证明△AOB是等边三角形是解题的关键.
4.(2024 南京模拟)一个圆锥的侧面积是12π,它的底面半径是3,则它的母线长等于( )
A.2 B.3 C.4 D.6
【点拨】圆锥的侧面积=底面周长×母线长÷2,把相应数值代入即可求解.
【解析】解:设母线长为R,底面半径是3cm,则底面周长=6π,侧面积=3πR=12π,
∴R=4cm.
故选:C.
【点睛】本题考查圆锥的计算,关键是利用了圆的周长公式和扇形面积公式求解.
5.(2025 无为市一模)如图,在矩形ABCD中,AB=3,AD=6,以点A为圆心,AD为半径的弧交BC于点E,则阴影部分的扇形面积是( )
A. B.π C.2π D.3π
【点拨】根据矩形的性质和“直角三角形30°所对的直角边等于斜边的一半”求出∠DAE的度数,再由扇形的面积公式计算阴影部分的扇形面积即可.
【解析】解:根据题意,得AE=AD=6,
∵四边形ABCD是矩形,
∴∠ABE=90°,BC∥AD,
∵AB=3,
∴∠AEB=30°,
∴∠DAE=∠AEB=30°,
∴阴影部分的扇形面积是π×62=3π.
故选:D.
【点睛】本题考查扇形面积的计算、矩形的性质,掌握矩形的性质、“直角三角形30°所对的直角边等于斜边的一半”、扇形的面积计算公式是解题的关键.
6.(2024 广安)如图,在等腰三角形ABC中,AB=AC=10,∠C=70°,以AB为直径作半圆,与AC,BC分别相交于点D,E,则的长度为( )
A. B. C. D.
【点拨】根据等腰三角形的性质和三角形的内角和定理求得∠A的度数,证明OE∥AC,再由OA=OD,再由等腰三角形的性质和平行线的性质求得∠DOE的度数,利用弧长公式即可求解.
【解析】解:连接OD,OE,
∵AB=AC,
∴∠ABC=∠C=70°,
∵OE=OB,
∴∠OEB=∠ABC=70°,
∴∠OEB=∠C=70°,
∴OE∥AC,
在△ABC中,∠A+∠ABC+∠C=180°,
∴∠A=180°﹣∠ABC﹣∠C=180°﹣70°﹣70°=40°,,
∵OE∥AC,
∴∠A=∠ADO=40°=∠DOE,
∴的长度为,
故选:C.
【点睛】本题考查了弧长的求解,得到圆心角和半径是解题的关键.
7.(2024 重庆)如图,在矩形ABCD中,分别以点A和C为圆心,AD长为半径画弧,两弧有且仅有一个公共点.若AD=4,则图中阴影部分的面积为( )
A.32﹣8π B.16﹣4π C.32﹣4π D.16﹣8π
【点拨】连接AC,在Rt△ADC 中利用勾股定理求出AC的长,根据矩形的面积公式求出矩形ABCD的面积,两个扇形为圆,根据扇形面积公式求出两个扇形面积之和,根据S阴影=S矩形ABCD﹣S两个扇形计算阴影部分的面积即可.
【解析】解:连接AC.
∵两弧有且仅有一个公共点,AD=4,
∴AC=2AD=8,
∴在Rt△ADC 中,CD===4,
∴S矩形ABCD=AD CD=16,
∵两个扇形均为圆,而且它们的半径相等,
∴两个扇形为圆,面积之和为S两个扇形=πAD2=8π,
∴S阴影=S矩形ABCD﹣S两个扇形=16﹣8π.
故选:D.
【点睛】本题考查扇形面积的计算,掌握勾股定理、矩形、扇形和圆的面积公式是解题的关键.
8.(2024 东阳市二模)如图所示是某几何体的三视图,根据图中数据计算,这个几何体侧面展开图的圆心角的度数为( )
A.75° B.90° C.108° D.120°
【点拨】根据圆锥的底面半径得到圆锥的底面周长,也就是圆锥的侧面展开图的弧长,根据勾股定理得到圆锥的母线长,利用弧长公式可求得圆锥的侧面展开图中扇形的圆心角.
【解析】解:∵圆锥的底面直径为4,则半径为2,
∴圆锥的底面周长为4π,
∵圆锥的高是2√2cm,
∴圆锥的母线长为6,
设扇形的圆心角为n°,
∴(nπ×6)÷180=4π,
解得n=120.
故这个几何体展开图的圆心角是120°.
故选:D.
【点睛】本题考查了圆锥的计算,圆锥的侧面展开图是一个扇形,此扇形的弧长等于圆锥底面周长,扇形的半径等于圆锥的母线长.本题就是把的扇形的弧长等于圆锥底面周长作为相等关系,列方程求解.
9.(2024 余姚市一模)将正六边形ABCDEF折叠成三角形后(如图1)用剪刀剪下一个角,展开后得到如图2所示的图形,图2中虚线为折叠时产生的折痕,折痕AG+BH=AB,若剪完后所得阴影图形的面积为原正六边形面积的.则的值为( )
A. B. C. D.
【点拨】由折叠的性质知,6个小三角形均为完全相同的三角形,阴影面积与正六边形面积的,则每个小三角形(如△OGH)面积占一个小正三角形(如△AOB)的,过点G作GR⊥OC于点R,过点O作OT⊥AB于点T,设AB=OB=OA=OB=OC=1,然后根据三角形面积公式及勾股定理可得方程,通过解方程可得答案.
【解析】解:由折叠的性质知,6个小三角形均为完全相同的三角形,阴影面积与正六边形面积的,则每个小三角形(如△OGH)面积占一个小正三角形(如△AOB)的1﹣.
过点G作GR⊥OC于点R,过点O作OT⊥AB于点T,设AB=OB=OA=OB=OC=1,
∴S△AOB=AB OT==,
S△GOH==OG(1﹣OG)×=,
OG﹣OG2=,
解得OG=或(舍),
∴OH=1﹣OG=,OR=,
∴HR=OR﹣OH==﹣,GR=OR=,
∴GR2+HR2=GH2,即+=GH2,
解得GH=(负值舍去),
∴=,
故选:A.
【点睛】此题考查的是正多边形和圆、翻折变换、勾股定理,正确作出辅助线是解决此题的关键.
10.(2024 浙江模拟)有一块半径为8米,圆心角为45°的扇形空地需要美化,某同学的设计图如图所示,在扇形空地上修建一个正方形水池,正方形的一条边DE在边OB上,点C在边OA上,其他部分种上花圃,已知花圃的面积为16平方米,设BE的长为x米,可列方程为( )
A. B. C.8π﹣(8﹣x)2=16 D.16π﹣(8﹣x)2=16
【点拨】根据扇形的面积公式计算出扇形的面积;根据∠AOB=45°和正方形的性质证明OD=CD=DE,从而将DE用x表示出来,进而表示出正方形CDEF的面积,再根据S花圃=S扇形﹣S正方形CDEF解答即可.
【解析】解:S扇形=π OA2=π×64=8π,
∵∠AOB=45°,∠ODC=90°,
∴∠OCD=45°,
∴OD=CD,
∵四边形CDEF是正方形,
∴CD=DE,
∴OD=DE,
∴DE==,
∴S正方形CDEF=DE2=()2,
根据S花圃=S扇形﹣S正方形CDEF,得8π﹣()2=16.
故选:A.
【点睛】本题考查扇形面积的计算,掌握扇形面积的计算公式是解题的关键.
二.填空题
11.(2025 泗阳县一模)若扇形的圆心角为120°,半径为3,则它的弧长为 2π .
【点拨】根据题目中的数据和弧长公式,可以计算出该扇形的弧长.
【解析】解:∵扇形的圆心角为120°,半径为3,
∴它的弧长为:=2π,
故答案为:2π.
【点睛】本题考查弧长的计算,解答本题的关键是明确弧长的计算公式l=.
12.(2024 盐城)已知圆锥的底面半径为4,母线长为5,该圆锥的侧面积为 20π .
【点拨】圆锥的侧面积=底面周长×母线长÷2.
【解析】解:由圆锥的底面半径为4,母线长为5,
则圆锥的侧面积为×2π×4×5=20π.
故答案为:20π.
【点睛】本题考查的是圆锥的计算,理解圆锥的侧面展开图与原来的扇形之间的关系是解决本题的关键.
13.(2024 润州区二模)如图,物理实验中利用一个半径为6cm的定滑轮提起砝码,小明向下拉动绳子一端,使得定滑轮逆时针转动了120°,此时砝码被提起了 4π cm.(结果保留π)
【点拨】直接根据弧长公式计算即可.
【解析】解:砝码被提起了:=4π(cm).
故答案为:4π.
【点睛】本题考查了弧长的计算,关键是熟练掌握弧长公式.
14.(2024 宁波模拟)将一张半径为13cm的扇形纸片卷成一个圆锥形桶(不重叠,无缝隙),通过测量,知该圆锥形桶高为12cm,则扇形纸片的面积为 65π cm2(结果保留π).
【点拨】首先利用勾股定理求得底面半径,然后利用公式求得面积即可.
【解析】解:∵扇形的半径为13cm,高为12cm,
∴圆锥的底面半径为=5cm,
∴圆锥的侧面积为13×5π=65πcm2,
故答案为:65π.
【点睛】本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.也考查了勾股定理.
15.(2024 钱塘区一模)如图,分别以等边△ABC的顶点A,B,C为圆心,以AB长为半径画弧,我们把这三条弧组成的封闭图形叫做莱洛三角形.若莱洛三角形的周长为2π,则莱洛三角形的面积为 .
【点拨】根据莱洛三角形的周长,可求出等边△ABC的边长,进而可求出莱洛三角形的面积.
【解析】解:由题知,
莱洛三角形的周长可转化为半径长为AB的圆周长的一半.
又因为莱洛三角形的周长为2π,
所以,
则AB=2,
所以等边△ABC的边长为2.
过点A作BC的垂线,垂足为M,
则BM=.
在Rt△ABM中,
AM=.
所以莱洛三角形的面积为:.
故答案为:.
【点睛】本题考查扇形面积的计算,能根据所给莱洛三角形的周长得出等边三角形的边长是解题的关键.
16.(2025 定兴县一模)如图,两个边长相等的正六边形的公共边为BD,点A,B,C在同一直线上,点O1,O2分别为两个正六边形的中心.则tan∠O2AC的值为 .
【点拨】根据正六边形的性质,直角三角形的边角关系以及锐角三角函数的定义进行计算即可.
【解析】解:如图,连接O2C,过O2点作O2E⊥BC,垂足为E,设正六边形的边长为a,则O1A=O1B=O2C=a,
在Rt△O2CE中,O2C=a,∠CO2E=30°,
∴EC=O2C=a=BE,O2E=O2C=a,
∴AE=2a+a=a,
∴tan∠O2AC==.
故答案为:.
【点睛】本题考查正多边形和圆,掌握正六边形的性质,直角三角形的边角关系以及锐角三角函数的定义是正确解答的关键.
17.(2025 盐城一模)公元前四世纪,希腊哲学家、科学史家欧德莫斯曾研究过对数学发展有重要影响的如下问题:如图,AB为⊙O的直径,过圆心O作OC⊥AB,交⊙O于点C,以C为圆心,CA为半径作,若S阴=4cm2,则S△ABC= 4 cm2.
【点拨】设⊙O的半径为r,则,根据,即,求r2,然后代入求面积即可.
【解析】解:由题意知,∠ACB=90°,设⊙O的半径为r,则,
∴,即,
解得r2=4,
∴,
故答案为:4.
【点睛】本题考查了直径所对的圆周角为直角,扇形面积等知识.解题的关键在于正确表示阴影部分面积.
三.解答题
18.(2024 垦利区三模)已知:如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,∠AOC=60°,AC=2.
(1)求弦CD的长;
(2)求图中阴影部分的面积.
【点拨】(1)根据AB是直径,∠AOC=60°,AC=2,可求出AB,CB的长度,弦CD⊥AB,可得CE=DE,即可求得CE的长度,继而得出CD的长;
(2)S阴影=S半圆﹣S△ABC.
【解析】解:(1)∵AB是⊙O的直径,
∴∠ACB=90°,
∵AC=2,∠AOC=60°,
∴△AOC是等边三角形,
则AO=AC=2,AB=4,
∵弦CD⊥AB,
∴CE=DE=CD=OC×sin60°=2×=,
∴CD=2CE=2;
(2)∵,S△ABC=AB CE=×4×=2,
∴S阴影=S半圆﹣S△ABC=π 22﹣2=2π﹣2.
【点睛】本题考查了扇形的面积计算,垂径定理,圆周角定理等知识点,熟练掌握性质及定理是解本题的关键.
19.(2024 亳州二模)如图,在△ABC中,AB=AC=6cm,∠BAC=45°,以AB为直径作半圆,交BC于点D,交AC于点E.
(1)求线段CE的长;
(2)求弧DE的长.
【点拨】(1)连接OE,OD,由等腰三角形的性质得∠AEO=∠BAC=45°,再根据勾股定理计算即可;
(2)由等腰三角形的性质推出∠C=∠ODB,得到OD∥AC,推出∠EOD=∠AEO=45°,因此∠EOD=∠AEO=45°,由弧长公式计算即可.
【解析】解:(1)如图,连接OE,OD,
∵∠BAC=45°,OA=OE,
∴∠AEO=∠BAC=45°,
∴∠AOE=90°,
∵OA=OE=3cm,
∴AE==3(cm),
∴CE=6﹣3(cm);
(2)∵OD=OB,
∴∠B=∠ODB,
∵AB=AC,
∴∠B=∠C,
∴∠C=∠ODB,
∴OD∥AC,
∴∠EOD=∠AEO=45°,
∴弧DE的长==π(cm).
【点睛】本题考查弧长的计算,等腰三角形的性质,平行线的性质,关键是由等腰三角形的性质推出OD∥AC,从而求出∠EOD的度数.
20.(2024 上海模拟)如图,正五边形ABCDE内接于⊙O,连结AC,BD交于点F.
(1)求证:AB=AF.
(2)若⊙O的半径为10,求正五边形ABCDE的面积(结果精确到0.1,参考数据:sin36°≈0.59,cos36°≈0.81,tan36°≈0.73).
【点拨】(1)证明∠AFB=∠ABF=72°,可得结论;
(2)过点B作BH⊥OA于点H.解直角三角形求出OH,AB,可得结论.
【解析】解:(1)证明:如图,连接OA,OD,OC,OB.
∵ABCDE是正五边形,
∴∠BOC=72°,∠AOD=144°,
∴∠BAC=∠BOC=36°,∠ABF=∠AOD=72°,
∴∠AFB=180°﹣36°﹣72°=72°,
∴∠AFB=∠ABF,
∴AB=AF;
(2)解:过点B作BH⊥OA于点H.则BH=OB sin36°,OH=OB cos36°,
∴五边形ABCDE的面积=5× AB OH
=5××2×OB2 sin30° cos36°
=5×102×0.59×0.81
≈239.0.
【点睛】本题考查正多边形与圆,圆周角定理,解直角三角形等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题.
21.(2024 阳西县一模)综合与实践
主题:制作圆锥形生日帽.
素材:一张圆形纸板、装饰彩带.
步骤1:如图1,将一个底面半径为r的圆锥侧面展开,可得到一个半径为l、圆心角为n°的扇形.制作圆锥形生日帽时,要先确定扇形的圆心角度数,再度量裁剪材料.
步骤2:如图2,把剪好的纸板粘合成圆锥形生日帽.
在制作好的生日帽中,AB=6cm,l=6cm,C是PB的中点,现要从点A到点C再到点A之间拉一条装饰彩带,求彩带长度的最小值.
【点拨】根据条件得出圆锥的侧面展开后可得到的扇形圆心角为180°,进而根据勾股定理即可求解.
【解析】解:∵l=6cm,AB=6cm,
∴r=3cm,
∵×2πr×l=,
n=,
∴.
∴圆锥的侧面展开后得到的扇形圆心角为180°,如图所示.
∴.
∵PA′=PB=6cm,
∴.
∴在Rt△A′PC中,由勾股定理得.
∴彩带长度的最小值为.
【点睛】本题考查了圆锥侧面展开图的圆心角的度数,勾股定理求最值问题,掌握以上知识是解题的关键.
22.(2024 东阳市二模)根据以下操作,完成任务.
如何折出正多边形?
操作1 如图①,先对折正方形,得到AB的垂直平分线,再摊开、铺平,把点D,C折到AB的垂直平分线上.折叠后的点D,点C重合,记为点O.得到△ABO.
操作2 将操作1中折出的△ABO剪下,如图②,将△ABO对折,记折痕为OH,再摊开、铺平,把点A,B折到OH上.折叠后的点A,点B重合,记为点G……
问题解决
任务1 判断△ABO的形状,并说明理由
任务2 某数学学科小组在操作2的基础上继续折叠,提供了以下三种方案: 方案①:将纸片沿EF向上折叠,使得点H落在点P处. 方案②:将∠OEG对折,使得角两边EO与EG重合,折痕交OH于点P. 方案③:将纸片向左上方折叠,使得点E与点H重合,折叠后的点F落在点P处. 以上方案中折出的四边形EHFP为正方形的是 ①②③ .(填写序号)
任务3 求操作1中的正方形ABCD与操作2中所折出的正方形EHFP的面积之比.
【点拨】任务1:根据折叠的性质得出△OAB是等边三角形;
任务2:由折叠的方法和对称性质可得∠EHF=90°,EH=FH,再由方案①②③的折叠方法可证明四边形EHFP是正方形;
任务3:根据含30° 直角三角形性质和等腰直角三角形性质求出正方形EHFP的边长EH与正方形ABCD边长AB之比的平方,即可解答.
【解析】解:任务1:△OAB是等边三角形,
理由:根据折叠的方法可知:OA=AD=AB=BC=OB,
∴△OAB是等边三角形;
任务2:连接EF,
∵△OAB是等边三角形,OH所在直线是△OAB的一条对称轴,
∴由折叠方法可知EH=FH,∠EHA=∠EHO=∠OHF=∠FHB=45°,E、F是关于OH的对称,
∴OH⊥EF,EK=FK,即OH是EF的垂直平分线,∠EHF=90°,
方案①,将纸片沿EF向上折叠,使得点H落在点P处,
∴EH=HF=FP=PE,
∴四边形EHFP是菱形,
又∠EHF=90°,
∴菱形EHFP是正方形;
方案②,将∠OEG对折,使得角两边EO与EG重合,折痕交OH于点P,
∵∠AEH=∠GEH=∠AEG,,
∴∠HEP=∠GEH+∠PEG=(∠AEG+∠OEG)=90°,
∴∠EPH=∠EHG=45°,
∴EP∥HF,
∴EP=EH=HF,
∴四边形EHFP是是正方形;
方案③:将纸片向左上方折叠,使得点E与点H重合,折叠后的点F落在点P处,
如图,
由折叠方法可知:∠PEH=∠FHE=90°,EP=HF,
∴EP∥HF,
∴四边形EHFP是平行四边形,
∵EH=HF,EH⊥HF,
∴四边形EHFP是正方形;
综上所述:方案中折出的四边形EHFP为正方形的是①②③,
故答案为:①②③;
任务3:如图,过点E作EM⊥AB,垂足为M,
∵∠A=60°,∠EHA=45°,
∴EM=MH,AE=2AM,
∴,,
∴,,
正方形ABCD与正方形EHFP的面积之比为:.
【点睛】本题考查了正方形与折叠问题,等腰三角形的性质与判定,轴对称的性质,勾股定理,熟练掌握折叠的性质是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
专题25 与圆有关的计算
一.选择题
1.(2024 安徽)若扇形AOB的半径为6,∠AOB=120°,则的长为( )
A.2π B.3π C.4π D.6π
2.(2025 柳州二模)已知扇形的半径为3,圆心角为120°,则这个扇形的面积为( )
A.9π B.6π C.3π D.2π
3.(2024 甘孜州)如图,正六边形ABCDEF内接于⊙O,OA=1,则AB的长为( )
A.2 B. C.1 D.
4.(2024 南京模拟)一个圆锥的侧面积是12π,它的底面半径是3,则它的母线长等于( )
A.2 B.3 C.4 D.6
5.(2025 无为市一模)如图,在矩形ABCD中,AB=3,AD=6,以点A为圆心,AD为半径的弧交BC于点E,则阴影部分的扇形面积是( )
A. B.π C.2π D.3π
6.(2024 广安)如图,在等腰三角形ABC中,AB=AC=10,∠C=70°,以AB为直径作半圆,与AC,BC分别相交于点D,E,则的长度为( )
A. B. C. D.
7.(2024 重庆)如图,在矩形ABCD中,分别以点A和C为圆心,AD长为半径画弧,两弧有且仅有一个公共点.若AD=4,则图中阴影部分的面积为( )
A.32﹣8π B.16﹣4π C.32﹣4π D.16﹣8π
8.(2024 东阳市二模)如图所示是某几何体的三视图,根据图中数据计算,这个几何体侧面展开图的圆心角的度数为( )
A.75° B.90° C.108° D.120°
9.(2024 余姚市一模)将正六边形ABCDEF折叠成三角形后(如图1)用剪刀剪下一个角,展开后得到如图2所示的图形,图2中虚线为折叠时产生的折痕,折痕AG+BH=AB,若剪完后所得阴影图形的面积为原正六边形面积的.则的值为( )
A. B. C. D.
10.(2024 浙江模拟)有一块半径为8米,圆心角为45°的扇形空地需要美化,某同学的设计图如图所示,在扇形空地上修建一个正方形水池,正方形的一条边DE在边OB上,点C在边OA上,其他部分种上花圃,已知花圃的面积为16平方米,设BE的长为x米,可列方程为( )
A. B. C.8π﹣(8﹣x)2=16 D.16π﹣(8﹣x)2=16
二.填空题
11.(2025 泗阳县一模)若扇形的圆心角为120°,半径为3,则它的弧长为 .
12.(2024 盐城)已知圆锥的底面半径为4,母线长为5,该圆锥的侧面积为 .
13.(2024 润州区二模)如图,物理实验中利用一个半径为6cm的定滑轮提起砝码,小明向下拉动绳子一端,使得定滑轮逆时针转动了120°,此时砝码被提起了 cm.(结果保留π)
14.(2024 宁波模拟)将一张半径为13cm的扇形纸片卷成一个圆锥形桶(不重叠,无缝隙),通过测量,知该圆锥形桶高为12cm,则扇形纸片的面积为 cm2(结果保留π).
15.(2024 钱塘区一模)如图,分别以等边△ABC的顶点A,B,C为圆心,以AB长为半径画弧,我们把这三条弧组成的封闭图形叫做莱洛三角形.若莱洛三角形的周长为2π,则莱洛三角形的面积为 .
16.(2025 定兴县一模)如图,两个边长相等的正六边形的公共边为BD,点A,B,C在同一直线上,点O1,O2分别为两个正六边形的中心.则tan∠O2AC的值为 .
17.(2025 盐城一模)公元前四世纪,希腊哲学家、科学史家欧德莫斯曾研究过对数学发展有重要影响的如下问题:如图,AB为⊙O的直径,过圆心O作OC⊥AB,交⊙O于点C,以C为圆心,CA为半径作,若S阴=4cm2,则S△ABC= cm2.
三.解答题
18.(2024 垦利区三模)已知:如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,∠AOC=60°,AC=2.
(1)求弦CD的长;
(2)求图中阴影部分的面积.
19.(2024 亳州二模)如图,在△ABC中,AB=AC=6cm,∠BAC=45°,以AB为直径作半圆,交BC于点D,交AC于点E.
(1)求线段CE的长;
(2)求弧DE的长.
20.(2024 上海模拟)如图,正五边形ABCDE内接于⊙O,连结AC,BD交于点F.
(1)求证:AB=AF.
(2)若⊙O的半径为10,求正五边形ABCDE的面积(结果精确到0.1,参考数据:sin36°≈0.59,cos36°≈0.81,tan36°≈0.73).
21.(2024 阳西县一模)综合与实践
主题:制作圆锥形生日帽.
素材:一张圆形纸板、装饰彩带.
步骤1:如图1,将一个底面半径为r的圆锥侧面展开,可得到一个半径为l、圆心角为n°的扇形.制作圆锥形生日帽时,要先确定扇形的圆心角度数,再度量裁剪材料.
步骤2:如图2,把剪好的纸板粘合成圆锥形生日帽.
在制作好的生日帽中,AB=6cm,l=6cm,C是PB的中点,现要从点A到点C再到点A之间拉一条装饰彩带,求彩带长度的最小值.
22.(2024 东阳市二模)根据以下操作,完成任务.
如何折出正多边形?
操作1 如图①,先对折正方形,得到AB的垂直平分线,再摊开、铺平,把点D,C折到AB的垂直平分线上.折叠后的点D,点C重合,记为点O.得到△ABO.
操作2 将操作1中折出的△ABO剪下,如图②,将△ABO对折,记折痕为OH,再摊开、铺平,把点A,B折到OH上.折叠后的点A,点B重合,记为点G……
问题解决
任务1 判断△ABO的形状,并说明理由
任务2 某数学学科小组在操作2的基础上继续折叠,提供了以下三种方案: 方案①:将纸片沿EF向上折叠,使得点H落在点P处. 方案②:将∠OEG对折,使得角两边EO与EG重合,折痕交OH于点P. 方案③:将纸片向左上方折叠,使得点E与点H重合,折叠后的点F落在点P处. 以上方案中折出的四边形EHFP为正方形的是 .(填写序号)
任务3 求操作1中的正方形ABCD与操作2中所折出的正方形EHFP的面积之比.
答案与解析
一.选择题
1.(2024 安徽)若扇形AOB的半径为6,∠AOB=120°,则的长为( )
A.2π B.3π C.4π D.6π
【点拨】利用弧长计算公式计算即可.
【解析】解:=,
故选:C.
【点睛】本题考查了弧长的计算,掌握弧长计算公式是解题的关键.
2.(2025 柳州二模)已知扇形的半径为3,圆心角为120°,则这个扇形的面积为( )
A.9π B.6π C.3π D.2π
【点拨】直接代入扇形的面积公式即可得出答案.
【解析】解:S扇形==3π.
故选:C.
【点睛】本题考查了扇形的面积公式,属于基础题,解答本题的关键是熟练掌握扇形的面积公式:S=.
3.(2024 甘孜州)如图,正六边形ABCDEF内接于⊙O,OA=1,则AB的长为( )
A.2 B. C.1 D.
【点拨】由正六边形ABCDEF内接于⊙O,求得∠AOB=60°,则△AOB是等边三角形,所以AB=OA=1,于是得到问题的答案.
【解析】解:∵正六边形ABCDEF内接于⊙O,
∴∠AOB=×360°=60°,
∵OA=OB,
∴△AOB是等边三角形,
∴AB=OA=1,
故选:C.
【点睛】此题重点考查正多边形的半径及中心角的定义、等边三角形的判定等知识,证明△AOB是等边三角形是解题的关键.
4.(2024 南京模拟)一个圆锥的侧面积是12π,它的底面半径是3,则它的母线长等于( )
A.2 B.3 C.4 D.6
【点拨】圆锥的侧面积=底面周长×母线长÷2,把相应数值代入即可求解.
【解析】解:设母线长为R,底面半径是3cm,则底面周长=6π,侧面积=3πR=12π,
∴R=4cm.
故选:C.
【点睛】本题考查圆锥的计算,关键是利用了圆的周长公式和扇形面积公式求解.
5.(2025 无为市一模)如图,在矩形ABCD中,AB=3,AD=6,以点A为圆心,AD为半径的弧交BC于点E,则阴影部分的扇形面积是( )
A. B.π C.2π D.3π
【点拨】根据矩形的性质和“直角三角形30°所对的直角边等于斜边的一半”求出∠DAE的度数,再由扇形的面积公式计算阴影部分的扇形面积即可.
【解析】解:根据题意,得AE=AD=6,
∵四边形ABCD是矩形,
∴∠ABE=90°,BC∥AD,
∵AB=3,
∴∠AEB=30°,
∴∠DAE=∠AEB=30°,
∴阴影部分的扇形面积是π×62=3π.
故选:D.
【点睛】本题考查扇形面积的计算、矩形的性质,掌握矩形的性质、“直角三角形30°所对的直角边等于斜边的一半”、扇形的面积计算公式是解题的关键.
6.(2024 广安)如图,在等腰三角形ABC中,AB=AC=10,∠C=70°,以AB为直径作半圆,与AC,BC分别相交于点D,E,则的长度为( )
A. B. C. D.
【点拨】根据等腰三角形的性质和三角形的内角和定理求得∠A的度数,证明OE∥AC,再由OA=OD,再由等腰三角形的性质和平行线的性质求得∠DOE的度数,利用弧长公式即可求解.
【解析】解:连接OD,OE,
∵AB=AC,
∴∠ABC=∠C=70°,
∵OE=OB,
∴∠OEB=∠ABC=70°,
∴∠OEB=∠C=70°,
∴OE∥AC,
在△ABC中,∠A+∠ABC+∠C=180°,
∴∠A=180°﹣∠ABC﹣∠C=180°﹣70°﹣70°=40°,,
∵OE∥AC,
∴∠A=∠ADO=40°=∠DOE,
∴的长度为,
故选:C.
【点睛】本题考查了弧长的求解,得到圆心角和半径是解题的关键.
7.(2024 重庆)如图,在矩形ABCD中,分别以点A和C为圆心,AD长为半径画弧,两弧有且仅有一个公共点.若AD=4,则图中阴影部分的面积为( )
A.32﹣8π B.16﹣4π C.32﹣4π D.16﹣8π
【点拨】连接AC,在Rt△ADC 中利用勾股定理求出AC的长,根据矩形的面积公式求出矩形ABCD的面积,两个扇形为圆,根据扇形面积公式求出两个扇形面积之和,根据S阴影=S矩形ABCD﹣S两个扇形计算阴影部分的面积即可.
【解析】解:连接AC.
∵两弧有且仅有一个公共点,AD=4,
∴AC=2AD=8,
∴在Rt△ADC 中,CD===4,
∴S矩形ABCD=AD CD=16,
∵两个扇形均为圆,而且它们的半径相等,
∴两个扇形为圆,面积之和为S两个扇形=πAD2=8π,
∴S阴影=S矩形ABCD﹣S两个扇形=16﹣8π.
故选:D.
【点睛】本题考查扇形面积的计算,掌握勾股定理、矩形、扇形和圆的面积公式是解题的关键.
8.(2024 东阳市二模)如图所示是某几何体的三视图,根据图中数据计算,这个几何体侧面展开图的圆心角的度数为( )
A.75° B.90° C.108° D.120°
【点拨】根据圆锥的底面半径得到圆锥的底面周长,也就是圆锥的侧面展开图的弧长,根据勾股定理得到圆锥的母线长,利用弧长公式可求得圆锥的侧面展开图中扇形的圆心角.
【解析】解:∵圆锥的底面直径为4,则半径为2,
∴圆锥的底面周长为4π,
∵圆锥的高是2√2cm,
∴圆锥的母线长为6,
设扇形的圆心角为n°,
∴(nπ×6)÷180=4π,
解得n=120.
故这个几何体展开图的圆心角是120°.
故选:D.
【点睛】本题考查了圆锥的计算,圆锥的侧面展开图是一个扇形,此扇形的弧长等于圆锥底面周长,扇形的半径等于圆锥的母线长.本题就是把的扇形的弧长等于圆锥底面周长作为相等关系,列方程求解.
9.(2024 余姚市一模)将正六边形ABCDEF折叠成三角形后(如图1)用剪刀剪下一个角,展开后得到如图2所示的图形,图2中虚线为折叠时产生的折痕,折痕AG+BH=AB,若剪完后所得阴影图形的面积为原正六边形面积的.则的值为( )
A. B. C. D.
【点拨】由折叠的性质知,6个小三角形均为完全相同的三角形,阴影面积与正六边形面积的,则每个小三角形(如△OGH)面积占一个小正三角形(如△AOB)的,过点G作GR⊥OC于点R,过点O作OT⊥AB于点T,设AB=OB=OA=OB=OC=1,然后根据三角形面积公式及勾股定理可得方程,通过解方程可得答案.
【解析】解:由折叠的性质知,6个小三角形均为完全相同的三角形,阴影面积与正六边形面积的,则每个小三角形(如△OGH)面积占一个小正三角形(如△AOB)的1﹣.
过点G作GR⊥OC于点R,过点O作OT⊥AB于点T,设AB=OB=OA=OB=OC=1,
∴S△AOB=AB OT==,
S△GOH==OG(1﹣OG)×=,
OG﹣OG2=,
解得OG=或(舍),
∴OH=1﹣OG=,OR=,
∴HR=OR﹣OH==﹣,GR=OR=,
∴GR2+HR2=GH2,即+=GH2,
解得GH=(负值舍去),
∴=,
故选:A.
【点睛】此题考查的是正多边形和圆、翻折变换、勾股定理,正确作出辅助线是解决此题的关键.
10.(2024 浙江模拟)有一块半径为8米,圆心角为45°的扇形空地需要美化,某同学的设计图如图所示,在扇形空地上修建一个正方形水池,正方形的一条边DE在边OB上,点C在边OA上,其他部分种上花圃,已知花圃的面积为16平方米,设BE的长为x米,可列方程为( )
A. B. C.8π﹣(8﹣x)2=16 D.16π﹣(8﹣x)2=16
【点拨】根据扇形的面积公式计算出扇形的面积;根据∠AOB=45°和正方形的性质证明OD=CD=DE,从而将DE用x表示出来,进而表示出正方形CDEF的面积,再根据S花圃=S扇形﹣S正方形CDEF解答即可.
【解析】解:S扇形=π OA2=π×64=8π,
∵∠AOB=45°,∠ODC=90°,
∴∠OCD=45°,
∴OD=CD,
∵四边形CDEF是正方形,
∴CD=DE,
∴OD=DE,
∴DE==,
∴S正方形CDEF=DE2=()2,
根据S花圃=S扇形﹣S正方形CDEF,得8π﹣()2=16.
故选:A.
【点睛】本题考查扇形面积的计算,掌握扇形面积的计算公式是解题的关键.
二.填空题
11.(2025 泗阳县一模)若扇形的圆心角为120°,半径为3,则它的弧长为 2π .
【点拨】根据题目中的数据和弧长公式,可以计算出该扇形的弧长.
【解析】解:∵扇形的圆心角为120°,半径为3,
∴它的弧长为:=2π,
故答案为:2π.
【点睛】本题考查弧长的计算,解答本题的关键是明确弧长的计算公式l=.
12.(2024 盐城)已知圆锥的底面半径为4,母线长为5,该圆锥的侧面积为 20π .
【点拨】圆锥的侧面积=底面周长×母线长÷2.
【解析】解:由圆锥的底面半径为4,母线长为5,
则圆锥的侧面积为×2π×4×5=20π.
故答案为:20π.
【点睛】本题考查的是圆锥的计算,理解圆锥的侧面展开图与原来的扇形之间的关系是解决本题的关键.
13.(2024 润州区二模)如图,物理实验中利用一个半径为6cm的定滑轮提起砝码,小明向下拉动绳子一端,使得定滑轮逆时针转动了120°,此时砝码被提起了 4π cm.(结果保留π)
【点拨】直接根据弧长公式计算即可.
【解析】解:砝码被提起了:=4π(cm).
故答案为:4π.
【点睛】本题考查了弧长的计算,关键是熟练掌握弧长公式.
14.(2024 宁波模拟)将一张半径为13cm的扇形纸片卷成一个圆锥形桶(不重叠,无缝隙),通过测量,知该圆锥形桶高为12cm,则扇形纸片的面积为 65π cm2(结果保留π).
【点拨】首先利用勾股定理求得底面半径,然后利用公式求得面积即可.
【解析】解:∵扇形的半径为13cm,高为12cm,
∴圆锥的底面半径为=5cm,
∴圆锥的侧面积为13×5π=65πcm2,
故答案为:65π.
【点睛】本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.也考查了勾股定理.
15.(2024 钱塘区一模)如图,分别以等边△ABC的顶点A,B,C为圆心,以AB长为半径画弧,我们把这三条弧组成的封闭图形叫做莱洛三角形.若莱洛三角形的周长为2π,则莱洛三角形的面积为 .
【点拨】根据莱洛三角形的周长,可求出等边△ABC的边长,进而可求出莱洛三角形的面积.
【解析】解:由题知,
莱洛三角形的周长可转化为半径长为AB的圆周长的一半.
又因为莱洛三角形的周长为2π,
所以,
则AB=2,
所以等边△ABC的边长为2.
过点A作BC的垂线,垂足为M,
则BM=.
在Rt△ABM中,
AM=.
所以莱洛三角形的面积为:.
故答案为:.
【点睛】本题考查扇形面积的计算,能根据所给莱洛三角形的周长得出等边三角形的边长是解题的关键.
16.(2025 定兴县一模)如图,两个边长相等的正六边形的公共边为BD,点A,B,C在同一直线上,点O1,O2分别为两个正六边形的中心.则tan∠O2AC的值为 .
【点拨】根据正六边形的性质,直角三角形的边角关系以及锐角三角函数的定义进行计算即可.
【解析】解:如图,连接O2C,过O2点作O2E⊥BC,垂足为E,设正六边形的边长为a,则O1A=O1B=O2C=a,
在Rt△O2CE中,O2C=a,∠CO2E=30°,
∴EC=O2C=a=BE,O2E=O2C=a,
∴AE=2a+a=a,
∴tan∠O2AC==.
故答案为:.
【点睛】本题考查正多边形和圆,掌握正六边形的性质,直角三角形的边角关系以及锐角三角函数的定义是正确解答的关键.
17.(2025 盐城一模)公元前四世纪,希腊哲学家、科学史家欧德莫斯曾研究过对数学发展有重要影响的如下问题:如图,AB为⊙O的直径,过圆心O作OC⊥AB,交⊙O于点C,以C为圆心,CA为半径作,若S阴=4cm2,则S△ABC= 4 cm2.
【点拨】设⊙O的半径为r,则,根据,即,求r2,然后代入求面积即可.
【解析】解:由题意知,∠ACB=90°,设⊙O的半径为r,则,
∴,即,
解得r2=4,
∴,
故答案为:4.
【点睛】本题考查了直径所对的圆周角为直角,扇形面积等知识.解题的关键在于正确表示阴影部分面积.
三.解答题
18.(2024 垦利区三模)已知:如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,∠AOC=60°,AC=2.
(1)求弦CD的长;
(2)求图中阴影部分的面积.
【点拨】(1)根据AB是直径,∠AOC=60°,AC=2,可求出AB,CB的长度,弦CD⊥AB,可得CE=DE,即可求得CE的长度,继而得出CD的长;
(2)S阴影=S半圆﹣S△ABC.
【解析】解:(1)∵AB是⊙O的直径,
∴∠ACB=90°,
∵AC=2,∠AOC=60°,
∴△AOC是等边三角形,
则AO=AC=2,AB=4,
∵弦CD⊥AB,
∴CE=DE=CD=OC×sin60°=2×=,
∴CD=2CE=2;
(2)∵,S△ABC=AB CE=×4×=2,
∴S阴影=S半圆﹣S△ABC=π 22﹣2=2π﹣2.
【点睛】本题考查了扇形的面积计算,垂径定理,圆周角定理等知识点,熟练掌握性质及定理是解本题的关键.
19.(2024 亳州二模)如图,在△ABC中,AB=AC=6cm,∠BAC=45°,以AB为直径作半圆,交BC于点D,交AC于点E.
(1)求线段CE的长;
(2)求弧DE的长.
【点拨】(1)连接OE,OD,由等腰三角形的性质得∠AEO=∠BAC=45°,再根据勾股定理计算即可;
(2)由等腰三角形的性质推出∠C=∠ODB,得到OD∥AC,推出∠EOD=∠AEO=45°,因此∠EOD=∠AEO=45°,由弧长公式计算即可.
【解析】解:(1)如图,连接OE,OD,
∵∠BAC=45°,OA=OE,
∴∠AEO=∠BAC=45°,
∴∠AOE=90°,
∵OA=OE=3cm,
∴AE==3(cm),
∴CE=6﹣3(cm);
(2)∵OD=OB,
∴∠B=∠ODB,
∵AB=AC,
∴∠B=∠C,
∴∠C=∠ODB,
∴OD∥AC,
∴∠EOD=∠AEO=45°,
∴弧DE的长==π(cm).
【点睛】本题考查弧长的计算,等腰三角形的性质,平行线的性质,关键是由等腰三角形的性质推出OD∥AC,从而求出∠EOD的度数.
20.(2024 上海模拟)如图,正五边形ABCDE内接于⊙O,连结AC,BD交于点F.
(1)求证:AB=AF.
(2)若⊙O的半径为10,求正五边形ABCDE的面积(结果精确到0.1,参考数据:sin36°≈0.59,cos36°≈0.81,tan36°≈0.73).
【点拨】(1)证明∠AFB=∠ABF=72°,可得结论;
(2)过点B作BH⊥OA于点H.解直角三角形求出OH,AB,可得结论.
【解析】解:(1)证明:如图,连接OA,OD,OC,OB.
∵ABCDE是正五边形,
∴∠BOC=72°,∠AOD=144°,
∴∠BAC=∠BOC=36°,∠ABF=∠AOD=72°,
∴∠AFB=180°﹣36°﹣72°=72°,
∴∠AFB=∠ABF,
∴AB=AF;
(2)解:过点B作BH⊥OA于点H.则BH=OB sin36°,OH=OB cos36°,
∴五边形ABCDE的面积=5× AB OH
=5××2×OB2 sin30° cos36°
=5×102×0.59×0.81
≈239.0.
【点睛】本题考查正多边形与圆,圆周角定理,解直角三角形等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题.
21.(2024 阳西县一模)综合与实践
主题:制作圆锥形生日帽.
素材:一张圆形纸板、装饰彩带.
步骤1:如图1,将一个底面半径为r的圆锥侧面展开,可得到一个半径为l、圆心角为n°的扇形.制作圆锥形生日帽时,要先确定扇形的圆心角度数,再度量裁剪材料.
步骤2:如图2,把剪好的纸板粘合成圆锥形生日帽.
在制作好的生日帽中,AB=6cm,l=6cm,C是PB的中点,现要从点A到点C再到点A之间拉一条装饰彩带,求彩带长度的最小值.
【点拨】根据条件得出圆锥的侧面展开后可得到的扇形圆心角为180°,进而根据勾股定理即可求解.
【解析】解:∵l=6cm,AB=6cm,
∴r=3cm,
∵×2πr×l=,
n=,
∴.
∴圆锥的侧面展开后得到的扇形圆心角为180°,如图所示.
∴.
∵PA′=PB=6cm,
∴.
∴在Rt△A′PC中,由勾股定理得.
∴彩带长度的最小值为.
【点睛】本题考查了圆锥侧面展开图的圆心角的度数,勾股定理求最值问题,掌握以上知识是解题的关键.
22.(2024 东阳市二模)根据以下操作,完成任务.
如何折出正多边形?
操作1 如图①,先对折正方形,得到AB的垂直平分线,再摊开、铺平,把点D,C折到AB的垂直平分线上.折叠后的点D,点C重合,记为点O.得到△ABO.
操作2 将操作1中折出的△ABO剪下,如图②,将△ABO对折,记折痕为OH,再摊开、铺平,把点A,B折到OH上.折叠后的点A,点B重合,记为点G……
问题解决
任务1 判断△ABO的形状,并说明理由
任务2 某数学学科小组在操作2的基础上继续折叠,提供了以下三种方案: 方案①:将纸片沿EF向上折叠,使得点H落在点P处. 方案②:将∠OEG对折,使得角两边EO与EG重合,折痕交OH于点P. 方案③:将纸片向左上方折叠,使得点E与点H重合,折叠后的点F落在点P处. 以上方案中折出的四边形EHFP为正方形的是 ①②③ .(填写序号)
任务3 求操作1中的正方形ABCD与操作2中所折出的正方形EHFP的面积之比.
【点拨】任务1:根据折叠的性质得出△OAB是等边三角形;
任务2:由折叠的方法和对称性质可得∠EHF=90°,EH=FH,再由方案①②③的折叠方法可证明四边形EHFP是正方形;
任务3:根据含30° 直角三角形性质和等腰直角三角形性质求出正方形EHFP的边长EH与正方形ABCD边长AB之比的平方,即可解答.
【解析】解:任务1:△OAB是等边三角形,
理由:根据折叠的方法可知:OA=AD=AB=BC=OB,
∴△OAB是等边三角形;
任务2:连接EF,
∵△OAB是等边三角形,OH所在直线是△OAB的一条对称轴,
∴由折叠方法可知EH=FH,∠EHA=∠EHO=∠OHF=∠FHB=45°,E、F是关于OH的对称,
∴OH⊥EF,EK=FK,即OH是EF的垂直平分线,∠EHF=90°,
方案①,将纸片沿EF向上折叠,使得点H落在点P处,
∴EH=HF=FP=PE,
∴四边形EHFP是菱形,
又∠EHF=90°,
∴菱形EHFP是正方形;
方案②,将∠OEG对折,使得角两边EO与EG重合,折痕交OH于点P,
∵∠AEH=∠GEH=∠AEG,,
∴∠HEP=∠GEH+∠PEG=(∠AEG+∠OEG)=90°,
∴∠EPH=∠EHG=45°,
∴EP∥HF,
∴EP=EH=HF,
∴四边形EHFP是是正方形;
方案③:将纸片向左上方折叠,使得点E与点H重合,折叠后的点F落在点P处,
如图,
由折叠方法可知:∠PEH=∠FHE=90°,EP=HF,
∴EP∥HF,
∴四边形EHFP是平行四边形,
∵EH=HF,EH⊥HF,
∴四边形EHFP是正方形;
综上所述:方案中折出的四边形EHFP为正方形的是①②③,
故答案为:①②③;
任务3:如图,过点E作EM⊥AB,垂足为M,
∵∠A=60°,∠EHA=45°,
∴EM=MH,AE=2AM,
∴,,
∴,,
正方形ABCD与正方形EHFP的面积之比为:.
【点睛】本题考查了正方形与折叠问题,等腰三角形的性质与判定,轴对称的性质,勾股定理,熟练掌握折叠的性质是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
