2025年甘肃省武威第二十中学中考数学人教版 对称轴 专项知识复习练习题(含答案)
文档属性
| 名称 | 2025年甘肃省武威第二十中学中考数学人教版 对称轴 专项知识复习练习题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-11 15:25:28 | ||
图片预览



文档简介
2025年甘肃省武威第二十中学中考数学人教版《对称轴》专项知识复习练习题
一、单选题
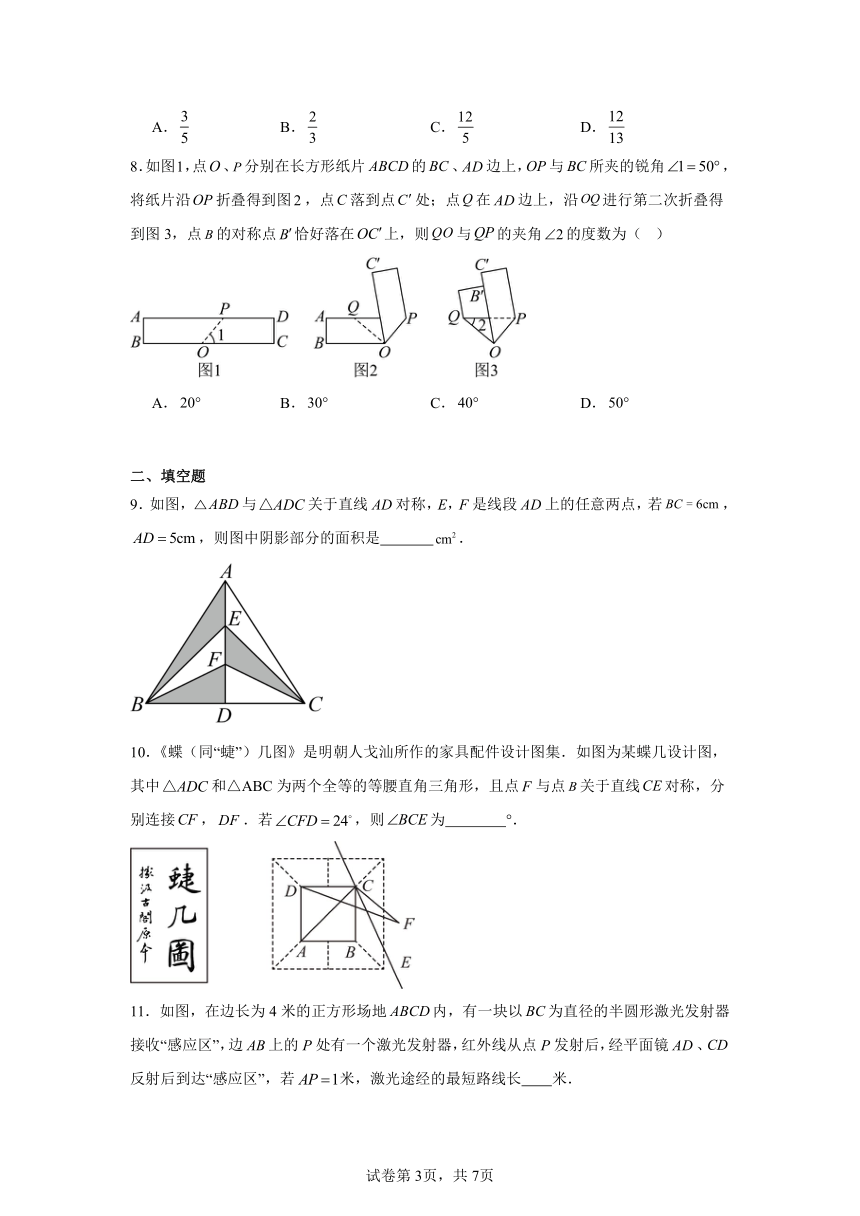
1.如图,,交于点O,和关于直线对称,点A,B的对称点分别是点C,D.下列结论中,不一定正确的是( ).
A. B. C. D.
2.如图,先将正方形纸片(,)对折,折痕为,再把点折叠到上,折痕为,点在上的对应点为,则的度数为( )
A. B. C. D.
3.如图在平面直角坐标系中,对△ABC进行循环往复的轴对称变换,若原来点的是,则经过第次变换后,所得点的坐标是( )
A. B. C. D.
4.小明用两个全等的等腰三角形设计了一个“蝴蝶”的平面图案.如图,其中与都是等腰三角形,且它们关于直线对称,点,分别是底边,的中点,.下列推断错误的是( )
A. B.
C. D.
5.在直角坐标系中,已知点,,其中m,n,p,q为互不相等的正数.作点A关于y轴的对称点C,点B关于x轴的对称点D.若直线经过原点,则下列关系式正确的是( )
A. B. C. D.
6.如图,△ABC与关于直线对称,连接,其中分别交于点,下列结论: ;;直线垂直平分;直线与的交点不一定在直线上.其中正确的是( )
A. B. C. D.
7.如图,三角形纸片中,,,.沿过点的直线将纸片折叠,使点落在边上的点处;再折叠纸片,使点与点重合,若折痕与的交点为,则( )
A. B. C. D.
8.如图,点、分别在长方形纸片的、边上,与所夹的锐角,将纸片沿折叠得到图,点落到点处;点在边上,沿进行第二次折叠得到图3,点的对称点恰好落在上,则与的夹角的度数为( )
A. B. C. D.
二、填空题
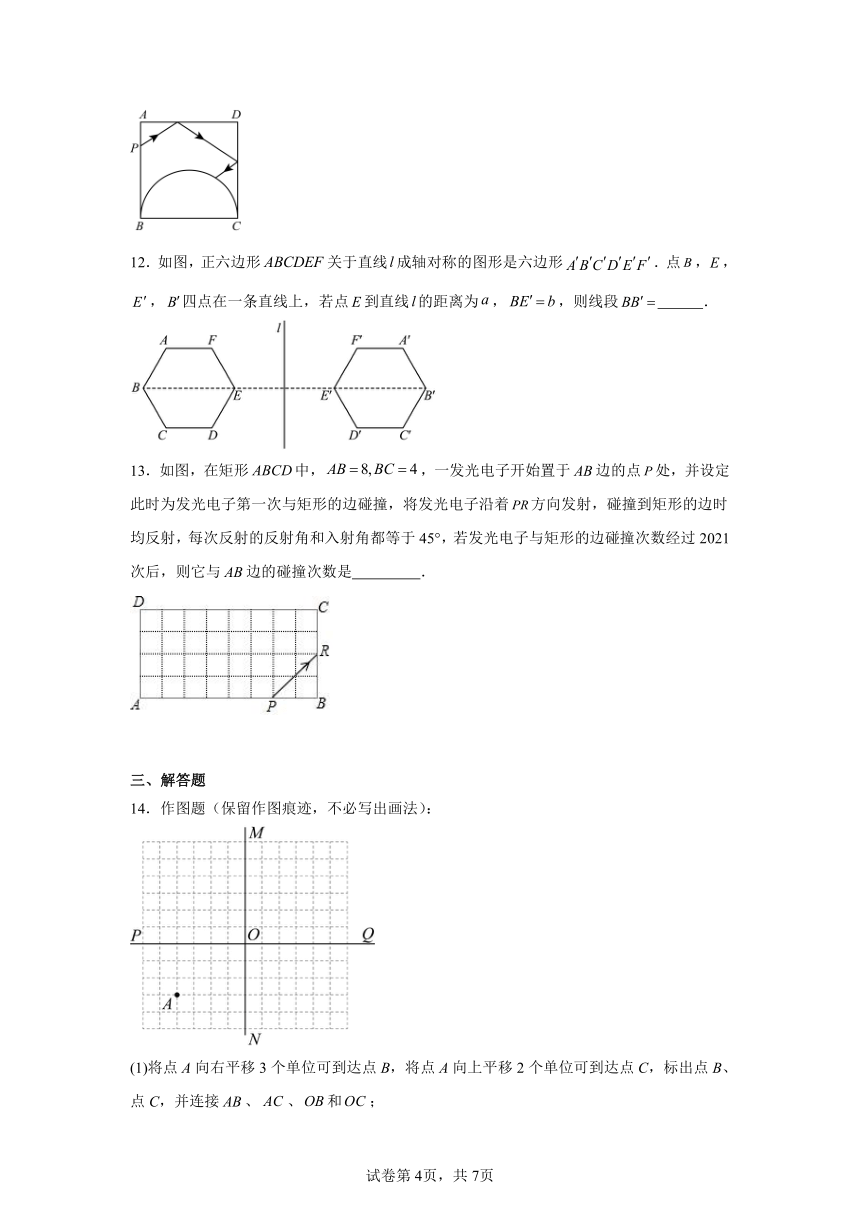
9.如图,与关于直线对称,E,F是线段上的任意两点,若,,则图中阴影部分的面积是 .
10.《蝶(同“蜨”)几图》是明朝人戈汕所作的家具配件设计图集.如图为某蝶几设计图,其中和△ABC为两个全等的等腰直角三角形,且点与点关于直线对称,分别连接,.若,则为 °.
11.如图,在边长为4米的正方形场地内,有一块以为直径的半圆形激光发射器接收“感应区”,边上的P处有一个激光发射器,红外线从点P发射后,经平面镜、反射后到达“感应区”,若米,激光途经的最短路线长 米.
12.如图,正六边形关于直线成轴对称的图形是六边形.点,,,四点在一条直线上,若点到直线的距离为,,则线段 .
13.如图,在矩形中,,一发光电子开始置于边的点处,并设定此时为发光电子第一次与矩形的边碰撞,将发光电子沿着方向发射,碰撞到矩形的边时均反射,每次反射的反射角和入射角都等于45°,若发光电子与矩形的边碰撞次数经过2021次后,则它与边的碰撞次数是 .
三、解答题
14.作图题(保留作图痕迹,不必写出画法):
(1)将点A向右平移3个单位可到达点B,将点A向上平移2个单位可到达点C,标出点B、点C,并连接、、和;
(2)在方格图中分别画出四边形和四边形,使四边形和四边形关于直线成轴对称;四边形和四边形关于点O成中心对称;
(3)四边形和四边形有没有对称关系?如果有,成怎样的对称关系?
15.如图,将平行四边形纸片沿一条直线折叠,使点与点重合,点落在点处,折痕为.
(1)求证:;
(2)若,,试判断的形状,并说明理由.
16.如图所示,是由△ABC经轴对称变换得到的,对称轴为直线.
(1)与△ABC全等吗?全等的两个三角形一定能经轴对称变换互相得到吗?
(2)分别找出点、点关于直线l的对称点,如果点在△ABC内,那么点关于直线的对称点一定在内吗?
(3)连接,线段与直线有怎样的关系?
17.如图,△ABC与△ADE关于直线对称,与的交点在直线上.若.
(1)求出的长度;
(2)求的度数;
(3)连接,线段与直线有什么关系?
18.如图1,在正方形中,点M,N分别是,上的点,,点E是上一点,将沿折叠,使点B落在N上的点F处.
(1)若,证明:点M是上的中点.
(2)如图2,延长与的延长线交于点G,交于点H,延长交于点P.
①求证:;
②当点E是的中点时,探究与的数量关系,并证明.
19.如图所示,在中,,,,点P从点A出发以每秒2个单位长度的速度沿向终点B运动,当点P不与点A,B重合时,作,边交折线于点D,点A关于直线的对称点为E,连接,得到.设点P的运动时间为t(秒).
(1)直接写出线段的长(用含t的代数式表示);
(2)当点E落在边上时,求t的值;
(3)设与△ABC重合部分图形的面积为S,求S与t之间的函数关系式,并写出自变量t的取值范围.
20.定义:如果一个凸四边形沿着它的一条对角线对折后能完全重合,我们就把这个四边形称为“忧乐四边形”.如图1,凸四边形沿对角线对折后完全重合,四边形是以直线为对称轴的“忧乐四边形”
(1)下列四边形一定是“忧乐四边形”的有_______ (填序号);
①平行四边形②菱形③矩形④正方形
(2)如图2,在矩形中,点是边上的中点,四边形是以直线为对称轴的“优乐四边形”(点在四边形内部),连接并延长交于点.
求证:四边形是“忧乐四边形”
(3)如图3,在四边形中,,,,,点是边上的中点,四边形是以直线为对称轴的“忧乐四边形”(点在四边形内部),连接并延长交于点.当是直角三角形时,请直接写出线段的长.
试卷第2页,共2页
试卷第1页,共3页
《2025年甘肃省武威第二十中学中考数学人教版《对称轴》专项知识复习练习题》参考答案
题号 1 2 3 4 5 6 7 8
答案 D C D B C A D C
9.
10.
11./
12.
13.673
14.(1)解:如图,点B、点C,、、和即为所求.
(2)解:如图,四边形和四边形即为所求.
(3)解:由图可知,四边形和四边形关于直线成轴对称.
15.(1)证明:∵四边形是平行四边形,
∴,,,
由折叠可得,,,,
∴,,,
∴,
∴,
∴;
(2)解:∵四边形是平行四边形,
∴,,
∴.
∵,
∴,
∴为等腰直角三角形.
16.(1)解:与△ABC全等,全等的两个三角形不一定能经轴对称变换互相得到,这要看这两个三角形的位置关系,
理由如下:
是由△ABC经轴对称变换得到的,
,
如图,,但和△ABC不是轴对称的关系,
;
(2)解:点、点关于直线的对称点分别是点、点;如果点在△ABC内,那么点关于直线的对称点一定在内,
如图,
;
(3)解:线段被直线垂直平分,
理由如下:
如图,设直线交直线于,
,
与△ABC关于直线对称,
点,是对称点,
将△ABC沿直线折叠后,点与点重合,则有,,
线段被直线垂直平分.
17.(1)解:∵△ABC与△ADE关于直线对称,,
∴,
∴.
(2)解:∵△ABC与△ADE关于直线对称,,
∴,
∴.
(3)解:直线垂直平分线段.理由如下:如图,
∵关于直线对称,
∴直线垂直平分线段.
18.(1)证明:∵四边形是正方形,
∴,
∵,
,
若,
则,
由折叠可知:,
,
∴点是的中点;
(2)①证明:∵四边形是正方形,
∴,,
由折叠可知:,
,,
,
∴△HPF∽△AOD
,
,
;
②解:当点是的中点时,与的数量关系是,
证明如下:
设,
则,
当点是的中点时,,
,
由折叠可知:,,
,
连接,如图:
在和中
,
,
,
,
而,
,
,
即有,
,
,
,
,
,
∴△PFN∽△PAD
,
,
或.
19.(1)①当时,
∵,
∴,
∵,
∴是等边三角形,
∴,
②当时,如图:
∵,
∴,
∵,
∴,
∴;
综上所述,,
(2)如图:
∵关于对称,
∴,
∴,
∴,
∵,
∴,
∴,
∴,
∴,
∵,
∴,
∴
(3)当时,如图:
重叠部分是∴△PED,
当时,如图
重叠部分是四边形,
∵,,
∴,
∴
∴,
∵,
∴
∴,
当时,如图:
重叠部分是,
∵
∴
综上所述,.
20.(1)①平行四边形,③矩形,沿着它的一条对角线对折后不能完全重合;②菱形,④正方形,沿着它的一条对角线对折后能完全重合.
②菱形,④正方形一定是忧乐四边形;
故答案为:②④;
(2)证明:如图2,连接,
四边形是矩形,
,
是的中点,
,
将沿折叠后得到,
,,,
,
,
,
四边形沿折叠完全重合,
四边形是“忧乐四边形”;
(3).
若,连接,则四边形是矩形,
,
由(2)知,,
设,则,,
,
,
,
;
若,连接,过点作于点,,交的延长线于点,如图,
由(2)知,
,
,
,
,
,
,,
,
,
,
,
,
,
设,
,
(负值舍),
.
综上所述,的长为或.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.如图,,交于点O,和关于直线对称,点A,B的对称点分别是点C,D.下列结论中,不一定正确的是( ).
A. B. C. D.
2.如图,先将正方形纸片(,)对折,折痕为,再把点折叠到上,折痕为,点在上的对应点为,则的度数为( )
A. B. C. D.
3.如图在平面直角坐标系中,对△ABC进行循环往复的轴对称变换,若原来点的是,则经过第次变换后,所得点的坐标是( )
A. B. C. D.
4.小明用两个全等的等腰三角形设计了一个“蝴蝶”的平面图案.如图,其中与都是等腰三角形,且它们关于直线对称,点,分别是底边,的中点,.下列推断错误的是( )
A. B.
C. D.
5.在直角坐标系中,已知点,,其中m,n,p,q为互不相等的正数.作点A关于y轴的对称点C,点B关于x轴的对称点D.若直线经过原点,则下列关系式正确的是( )
A. B. C. D.
6.如图,△ABC与关于直线对称,连接,其中分别交于点,下列结论: ;;直线垂直平分;直线与的交点不一定在直线上.其中正确的是( )
A. B. C. D.
7.如图,三角形纸片中,,,.沿过点的直线将纸片折叠,使点落在边上的点处;再折叠纸片,使点与点重合,若折痕与的交点为,则( )
A. B. C. D.
8.如图,点、分别在长方形纸片的、边上,与所夹的锐角,将纸片沿折叠得到图,点落到点处;点在边上,沿进行第二次折叠得到图3,点的对称点恰好落在上,则与的夹角的度数为( )
A. B. C. D.
二、填空题
9.如图,与关于直线对称,E,F是线段上的任意两点,若,,则图中阴影部分的面积是 .
10.《蝶(同“蜨”)几图》是明朝人戈汕所作的家具配件设计图集.如图为某蝶几设计图,其中和△ABC为两个全等的等腰直角三角形,且点与点关于直线对称,分别连接,.若,则为 °.
11.如图,在边长为4米的正方形场地内,有一块以为直径的半圆形激光发射器接收“感应区”,边上的P处有一个激光发射器,红外线从点P发射后,经平面镜、反射后到达“感应区”,若米,激光途经的最短路线长 米.
12.如图,正六边形关于直线成轴对称的图形是六边形.点,,,四点在一条直线上,若点到直线的距离为,,则线段 .
13.如图,在矩形中,,一发光电子开始置于边的点处,并设定此时为发光电子第一次与矩形的边碰撞,将发光电子沿着方向发射,碰撞到矩形的边时均反射,每次反射的反射角和入射角都等于45°,若发光电子与矩形的边碰撞次数经过2021次后,则它与边的碰撞次数是 .
三、解答题
14.作图题(保留作图痕迹,不必写出画法):
(1)将点A向右平移3个单位可到达点B,将点A向上平移2个单位可到达点C,标出点B、点C,并连接、、和;
(2)在方格图中分别画出四边形和四边形,使四边形和四边形关于直线成轴对称;四边形和四边形关于点O成中心对称;
(3)四边形和四边形有没有对称关系?如果有,成怎样的对称关系?
15.如图,将平行四边形纸片沿一条直线折叠,使点与点重合,点落在点处,折痕为.
(1)求证:;
(2)若,,试判断的形状,并说明理由.
16.如图所示,是由△ABC经轴对称变换得到的,对称轴为直线.
(1)与△ABC全等吗?全等的两个三角形一定能经轴对称变换互相得到吗?
(2)分别找出点、点关于直线l的对称点,如果点在△ABC内,那么点关于直线的对称点一定在内吗?
(3)连接,线段与直线有怎样的关系?
17.如图,△ABC与△ADE关于直线对称,与的交点在直线上.若.
(1)求出的长度;
(2)求的度数;
(3)连接,线段与直线有什么关系?
18.如图1,在正方形中,点M,N分别是,上的点,,点E是上一点,将沿折叠,使点B落在N上的点F处.
(1)若,证明:点M是上的中点.
(2)如图2,延长与的延长线交于点G,交于点H,延长交于点P.
①求证:;
②当点E是的中点时,探究与的数量关系,并证明.
19.如图所示,在中,,,,点P从点A出发以每秒2个单位长度的速度沿向终点B运动,当点P不与点A,B重合时,作,边交折线于点D,点A关于直线的对称点为E,连接,得到.设点P的运动时间为t(秒).
(1)直接写出线段的长(用含t的代数式表示);
(2)当点E落在边上时,求t的值;
(3)设与△ABC重合部分图形的面积为S,求S与t之间的函数关系式,并写出自变量t的取值范围.
20.定义:如果一个凸四边形沿着它的一条对角线对折后能完全重合,我们就把这个四边形称为“忧乐四边形”.如图1,凸四边形沿对角线对折后完全重合,四边形是以直线为对称轴的“忧乐四边形”
(1)下列四边形一定是“忧乐四边形”的有_______ (填序号);
①平行四边形②菱形③矩形④正方形
(2)如图2,在矩形中,点是边上的中点,四边形是以直线为对称轴的“优乐四边形”(点在四边形内部),连接并延长交于点.
求证:四边形是“忧乐四边形”
(3)如图3,在四边形中,,,,,点是边上的中点,四边形是以直线为对称轴的“忧乐四边形”(点在四边形内部),连接并延长交于点.当是直角三角形时,请直接写出线段的长.
试卷第2页,共2页
试卷第1页,共3页
《2025年甘肃省武威第二十中学中考数学人教版《对称轴》专项知识复习练习题》参考答案
题号 1 2 3 4 5 6 7 8
答案 D C D B C A D C
9.
10.
11./
12.
13.673
14.(1)解:如图,点B、点C,、、和即为所求.
(2)解:如图,四边形和四边形即为所求.
(3)解:由图可知,四边形和四边形关于直线成轴对称.
15.(1)证明:∵四边形是平行四边形,
∴,,,
由折叠可得,,,,
∴,,,
∴,
∴,
∴;
(2)解:∵四边形是平行四边形,
∴,,
∴.
∵,
∴,
∴为等腰直角三角形.
16.(1)解:与△ABC全等,全等的两个三角形不一定能经轴对称变换互相得到,这要看这两个三角形的位置关系,
理由如下:
是由△ABC经轴对称变换得到的,
,
如图,,但和△ABC不是轴对称的关系,
;
(2)解:点、点关于直线的对称点分别是点、点;如果点在△ABC内,那么点关于直线的对称点一定在内,
如图,
;
(3)解:线段被直线垂直平分,
理由如下:
如图,设直线交直线于,
,
与△ABC关于直线对称,
点,是对称点,
将△ABC沿直线折叠后,点与点重合,则有,,
线段被直线垂直平分.
17.(1)解:∵△ABC与△ADE关于直线对称,,
∴,
∴.
(2)解:∵△ABC与△ADE关于直线对称,,
∴,
∴.
(3)解:直线垂直平分线段.理由如下:如图,
∵关于直线对称,
∴直线垂直平分线段.
18.(1)证明:∵四边形是正方形,
∴,
∵,
,
若,
则,
由折叠可知:,
,
∴点是的中点;
(2)①证明:∵四边形是正方形,
∴,,
由折叠可知:,
,,
,
∴△HPF∽△AOD
,
,
;
②解:当点是的中点时,与的数量关系是,
证明如下:
设,
则,
当点是的中点时,,
,
由折叠可知:,,
,
连接,如图:
在和中
,
,
,
,
而,
,
,
即有,
,
,
,
,
,
∴△PFN∽△PAD
,
,
或.
19.(1)①当时,
∵,
∴,
∵,
∴是等边三角形,
∴,
②当时,如图:
∵,
∴,
∵,
∴,
∴;
综上所述,,
(2)如图:
∵关于对称,
∴,
∴,
∴,
∵,
∴,
∴,
∴,
∴,
∵,
∴,
∴
(3)当时,如图:
重叠部分是∴△PED,
当时,如图
重叠部分是四边形,
∵,,
∴,
∴
∴,
∵,
∴
∴,
当时,如图:
重叠部分是,
∵
∴
综上所述,.
20.(1)①平行四边形,③矩形,沿着它的一条对角线对折后不能完全重合;②菱形,④正方形,沿着它的一条对角线对折后能完全重合.
②菱形,④正方形一定是忧乐四边形;
故答案为:②④;
(2)证明:如图2,连接,
四边形是矩形,
,
是的中点,
,
将沿折叠后得到,
,,,
,
,
,
四边形沿折叠完全重合,
四边形是“忧乐四边形”;
(3).
若,连接,则四边形是矩形,
,
由(2)知,,
设,则,,
,
,
,
;
若,连接,过点作于点,,交的延长线于点,如图,
由(2)知,
,
,
,
,
,
,,
,
,
,
,
,
,
设,
,
(负值舍),
.
综上所述,的长为或.
答案第1页,共2页
答案第1页,共2页
同课章节目录
