第二十二章 二次函数 学情评估卷(含答案)2024-2025学年人教版数学九年级上册
文档属性
| 名称 | 第二十二章 二次函数 学情评估卷(含答案)2024-2025学年人教版数学九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 189.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-11 21:12:44 | ||
图片预览




文档简介
第二十二章 二次函数 学情评估卷
时间:45分钟 满分:100分
一、选择题(本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.下列属于二次函数的是( )
A. B. C. D.
2.抛物线与轴的交点为( )
A. B. C. D.
3.若抛物线经过平移得到抛物线,则平移的方法是( )
A. 向左平移1个单位长度,再向下平移3个单位长度
B. 向左平移1个单位长度,再向上平移3个单位长度
C. 向右平移1个单位长度,再向上平移3个单位长度
D. 向右平移1个单位长度,再向下平移3个单位长度
4.已知抛物线,下列结论错误的是( )
A. 抛物线开口向上 B. 抛物线与轴没有交点
C. 抛物线的顶点坐标为 D. 当时,随的增大而减小
5.如图,抛物线与直线交于,两点,则不等式的解集为( )
A. B.
C. 或 D.
6.根据下表中二次函数,,为常数,的自变量与函数值的对应值,判断方程的一个解的取值范围是( )
6.17 6.18 6.19 6.20
0.02 0.06
A. B.
C. D.
7.已知抛物线,若点,,都在该抛物线上,则,,的大小关系为( )
A. B.
C. D.
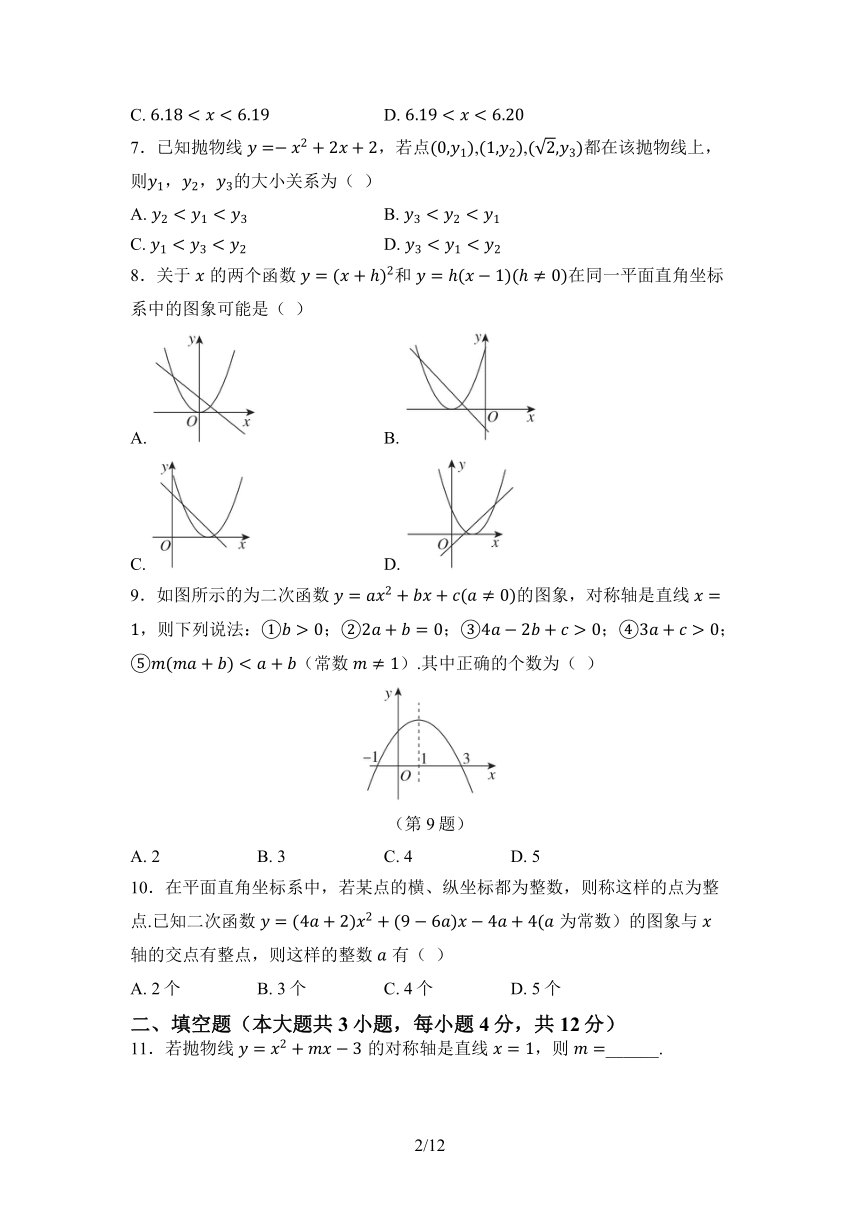
8.关于的两个函数和在同一平面直角坐标系中的图象可能是( )
A. B.
C. D.
9.如图所示的为二次函数的图象,对称轴是直线,则下列说法:;;;;(常数).其中正确的个数为( )
(第9题)
A. 2 B. 3 C. 4 D. 5
10.在平面直角坐标系中,若某点的横、纵坐标都为整数,则称这样的点为整点.已知二次函数为常数)的图象与轴的交点有整点,则这样的整数有( )
A. 2个 B. 3个 C. 4个 D. 5个
二、填空题(本大题共3小题,每小题4分,共12分)
11.若抛物线的对称轴是直线,则_ _ _ _ _ _ .
12.某西瓜经营户以2元/的价格购进一批西瓜,以3元/的单价售出,每天可售出,经调查,售价每降0.1元/,每天多卖,另外,每天的其他固定成本为24元.当定价为_ _ 元/时,每天能获得最大利润.
13.如图,抛物线与轴只有一个交点(交点在轴正半轴上),与轴平行的直线交抛物线于点,,交轴于点.若,则_ _ _ _ _ _ .
(第13题)
三、解答题(本大题共4小题,共48分.解答时应写出文字说明、证明过程或演算步骤)
14.(本小题满分8分)如图,已知抛物线对应的函数解析式为,抛物线的顶点为,其对称轴为直线.
(1) 求拋物线对应的函数解析式和点的坐标;
(2) 将抛物线向下平移个单位长度后,得到新的抛物线,求的值.
15.(本小题满分12分)如图,抛物线与直线交于点和点.
(1) 求出和的值;
(2) 求出点的坐标,并结合图象直接写出不等式的解集;
(3) 点为抛物线上一动点,当的面积为3时,求出点的坐标.
16.(本小题满分13分)如图,在平面直角坐标系中,抛物线与轴交于,两点,与轴交于点.
(1) 求该抛物线的解析式;
(2) 若点是直线下方抛物线上的一动点,过点作轴的平行线交于点,过点作轴的平行线交轴于点,求的最大值及此时点的坐标.
17.(本小题满分15分)如图①,灌溉车沿着平行于绿化带底部边缘的方向行驶,为绿化带浇水,喷水口离地面的高度为.如图②,可以把灌溉车喷出水的上下边缘抽象为平面直角坐标系中的两条抛物线的部分图象,把绿化带横截面抽象为矩形,其水平宽度,竖直高度,喷水口点是下边缘抛物线的最高点,上边缘抛物线的最高点离喷水口的水平距离为,高出喷水口,灌溉车到绿化带底部边缘的距离为.
(1) 求上边缘喷出水的最大射程;
(2) 当时,灌溉车在行驶时喷出的水能浇灌到整个绿化带吗?请你通过计算说明理由;
(3) 为保证灌溉车在行驶时喷出的水能浇灌到整个绿化带,请直接写出的取值范围.
第二十二章 二次函数 学情评估卷
时间:45分钟 满分:100分
一、选择题(本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.下列属于二次函数的是( )
A. B. C. D.
【答案】A
2.抛物线与轴的交点为( )
A. B. C. D.
【答案】B
3.若抛物线经过平移得到抛物线,则平移的方法是( )
A. 向左平移1个单位长度,再向下平移3个单位长度
B. 向左平移1个单位长度,再向上平移3个单位长度
C. 向右平移1个单位长度,再向上平移3个单位长度
D. 向右平移1个单位长度,再向下平移3个单位长度
【答案】C
4.已知抛物线,下列结论错误的是( )
A. 抛物线开口向上 B. 抛物线与轴没有交点
C. 抛物线的顶点坐标为 D. 当时,随的增大而减小
【答案】D
5.如图,抛物线与直线交于,两点,则不等式的解集为( )
A. B.
C. 或 D.
【答案】C
6.根据下表中二次函数,,为常数,的自变量与函数值的对应值,判断方程的一个解的取值范围是( )
6.17 6.18 6.19 6.20
0.02 0.06
A. B.
C. D.
【答案】C
7.已知抛物线,若点,,都在该抛物线上,则,,的大小关系为( )
A. B.
C. D.
【答案】C
8.关于的两个函数和在同一平面直角坐标系中的图象可能是( )
A. B.
C. D.
【答案】C
9.如图所示的为二次函数的图象,对称轴是直线,则下列说法:;;;;(常数).其中正确的个数为( )
(第9题)
A. 2 B. 3 C. 4 D. 5
【答案】B
10.在平面直角坐标系中,若某点的横、纵坐标都为整数,则称这样的点为整点.已知二次函数为常数)的图象与轴的交点有整点,则这样的整数有( )
A. 2个 B. 3个 C. 4个 D. 5个
【答案】C
二、填空题(本大题共3小题,每小题4分,共12分)
11.若抛物线的对称轴是直线,则_ _ _ _ _ _ .
【答案】
12.某西瓜经营户以2元/的价格购进一批西瓜,以3元/的单价售出,每天可售出,经调查,售价每降0.1元/,每天多卖,另外,每天的其他固定成本为24元.当定价为_ _ 元/时,每天能获得最大利润.
【答案】2.75
13.如图,抛物线与轴只有一个交点(交点在轴正半轴上),与轴平行的直线交抛物线于点,,交轴于点.若,则_ _ _ _ _ _ .
(第13题)
【答案】
三、解答题(本大题共4小题,共48分.解答时应写出文字说明、证明过程或演算步骤)
14.(本小题满分8分)如图,已知抛物线对应的函数解析式为,抛物线的顶点为,其对称轴为直线.
(1) 求拋物线对应的函数解析式和点的坐标;
(2) 将抛物线向下平移个单位长度后,得到新的抛物线,求的值.
【答案】
(1) 解: 抛物线的对称轴为直线,,解得,故抛物线对应的函数解析式为,将解析式化为顶点式得到,
.
(2) 由“上加下减”得平移后新的函数解析式为.
平移后新抛物线对应的函数解析式为,
,
,解得.
15.(本小题满分12分)如图,抛物线与直线交于点和点.
(1) 求出和的值;
(2) 求出点的坐标,并结合图象直接写出不等式的解集;
(3) 点为抛物线上一动点,当的面积为3时,求出点的坐标.
【答案】
(1) 解:把的坐标代入,得,解得.
把的坐标代入,得,
解得.
(2) 联立
解得或(舍去)
.
由题意得不等式的解集为或.
(3) ,.
的面积为3,
,,
.在中,当时,解得或;
当时,方程无解.
点的坐标为或.
16.(本小题满分13分)如图,在平面直角坐标系中,抛物线与轴交于,两点,与轴交于点.
(1) 求该抛物线的解析式;
(2) 若点是直线下方抛物线上的一动点,过点作轴的平行线交于点,过点作轴的平行线交轴于点,求的最大值及此时点的坐标.
【答案】
(1) 解:由题意,得
解得
抛物线的解析式为.
(2) ,, 易得直线的解析式为.
设,则,
.
, 当时,有最大值,最大值为,此时.
17.(本小题满分15分)如图①,灌溉车沿着平行于绿化带底部边缘的方向行驶,为绿化带浇水,喷水口离地面的高度为.如图②,可以把灌溉车喷出水的上下边缘抽象为平面直角坐标系中的两条抛物线的部分图象,把绿化带横截面抽象为矩形,其水平宽度,竖直高度,喷水口点是下边缘抛物线的最高点,上边缘抛物线的最高点离喷水口的水平距离为,高出喷水口,灌溉车到绿化带底部边缘的距离为.
(1) 求上边缘喷出水的最大射程;
(2) 当时,灌溉车在行驶时喷出的水能浇灌到整个绿化带吗?请你通过计算说明理由;
(3) 为保证灌溉车在行驶时喷出的水能浇灌到整个绿化带,请直接写出的取值范围.
【答案】
(1) 解:由题意得点的横坐标为2,纵坐标为,
设,
将的坐标代入,
得,解得,
的解析式为.
当时,,
,(舍去),
上边缘喷出水的最大射程为.
(2) 不能.理由:当时,根据题意得点的横坐标为,
,,
当时,.
, 当时,灌溉车在行驶时喷出的水不能浇灌到整个绿化带.
(3) .
/
时间:45分钟 满分:100分
一、选择题(本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.下列属于二次函数的是( )
A. B. C. D.
2.抛物线与轴的交点为( )
A. B. C. D.
3.若抛物线经过平移得到抛物线,则平移的方法是( )
A. 向左平移1个单位长度,再向下平移3个单位长度
B. 向左平移1个单位长度,再向上平移3个单位长度
C. 向右平移1个单位长度,再向上平移3个单位长度
D. 向右平移1个单位长度,再向下平移3个单位长度
4.已知抛物线,下列结论错误的是( )
A. 抛物线开口向上 B. 抛物线与轴没有交点
C. 抛物线的顶点坐标为 D. 当时,随的增大而减小
5.如图,抛物线与直线交于,两点,则不等式的解集为( )
A. B.
C. 或 D.
6.根据下表中二次函数,,为常数,的自变量与函数值的对应值,判断方程的一个解的取值范围是( )
6.17 6.18 6.19 6.20
0.02 0.06
A. B.
C. D.
7.已知抛物线,若点,,都在该抛物线上,则,,的大小关系为( )
A. B.
C. D.
8.关于的两个函数和在同一平面直角坐标系中的图象可能是( )
A. B.
C. D.
9.如图所示的为二次函数的图象,对称轴是直线,则下列说法:;;;;(常数).其中正确的个数为( )
(第9题)
A. 2 B. 3 C. 4 D. 5
10.在平面直角坐标系中,若某点的横、纵坐标都为整数,则称这样的点为整点.已知二次函数为常数)的图象与轴的交点有整点,则这样的整数有( )
A. 2个 B. 3个 C. 4个 D. 5个
二、填空题(本大题共3小题,每小题4分,共12分)
11.若抛物线的对称轴是直线,则_ _ _ _ _ _ .
12.某西瓜经营户以2元/的价格购进一批西瓜,以3元/的单价售出,每天可售出,经调查,售价每降0.1元/,每天多卖,另外,每天的其他固定成本为24元.当定价为_ _ 元/时,每天能获得最大利润.
13.如图,抛物线与轴只有一个交点(交点在轴正半轴上),与轴平行的直线交抛物线于点,,交轴于点.若,则_ _ _ _ _ _ .
(第13题)
三、解答题(本大题共4小题,共48分.解答时应写出文字说明、证明过程或演算步骤)
14.(本小题满分8分)如图,已知抛物线对应的函数解析式为,抛物线的顶点为,其对称轴为直线.
(1) 求拋物线对应的函数解析式和点的坐标;
(2) 将抛物线向下平移个单位长度后,得到新的抛物线,求的值.
15.(本小题满分12分)如图,抛物线与直线交于点和点.
(1) 求出和的值;
(2) 求出点的坐标,并结合图象直接写出不等式的解集;
(3) 点为抛物线上一动点,当的面积为3时,求出点的坐标.
16.(本小题满分13分)如图,在平面直角坐标系中,抛物线与轴交于,两点,与轴交于点.
(1) 求该抛物线的解析式;
(2) 若点是直线下方抛物线上的一动点,过点作轴的平行线交于点,过点作轴的平行线交轴于点,求的最大值及此时点的坐标.
17.(本小题满分15分)如图①,灌溉车沿着平行于绿化带底部边缘的方向行驶,为绿化带浇水,喷水口离地面的高度为.如图②,可以把灌溉车喷出水的上下边缘抽象为平面直角坐标系中的两条抛物线的部分图象,把绿化带横截面抽象为矩形,其水平宽度,竖直高度,喷水口点是下边缘抛物线的最高点,上边缘抛物线的最高点离喷水口的水平距离为,高出喷水口,灌溉车到绿化带底部边缘的距离为.
(1) 求上边缘喷出水的最大射程;
(2) 当时,灌溉车在行驶时喷出的水能浇灌到整个绿化带吗?请你通过计算说明理由;
(3) 为保证灌溉车在行驶时喷出的水能浇灌到整个绿化带,请直接写出的取值范围.
第二十二章 二次函数 学情评估卷
时间:45分钟 满分:100分
一、选择题(本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.下列属于二次函数的是( )
A. B. C. D.
【答案】A
2.抛物线与轴的交点为( )
A. B. C. D.
【答案】B
3.若抛物线经过平移得到抛物线,则平移的方法是( )
A. 向左平移1个单位长度,再向下平移3个单位长度
B. 向左平移1个单位长度,再向上平移3个单位长度
C. 向右平移1个单位长度,再向上平移3个单位长度
D. 向右平移1个单位长度,再向下平移3个单位长度
【答案】C
4.已知抛物线,下列结论错误的是( )
A. 抛物线开口向上 B. 抛物线与轴没有交点
C. 抛物线的顶点坐标为 D. 当时,随的增大而减小
【答案】D
5.如图,抛物线与直线交于,两点,则不等式的解集为( )
A. B.
C. 或 D.
【答案】C
6.根据下表中二次函数,,为常数,的自变量与函数值的对应值,判断方程的一个解的取值范围是( )
6.17 6.18 6.19 6.20
0.02 0.06
A. B.
C. D.
【答案】C
7.已知抛物线,若点,,都在该抛物线上,则,,的大小关系为( )
A. B.
C. D.
【答案】C
8.关于的两个函数和在同一平面直角坐标系中的图象可能是( )
A. B.
C. D.
【答案】C
9.如图所示的为二次函数的图象,对称轴是直线,则下列说法:;;;;(常数).其中正确的个数为( )
(第9题)
A. 2 B. 3 C. 4 D. 5
【答案】B
10.在平面直角坐标系中,若某点的横、纵坐标都为整数,则称这样的点为整点.已知二次函数为常数)的图象与轴的交点有整点,则这样的整数有( )
A. 2个 B. 3个 C. 4个 D. 5个
【答案】C
二、填空题(本大题共3小题,每小题4分,共12分)
11.若抛物线的对称轴是直线,则_ _ _ _ _ _ .
【答案】
12.某西瓜经营户以2元/的价格购进一批西瓜,以3元/的单价售出,每天可售出,经调查,售价每降0.1元/,每天多卖,另外,每天的其他固定成本为24元.当定价为_ _ 元/时,每天能获得最大利润.
【答案】2.75
13.如图,抛物线与轴只有一个交点(交点在轴正半轴上),与轴平行的直线交抛物线于点,,交轴于点.若,则_ _ _ _ _ _ .
(第13题)
【答案】
三、解答题(本大题共4小题,共48分.解答时应写出文字说明、证明过程或演算步骤)
14.(本小题满分8分)如图,已知抛物线对应的函数解析式为,抛物线的顶点为,其对称轴为直线.
(1) 求拋物线对应的函数解析式和点的坐标;
(2) 将抛物线向下平移个单位长度后,得到新的抛物线,求的值.
【答案】
(1) 解: 抛物线的对称轴为直线,,解得,故抛物线对应的函数解析式为,将解析式化为顶点式得到,
.
(2) 由“上加下减”得平移后新的函数解析式为.
平移后新抛物线对应的函数解析式为,
,
,解得.
15.(本小题满分12分)如图,抛物线与直线交于点和点.
(1) 求出和的值;
(2) 求出点的坐标,并结合图象直接写出不等式的解集;
(3) 点为抛物线上一动点,当的面积为3时,求出点的坐标.
【答案】
(1) 解:把的坐标代入,得,解得.
把的坐标代入,得,
解得.
(2) 联立
解得或(舍去)
.
由题意得不等式的解集为或.
(3) ,.
的面积为3,
,,
.在中,当时,解得或;
当时,方程无解.
点的坐标为或.
16.(本小题满分13分)如图,在平面直角坐标系中,抛物线与轴交于,两点,与轴交于点.
(1) 求该抛物线的解析式;
(2) 若点是直线下方抛物线上的一动点,过点作轴的平行线交于点,过点作轴的平行线交轴于点,求的最大值及此时点的坐标.
【答案】
(1) 解:由题意,得
解得
抛物线的解析式为.
(2) ,, 易得直线的解析式为.
设,则,
.
, 当时,有最大值,最大值为,此时.
17.(本小题满分15分)如图①,灌溉车沿着平行于绿化带底部边缘的方向行驶,为绿化带浇水,喷水口离地面的高度为.如图②,可以把灌溉车喷出水的上下边缘抽象为平面直角坐标系中的两条抛物线的部分图象,把绿化带横截面抽象为矩形,其水平宽度,竖直高度,喷水口点是下边缘抛物线的最高点,上边缘抛物线的最高点离喷水口的水平距离为,高出喷水口,灌溉车到绿化带底部边缘的距离为.
(1) 求上边缘喷出水的最大射程;
(2) 当时,灌溉车在行驶时喷出的水能浇灌到整个绿化带吗?请你通过计算说明理由;
(3) 为保证灌溉车在行驶时喷出的水能浇灌到整个绿化带,请直接写出的取值范围.
【答案】
(1) 解:由题意得点的横坐标为2,纵坐标为,
设,
将的坐标代入,
得,解得,
的解析式为.
当时,,
,(舍去),
上边缘喷出水的最大射程为.
(2) 不能.理由:当时,根据题意得点的横坐标为,
,,
当时,.
, 当时,灌溉车在行驶时喷出的水不能浇灌到整个绿化带.
(3) .
/
同课章节目录
