2025年甘肃省武威第二十中学中考数学人教版 全等三角形 专项训练练习题(含答案)
文档属性
| 名称 | 2025年甘肃省武威第二十中学中考数学人教版 全等三角形 专项训练练习题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-11 15:25:53 | ||
图片预览

文档简介
2025年甘肃省武威第二十中学中考数学人教版《全等三角形》专项训练练习题
一、单选题
1.如图,在的两边上,分别取,再分别过点,作、的垂线交点为画射线,判断依据是( )
A. B. C. D.
2.如图,在∴△ABC与中,,且点A在上,点D在上,添加下列一个条件后,仍然不能判定的是( )
A. B. C. D.
3.已知,在△ABC中,,,垂足为点H,平分,与相交于点D,过点D作,与边相交于点E,那么下列结论中一定正确的是( )
A. B.
C. D.
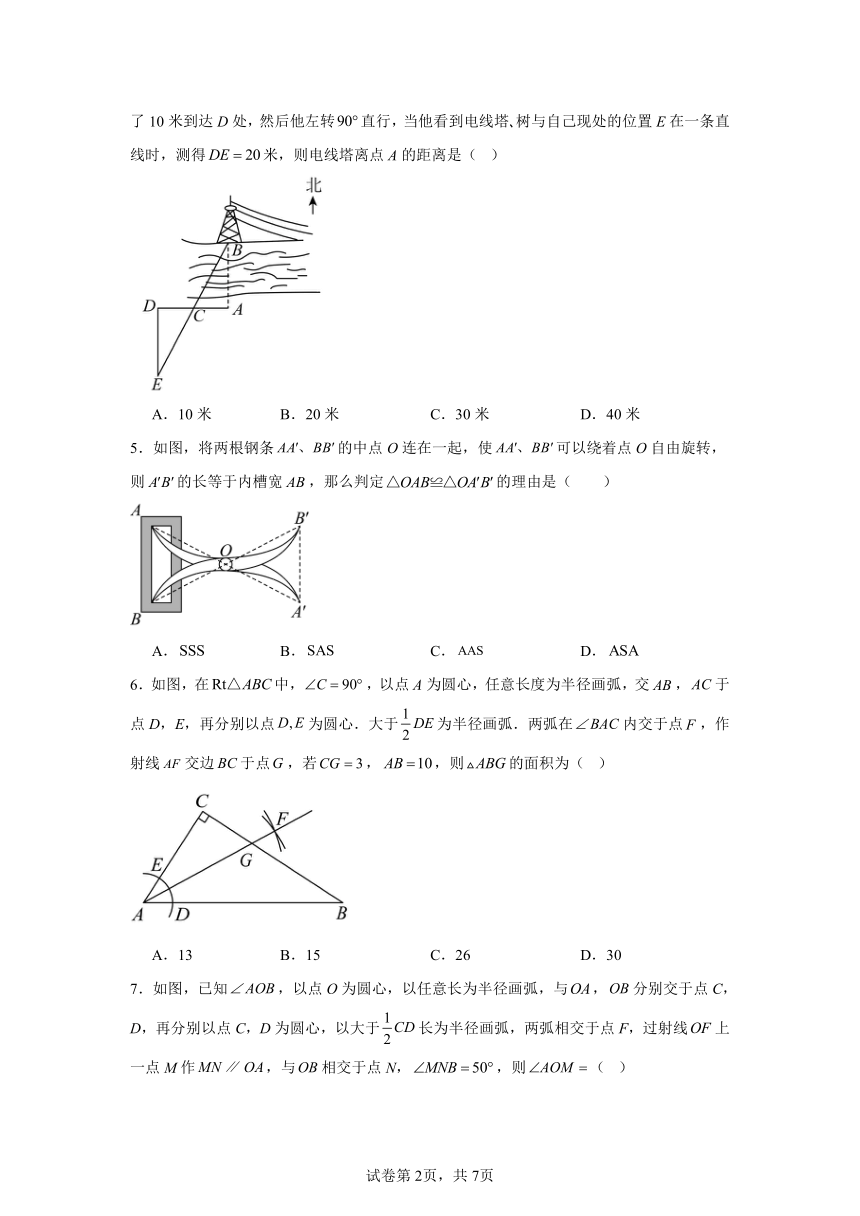
4.如图,嘉琪站在河边的点A处,在河对面(嘉珙正北方向)的点B处有一电线塔,他想知道此时电线塔离他有多远,于是他向正西方向走了10米到达一棵树C处,接着再向前走了10米到达D处,然后他左转直行,当他看到电线塔 树与自己现处的位置E在一条直线时,测得米,则电线塔离点A的距离是( )
A.10米 B.20米 C.30米 D.40米
5.如图,将两根钢条的中点O连在一起,使可以绕着点O自由旋转,则的长等于内槽宽,那么判定的理由是( )
A. B. C. D.
6.如图,在中,,以点A为圆心,任意长度为半径画弧,交,于点D,E,再分别以点为圆心.大于为半径画弧.两弧在内交于点,作射线交边于点,若,,则的面积为( )
A.13 B.15 C.26 D.30
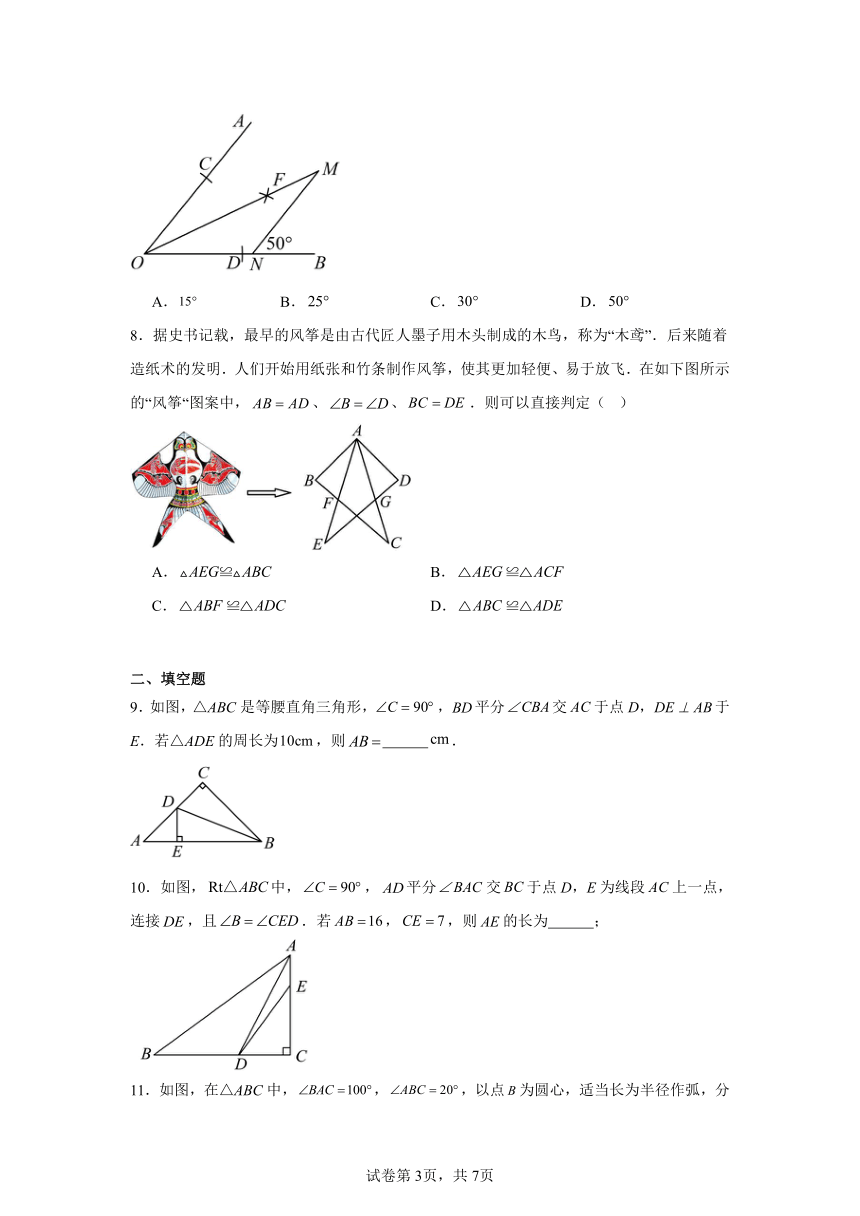
7.如图,已知,以点O为圆心,以任意长为半径画弧,与,分别交于点C,D,再分别以点C,D为圆心,以大于长为半径画弧,两弧相交于点F,过射线上一点M作,与相交于点N,,则( )
A. B. C. D.
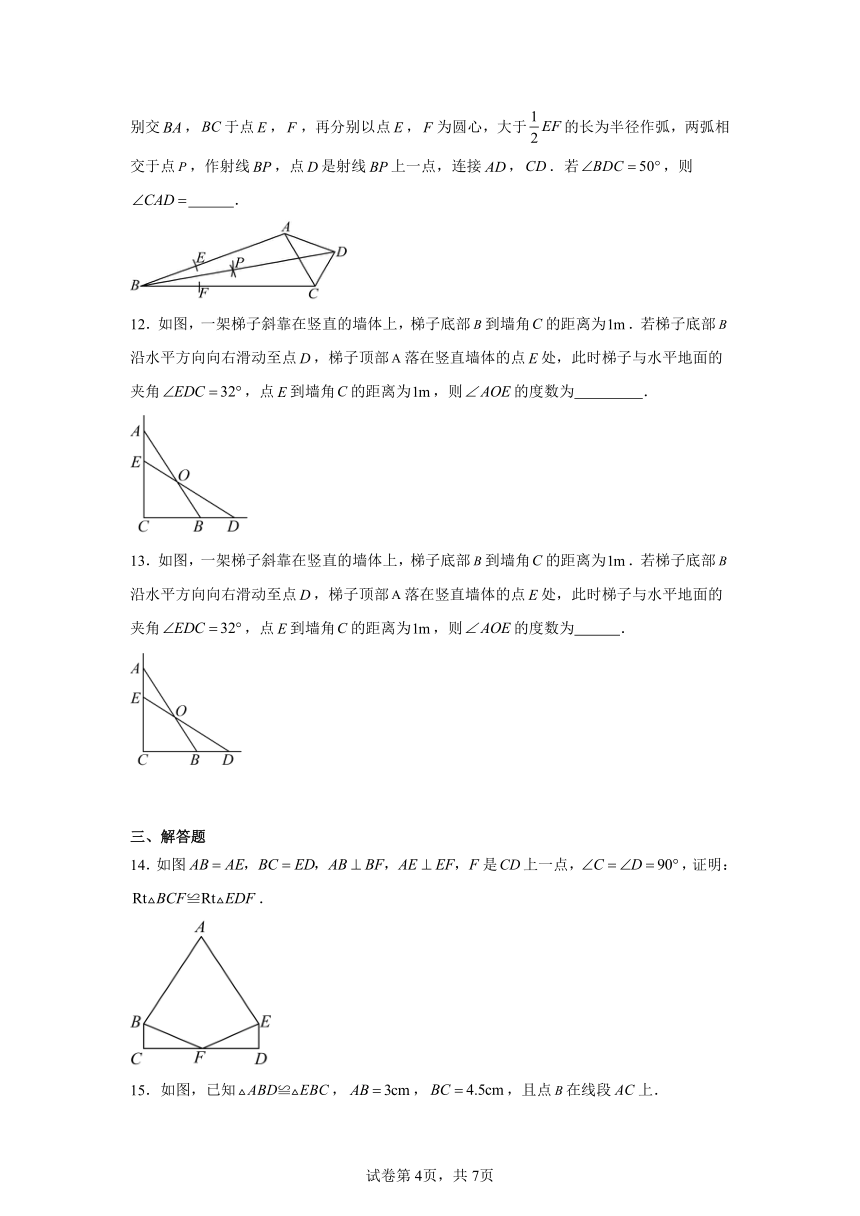
8.据史书记载,最早的风筝是由古代匠人墨子用木头制成的木鸟,称为“木鸢”.后来随着造纸术的发明.人们开始用纸张和竹条制作风筝,使其更加轻便、易于放飞.在如下图所示的“风筝“图案中,、、.则可以直接判定( )
A. B.
C. D.
二、填空题
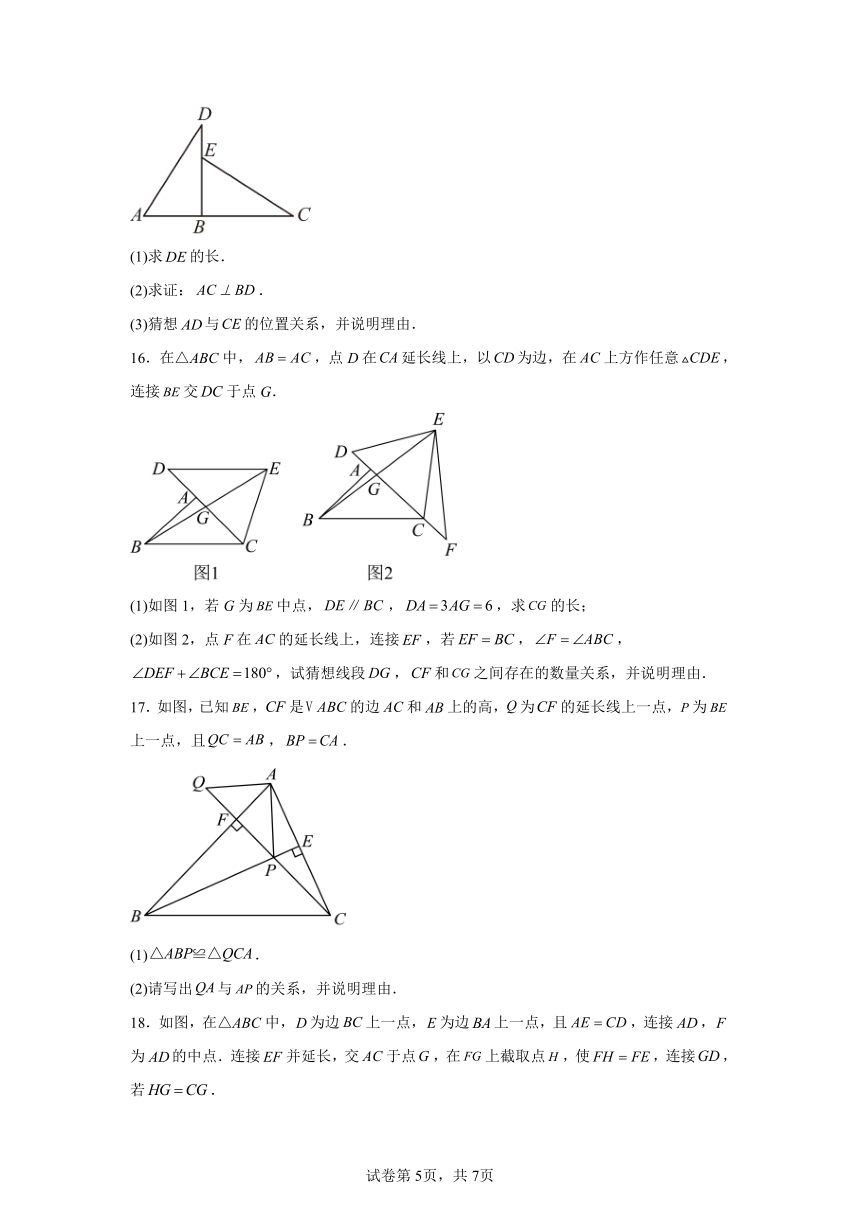
9.如图,△ABC是等腰直角三角形,,平分交于点D,于E.若△ADE的周长为,则 .
10.如图,中,,平分交于点D,E为线段上一点,连接,且.若,,则的长为 ;
11.如图,在△ABC中,,,以点为圆心,适当长为半径作弧,分别交,于点,,再分别以点,为圆心,大于的长为半径作弧,两弧相交于点,作射线,点是射线上一点,连接,.若,则 .
12.如图,一架梯子斜靠在竖直的墙体上,梯子底部到墙角的距离为.若梯子底部沿水平方向向右滑动至点,梯子顶部落在竖直墙体的点处,此时梯子与水平地面的夹角,点到墙角的距离为,则的度数为 .
13.如图,一架梯子斜靠在竖直的墙体上,梯子底部到墙角的距离为.若梯子底部沿水平方向向右滑动至点,梯子顶部落在竖直墙体的点处,此时梯子与水平地面的夹角,点到墙角的距离为,则的度数为 .
三、解答题
14.如图是上一点,,证明:.
15.如图,已知,,,且点在线段上.
(1)求的长.
(2)求证:.
(3)猜想与的位置关系,并说明理由.
16.在△ABC中,,点D在延长线上,以为边,在上方作任意,连接交于点G.
(1)如图1,若G为中点,,,求的长;
(2)如图2,点F在的延长线上,连接,若,,,试猜想线段,和之间存在的数量关系,并说明理由.
17.如图,已知,是的边和上的高,为的延长线上一点,为上一点,且,.
(1).
(2)请写出与的关系,并说明理由.
18.如图,在△ABC中,为边上一点,为边上一点,且,连接,为的中点.连接并延长,交于点,在上截取点,使,连接,若.
(1)求证:;
(2)求证:.
19.如图,在四边形中,,过点作于点,,在上截取,连接,平分交的延长线于点,连接.
【问题解决】(1)证明:;
【问题探究】(2)探索线段之间的数量关系并说明理由.
20.综合与实践:
(1)某学习小组在探究三角形全等时,发现了下面这种典型的基本图形.如图1.已知:在中.,,直线l经过点A,直线l,直线l,垂足分别为点D、E.证明:.
(2)组员小刘对图2(,,直线l经过点A,直线l,直线l,垂足分别为点D、E.)进行了探究,他发现线段、、之间也存在着类似的数量关系,请你直接写出这个发现.
数学老师赞赏了他们的探索精神,并鼓励他们运用这个知识来解决问题:
(3)如图3,已知△ABC,是边上的高,.过△ABC的边、向外作正方形和正方形,延长交于点I,若,请直接写出的面积.
(4)如图4,在△ABC中,是钝角,,,直线m与的延长线交于点F,若,△ABC的面积是12,请直接写出与的面积之和.
21.利用全等三角形面积相等可以解决与图形面积相关的问题.
初步感知
如图1,在△ABC中,为中线,过点作于点,过点作交的延长线于点.在延长线上取一点,连接,使.
(1)填空:________.(填“”“”或“”)
(2)求证:.
(3)试说明:.
拓展应用
(4)如图2,在△ABC中,是钝角,点在边上,,点在边上,点在边的延长线上,,,若,的面积是9,求与的面积之和.
试卷第1页,共3页
试卷第1页,共3页
《2025年甘肃省武威第二十中学中考数学人教版《全等三角形》专项训练练习题》参考答案
题号 1 2 3 4 5 6 7 8
答案 D A D B B B B D
9.10
10.2
11./度
12./26度
13./26度
14.证明:连接,
∵,
∴,
∵,,
∴,
∴,
∵,,
在和中,
,
∴.
15.(1)解:∵,
∴,,
∴;
(2)证明:∵,
∴,
∵点在线段上,
∴
∴,
∴;
(3)解:直线与直线垂直,理由:
如图,延长交于点,
∵,
∴,
∵中,,
∴,
∴,
∴.
16.(1)解:∵,
∴,
∴,
∵G为中点,
∴,
∵,
∴,.
在和中,
,
∴,
∴.
(2)解:线段,和之间存在的数量关系为.
理由如下:
在上截取,如图,
∵,
∵,
∴,
在和中,
,
∴,
∴,,
∴,
∵,,
∴,
∴,
∴.
在和中,
,
∴,
∴,
∴.
17.(1)解:∵是的高,
,
,
,
在和中:
,
∴ △ABP≌△QCA(SAS)
(2)解:,
理由如下:
∵△ABP≌△QCA
,,
,
,
,
即,
.
18.(1)证明:点是的中点,
,
在和中,
,
;
(2)证明:,
,
,
,
,
,
在和中,
,
,
,
,
.
19.证明:(1)∵,
∴,
∴,
在和△CBF中,
,
∴,
∴.
∵平分,
∴,
∴.
(2).理由如下:
∵,
∴,
在和中,
,
∴,
∴.
∵,
∴.
20.(1)证明:∵直线,直线,
∴,
∵,
∴,
∵,
∴,
在和中,
,
∴,
∴,
∴.
(2)解:,理由如下:
∵直线,直线,
∴,
∵,
∴,
∵,
∴,
在和中,
,
∴,
∴,
∴.
(3)解:如图3,过E作于M,的延长线于N,
∴,
由(1)和(2)的结论可知,
在和中,
,
∴,
∴,
∴,
则
.
(4)∵,,
∴,
又∵,
∴,
.
如图所示,过点A作于,则,.
,
.
,
与的面积之和为6.
21.(1)解:∵在△ABC中,为中线,
∴,
∵,,
∴,
∵,
∴,
∴,
故答案为:;
(2)证明:由(1)可知:,
,
,
,
,
;
(3)证明:由(1)可知,由(2)可知,
,,
;
(4)解:,,,
,
在和中,
,
∴ △ABF≌△DAE(AAS)
,
设的底边上的高为h,则的底边上的高为h,
,,
,
,
,
与的面积之和为.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.如图,在的两边上,分别取,再分别过点,作、的垂线交点为画射线,判断依据是( )
A. B. C. D.
2.如图,在∴△ABC与中,,且点A在上,点D在上,添加下列一个条件后,仍然不能判定的是( )
A. B. C. D.
3.已知,在△ABC中,,,垂足为点H,平分,与相交于点D,过点D作,与边相交于点E,那么下列结论中一定正确的是( )
A. B.
C. D.
4.如图,嘉琪站在河边的点A处,在河对面(嘉珙正北方向)的点B处有一电线塔,他想知道此时电线塔离他有多远,于是他向正西方向走了10米到达一棵树C处,接着再向前走了10米到达D处,然后他左转直行,当他看到电线塔 树与自己现处的位置E在一条直线时,测得米,则电线塔离点A的距离是( )
A.10米 B.20米 C.30米 D.40米
5.如图,将两根钢条的中点O连在一起,使可以绕着点O自由旋转,则的长等于内槽宽,那么判定的理由是( )
A. B. C. D.
6.如图,在中,,以点A为圆心,任意长度为半径画弧,交,于点D,E,再分别以点为圆心.大于为半径画弧.两弧在内交于点,作射线交边于点,若,,则的面积为( )
A.13 B.15 C.26 D.30
7.如图,已知,以点O为圆心,以任意长为半径画弧,与,分别交于点C,D,再分别以点C,D为圆心,以大于长为半径画弧,两弧相交于点F,过射线上一点M作,与相交于点N,,则( )
A. B. C. D.
8.据史书记载,最早的风筝是由古代匠人墨子用木头制成的木鸟,称为“木鸢”.后来随着造纸术的发明.人们开始用纸张和竹条制作风筝,使其更加轻便、易于放飞.在如下图所示的“风筝“图案中,、、.则可以直接判定( )
A. B.
C. D.
二、填空题
9.如图,△ABC是等腰直角三角形,,平分交于点D,于E.若△ADE的周长为,则 .
10.如图,中,,平分交于点D,E为线段上一点,连接,且.若,,则的长为 ;
11.如图,在△ABC中,,,以点为圆心,适当长为半径作弧,分别交,于点,,再分别以点,为圆心,大于的长为半径作弧,两弧相交于点,作射线,点是射线上一点,连接,.若,则 .
12.如图,一架梯子斜靠在竖直的墙体上,梯子底部到墙角的距离为.若梯子底部沿水平方向向右滑动至点,梯子顶部落在竖直墙体的点处,此时梯子与水平地面的夹角,点到墙角的距离为,则的度数为 .
13.如图,一架梯子斜靠在竖直的墙体上,梯子底部到墙角的距离为.若梯子底部沿水平方向向右滑动至点,梯子顶部落在竖直墙体的点处,此时梯子与水平地面的夹角,点到墙角的距离为,则的度数为 .
三、解答题
14.如图是上一点,,证明:.
15.如图,已知,,,且点在线段上.
(1)求的长.
(2)求证:.
(3)猜想与的位置关系,并说明理由.
16.在△ABC中,,点D在延长线上,以为边,在上方作任意,连接交于点G.
(1)如图1,若G为中点,,,求的长;
(2)如图2,点F在的延长线上,连接,若,,,试猜想线段,和之间存在的数量关系,并说明理由.
17.如图,已知,是的边和上的高,为的延长线上一点,为上一点,且,.
(1).
(2)请写出与的关系,并说明理由.
18.如图,在△ABC中,为边上一点,为边上一点,且,连接,为的中点.连接并延长,交于点,在上截取点,使,连接,若.
(1)求证:;
(2)求证:.
19.如图,在四边形中,,过点作于点,,在上截取,连接,平分交的延长线于点,连接.
【问题解决】(1)证明:;
【问题探究】(2)探索线段之间的数量关系并说明理由.
20.综合与实践:
(1)某学习小组在探究三角形全等时,发现了下面这种典型的基本图形.如图1.已知:在中.,,直线l经过点A,直线l,直线l,垂足分别为点D、E.证明:.
(2)组员小刘对图2(,,直线l经过点A,直线l,直线l,垂足分别为点D、E.)进行了探究,他发现线段、、之间也存在着类似的数量关系,请你直接写出这个发现.
数学老师赞赏了他们的探索精神,并鼓励他们运用这个知识来解决问题:
(3)如图3,已知△ABC,是边上的高,.过△ABC的边、向外作正方形和正方形,延长交于点I,若,请直接写出的面积.
(4)如图4,在△ABC中,是钝角,,,直线m与的延长线交于点F,若,△ABC的面积是12,请直接写出与的面积之和.
21.利用全等三角形面积相等可以解决与图形面积相关的问题.
初步感知
如图1,在△ABC中,为中线,过点作于点,过点作交的延长线于点.在延长线上取一点,连接,使.
(1)填空:________.(填“”“”或“”)
(2)求证:.
(3)试说明:.
拓展应用
(4)如图2,在△ABC中,是钝角,点在边上,,点在边上,点在边的延长线上,,,若,的面积是9,求与的面积之和.
试卷第1页,共3页
试卷第1页,共3页
《2025年甘肃省武威第二十中学中考数学人教版《全等三角形》专项训练练习题》参考答案
题号 1 2 3 4 5 6 7 8
答案 D A D B B B B D
9.10
10.2
11./度
12./26度
13./26度
14.证明:连接,
∵,
∴,
∵,,
∴,
∴,
∵,,
在和中,
,
∴.
15.(1)解:∵,
∴,,
∴;
(2)证明:∵,
∴,
∵点在线段上,
∴
∴,
∴;
(3)解:直线与直线垂直,理由:
如图,延长交于点,
∵,
∴,
∵中,,
∴,
∴,
∴.
16.(1)解:∵,
∴,
∴,
∵G为中点,
∴,
∵,
∴,.
在和中,
,
∴,
∴.
(2)解:线段,和之间存在的数量关系为.
理由如下:
在上截取,如图,
∵,
∵,
∴,
在和中,
,
∴,
∴,,
∴,
∵,,
∴,
∴,
∴.
在和中,
,
∴,
∴,
∴.
17.(1)解:∵是的高,
,
,
,
在和中:
,
∴ △ABP≌△QCA(SAS)
(2)解:,
理由如下:
∵△ABP≌△QCA
,,
,
,
,
即,
.
18.(1)证明:点是的中点,
,
在和中,
,
;
(2)证明:,
,
,
,
,
,
在和中,
,
,
,
,
.
19.证明:(1)∵,
∴,
∴,
在和△CBF中,
,
∴,
∴.
∵平分,
∴,
∴.
(2).理由如下:
∵,
∴,
在和中,
,
∴,
∴.
∵,
∴.
20.(1)证明:∵直线,直线,
∴,
∵,
∴,
∵,
∴,
在和中,
,
∴,
∴,
∴.
(2)解:,理由如下:
∵直线,直线,
∴,
∵,
∴,
∵,
∴,
在和中,
,
∴,
∴,
∴.
(3)解:如图3,过E作于M,的延长线于N,
∴,
由(1)和(2)的结论可知,
在和中,
,
∴,
∴,
∴,
则
.
(4)∵,,
∴,
又∵,
∴,
.
如图所示,过点A作于,则,.
,
.
,
与的面积之和为6.
21.(1)解:∵在△ABC中,为中线,
∴,
∵,,
∴,
∵,
∴,
∴,
故答案为:;
(2)证明:由(1)可知:,
,
,
,
,
;
(3)证明:由(1)可知,由(2)可知,
,,
;
(4)解:,,,
,
在和中,
,
∴ △ABF≌△DAE(AAS)
,
设的底边上的高为h,则的底边上的高为h,
,,
,
,
,
与的面积之和为.
答案第1页,共2页
答案第1页,共2页
同课章节目录
