苏科版七年级数学下册 第八章 整式乘法 章节测试卷 (含解析)
文档属性
| 名称 | 苏科版七年级数学下册 第八章 整式乘法 章节测试卷 (含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 369.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-12 00:00:00 | ||
图片预览




文档简介
第八章《整式乘法》章节测试卷
一、选择题(本大题共8小题,每小题3分,共24分).
1.的计算结果为( )
A. B. C. D.
2.已知单项式与的积为,则的值为( )
A.12 B.9 C.6 D.3
3.如果,则括号里应填的式子是( )
A. B. C. D.
4.已知关于的多项式与的乘积的展开式中不含的二次项,则的值为( )
A. B. C. D.3
5.下列能用平方差公式直接计算的是( )
A. B.
C. D.
6.已知,则的值为( )
A. B. C.-8 D.9
7.杨辉三角形,又称贾宪三角形,是二项式系数在三角形中的一种几何排列,如图是杨辉三角形的部分排列规律,则第八行从左数第三个数为( )
A.十五 B.二十一 C.二十五 D.三十五
8.有两个正方形A,B,现将B放在A的内部得图甲,将A,B并列放置后构造新的正方形得图乙.若图甲和图乙中阴影部分的面积分别为1和12,则正方形A,B的面积之和为( )
A.9 B.11 C.12 D.13
二、填空题(本大题共8小题,每小题3分,共24分)
9.计算:
(1) ;
(2) .
10.若一个三角形的底边长为,这条底边上的高为,则它的面积为 .
11.若等式□成立,则□内应填 .
12.张某有一块长方形农田,长,宽.后来张某开垦荒田,使该农田的长、宽都增加了,那么面积增加了 .
13.如果,那么的结果是 .
14.如图,两个正方形的边长分别为a,b.若,,则图中阴影部分的面积为 .
15.由,反过来可以得到.计算: .
16.“幻方”最早记载于春秋时期的《大戴礼记》中,现将数字填入如图所示的“幻方”中,使得每个圆圈上的四个数字的和都等于,若每个圆圈上的四个数字的平方和分别记、、,且.如果将交点处的三个圆圈填入的数字分别记作为、、,则 ; .
三、解答题(本大题共9小题,共72分.)
17.化简:
(1); (2);(3).
18.先化简,再求值:
(1),其中;
(2),其中.
19.利用乘法公式计算:
(1); (2).
20.用简便方法计算:
(1); (2);
(3)
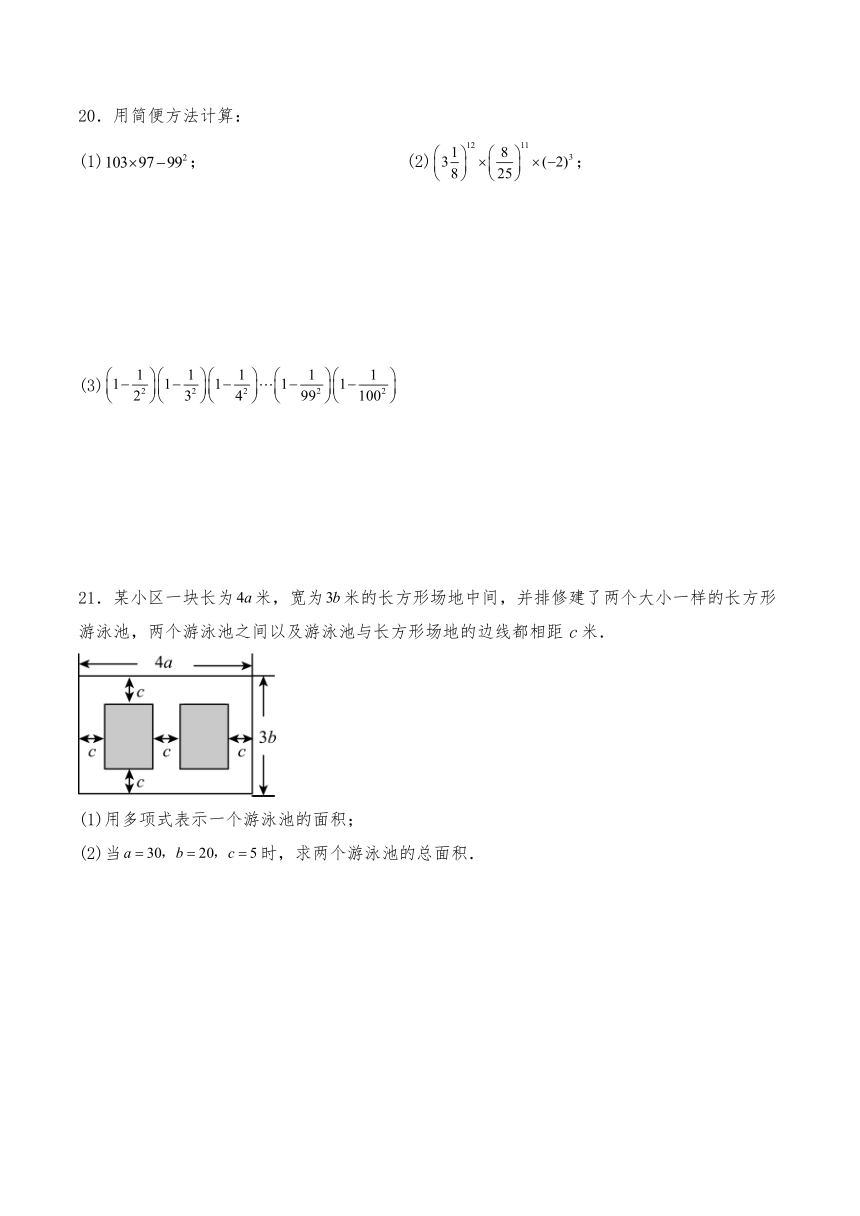
21.某小区一块长为米,宽为米的长方形场地中间,并排修建了两个大小一样的长方形游泳池,两个游泳池之间以及游泳池与长方形场地的边线都相距c米.
(1)用多项式表示一个游泳池的面积;
(2)当时,求两个游泳池的总面积.
22.小迪同学在计算时,把4写成后,得.受此启发,在求的值时,先乘得
.
阅读上面的材料,解答下列问题:
(1)计算:;
(2)借用上面的方法,逆用平方差公式计算:.
23.定义:是以为系数的二次多项式,即,其中均为实数.例如,.若,求的值.
24.图①是四个全等的小长方形拼成的大正方形,大正方形的边长为,小正方形(阴影部分)的边长为.
(1)观察图①,直接写出三者之间的数量关系式:_______;
(2)根据(1)的结论解答:如图②,两个正方形的边长分别为,且三点在一条直线上.若,,求图②中阴影部分的面积.
25.拓广探索:
若x满足,求的值.
解:设,
则,
∴.
请仿照上面的方法求解问题:
(1)若x满足,求的值.
(2)已知正方形的边长为分别是、上的点,且,,长方形的面积是,分别以、为边作正方形,求阴影部分的面积.
参考答案
一、选择题.
1.B
【分析】本题考查完全平方公式,熟记完全平方公式是解答的关键.根据完全平方公式展开求解即可.
【详解】解:
,
故选:B.
2.C
【分析】本题考查了单项式乘单项式法则:把它们的系数、相同字母的幂分别相乘,其余字母连同它的指数不变,作为积的因式,据此即可求出答案.
【详解】解,
,
,,
,
故选: C.
3.C
【分析】本题主要考查了平方差公式,根据进行求解即可.
【详解】解:,
故选:C.
4.C
【分析】本题考查了多项式乘以多项式,掌握多项式乘以多项式法则进行运算是关键.
根据多项式乘以多项式法则进行计算.
【详解】解:
∵多项式与的乘积的展开式中不含的二次项,
∴.
解得.
故选:C.
5.C
【分析】本题考差了平方差公式的特征,解题的关键是掌握平方差公式,据此逐个判断即可.
【详解】解:A、,不能用平方差公式,不符合题意;
B、,不能用平方差公式,不符合题意;
C、,能用平方差公式,符合题意;
D、不能用平方差公式,不符合题意;
故选:C.
6.B
【分析】本题主要考查了多项式乘以多项式运算,掌握多项式乘以多项式的运算法则是解题关键.
先根据多项式相等则对应项的系数相等求出m与n的值,然后代入计算即可.
【详解】解:∵,
∴,
∴,
∴.
故选:B.
7.B
【分析】本题考查了完全平方公式,各项是按a的降幂排列的,它的两端都是由数字1组成的,而其余的数则是等于它肩上的两个数之和.
从第3行开始依次确定第三个数,即是完全平方公式中的第三项的系数,找到规律即可确定第八行第三个数.
【详解】解:依据规律可得到:的展开式的系数是杨辉三角第8行的数,
第3行第三个数为1,
第4行第三个数为,
第5行第三个数为,
…
第8行第三个数为:.
故选:B.
8.D
【分析】本题主要考查了完全平方公式在几何图形中的应用和整体代入的数学思想,根据图形得出数量关系是解题的关键.设正方形A的边长为a,正方形B的边长为b,根据图形列出a、b的关系式求解即得.
【详解】解:设正方形A的边长为a,正方形B的边长为b,
由图甲得:,即,
由图乙得:,整理得,
所以
所以.
即正方形A、B的面积之和为13.
故选D.
二、填空题
9.
【分析】本题考查了单项式乘单项式,积的乘方,同底数幂相乘,正确掌握相关性质内容是解题的关键.
(1)根据单项式乘单项式的运算法则进行计算,即可作答.
(2)先运算积的乘方,再运算同底数幂相乘,即可作答.
【详解】解:(1),
故答案为:;
(2),
故答案为:.
10.
【分析】本题考查了单项式乘单项式,根据三角形的面积底乘高进行列式计算,即可作答.
【详解】解:∵一个三角形的底边长为,这条底边上的高为,
∴,
则它的面积为,
故答案为:.
11.
【分析】本题考查了去括号与添括号,根据去括号法则计算即可作出判断.
【详解】解:,
所以□内应填写,
故答案为:.
12.
【分析】本题主要考查了用多项式乘以多项式表示面积,同底数幂的乘法,以及整式加减的应用,先分别计算出原来与后来的长方形农田面积,然后相减即可求解.
【详解】解:原来的长方形农田面积为:()
后来的长方形农田面积为:(),
∴面积增加了:()
故答案为:
13.6
【分析】本题考查了整式乘法公式,根据完全平方公式和平方差公式,把 化简整理为,再将整体代入计算即可.
【详解】解:
,
∵,
∴
故答案为:.
14.16
【分析】本题考查的是完全平方公式在几何图形中的应用.先利用阴影部分的面积等于大的正方形的面积的一半减去三个三角形的面积得到阴影面积为:,再利用完全平方公式的变形求解即可.
【详解】解:两个正方形的边长分别为a,b,
,
,,
∴.
故答案为:16.
15.
【分析】本题考查平方差公式,逆用平方差公式进行简算即可.
【详解】解:原式
;
故答案为:.
16.
【分析】根据、、的位置可知这三个数每个都加了两次,三个圆圈上的数字之和是,但是这个数字之和是,所以可得,从而求出的值;因为,可以得到,配方得,把代入即可求出的值.本题考查了整式的运算、完全平方公式以及有理数的乘方运算.解决本题的关键是理解、、这三个数每个都加了两次,并且能把凑成完全平方式.
【详解】解:每个圆圈上的四个数字的和都等于,
三个圆上的数字之和应为,
其中的、、这三个数每个都加了两次,
,
,
则有,
解得:;
每个圆圈上的四个数字的平方和分别记、、,且,
,
,
,
,
整理得:,
,
;
,
,
,
解得:.
故答案为:.
三、解答题
17.(1)解:
.
(2)解:
.
(3)解:
.
18.(1)
.
当时,
原式.
(2)
.
∵,
∴,
∴原式.
19.(1)解:
.
(2)解:
.
20.(1)解:
.
(2)解:
.
(3)解:
.
21.(1)根据题意得:;
(2)两个游泳池的面积为,
将代入上式,得.
∴两个游泳池的总面积为.
22.(1)解:
;
(2)解:
.
23.解: ,
,
,
,
,,
,
,
,
,
,
,
,
.
的值为.
24.(1)解:根据题意可得,;
故答案为:
(2)解:由(1)可得,
∴,
把,代入上式,得:
.
∴图2中阴影部分的面积为.
25.(1)解:设,,
则,,
∴;
(2)∵正方形的边长为 ,,
∴,,
设,,
则,,
∴,
∴,
∴ ,
∴阴影部分的面积为.
一、选择题(本大题共8小题,每小题3分,共24分).
1.的计算结果为( )
A. B. C. D.
2.已知单项式与的积为,则的值为( )
A.12 B.9 C.6 D.3
3.如果,则括号里应填的式子是( )
A. B. C. D.
4.已知关于的多项式与的乘积的展开式中不含的二次项,则的值为( )
A. B. C. D.3
5.下列能用平方差公式直接计算的是( )
A. B.
C. D.
6.已知,则的值为( )
A. B. C.-8 D.9
7.杨辉三角形,又称贾宪三角形,是二项式系数在三角形中的一种几何排列,如图是杨辉三角形的部分排列规律,则第八行从左数第三个数为( )
A.十五 B.二十一 C.二十五 D.三十五
8.有两个正方形A,B,现将B放在A的内部得图甲,将A,B并列放置后构造新的正方形得图乙.若图甲和图乙中阴影部分的面积分别为1和12,则正方形A,B的面积之和为( )
A.9 B.11 C.12 D.13
二、填空题(本大题共8小题,每小题3分,共24分)
9.计算:
(1) ;
(2) .
10.若一个三角形的底边长为,这条底边上的高为,则它的面积为 .
11.若等式□成立,则□内应填 .
12.张某有一块长方形农田,长,宽.后来张某开垦荒田,使该农田的长、宽都增加了,那么面积增加了 .
13.如果,那么的结果是 .
14.如图,两个正方形的边长分别为a,b.若,,则图中阴影部分的面积为 .
15.由,反过来可以得到.计算: .
16.“幻方”最早记载于春秋时期的《大戴礼记》中,现将数字填入如图所示的“幻方”中,使得每个圆圈上的四个数字的和都等于,若每个圆圈上的四个数字的平方和分别记、、,且.如果将交点处的三个圆圈填入的数字分别记作为、、,则 ; .
三、解答题(本大题共9小题,共72分.)
17.化简:
(1); (2);(3).
18.先化简,再求值:
(1),其中;
(2),其中.
19.利用乘法公式计算:
(1); (2).
20.用简便方法计算:
(1); (2);
(3)
21.某小区一块长为米,宽为米的长方形场地中间,并排修建了两个大小一样的长方形游泳池,两个游泳池之间以及游泳池与长方形场地的边线都相距c米.
(1)用多项式表示一个游泳池的面积;
(2)当时,求两个游泳池的总面积.
22.小迪同学在计算时,把4写成后,得.受此启发,在求的值时,先乘得
.
阅读上面的材料,解答下列问题:
(1)计算:;
(2)借用上面的方法,逆用平方差公式计算:.
23.定义:是以为系数的二次多项式,即,其中均为实数.例如,.若,求的值.
24.图①是四个全等的小长方形拼成的大正方形,大正方形的边长为,小正方形(阴影部分)的边长为.
(1)观察图①,直接写出三者之间的数量关系式:_______;
(2)根据(1)的结论解答:如图②,两个正方形的边长分别为,且三点在一条直线上.若,,求图②中阴影部分的面积.
25.拓广探索:
若x满足,求的值.
解:设,
则,
∴.
请仿照上面的方法求解问题:
(1)若x满足,求的值.
(2)已知正方形的边长为分别是、上的点,且,,长方形的面积是,分别以、为边作正方形,求阴影部分的面积.
参考答案
一、选择题.
1.B
【分析】本题考查完全平方公式,熟记完全平方公式是解答的关键.根据完全平方公式展开求解即可.
【详解】解:
,
故选:B.
2.C
【分析】本题考查了单项式乘单项式法则:把它们的系数、相同字母的幂分别相乘,其余字母连同它的指数不变,作为积的因式,据此即可求出答案.
【详解】解,
,
,,
,
故选: C.
3.C
【分析】本题主要考查了平方差公式,根据进行求解即可.
【详解】解:,
故选:C.
4.C
【分析】本题考查了多项式乘以多项式,掌握多项式乘以多项式法则进行运算是关键.
根据多项式乘以多项式法则进行计算.
【详解】解:
∵多项式与的乘积的展开式中不含的二次项,
∴.
解得.
故选:C.
5.C
【分析】本题考差了平方差公式的特征,解题的关键是掌握平方差公式,据此逐个判断即可.
【详解】解:A、,不能用平方差公式,不符合题意;
B、,不能用平方差公式,不符合题意;
C、,能用平方差公式,符合题意;
D、不能用平方差公式,不符合题意;
故选:C.
6.B
【分析】本题主要考查了多项式乘以多项式运算,掌握多项式乘以多项式的运算法则是解题关键.
先根据多项式相等则对应项的系数相等求出m与n的值,然后代入计算即可.
【详解】解:∵,
∴,
∴,
∴.
故选:B.
7.B
【分析】本题考查了完全平方公式,各项是按a的降幂排列的,它的两端都是由数字1组成的,而其余的数则是等于它肩上的两个数之和.
从第3行开始依次确定第三个数,即是完全平方公式中的第三项的系数,找到规律即可确定第八行第三个数.
【详解】解:依据规律可得到:的展开式的系数是杨辉三角第8行的数,
第3行第三个数为1,
第4行第三个数为,
第5行第三个数为,
…
第8行第三个数为:.
故选:B.
8.D
【分析】本题主要考查了完全平方公式在几何图形中的应用和整体代入的数学思想,根据图形得出数量关系是解题的关键.设正方形A的边长为a,正方形B的边长为b,根据图形列出a、b的关系式求解即得.
【详解】解:设正方形A的边长为a,正方形B的边长为b,
由图甲得:,即,
由图乙得:,整理得,
所以
所以.
即正方形A、B的面积之和为13.
故选D.
二、填空题
9.
【分析】本题考查了单项式乘单项式,积的乘方,同底数幂相乘,正确掌握相关性质内容是解题的关键.
(1)根据单项式乘单项式的运算法则进行计算,即可作答.
(2)先运算积的乘方,再运算同底数幂相乘,即可作答.
【详解】解:(1),
故答案为:;
(2),
故答案为:.
10.
【分析】本题考查了单项式乘单项式,根据三角形的面积底乘高进行列式计算,即可作答.
【详解】解:∵一个三角形的底边长为,这条底边上的高为,
∴,
则它的面积为,
故答案为:.
11.
【分析】本题考查了去括号与添括号,根据去括号法则计算即可作出判断.
【详解】解:,
所以□内应填写,
故答案为:.
12.
【分析】本题主要考查了用多项式乘以多项式表示面积,同底数幂的乘法,以及整式加减的应用,先分别计算出原来与后来的长方形农田面积,然后相减即可求解.
【详解】解:原来的长方形农田面积为:()
后来的长方形农田面积为:(),
∴面积增加了:()
故答案为:
13.6
【分析】本题考查了整式乘法公式,根据完全平方公式和平方差公式,把 化简整理为,再将整体代入计算即可.
【详解】解:
,
∵,
∴
故答案为:.
14.16
【分析】本题考查的是完全平方公式在几何图形中的应用.先利用阴影部分的面积等于大的正方形的面积的一半减去三个三角形的面积得到阴影面积为:,再利用完全平方公式的变形求解即可.
【详解】解:两个正方形的边长分别为a,b,
,
,,
∴.
故答案为:16.
15.
【分析】本题考查平方差公式,逆用平方差公式进行简算即可.
【详解】解:原式
;
故答案为:.
16.
【分析】根据、、的位置可知这三个数每个都加了两次,三个圆圈上的数字之和是,但是这个数字之和是,所以可得,从而求出的值;因为,可以得到,配方得,把代入即可求出的值.本题考查了整式的运算、完全平方公式以及有理数的乘方运算.解决本题的关键是理解、、这三个数每个都加了两次,并且能把凑成完全平方式.
【详解】解:每个圆圈上的四个数字的和都等于,
三个圆上的数字之和应为,
其中的、、这三个数每个都加了两次,
,
,
则有,
解得:;
每个圆圈上的四个数字的平方和分别记、、,且,
,
,
,
,
整理得:,
,
;
,
,
,
解得:.
故答案为:.
三、解答题
17.(1)解:
.
(2)解:
.
(3)解:
.
18.(1)
.
当时,
原式.
(2)
.
∵,
∴,
∴原式.
19.(1)解:
.
(2)解:
.
20.(1)解:
.
(2)解:
.
(3)解:
.
21.(1)根据题意得:;
(2)两个游泳池的面积为,
将代入上式,得.
∴两个游泳池的总面积为.
22.(1)解:
;
(2)解:
.
23.解: ,
,
,
,
,,
,
,
,
,
,
,
,
.
的值为.
24.(1)解:根据题意可得,;
故答案为:
(2)解:由(1)可得,
∴,
把,代入上式,得:
.
∴图2中阴影部分的面积为.
25.(1)解:设,,
则,,
∴;
(2)∵正方形的边长为 ,,
∴,,
设,,
则,,
∴,
∴,
∴ ,
∴阴影部分的面积为.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
